基于ARIMA-GM(1,1)模型的温度二次仪表误差修正方法

摘 要：针对化工设备的温度二次仪表在超高温阶段存在的误差无法检测的问题，文章提出了一种基于ARIMA-GM（1，1）模型的温度误差修正方法。首先，将温度二次仪表和标准器静置在稳定的环境中，通过标准器输出电信号来计算标准器与二次仪表之间的误差；其次，通过误差序列建立ARIMA模型，得到一组预测值；再次，计算实际误差与预测值之间的残差，为了提高ARIMA模型的预测精度，截取残差序列的尾部数据建立 GM（1，1）修正模型；最后，将ARIMA模型与GM（1，1）模型相结合，建立了ARIMA-GM（1，1）修正模型，预测下一个阶段仪表可能存在的误差，实现温度二次仪表的自修正功能。对比实验证明，本研究提出的ARIMA-GM（1，1） 模型的相对平均误差最低，预测精度较高，能够较好地预测出下一个阶段仪表可能存在的误差，为后续仪表的自修正提供科学依据。

关键词：误差修正模型；ARIMA模型；GM（1，1）模型；ARIMA-GM（1，1）模型

中图分类号：TH814"" 文献标识码：A"" 文章编号：1673-1794（2024）05-0001-04

作者简介：冯鑫，南京市计量监督检测院高级工程师，博士，研究方向：热工仪表计量检测、大数据分析与建模；李舒，南京市计量监督检测院正高级工程师，硕士，研究方向：热工计量；李磊， 南京市计量监督检测院工程师；封海兵，南京市计量监督检测院高级工程师（南京 210036）。

在实际检测过程中，经常会遇到被检的仪表超出标准器检测能力范围，因此，其存在的误差就无法获取。为了解决上述问题，文章提出一种基于ARIMA-GM（1，1）模型的温度二次仪表误差自修正方法。

关于ARIMA和GM（1，1）模型国内外的学者也对其开展了相关研究：尤金辉等^[1]利用兴化市2012—2019年结核病月发病率情况，分别建立ARIMA和GM（1，1）模型预测结核病的发展趋势；潘红宝等^[2]以武汉华中科创产业园超大深基坑工程实际沉降数据为依据，分别建立了ARIMA和GM（1，1）模型预测后期的沉降情况；Sheoran等^[3]研究了滑动窗口ARIMA（WS-ARIMA）方法用于每日和每周风速预测；Ding等^[4]提出了一种新的自适应结构GM（1，1）核能消耗预测模型；Feng等^[5]提出了一种Markov-C-GM（1，1）模型来预测每个月南京市电梯故障率；Aasim等^[6]提出了一种用于极短期风速预测的RWT-ARIMA模型，并证明了该模型在风速预测中的优越性。

分析上述文献可以发现：ARIMA和GM（1，1）适用于中短期的预测，并且适用于少样本量的数据；单独的ARIMA、GM（1，1）及其相关改进的模型研究较多，但是混合ARIMA-GM（1，1）模型的研究还没有。结合ARIMA和GM（1，1）模型，以及温度二次仪表样本量特征，文章提出了温度二次仪表的ARIMA-GM（1，1）误差修正模型。

1 ARIMA-GM（1，1） 模型

ARIMA预测模型的理论以及具体步骤可参看文献[7-8]，GM（1，1）模型的建模思路可参看文献[9]。

文章主要根据温度二次仪表的误差数据建立ARIMA模型，为了提高ARIMA的预测精度，截取ARIMA模型预测和实际误差的尾部部分绝对差值，建立GM（1，1）修正模型，其模型可以表示为：

y︿t=ARIMA+GM（1，1）=a+byt－1+cet－1+…±de^wt

ARIMA=a+byt－1+cet－1+…GM（1，1）=de^wt（1）

上式中，a为ARIMA模型常数项，b，c分别为ARIMA模型的系数；d，w分别为GM（1，1）模型系数。

具体步骤如下所示：

步骤1：在温度循环箱中给二次仪表提供标准源，计算不同的温度电信号和二次仪表之间的误差序列；

步骤2：利用误差序列建立ARIMA预测模型，同时得到一组预测值；

步骤3：计算误差值和预测值之间的残差，截取尾部的残差序列建立GM（1，1）残差修正模型；

步骤4：将步骤2中ARIMA预测模型和步骤3中GM（1，1）残差修正模型相加，建立ARIMA-GM误差自修正模型；

步骤5：根据ARIMA-GM误差自修正模型计算二次仪表下一个阶段误差值，实现仪表的自我修正。

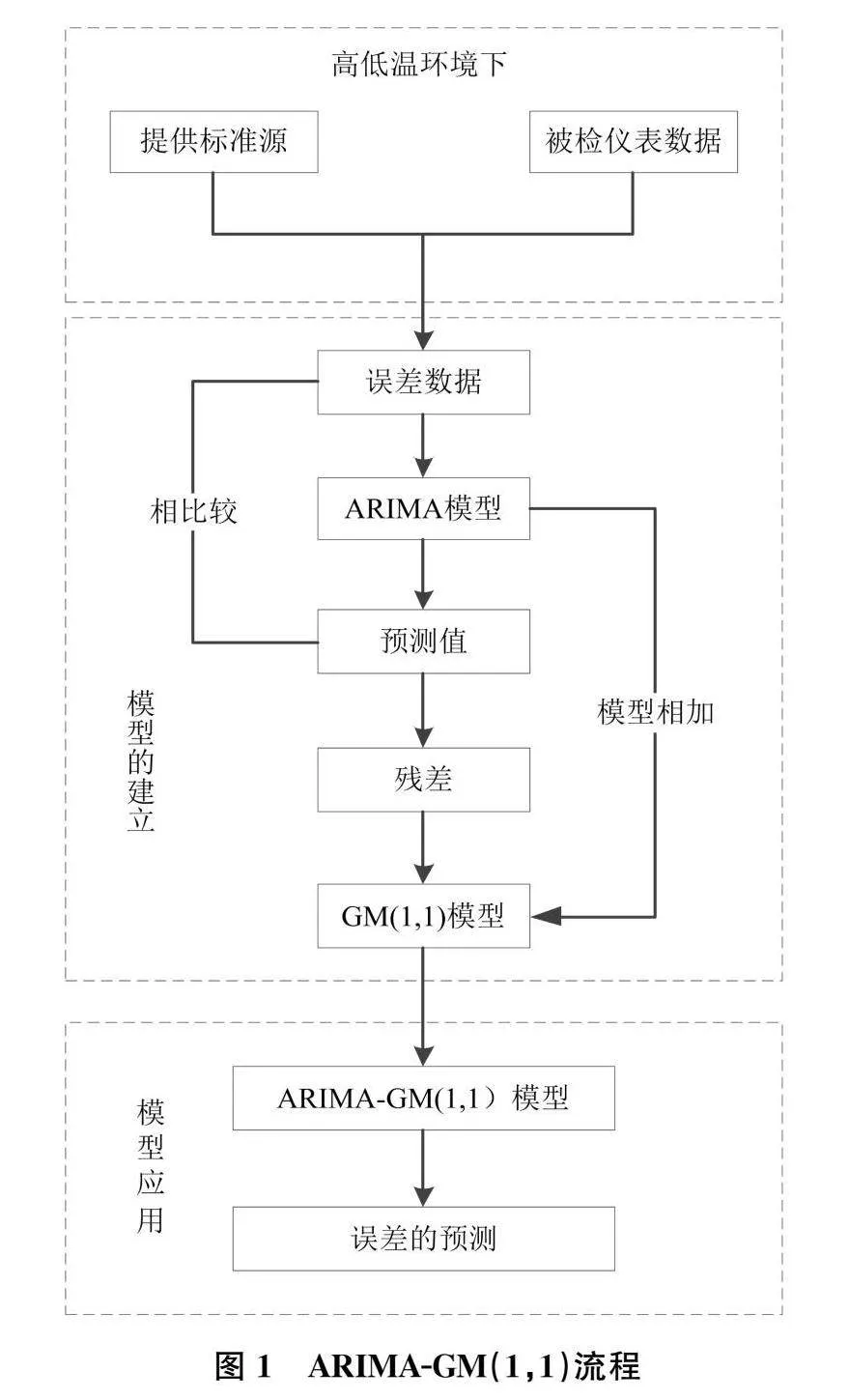
建立ARIMA-GM（1，1）的流程如图1所示。

2 工程应用

将被检的温度二次仪表和标准器放置在温度循环箱中，通过连接线将标准温度源和被检仪表相连接，设定高低温循环箱的温度值，使其在一个稳定的温度环境中，标准温度源从低到高输出电信号，同时读取被检仪表的示值，计算其误差值。具体如下。

参考《JJG 617-1996 数字温度指示调节仪检定规程》^[10]中的测试方法，选取某品牌的温度指示调节仪20块，量程范围（0～1500）℃，精度等级±1%，本研究使用的标准仪器能力范围为（0～1300）℃，超出能力范围外的无法测试，本研究以（450～1300）℃为试验，共计得到18个数据，利用前面17个数据作为训练样本建立预测模型，最后一个数据作为测试数据，具体数据如表1所示。

2.1 ARIMA 模型

建立ARIMA模型，具体计算过程如下：

步骤1：对误差数据进行平稳性检查。如果数据不稳定需要进行平稳性处理。

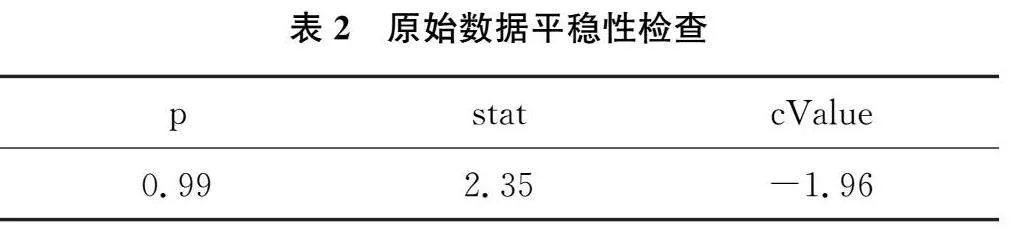
对原始数据进行平稳性检查，得到的结果如表2所示：

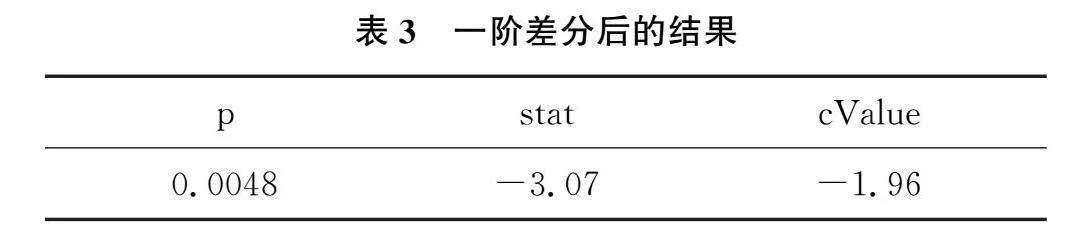
根据表2值p=0.990.05，因此，需要做差分处理，经过一阶差分后的结果如表3所示：

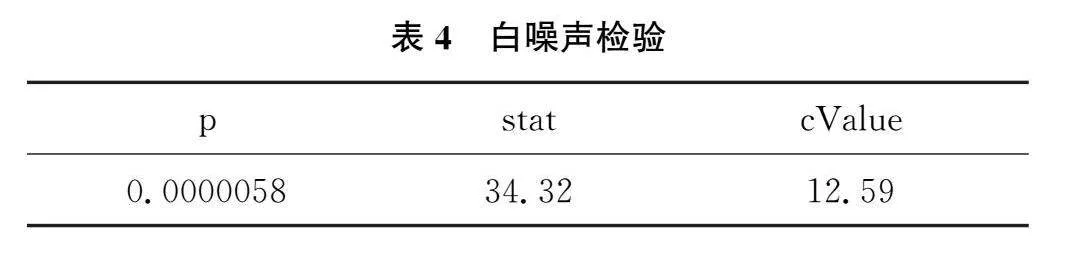
根据表3的结果，经过一阶差分后原始数据平稳，同时对原始数据的白噪声检验，得到的结果如下表4所示：

根据表4的结果，白噪声的p=0.00000580.05，说明为非白噪声，原始数据有意义，可以进行ARIMA模型的建立，同时得到模型中d=1。

步骤2：模型参数的选择。主要确定ARIMA模型中的p、q值。p、q值的确定有两种方法，本研究通过计算BIC值。

其计算公式如下：

BIC=kln（n）－2ln（L）（2）

其中，k为模型参数，n为样本数量，L为似然函数，在该方法中，先利用经验公式确定p、q的最大值：

pmax=length（n）/10（3）

pmax=length（n）/10（4）

其中，pmax、qmax代表最大值，length（n）代表样本数据长度。例如，表1中样本数据个数为17，根据上述公式，计算得到pmax、qmax的值为2。

根据计算软件，直接计算得到BIC矩阵为：

AR（0）39.58241.30642.339AR（1）42.39238.01840.845AR（2）44.67347.88641.564MA（0）MA（1）MA（2）

根据上述的BIC 矩阵可以确定第AR（1）行MA（1）列的值最小，且最小值为38.018，因此，可以确定p=1、q=1。

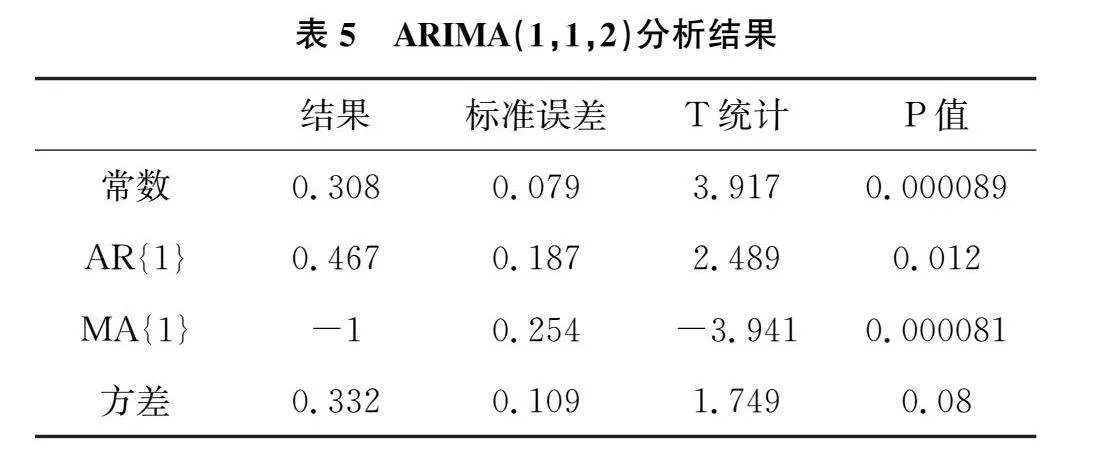
步骤3：模型的建立。根据上述步骤的分析结果，可以确定d=1，p=1，q=1，建立的模型为ARIMA（1，1，1），得到的具体分析结果如表5所示：

根据表5，建立ARIMA（1，1，1）模型为：

ARIMA（1，1，2）=y︿t=0.308+0.467yt－1－1.00et－1

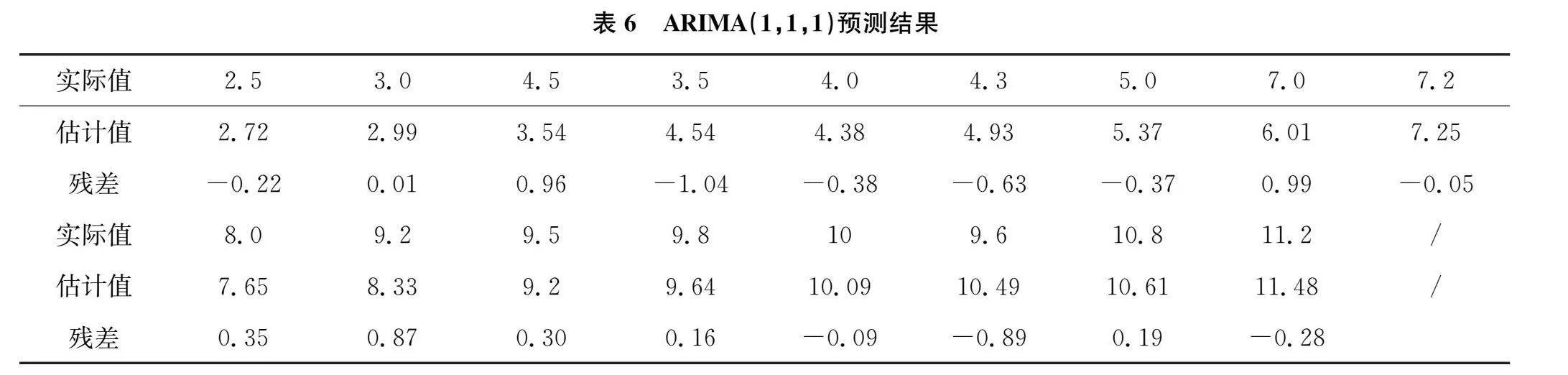
利用ARIMA（1，1，1）模型对表1数据进行预测，得到的结果如下表6所示：

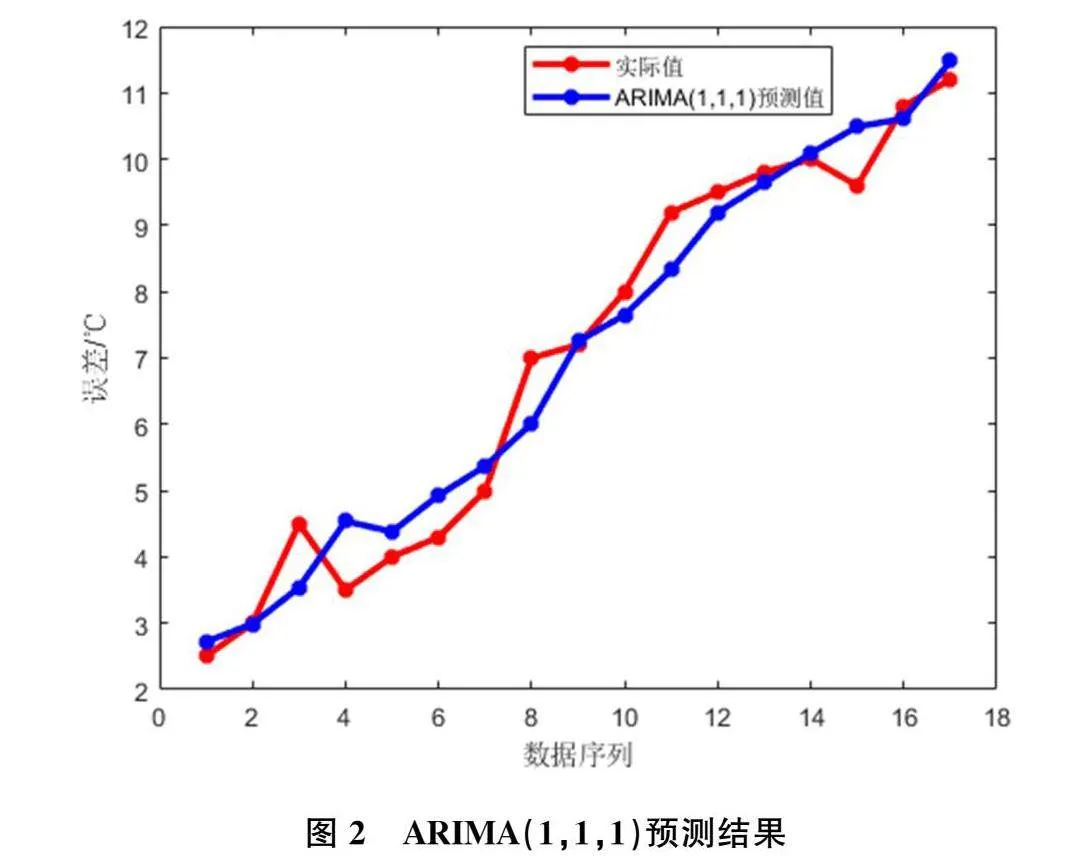
同时得到预测曲线如下图2所示：

通过图2可以发现，ARIMA（1，1，1）模型呈现平稳上升的趋势，基本上能预测出实际误差的整体变化情况。

2.2 GM（1，1） 修正模型

建立GM（1，1）修正模型，具体的步骤如下：

步骤1：截取最后的残差数据作为训练样本，本研究截取表6中的最后4个数据作为训练样本，其结果如下：

x=（0.09 0.89 0.19 0.28）

步骤2：对步骤1中数据进行一次累加，得到的结果为：

x1－ago=（0.09 0.98 1.17 1.45）

步骤3：基于单次累加生成的结果，进行最近邻近均值生成，其结果为：

x1－ago－m=（0.535 1.075 1.31）

步骤4：根据GM（1，1）模型的理论，构造矩阵向量B和常数向量Yn，其结果为：

B=－0.5351－1.0751－1.311" Y=［0.89 0.19 0.28］

步骤5：计算参数a和b的值为：

a︿=ab=（BTB）－1BTYn=

－0.5351－1.0751－1.311T·－0.5351－1.0751－1.311^－1·

－0.5351－1.0751－1.311T·0.890.190.28" =0.881.31

根据上述结果可以得到GM（1，1）修正模型为：

x︿^（0）（t+1）=（1－ea）（x^（0）（1）－ba）e^－at=

（1－e^0.88）（－1.4）e^－0.88t=1.97e^－0.88t

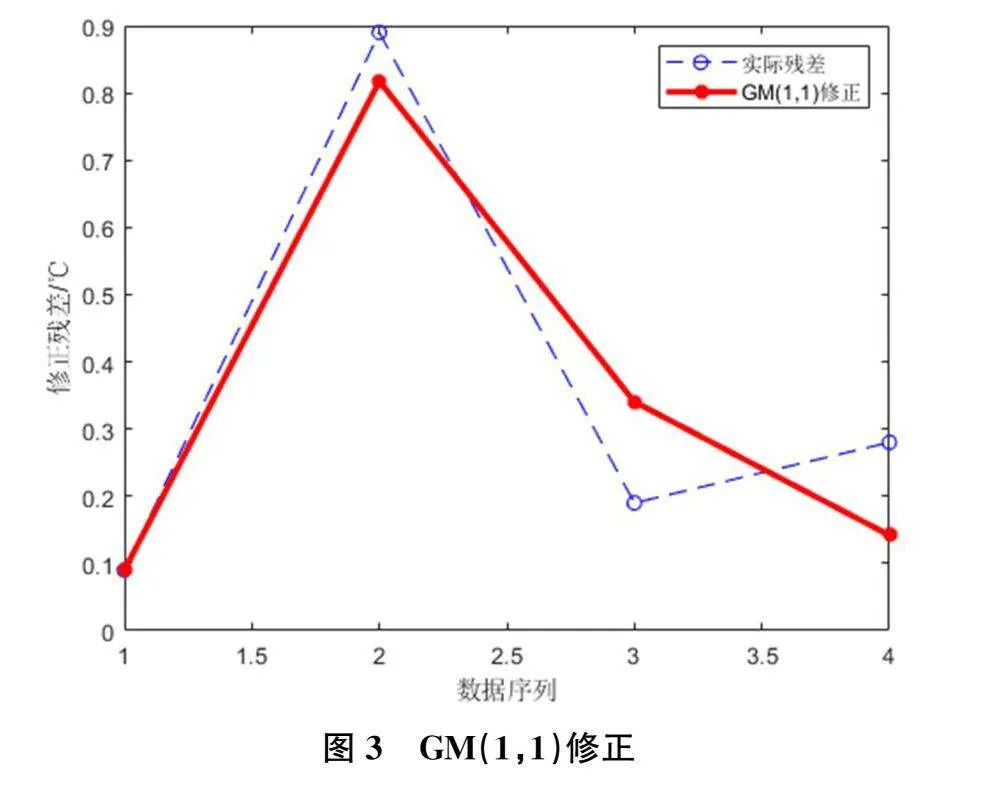
得到的GM（1，1）残差修正情况，如图3所示：

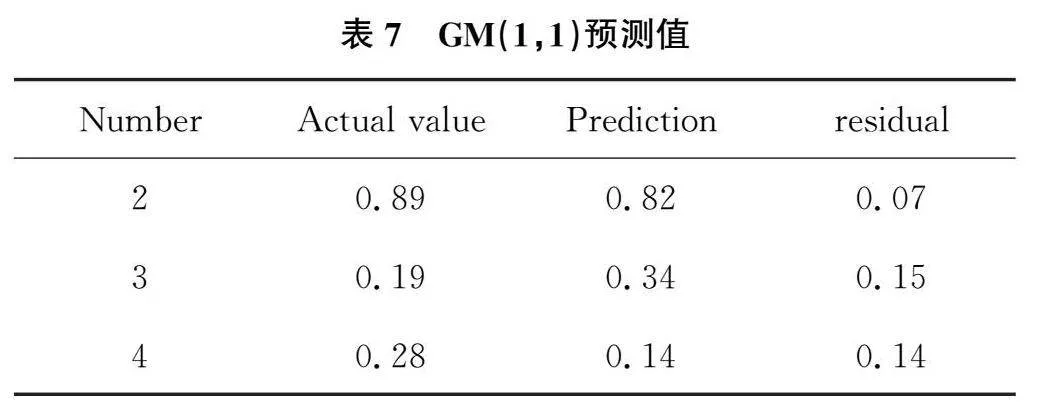
根据GM（1，1）上述的修正模型，得到的预测结果如表7所示：

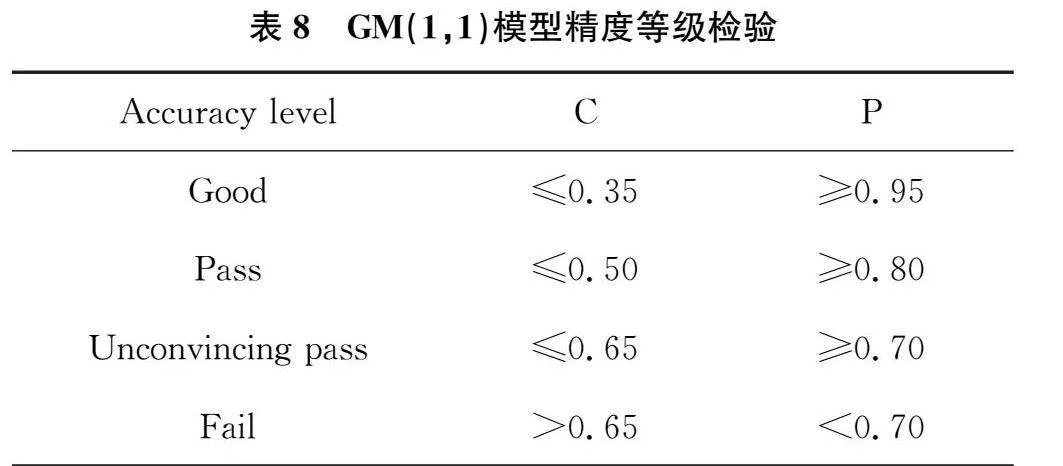
为了验证GM（1，1）模型的优劣程度，一般可以通过计算标准偏差比C和小误差概率P来判断，本研究计算得到C=0.34，P=1.0。对比表8，可以认为该GM（1，1）修正模型的精度等级最好。

2.3 ARIMA-GM（1，1） 修正模型

已经建立了ARIMA（1，1，1）模型以及GM（1，1）修正模型，将两个模型相加得到最终的预测模型为：

y︿t=0.308+0.467yt－1－1.00et－1±1.97e^－0.88tstARIMA（1，1，2）=0.308+0.467yt－1－

1.00et－1， 2≤t≤nGM（1，1）=1.97e^－0.88t，""" n－3≤t≤n（5）

其中，n 为训练样本数据个数，根据ARIMA-GM（1，1）模型可知，ARIMA（1，1，1）为主体预测模型，GM（1，1）为截尾的修正模型。

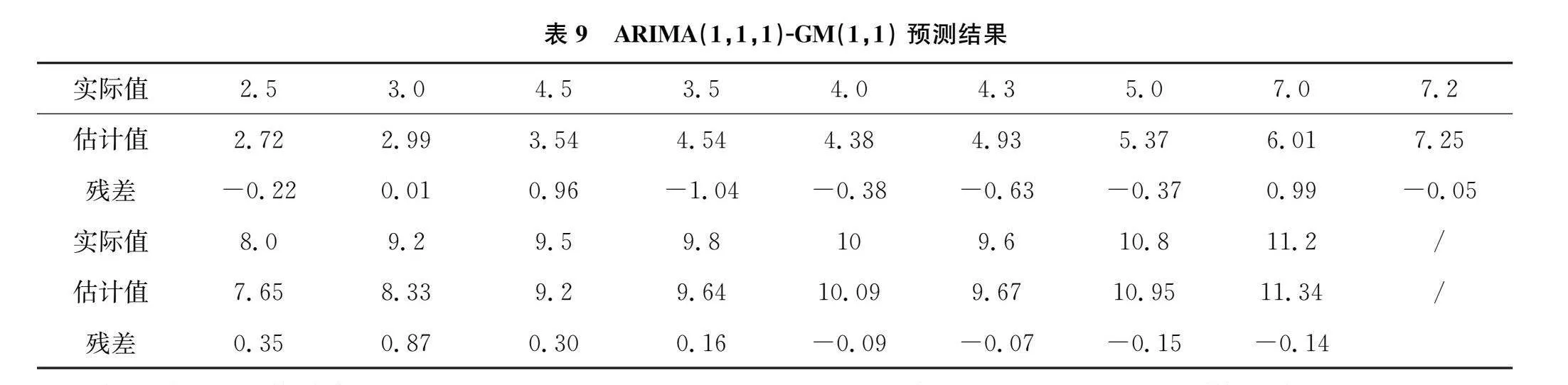
根据公式（5）得到其预测结果如表9所示：

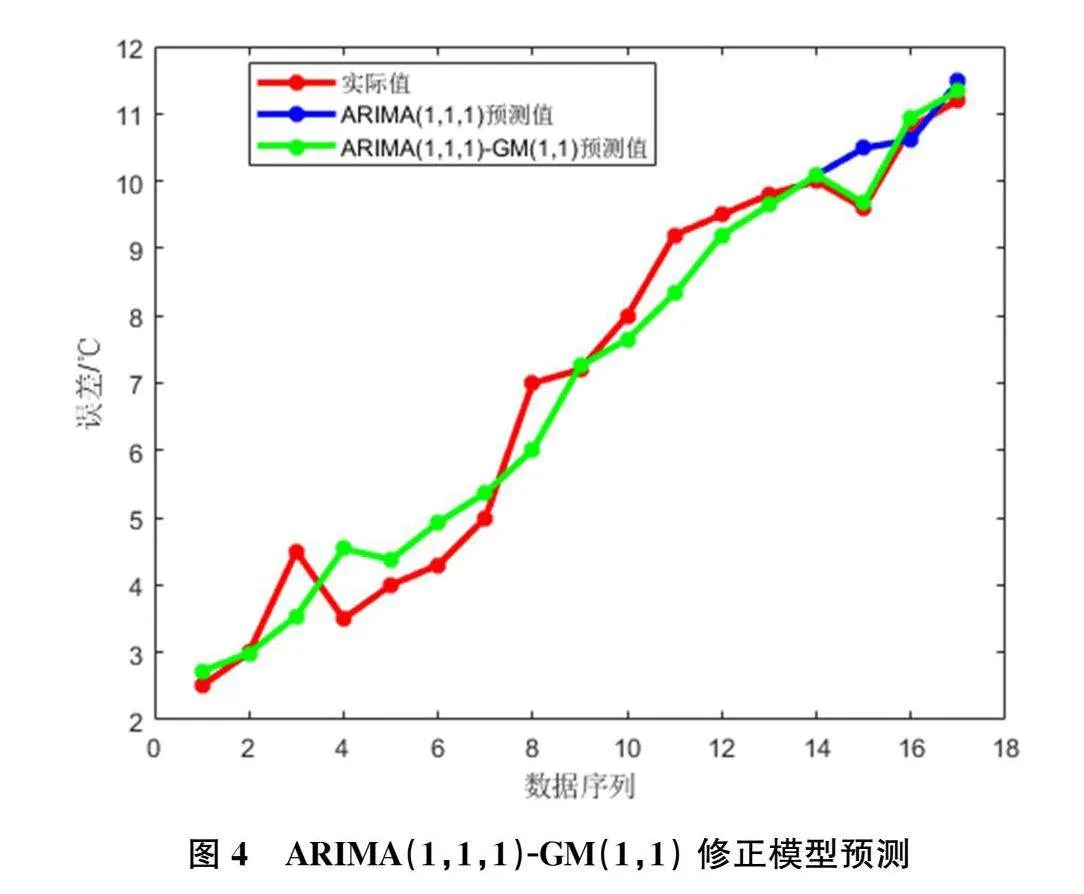
得到的预测曲线如图4所示：

通过图4明显可以得到，与传统的ARIMA（1，1，1）模型相比，ARIMA（1，1，1）-GM（1，1） 尾部的四个数据的变化曲线与实际数据几乎重合。

根据ARIMA（1，1，1）模型在1300℃时的误差值为11.97，利用GM（1，1）修正模型预测出下一个阶段的误差修正值为0.06，因此，根据计量校准进位原则可以推断出在1300℃时的误差范围在[11.9，12.1]，对比表1，其在1300℃时的误差为12.0℃，预测效果较好，以此类推，通过更新样本数据可以预测更高阶段的温度误差。

3 对比实验

为了验证ARIMA（1，1，1）-GM（1，1） 模型的优劣性，一般利用相对平均误差来衡量，其计算公式为：

E_R=∑Ni=1y1－y2N（6）

式中，y1为实际值，y2为预测值。

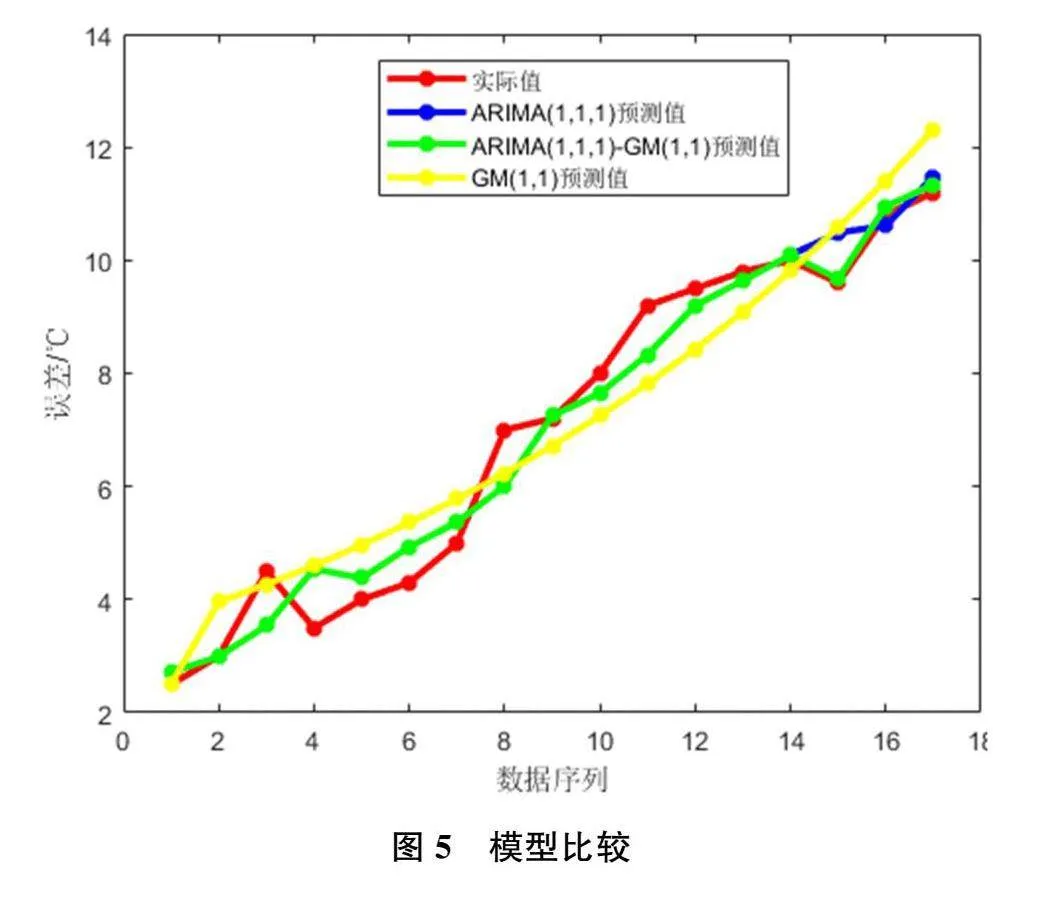
本研究将ARIMA-GM（1，1）模型与传统的ARIMA以及GM（1，1）模型相比，根据公式（6）计算得到ARIMA（1，1，1）模型的相对平均误差值E_R为0.46，GM（1，1）模型的相对平均误差值E_R为0.77，ARIMA（1，1，1）-GM（1，1）模型的相对平均误差E_R为0.40，因此，ARIMA（1，1，2）-GM（1，1）模型与实际误差值更加接近。

其具体结果如图5所示：

本研究提出的ARIMA-GM（1，1）修正模型具有较好的预测效果。

4 结论

针对温度二次仪表温度误差的问题，提出了一种基于ARIMA-GM（1，1）模型的温度校正方法。使用标准源和检测仪器获得残差，并通过残差建立ARIMA模型，为了提高ARIMA模型的准确性，建立GM（1，1）模型来修正ARIMA模型。主要结论如下：

（1）绝大多数企业不熟悉设备性能，也不具备定期开展校准工作的条件。本研究提出的ARIMA-GM模型解决了温度误差修正问题，企业在了解设备已有误差的基础上，可以推断出设备下一个阶段存在的误差，为开展设备的自修正提供科学依据；

（2）与传统的ARIMA、GM（1，1）以及混合的GM-ARIMA模型相比较，本研究提出的ARIMA-GM（1，1）修正模型预测精度高，可以应用在实际误差无法检测的工况下。

［参 考 文 献］

［1］

尤金辉，范国锋.ARIMA模型与GM（1，1）模型对兴化市结核病发病数预测效果比较[J].江苏预防医学，2022， 33（5）：551-553.

[2] 潘红宝，宋绍溥，傅志峰，等.ARIMA与GM（1，1）模型在某深基坑沉降预测中的对比分析[J].勘察科学技术， 2022（4）：39-43.

[3] SARITA S.，SUMANTA P.Efficacy and application of the window-sliding ARIMA for daily and weekly wind speed forecasting[J].Journal of Renewable and Sustainable Energy，2022，14 （5）.

[4] DING S，LI R，WU S，et al.Application of a novel structure-adaptative grey model with adjustable time power item for nuclear energy consumption forecasting[J].Applied Energy，2021，298（3）：117114.

[5] LI L，BAI X，XIA H.Prediction of the trend of higher education development using a weakening bufer operatorbased GM （1， 1） model[J].Education and Information Technologies，2024，29：2523-2538.

[6] FENG X， JIANG J， WANG W， et al.Predictive model for the number of elevator failures based on the residual error correction model and a GM （1，1）-Markov chain[J].The Journal of grey system，2021，33（4）：46-60.

[7] 翟小伟，周翔，宋波波，等.基于ARIMA模型的矿井灾害预测方法研究[J/OL]．煤炭技术. https：//doi.org/10.13301/j.cnki.ct.2024.06.034.

[8] 张良均. MATLAB数据分析与挖掘实战[M].北京：机械工业出版社， 2015： 118-120.

[9] 张庆伟，肖建清.GM（1，1）与Verhulst模型在地基沉降预测中的适用性比较[J].沈阳工业大学学报， 2014（6）：716-720.

[10] JJG 617-1996 数字温度指示调节仪检定规程[S].北京： 中国标准出版社，1996.

Error Morrection Method for Secondary Temperature Instruments Based on ARIMA-GM （1， 1） Model

Feng Xin， Ni Lei， Li Shu， Li Lei

Abstract： the problem of undetectable errors in secondary temperature instruments for chemical equipment during ultra-high temperature stages， this paper proposed a temperature error correction method based on ARIMA-GM （1，1） model. Firstly， put the secondary temperature instrument and standard in a stable environment， and calculate the error between the standard and secondary instrument by outputting electrical signals from the standard instrument; Secondly， an ARIMA model was established through error sequences to obtain a set of predicted values; Then， the residual between the actual error and the predicted value is calculated， to improve the prediction accuracy of the ARIMA model， the tail data of the residual sequence is truncated to establish a GM （1，1） correction model; Finally， the ARIMA model was combined with the GM （1，1） model to establish an ARIMA-GM （1，1） correction model， which predicts the possible errors of the instrument in the next stage and realizes the self-correction function of the secondary temperature instrument. Comparative experiments have shown that the ARIMA-GM （1，1） model proposed in this paper has the lowest relative average error， higher prediction accuracy， and can better predict the possible errors of the instrument in the next stage， and this method provided a scientific basis for the self-correction of subsequent instruments.

Key words：error correction model; ARIMA model; GM（1，1） model; ARIMA-GM（1，1） model

责任编辑：陈星宇