阶跃函数模拟桥梁断面气动自激力的精度研究

摘要： 介绍了采用阶跃函数模拟桥梁断面时域气动自激力的方法并对模拟的精度进行了研究。提出了采用现代遗传优化算法进行阶跃函数参数识别的方法。在模拟桥梁断面时域自激力的过程中，建立了颤振导数与阶跃函数各参数之间的等量关系，基于MATLAB平台实现了遗传优化算法并识别了阶跃函数的各个参数，根据参数值与上述等量关系反算得到颤振导数的拟合值，并通过对比颤振导数的拟合值与试验值来评估模拟的精度。数值算例表明，遗传优化算法的计算效率很高且不受参数个数与参数取值范围的影响；阶跃函数参数个数对颤振导数拟合精度存在较大的影响；当参数个数较少时，对于较为复杂的颤振导数曲线，拟合精度不高。随着参数个数的增加，拟合精度显著提高。拟合精度直接影响后续时域颤振分析得到的桥梁颤振性能；因此，需要依据颤振导数曲线规律，合理地选取阶跃函数的参数个数，才能建立精度较高的时域自激力模型，进而准确评估桥梁的颤振稳定性能。

关键词： 桥梁； 颤振； 时域； 阶跃函数； 遗传优化

中图分类号： U441+.3； TU312+.3 文献标志码： A 文章编号： 1004-4523（2024）06-0997-09

DOI：10.16385/j.cnki.issn.1004-4523.2024.06.010

引 言

颤振是大跨桥梁抗风设计的关键问题之一。目前研究桥梁颤振的方法主要包括频域法与时域法两类。频域方法很成熟，能够较为准确地描述桥梁断面的气动力特性，已被广泛应用于桥梁颤振临界问题的研究中［1⁃2］。较晚形成的时域方法也具有其独特的优势，不仅便于考虑多种非线性效应的影响，还能与结构的有限元计算模型相结合，在桥梁颤振、非线性颤振、颤抖振一体化研究中得到了广泛的应用［3⁃9］。桥梁断面的气动自激力一般采用由气动导数描述的Scanlan自激力模型模拟，直接基于该模型进行的颤振分析属于频域方法。若建立合适的与试验气动导数相应的过渡函数，将Scanlan自激力模型转换为纯时域模型，然后基于时域自激力模型进行颤振分析，这类方法属于时域方法。

建立桥梁断面时域自激力模型的主要方法有阶跃函数法与有理函数法［10］。阶跃函数（Indicial Functions， IFs）已被广泛用于描述桥梁的气弹效应与时域颤振分析［11⁃14］。阶跃函数时域表达桥梁断面自激力的本质是通过已知的气动导数来拟合未知的阶跃函数，即确定阶跃函数的参数值，这属于最优化问题，且拟合精度必须满足工程要求才能保证后续时域颤振分析的可靠性。在以往的研究中，常采用传统的最小二乘优化方法，为了提高拟合效率，期望阶跃函数所含的参数个数越少越好，通常参数取4个或6个，且各参数的搜索范围也不宜太大。当颤振导数随折算风速的变化较为平顺时，较少的参数可能达到较高的拟合精度；当颤振导数随折算风速的变化较为复杂时，较少的参数将无法满足精度要求，此时只能增加阶跃函数的指数项个数即增加参数个数来提高拟合精度，然而参数个数的增加，将会导致优化算法的效率降低。鉴于此，本文引入了现代智能优化方法中的遗传算法［15］，并基于MATLAB平台实现了阶跃函数参数的快速识别，该方法计算效率高，且不受参数个数及搜索域的影响，可同时求解多个参数的最优解。

以江底河大桥为例，基于遗传优化算法，分别选取含有4，6，8，10与12参数的阶跃函数对主梁断面的试验颤振导数进行拟合，得到阶跃函数的参数值与颤振导数的拟合值。通过考查颤振导数试验值与拟合值的吻合情况来评估参数个数对颤振导数拟合精度的影响。基于ANSYS有限元软件，分别采用不同类型阶跃函数建立的时域自激力模型对桥梁进行时域颤振分析，得到相应的颤振临界风速，并进一步讨论采用阶跃函数法进行桥梁时域颤振分析的可靠性。

1 颤振导数与IFs参数等价关系

Scanlan自激力模型描述的是微小振幅简谐运动引起的自激气动力［16］，以桥梁断面二维自激气动力为例，其表达式如下式所示：

（1）

（2）

式中 及分别为单位长度主梁的自激气动升力及升力矩；与分别表示竖向运动引起的升力与升力矩时程，与分别表示扭转运动引起的升力与升力矩时程；为空气密度；U为来流风速；B为桥面宽度；K为无量纲折算频率，K=Bω/U，其中ω为结构振动频率；与 （i=1，2，3，4）为颤振导数；与分别为竖向位移及其对时间的一阶导数；与分别为扭转位移及其对时间的一阶导数。

阶跃函数可以描述阶跃响应所引起的结构断面气动力变化时程。在描述桥梁断面自激气动力中，阶跃函数通常采用如下的形式：

（3）

式中 ，为待定参数；r为指数项个数。

借助上述阶跃函数，任意微小扭转振动所引起的升力时程可以表示为如下式所示的卷积形式：

（4）

式中 ，为积分变量，表示无量纲时间s的变化。

对于桥梁断面，通常分开处理竖向与扭转运动所引起的自激气动力后再叠加，即单位长度主梁所受的气动升力与升力矩分别表示如下：

（5）

（6）

式中 s为无量纲时间，s=Ut/B，其中t为时间；与分别为升力与升力矩系数对攻角的导数；为扭转位移对s的一阶导数；为竖向位移对s的二阶导数；，，与为阶跃函数，其表达式可统一为如下形式：

（7）

式中 与为阶跃函数参数，其中x表示L或M，y表示h或，如为描述扭转阶跃响应引起断面升力变化的阶跃函数。将公式（5）和（6）称为IF型时域自激力模型。

通过Scanlan自激力模型来建立与之等价的IF型时域自激力模型，其实质是根据已知的气动导数（包括颤振导数与三分力系数）来识别阶跃函数各个参数值的过程。下面介绍一种直观简便的方法来建立气动导数与阶跃函数各参数之间的等量关系。

假设结构做单位幅值的正弦竖向运动与扭转运动，表达式分别如下：

竖向：（8）

扭转：（9）

将公式（8）和（9）代入公式（1）和（2）中可得Scanlan自激力模型的具体表达式如下式所示：

（10）

（11）

（12）

（13）

将公式（8）和（9）代入公式（5）和（6）中可得IF型自激力模型的具体表达式如下式所示：

（14）

（15）

（16）

（17）

对比公式（10）～（13）与（14）～（17）可知，后者均比前者多一个含的指数项，根据指数型函数的曲线规律，假如参数为负值，指数项将会发散，此时IF型时域自激力无法与Scanlan自激力等价。因此，必须为一正值，让指数项随时间衰减；但需要说明的是，为正值的前提下，IF型自激力时程在起初的一段时间内也可能会出现较为明显的瞬态现象，但随着时间的推移，自激力时程最终会趋于稳态，如图1所示。

综上可知，要建立与Scanlan模型等价的IF型时域自激力模型，必须满足以下两个条件：首先，IF型自激力模型中的指数项必须随时间衰减为零，即要求参数必须为正值；其次，在保证拟合精度的前提下，的下限可以适当地提高，促使指数项在较短时间内衰减；最后，两类自激力模型的正弦项与余弦项的系数必须对应相等，即如下式所示：

（18）

（19）

（20）

（21）

整理即可建立气动导数与阶跃函数各待定参数之间的等价关系，如下式所示：

（22）

（23）

（24）

（25）

根据上述等价关系，建立如下式所示的目标函数，通过求解目标函数的极小值来识别阶跃函数的参数值，进而确定公式（5）和（6）所示时域自激力模型的具体表达式。显然，阶跃函数参数识别是一个典型的最优化问题。

（26）

（27）

（28）

（29）

式中 与（m=1，2，3，4）为颤振导数的试验值；n为试验数据组数。

由于公式（26）～（29）中分式的分母存在待识别的参数，因此它是一个较为复杂的非线性最优化问题。针对此类非线性优化问题，下面介绍现代优化算法中的遗传算法，并基于MATLAB平台进行求解。

2 阶跃函数参数识别

2.1 遗传优化算法

遗传算法是基于优胜劣汰、适者生存的进化论原理，模拟生物在自然环境中遗传进化过程的一种随机搜索优化算法［15］。具体来说，就是依照遗传进化原理，将随机产生的初始种群作为优化问题的一组初始解，通过对初始种群施加选择、交叉、变异等一系列遗传进化操作来产生适应性较好的新一代种群，重复上述操作直至种群优化到包含近似最优解的状态。

遗传优化算法的具体思路为：针对某一具体的优化问题，建立相应的目标函数作为个体评价的适应度函数。在进化过程的每一代中，分别计算所有个体的适应度，适应度小的个体淘汰，适应度大的个体留下作为产生新一代种群的母体。若某一代个体的适应度达到目标容许误差，或遗传代数达到预先设定的最大值，则停止计算，返回最优解。与传统优化方法相比，遗传优化算法具有较广的搜索域，较强的并行运算能力，灵活性更强，效率更高，有利于获取全局最优解。

阶跃函数参数识别实质上是求解公式（26）～（29）所示目标函数取得极小值时的参数值。根据上述优化问题的性质，借助MATLAB遗传工具箱的“ga”函数进行优化计算，“ga”函数的一般格式如下：

该函数主要的输出与输入参数如下：

输出参数：x表示阶跃函数所有参数（，，，…，；，，，…，）组成的数组；fval为x对应的适应度值。

输入参数：fitnessfcn为适应度函数，公式（26）～（29）所示的目标函数即为适应度函数，用于计算x对应的适应度值；nvars为适应度函数中独立变量的个数，即待拟合参数的个数；lb，ub分别为x搜索域的下限与上限；options为算法结构参数，主要包括种群大小、最大遗传代数、交叉概率、变异概率、适应度的阈值等，可以根据具体问题的性质调整结构参数的范围。采用遗传优化算法进行阶跃函数参数识别的流程如图2所示。

2.2 参数识别结果与精度讨论

以江底河悬索桥为例，通过上述遗传优化算法来识别得到阶跃函数的各个参数值，相关的计算参数如表1所示。由表1可知，风攻角为+3°，与分别为升力与升力矩系数对攻角的一阶导数，参数（i=1，2，…，r）的搜索域设置为全体实数，（i=1，2，…，r）的搜索域设置为≥0.1。阶跃函数的指数项个数分别取2，3，4，5，6项时，对应的参数个数依次为4，6，8，10，12，如表2所示。若阶跃函数的指数项个数为2，即含有4个参数，则称为4参数阶跃函数，其他情形类推。

分别采用4，6，8，10与12参数阶跃函数对桥梁断面的试验颤振导数进行拟合。当遗传优化算法的种群大小取1000，遗传代数取1000，其余计算参数采用默认值时，5种工况的计算时间成本均低于2 min，计算效率非常高。表3～7分别给出了4，6，8，10与12参数阶跃函数的参数识别结果。

将阶跃函数参数值代入公式（22）～（25）即可求得颤振导数的拟合值。通过比较颤振导数的拟合曲线与试验曲线，即可判断颤振导数的拟合精度。

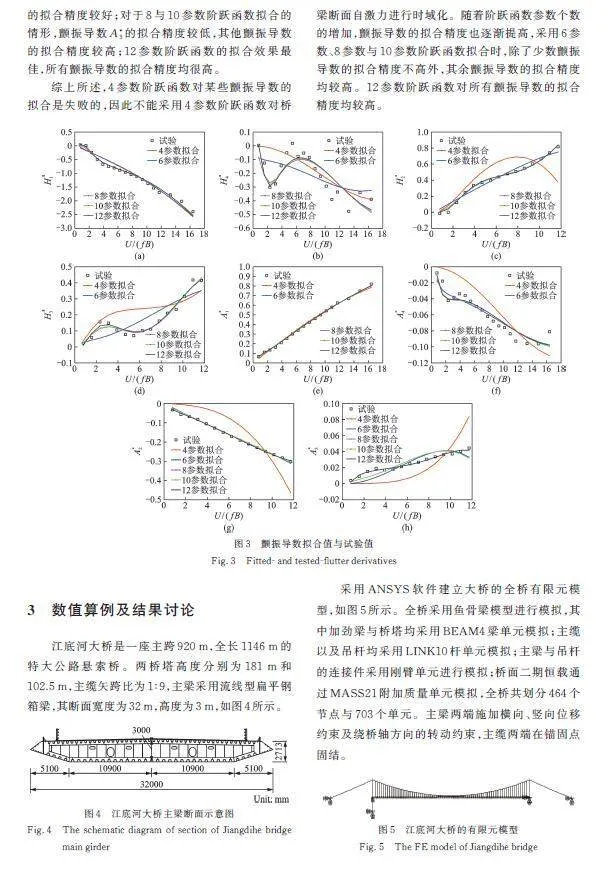
由公式（26）～（29）可知，参数拟合过程均是以两组颤振导数成对的形式进行拟合的，如与为一对，因此往往也将成对的两组颤振导数曲线绘制在同一个图形中，然而当成对的两组颤振导数的数值范围相差较大时，这样绘制的颤振导数曲线图很可能从视觉上掩盖了数值较小的那一组颤振导数的拟合误差。鉴于此，本文将8组颤振导数分别绘制在独立的图形中，这样便可很直观地考查各组颤振导数的拟合精度。

图3给出了桥梁断面颤振导数试验值与由阶跃函数参数反算得到的颤振导数拟合值。由图3可知，对于4参数阶跃函数拟合的情形，除了颤振导数与的拟合精度较好之外，其他颤振导数的拟合均是失败的；对于6参数阶跃函数拟合的情形，颤振导数，与的拟合精度较低，其他颤振导数的拟合精度较好；对于8与10参数阶跃函数拟合的情形，颤振导数的拟合精度较低，其他颤振导数的拟合精度较高；12参数阶跃函数的拟合效果最佳，所有颤振导数的拟合精度均很高。

综上所述，4参数阶跃函数对某些颤振导数的拟合是失败的，因此不能采用4参数阶跃函数对桥梁断面自激力进行时域化。随着阶跃函数参数个数的增加，颤振导数的拟合精度也逐渐提高，采用6参数、8参数与10参数阶跃函数拟合时，除了少数颤振导数的拟合精度不高外，其余颤振导数的拟合精度均较高。12参数阶跃函数对所有颤振导数的拟合精度均较高。

3 数值算例及结果讨论

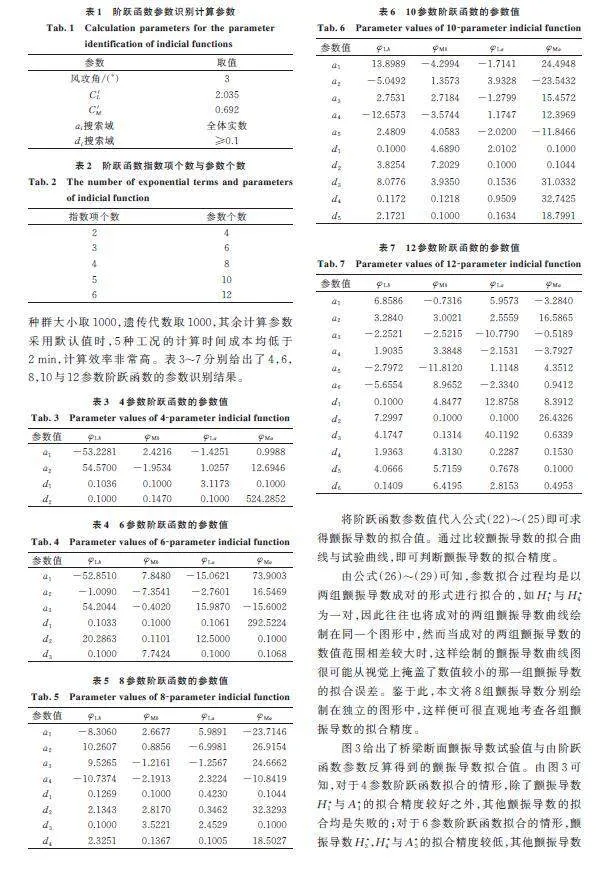
江底河大桥是一座主跨920 m，全长1146 m的特大公路悬索桥。两桥塔高度分别为181 m和102.5 m，主缆矢跨比为1∶9，主梁采用流线型扁平钢箱梁，其断面宽度为32 m，高度为3 m，如图4所示。

采用ANSYS软件建立大桥的全桥有限元模型，如图5所示。全桥采用鱼骨梁模型进行模拟，其中加劲梁与桥塔均采用BEAM4梁单元模拟；主缆以及吊杆均采用LINK10杆单元模拟；主梁与吊杆的连接件采用刚臂单元进行模拟；桥面二期恒载通过MASS21附加质量单元模拟，全桥共划分464个节点与703个单元。主梁两端施加横向、竖向位移约束及绕桥轴方向的转动约束，主缆两端在锚固点固结。

基于ANSYS软件分别采用6，8，10与12参数阶跃函数拟合得到的自激力时程对江底河大桥进行时域颤振分析，得到各工况对应的颤振临界风速及频率。时域颤振计算的参数如表8所示。结构阻尼采用瑞利阻尼模型进行描述，其表达式如下式所示：

（30）

式中 ，与分别为结构的阻尼、质量与刚度矩阵；和为瑞利阻尼系数。根据表8的参数可得到阻尼比与圆频率的关系如图6所示。

图7给出了桥梁不同工况的颤振临界风速及频率。由图7可知，8与10参数所对应的颤振临界风速相差不大，且略低于6参数所对应的风速值，但均明显低于12参数的风速值。这一结果可从图3所示的颤振导数拟合效果来解释，相比6参数阶跃函数的拟合效果，8与10参数阶跃函数的拟合效果得到了一定的改善，且8与10参数的拟合效果相差不大；相比之下，12参数阶跃函数的整体拟合效果最佳。不同工况对应的颤振频率相差甚微，表明4种工况在颤振临界点的气动刚度相差很小。

表9给出了江底河大桥不同工况对应的颤振临界风速相对风洞试验结果的误差。由表9可知，12参数对应的颤振临界风速为90.05 m/s，与风洞试验结果十分接近，误差仅为0.39%，而其他工况对应的颤振临界风速显著低于风洞试验结果，即明显地低估了此桥的颤振稳定性能。

综上所述，阶跃函数的参数个数对颤振导数的拟合精度存在显著的影响，参数个数较少时，有些颤振导数的拟合精度不高，将会导致时域颤振计算得到的颤振临界风速与试验值存在较大的偏差，因此需要增加参数个数，提高所有颤振导数的拟合精度，这样才能保证时域法进行桥梁颤振稳定分析的可靠性。

4 结 论

本文详细地介绍了采用阶跃函数时域表达桥梁断面自激气动力的方法。采用现代优化算法中的遗传算法进行阶跃函数参数识别并基于MATLAB平台实现。以江底河大桥为例，研究了阶跃函数的参数个数对颤振导数拟合效果的影响；基于ANSYS平台进行了大跨桥梁的时域颤振分析，并讨论了应用阶跃函数法进行时域颤振分析的可靠性。主要结论如下：

（1） 阶跃函数参数识别的遗传优化算法具有很高的计算效率，且能在很广的搜索域内识别出最优参数值。在本文设置的计算参数与搜索域的条件下，5种工况的计算成本均低于2 min。因此，遗传优化算法的引入显著地提高了大跨桥梁时域颤振分析的效率与精度；

（2） 对江底河大桥断面而言，采用4参数阶跃函数对其试验颤振导数进行拟合的精度很差，甚至对于某些颤振导数的拟合是失败的，因此4参数阶跃函数不能用于此桥自激气动力的时域表达。算例表明，随着阶跃函数参数个数的增加，颤振导数的拟合精度得到逐步提高。

（3） 由于不同类型阶跃函数在自激力时程的拟合精度上存在差异，因此时域颤振计算得到的颤振临界风速也会存在差异。5种工况中，12参数阶跃函数拟合精度最高，它对应的颤振临界风速为90.05 m/s，与节段模型风洞试验结果的89.7 m/s十分接近。而6， 8与10参数阶跃函数对于某些颤振导数的拟合精度不高，因此得到的颤振临界风速与试验值相差较大。

由于遗传优化算法具有很高的计算效率，因此对于颤振导数曲线较为复杂的桥梁钝体断面，建议选取参数个数较多的阶跃函数进行颤振导数拟合，建立精度较高的时域自激力模型，进而保证后续时域颤振分析的可靠性。

参考文献：

［1］ Ge Y J， Tanaka H. Aerodynamic flutter analysis of cable-supported bridge by multi-mode and full-mode approaches［J］. Journal of Wind Engineering and Industrial Aerodynamics， 2000， 86（2-3）： 123-153.

［2］ Ding Q S， Chen A R， Xiang H F. Coupled flutter analysis of long-span bridges by multimode and full-order approaches［J］. Journal of Wind Engineering and Industrial Aerodynamics， 2002， 90（12-15）： 1981-1993.

［3］ Chen X Z， Matsumoto M， Kareem A. Time domain flutter and buffeting response analysis of bridges［J］. Journal of Engineering Mechanics， 2000， 126（1）： 7-16.

［4］ Miyata T， Yamada H， Boonyapingo V， et al. Analytical investigation on the response of a very long suspension bridge under gust wind［C］//In Proceedings of 9th International Conference on Wind Engineering. New Delhi， 1995： 1006-1017.

［5］ Zhang Z T. Multistage indicial functions and post flutter simulation of long-span bridges［J］. Journal of Bridge Engineering， 2018， 23（4）： 04018010.

［6］ 吴长青， 张志田， 张伟峰. 考虑几何非线性的桥梁后颤振极限环特性［J］. 湖南大学学报（自然科学版）， 2018， 45（5）：1-10.

WU Changqing， ZHANG Zhitian， Zhang Weifeng. Limit cycle oscillation of bridge post-flutter with geometric nonlinearities［J］. Journal of Hunan University （Natural Sciences）， 2018， 45（5）：1-10.

［7］ 吴长青，张志田. 平均风与气弹效应一体化的桥梁非线性后颤振分析［J］. 振动工程学报， 2018，31（3）： 399-410.

WU Changqing， ZHANG Zhitian. Nonlinear post-flutter analysis of bridge decks with the integrated mean and aero-elastic wind effects［J］. Journal of Vibration Engineering， 2018， 31（3）： 399-410.

［8］ Zhang Z T. Mean wind load induced incompatibility in nonlinear aeroelastic simulations of bridge spans［J］. Frontiers of Structural and Civil Engineering， 2019， 13： 605-617.

［9］ 汪志雄， 张志田， 吴长青，等. π型叠合梁颤振试验及数值研究［J］. 振动工程学报， 2021， 34（2）：301-310.

WANG Zhixiong， Zhang Zhitian， WU Changqing， et al. Experimental and numerical investigations on flutter of π-shaped side-girders［J］. Journal of Vibration Engineering， 2021， 34（2）： 301-310.

［10］ Salvatori L， Borri C. Frequency- and time-domain methods for the numerical modeling of full-bridge aeroelasticity［J］. Computers & Structures， 2007， 85（11-14）： 675-687.

［11］ 张志田， 陈政清， 李春光. 桥梁气动自激力时域表达式的瞬态与极限特性［J］. 工程力学， 2011， 28（2）： 75-85.

ZHANG Zhitian， CHEN Zhengqing， LI Chunguang. Limiting and transient characteristics of time-domain expressions for bridge self-excited aerodynamic forces［J］. Engineering Mechanics， 2011， 28（2）： 75-85.

［12］ de Miranda S， Patruno L， Ubertini F， et al. Indicial functions and flutter derivatives： a generalized approach to the motion-related wind loads［J］. Journal of Fluids & Structures， 2013， 42： 466-487.

［13］ Farsani H Y， Valentine D T， Arena A， et al. Indicial functions in the aeroelasticity of bridge decks［J］. Journal of Fluids & Structures， 2014， 48： 203-215.

［14］ Zhang Z T， Chen Z Q， Cai Y Y， et al. Indicial functions for bridge aero-elastic forces and time-domain flutter analysis［J］. Journal of Bridge Engineering， 2011， 16（4）： 546-557.

［15］ 吴长青. 大跨度桥梁非线性颤振及后颤振强健性研究［D］. 长沙：湖南大学， 2019.

WU Changqing. Investigation on nonlinear flutter and post flutter robustness of long span bridges［D］. Changsha： Hunan University， 2019.

［16］ Scanlan R H. Problematics in formulation of wind-force models for bridge decks［J］. Journal of Engineering Mechanics， 1993， 119（7）： 1353-1375.

Precision investigation on the self-excited aerodynamic force model of bridge decks simulated by indicial functions

WU Chang-qing1， ZHANG Zhi-tian2

（1.College of Civil Engineering and Architecture， Hunan Institute of Science and Technology， Yueyang 414006， China；2.School of Civil Engineering and Architecture， Hainan University， Haikou 570228， China）

Abstract： This paper introduces a method of using indicial functions （IFs） to simulate the time-domain expressions of self-excited aerodynamic loads of bridge decks， and studies the precision of this simulation. A modern genetic optimization algorithm is proposed to identify the parameters of IFs based on the tested flutter derivatives. During the simulation process， the equivalent relation between flutter derivatives and IFs parameters is first established. Then， the genetic optimization algorithm is implemented to identify all the IFs parameters using the MATLAB software. Based on the obtained IFs parameters， the fitted flutter derivatives are calculated according to the relation expression between IFs parameters and flutter derivatives. Finally， the simulation precision is evaluated by comparing the fitted and tested flutter derivatives. Numerical results indicate that the genetic optimization algorithm has high computational efficiency and is not affected by the number or range of parameters. The number of IFs parameters greatly influences the fitting precision of the flutter derivative. When the number of IFs parameters is small， the fitting precision is not ideal for complex flutter derivative curves. As the number of IFs parameters increases， the fitting precision significantly improves. The difference in fitting precision directly affects the critical wind speed of flutter obtained by the subsequent time-domain flutter analysis. Therefore， it is necessary to carefully select the number of IFs parameters based on the properties of flutter derivative curves. This allows for the simulation of a high-precision time-domain self-excited aerodynamic loads model， which can accurately evaluate the flutter stability of long-span bridges.

Key words： bridges；flutter；time-domain；indicial functions；genetic optimization

作者简介： 吴长青（1987―），男，博士，讲师。E-mail：12021048@hnist.edu.cn。