地震作用下桩⁃土⁃核电结构相互作用的异步分析方法

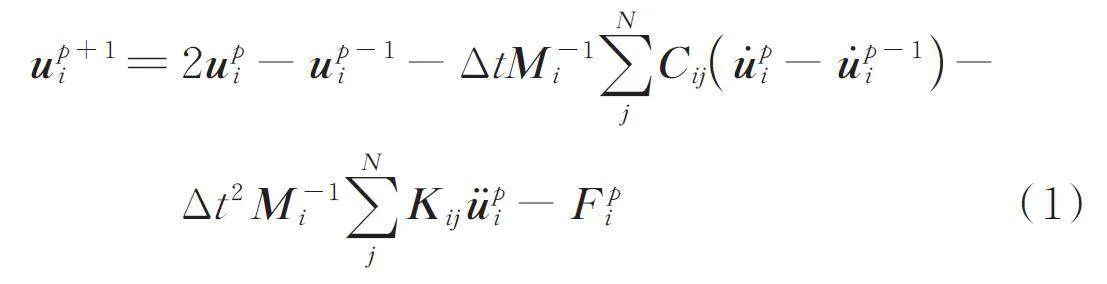
摘要： 为拓展核电厂的选址范围，有必要对非基岩场地桩基情形的核电结构进行地震安全性评估。在目前的桩⁃土⁃结构相互作用分析方法中，Winkler地基梁模型以及p⁃y法都将桩⁃土⁃结构相互作用问题进行了简化，难以反映复杂地基情形。整体有限元法可考虑复杂地基情形，但计算量较大，效率较低。本文基于高效的三维时域土⁃结构相互作用分区分析（Partitioned Analysis of Soil⁃Structure Interaction，PASSI）方法，实现桩基与土体分别采用不同时间步距的计算方法，避免土体采用桩基相对较小的时间步距而增加不必要的计算量。本文以AP1000核岛结构作为研究对象，建立了桩⁃土⁃核电结构相互作用的三维有限元模型并对其进行分析。通过输入脉冲波验证了该异步算法的有效性，并结合运动相互作用和惯性相互作用，分析了桩身最大剪力和最大弯矩的特点。分析了桩⁃土⁃核电结构在地震波输入下的响应。由于桩的自由度数相对于土体的自由度数可以忽略不计，采用桩⁃土异步算法时，桩附加的计算量可以忽略，这种高效方法有望用于大型核电结构的桩⁃土⁃结构动力相互作用分析中。

关键词： 桩⁃土⁃结构相互作用； 土⁃结构相互作用分区分析方法； 运动相互作用； 异步算法； 核电抗震设计

中图分类号： TU311.3； TU473.1 文献标志码： A 文章编号： 1004-4523（2024）06-1033-10

DOI： 10.16385/j.cnki.issn.1004-4523.2024.06.014

引 言

为拓展核电厂的选址需求，考虑桩基情形的核电抗震设计十分必要。场地放大效应和桩⁃土体系的柔性对桩⁃土⁃结构系统的地震响应有较大影响，需要考虑桩⁃土⁃结构相互作用。目前关于桩⁃土⁃结构相互作用的研究较多，其分析方法仍可沿用土⁃结构相互作用的分类：子结构法［1］和直接法［2⁃4］，只是在考虑桩⁃土相互作用时，采用Winkler地基模型［5⁃7］或整体建模［4］。Castelli等［8］采用一种简化的方法分析了桩基础的地震响应，该方法分两步进行计算：（1）自由场分析，得到沿桩身的最大位移；（2）将上部结构的惯性力等效为静力荷载施加于桩头，并将沿桩身的最大自由场位移施加于桩上，进行静力分析，其中桩⁃土相互作用通过p⁃y曲线刻画，群桩效应采用p乘子法考虑。Carbonari等［9］采用子结构方法，运用频域方法分析动力刚度和运动相互作用，再将动力刚度进行时域参数化，然后对结构进行时域动力分析，并对铁路桥梁进行了分析。Maheshwari等［10］为了评估非线性效应，采用了一种先进的、基于塑性的分层单表面（HISS）土体模型，利用频域⁃时域混合算法分析了三维空间中桩基的非线性响应。利用这些结果，根据不同桩间距的动力阻抗和运动相互作用系数，给出了弹性和非弹性土壤条件下桩基的频率响应。Boulanger等［11］采用非线性Winkler地基梁模型，通过动力非线性p⁃y单元实现桩⁃土相互作用分析，并与离心机的试验进行对比，验证了该方法的有效性。Kojima等［12］采用复杂模态量的反应谱方法评估结构⁃桩⁃土系统的地震反应，得出复杂模式的响应谱方法适用于桩⁃土模型，运动响应、惯性响应和总响应可以以统一的方式进行评估的结论。Won等［13］采用t⁃z/q⁃z和p⁃y曲线的荷载转移方法分析单桩，运用有限元技术将桩的刚度与桩帽和柱的刚度相结合，通过与其他桩群的数值方法进行比较，验证了所开发的数值方法。Kavvads等［14］采用动力Winkler地基梁模型，分析了层状地基中的桩⁃土运动相互作用，并通过有限元结果的对比，给出了Winkler刚度的取值。

目前针对核电结构的桩⁃土⁃结构相互作用分析还较少，Sayed等［15］比较了采用刚性地基和考虑非线性桩⁃土相互作用两种情况下核电站的抗震性能，结果表明，高频波动输入下后者的响应要大于前者。但其自由场输入是基于等效线性化的一维场地响应分析，所采用核电站模型为仅包含13个单元和14个节点的简化一维梁模型。王桂萱等［16］在国内某软土地基上的核电厂房地震响应分析中，考虑了桩⁃土⁃结构动力相互作用，但其并未直接使用三维模型进行计算，而是通过简化为x⁃z，y⁃z两个平面模型进行拟三维分析。Luo等［17］采用罚函数法对核电站的非线性桩⁃土⁃结构动力相互作用进行了三维有限元数值模拟，比较了水平成层场地中有桩和无桩情况下核电结构的响应，其计算在LS⁃DYNA中进行，土体单元数目达1806508个，节点数目达1896478个，输入时长为40 s的地震波。

进行桩⁃土⁃结构相互作用数值模拟的关键在于建立合理的动力分析模型，但受制于桩⁃土⁃结构动力相互作用的复杂性，通常将地基模型或结构模型进行简化。Winkler地基模型将桩⁃土相互作用问题进行简化，但难以反映复杂地基情形。整体有限元法可考虑复杂地基情形，但计算量较大，效率较低。随着计算机技术和计算方法的快速发展，可以通过整体有限元方法分析桩⁃土⁃核电结构的地震响应，以避免简易方法的假设和参数不易确定等引起的误差。陈少林等［18⁃21］发展了一套土⁃结构相互作用分区分析（PASSI）方法，将结构和土体分区计算，各分区选用适合的分析方法，结构可采用隐式积分方法或模态叠加方法，土体采用显式积分方法。PASSI方法可以考虑土体的非线性和土体与基础间的接触非线性，人工边界可采用透射边界或者黏弹性边界，可考虑地震波斜入射，并且在每一时间步距，土体（基础）子域完成计算后，将基础位移传递给结构，当结构分析完成后，土体（基础）又接收来自结构的反作用力，这样就实现了不同子域之间的耦合和并行计算，具有较高的效率，已应用于AP1000的土⁃结构相互作用分析中。该方法可应用于桩基情形，桩⁃土体系应用显式积分格式，但由于桩的波速远大于土体，导致其满足稳定性要求的时间步距较小，若桩⁃土体系采用同一时间步距，必将导致土体子系统的计算量和计算时间显著增加。考虑桩⁃土体系中的桩节点数要远小于土节点数，若桩节点和土节点采用不同的时间步距，可以大大提高计算效率。

为解决上述问题，本文在水平成层软土场地条件下建立了桩⁃土⁃核电结构动力相互作用模型，在土⁃结构相互作用分区分析（PASSI）方法的基础上，实现了桩基和土体单元的异步计算，通过简单算例对提出的异步算法进行了验证。并进一步分析了核电结构在脉冲波和实际地震波输入下的响应及桩基受力情况。

1 分析方法

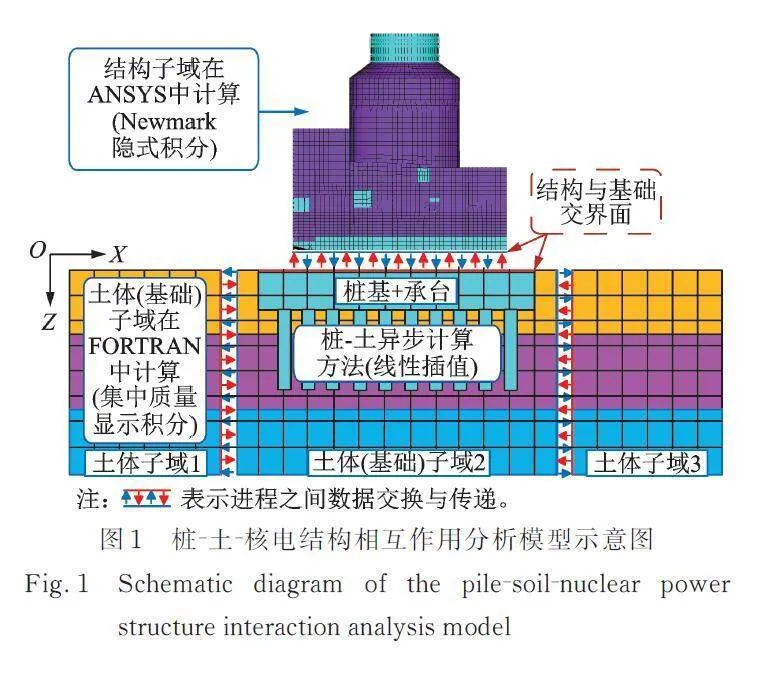
模型由地基土、群桩、承台及核电结构组成，如图1所示。上部核电结构的总高度约为86.50 m，最大平面尺寸为42.32 m×90.80 m。该模型包含32467个节点和35162个单元（包括质量单元Mass 21）。对于上部结构很难一次建立包括所有设备在内的所有模型，因此内部设备和管道采用壳单元（Shell 181）和质量单元（Mass 21）进行简化，屏蔽厂房主体采用壳单元建模，内部钢架采用梁单元（Beam 188）建模。

采用土⁃结构相互作用分区分析（PASSI）方法，根据计算地基（包括桩和土）节点位移响应所采用方法的不同，将地基节点分为3类：内节点（包含自由表面节点），与承台相接触的节点和人工边界节点。其中，与承台相接触的节点的运动，根据连续条件，由承台的运动所决定。在地基的侧边界和底边界设置黏弹性人工边界［22‑23］，采用集中质量有限元方法计算内节点和人工边界节点的运动，其公式为：

（1）

式中 为时间步距；，和分别为时刻节点i的加速度、速度和位移；为时刻节点i的位移；为时刻节点i的位移；为节点i的集中质量；N为所有与节点i相连的节点总数；和分别为节点i与其相邻节点j之间的刚度矩阵和阻尼矩阵；为p时刻作用于节点i的集中外荷载。

当计算内节点运动时，；当计算人工边界节点运动时，为作用在边界节点上的等效荷载，且方程（1）的计算考虑了人工边界节点的阻尼和弹簧系数。

桩⁃土节点采用集中质量显式有限元求解时（如公式（1）所示），其时间步距受稳定性条件限制，与介质波速成反比。因此桩节点的稳定时间步距要远小于土节点的稳定时间步距，且土节点数要远大于桩节点数，导致桩⁃土体系的计算效率因采用桩的计算时间步距而大大降低。因此，为提高计算效率，基于PASSI方法异步计算的思想，有必要对桩节点和土节点采用异步计算的方法，即桩和土体分别采用不同的时间步距。这里，假设土节点采用，桩节点采用，且。

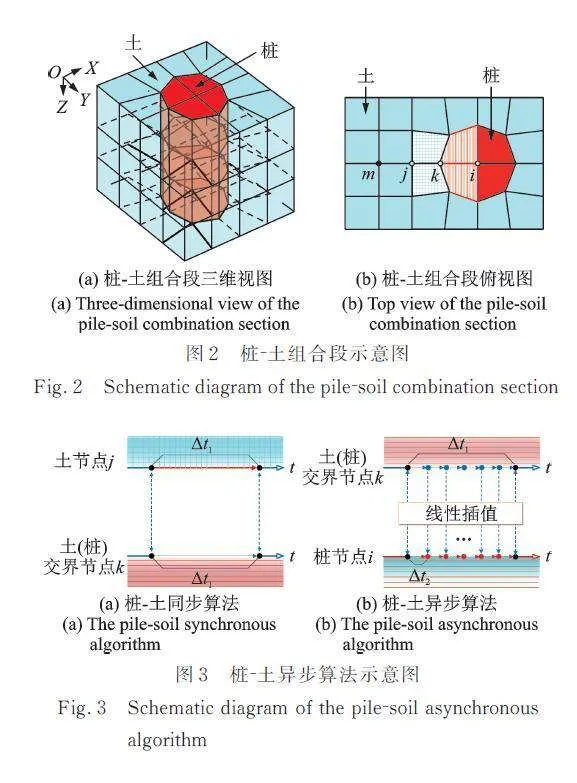
桩⁃土组合段示意图如图2所示，其中蓝色区域为土体单元，红色区域为桩基单元。桩节点（如i）和桩⁃土界面点（如k）按桩节点时间步距计算；土节点（如m和j）按土节点时间步距计算。在计算桩⁃土界面点i时，需用到相邻节点系（如图中画线阴影部分）的反应，首先土节点j和土（桩）交界节点k之间按步距进行计算，而土（桩）交界节点k按时间步距进行线性插值用于桩节点i的计算，如图3的桩⁃土异步算法示意图所示。

承台假设为刚性，其运动可以由3个平动分量和3个转动分量来描述。土体、桩基和结构作用在承台上的合力使承台产生刚体运动。

采用中心差分格式，承台在时刻的位移表示为：

（2）

式中 ，和分别为承台在，和时刻的位移；为承台的时间步距，与土体的相同；为承台的质量矩阵；为承台中心在时刻受到的来自土体、桩基和上部结构的作用力。

由刚性承台与土体和结构间的位移连续条件，土体、桩基和结构与承台相接触的节点的运动可表示为：

（3）

式中 为一几何转换矩阵，可以根据节点和承台质心的相对坐标求出。

由于计算承台响应的时间步距为土体的时间步距，所以，由公式（3）得到的与承台相连的桩节点响应，需要插值成以为时间步距的响应。

上部结构的运动方程可以表示为：

（4）

式中 ，和分别为质量矩阵、刚度矩阵和阻尼矩阵；F为外部激励；u为系统节点处的位移场。

采用Newmark隐式积分算法进行计算，其时间步距根据精度要求选取，可远大于土体的时间步距。

2 算例分析

2.1 方法验证

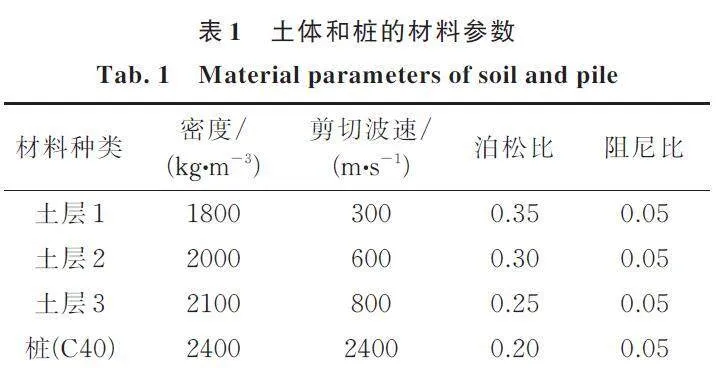
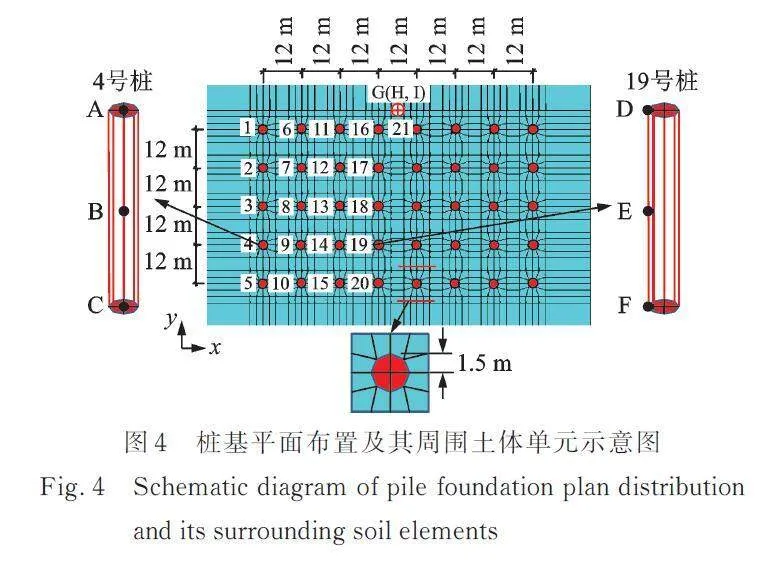
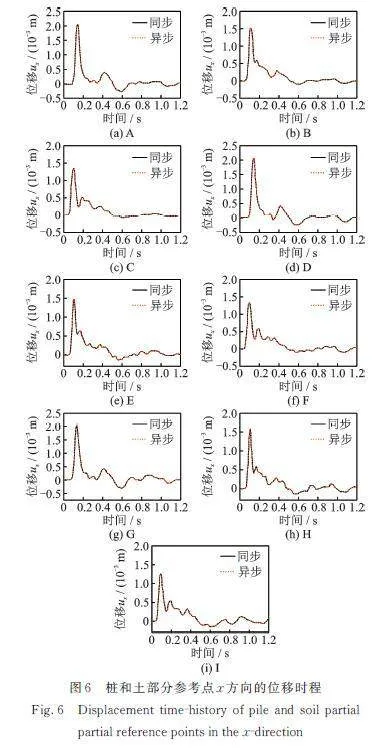
首先通过群桩的运动相互作用分析验证本文桩⁃土异步分析方法的精度和效率，分析模型如图1所示。土体为3层水平成层土，土体和桩的材料参数如表1所示。桩基分布如图6所示，共有40根圆桩，x方向8根，间距为12 m，y方向5根，间距12 m，圆桩直径均为3 m，长度均为20 m。刚性承台尺寸为92 m×60 m×10 m。

土体计算区域的尺寸为640 m×360 m×60 m（3层土，每层土厚20 m），将土体离散为2 m×2 m×2 m的六面体八节点实体单元，桩及周围土体的单元剖分如图4所示，图中蓝色区域为土体单元，红色区域为桩单元。单元总数为1728000个，节点总数为1801131个。场地和上部结构共4个进程进行并行计算。

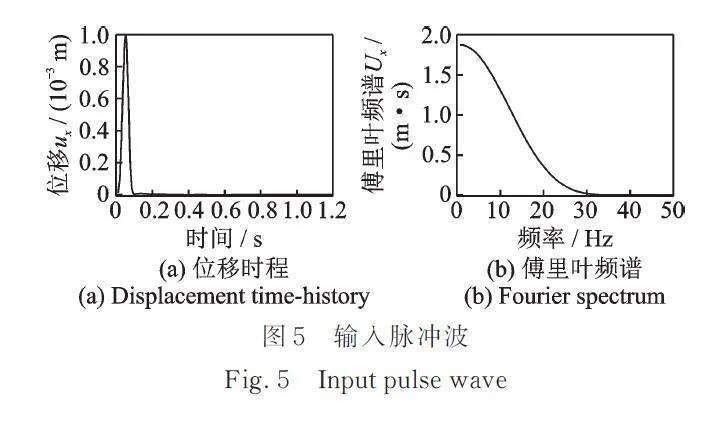
选取如图5所示的脉冲位移作为SV波由基岩表面垂直入射。计算总时长为1.2 s。对土体和群桩分别采用相同的时间步距（∆t1=∆t2=2×10-5 s）和不同的时间步距（∆t1=5∆t2=1×10-4 s）进行计算，以验证异步算法的准确性和有效性。

图6给出了桩和土部分参考点x方向的位移时程曲线。参考点位置如图4所示，其中，点A，B和C分别为4号桩顶部、中部和底部的中心点；点D，E和F分别为19号桩顶部、中部和底部的左侧点；点G，H和I分别为16号和21号桩之间土体10，20和30 m深度处的点。图6中实线为桩、土体采用相同的时间步距时的计算结果，虚线为桩、土体采用不同的时间步距时的计算结果，两者完全重合，验证了该方法的精度。当∆t1=∆t2=2×10-5 s时，此时桩与土体计算时间步距一致，同步计算，完成计算所需时间为10422 s（约174 min）；当∆t1=5∆t2=1×10-4 s时，桩与土体异步计算，完成计算所需时间为2097 s（约35 min），大概为相同步距时的1/5，计算效率大大提高。这是因为桩节点总数远小于土节点总数，在总的计算时间中占比很小，计算效率主要取决于土节点的计算量。

2.2 桩⁃土⁃核电结构相互作用分析

2.2.1 计算模型

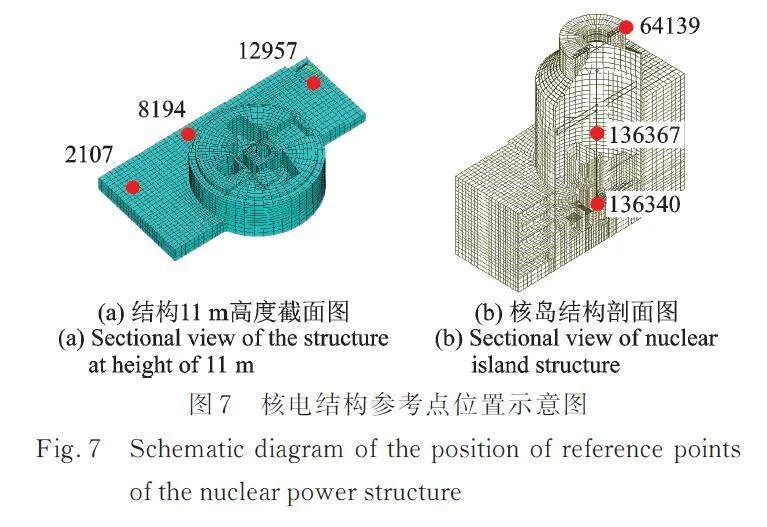
采用PASSI方法对AP1000核电结构进行桩⁃土⁃结构相互作用分析，地基和结构可独立建模。土体和桩基模型如图1所示，核电结构的总高度约为86.50 m，最大平面尺寸为42.32 m×90.80 m。该模型包含32467个节点和35162个单元（包括质量单元Mass 21）。图7为核电结构参考点位置示意图。

2.2.2 脉冲波输入情形

由于各桩的反应在定量上略有差异，但在定性上基本相同，因此以1号桩为例进行分析。图例中“土⁃结构相互作用”情形是指计算模型包括土体、桩基、承台和上部核电结构，包括运动相互作用和惯性相互作用；“运动相互作用”情形中，计算模型包含土体、桩基和无质量承台，但不包括上部结构。

以宽度为0.1 s，峰值为1×10-3 s的脉冲位移（如图5所示）作为SV波，垂直入射。计算总时长为1.2 s，土体计算时间步距为1×10-4 s，计算步数为12000；桩基计算时间步距为2×10-5 s，计算步数为60000；上部结构计算时间步距为0.0025 s，计算步数为480。

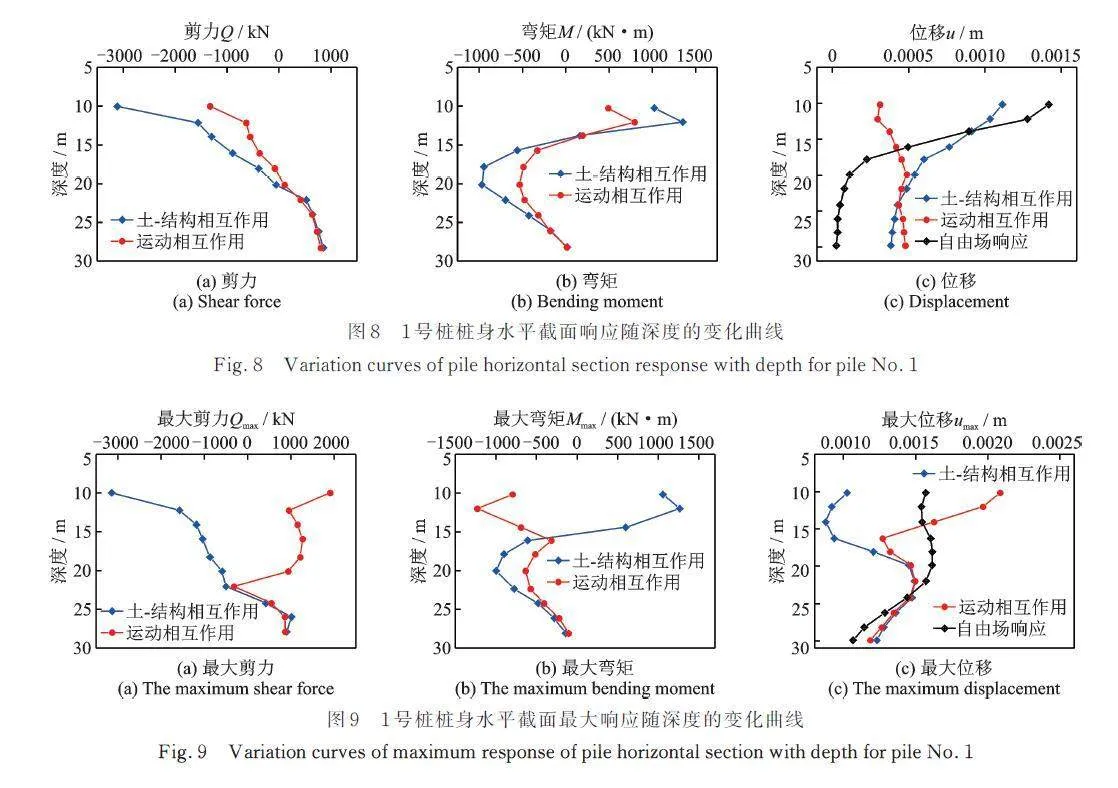
图8（a）和（b）为1号桩桩顶剪力和弯矩分别达到最大值时，桩身水平截面剪力和弯矩随深度的变化曲线；图8（c）为1号桩桩顶位移达到最大值时，桩身水平截面位移随深度的变化曲线。从图8（a）和（b）中可以看出，剪力在20 m深度以下，弯矩则在24 m深度以下，主要是由运动相互作用控制，也即惯性相互作用只能影响到地表以下一定的深度。在20 m深度左右，该处为软硬土层分层界面，自由场应变在该处不连续（如图8（c）所示），曲率无穷大，引起桩身在该处的曲率较大，导致此时弯矩为一极大值。而由桩的弯矩和剪力的关系可知，剪力在此处为零。

图9（a）和（b）为1号桩桩身水平截面最大剪力和最大弯矩随深度的变化曲线；图9（c）为该桩身水平截面最大位移随深度的变化曲线。同样地，在22 m深度以下，主要由运动相互作用控制。惯性相互作用与运动相互作用引起桩顶部剪力与弯矩反向。从图9（a）和（b）中可以看出，各桩的最大剪力和最大弯矩均位于桩顶。一方面，由于承台的约束，入射应力波遇到承台底面发生反射，剪力放大，因此仅考虑运动相互作用时，桩顶部的剪力也最大；另一方面，由于惯性相互作用，导致桩顶部的弯矩和剪力均较大，但与运动相互作用引起的剪力和弯矩反向。在土层分界面（20 m深度处）附近，弯矩有一极大值，而剪力较小，主要是由于运动相互作用引起的。

图10给出了1号桩顶部（Depth=10 m）、中部（Depth=20 m）和底部（Depth=28 m）的内力时程。对比可以发现，靠近承台的桩顶部位置，桩的剪力和弯矩都是最大的，而随着深度的增加，内力逐渐减小。同时，从图10（a）中可以看出，在桩顶部出现剪力与弯矩反向的情况。这也验证了上述图8和9中关于桩顶部最大剪力和最大弯矩的描述。

2.2.3 地震波输入情形

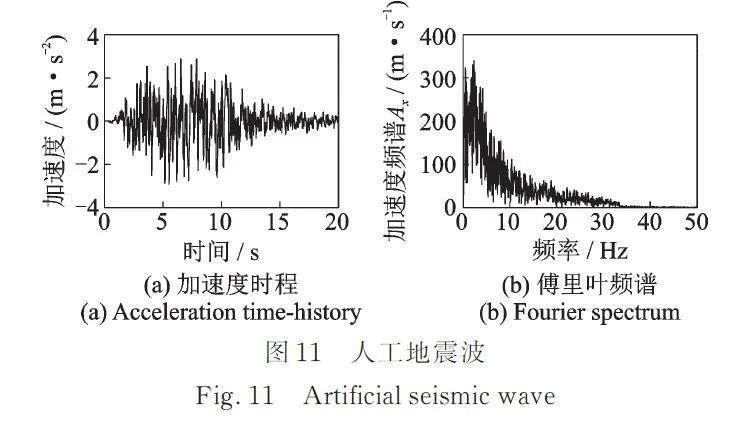
人工地震波（如图11所示）作为SV波由基岩表面垂直入射，峰值加速度为0.3g，总持续时长为20.48 s。桩基和土体采用异步算法，其中土体计算步距为1×10-4 s，步数为204800；桩基计算步距为2×10-5 s，步数为1024000；上部结构计算步距为0.0025 s，步数为8192。

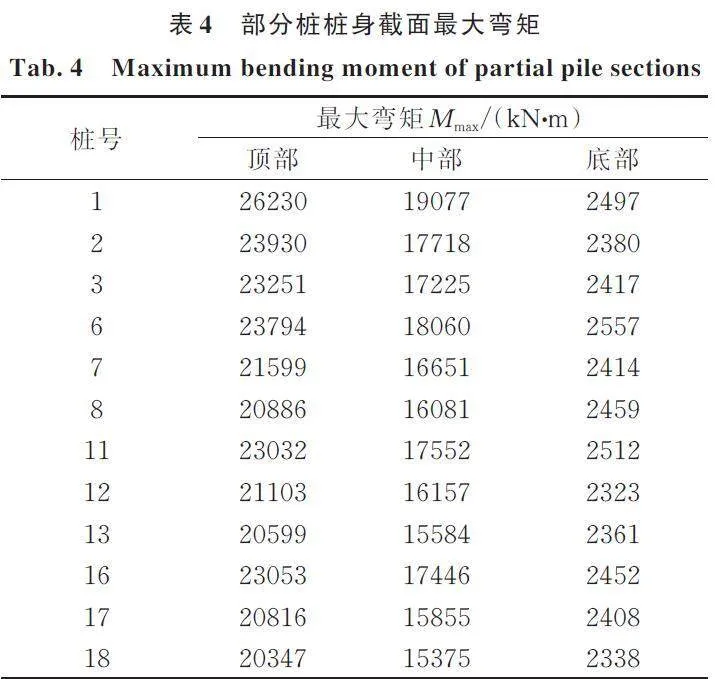
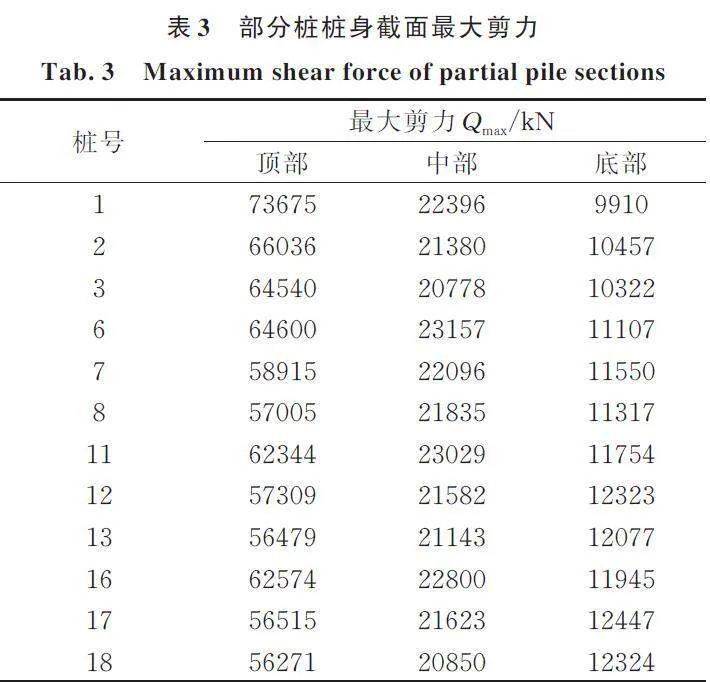
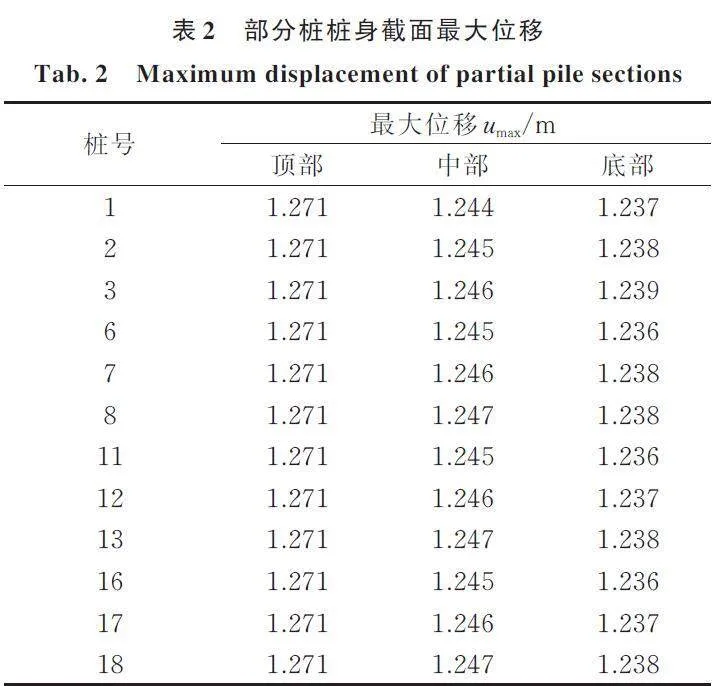
表2～4分别给出了部分桩桩身截面的最大位移、最大剪力和最大弯矩。图12（a）和（b）为1号桩桩身水平截面最大剪力和最大弯矩随深度的变化曲线；图12（c）为1号桩桩身水平截面最大位移随深度的变化曲线。与脉冲波情形相似，剪力在桩顶部最大，桩顶部附近和软硬土层界面附近弯矩较大。桩身最大位移值随深度变化较脉冲波情形平缓，可能是由于脉冲波频率较地震波高的原因。

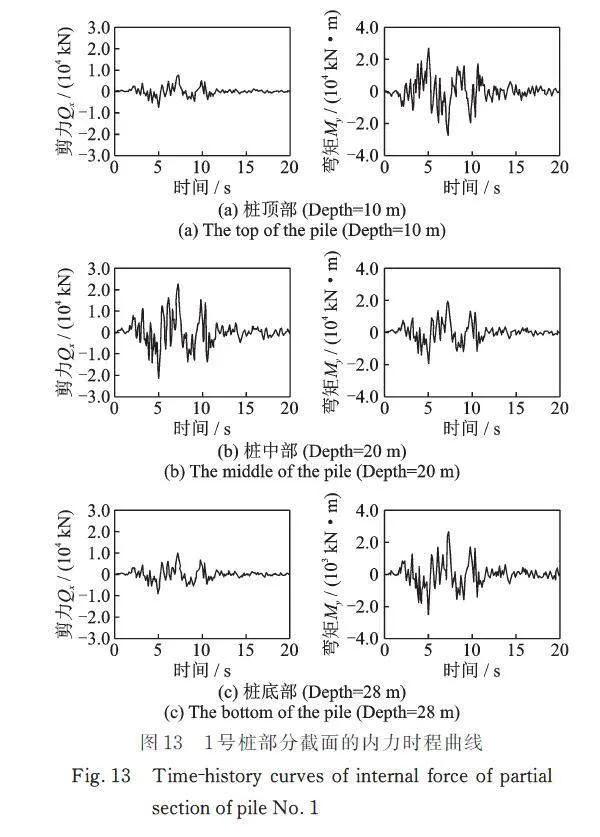
图13为1号桩顶部（Depth=10 m）、中部（Depth=20 m）和底部（Depth=28 m）的内力时程曲线。图13中地震波作用下的内力时程曲线与图10中脉冲响应下的内力时程曲线相比，发生了较大变化。由图13可以看出，桩身截面最大剪力出现在桩身中部位置，与图12（a）中桩身最大剪力随深度的变化曲线相吻合。由图13中桩身不同位置的弯矩变化曲线可以看出，最大弯矩出现在桩顶部和桩底部，桩中部较小，这与图12（b）中桩身最大弯矩随深度的变化曲线也基本相符。

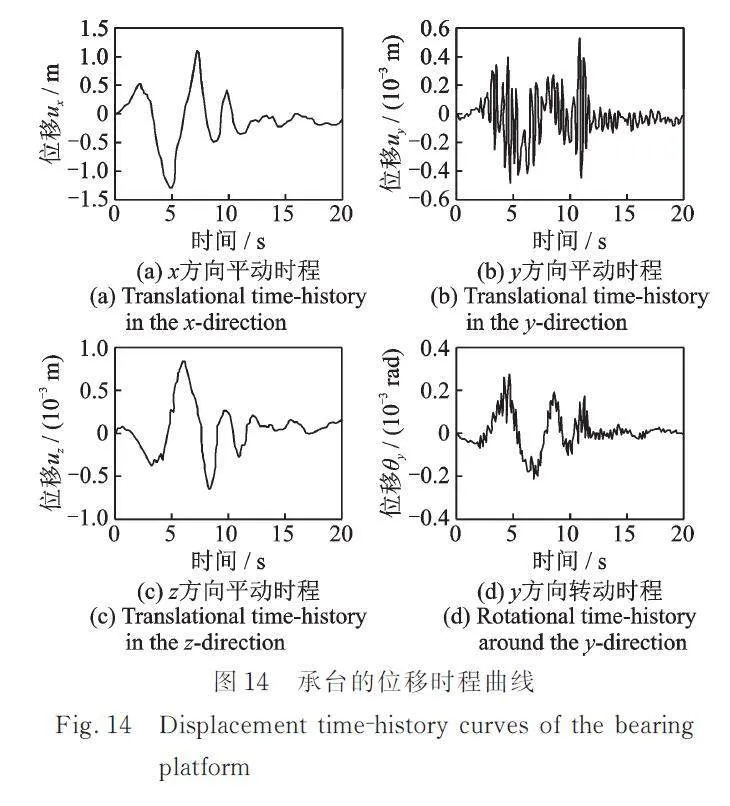
图14为承台的位移时程曲线。由于SV波垂直入射，以x方向反应为主。由图14可以看出，即使SV波垂直入射，也会引起承台的转动。虽然转动幅值较小，但由于核电结构较高，故基础的转动不可忽略。

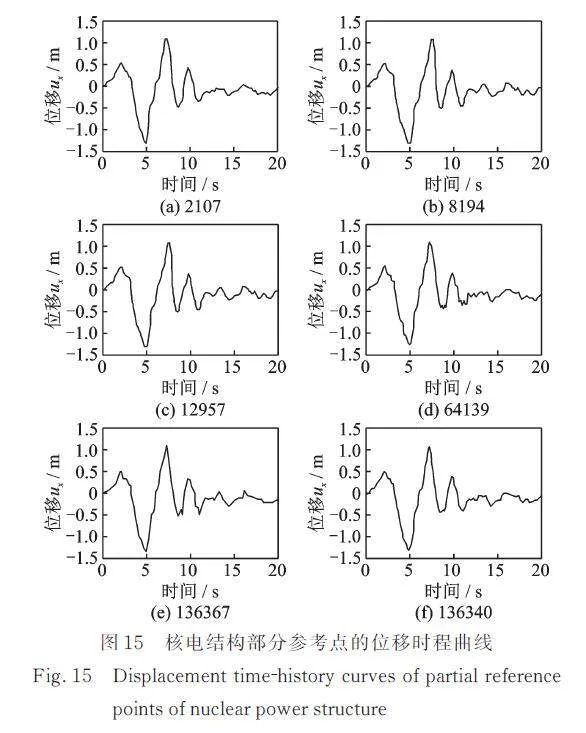
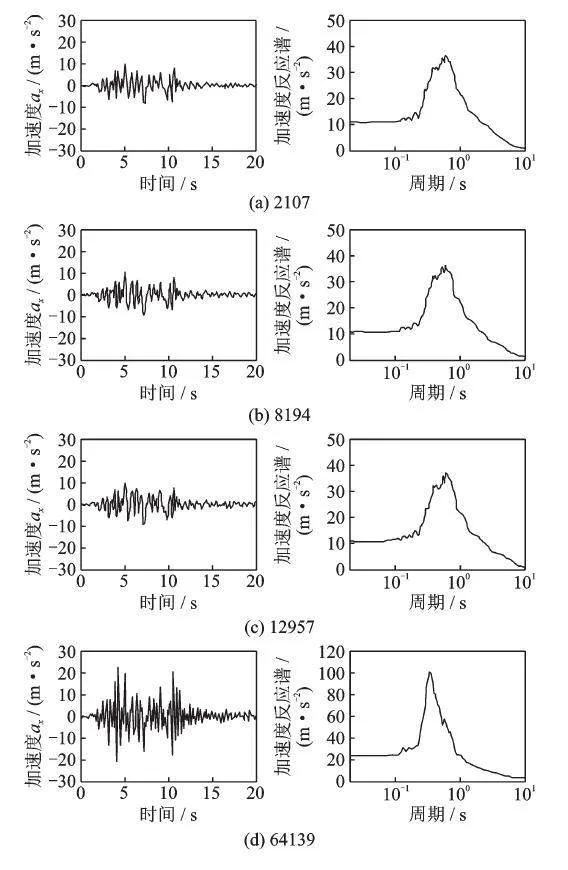
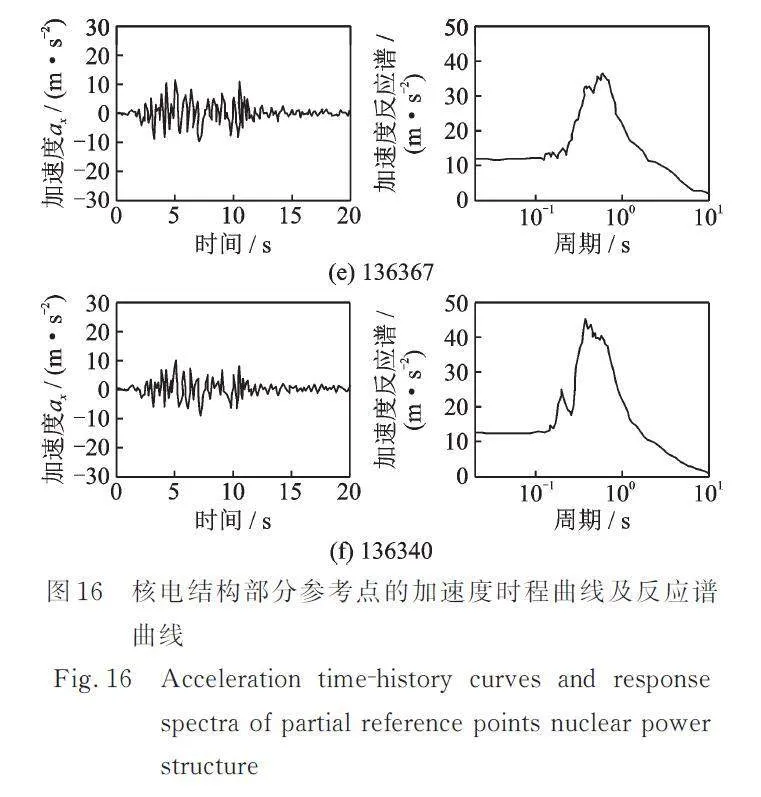
图15和16分别给出了核电结构部分参考点（位置如图7所示）的位移时程曲线和加速度时程曲线及反应谱。由于核电结构较刚，位移主要由低阶模态控制，因此各点的位移差异不大，而加速度和加速度反应谱差异较大。沿核电结构高程方向，加速度和加速度反应谱的响应逐渐增加，加速度反应谱的峰值频率也有所增加。因此，核电的最高点是整个结构响应的最值点，也是抗震设计的重点。结构各点的加速度时程及反应谱可为设备的抗震分析提供输入。

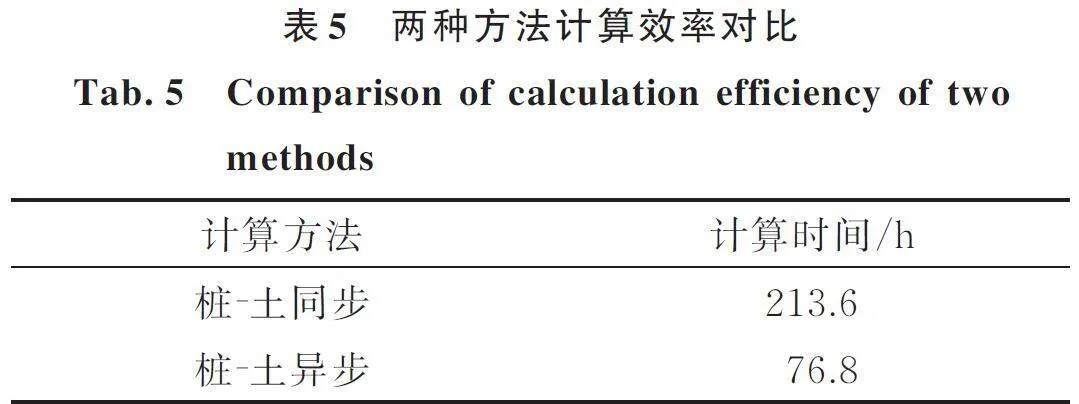
表5为在人工地震波作用下，两种方法计算效率的对比。由表5可以发现，采用桩⁃土异步算法可以极大地提高计算效率。

本文所有相关算例在DELL小型工作站上完成计算（处理器：英特尔酷睿i7；主频：3.40 GHz，内存：16 G）。

3 结 论

本文在土⁃结构相互作用分区分析（PASSI）方法的基础上，考虑桩⁃土⁃结构相互作用，通过对桩基、土体采用不同时间步距，避免土体与桩基因采用相同的时间步距而增加不必要的计算量。考虑到桩的自由度在桩⁃土体系的自由度总数中占比很小，这种异步算法中桩的计算量较小，可大大提高计算效率。本文通过简单算例验证了该异步算法的精度和效率，并采用桩⁃土异步算法对某软土场地上的桩基核电结构进行了三维桩⁃土⁃结构动力相互作用分析，探究了运动相互作用和惯性相互作用对桩基内力的影响，得到如下结论：

（1）桩顶附近一定深度范围内的剪力和弯矩主要由惯性相互作用控制，且由于惯性相互作用，桩顶的剪力和弯矩均较大；随着深度的增加，惯性相互作用的影响越来越小，在一定深度后，桩的剪力和弯矩主要由运动相互作用控制。

（2）在软硬土层界面附近，由于自由场位移曲率在该处突变，桩的弯矩为一极大值，相应的剪力较小，接近为零。

（3）在桩基设计时，应注意桩顶抗弯和抗剪验算，以及在软硬土层界面处桩的抗弯验算。

影响桩⁃土⁃结构动力相互作用的参数较多，进一步的参数分析需另外讨论。

参考文献：

［1］ Makris N， Gazetas G， Delis E. Dynamic soil-pile-foundation structure interaction： records and predictions［J］. Geotechnique， 1996， 46（1）： 33-50.

［2］ Mylonakis G， Nikolaou A， Gazetas G. Soil-pile-bridge seismic interaction： kinematic and inertial effects. Part Ⅰ： soft soil［J］. Earthquake Engineering & Structural Dynamics， 1997， 26（3）： 337-359.

［3］ Guin J， Banerjee P K. Coupled soil-pile-structure interaction analysis under seismic excitation［J］. Journal of Structural Engineering， 1998， 124（4）： 434-444.

［4］ Hussien M N， Iai S， Karray M. Analysis of characteristic frequencies of coupled soil-pile-structure system［J］. International Journal of Geomechanics， 2018， 18（6）： 04018047.

［5］ Shintaro Y， Toyoaki N. Lateral cyclic response of piles in viscoelastic Winkler subgrade［J］. Journal of Engineering Mechanics， ASCE， 1994， 120（4）： 758-775.

［6］ Finn W D L. A study of piles during earthquakes： issues of design and analysis［J］. Bulletin of Earthquake Engineering， 2005， 3（2）： 141-234.

［7］ Allotey N， El Naggar M H. Generalized dynamic Winkler model for nonlinear soil-structure interaction analysis［J］. Canadian Geotechnical Journal， 2008， 45（4）： 560-573.

［8］ Castelli F， Maugeri M. Simplified approach for the seismic response of a pile foundation［J］. Journal of Geotechnical and Geoenvironmental Engineering， 2009， 135（10）： 1440-1451.

［9］ Carbonari S， Dezi F， Leoni G. Seismic soil-structure interaction in multi-span bridges： application to a railway bridge［J］. Earthquake Engineering & Structural Dynamics， 2011， 40（11）： 1219-1239.

［10］ Maheshwari B K， Emani P K. Three-dimensional nonlinear seismic analysis of pile groups using FE-CIFECM coupling in a hybrid domain and HISS plasticity model［J］. International Journal of Geomechanics， 2015， 15（3）： 04014055.

［11］ Boulanger R W， Curras C J， Kutter B L， et al. Seismic soil-pile-structure interaction experiments and analyses［J］. Journal of Geotechnical and Geoenvironmental Engineering， 1999， 125（9）： 750-759.

［12］ Kojima K， Fujita K， Takewaki I. Unified analysis of kinematic and inertial earthquake pile responses via the single-input response spectrum method［J］. Soil Dynamics and Earthquake Engineering， 2014， 63： 36-55.

［13］ Won J， Ahn S Y， Jeong S， et al. Nonlinear three-dimensional analysis of pile group supported columns considering pile cap flexibility［J］. Computers and Geotechnics， 2006，33： 355-370.

［14］ Kavvads M， Gazetas G. Kinematic seismic response and bending of free-head piles in layered soil［J］. Geotechnique， 1993， 43（2）： 207-222.

［15］ Sayed M A， Kim D， Cho S G. Seismic analysis of base isolated nuclear power plant considering nonlinear pile-soil interaction［C］. 22nd Conference on Structural Mechanics in Reactor Technology. San Francisco， California， USA： Transactions， 2013.

［16］ 王桂萱， 张睿， 赵杰. 某沿海软土地区核电厂核岛天然地基及桩基抗震承载力分析［J］. 地震研究， 2016， 39（1）： 15-21.

WANG Guixuan， ZHANG Rui， ZHAO Jie. Analysis on seismic bearing capacity of natural and pile foundations about a coastal nuclear power plant in soft ground［J］. Journal of Seismological Research， 2016， 39（1）： 15-21.

［17］ Luo Chuan， Yang Xun， Zhan Changbao， et al. Nonlinear 3D finite element analysis of soil-pile-structure interaction system subjected to horizontal earthquake excitation［J］. Soil Dynamics and Earthquake Engineering， 2016， 84： 145-156.

［18］ 陈少林， 唐敢， 刘启方， 等. 三维土-结构动力相互作用的一种时域直接分析方法［J］. 地震工程与工程振动， 2010， 30（2）： 24-31.

Chen Shaolin， Tang Gan， Liu Qifang， et al. A direct time-domain method for analysis of three-dimensional soil-structure dynamic interaction［J］. Journal of Earthquake Engineering and Engineering Vibration， 2010， 30（2）： 24-31.

［19］ 陈少林， 赵宇昕. 一种三维饱和土-基础-结构动力相互作用分析方法［J］. 力学学报， 2016， 48（6）： 1362-1371.

Chen Shaolin， Zhao Yuxin. A method for three-dimensional saturated soil-foundation-structure dynamic interaction analysis［J］. Chinese Journal of Theoretical and Applied Mechanics， 2016， 48（6）： 1362-1371.

［20］ 陈少林， 王俊泉， 刘启方， 等. 基于显-隐式格式的三维时域土-结相互作用分析的异步并行算法［J］. 中国科学： 技术科学， 2017， 47（12）： 1321-1330.

Chen Shaolin， Wang Junquan， Liu Qifang， et al. Asynchronous parallel algorithm for three-dimensional soil-structure interaction analysis based on explicit-implicit integration scheme［J］. Scientia Sinica Technologica， 2017， 47（12）： 1321-1330.

［21］ Chen S L， Lü H， Zhou G L. Partitioned analysis of soil-structure interaction for nuclear island building［J］. Earthquake Engineering & Structural Dynamics， 2022， 51（10）： 2220-2247.

［22］ 刘晶波， 李彬. 三维黏弹性静-动力统一人工边界［J］. 中国科学E辑： 工程科学 材料科学， 2005， 35（9）： 966-980.

Liu Jingbo， Li Bin. 3D viscoelastic static-dynamic unified artificial boundary［J］. Scientia Sinica Series E： Engineering Science and Materials Science， 2005， 35（9）： 966-980.

［23］ 谷音， 刘晶波， 杜义欣. 三维一致粘弹性人工边界及等效粘弹性边界单元［J］. 工程力学， 2007， 24（12）： 31-37.

Gu Yin， Liu Jingbo， Du Yixin. 3D consistent viscous-spring artificial boundary and viscous-spring boundary element［J］. Engineering Mechanics， 2007， 24（12）： 31-37.

Asynchronous analysis method for pile-soil-nuclear power structure interaction under seismic action

LÜ Hao1，2， CHEN Shao-lin1，2， LU Xin-yu3， SUN Xiao-ying3，4

（1. Department of Structural Engineering and Mechanics， College of Aerospace Engineering，Nanjing University of Aeronautics and Astronautics， Nanjing 210016， China； 2. Department of Civil and Airport Engineering，College of Civil Aviation， Nanjing University of Aeronautics and Astronautics， Nanjing 211106， China；3. Institute of Engineering Mechanics， China Earthquake Administration， Harbin 150080， China；4. China Nuclear Power Engineering Co.， Ltd.， Beijing 100840， China）

Abstract： To broaden the site selection for nuclear power plants， it is vital to assess the seismic safety of nuclear power structures in non-rock sites with pile foundations. Current pile-soil-structure interaction analysis methods， such as the Winkler foundation model and the p-y method， simplify the interaction problem and struggle to reflect complex foundation situations. While the integral finite element method can consider complex foundation situations， it is computationally intensive and inefficient. This paper introduces an efficient three-dimensional time-domain method， Partitioned Analysis of Soil-Structure Interaction （PASSI）， which uses different time steps for pile foundation and soil to avoid unnecessary calculations. A three-dimensional finite element model of the pile-soil-nuclear power structure interaction is established， with the AP1000 nuclear island structure as the research object. The effectiveness of this asynchronous algorithm is verified by inputting pulse waves， and the characteristics of the maximum shear force and bending moment of the pile are analyzed by combining the kinematic and inertial interactions. The response of the pile-soil-nuclear power structure under the seismic wave input is then analyzed. Since the degrees of freedom of the pile are insignificant compared to the soil， the additional computational volume of the pile can be neglected when using the pile-soil asynchronous algorithm. This efficient method is expected to be used in the analysis of the dynamic interaction of large nuclear power structures with pile-soil-structures.

Key words： pile-soil-structure interaction； partitioned analysis method of soil-structure interaction； kinematic interactions； asynchronous algorithm； seismic design for nuclear power

作者简介： 吕 昊（1988―），男，博士研究生。E-mail： lvhao_happy@sina.com。

通讯作者： 陈少林（1974―），男，博士，教授。E-mail： iemcsl@nuaa.edu.cn。