质心动态路径规划的变转速齿轮箱时频脊线索引算法

摘要： 针对强噪声下难以估计信号瞬时频率的问题，提出了基于质心动态路径规划（DPPB）的变转速齿轮箱时频脊线索引算法。该算法在剖析多路径匹配追踪（MMP）脊线索引算法及其在强噪声下失效原因的基础上，通过对MMP算法得到的脊线集加窗求质心，构建信号的脊线质心稀疏矩阵，并针对质心稀疏矩阵设计动态路径规划函数索引脊线上的质心点，根据脊线代价函数值计算最优时频脊线。将相似度系数Ra和置信度σRa作为脊线提取效果的衡量指标，通过仿真和试验验证了DPPB算法可有效提取强噪声信号的时频脊线，且不同程度噪声下的可靠性和鲁棒性均优于峰值索引算法和MMP脊线索引算法。

关键词： 故障诊断； 齿轮箱； 质心动态路径规划（DPPB）； 时频脊线索引； 多路径匹配追踪（MMP）； 时频分析

中图分类号： TH165+.3； TH132.41 文献标志码： A 文章编号： 1004-4523（2024）06-1077-12

DOI：10.16385/j.cnki.issn.1004-4523.2024.06.018

引 言

齿轮箱在变转速工况下会产生与转速相关的非平稳振动信号，使用传统的平稳信号分析方法难以诊断齿轮箱故障［1］。瞬时转速不仅是反映齿轮箱运行状态的重要参数，也是阶次跟踪算法、广义解调分析等非平稳信号分析方法的必需参量［2‑4］。所以准确获得变转速齿轮箱瞬时转速对齿轮箱健康状态监测和故障诊断具有重要意义。

利用高精度转速测量设备可获得振动信号对应的转速，但是由于实际工作环境的制约，大部分齿轮箱不具备安装转速测量设备的条件。齿轮箱振动信号中的特征频率通常与转速相关，所以通过估计瞬时频率（Instantaneous Frequency，IF）可达到求取瞬时转速的目的［5］。郭瑜等［6］针对变转速旋转机械，利用峰值索引算法在振动信号时频分布中获得一阶转速对应的IF时频脊线，实现了无转速计条件下估计振动信号的转频信息。峰值索引算法计算简单但对噪声较为敏感，在实际工程中往往难以得到满足要求的时频曲线。为了提高估计算法对噪声的鲁棒性， latsenko等［7］以频率平均值和标准差构造自适应代价函数代替时频峰值进行脊线索引，引入跳频惩罚保证脊线的连续性，一定程度上降低了噪声对脊线索引的影响。江星星等［8］提出了一种双向搜索时频脊融合算法，运用代价函数脊线索引方法从正反两个方希搜索同一IF分量的时频脊线，通过脊线融合算法合并最优脊线段从而消除噪声引起的局部误差。Ding等［9］则根据轴承振动信号的频率特征，运用概率密度函数将基频与其对应的倍频进行融合，从而达到修正时频脊线、提高转速估计精度的目的。由于受到Heisenberg不确定原理的影响，时频分布中频率发散、多分量频率信号混叠等现象严重影响时频脊线的索引结果。张炎等［10］运用同步压缩小波变换（Synchrosqueezing Wavelet Transform，SWT）对轴承振动信号的包络谱进行时频重排，通过提高时频包络谱的分辨率和聚集性，减小频谱发散对脊线提取的影响，从而准确提取轴承的特征频率曲线。上述算法一定程度上提高了时频脊线索引的精度，但对索引初始点的依赖性很高，若选择错误的索引初始点便无法提取正确的时频脊线。多路径匹配追踪（Multipath Matching Pursuit，MMP）［11］通过建立基于树的路径搜索模型，运用贪心算法搜寻最优路径，降低初始搜索点选择对搜索结果的影响。相继有学者利用同步压缩变换（Synchro‑Squeezing Transform， SST）［12］、Multisynchro‑squeezing Transform（MSST）［13］、同步提取变换（Synchro‑Extracting Transform，SET）［14］、Synchro‑Reassigning Transform（SRT）［15］算法获得变转速齿轮箱振动信号的重排时频分布，运用MMP算法提取到了较为准确的瞬时频率。然而对于强噪声信号，重排时频分布会出现大量噪声分量，MMP算法在干扰下依然难以识别正确的时频脊线。

目前脊线索引算法均是以时频分布上的离散时频点作为索引对象，强噪声产生的局部幅值极值会对脊线索引造成很强的干扰；同时现有算法将局部最优点的集合作为最终的脊线，所以其结果不一定满足全局最优。针对现有算法的不足，本文提出一种质心动态路径规划（Dynamic Path Planning for Barycenter， DPPB）时频脊线索引算法。算法在MMP算法的基础上构建脊线质心稀疏矩阵，将索引的对象由时频离散点转换为质心点，减少噪声对脊线索引的干扰并降低时频分布的维度；运用动态路径规划算法索引时频脊线，尽可能使索引结果达到全局最优。

1 MMP脊线索引算法

1.1 MMP算法原理及实现

对于信号，窗函数，通过滑动窗口可得到不同时间段信号的频谱图，从而获得信号的时频分布如下式所示：

（1）

式中 和表示时间；表示频率；表示g的共轭。

根据时频曲线附近局部能量突出且具有一定连续性的特点，建立最优脊线路径代价函数［16］：

（2）

式中 表示幅值对代价函数的权重系数；表示第k阶导数对代价函数的权重系数；k为求导阶数。

对式（2）进行离散变换，忽略高阶项的影响，同时设置脊线搜索频率半径为，得到如下式所示的脊线索引代价函数：

（3）

式中 为权重系数，用于确定幅值（时频分布）和频率变化量对代价函数的贡献率。由于噪声的影响，时频分布中可能出现噪声时频点幅值高于脊线上的幅值，若索引初始点落在噪声点上则无法索引到正确脊线。

MMP脊线索引算法通过选择多个索引初始点的方法消除索引结果过于依赖初始点的问题。对于时频分布构建基于树的脊线索引模型，选取n个起始点作为路径搜索树的支集起点，以代价函数C更新支集原子，通过贪心算法搜索每个支集上的原子，得到个支集作为时频脊线，然后根据下式确定最优时频脊线：

（4）

式中 为离散信号总长度。

MMP脊线索引算法具体步骤如下：

（1） 对于时频矩阵，取个索引初始点将时间平均分为n段，每一段的时间间隔为，每个初始点对应的时刻为，初始化；

（2） 令，找到第个初始时刻的最大幅值点作为脊线搜索的起始点；

（3） 正向搜索：令，根据式（3）以半径搜索处的脊线点；

（4） 重复步骤（3），直到停止迭代，；

（5） 负向搜索：令，根据式（3）以半径搜索处的脊线所在位置，；

（6） 重复步骤（5） ，直到停止迭代，得到时频脊线；

（7） 重复步骤（2）～（6） ，直到停止迭代；根据式（4）得到最终的脊线。

1.2 强噪声下MMP算法失效机理分析

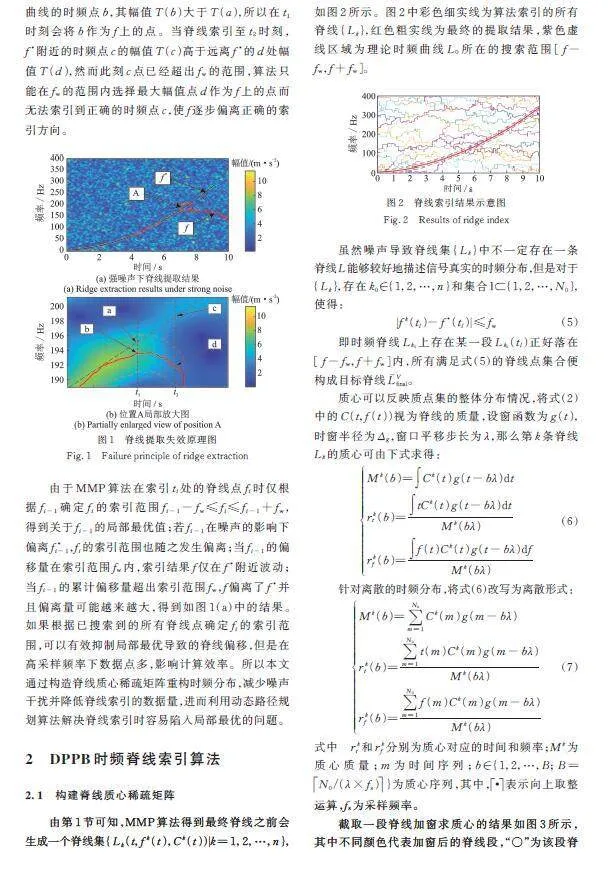
图1（a）为信噪比为-10 dB的强噪声下利用MMP算法得到的时频脊线，其中黑色虚线代表理论时频曲线，红色实线为MMP算法提取的结果。从图1（a）中可以看出，时间在0～7.5 s时与基本重合，提取效果较好；在7.5 s时与发生偏离，然后便沿着偏离后的结果继续搜寻，致使7.5 s后未能提取到有效的时频脊线。

图1（b）为图1（a）中位置A的局部放大图，红色虚线表示式（3）中的搜索频率半径。在时刻，时频点a虽然在附近，但在噪声的影响下幅值并不是搜索半径内的最大值，存在一个远离理论曲线的时频点b，其幅值大于，所以在时刻会将b作为上的点。当脊线索引至时刻，附近的时频点c的幅值高于远离的d处幅值，然而此刻c点已经超出的范围，算法只能在的范围内选择最大幅值点d作为f上的点而无法索引到正确的时频点c，使逐步偏离正确的索引方向。

由于MMP算法在索引处的脊线点时仅根据确定的索引范围，得到关于的局部最优值；若在噪声的影响下偏离，的索引范围也随之发生偏离；当的偏移量在索引范围内，索引结果仅在附近波动；当的累计偏移量超出索引范围，偏离了并且偏离量可能越来越大，得到如图1（a）中的结果。如果根据已搜索到的所有脊线点确定的索引范围，可以有效抑制局部最优导致的脊线偏移，但是在高采样频率下数据点多，影响计算效率。所以本文通过构造脊线质心稀疏矩阵重构时频分布，减少噪声干扰并降低脊线索引的数据量，进而利用动态路径规划算法解决脊线索引时容易陷入局部最优的问题。

2 DPPB时频脊线索引算法

2.1 构建脊线质心稀疏矩阵

由第1节可知，MMP算法得到最终脊线之前会生成一个脊线集，如图2所示。图2中彩色细实线为算法索引的所有脊线，红色粗实线为最终的提取结果，紫色虚线区域为理论时频曲线所在的搜索范围。

虽然噪声导致脊线集中不一定存在一条脊线能够较好地描述信号真实的时频分布，但是对于，存在和集合，使得：

（5）

即时频脊线上存在某一段正好落在内，所有满足式（5）的脊线点集合便构成目标脊线。

质心可以反映质点集的整体分布情况，将式（2）中的视为脊线的质量，设窗函数为，时窗半径为，窗口平移步长为λ，那么第k条脊线的质心可由下式求得：

（6）

针对离散的时频分布，将式（6）改写为离散形式：

（7）

式中 和分别为质心对应的时间和频率；为质心质量；m为时间序列；为质心序列，其中，表示向上取整运算，为采样频率。

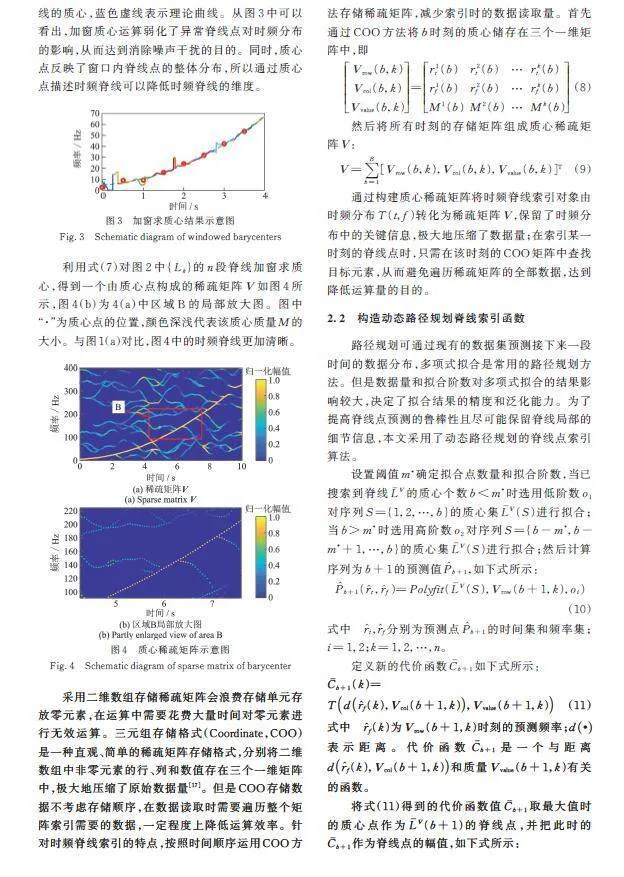
截取一段脊线加窗求质心的结果如图3所示，其中不同颜色代表加窗后的脊线段，“○”为该段脊线的质心，蓝色虚线表示理论曲线。从图3中可以看出，加窗质心运算弱化了异常脊线点对时频分布的影响，从而达到消除噪声干扰的目的。同时，质心点反映了窗口内脊线点的整体分布，所以通过质心点描述时频脊线可以降低时频脊线的维度。

利用式（7）对图2中的n段脊线加窗求质心，得到一个由质心点构成的稀疏矩阵V如图4所示，图4（b）为4（a）中区域B的局部放大图。图中“·”为质心点的位置，颜色深浅代表该质心质量的大小。与图1（a）对比，图4中的时频脊线更加清晰。

采用二维数组存储稀疏矩阵会浪费存储单元存放零元素，在运算中需要花费大量时间对零元素进行无效运算。三元组存储格式（Coordinate，COO）是一种直观、简单的稀疏矩阵存储格式，分别将二维数组中非零元素的行、列和数值存在三个一维矩阵中，极大地压缩了原始数据量［17］。但是COO存储数据不考虑存储顺序，在数据读取时需要遍历整个矩阵索引需要的数据，一定程度上降低运算效率。针对时频脊线索引的特点，按照时间顺序运用COO方法存储稀疏矩阵，减少索引时的数据读取量。首先通过COO方法将b时刻的质心储存在三个一维矩阵中，即

（8）

然后将所有时刻的存储矩阵组成质心稀疏矩阵V：

（9）

通过构建质心稀疏矩阵将时频脊线索引对象由时频分布转化为稀疏矩阵V，保留了时频分布中的关键信息，极大地压缩了数据量；在索引某一时刻的脊线点时，只需在该时刻的COO矩阵中查找目标元素，从而避免遍历稀疏矩阵的全部数据，达到降低运算量的目的。

2.2 构造动态路径规划脊线索引函数

路径规划可通过现有的数据集预测接下来一段时间的数据分布，多项式拟合是常用的路径规划方法。但是数据量和拟合阶数对多项式拟合的结果影响较大，决定了拟合结果的精度和泛化能力。为了提高脊线点预测的鲁棒性且尽可能保留脊线局部的细节信息，本文采用了动态路径规划的脊线点索引算法。

设置阈值确定拟合点数量和拟合阶数，当已搜索到脊线的质心个数时选用低阶数对序列的质心集进行拟合；当时选用高阶数对序列的质心集进行拟合；然后计算序列为的预测值，如下式所示：

（10）

式中 ，分别为预测点的时间集和频率集；；。

定义新的代价函数如下式所示：

（11）

式中 为时刻的预测频率；表示距离。代价函数是一个与距离和质量有关的函数。

将式（11）得到的代价函数值取最大值时的质心点作为的脊线点，并把此时的作为脊线点的幅值，如下式所示：

（12）

将每条脊线各点的幅值合作为脊线的判别参数，选择最大幅值合的脊线作为最终脊线，如下式所示：

（13）

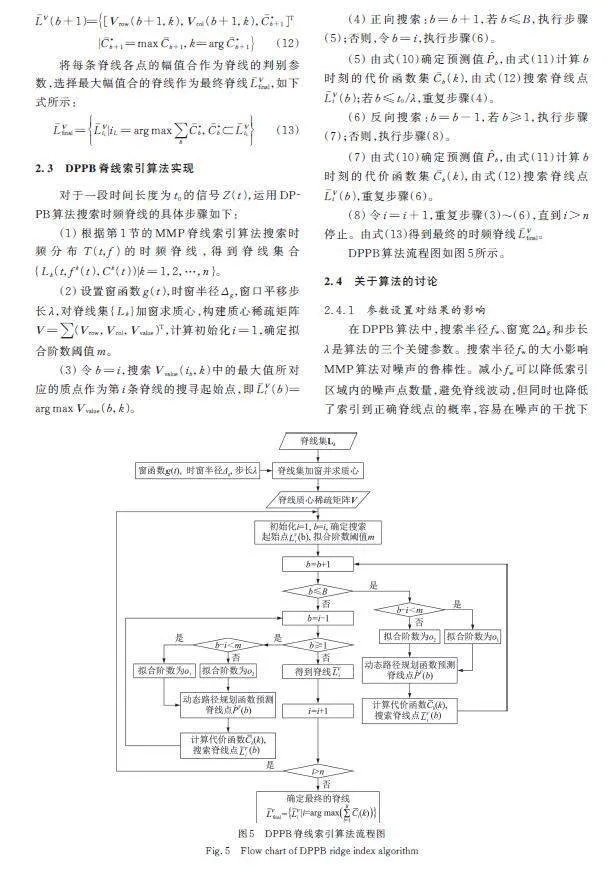
2.3 DPPB脊线索引算法实现

对于一段时间长度为的信号，运用DPPB算法搜索时频脊线的具体步骤如下：

（1） 根据第1节的MMP脊线索引算法搜索时频分布的时频脊线，得到脊线集合。

（2） 设置窗函数，时窗半径，窗口平移步长λ，对脊线集加窗求质心，构建质心稀疏矩阵，计算初始化，确定拟合阶数阈值m。

（3） 令，搜索中的最大值所对应的质点作为第i条脊线的搜寻起始点，即。

（4） 正向搜索：，若，执行步骤（5）；否则，令，执行步骤（6）。

（5） 由式（10）确定预测值，由式（11）计算时刻的代价函数集，由式（12）搜索脊线点；若，重复步骤（4）。

（6） 反向搜索：，若，执行步骤（7）；否则，执行步骤（8）。

（7） 由式（10）确定预测值，由式（11）计算时刻的代价函数集，由式（12）搜索脊线点，重复步骤（6）。

（8） 令，重复步骤（3）～（6），直到停止。由式（13）得到最终的时频脊线。

DPPB算法流程图如图5所示。

2.4 关于算法的讨论

2.4.1 参数设置对结果的影响

在DPPB算法中，搜索半径、窗宽和步长是算法的三个关键参数。搜索半径的大小影响MMP算法对噪声的鲁棒性。减小可以降低索引区域内的噪声点数量，避免脊线波动，但同时也降低了索引到正确脊线点的概率，容易在噪声的干扰下偏离正确索引路径；增大可以增加索引到正确脊线点的概率，当索引路径偏离理论脊线时有更大的机会重新返回正确的索引路径，但是也增加了噪声点的数量，容易使提取结果产生波动。加窗求质心的目的是降低噪声对脊线提取的干扰，使质心点能够准确描述理论脊线。窗口大小和步长会影响质心计算的准确性、抗噪声干扰能力和复杂度。随着增大，质心计算的抗噪声干扰能力增强，而准确性则先增高后降低；增大时，质心计算的准确性提高，但是提升效果会随的减小而降低。同时，和影响算法的复杂度，增大和会增加运算量。

目前尚未有合适的理论确定数据的最优搜索半径、窗宽和步长，本文仅根据经验和试验分析获得各参数的较优取值范围。对于，一般取10～35 Hz效果较好。对于，如果待提取的脊线变化较为剧烈，通常选择0.1～0.5 s的较小窗口；如果变化较为缓慢，通常选择0.5～1 s的较大窗口。对于，原则上越小越好，但是考虑到运算量，一般选择。

2.4.2 算法的计算成本

本文所提算法的计算成本主要包括MMP索引、质心求解和动态路径规划三部分。若信号时频分布的数据量为×，为离散信号总长度，为频率维度，算法的计算成本可以表示为：

（14）

式中 ，，和分别为算法总成本、MMP索引成本、质心计算成本和动态路径规划成本；为脊线段的数量；为个点的多项式拟合计算成本。

所提算法以较高的计算成本来换取较好的提取性能，所以计算成本较大。特别注意的是，的系数对计算成本产生较大的影响，所以在保证索引精度的前提下，合理减小和、增大可以有效降低算法的计算成本。

3 仿真分析

3.1 构建仿真模型

设仿真信号x及瞬时频率曲线f如下式所示：

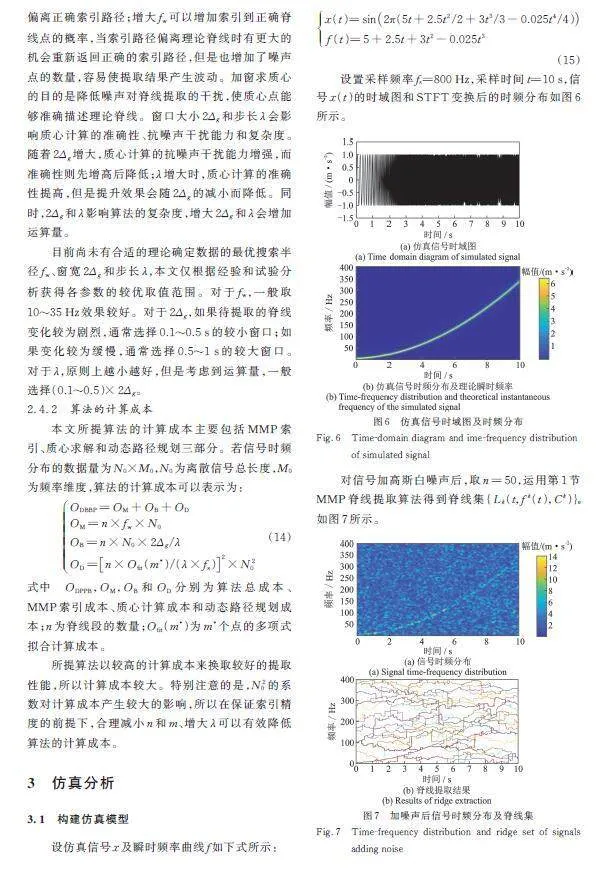
（15）

设置采样频率fs=800 Hz，采样时间t=10 s，信号的时域图和STFT变换后的时频分布如图6所示。

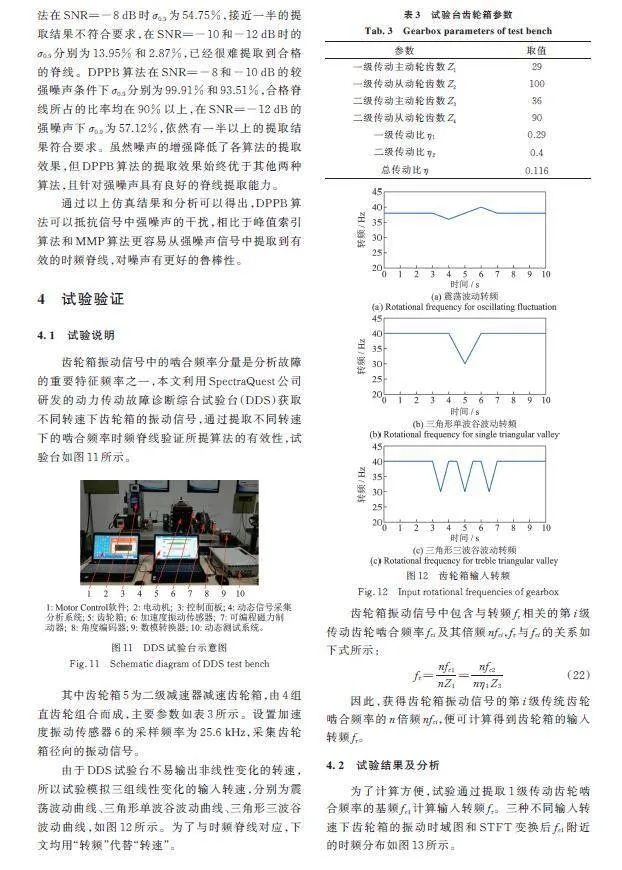
对信号加高斯白噪声后，取，运用第1节MMP脊线提取算法得到脊线集如图7所示。

由式（7）构建质心稀疏矩阵V，其中总采样点数N=fs·t=8000，窗宽度g=0.5 s，步长λ=0.1 s，时间序列总长度B=t/λ=100。

令式（10）中的，，，，，则仿真模型的动态路径规划函数可表示为：

（16）

根据式（11）构造仿真信号的代价函数为：

（17）

式中 为归一化质心质量；为距离权重，用来平衡归一化质心质量和距离对代价函数的贡献度，通常的取值范围为。

3.2 时频脊线提取效果衡量指标

为了更直观地分析不同算法的优劣，此处构造两个量化衡量指标：相似度系数和置信度。

绝对值倒数法是确定两个向量间相似度的一种方法，对于提取的第j条脊线上任意一点的频率与对应的理论值之间的相关程度可以由下式确定：

（18）

式中 c为误差允许值，表示接受与理论值的距离不大于c的提取结果。

对于某一算法O提取的第j条脊线与理论曲线的相似度，计算公式如下：

（19）

式中 Ra∈［0，1］，Ra越接近1，说明算法提取的脊线与理论曲线相似度越高，脊线提取效果越好；反之Ra越接近0，则说明相似度越低，提取效果越差。

图8所示为不同相似度Ra时的时频脊线对比图，图中误差上、下限之间为允许误差c的范围。当Ra≥0.9时，脊线与理论时频曲线基本吻合，提取结果误差较小；当0.9≤Ra≤0.8时，脊线在理论曲线附近波动变大，且存在少量脊线点超出了误差范围，但是脊线基本落在误差范围以内；当Ra≤0.7时，脊线与理论曲线保持相同的变化趋势，但是有部分脊线严重超出误差范围，提取效果欠佳。

运用算法O对M个信号进行脊线提取，获得M条脊线，根据式（19）计算得到所有脊线与理论曲线的相关系数，算法O的平均相似度系数为：

（20）

对于任意，存在k条脊线满足，则置信水平在上的置信度为：

（21）

平均相似系数表示提取结果与理论结果偏差的统计平均值，可以反映算法的稳定程度。置信度表示将与理论结果的相似度在的提取结果视为合格结果，则在整个试验结果中合格的提取结果所占的比率为，值越大，代表算法的提取效果越好。

3.3 仿真结果及分析

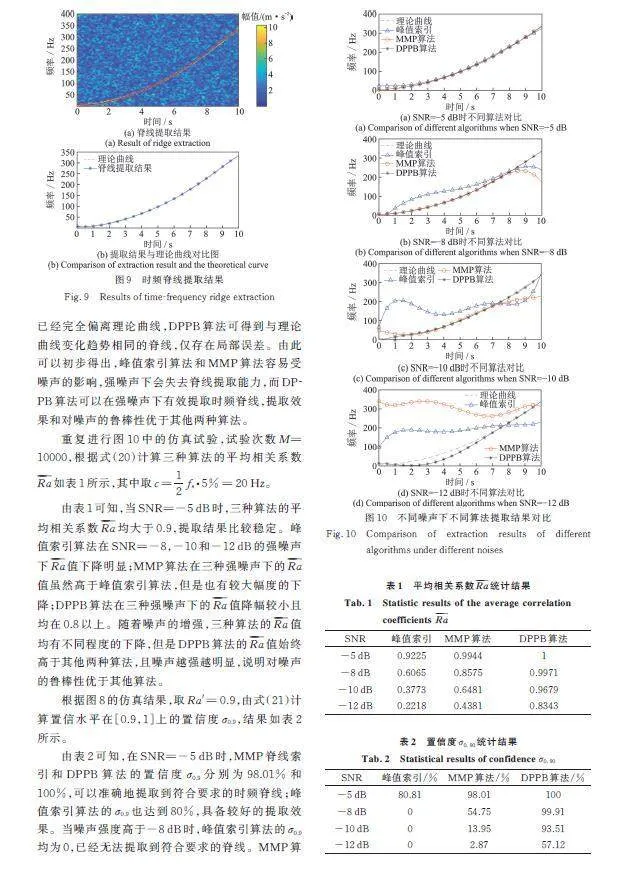
脊线提取结果及其与理论曲线对比结果如图9所示。图9（a）中红色曲线为提取到的时频脊线，脊线索引到了理论脊线附近所有的高幅值时频点；从图9（b）中可以看到，提取到的脊线与理论曲线基本重合，表明本算法可以提取得到较为准确的时频脊线。

为了分析噪声对脊线提取结果的影响，运用峰值索引、MMP脊线索引、DPPB脊线索引三种算法对信噪比的信号进行脊线提取，结果如图10所示。

在图10（a）中，对于信噪比SNR=-5 dB的低噪声信号，3种算法均能较好地提取时频脊线。在SNR=-8和-10 dB的较强噪声时（图10（b）和（c）所示），峰值索引算法得到的脊线已经完全偏离理论曲线，MMP算法得到的脊线与理论曲线有相同的变化趋势，但存在局部误差而偏离理论曲线，DPPB算法提取的脊线与理论曲线基本重合。在SNR=-12 dB的强噪声下（图10（d）所示），其他两种算法已经完全偏离理论曲线，DPPB算法可得到与理论曲线变化趋势相同的脊线，仅存在局部误差。由此可以初步得出，峰值索引算法和MMP算法容易受噪声的影响，强噪声下会失去脊线提取能力，而DPPB算法可以在强噪声下有效提取时频脊线，提取效果和对噪声的鲁棒性优于其他两种算法。

重复进行图10中的仿真试验，试验次数M=10000，根据式（20）计算三种算法的平均相关系数如表1所示，其中取 Hz。

由表1可知，当SNR=-5 dB时，三种算法的平均相关系数均大于0.9，提取结果比较稳定。峰值索引算法在SNR=-8，-10和-12 dB的强噪声下值下降明显；MMP算法在三种强噪声下的值虽然高于峰值索引算法，但是也有较大幅度的下降；DPPB算法在三种强噪声下的值降幅较小且均在0.8以上。随着噪声的增强，三种算法的值均有不同程度的下降，但是DPPB算法的值始终高于其他两种算法，且噪声越强越明显，说明对噪声的鲁棒性优于其他算法。

根据图8的仿真结果，取，由式（21）计算置信水平在［0.9，1］上的置信度，结果如表2所示。

由表2可知，在SNR=-5 dB时，MMP脊线索引和DPPB算法的置信度分别为98.01%和100%，可以准确地提取到符合要求的时频脊线；峰值索引算法的也达到80%，具备较好的提取效果。当噪声强度高于-8 dB时，峰值索引算法的均为0，已经无法提取到符合要求的脊线。MMP算法在SNR=-8 dB时为54.75%，接近一半的提取结果不符合要求，在SNR=-10和-12 dB时的分别为13.95%和2.87%，已经很难提取到合格的脊线。DPPB算法在SNR=-8和-10 dB的较强噪声条件下分别为99.91%和93.51%，合格脊线所占的比率均在90%以上，在SNR=-12 dB的强噪声下为57.12%，依然有一半以上的提取结果符合要求。虽然噪声的增强降低了各算法的提取效果，但DPPB算法的提取效果始终优于其他两种算法，且针对强噪声具有良好的脊线提取能力。

通过以上仿真结果和分析可以得出，DPPB算法可以抵抗信号中强噪声的干扰，相比于峰值索引算法和MMP算法更容易从强噪声信号中提取到有效的时频脊线，对噪声有更好的鲁棒性。

4 试验验证

4.1 试验说明

齿轮箱振动信号中的啮合频率分量是分析故障的重要特征频率之一，本文利用SpectraQuest公司研发的动力传动故障诊断综合试验台（DDS）获取不同转速下齿轮箱的振动信号，通过提取不同转速下的啮合频率时频脊线验证所提算法的有效性，试验台如图11所示。

其中齿轮箱5为二级减速器减速齿轮箱，由4组直齿轮组合而成，主要参数如表3所示。设置加速度振动传感器6的采样频率为25.6 kHz，采集齿轮箱径向的振动信号。

由于DDS试验台不易输出非线性变化的转速，所以试验模拟三组线性变化的输入转速，分别为震荡波动曲线、三角形单波谷波动曲线、三角形三波谷波动曲线，如图12所示。为了与时频脊线对应，下文均用“转频”代替“转速”。

齿轮箱振动信号中包含与转频相关的第i级传动齿轮啮合频率及其倍频，与的关系如下式所示：

（22）

因此，获得齿轮箱振动信号的第i级传统齿轮啮合频率的n倍频，便可计算得到齿轮箱的输入转频。

4.2 试验结果及分析

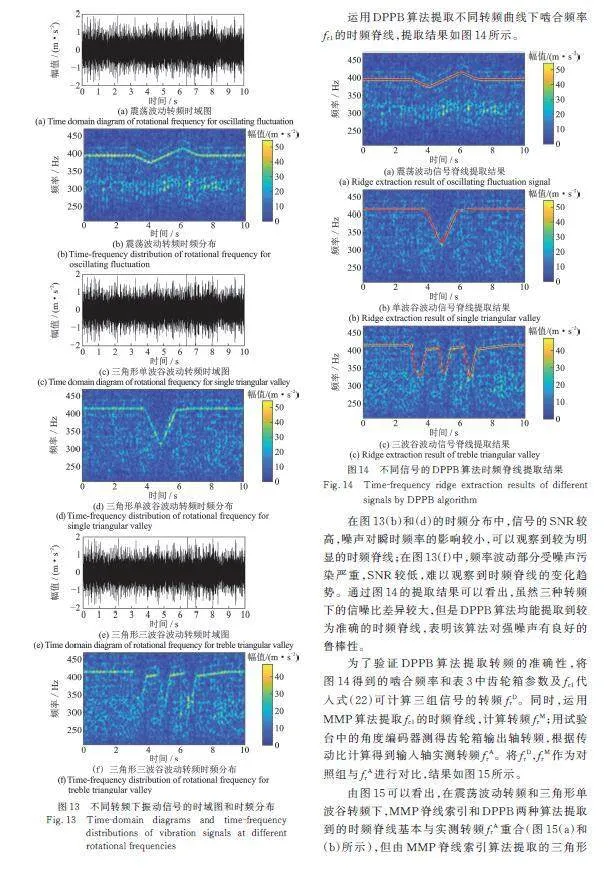
为了计算方便，试验通过提取1级传动齿轮啮合频率的基频计算输入转频。三种不同输入转速下齿轮箱的振动时域图和STFT变换后附近的时频分布如图13所示。

运用DPPB算法提取不同转频曲线下啮合频率的时频脊线，提取结果如图14所示。

在图13（b）和（d）的时频分布中，信号的SNR较高，噪声对瞬时频率的影响较小，可以观察到较为明显的时频脊线；在图13（f）中，频率波动部分受噪声污染严重，SNR较低，难以观察到时频脊线的变化趋势。通过图14的提取结果可以看出，虽然三种转频下的信噪比差异较大，但是DPPB算法均能提取到较为准确的时频脊线，表明该算法对强噪声有良好的鲁棒性。

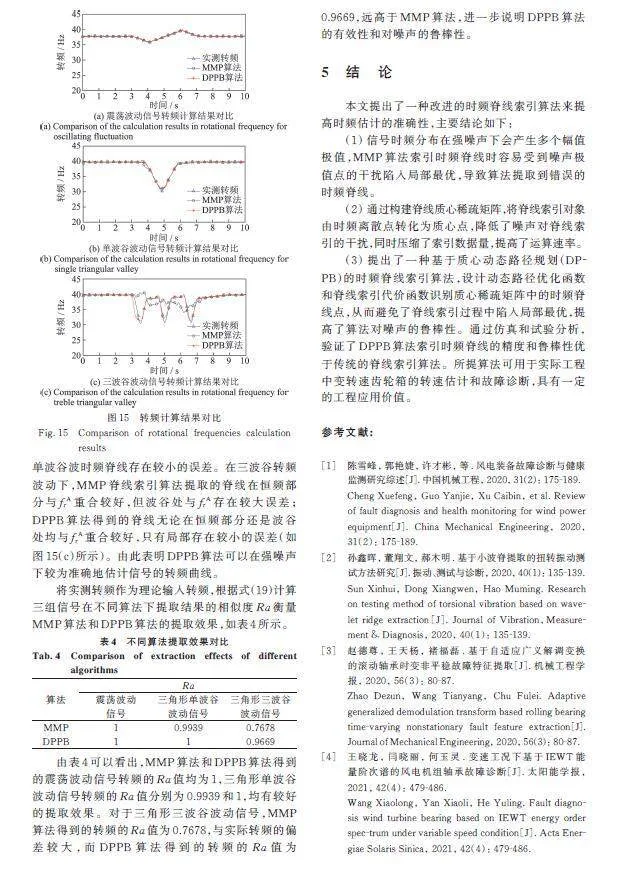
为了验证DPPB算法提取转频的准确性，将图14得到的啮合频率和表3中齿轮箱参数及代入式（22）可计算三组信号的转频。同时，运用MMP算法提取的时频脊线，计算转频；用试验台中的角度编码器测得齿轮箱输出轴转频，根据传动比计算得到输入轴实测转频。将，作为对照组与进行对比，结果如图15所示。

由图15可以看出，在震荡波动转频和三角形单波谷转频下，MMP脊线索引和DPPB两种算法提取到的时频脊线基本与实测转频重合（图15（a）和（b）所示），但由MMP脊线索引算法提取的三角形单波谷波时频脊线存在较小的误差。在三波谷转频波动下，MMP脊线索引算法提取的脊线在恒频部分与重合较好，但波谷处与存在较大误差；DPPB算法得到的脊线无论在恒频部分还是波谷处均与重合较好，只有局部存在较小的误差（如图15（c）所示）。由此表明DPPB算法可以在强噪声下较为准确地估计信号的转频曲线。

将实测转频作为理论输入转频，根据式（19）计算三组信号在不同算法下提取结果的相似度Ra衡量MMP算法和DPPB算法的提取效果，如表4所示。

由表4可以看出，MMP算法和DPPB算法得到的震荡波动信号转频的Ra值均为1，三角形单波谷波动信号转频的Ra值分别为0.9939和1，均有较好的提取效果。对于三角形三波谷波动信号，MMP算法得到的转频的Ra值为0.7678，与实际转频的偏差较大，而DPPB算法得到的转频的Ra值为0.9669，远高于MMP算法，进一步说明DPPB算法的有效性和对噪声的鲁棒性。

5 结 论

mhqytu3B96llJVmdX9+jYw==本文提出了一种改进的时频脊线索引算法来提高时频估计的准确性，主要结论如下：

（1） 信号时频分布在强噪声下会产生多个幅值极值，MMP算法索引时频脊线时容易受到噪声极值点的干扰陷入局部最优，导致算法提取到错误的时频脊线。

（2） 通过构建脊线质心稀疏矩阵，将脊线索引对象由时频离散点转化为质心点，降低了噪声对脊线索引的干扰，同时压缩了索引数据量，提高了运算速率。

（3） 提出了一种基于质心动态路径规划（DPPB）的时频脊线索引算法，设计动态路径优化函数和脊线索引代价函数识别质心稀疏矩阵中的时频脊线点，从而避免了脊线索引过程中陷入局部最优，提高了算法对噪声的鲁棒性。通过仿真和试验分析，验证了DPPB算法索引时频脊线的精度和鲁棒性优于传统的脊线索引算法。所提算法可用于实际工程中变转速齿轮箱的转速估计和故障诊断，具有一定的工程应用价值。

参考文献：

［1］ 陈雪峰， 郭艳婕， 许才彬， 等. 风电装备故障诊断与健康监测研究综述［J］. 中国机械工程， 2020， 31（2）： 175-189.

Cheng Xuefeng， Guo Yanjie， Xu Caibin， et al. Review of fault diagnosis and health monitoring for wind power equipment［J］. China Mechanical Engineering， 2020， 31（2）： 175-189.

［2］ 孙鑫晖， 董翔文， 郝木明. 基于小波脊提取的扭转振动测试方法研究［J］. 振动、测试与诊断， 2020， 40（1）： 135-139.

Sun Xinhui， Dong Xiangwen， Hao Muming. Research on testing method of torsional vibration based on wavelet ridge extraction［J］. Journal of Vibration，Measurement & Diagnosis， 2020， 40（1）： 135-139.

［3］ 赵德尊， 王天杨， 褚福磊. 基于自适应广义解调变换的滚动轴承时变非平稳故障特征提取［J］. 机械工程学报， 2020， 56（3）： 80-87.

Zhao Dezun， Wang Tianyang， Chu Fulei. Adaptive generalized demodulation transform based rolling bearing time-varying nonstationary fault feature extraction［J］. Journal of Mechanical Engineering， 2020， 56（3）： 80-87.

［4］ 王晓龙， 闫晓丽， 何玉灵. 变速工况下基于IEWT能量阶次谱的风电机组轴承故障诊断［J］. 太阳能学报， 2021， 42（4）： 479-486.

Wang Xiaolong， Yan Xiaoli， He Yuling. Fault diagnosis wind turbine bearing based on IEWT energy order spec-trum under variable speed condition［J］. Acta Energiae Solaris Sinica， 2021， 42（4）： 479-486.

［5］ 陈是扦， 彭志科， 周鹏. 信号分解及其在机械故障诊断中的应用研究综述［J］. 机械工程学报， 2020， 56（17）： 91-107.

Chen Shiqian， Peng Zhike， Zhou Peng. Review of signal decomposition theory and its applications in machine fault diagnosis［J］. Journal of Mechanicla Egnineering， 2020， 56（17）： 91-107.

［6］ 郭瑜， 秦树人， 汤宝平， 等. 基于瞬时频率估计的旋转机械阶比跟踪［J］. 机械工程学报， 2003， 39（3）： 32-36.

Guo Yu， Qin Shuren， Tang Baoping， et al. Order tracking of rotating machinery based on instantaneous frequency estimation［J］. Journal of Mechanical Engineering， 2003， 39（3）： 32-36.

［7］ Iatsenko D， McClintock P V E， Stefanovska A. Extrac-tion of instantaneous frequencies from ridges in time–frequency representations of signals［J］. Signal Processing， 2016， 125： 290-303.

［8］ 江星星， 李舜酩， 周东旺， 等. 时频脊融合方法及时变工况行星齿轮箱故障识别［J］. 振动工程学报， 2017， 30（1）： 127-134.

Jiang Xingxing， Li Shunming， Zhou Dongwang， et al. Time-frequency ridge fusion method and defective identification of planetary gearbox running on time-varying condition［J］. Journal of Vibration Engineering， 2017， 30（1）： 127-134.

［9］ Ding Rongmei， Shi Juanjuan， Jiang Xingxing， et al. Multiple instantaneous frequency ridge based integration strategy for bearing fault diagnosis under variable speed operations［J］. Measurement Science and Technology， 2018， 29（11）： 115002.

［10］ 张焱， 何姝钡， 王平， 等. 无转速计下变工况滚动轴承故障特征量化表征提取［J］. 仪器仪表学报， 2021， 42（8）： 104-114.

Zhang Yan， He Shubei， Wang Ping， et al. Tacholess quanti-tative characterization of rolling bearing fault feature under varying conditions［J］. Chinese Journal of Scientific Instrument， 2021， 42（8）： 104-114.

［11］ Wu M， Wu F， Yang K， et al. A multipath matching pursuit algorithm based on improved-inner product matching criterion［C］.2020 IEEE International Conference on Signal Processing， Communications and Computing （ICSPCC）. IEEE， 2020： 1-5.

［12］ Fourer D， Auger F， Flandrin P. Recursive versions of the Levenberg-Marquardt reassigned spectrogram and of the synchrosqueezed STFT［C］.2016 IEEE International Conference on Acoustics， Speech and Signal Processing （ICASSP）. IEEE， 2016： 4880-4884.

［13］ Yu G， Wang Z H， Zhao P. Multisynchrosqueezing transform［J］. IEEE Transactions on Industrial Electronics， 2018， 66（7）： 5441-5455.

［14］ Yu G， Yu M J， Xu C Y. Synchroextracting transform［J］. IEEE Transactions on Industrial Electronics， 2017， 64（10）： 8042-8054.

［15］ Li M F， Wang T Y， Kong Y， et al. Synchro-reassigning transform for instantaneous frequency estimation and signal reconstruction［J］. IEEE Transactions on Industrial Electronics， 2021， 69（7）： 7263-7274.

［16］ 江星星. 齿轮箱关键部件非平稳振动信号分析及诊断方法研究［D］. 南京：南京航空航天大学， 2016.

Jiang Xingxing. Research on the nonstationary vibration signal of key parts of gearbox and its fault diagnosis method［D］. Nanjing：Nanjing University of Aeronautics and Astronautics， 2016.

［17］ 杨世伟， 蒋国平， 宋玉蓉， 等. 基于GPU的稀疏矩阵存储格式优化研究［J］. 计算机工程， 2019， 45（9）： 23-31.

Yang Shiwei， Jiang Guoping， Song Yurong， et al. Research on storage format optimization of sparse matrix based on GPU［J］. Computer Engineering， 2019， 45（9）： 23-31.

Time-frequency ridge index algorithm for gearbox under variable speed based on dynamic path planning of barycenter

ZHANG Bo-lin1， WAN Shu-ting1， ZHAO Xiao-yan1， ZHANG Xiong1， GU Xiao-hui2

（1.Hebei Key Laboratory of Electric Machinery Health Maintenance & Failure Prevention，North China Electric Power University， Baoding 071003， China；2.State Key Laboratory of Mechanical Behavior and System Safety of Traffic Engineering Structures，Shijiazhuang Tiedao University， Shijiazhuang 050043， China）

Abstract： The paper proposes a time-frequency ridge index algorithm for gearboxes under variable speed conditions， based on Dynamic Path Planning of Barycenter （DPPB）. This algorithm addresses the challenge of estimating the instantaneous frequency of signals in a high-noise environment. The algorithm builds upon the analysis of the Multi-Path Matching Pursuit （MMP） ridge index algorithm and its limitations under high noise. By adding windows to the ridge set obtained by the MMP algorithm， a ridge barycenter sparse matrix of the signal is constructed. A dynamic path planning function is then designed for the barycenter sparse matrix to index the barycenters on the ridge line. The optimal time-frequency ridge line is calculated based on the values of the ridge line cost function. The similarity coefficient Ra and confidence σRa are used as measures of the ridge extraction effect. Simulations and experiments indicate that the DPPB algorithm can effectively extract the time-frequency ridge of signals in high-noise environments， and it is more reliable and robust than the peak index algorithm and the MMP algorithm under various noise intensities.

Key words： fault diagnosis； gearbox；dynamic path planning barycenter （DPPB）； time-frequency ridge index； multipath matching pursuit （MMP）； time-frequency analysis

作者简介： 张伯麟（1993—），男，博士研究生。电话：（0312）7525428； E-mail：393696838@qq.com。

通讯作者： 万书亭（1970—），男，博士，教授，博士生导师。电话：（0312）7525455； E-mail：52450809@ncepu.edu.cn。