单双向循环荷载作用下砂砾料动模量和阻尼比试验研究

摘要： 通过大型振动三轴试验，研究了单双向循环荷载作用下砂砾料动弹性模量和阻尼比的变化规律，分析围压和径向循环动应力对砂砾料动力参数的影响。研究结果表明：在双向振动三轴试验中，砂砾料的轴向动应变受径向动应力的影响较小，动应变主要与施加的轴向动应力大小有关；单双向振动下砂砾料的动弹性模量均随着动应变的增大而逐渐降低，双向振动时砂砾料动弹性模量随动应变的衰减速率基本不变，在相同动应变下双向振动的动模量均低于单向振动；砂砾料在双向振动时的阻尼比大于单向振动，双向振动时消耗的动应变能更大。通过对两种试验条件下的最大动弹性模量、动模量比进行分析，建立了表述单双向试验条件下最大动弹性模量的换算关系式和双向振动试验中动模量比和动应变的修正模型。

关键词： 砂砾料； 动三轴试验； 动弹性模量； 阻尼比； 双向振动； 径向动应力

中图分类号： TV641；TU441+.4 文献标志码： A 文章编号： 1004-4523（2024）06-1055-09

DOI：10.16385/j.cnki.issn.1004-4523.2024.06.016

引 言

砂砾料是广泛分布于河床及岸坡滩地的天然筑坝材料，开采成本低，且具有强度高、压实性好、透水性强及碾压后不易破碎等优点［1］，被广泛地用于土石坝建设中。由于土石坝结构简单、施工方便、坝体稳定且具有良好的抗震性能，土石坝的坝高已达到250 m级，如在建的新疆大石峡面板砂砾石坝（最大坝高247 m）、青海茨哈峡面板砂砾石坝（最大坝高256 m）［2‑3］。随着大坝高度的增加及建坝地质条件的恶化，坝体内应力水平增大和应力分布复杂，在地震动荷载作用下坝体抗震性能安全备受关注。

地震动荷载下土体的软化、破坏以及沉降一直是土动力学研究的重要内容［4‑5］。目前通常采用动三轴试验模拟地震动荷载，且根据Seed等［5‑7］的假设将地震荷载简化为水平剪切动荷载，应力条件主要用单向激振、均等固结时45°面上的应力来模拟［8‑9］。研究发现地震烈度高，震源浅时，需要考虑纵波和横波对土体动力特性的影响［10］，常规的动三轴试验无法模拟纵波和横波同时作用时土体的复杂应力状态。因此可采用双向动三轴试验进行研究，通过同时施加轴向和径向循环荷载模拟土体的应力状态。目前，关于轴向拉压和径向拉压耦合作用下土体的动力特性，国内外学者已经进行了一些研究，张希栋等［11］研究了双向循环荷载下黄土的动变形特性，发现初始动应力状态和径向动荷载对黄土的动剪切变形影响显著；黄钰皓等［12］对饱和软黏土进行双向循环动荷载试验研究，发现循环围压对土体的孔压影响明显；栾茂田等［13‑14］通过双向耦合剪切荷载下松砂的动力特性试验，发现不同应力路径下，剪应变均表现为双向积累。文献［15‑18］也研究了不同土体双向循环荷载作用下的动力特性。赵凯等［19］在双向循环剪切条件下研究了饱和砂土的剪胀性与累计体应变的关系。

目前土体双向循环动荷载试验所采用的试样尺寸较小，研究对象以黏土、黄土和松砂等粒径较小的土为主，而对于含有大粒径的砂砾料在双向振动作用下的动力特性研究较少。本文通过大型动三轴试验研究单双向振动荷载作用下砂砾料的动力特性，探寻单双向循环荷载作用下砂砾料动模量和阻尼比的变化规律，分析围压和径向循环动应力对砂砾料动模量和阻尼比的影响，对比分析单双向循环动应力作用下动力模型参数的变化规律。

1 试验内容及方法

1.1 试验仪器

试验仪器采用新疆水利工程安全与水灾害防治重点实验室的WYS‑2000大型多功能动静三轴试验机，如图1所示。仪器由主机、液压系统、饱和（体变）控制系统和数据采集系统等组成，该仪器最大轴向动荷载为1000 kN，最大围压为5.0 MPa，振动频率为0.01～10 Hz，试样尺寸为Φ300 mm× 700 mm。加载系统采用液压伺服作动器，位移、围压、反压可独立控制，从而实现双向的动、静荷载加载。本次双向循环动力试验在试样固结完成后，采用应力控制方式加载动应力，轴向通过顶部的液压伺服作动器加载动应力，径向应力（即围压）通过围压缸内活塞的循环运动控制，实现围压按设计波形循环变化，从而实现双向循环振动三轴试验。

1.2 试验土样

试验所用砂砾料取自新疆尼雅水库料场区，实验室进行筛分后得到不同粒组砂砾料。现场砂砾料最大可见粒径600 mm，呈磨圆度较高的圆形或亚圆形，岩石质地坚硬，无明显的棱角。受仪器尺寸的限制，同时为减小粒径尺寸对试验结果的影响，试验所选用的最大粒径为试样直径的1/5，即最大粒径为60 mm。依据《土工试验方法标准》（GB/T 50123—2019）［20］采用等量替代法对砂砾料原级配进行缩尺处理，以满足室内试验要求。试验级配曲线如图2所示，砂砾料各分级粒组如图3所示。通过相对密度试验，得出砂砾料的最大干密度和最小干密度，如表1所示，试验密度按相对密度Dr=0.85控制，密度为2.258 g/cm3。

1.3 试验过程

试验在大型多功能动静三轴试验机上进行，试样尺寸为Φ300 mm×700 mm的圆柱体试样。根据试样用料按级配准确称取每一级试料，加入适量的水拌和均匀后分7层装入动三轴成型筒中进行击实，为保证成型后的试样填筑密度均匀，每层试料击实后的厚度为100 mm，即认为达到试验控制密度。试样制备完毕后安装围压室，推入试验平台，然后对试样进行饱和，要求饱和度达到95%以上。试样固结过程中按给定围压进行等向固结，直至试样排水量稳定后进行振动三轴试验。动模量和阻尼比试验中，采用一个试样多级加载进行，每个试样以从小到大等差方式施加轴向循环应力或径向循环应力，轴向和径向循环荷载均采用应力控制。单向振动时，固结完成后第一级轴向循环应力为50 kPa，后面每级循环动应力增量为50 kPa，直至轴向循环应力等于最大轴向应力的90%时停止；双向激振时，在轴向循环应力施加的同时施加径向循环应力，相位差为0°，每个试样在试验中径向动应力幅值保持不变。为减少前期振动对试验结果的影响［21‑22］，每级动应力下振动6次，以6次循环振动的应力‑应变平均值作为试验结果。为避免预剪应力对试验结果的影响，试验选取固结应力比Kc=1.0；根据研究发现地震波的卓越频率为1.40～7.25 Hz，而基频一般约为1 Hz，且由于长周期的低频振动比短周期的高频振动对建筑物上部影响更大［23］，因此本次试验振动频率选为1 Hz，振动波形为正弦波。

双向振动试验中循环偏应力定义为轴向动应力与径向动应力的差值，即，如图4所示。为保证试样内部全部为压应力且在振动过程中不产生剪应力反向情况，在每个试验开始时给试样施加初始循环偏应力为50 kPa。为研究单双向振动条件下砂砾料的动模量和阻尼比变化规律，共进行了5个围压、4个径向循环动应力作用下的振动三轴试验，具体试验方案如表2所示。

2 试验结果与分析

2.1 循环偏应力与动应变关系

图5为单双向振动条件下试验测得的循环偏应力与轴向动应变关系曲线（骨干曲线）。从图5中可以看出，砂砾料的骨干曲线随轴向动应变增大，其斜率逐渐降低，符合双曲线增长趋势。在单向和双向振动工况下，曲线均表现出随围压的增大而变陡，大围压下的试验结果均位于小围压的上方。说明围压的增大，增加了砂砾料的刚度，这主要是由于围压增大提高了试样的固结应力，使固结后的试样密度增大，表现出受循环偏应力作用时的骨干曲线变陡。在5个试验围压下，均表现出双向振动试验的骨干曲线位于单向试验的下方，且随轴向动应变的增加，两种振动条件下的骨干曲线间距基本保持不变。其原因在于双向振动试验中所采用的轴向与径向动应力是同时加载的，不存在相位差，在周期内的最大循环偏应力为，而在单向振动试验时的最大循环偏应力为，所以出现在相同轴向动应力作用时，双向振动试验的最大循环偏应力小于单向振动试验；并且双向振动试验受径向动应力大小的影响，相当于给试样增加了一个数值等于的固结应力，使试样的固结应力增大，而单向振动时径向应力是不变的，所以在轴向动应力相等时，双向振动试验时的轴向动应变略小于单向振动试验，致使双向振动条件下的骨干曲线低于单向振动。

图6为围压=800 kPa时不同径向动应力作用下砂砾料循环偏应力与轴向动应变关系曲线。由图6可知，径向动应力幅值变化对砂砾料的骨干曲线有显著影响。随着径向动应力增大，骨干曲线逐渐降低，主要受径向动应力的影响使施加在试样上的循环偏应力减小，而轴向动应变受径向动应力的影响较小。在相同的轴向动应力作用下，砂砾料所产生的轴向动应变差异不明显，导致在径向动应力越大时骨干曲线位置越低。说明在双向振动三轴试验中，砂砾料的轴向动应变受径向动应力的影响较小，动应变大小主要与施加的轴向动应力有关。

2.2 动弹性模量Ed的变化规律

根据动弹性模量的定义，砂砾料的动弹性模量采用下式计算［9］：

（1）

式中 和分别为每次振动循环中试样的最大和最小循环偏应力；和分别为每次循环中对应的最大和最小轴向动应变。

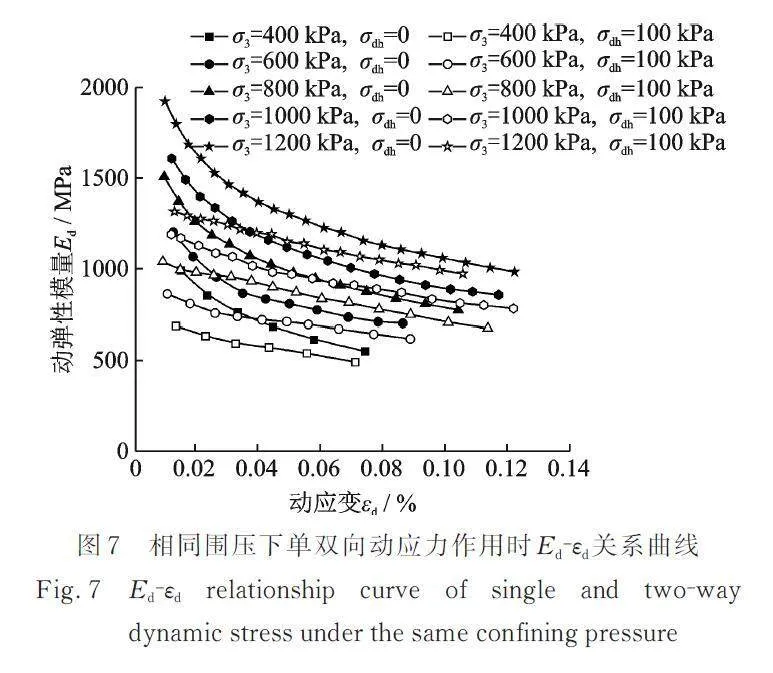
绘制不同围压下单向和双向振动三轴试验的关系曲线，如图7所示。从图7中可以看出：在5个试验围压下，砂砾料的动弹性模量均随动应变的增大而逐渐减小，但径向动应力作用使单双向振动试验的结果差异明显。单向振动试验时（=0），砂砾料的动弹性模量随动应变的增大而减小；动应变较小时，动弹性模量衰减速率较快，随着动应变的增大，其衰减速率逐渐降低。双向振动时（），砂砾料的动弹性模量随动应变的增大而减小，且随动应变的增大，动弹性模量的衰减速率基本保持不变，砂砾料的动弹性模量随动应变增大呈线性减小。对比单双向振动下的关系曲线发现，相同围压下径向动应力的存在使得相同动应变水平下动弹性模量明显减小；且动应变越小，其差值越大，随着动应变的增大，其差值逐渐减小。

图8为相同围压、不同径向动应力幅值作用下砂砾料的动弹性模量与动应变关系曲线。由图8可知，不同径向动应力作用下，砂砾料的动弹性模量随动应变的增大而减小。在单向振动试验中，动应变较小时，动弹性模量衰减较快，而随着动应变的增大，动弹性模量的衰减速率逐渐减小。在双向振动试验时，动弹性模量随动应变的衰减速率基本保持不变，呈线性减小规律；并且径向动应力越大，动弹性模量与动应变关系曲线越低。这主要是在相同轴向动应力作用下径向动应力增大，使循环偏应力减小，从而在相同动应变下的动弹性模量减小。在不同的径向动应力下，动弹性模量在较大动应变时的差值逐渐减小。

2.3 阻尼比λ变化规律

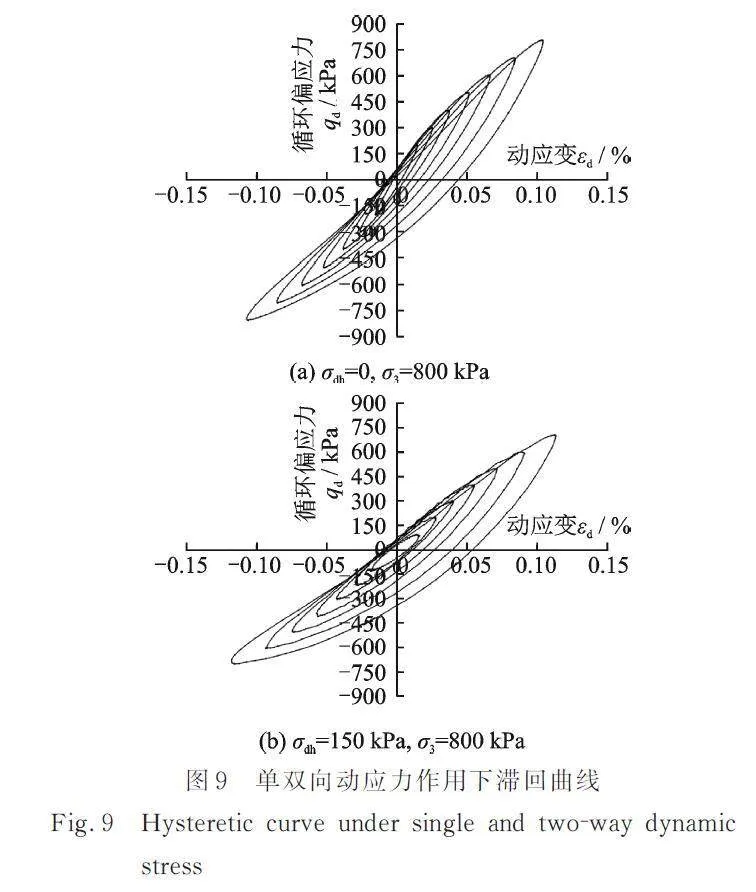
土的动变形特性常采用土体在循环荷载作用下的动应力‑动应变关系来描述，即滞回曲线。图9为围压=800 kPa，径向动应力幅值分别为0和150 kPa时砂砾料的滞回曲线。从图9中可以看出，双向振动条件下的滞回曲线椭圆度较高，对称性较好，但随动应力的增大，对称性降低；而在单向振动下的滞回曲线整体较狭长，对称性相较双向振动时低。受径向动应力的影响，双向振动时的滞回曲线倾斜度比单向振动时大。在两种试验工况下，滞回曲线的加载和卸载过程的曲线斜率差异较大，滞回曲线的对称性不高的原因在于本次试验采用同一试样连续加载，在较大动应力加载时试样已经受到了较小动应力作用，表现出在小应力加载过程为近似线性增长，且不同动应力下的加载曲线较为接近。

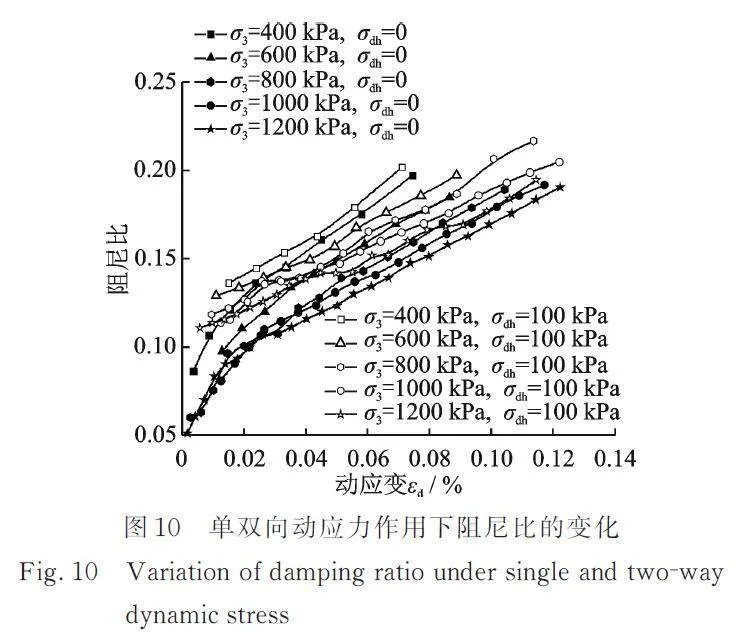
根据等效阻尼比的定义，可采用动三轴试验中一次循环振动所消耗的能量与施加总能量的比值来计算［24］。针对滞回曲线对称性不好情况，前文分析已指出是由于同一试样连续加载所致，为消除连续加载对阻尼比计算造成的影响，本文采用滞回曲线卸载段与过原点的中轴所围成的面积作为滞回圈面积的0.5倍进行计算。通过该方法计算得到砂砾料在单双向振动三轴试验下的阻尼比与动应变的关系曲线如图10所示。由图10可知，阻尼比随动应变的发展不断增大；动应变相同时，双向振动试验中径向动应力对阻尼比具有一定的增大作用。表明径向动应力的存在导致土体间相对变形增加，颗粒间的接触面积增大，土体消耗的动应变能增大，在颗粒间传递消耗的能量增加，表现为双向振动条件下砂砾料的阻尼比高于单向振动试验。单双向动应力作用下砂砾料的阻尼均随着围压的增大而减小，这与以往研究结果是一致的［25］。

3 单双向振动下动弹性模量分析

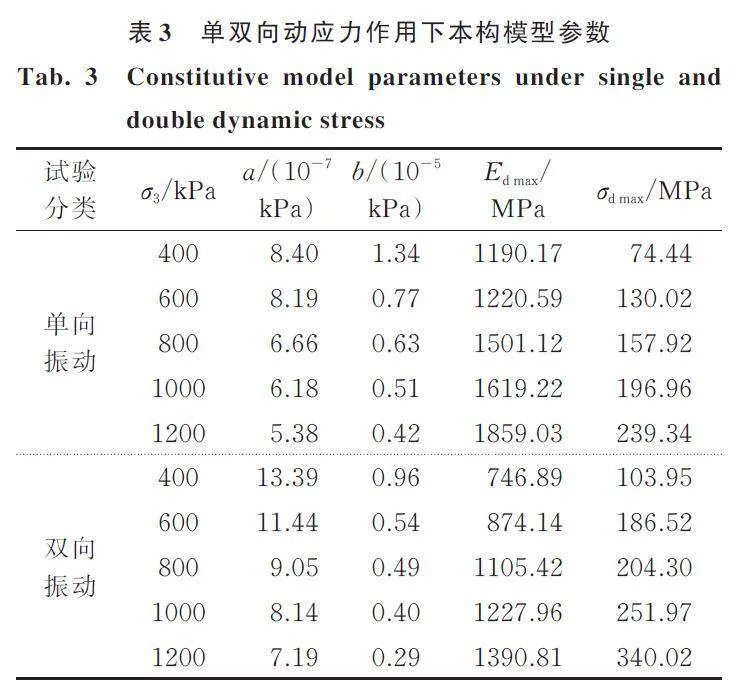
3.1 Edmax模型

目前，由于等效线性黏弹性模型概念明确，能较合理地确定土体在地震加速度作用下的动应力与动应变反应，在土体动力分析中被广泛应用，等效线性黏弹性模型认为动应力与动应变的关系服从双曲线模型，即

（2）

式中 σd为轴向动应力；εd为轴向动应变；a，b为试验常数。Ed max=1/a，表示趋近于0时的动弹性模量；σd max=1/b，表示相对于趋近于无穷大时的σd。

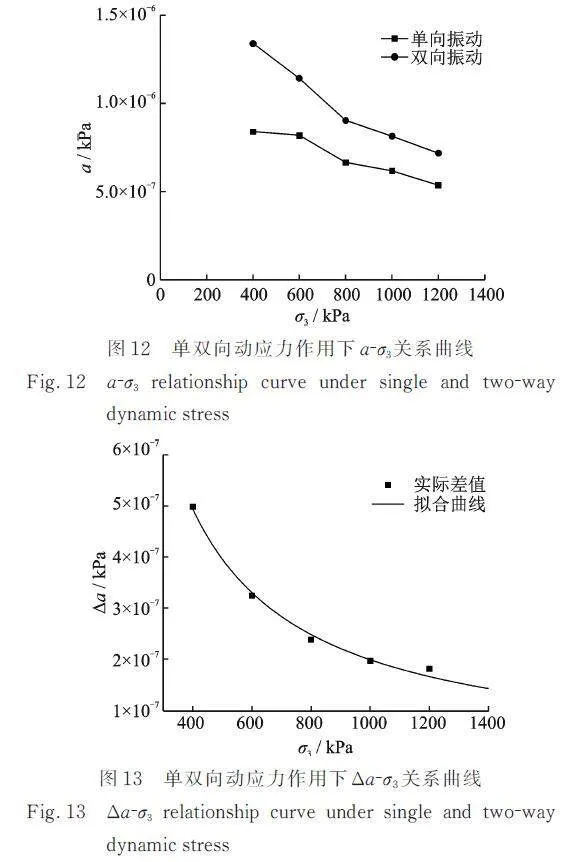
图11为不同试验条件下1/Ed‑εd关系曲线。由图11可知，单双向循环荷载作用下砂砾料1/Ed‑εd关系呈线性变化，1/Ed随动应变的增大线性增大，双向动荷载作用下砂砾料的1/Ed‑εd关系仍可用等效线性模型进行描述。为比较单双向循环荷载作用下砂砾料的差异性，将不同试验条件下模型参数列于表3中。可以看出相同围压作用下单双向循环荷载条件下模型参数a存在明显的差异。由于模型参数a反映材料的最大动弹性模量，绘制单双向振动条件下a与围压的关系，如图12所示。由图12可知，模型参数a随围压的增大而变化。单双向循环荷载作用下砂砾料的模型参数a均不断的减小，且在相同围压下两种振动方式所得参数a的差值也不断减小。为分析两种振动方式下的变化规律，绘制围压‑σ3关系曲线，如图13所示。由图13可知，与围压σ3呈非线性关系，采用幂函数进行拟合，表达式为：

=1.91×10-4σ3-0.99（3）

从拟合结果中可知，围压较小时，二者差异较大，而随着围压不断增大，单双向循环荷载作用下模型参数a的差值将不断缩小，可认为当围压足够大时，单双向振动条件下的试验参数a相同。将式（3）代入式（2）可以得到单双向循环动应力作用下最大动弹性模量之间的关系，可按如下公式计算：

（4）

或

（5）

式中 和分别为单向和双向动应力作用下的最大动模量。

3.2 Ed/Ed max模型

在描述土体动力特性时，通常选用等效线性模型或修正的双曲线模型来表述动弹性模量的衰减关系，即动弹性模量比或随动应变的变化关系。

（6）

式中 为参考动应变，。文献［9］中提出了双向循环荷载作用下软黏土模型，且关系曲线对试验结果的准确性具有决定作用。Hardin‑Drnevich模型对土的动弹性模量衰减模式适用性较强，表达式简单，学者们常采用该模型描述不同类土的动模量随动应变变化的衰减规律。

本次单双向振动试验下的关系曲线如图14所示。从图14中可以看出：单向振动时，砂砾料随动应变增大迅速减小；而双向振动时，轴向动应变在10-4～10-2范围内的动弹性模量减小速率较单向振动缓慢，在动应变为10-3时动弹性模量比仍大于0.5。这与单向振动三轴试验所得的结果存在明显差异［26‑27］，表明双向振动试验中，砂砾料的动应力‑动应变关系与Hardin‑Drnevich模型存在一定的差别。针对动模量比衰减速率慢和试验结束时动模量比较大的情况，在Hardin‑Drnevich模型的基础上，增加描述曲线降低速率和极限值的参数来描述双向振动三轴试验中砂砾料动弹性模量的衰减关系，表达式为：

（7）

式中 m为动弹性模量比衰减曲线在动应变变化范围内的最小值；n为曲线拐点值，用于调整曲线在应变轴上的位置；k为指数，用于调整曲线的曲度。

根据式（7）对双向循环荷载作用下砂砾料动弹性模量比关系进行拟合，如图14所示。由图14可知，试验点分部在拟合曲线两侧狭窄的区域内，拟合效果较好，说明修正后的模型能合理描述双向振动下砂砾料的动模量与动应变的关系，本次试验的参数m=0.246，n=0.132，k=1.056。

4 结 论

通过大型振动三轴试验，研究了单双向循环荷载在固定振动频率（f=1 Hz）下砂砾料动弹性模量和阻尼比的变化规律，分析了围压和径向动应力对砂砾料动弹性模量和阻尼比的影响，探讨了不同试验条件下砂砾料的动弹性模量间的关系，主要得出以下结论：

（1）在双向振动三轴试验中，砂砾料的轴向动应变受径向动应力的影响较小，其变化主要与施加的轴向动应力大小有关。

（2）单双向振动下，砂砾料的动弹性模量均随着动应变的增大而逐渐减小。单向振动时动弹性模量衰减速率随着动应变的增大逐渐减小；双向振动时动弹性模量衰减速率随动应变的增大基本保持不变，且双向振动下的动弹性模量略低于单向振动。

（3）单双向振动下，砂砾料的阻尼比均随动应变的增大而增大；动应变相同时，双向振动的阻尼比大于单向振动，说明砂砾料在双向振动时消耗的动应变能更大。

（4）围压相同时，单双向振动试验的模型参数a存在明显差异；并随着围压的增大，模型参数a不断减小，且a的差值Δa也不断减小；Δa与围压σ3呈幂函数关系，建立了单双向振动三轴试验砂砾料最大动弹性模量Ed max的换算关系式。

（5）双向振动三轴试验的动弹性模量比随动应变的增大而减小，但衰减速率较小，在动应变为10-3时的动模量比仍大于0.5；基于Hardin‑Drnevich模型建立了双向振动下砂砾料动弹性模量比与动应变的修正模型。

参考文献：

［1］ 陈生水， 凤家骥， 袁辉. 砂砾石面板坝关键技术研究［J］. 岩土工程学报， 2004， 26（1）： 16‑20.

CHEN Shengshui， FENG Jiaji， YUAN Hui. Research on key techniques of facing sandy gravel dam［J］. Chinese Journal of Geotechnical Engineering， 2004， 26（1）： 16‑20.

［2］ 陈生水， 阎志坤， 傅中志， 等. 特高面板砂砾石坝结构安全性论证［J］. 岩土工程学报， 2017， 39（11）： 1949‑1958.

CHEN Shengshui， YAN Zhikun， FU Zhongzhi， et al. Evaluation of safety performance of extremely high slab‑faced gravel dams［J］. Chinese Journal of Geotechnical Engineering， 2017， 39（11）： 1949‑1958.

［3］ MA Hongqi， CHI Fudong. Technical progress on researches for the safety of high concrete‑faced rockfill dams［J］. Engineering， 2016， 2（3）： 332‑339.

［4］ Thiers G R， Seed H B. Cyclic stress‑strain characteristics of clay［J］. ASCE Soil Mechanics and Foundation Division Journal， 1968， 94（2）： 555‑569.

［5］ Seed H B， Lee K L. Liquefaction of saturated sands during cyclic loading［J］. Journal of the Geotechnical and Geoenvironmental Engineering， 1966， 92（6）：105‑134.

［6］ Seed H B， Peacock W H. Test procedures for measuring soil liquefaction characteristics［J］. Journal of Geotechnical and Geoenvironmental Engineering， 1971， 97（8）： 1099‑1119.

［7］ Seed H B， Idriss I M. Simplified procedure for evaluating soil liquefaction potential［J］. ASCE Soil Mechanics and Foundation Division Journal， 1971， 97（9）： 1249‑1273.

［8］ 常建梅， 李晓慧， 张伏光， 等. 基于大型动三轴试验和图形分析法的有砟道床劣化特性研究［J］. 铁道学报， 2022， 44（7）： 107‑116.

CHANG Jianmei， LI Xiaohui， ZHANG Fuguang， et al. Degradation mechanism of railway ballast by large‑scale cyclic triaxial test and image analysis method［J］. Journal of the China Railway Society， 2022， 44（7）： 107‑116.

［9］ 蔡袁强， 王军， 海钧. 双向激振循环荷载作用下饱和软黏土强度和变形特性研究［J］. 岩石力学与工程学报， 2008， 27（3）： 495‑504.

CAI Yuanqiang， WANG Jun， HAI Jun. Study on strength and deformation behaviors of soft clay under bidirectional exciting cyclic loading［J］. Chinese Journal of Rock Mechanics and Engineering，2008， 27（3）： 495‑504.

［10］ 王军， 蔡袁强， 丁光亚， 等. 双向激振下饱和软黏土动模量与阻尼变化规律试验研究［J］. 岩石力学与工程学报， 2010， 29（2）： 423‑432.

WANG Jun， CAI Yuanqiang， DING Guangya， et al. Experimental research on changing rules of dynamic modulus and damping ratio of saturated soft clay under bidirectional exciting cyclic loading［J］. Chinese Journal of Rock Mechanics and Engineering， 2010， 29（2）： 423‑432.

［11］ 张希栋， 骆亚生. 双向循环荷载下黄土的动变形特性研究［J］. 地震工程与工程振动， 2016， 36（1）： 186‑192.

ZHANG Xidong， LUO Yasheng. Study on dynamic deformation characteristics of loess under bidirectional cyclic loads［J］. Earthquake Engineering and Engineering Dynamics， 2016， 36（1）： 186‑192.

［12］ 黄珏皓， 陈健， 柯文汇， 等. 双向激振循环荷载和振动频率共同作用下饱和软黏土孔压试验研究［J］. 岩土工程学报， 2017， 39（增刊2）： 71‑74.

HUANG Juehao， CHEN Jian， KE Wenhui， et al. Coupling effects of bidirectional cyclic loading and loading frequency on pore water pressure of saturated soft clay［J］. Chinese Journal of Geotechnical Engineering， 2017， 39（Sup2）： 71‑74.

［13］ 栾茂田， 金丹， 张振东， 等. 饱和松砂的双向耦合剪切特性试验研究［J］. 岩土工程学报， 2009， 31（3）： 319‑325.

LUAN Maotian， JIN Dan， ZHANG Zhendong， et al. Liquefaction of sand under bi‑directional cyclic loading［J］. Chinese Journal of Geotechnical Engineering， 2009， 31（3）： 319‑325.

［14］ 栾茂田， 金丹， 许成顺， 等. 双向耦合剪切条件下饱和松砂的液化特性试验研究［J］. 岩土工程学报， 2008， 30（6）： 790‑794.

LUAN Maotian， JIN Dan， XU Chengshun， et al. Liquefaction of sand under bidirectional cyclic loading［J］. Chinese Journal of Geotechnical Engineering， 2008， 30（6）： 790‑794.

［15］ 刘潇， 张学， 赵俭斌， 等. 单、双向振动条件下饱和粉砂变形特性对比试验研究［J］. 地震工程学报， 2015， 37（3）： 748‑753.

LIU Xiao， ZHANG Xue， ZHAO Jianbin， et al. Study on deformation characteristics of saturated silty sand in uni‑and bidirectional cyclic triaxial tests［J］. China Earthquake Engineering Journal， 2015， 37（3）： 748‑753.

［16］ 王军， 蔡袁强， 潘林有. 双向激振下饱和软黏土应变软化现象试验研究［J］. 岩土工程学报， 2009， 31（2）： 178‑185.

WANG Jun， CAI Yuanqiang， PAN Linyou. Degardation of stiffness of soft clay under bidirectional cyclic loading［J］. Chinese Journal of Geotechnical Engineering， 2009， 31（2）： 178‑185.

［17］ 谷川， 蔡袁强， 王军. 地震P波和S波耦合的变围压动三轴试验模拟［J］. 岩土工程学报， 2012， 34（10）： 1903‑1909.

GU Chuan， CAI Yuanqiang， WANG Jun. Coupling effects of P‑waves and S‑waves based on cyclic triaxial tests with cyclic confining pressure［J］. Chinese Journal of Geotechnical Engineering， 2012， 34（10）： 1903‑1909.

［18］ 王军， 蔡袁强， 海钧. 双向激振对饱和软黏土应力应变循环刚度软化的影响［J］. 水利学报， 2008， 39（9）： 1083‑1091.

WANG Jun， CAI Yuanqiang， HAI Jun. Stiffness degradation of saturated soft clay under the action of bidirectional cyclic loading［J］. Journal of Hydraulic Engineering， 2008， 39（9）： 1083‑1091.

［19］ 赵凯， 吴琪， 熊浩， 等. 双向耦合循环剪切条件下饱和砂土体应变发展规律试验研究［J］. 岩土工程学报， 2019， 41（7）： 1260‑1269.

ZHAO Kai， WU Qi， XIONG Hao， et al. Experimental investigations on volumetric train behavior of saturated sands under bi‑directional cyclic loadings［J］. Chinese Journal of Geotechnical Engineering， 2019， 41（7）： 1260‑1269.

［20］ 中华人民共和国水利部. 土工试验方法标准：GB/T 50123—2019［S］. 北京： 中国计划出版社， 2019.

Ministry of Water Resources of the People’s Republic of China. Standard for geotechnical testing method： GB/T 50123—2019［S］. Beijing： China Planning Press， 2019.

［21］ 刘平， 刘汉龙， 孟敏强， 等.先期振动对高聚物胶凝堆石料动变形特性的影响［J］.中国公路学报， 2022， 35（6）： 230‑239.

LIU Ping， LIU Hanlong， MENG Minqiang， et al. Effect of previous cyclic loading on dynamic deformation behaviors of PFA‑reinforced rockfill materials［J］. China Journal of Highway and Transport， 2022， 35（6）： 230‑239.

［22］ 陆晓炎. 前期加载振动对堆石料动力变形特性的影响［D］. 大连： 大连理工大学， 2020.

LU Xiaoyan. Effect of loading history on the cyclic residual deformation behaviors of rockfill material［D］. Dalian： Dalian University of Technology， 2020.

［23］ 王汝恒， 贾彬， 邓安福， 等. 砂卵石土动力特性的动三轴试验研究［J］. 岩石力学与工程学报， 2006， 25（增刊2）： 4059‑4064.

WANG Ruheng， JIA Bin， DENG Anfu， et al. Dynamic triaxial testing study on dynamic characteristics of sandy pebble soil［J］. Chinese Journal of Rock Mechanics and Engineering， 2006， 25（Sup2）： 4059‑4064.

［24］ 庄海洋， 刘启菲， 吴琪， 等. 饱和橡胶颗粒‑砂混合料的动力学特性［J］. 建筑材料学报， 2021， 24（3）： 597‑605.

ZHUANG Haiyang， LIU Qifei， WU Qi， et al. Dynamic behavior of saturated rubber particle‑sand mixture［J］. Journal of Building Materials， 2021， 24（3）： 597‑605.

［25］ ZHU S，YANG G，WEN Y，et al. Dynamic shear modulus reduction and damping under high confining pressures for gravels［J］. Geotechnique Letters，2014，4（3）：179‑186

［26］ 董威信， 孙书伟， 于玉贞， 等. 堆石料动力特性大型三轴试验研究［J］. 岩土力学， 2011， 32（增刊2）： 296‑301.

DONG Weixin， SUN Shuwei， YU Yuzhen， et al. Large scale triaxial shear test on dynamic properties of rockfill materials［J］. Rock and Soil Mechanics， 2011， 32（Sup2）： 296‑301.

［27］ 齐剑峰， 栾茂田， 杨庆， 等. 饱和黏土动剪切模量与阻尼比的试验研究［J］. 岩土工程学报， 2008， 30（4）： 518‑523.

QI Jianfeng， LUAN Maotian， YANG Qing， et al. Dynamic shear modulus and damping ratio of saturated clay［J］. Chinese Journal of Geotechnical Engineering， 2008， 30（4）： 518‑523.

Experimental study on dynamic modulus and damping ratio of sand and gravel under single and double cyclic loads

HE Jian‑xin1，2， WANG Jing3， YANG Hai‑hua1，2， LIU Liang1，2， YANG Zhi‑hao1

（1.College of Water Conservancy and Civil Engineering，Xinjiang Agricultural University，Urumqi 830052，China；2.Xinjiang Key Laboratory of Hydraulic Engineering Security and Water Disasters Prevention， Urumqi 830052，China；3.Xinjiang Water Resources and Hydropower Survey Design and Research Institute Company with Limited Liability，Urumqi 830000，China）

Abstract： The study investigates the dynamic elastic modulus and damping ratio of sand and gravel under single and bidirectional cyclic loads using a large-scale vibration triaxial test. It also analyzes the effects of confining pressure and radial cyclic stress on the dynamic parameters of sand and gravel. The results show that in the bidirectional vibration triaxial test， the axial dynamic strain of sand and gravel is less influenced by the radial dynamic stress， with the dynamic strain primarily related to the applied axial dynamic stress. Under both unidirectional and bidirectional vibration， the dynamic elastic modulus of sand and gravel gradually decreases with the increase of dynamic strain. Under bidirectional vibration， the decay rate of dynamic elastic modulus of sand and gravel remains essentially unchanged， and the dynamic modulus of bidirectional vibration is lower than that of unidirectional vibration under the same dynamic strain. The damping ratio of sand and gravel under bidirectional vibration is larger than that under unidirectional vibration， and the dynamic strain energy consumed under bidirectional vibration is larger. Based on the analysis of the maximum dynamic elastic modulus and dynamic modulus ratio under the two test conditions， a conversion relation expressing the maximum dynamic elastic modulus under single and double direction test conditions and a correction model of the dynamic modulus ratio and dynamic strain in the bidirectional vibration test were established. The research results can provide a theoretical basis for the seismic design of sand and gravel in high earth-rock dams.

Key words： gravel material； dynamic triaxial test； dynamic elastic modulus； damping ratio； bidirectional vibration； radial dynamic stress

作者简介： 何建新（1973―），男，硕士，教授。 E‑mail： 604690896@qq.com。