风力机叶片预弯状态颤振效应分析

摘要： 风力机叶片预弯设计大多采用静气弹分析方法，忽略了叶片气动力、惯性力和弹性力三者相互作用而引发的气弹耦合失稳问题，而预弯对百米量级超长柔性叶片的颤振性能影响尤为显著。为对比分析不同预弯尺寸对叶片颤振临界状态的影响，基于主梁刚度等效原则进行叶片气弹模型设计，通过风洞试验发现了15 MW两种预弯叶片颤振区间及其临界风速的差异；进一步基于修正的叶素动量理论和几何精确梁理论（Blade Element Momentum Theory⁃Geometrically Exact Beam Theory，BEM⁃GEBT）耦合计算方法对4种预弯叶片进行分析，对比了不同预弯尺寸叶片的颤振临界风速、气动力分布和位移频谱特性，并揭示了颤振耦合模态机理。研究表明：BEM⁃GEBT耦合计算方法结果与风洞试验结果吻合较好；随着预弯尺寸的增大，挥舞⁃摆振耦合颤振临界风速提高，颤振区间范围基本一致；不同预弯尺寸叶片升力系数和俯仰力矩系数发散速率与位移发散速率呈正相关，平均风压曲线在预弯3～4 m范围内出现显著变化，挥舞⁃摆振耦合效应大于挥舞⁃扭转耦合效应，其颤振耦合频率由一阶挥舞频率主导。

关键词： 超长柔性叶片； 预弯效应； 风洞试验； 气动弹性耦合； 颤振失稳

中图分类号： TK83 文献标志码： A 文章编号： 1004-4523（2024）06-0986-11

DOI：10.16385/j.cnki.issn.1004-4523.2024.06.009

引 言

预弯［1］作为大兆瓦级风力机叶片设计的关键环节，是防止超长柔性叶片出现扫塔事故的主要措施。预弯改变了叶片气动外形和结构特性，影响其气动力、惯性力和弹性力的相互作用和不同模态间的耦合振动，易造成叶片气动弹性耦合颤振失稳。现有预弯设计大多采用静气弹设计方法［2⁃3］，未考虑动气弹耦合影响。然而在强/台风作用下，风力机叶片因预弯效应发生气弹失稳破坏的事故［4⁃7］屡见不鲜，如2008年台风“蔷薇”导致风力机叶片发生严重破坏，2013年台风“鲇鱼”造成风力机叶片折断等。系统研究预弯尺寸效应对叶片气弹失稳的发生机制具有重要意义。

目前针对风力机叶片预弯效应的研究大多采用数值模拟方法，主要内容涉及叶片稳定性能［8］、预弯静力响应［9⁃10］、机组输出功率［3，11］等。研究发现，预弯有助于叶片扭转载荷的降载和稳定，预弯叶片截面的扭转变形则使风力机的实际气动功率减小，其轴向弹性变形有利于实际功率的提高。但静气弹分析方法忽略了结构附加变形效应、结构运动位移和速度与气动力耦合效应，很难精确反映预弯效应的颤振失稳影响。气弹风洞试验是研究颤振预弯效应最有效的手段之一，但由于风力机叶片翼型不规则，其截面、刚度、剪心等沿展长不规则分布使得气弹模型设计难，又因其大缩尺比带来的测点布置难、采集干扰性强和测量精度低等试验因素，导致国内外缺少风力机叶片的三维气弹风洞试验。现主要采用节段翼型［12⁃15］进行测压、测力试验，探讨二维翼型测压、测力的一致性，但二维翼型试验难以真实反映三维叶片预弯效应对于颤振的影响。

鉴于此，本文以NREL⁃15 MW风力机超长柔性叶片为研究对象，首先基于主梁刚度等效原则设计超长柔性叶片三维气弹模型，并采用高速摄像技术和高频六分量天平进行同步测振、测力气弹风洞试验，提炼预弯尺寸对颤振区间及临界风速的组合规律；然后基于BEM⁃GEBT耦合计算方法研究预弯尺寸对叶片颤振性能的影响，最后揭示预弯尺寸对气弹耦合模态的影响机理，研究结论可为超长柔性风力机叶片预弯设计提供参考依据。

1 气弹模型风洞试验

1.1 气弹模型设计

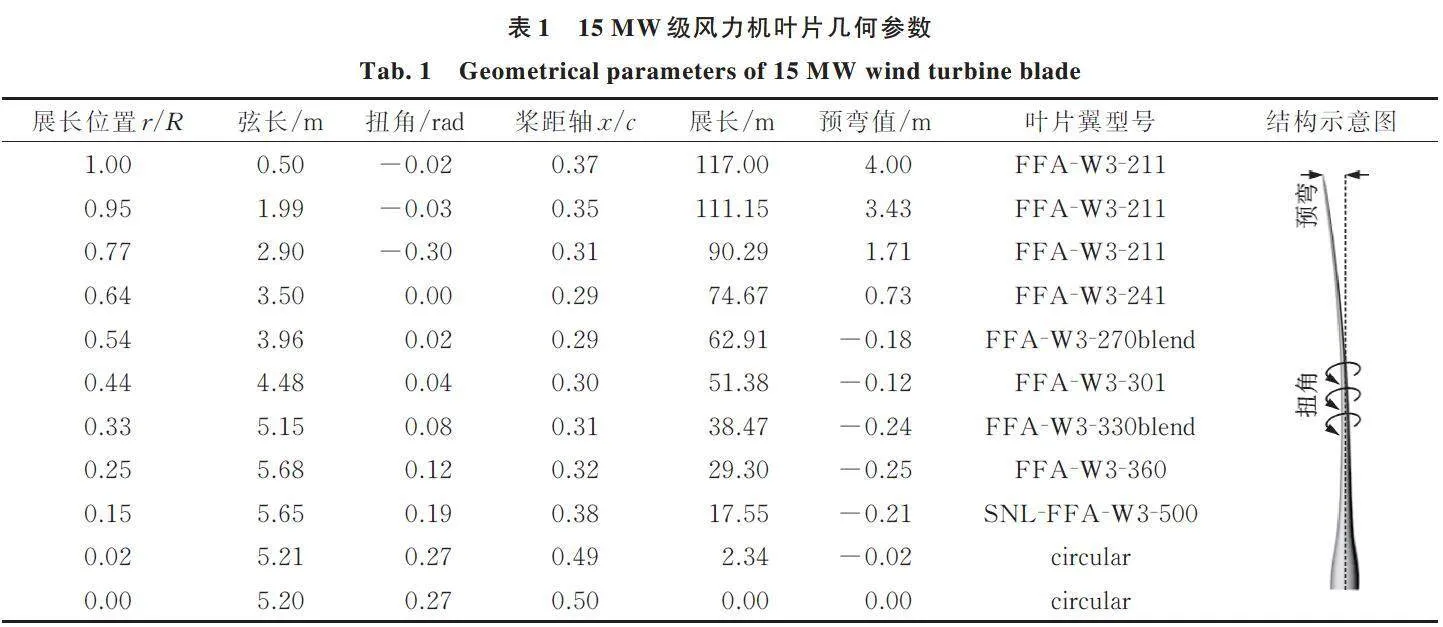
以美国国家可再生能源实验室NREL⁃15 MW风力机叶片［16］为研究对象，该叶片全长117 m，叶片设计采用DTU FFA⁃W3翼型族，叶片根部直径为5.2 m，在27.2 m（23.3%）处弦长最大为5.77 m，单叶片质量为65.252 t，叶片质心为26.8 m，最大叶尖预弯位移量为4 m。叶片具体几何参数如表1所示。表1中，r为以叶根处为起点，沿叶根到叶尖方向的实际位置；R为叶片总长度；x为截面桨距中心位置；c为截面弦长。

气动外形相似和结构动力学相似是气弹模型设计的基本原则，风洞试验叶片气弹模型需要模拟几何尺寸、风场特性和气动弹性特性。气弹相似条件物理量可采用无量纲参数来表示，如Reynolds数、Froude数、Cauchy数、密度比、阻尼比等。而风力机叶片所在流场空气为低速、不可压缩、牛顿黏性流，其流体运动方程与结构运动方程分别为：

（1）

（2）

式中 u为流体运动广义速度；f为流体广义外力；ρ为空气密度；P为压强；为空气动力黏度；x为坐标系主轴；ω为锁频风振频率；M为广义质量；K为广义刚度；g为阻尼系数；V为流场速度；b1为参考长度；A为广义空气动力系数；q为广义坐标。

引用符号λX表示模型的Xm同实物的Xa之比，即λX=Xm/Xa，可以用实物参数写为：

（3）

（4）

对流体运动方程所有项乘以λl/λ，对结构运动方程考虑减缩频率相同，即λbλω/λV=1。为保证原型和模型流体运动与结构运动的相似性，物理量的比值需满足下式：

（5）

（6）

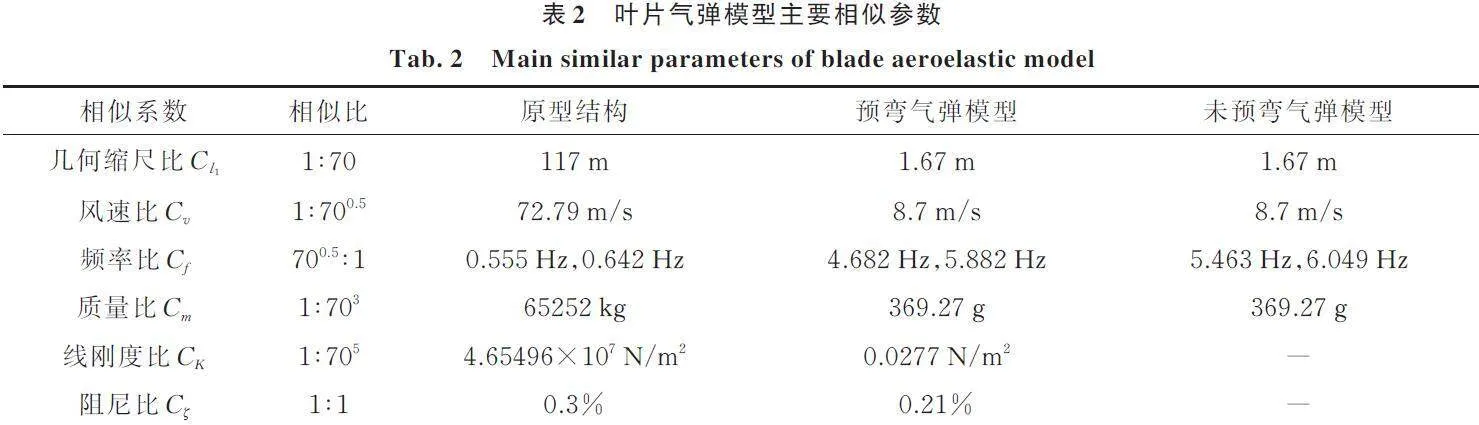
考虑风洞试验条件限制，不易保证Re数相等，且模型与原型Re数均处于自模区［17］，不是决定性相似准则，因此忽略Re数相等准则。根据风洞阻塞率要求，预弯与未预弯气弹模型缩尺比均选为1∶70，其中，未预弯气弹模型沿展长预弯尺寸设为零，缩尺后的模型叶片底部最大直径为0.074 m，高度为1.67 m，满足阻塞率要求。因添加质量块和安装叶片底座连接件产生了附加质量，使得模型质量与目标质量偏差稍大，模型动力相似通过控制试验模型的固有振动特性来保证。其余无量纲参数由相似准则推算得出，叶片气弹模型主要相似参数如表2所示。

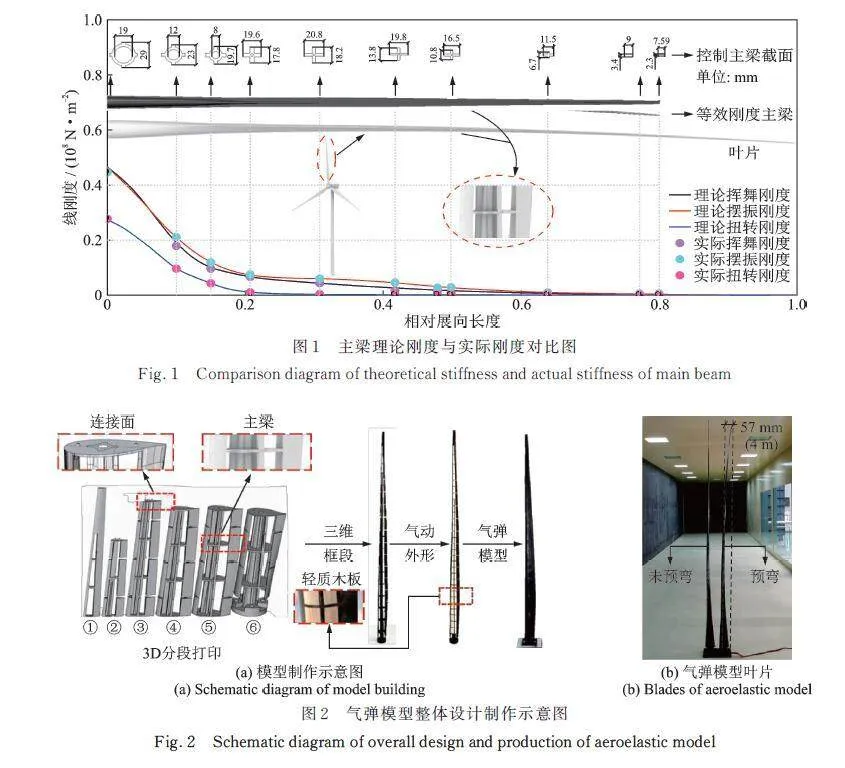
结构动力特性是进行结构动力试验和动力响应分析的基础，气弹模型需考虑结构频率分布特点。为了便于调节叶片挥舞刚度、摆振刚度和扭转刚度，基于变分渐进梁截面法（VABS）提出等效梁截面法进行风力机叶片的气弹模型制作，叶片通过变截面异形梁提供全部刚度，每段梁截面具体尺寸根据模型控制截面的目标刚度设计，梁截面尺寸由叶根到叶尖逐渐减小，气弹模型主梁理论刚度与实际刚度对比曲线及主梁截面形状如图1所示。

气弹模型的气动外形采用“维形框段”结构形式，维形框段保证模型的气动外形，框段和主梁连接方式采用单点连接。为保证框段不对整体结构提供额外刚度，框段采用分段式打印，相邻框段间有3 mm间隙，分段缝隙采用高密泡沫进行填充，前后缘和檩条之间的镂空区域采用轻质木片填充打磨，以保证气动外形封闭。风力机叶片整体采用聚酰胺纤维（未来7500尼龙）分段式3D打印，重心和转动惯量通过质量块调整配重进行模拟。预弯与未预弯气弹模型整体设计制作示意图如图2所示。

1.2 动力特性分析

为验证气弹模型与原型结构的相似性，基于锤击法测量气弹模型固有频率，采用随机减量法［18］处理得到结构模态参数。表3为气弹模型与原型结构动力特性对比分析列表，其中NREL⁃15 MW研究报告［16］仅给出结构前2阶模态频率。分析发现：预弯气弹数值模型和预弯气弹模型与原型结构的前2阶模态固有频率基本吻合，误差均在10%以内，表明气弹模型的动力学特性与原型结构匹配较好，保证了气弹模型的颤振特性与原型结构的相似精度；未预弯气弹模型前2阶频率明显大于预弯气弹模型。

1.3 风洞测量系统

风洞试验段长20 m，高2 m，宽2.5 m，最大试验风速为30 m/s，风洞上游来流风速通过眼镜蛇三维脉动风速测量仪测量。叶片模型竖直放置在风洞的转盘中心处，通过连接件与高频六分量天平固定，其底端与风洞转盘固结，模型可以随转盘360°转动，通过采集系统实时测量根部六分力。叶尖位移采集通过补光灯照射叶尖反光点，并使用高速摄像系统记录叶尖反光点移动轨迹，高速摄像采样频率为330 Hz，每个试验工况采集60 s叶尖运动高帧视频，再使用编程处理高速摄像视频，得到叶尖挥舞和摆振方向位移。风洞气弹模型测量系统示意图如图3所示。

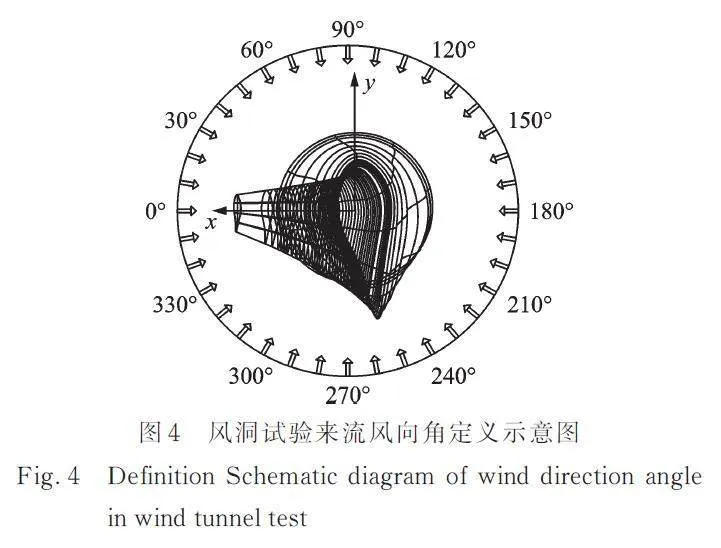
鉴于风洞试验中叶片桨距角不能主动调节，又考虑到实际风向的突变性［19⁃20］，叶片的风攻角区间为0°～360°，以每10°为间隔共设置36个桨距角，每个桨距角测量7个风速工况，逐级加载，在风振响应显著的工况下每隔0.5°进行内插，提取风振响应敏感桨距角。定义叶片正常运行状态下的转盘为0°，转盘以面向来流方向顺时针旋转为正，顺风向为叶片挥舞方向，垂直顺风向为叶片摆振方向，风洞试验来流风向角定义示意图如图4所示。

1.4 试验结果分析

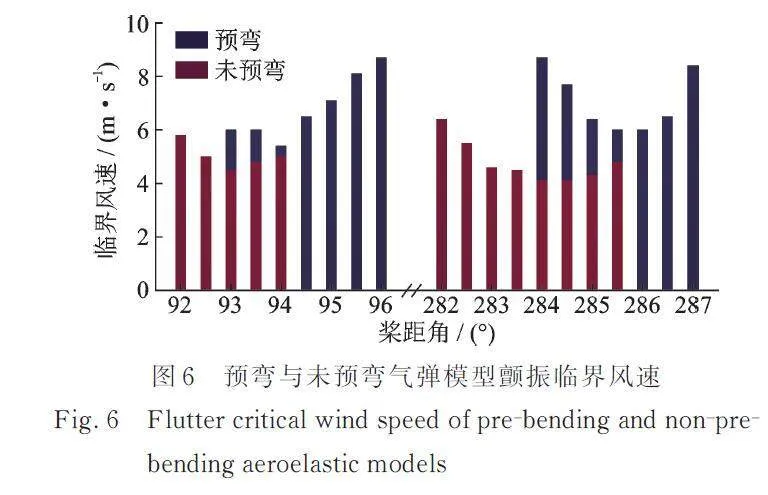
图5给出了全桨距角下风速为8.7 m/s（实际风速为72.8 m/s）时，预弯与未预弯气弹模型的叶尖位移均方根对比图。由图5可知，在桨距角0°～180°范围内，预弯与未预弯气弹模型颤振区间分别为93°～96°和92°～94°；在桨距角180°～360°范围内，预弯与未预弯气弹模型颤振区间分别为284°～287°和282°～285.5°；叶尖挥舞位移均方根显著大于叶尖摆振位移均方根。

将风速从4 m/s开始每隔0.1 m/s逐级加载，预弯与未预弯气弹模型的颤振临界风速结果如图6所示。对比发现：两叶片在颤振区间内颤振临界风速均呈现先减小后增大的趋势；在桨距角0°～180°范围内，预弯与未预弯气弹模型最小颤振临界风速分别为5.4和4.5 m/s，最大颤振临界风速分别为8.7和5.8 m/s；在桨距角180°～360°范围内，预弯与未预弯气弹模型最小颤振临界风速分别为5.4和4.1 m/s，最大颤振临界风速分别为8.7和6.4 m/s；在二者相交的颤振区间内，预弯模型的颤振临界风速比未预弯模型的大。

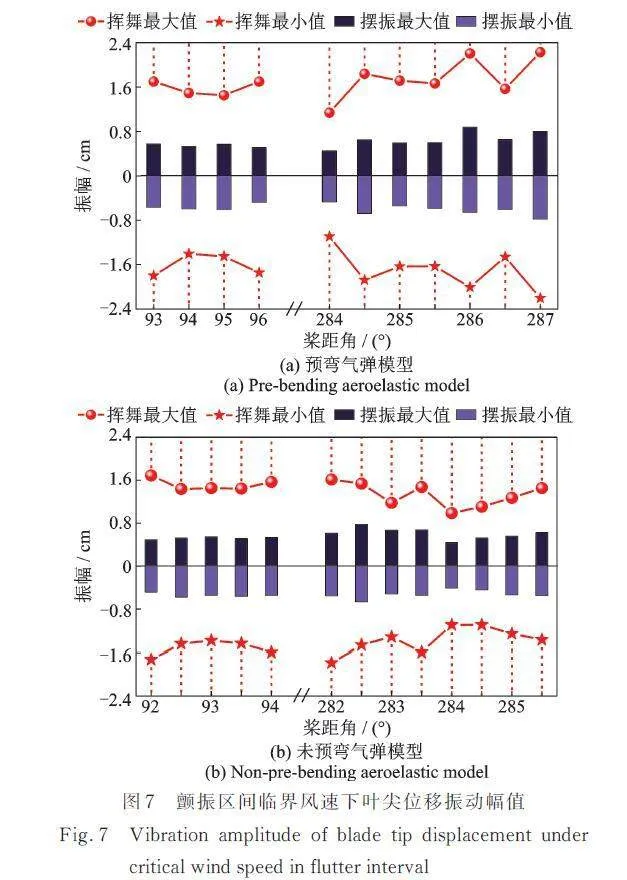
图7给出了颤振区间临界风速下叶尖位移振动幅值随桨距角变化的曲线。对比颤振区间临界风速下叶尖位移振动幅值的变化可知：预弯与未预弯气弹模型的挥舞位移明显大于摆振位移，挥舞位移最大值和最小值的绝对值基本相等，摆振位移亦呈现相同特点。结合图7分析可知：预弯与未预弯气弹模型在颤振桨距角0°～180°范围内，挥舞/摆振振幅与颤振临界风速变化趋势一致；在颤振桨距角180°～360°范围内，挥舞/摆振振幅与颤振临界风速呈非线性关系。

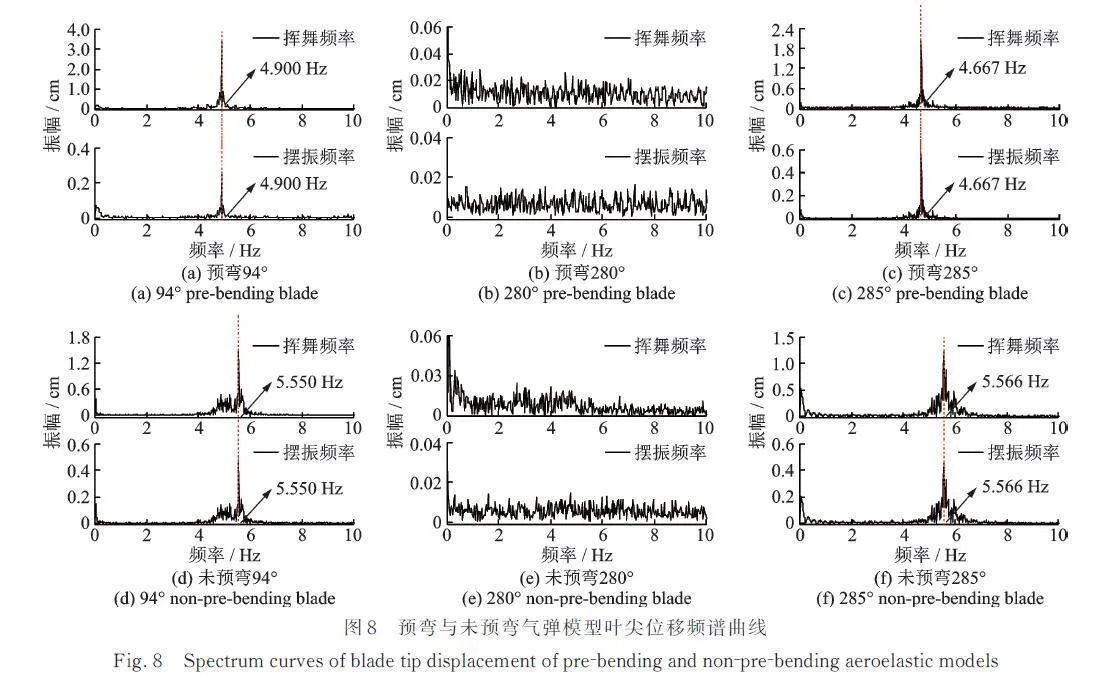
图8给出了风速为8.7 m/s，桨距角分别为94°，280°和285°时，预弯与未预弯气弹模型的挥舞/摆振叶尖位移频谱曲线。由图8可知：预弯与未预弯气弹模型发生颤振时，挥舞位移主导频率与摆振位移主导频率基本相等，耦合主导频率与各自的一阶挥舞频率（4.682和5.463 Hz）基本一致；预弯与未预弯气弹模型未发生颤振时，叶尖位移频谱曲线呈平缓波动趋势，均没有主导频率。

2 BEM-GEBT耦合计算方法

叶片发生大幅振动时结构变形较大，超长预弯叶片的柔性变形具有明显的几何非线性特点，且沿展长方向各翼型攻角随时间发生周期性变化，从而影响翼型气动力。为了研究预弯尺寸的颤振机理，结合修正的叶素动量理论与几何精确梁理论分析叶片非定常效应。

2.1 BEM-GEBT耦合方法

2.1.1 气动控制方程

基于叶素动量理论计算风力机叶片气动力，假设风轮所受气动载荷沿叶片展向均匀分布，且作用在叶片截面弦上距离前缘1/4即气动中心处。为了获得较为准确的计算结果，采用Prandtl叶尖损失修正［21］、Pitt/Peters模型［22］、动态失速模型［23］对该算法进行修正，进行非线性迭代求解。

由叶素定理和动量定理可得，作用在风轮半径r1处的微元环所受推力和转矩分别为：

（7）

（8）

式中 B为叶片数；V0为自由来流速度；Cn和Ct分别为法向力系数和切向力系数；ϕ为入流角；askew为修正后的轴向诱导因子；a′为切向诱导因子；F为叶尖损失修正因子。

2.1.2 结构控制方程

几何精确梁理论［24］适用于几何非线性及大挠度变形结构，具有伸展、弯曲、剪切和扭转自由度，使用完整的6×6质量和刚度矩阵，其运动控制方程为：

（9）

（10）

式中 和分别为惯性系中的线动量和角动量；和分别为梁的截面力和力矩；为梁参考线上一点的一维偏移量；为沿着梁参考线上一点的方向向量；和分别为作用在梁结构上的分布力和力矩；其中，变量下方加下划线标记表示向量或相应矩阵的维度，加双下划线标记表示张量；另外，上角标“'”表示对梁的轴线求导数，变量上方加“∙”表示对时间求导数，变量上方加“～”表示给定向量的反对称张量。

叶片的阻尼力与应变率成正比，针对6个自由度（3个平移，3个旋转）给定叶片6个阻尼系数。通过每个截面的刚度矩阵和阻尼系数矩阵以及应变率可以得到阻尼力为：

（11）

式中 为阻尼力；为应变率；为6×6刚度矩阵；为阻尼系数矩阵。

2.2 OpenFAST二次开发建模

为进一步研究不同预弯尺寸对颤振性能的影响，设计了4种预弯叶片，其尺寸分别为0，3，4和5 m，叶片翼型选用与NREL⁃15 MW风力机叶片相同数据，基于积叠线形状设计方法［2］，采用与叶片展向线性和二次曲线结合的形式对叶片进行预弯，预弯起于叶片根部。预弯表达式如下式所示：

（12）

式中 为沿展向的预弯位移；R0为叶片长度；a和b分别为线性和二次项系数。

综合考虑风力机输出功率随叶片预弯尺寸增大呈非线性减小［11］及叶片扫塔因素，预弯尺寸参数分别取a=2.5，b=5.5（预弯3 m）；a=3.3，b=7.3（预弯4 m）；a=4.1，b=9.1（预弯5 m）进行设计。

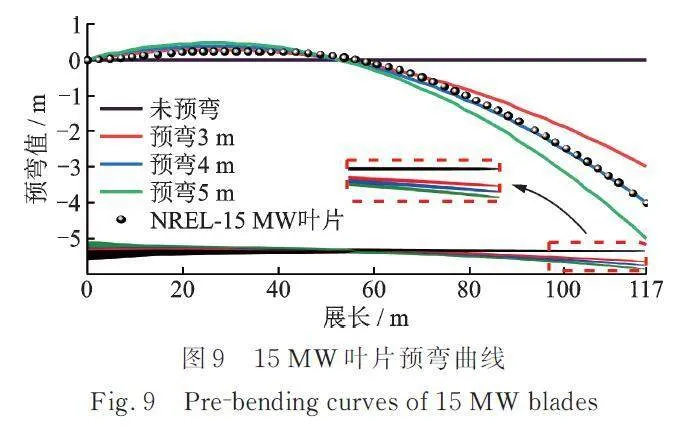
根据公式（12）得到4种叶片预弯曲线，并将叶片与NREL⁃15 MW原型结构进行对比，结果如图9所示。由图9可知：基于积叠线形状设计方法得到的预弯4 m曲线与NREL⁃15 MW原型结构拟合较好。

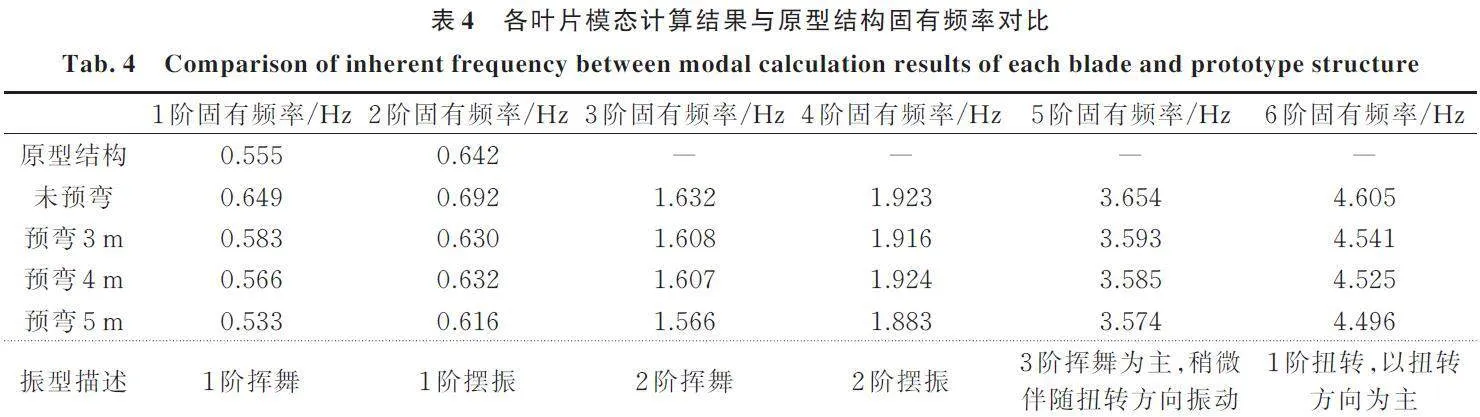
对4种预弯叶片进行模态计算，表4给出了模态计算结果与NREL⁃15 MW原型结构（预弯4 m）前2阶固有频率［16］的对比。对比4种预弯叶片固有频率可知：所设计的预弯叶片具有较高的精度；叶片前4阶振型以挥舞或摆振方向为主；第5阶振型以挥舞方向为主，稍微伴随扭转方向振动；第6阶振型主要表现为扭转方向振动；叶片前3阶固有频率随预弯尺寸的增大均有所降低，且一阶挥舞频率与一阶摆振频率偏离程度逐渐增大。

2.3 有效性验证

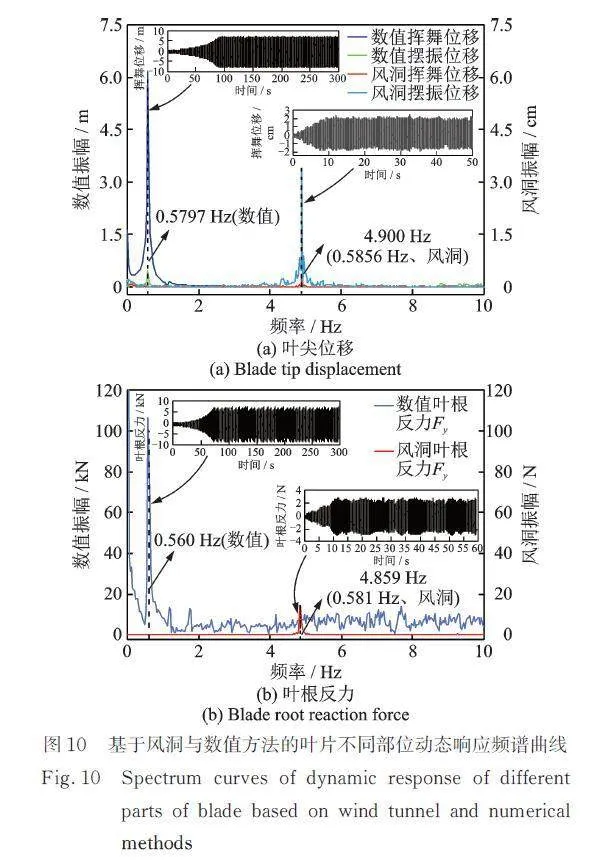
为验证数值模拟与风洞试验数据结果的一致性，选取风洞试验风速为8.7 m/s及桨距角为94°的工况结果进行验证对比。考虑数值模拟采用足尺模型，风洞试验相应数据按缩尺比进行调整，其足尺模型对应风速为72.8 m/s，叶尖位移和叶根反力动态响应频谱曲线如图10所示。对比叶尖位移和叶根反力动态响应频谱曲线可知：数值频率分别为0.578和0.560 Hz，与一阶挥舞频率（0.555 Hz）基本对应，风洞试验频率分别为4.900和4.859 Hz，按照缩尺比换算全尺寸模型为0.586和0.581 Hz；数值挥舞/摆振位移及挥舞方向叶根反力的主导频率与风洞试验结果基本一致，误差均小于5%，表明BEM⁃GEBT耦合计算方法结果与风洞试验结果吻合较好。

3 预弯效应分析

3.1 颤振临界风速

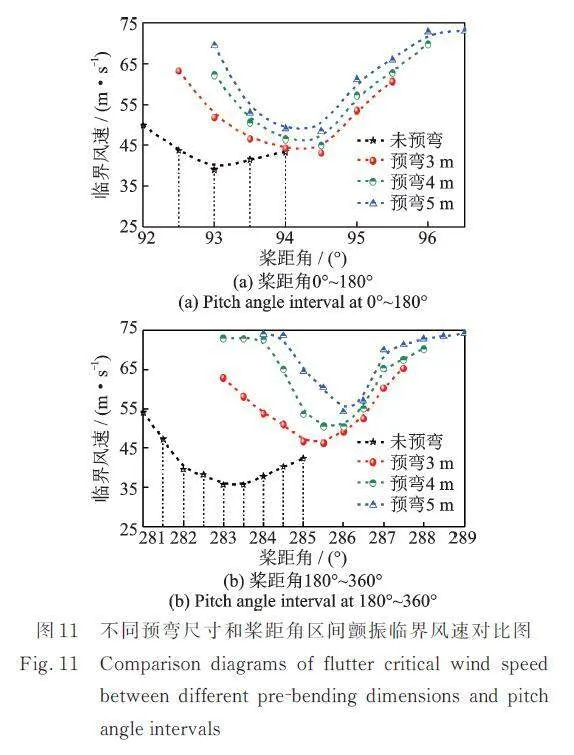
图11给出了由BEM⁃GEBT耦合计算方法计算来流风速为72.8 m/s时，4种预弯叶片的颤振区间及颤振临界风速。由图11可知：4种预弯叶片在桨距角0°～180°和180°～360°范围内均会发生颤振，定义桨距角0°～180°范围内的颤振区间为颤振Ⅰ区间，180°～360°范围内的颤振区间为颤振Ⅱ区间。4种预弯叶片的颤振区间有较大重合部分，颤振Ⅰ，Ⅱ区间的临界风速均呈抛物线趋势，初始颤振桨距角随预弯尺寸的增大呈后移现象，与风洞试验得到的规律一致；同一颤振桨距角下，颤振临界风速随预弯尺寸的增大而增大；随着预弯尺寸改变，颤振区间未发生明显变化。

3.2 气动力特性

为分析预弯尺寸对叶片颤振气动力的影响，选取未预弯叶片和预弯4 m叶片两种典型工况进行分析。图12给出了来流风速为72.8 m/s及桨距角为94°时，两种工况叶片的叶尖截面升力系数Cl和俯仰力矩系数CT的归一化曲线。由图12可知：升力系数随时间变化呈发散状态，叶尖截面翼型攻角随叶片大幅发散呈现周期性变化；升力系数与俯仰力矩系数幅值增长速度随预弯尺寸的增大而减缓；同一预弯尺寸的升力系数曲线与俯仰力矩系数曲线波动相位一致，可以看出不同预弯尺寸的升力特性主要受叶片扭转的影响。

图13给出了来流风速为72.8 m/s及桨距角为94°时，4种预弯叶片沿展长平均风压变化的曲线。由图13可知：4种预弯叶片平均风压曲线变化趋势基本一致，沿展长呈现先减小后增大的趋势，且平均风压变化速率随预弯尺寸的增大而减小；在叶片展长0～47 m范围内，平均风压相差不明显，展长超过47 m后，平均风压随预弯尺寸的增大呈减小趋势且在3～4 m范围内减小趋势显著；沿展长方向平均风压呈非线性增长且随预弯尺寸的增大趋于平缓分布。

3.3 气弹耦合模态

图14给出了4种预弯叶片的典型响应对比曲线。由位移时程曲线可知：颤振位移发展阶段随预弯尺寸的增加而逐渐延长，但位移不会无限发散，最终发展为锁幅振动且4种预弯叶片振动幅值基本一致。由频谱对比曲线可知：不同预弯尺寸叶片挥舞、摆振和扭转的主导频率基本相等并对应各自一阶挥舞频率，即叶尖颤振变形主要受一阶挥舞振动的影响。由振动幅值可知：耦合频率处的振动幅值随预弯尺寸的增大而减小，叶尖运动能量随预弯尺寸的增大呈减小趋势，4种预弯叶片的挥舞⁃摆振耦合效应大于挥舞⁃扭转耦合效应。

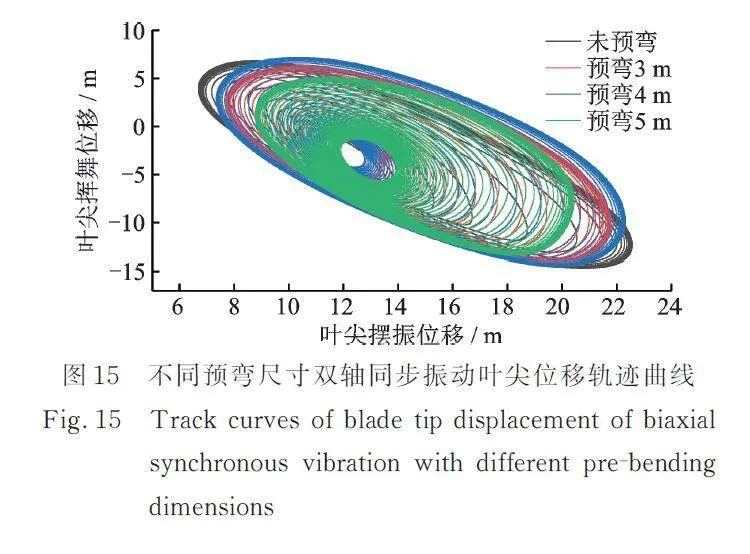
图15给出了4种预弯叶片的挥舞⁃摆振双轴同步振动叶尖位移轨迹曲线。由图15可知：摆振方向位移随预弯尺寸的增大呈现先减小后增大再减小的趋势，挥舞方向位移随预弯尺寸的增大出现先增大再减小的趋势；4种预弯叶片双轴轨迹图由初始振动逐步增大，发展到一定阶段达到稳态，随后进入锁幅振动状态，双轴位移轨迹表现为类椭圆闭合曲线。

4 结 论

（1）基于主梁刚度等效原则设计了三维叶片气弹模型，发展了基于修正的叶素动量和几何精确梁理论耦合的颤振分析方法，与风洞试验结果对比，表明BEM⁃GEBT耦合计算方法能有效模拟风力机叶片的颤振预弯效应，最大误差为5%。

（2）风力机叶片固有频率随预弯尺寸的增大逐渐减小，且一阶挥舞频率与一阶摆振频率偏离程度呈加大趋势；颤振区间随预弯尺寸的增大呈现小幅度后移趋势，相同桨距角下颤振临界风速亦随预弯尺寸的增大而增大，颤振区间范围基本一致。

（3）升力系数与俯仰力矩系数发散速率随预弯尺寸的增大而减缓，并与位移发散速率呈正相关，且不同预弯尺寸的升力特性主要受叶片扭转的影响；4种预弯叶片平均风压曲线变化趋势基本一致，沿展长呈现先减小后增大的趋势。

（4）叶尖运动能量积累随预弯尺寸的增大呈减小趋势；不同预弯超长柔性叶片的挥舞⁃摆振耦合效应大于挥舞⁃扭转耦合效应，其颤振耦合频率由一阶挥舞频率主导，双轴位移轨迹表现为规则的类椭圆闭合曲线。

参考文献：

［1］ OLESEN E E， KOEFOED M S， PEDERSEN S H， et al. Method of manufacturing pre-bent wind turbine blades： US13176419［P］. 2012-07-10.

［2］ HANSEN M H. Aeroelastic properties of backward swept blades［C］. 49th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Orlando， Florida， 2011： 260.

［3］ 郭小锋， 陈进， 李松林. 风力机叶片预弯设计机理与方法［J］. 东北大学学报（自然科学版）， 2016， 37（6）： 851-855.

GUO X F， CHEN J， LI S L. Mechanism and method of pre-bending design for the wind turbine blades［J］. Journal of Northeastern University （Natural Science）， 2016， 37（6）： 851-855.

［4］ CHOU J S， CHIU C K， HUANG I K， et al. Failure analysis of wind turbine blade under critical wind loads［J］. Engineering Failure Analysis， 2013， 27： 99-118.

［5］ 王浩， 柯世堂， 王同光. 台风过境全过程大型风力机风荷载特性［J］. 空气动力学学报， 2020， 38（5）： 915-923.

WANG H， KE S T， WANG T G. Wind loads characteristic of large wind turbine considering typhoon transit process［J］ Acta Aerodynamica Sinica， 2020， 38（5）： 915-923.

［6］ 柯世堂， 徐璐， 王同光， 等. 考虑停机位置风力机塔架-叶片耦合体系风致稳定性能分析［J］. 太阳能学报， 2020， 41（1）： 264-272.

KE S T， XU L， WANG T G， et al. Analysis of wind-induced stability tower-blade coupling system of wind turbine considering stopping positions［J］. Acta Energiae Solaris Sinica， 2020， 41（1）： 264-272.

［7］ CHEN X， XU J Z. Structural failure analysis of wind turbines impacted by super typhoon Usagi［J］. Engineering Failure Analysis， 2016， 60： 391-404.

［8］ BAZILEVS Y， HSU M C， KIENDL J， et al. A computational procedure for prebending of wind turbine blades［J］. International Journal for Numerical Methods in Engineering， 2012， 89（3）： 323-336.

［9］ RIZIOTIS V A， VOUTSINAS S G， MANOLAS D I， et al. Aeroelastic analysis of pre-curved rotor blades［C］. Proceedings of the European Wind Energy Conference and Exhibition 2010. Warsaw， Poland， 2010： 1173-1202.

［10］ 田德， 罗涛， 梁俊宇， 等. 风电机组预弯叶片模型的有限元分析［J］. 太阳能学报， 2017， 38（6）： 1482-1488.

TIAN D， LUO T， LIANG J Y， et al. Finite element analysis of pre-bending blade model for wind turbine generation system［J］. Acta Energiae Solaris Sinica， 2017， 38（6）： 1482-1488.

［11］ 郭婷婷， 吴殿文， 王成荫， 等. 风力发电机叶片预弯设计及其数值研究［J］. 动力工程学报， 2010， 30（6）： 450-455.

GUO T T， WU D W， WANG C Y， et al. Pre-bend design and numerical simulation of wind turbo-generator［J］. Journal of Chinese Society of Power Engineering， 2010， 30（6）： 450-455.

［12］ 程鹏. 水平轴风力机叶片气动弹性的风洞试验研究［D］. 哈尔滨： 哈尔滨工业大学， 2009.

CHENG P. Experimental study of aeroelasticity for the blades of horizontal axis wind turbines［D］. Harbin： Harbin Institute of Technology， 2009.

［13］ RAZAK N A， ANDRIANNE T， DIMITRIADIS G. Flutter and stall flutter of a rectangular wing in a wind tunnel［J］. AIAA Journal， 2011， 49（10）： 2258-2271.

［14］ DIMITRIADIS G， LI J. Bifurcation behavior of airfoil undergoing stall flutter oscillations in low-speed wind tunnel［J］. AIAA Journal， 2009， 47（11）： 2577-2596.

［15］ 张超宇. 后掠叶段气动及气弹特性的风洞实验研究［D］. 北京： 中国科学院大学（中国科学院工程热物理研究所）， 2020.

ZHANG C Y. Study on aerodynamic and aeroelastic characteristic of swept-back airfoil model based on wind tunnel experiments［D］. Beijing： University of Chinese Academy of Sciences （Institute of Engineering Thermophysics， Chinese Academy of Sciences）， 2020.

［16］ GAERTNER E， RINKER J， SETHURAMAN L， et al. IEA wind TCP task 37： definition of the IEA wind 15-megawatt offshore reference wind turbine： NREL/TP-5000-75698［R］. Golden， C.O.， United States： National Renewable Energy Laboratory （NREL）， 2020.

［17］ 黄本才， 汪丛军. 结构抗风分析原理及应用［M］. 2版. 上海： 同济大学出版社， 2008： 112-113.

HUANG B C， WANG C J. Principle and Application of Structural Wind Resistance Analysis［M］. 2nd ed. Shanghai： Tongji University Press， 2008： 112-113.

［18］ IBRAHIM S R. Random decrement technique for modal identification of structures［J］. Journal of Spacecraft and Rockets， 1977， 14（11）： 696-700.

［19］ 吴金城， 张容焱， 张秀芝. 海上风电机的抗台风设计［J］. 中国工程科学， 2010， 12（11）： 25-31.

WU J C， ZHANG R Y， ZHANG X Z. Anti-typhoon design for offshore wind turbines［J］. Strategic Study of CAE， 2010， 12（11）： 25-31.

［20］ 宋丽莉， 毛慧琴， 钱光明， 等. 热带气旋对风力发电的影响分析［J］. 太阳能学报， 2006， 27（9）： 961-965.

SONG L L， MAO H Q， QIAN G M， et al. Analysis on the wind power by tropical cyclone［J］. Acta Energiae Solaris Sinica， 2006， 27（9）： 961-965.

［21］ SHEN W Z， MIKKELSEN R， SØRENSEN J N， et al. Tip loss corrections for wind turbine computations［J］. Wind Energy， 2005， 8（4）： 457-475.

［22］ NING S A， HAYMAN G， DAMIANI R， et al. Development and validation of a new blade element momentum skewed-wake model within AeroDyn［C］//33rd Wind Energy Symposium. Kissimmee， Florida， 2015： 0215.

［23］ LEISHMAN J G， BEDDOES T S. A semi-empirical model for dynamic stall［J］. Journal of the American Helicopter Society， 1989， 34（3）： 3-17.

［24］ JÚNIOR C J F， CARDOZO A C P， JÚNIOR V M， et al. Modeling wind turbine blades by geometrically-exact beam and shell elements： a comparative approach［J］. Engineering Structures， 2019， 180： 357-378.

Analysis of flutter effect in the pre‑bending state of wind turbine blade

GAO Mu-en1， KE Shi-tang1，2， WU Hong-xin1，2， ZHANG Chun-wei1，2，

TIAN Wen-xin1， LU Man-man1

（1.Department of Civil and Airport Engineering， College of Civil Aviation， Nanjing University of Aeronautics and Astronautics， Nanjing 211106， China； 2.Jiangsu Key Laboratory of Hi-Tech Research for Wind Turbine Design，Nanjing University of Aeronautics and Astronautics， Nanjing 210016， China）

Abstract： Most wind turbine blade pre-bending designs use the static aeroelastic analysis method. This approach often overlooks the aeroelastic coupling instability caused by the interaction of blade aerodynamic force， inertial force and elastic force. This oversight is particularly significant when considering flutter performance of ultra-long flexible blades of around 100 meters. To analyze the influence of different pre-bending sizes on flutter critical state of blade， aeroelastic model of the blade was designed based on the stiffness equivalence principle of the main beam. Wind tunnel tests revealed differences between the flutter interval and the critical wind speed of two pre-bending blades of a 15 MW wind turbine. Further analysis was conducted on four pre-bending blades using the corrected Blade Element Momentum Theory-Geometrically Exact Beam Theory （BEM-GEBT） coupling calculation method. This analysis compared and analyzed the flutter critical wind speed， aerodynamic force distribution and displacement spectrum characteristics of blades with different pre-bending sizes， revealing the flutter coupling modal mechanism. The research shows that the results of BEM-GEBT coupling calculation method align well with those of wind tunnel test. As the pre-bending size increases， the flutter critical wind speed of flap-edge coupling increases， and the flutter interval range remains essentially the same. The divergence rates of lift coefficient and pitching moment coefficient of different pre-bending blades are positively correlated with the displacement divergence rate. The average wind pressure curve shows significant changes in the pre-bending range of 3～4 m. The flap-edge coupling effect is larger than the flap-torsion coupling effect， and the flutter coupling frequency is dominated by the first-order flapwise frequency.

Key words： ultra-long flexible blades；pre-bending effect；wind tunnel test；aeroelastic coupling；flutter instability

作者简介： 高沐恩（1997―），男，硕士。E-mail：gaomuen@nuaa.edu.cn。

通讯作者： 柯世堂（1982―），男，博士，教授。E-mail：keshitang@163.com。