旋转环境下的磁耦合双稳态能量俘获机理研究

摘要： 环境中存在大量的旋转运动能量，可以使用能量俘获技术将其转换为可用的电能，进而为嵌入式设备和无线传感器提供持续稳定的电能，以解决传统化学电池供电带来的环境污染和维护成本高等问题。为了提高能量俘获系统在超低频（低于3 Hz）旋转环境中的能量俘获性能，本文提出一种具有低势垒特性的时变势阱磁耦合双稳态能量俘获系统。在充分考虑了离心效应影响的前提下，基于能量法和拉格朗日方程在旋转坐标系下推导了该系统的分布式参数机电耦合方程。通过建立该系统的磁力计算模型以分析磁间距和离心效应对系统势能阱及能量俘获特性的影响。数值仿真结果和实验结果均验证了与传统线性能量俘获系统相比，本文提出的时变势阱磁耦合双稳态能量俘获系统具有更宽的工作频率范围（0～2.67 Hz）和更高的输出电压（大于2 V）。

关键词： 旋转能量俘获； 超低频； 双稳态； 时变势阱； 低势垒

中图分类号： TN712+.1； O322 文献标志码： A 文章编号： 1004-4523（2024）06-0964-12

DOI：10.16385/j.cnki.issn.1004-4523.2024.06.007

引 言

能量俘获技术被认为是解决传统化学电池供电存在的寿命有限、环境污染和维修更换困难等问题的新兴技术，该技术能够实现对无线传感器网络和物联网中的低功耗无线传感器的长期可靠供电［1⁃2］，具有广阔的工程应用前景。衡量能量俘获系统性能的两个关键指标是其输出功率和工作频率范围。然而，环境中的振动可能是时变的，并具有宽频特性，当线性能量俘获系统的工作频率与环境激励频率不匹配时，其能量俘获性能将显著降低。为了解决上述问题，学者们提出了非线性单稳态［3⁃4］、双稳态［5］、多稳态［6⁃7］和自调谐［8⁃9］等方法，并进行了理论和实验研究。此外，环境中存在着大量旋转运动，为能量俘获技术的应用提供了基础。从而使得旋转运动能量俘获技术在近年来受到了广泛的关注和研究［10⁃11］。

Gu等［12］利用离心力设计了一种被动调谐旋转能量俘获系统，实验结果验证了该系统具备频宽为11 Hz的自调谐性能。Hsu等［13］提出了一种利用离心硬化效应实现自调谐的能量俘获系统，采用有限元方法对该系统进行分析，同时进行了实验验证。Mei等［14］提出了四稳态自调谐能量俘获系统。Guan等［15］提出了一种压电倒置压电悬臂梁结构，利用离心软化效应增加输出功率，实验结果表明旋转频率在7～13.5 Hz范围内时，系统输出功率为83.5～825 μW。Liu等［16］提出了一种被动自调谐能量俘获器。

Mei等［17］研究了三稳态旋转压电能量俘获器在旋转运动中的性能，实验结果表明该系统的有效带宽为4～7.33 Hz。Zhou等［18］提出了一种具有时变势能特性的柔性双稳态能量俘获系统，该系统不仅具有较小的突跳阈值，而且在激振强度大于临界激振强度时可以产生较大的输出功率。Fang等［19］设计了一种碰撞式旋转能量俘获器，通过引入非线性碰撞力实现压电悬臂梁上的变频转换。Zou等［20］提出了一种磁耦合的双倒置压电悬臂梁结构，实验结果表明该系统适用于低频旋转运动，能俘获多频段的旋转运动能量。Febbo等［21］将双自由度悬臂梁型旋转能量俘获系统安装在轮毂上，在0.83～2.5 Hz频率范围内得到的输出功率为26～105 μW。Mei等［22］结合非线性磁力和离心软化效应设计了一种压电振动能量俘获系统，得到了大于4 V的均方根输出电压。Zhang等［23］设计了一种可安装在汽车轮胎上的旋转能量俘获器，其优点是可以扩大旋转频率带宽，同时在高能轨道稳定振荡；在车辆驱动实验中，该系统的有效工作范围可从15～25 km/h拓展至10～40 km/h，并且在40 km/h的驱动速度下，平均输出功率为61 μW。

目前，在超低频旋转运动能量俘获方面的研究相对较少。因此，为了实现在超低频旋转环境下高效俘获能量的目的，本文在上述研究的基础上，设计了一种具有低势垒特性的时变势阱磁耦合双稳态能量俘获系统。该系统能够在超低的旋转激励水平下跨越势垒实现大振幅阱间振荡，与线性能量俘获系统相比具有更宽的工作频率范围和更高的输出电压。

1 结构设计与工作原理

本文所提出的时变势阱磁耦合双稳态能量俘获系统如图1所示，一个正置悬臂梁和一个倒置压电悬臂梁共同安装在一个绕中心轴以超低频匀速转动的旋转圆盘上，且沿同一径向布置，旋转圆盘的角速度为，角位移为。其中，“正置”指的是悬臂梁固定端到自由端的方向与端部磁铁所受离心力方向一致，“倒置”指的是悬臂梁固定端到自由端的方向与端部磁铁所受离心力方向相反。正置悬臂梁和倒置压电悬臂梁的端部磁铁磁极相对且相斥，在静止状态下有两个对称的稳定平衡位置。正置悬臂梁的固定端到旋转中心的距离为，倒置压电悬臂梁固定端到旋转中心的距离为。当旋转圆盘做匀速转动时，两个悬臂梁在周期性重力分量的作用下发生振动，自适应调节两个端部磁铁之间的距离从而使系统具有时变势阱特性，有效地降低了双稳态系统的势阱深度，有利于该系统在超低频旋转激励下实现大振幅势阱间振荡，提高能量俘获性能。

2 动力学建模

2.1 系统的能量描述

时变势阱磁耦合双稳态能量俘获系统的几何关系如图2所示。由于在旋转运动中正置悬臂梁和倒置压电悬臂梁的横向位移是时变的，因此在旋转坐标系中建立其数学模型更为简便。

（1）动能计算

正置悬臂梁上任意一点在旋转坐标系中的方向矢量和速度矢量可表示为：

（1）

式中 ，分别为旋转坐标系中，方向上的单位向量；为正置悬臂梁在方向上的横向位移；为对时间的一阶导数。

同理，倒置压电悬臂梁上任意一点在旋转坐标系中的方向矢量和速度矢量可表示为：

（2）

式中 为倒置悬臂梁在方向上的横向位移；为对时间的一阶导数。

系统总动能的表达式为：

（3）

式中 为正置悬臂梁长度；为倒置压电悬臂梁长度；和分别为正置悬臂梁和倒置压电悬臂梁的单位长度质量；和分别为正置悬臂梁和倒置压电悬臂梁的端部质量。

（4）

式中 为悬臂梁基底的密度；为悬臂梁基底横截面面积（正置悬臂梁和倒置压电悬臂梁基底的厚度、宽度和材料参数完全一致，因此二者相关的参数用同一变量表示）。

（5）

式中 为压电片的密度；为压电片的横截面面积；为压电片长度。

（2）势能计算

正置悬臂梁弹性势能的表达式为：

（6）

式中 为对的二阶偏导数；为对的二阶偏导数；和分别为正置悬臂梁和倒置压电悬臂梁的抗弯刚度。

当时，的表达式为：

（7）

式中 为正置悬臂梁基底的杨氏模量；为正置悬臂梁基底的宽度；为正置悬臂梁基底的厚度。

当时，的表达式为：

（8）

式中 为压电片的杨氏模量；为压电片和悬臂梁基底的宽度（悬臂梁基底和压电片宽度一致用同一变量b表示）；为压电片的厚度。

当时，的表达式为：

（9）

式中 为倒置悬臂梁基底的杨氏模量；为倒置悬臂梁基底的厚度。

重力势能的表达式为：

（10）

式中 为重力加速度，。

离心势能的表达式为［22］：

（11）

目前磁偶极子模型已被广泛应用于计算磁力，并在参考文献［6，14］中被证明是有效的。因此，本文采用磁偶极子模型计算磁铁2fd0c9fbe96ffd1d7fa52157fd79a6e8A和磁铁B之间的非线性磁力。

如图3所示，在旋转坐标系中，磁铁A到磁铁B的向量的表达式为：

（12）

其中：

（13）

式中 为端部磁铁A的厚度；为端部磁铁B的厚度；为端部磁铁A和端部磁铁B之间在方向上的间距。

端部磁铁A的磁矩和端部磁铁B的磁矩可表示为：

（14）

式中 为端部磁铁A的磁化强度；为端部磁铁B的磁化强度；为端部磁铁A的体积；为端部磁铁B的体积；为端部磁铁A的转角；为端部磁铁B的转角。

式（14）中，和的表达式为：

（15）

式中 为磁铁A的剩余磁通量；为磁铁B的剩余磁通量；为真空磁导率。

式（15）中，和的表达式为：

（16）

根据磁偶极子模型，磁场中的磁感应强度的表达式为：

（17）

磁场中的磁力势能表达式为［21］：

（18）

磁铁A受到的磁力和磁铁B受到的磁力的表达式分别为：

（19）

（20）

式中 为的单位向量；为的单位向量；为的单位向量。

因此，磁力在Y*方向上的分力F1和磁力在Y*方向上的分力F2的表达式分别为：

（21）

（22）

该系统的势能为弹性势能、重力势能、离心势能和磁势能之和，即

（23）

（3）压电片的内部电能计算

倒置压电悬臂梁上压电片的内部电能的表达式为：

（24）

式中 为压电片的机电耦合系数；为倒置压电悬臂梁上的压电片的输出电压；为压电片的内部电容。

式（24）中，和的表达式分别为：

（25）

（26）

式中 为压电片的压电常数；为压电片的夹持介电常数；为压电片的厚度。

2.2 机电耦合方程推导

根据假设模态法，正置悬臂梁和倒置压电悬臂梁振动响应的横向位移可表示为有限展开项。考虑到旋转圆盘做超低频旋转运动，压电悬臂梁振动响应展开式中一阶模态占据主导地位，则和可表示为：

（27）

式中 为正置悬臂梁运动学上的一阶容许试探函数；为倒置压电悬臂梁运动学上的一阶容许试探函数；为正置悬臂梁运动学上的广义时间坐标；为倒置压电悬臂梁运动学上的广义时间坐标。和满足各自的边界条件［22］，具体表达式为：

（28）

（29）

式中 ～，～，～，～为待定系数，可根据悬臂梁边界条件求得。

不考虑机械耗散效应，时变势阱磁耦合双稳态能量俘获系统的拉格朗日方程为：

（30）

不考虑机械损失，非保守力所做的虚功（负载电阻和阻尼力耗散）可以表示为：

（31）

式中 和分别为正置悬臂梁和倒置悬臂梁的应变阻尼系数；为压电片产生的电荷量。

基于拓展的哈密顿原理，该结构的拉格朗日机电耦合方程为：

（32）

将式（3），（6），（10），（11），（21），（22），（23）和（30）代入式（32）得：

（33）

其中，各系数的表达式如下：

（34）

（35）

（36）

（37）

（38）

（39）

（40）

（41）

（42）

3 理论分析

3.1 磁间距对系统势能阱的影响

材料参数如表1～3所示。

在不考虑离心效应的情况下，数值分析磁间距d对系统势能阱的影响。势能为系统弹性势能和磁力势能之和，重力视作外部激励（在此不计算重力势能），的表达式为：

（43）

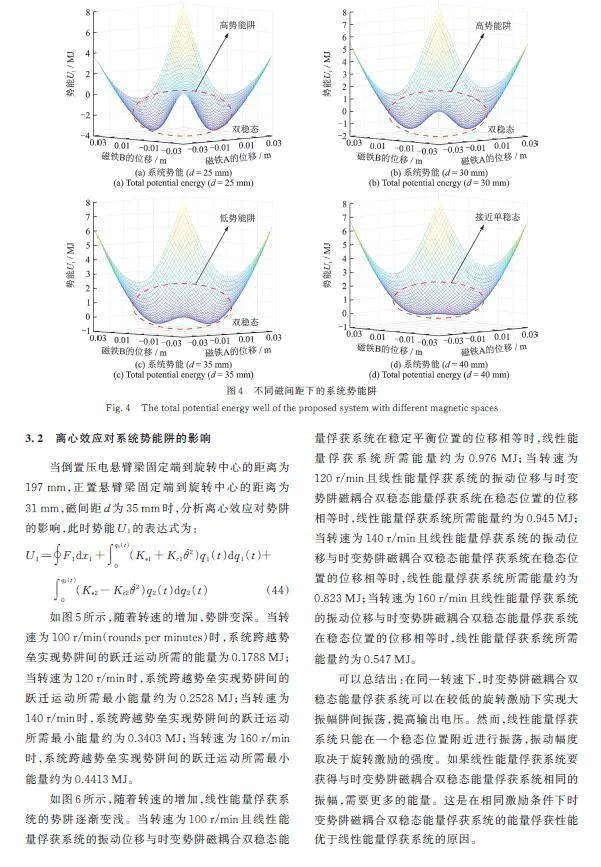
如图4所示，随着端部磁铁A和B之间的磁间距d的增加，系统的势阱深度逐渐降低，对应不同的非线性程度。当磁间距d为25和30 mm时，系统为对称双稳态系统，其势垒过高，难以实现有利于高输出电压的阱间振荡。当磁间距为35 mm时，系统为对称双稳态系统，其势垒显著减小，有利于系统在超低频旋转环境中实现阱间振荡，从而提高了输出电压。随着磁间距d进一步增大到40 mm，系统的非线性较弱，趋近于单稳态特征。

当系统在旋转圆盘上工作时，旋转运动过程中的周期性重力分量被看作是驱动系统跨越势垒的激励力。因此，当其势垒足够低时，即使在较低的旋转激励下，也可以获得较大的振幅（阱间运动），对应较高的输出电压，达到本文在超低频旋转运动中高效俘获能量的目的。因此为了在较低的旋转频率下提高输出电压，以上四组磁间距的值中取35 mm最佳。

3.2 离心效应对系统势能阱的影响

当倒置压电悬臂梁固定端到旋转中心的距离为197 mm，正置悬臂梁固定端到旋转中心的距离为31 mm，磁间距d为35 mm时，分析离心效应对势阱的影响，此时势能的表达式为：

（44）

如图5所示，随着转速的增加，势阱变深。当转速为100 r/min（rounds per minutes）时，系统跨越势垒实现势阱间的跃迁运动所需的能量为0.1788 MJ；当转速为120 r/min时，系统跨越势垒实现势阱间的跃迁运动所需最小能量约为0.2528 MJ；当转速为140 r/min时，系统跨越势垒实现势阱间的跃迁运动所需最小能量约为0.3403 MJ；当转速为160 r/min时，系统跨越势垒实现势阱间的跃迁运动所需最小能量约为0.4413 MJ。

如图6所示，随着转速的增加，线性能量俘获系统的势阱逐渐变浅。当转速为100 r/min且线性能量俘获系统的振动位移与时变势阱磁耦合双稳态能量俘获系统在稳定平衡位置的位移相等时，线性能量俘获系统所需能量约为0.976 MJ；当转速为120 r/min且线性能量俘获系统的振动位移与时变势阱磁耦合双稳态能量俘获系统在稳态位置的位移相等时，线性能量俘获系统所需能量约为0.945 MJ；当转速为140 r/min且线性能量俘获系统的振动位移与时变势阱磁耦合双稳态能量俘获系统在稳态位置的位移相等时，线性能量俘获系统所需能量约为0.823 MJ；当转速为160 r/min且线性能量俘获系统的振动位移与时变势阱磁耦合双稳态能量俘获系统在稳态位置的位移相等时，线性能量俘获系统所需能量约为0.547 MJ。

可以总结出：在同一转速下，时变势阱磁耦合双稳态能量俘获系统可以在较低的旋转激励下实现大振幅阱间振荡，提高输出电压。然而，线性能量俘获系统只能在一个稳态位置附近进行振荡，振动幅度取决于旋转激励的强度。如果线性能量俘获系统要获得与时变势阱磁耦合双稳态能量俘获系统相同的振幅，需要更多的能量。这是在相同激励条件下时变势阱磁耦合双稳态能量俘获系统的能量俘获性能优于线性能量俘获系统的原因。

4 实验验证

4.1 实验装置

如图7和8所示，旋转装置固定安装在光学平台上，由旋转圆盘、旋转轴、底座、伺服电机和电滑环组成。伺服驱动器（SGD7S， YASKAWA）控制的伺服电机（SGM7J， YASKAWA）带动旋转轴为旋转圆盘提供动力。转轴的转速可以通过电脑上的SigmaWin+（Version 7.0，YASKAWA）软件进行参数设置，软件将控制信号输入电机执行器从而对伺服电机进行控制。能量俘获结构和激光位移传感器（HG⁃C1100，Panasonic）安装在旋转圆盘上，它们的输出信号（电压信号和位移信号）通过电滑环中的导线输出到数字示波器（DSOX3014T， KEYSIGHT）中。示波器的内阻为1 MΩ，用于监测和测量输出电压和位移，数字示波器的采样频率为每秒500个采样点。电滑环（SENRING，CHINA）由定子和转子组成，安装在旋转轴上，导线从电滑环转子中穿过，因此在旋转过程中导线与旋转圆盘保持相对静止状态，从而解决了旋转运动中导线的缠绕问题。

如图9所示，倒置压电悬臂梁固定端到旋转中心的距离R为197 mm，正置悬臂梁固定端到旋转中心距离r为31 mm，磁间距d为35 mm。实验中采集的电压和位移信号均在稳定状态下获得，时间为零时表示的是在稳定状态下进行信号采集的初始时刻。激光位移传感器的激光照射点位于倒置压电悬臂梁上距固定端35 mm处，倒置压电悬臂梁在两个稳态下激光测量处的位移分别为±0.6 mm。如图10所示，线性能量俘获系统的安装位置和材料参数与时变势阱磁耦合双稳态能量俘获系统中的倒置压电悬臂梁保持一致。

4.2 实验结果

如图11所示，在全转速范围内时变势阱磁耦合双稳态能量俘获系统的输出电压大于线性能量俘获系统。当转速从0增加到115 r/min时，前者的均方根电压缓慢升高，在该转速范围内旋转运动的激励水平较低，无法跨越势垒实现阱间运动，仅在其中一个稳态位置附近振动。如图12（a）所示，当转速为60 r/min时，倒置压电悬臂梁激光测量处的位移范围约为-2.065～0.49 mm，可以判断系统在稳态位置1附近振动。如图12（b）所示，当转速为90 r/min时，倒置压电悬臂梁激光测量处的位移范围约为0～1.88 mm，可以判断系统在稳态位置2附近振动。如图12（c）所示，当转速为115 r/min时，系统中倒置压电悬臂梁激光测量处的位移范围约为-2.21～0.21 mm，可以判断系统在稳态位置1附近振动。

转速在120 ～160 r/min范围内，时变势阱磁耦合双稳态能量俘获系统跨越势垒实现了阱间振荡，其均方根输出电压大幅度升高，在160 r/min达到最大值8.6 V左右。如图12（d）所示，当转速为120 rpm时，倒置压电悬臂梁激光测量处的位移范围约为-3.12～5.49 mm，可以判断系统开始跨越势垒实现阱间振荡。如图12（e）所示，当转速为150 r/min时，倒置压电悬臂梁激光测量处的位移范围约为-3.78 ～3.96 mm，系统跨越了势垒实现阱间振荡，电压大幅度升高。

示波器和电阻箱R1并联，即时变势阱磁耦合双稳态能量俘获系统的外接电阻的总阻值大小满足以下关系式：

（45）

图13为时变势阱磁耦合双稳态能量俘获系统在不同电阻箱阻值R1下的均方根输出电压。当电阻箱阻值由0.02 MΩ增加到2 MΩ的过程中，倒置压电悬臂梁的均方根输出电压均缓慢上升；当电阻箱阻值由2 MΩ增加到6 MΩ的过程中，倒置压电悬臂梁的均方根输出电压基本保持稳定。图14所示为倒置压电悬臂梁在不同负载电阻下的均方根输出功率。当电阻箱阻值由0.02 MΩ增加到2 MΩ的过程中，倒置压电悬臂梁的均方根输出功率整体呈上升趋势，在电阻箱阻值为2 MΩ时达到最大值。电阻箱阻值由2 MΩ增加到6 MΩ的过程中，转速为60，80和100 r/min的倒置压电悬臂梁的均方根输出功率基本保持平稳；转速为120和140 r/min的倒置压电悬臂梁的均方根输出电压略有下降但最终基本保持稳定。

综合以上分析，可以得出时变势阱磁耦合双稳态能量俘获系统中倒置压电悬臂梁的最佳外接电阻R0≈0.667 MΩ ，对应的电阻箱阻值R1＝2 MΩ。

如图15和16所示，当转速从60 r/min增加至160 r/min时，实验均方根输出电压和功率整体呈上升趋势，在转速为160 r/min处达到最大值，此时对应的均方根输出电压和功率分别约为7.4 V和82 μW。数值仿真的均方根输出电压和功率随着转速增加整体也呈上升趋势，在转速为160 r/min处达到最大值，此时对应的均方根输出电压和功率分别约为8.0 V和97 μW。均方根输出电压和功率的数值仿真结果与实验结果的平均误差分别约为28%和26%。数值仿真结果和实验结果存在一定误差，但随转速增加的变化趋势基本一致，因此本文建立的动力学模型可以作为理论参考。

5 结 论

本文提出了一种超低频旋转环境下的时变势阱磁耦合双稳态能量俘获系统，建立了完整的动力学模型，并分析了其特性和能量俘获性能，得到了以下结论：

（1）充分考虑离心效应影响的情况下，基于能量法和拉格朗日方程等在旋转坐标系下推导了系统的分布式参数机电耦合方程。建立了相应的磁力计算模型用以分析磁间距和离心效应对势阱的影响。分析结果表明随着磁间距的增大，势阱逐渐变浅，对应不同的非线性和稳态特性。由于离心效应的影响，系统的势阱随着转速增大而变深。

（2）理论分析与实验验证了本文提出的时变势阱磁耦合双稳态能量俘获系统具有低势垒特性，在超低旋转激励水平下能够实现大振幅阱间振荡，与线性能量俘获系统相比，该系统具有更宽的工作频率范围和更高的输出电压。

（3）实验中，时变势阱磁耦合双稳态能量俘获系统的最大均方根输出电压和功率分别约为7.4 V和82 μW，可以满足低功耗嵌入式设备和无线传感器的供能需求。

参考文献：

［1］ Tan Q， Fan K， Guo J， et al. A cantilever-driven rotor for efficient vibration energy harvesting［J］. Energy， 2021， 235： 121326.

［2］ 芮小博，李一博，曾周末. 压电悬臂梁振动能量收集器研究进展［J］. 振动与冲击， 2020， 39（17）： 112-123．

Rui Xiaobo， Li Yibo， Zeng Zhoumo. Research progress of piezoelectric cantilever vibration energy collector［J］. Journal of Vibration and Shock， 2020， 39（17）： 112-123.

［3］ 杨涛，周生喜，曹庆杰， 等. 非线性振动能量俘获技术的若干进展［J］. 力学学报， 2021， 53（11）： 2894-2909.

Yang Tao， Zhou Shengxi， Cao Qingjie， et al. Some advances in nonlinear vibration energy harvesting technology［J］. Chinese Journal of Theoretical and Applied Mechanics， 2021， 53（11）： 2894-2909.

［4］ 刘久周， 张凤玲， 辛健强， 等. 一种非线性宽频压电能量收集系统的动力学特性分析［J］. 振动工程学报， 2021， 34（3）： 567-576.

Liu Jiuzhou， Zhang Fengling， Xin Jianqiang， et al. Dynamic characteristics of a nonlinear wideband energy harvester based on piezoelectric material［J］. Journal of Vibration Engineering， 2021， 34（3）： 567-576.

［5］ 李魁， 杨智春， 谷迎松， 等. 变势能阱双稳态气动弹性能量收集的性能增强研究［J］. 航空学报， 2020， 41（9）： 136-147.

Li Kui， Yang Zhichun， Gu Yingsong， et al. Performance enhancement of variable-potential-well bi-stable aeroelasticity energy harvesting［J］. Acta Aeronautica et Astronautica Sinica， 2020， 41（9）： 136-147.

［6］ 张颖， 王伟， 曹军义. 多稳态俘能系统的准确磁力建模方法［J］. 力学学报， 2021， 53（11）： 2984-2995

Zhang Ying， Wang Wei， Cao Junyi. An accurate modelling method of magnetic force in multi-stable energy harvesting system［J］. Chinese Journal of Theoretical and Applied Mechanics， 2021， 53（11）： 2984-2995.

［7］ 高鸣源， 李守太， 孙玉华， 等. 多稳态电磁俘能系统的非线性动力学实验研究［J］. 振动工程学报， 2021， 34（4）： 775-781.

Gao Mingyuan， Li Shoutai， Sun Yuhua， et al. Experimental study of non-linear dynamics of multi-stable electromagnetic energy harvesting system［J］. Journal of Vibration Engineering， 2021， 34（4）： 775-781.

［8］ 张旭辉， 吴中华， 邓鹏飞， 等. 自调谐全方向振动能量收集装置的设计及优化［J］. 压电与声光， 2016， 38（6）： 915-919.

Zhang Xuhui， Wu Zhonghua， Deng Pengfei， et al. Design and optimization of self-tuning omnidirectional vibration energy harvester［J］. Piezoelectrics and Acoustooptics， 2016， 38（6）： 915-919.

［9］ 朱莉娅， 陈仁文， 刘祥建， 等. 自调谐宽频带压电振动发电机的改进［J］. 南京航空航天大学学报， 2012， 44（3）： 327-332.

Zhu Liya， Chen Renwen， Liu Xiangjian， et al9SFVNRBl1kjgLCqmxOuuX0QnsStwKybh4CJEa5+JugQ=. Improved design of self-tuning broadband piezoelectric vibration generator［J］. Journal of Nanjing University of Aeronautics and Astronautics， 2012， 44（3）： 327-332.

［10］ 赵林川， 邹鸿翔， 刘丰瑞， 等. 压电与摩擦电复合型旋转能量采集动力学协同调控机制研究［J］. 力学学报， 2021， 53（11）： 2961-2971

Zhao Linchuan， Zou Hongxiang， Liu Fengrui， et al. Hybrid piezoelectric-triboelectric rotational energy harvester using dynamic coordinated modulation mechanism［J］. Chinese Journal of Theoretical and Applied Mechanics， 2021， 53（11）： 2961-2971.

［11］ Zhang B， Li H， Zhou S， et al. Modeling and analysis of a three-degree-of-freedom piezoelectric vibration energy harvester for broadening bandwidth［J］. Mechanical Systems and Signal Processing， 2022， 176： 109169.

［12］ Gu L， Livermore C. Passive self-tuning energy harvester for extracting energy from rotational motion［J］. Applied Physics Letters， 2010， 97（8）： 081904.

［13］ Hsu J C， Tseng C T， Chen Y S. Analysis and experiment of self-frequency-tuning piezoelectric energy harvesters for rotational motion［J］. Smart Materials and Structures， 2014， 23（7）： 075013.

［14］ Mei X， Zhou S， Yang Z， et al. Enhancing energy harvesting in low-frequency rotational motion by a quad-stable energy harvester with time-varying potential wells［J］. Mechanical Systems and Signal Processing， 2021， 148： 107167.

［15］ Guan M， Liao W H. Design and analysis of a piezoelectric energy harvester for rotational motion system［J］. Energy Conversion and Management， 2016， 111： 239-244.

［16］ Liu T， Livemore C. Passively tuning harvesting beam length to achieve very high harvesting bandwidth in rotating applications［J］. Proceedings of PowerMEMS， 2012， 2012： 492-495.

［17］ Mei X， Zhou S， Yang Z， et al. A tri-stable energy harvester in rotational motion： modeling， theoretical analyses and experiments［J］. Journal of Sound and Vibration， 2020， 469： 115142.

［18］ Zhou Z， Qin W， Du W， et al. Improving energy harvesting from random excitation by nonlinear flexible bi-stable energy harvester with a variable potential energy function［J］. Mechanical Systems and Signal Processing， 2019， 115： 162-172.

［19］ Fang S， Fu X， Liao W H. Modeling and experimental validation on the interference of mechanical plucking energy harvesting［J］. Mechanical Systems and Signal Processing， 2019， 134： 106317.

［20］ Zou H， Zhang W， Li W， et al. Design and experimental investigation of a magnetically coupled vibration energy harvester using two inverted piezoelectric cantilever beams for rotational motion［J］. Energy Conversion and Management， 2017， 148： 1391-1398.

［21］ Febbo M， Machado S P， Gatti C D， et al. An out-of-plane rotational energy harvesting system for low frequency environments［J］. Energy conversion and management， 2017， 152： 166-175.

［22］ Mei X， Zhou R， Yang B， et al. Combining magnet-induced nonlinearity and centrifugal softening effect to realize high-efficiency energy harvesting in ultralow-frequency rotation［J］. Journal of Sound and Vibration， 2021， 505： 116146.

［23］ Zhang Y， Zheng R， Nakano K， et al. Stabilising high energy orbit oscillations by the utilisation of centrifugal effects for rotating-tyre-induced energy harvesting［J］. Applied Physics Letters， 2018， 112（14）： 143901.

Mechanism of magnetic⁃coupled bistable energy harvesting in rotational environment

WU Zhi-xian1，2， WANG Suo1，2， LI Zhi-yuan1，2， MEI Xu-tao3， ZHOU Sheng-xi1，2

（1.School of Aeronautics， Northwestern Polytechnical University， Xi’an 710072， China；2.Research and Development Institute in Shenzhen， Northwestern Polytechnical University， Shenzhen 518057， China；3.Faculty of Engineering， The University of Tokyo， Tokyo 153-8505， Japan）

Abstract： Ambient environments are rich in rotational energy resources. These can be converted into useful electric energy through energy conversion materials to， powering embedded devices and wireless sensors in the Internet of Things. As such， energy harvesting technology could potentially address the environmental pollution and high maintenance costs associated with traditional chemical batteries. This paper proposes a novel time-varying potential well magnetic-coupled bistable energy harvesting system with low potential barriers to enhance the energy harvesting performance in ultra-low frequency rotating environments （below 3 Hz）. The proposed system comprises a forward steel beam and an inverted piezoelectric beam installed on a rotational plate. Mutually exclusive magnets are attached to the free ends of both beams， creating three equilibrium positions due to the magnetic force， two of which are stable. This gives the system its coupled bistable characteristics. The free end of the forward steel beam is distanced from the center of the rotational plate， making it a centrifugal hardening beam. Conversely， the free end of the inverted piezoelectric beam is closer to the center， making it a centrifugal softening beam. Taking into account the influence of the centrifugal effect， the distributed parameter electromechanical coupling equation of the system is derived in the rotational coordinate system using the energy method， Lagrange equation， piezoelectric theory， and more. A magnetic calculation model is used to analyze the influence of magnetic spacing and the centrifugal effect on the potential energy well and the energy harvesting performance of the system. Finally， numerical simulations and experimental results verify that， compared to the linear energy harvesting system， the proposed magnetic-coupled bistable energy harvesting system has a wider operating frequency range （0～2.67 Hz） and higher output voltage （greater than 2 V）.

Key words： rotational energy harvesting；ultra-low frequency； bistable state； time-varying potential well； low potential barrier

作者简介： 伍芷娴（1997—），女，硕士研究生。E-mail：2856932332@qq.com。

通讯作者： 周生喜（1987—），男，博士，教授。E-mail：zhoushengxi@nwpu.edu.cn。