含分段阻尼特性动力吸振器的吸振性能

摘要： 利用凸轮机构设计了一种分段阻尼装置。以传统Voigt型动力吸振器为基础，将该装置安装于动力吸振器的主系统与子系统之间，建立了吸振器的动力学方程。利用在一个振动周期内阻尼耗能等效这一原理，在相同振动频率下得到了分段阻尼装置的等效阻尼系数。推导得出了具有分段阻尼特性的动力吸振器的理论解，并用数值解进行了验证。比较分析了无阻尼、传统线性阻尼及具有分段阻尼特性的动力吸振器的吸振特性。结果表明，具有分段阻尼特性的动力吸振器的幅频特性综合了无阻尼和传统线性阻尼动力吸振器的特点，能保证反共振点处主系统的振幅很低，同时对主系统的共振振幅的抑制效果接近于传统线性阻尼动力吸振器。

关键词： 动力吸振器； 分段阻尼； 共振； 反共振； 能量等效

中图分类号： O322； TH113.1 文献标志码： A 文章编号： 1004-4523（2024）06-0945-09

DOI：10.16385/j.cnki.issn.1004-4523.2024.06.005

引 言

动力吸振器是一种振动控制装置，通过辅助质量、弹簧和阻尼作用来减小被控对象的振动，同时附加质量会产生一定的振动，如同附加质量将被控对象的振动吸收［1］。Frahm［2］发明了一种窄频带无阻尼动力吸振器，这种吸振器只能在较窄的频带范围内实现良好的振动抑制效果，而在带宽附近会使系统产生较大的振幅。Ormondroyd等［3］首次将阻尼添加到动力吸振器中，并提出了固定点理论。Den Hartog［4］将这一理论总结到其著作中，完善了传统Voigt型动力吸振器模型及其参数优化方法。Nishihara等［5‑6］进一步得到了此模型的精确级数解。Crandall等［7］提出了优化设计准则，可使系统输入功率达到最小。Yamaguchi［8］提出了最大稳定性优化准则，得到了主系统瞬态响应最快稳定的方案。Asami等［9］得到了主系统无阻尼状态下H‑infinity优化的级数解和精确解。此后线性动力吸振器模型逐渐丰富。Asami等［10］提出了三要素型动力吸振器基于固定点理论的优化方法。Ren［11］提出了一种接地式动力吸振器及其参数优化方法。Liu等［12‑13］运用不同方法得到了类似的优化参数，并应用到了主系统含阻尼的接地式动力吸振器最优参数优化过程中。背户一登［14］将不同类型的线性动力吸振器设计方法进行了推广，使其在实用性上得到了进一步提高。胡海岩［15］分析了无阻尼二自由度系统反共振现象，对原点反共振、跨点反共振机理进行了分析。

由于早期的线性动力吸振器存在带宽较窄等问题，人们开始广泛地研究非线性动力吸振器，非线性动力吸振器逐渐成为动力吸振器的研究热点［16］。Bellizzi等［17］研究了一种含立方刚度和时滞控制策略黏滞阻尼器的非线性吸振器，其质量较轻、鲁棒性较强且减振频带宽，因此在许多场合得到了应用［18］。刘丽兰等［19］设计了一种含非线性阻尼的双稳态动力吸振器，该吸振器考虑了双稳态吸振器分岔情况，能够得到相较于线性阻尼双稳态吸振器更好的减振效果。Milovanovic等［20］考虑了并联立方刚度和三次非线性阻尼的单自由度隔振系统。Jing［21］研究了一种基于Voigt系统含立方项刚度和非线性阻尼的动力吸振器，发现其对主系统控制有许多优势。Koo等［22］研究了一种半主动调谐吸振器控制方法，分别基于速度和位移的on‑off和continues控制策略分析了吸振性能。Shen等［23‑24］利用平均法得到了半主动on‑off控制的近似解析解。郎君等［25‑26］ 将on‑off 控制策略引入到Voigt型动力吸振器和接地型动力吸振器中，应用该控制策略使系统在随机激励下得到了较好的位移响应。刘中坡等［27‑28］研究了一种安装在高层结构的轨道型被动NES能量阱模型，分析结构在不同模态下承受风振激励和地震波激励时的顶层位移响应和加速响应，其研究对象属于一种连续系统。

无阻尼动+uR33vRh4+6dhStRosKECg==力吸振器存在反共振点，当激励频率与反共振点频率一致时，被控对象不动，振动完全被子系统“吸收”，振动控制效果最好，但激励频率偏离反共振点频率，尤其是接近系统的固有频率时，被控对象反而振动剧烈。为了拓宽无阻尼动力吸振器的吸振频带，动力吸振器要有一定的阻尼，但阻尼的存在会恶化反共振点频率处的吸振效果。为了解决这一矛盾，本文提出了一种分段阻尼装置，该装置在反共振点频率附近时体现为无阻尼特性，在偏离反共振点频率时体现一定的阻尼特性。

1 分段阻尼装置及阻尼特性分析

图1为基于移动凸轮设计的非线性阻尼装置，该装置两侧为横向且对称布置的线性黏滞阻尼器，中间为可以上下移动的凸轮块。凸轮块两侧为对称的轮廓线，轮廓线设计成T形导轨槽样式。每个T形槽内嵌入一个滚动轴承，凸轮两边分别放置一个横向的阻尼器，阻尼器的活塞杆与滚动轴承内圈相连。工作状态下凸轮与横向布置的阻尼器相对上下移动，滚动轴承在导轨槽的引导下可以自由滚动。运动过程产生的摩擦力很小，本文分析时忽略该摩擦力。

设计不同的凸轮轮廓线可以使阻尼产生不同的效果。本文选取如图1（d）所示的轮廓曲线进行探讨。整个运动过程中，凸轮与阻尼活塞杆之间相对竖直分位移方向为轴，相对水平分位移方向为轴，轮廓线与轴之间形成的倾角为。为阻尼开始产生的位置相对凸轮横向对称线的距离，即图1（d）中T形导轨槽方向改变的位置到水平对称轴的距离。运动过程中，当轴承与凸轮块之间相对位移小于时，阻尼活塞杆与阻尼油缸之间无水平分速度，系统瞬时不会产生阻尼力。当相对位移大于时，阻尼活塞杆与阻尼油缸之间会产生一对水平分速度，系统瞬时产生阻尼力。该轮廓曲线对应的位移几何关系式为：

（1）

（2）

令两侧单个线性阻尼器的阻尼系数为。在有阻尼范围内，阻尼力作用在凸轮轮廓线上的水平分力自相平衡，竖直分力等效为由阻尼系数为的垂向布置阻尼产生，等效阻尼与实际阻尼瞬时功率相等，即

（3）

化简可得：

（4）

结合式（1）相对位移小于部分，可以得出图1（d）形式的凸轮轮廓曲线对应的等效阻尼系数：

（5）

2 动力吸振器动力学方程及求解

如图2所示，传统Voigt型动力吸振器模型用弹簧和阻尼连接主系统与吸振器，其中，为主系统质量，为主系统刚度，为附加吸振器质量，为附加吸振器刚度，为阻尼系数，为主系统的位移，为附加动力吸振器位移，为激励力幅值，为激振频率。本文将模型中的线性阻尼的阻尼系数变为图1（b）所示的分段阻尼的阻尼系数，该模型可以利用主系统与吸振器之间相对振幅来被动调节阻尼大小。设置图1（c）凸轮两端轮廓曲线倾角为，即图1（d）的倾角α为，则垂向阻尼系数为：

（6）

2.1 无阻尼部分动力学分析

对于Voigt型动力吸振器来说，主系统与吸振器之间的相对位移相当于凸轮与滚子沿轴方向的相对位移，所以需要求出无阻尼条件下主系统与吸振器的稳态相对振幅。当稳态相对振幅小于时，滚动轴承在变阻尼点位置以下移动，系统为无阻尼系统。此时系统的动力学方程为：

（7）

令模型各部分稳态响应形式为：

（8）

式中 为主系统与吸振器之间的相对位移；X1，X2及X12分别为主系统、吸振器及主系统与吸振器之间的相对位置位移变振幅。

引入归一化参数：

。

将上述参数代入式（7）中，得到：

（9）

引入归一化振幅：

，解得主系统归一化振幅、吸振器归一化振幅，以及主系统与吸振器之间相对归一化振幅分别为：

（10）

（11）

（12）

根据文献［29］可知，当激励频率达到系统反共振频率，即频率化时，主系统归一化振幅为0，将代入式（11）和（12），获得吸振器归一化振幅与相对归一化振幅为：

（13）

在此引入归一化振幅：

（14）

上述过程表明在反共振频率处，主系统归一化振幅为0，吸振器归一化振幅为，在对应的实际位置设置第1节所述的模型阻尼产生，即可使系统在反共振频率处无阻尼参与，能够达到归一化振幅为0的特性。

由式（12）和（14）得到归一化振幅为时对应的四个频率比分界点分别为：

（15）

（16）

（17）

（18）

图3为改变参数时分界点处四个频率比的大小关系。图4为在根据式（12）得到的动力吸振器无阻尼频率范围内，归一化振幅的幅频曲线低于的部分。由图3和4可以得到动力吸振器无阻尼频率区间为：

（19）

式中 ；。

由图4可见，在式（19）所示的区间内，稳态相对振幅低于阻尼分界点，所以可适用无阻尼公式（10）～（12）来获得系统各稳态振幅。

2.2 有阻尼部分动力学分析

当稳态归一化振幅大于时，系统存在分段阻尼。对应的频率比区间为：

（20）

系统在稳态振动阶段的相对稳态振幅曲线与稳态响应一般形式（8）基本相同。图5为相对稳态振幅在一个振动周期内所经历的时程曲线，在一个稳态周期内滚子会四次经过对称的阻尼产生位置，此位置对应归一化振幅，设第一次经过变阻尼点时主系统与吸振器之间的相角为：

（21）

由对称性和循环性可以得到其他三个变阻尼点对应的相角关系。

图5表明系统在一个振动周期内的有阻尼频率区间由三部分组成。在有阻尼的三部分频率区间内对阻尼力进行积分，得到一个周期内的分段阻尼耗能。同时对系统一个周期内的等效线性阻尼做功积分得到等效线性阻尼耗能。根据能量等效的方法，一个周期内分段线性阻尼的三部分做功与等效阻尼做功相等，可获得如下关系式：

（22）

解得等效阻尼为：

（23）

由式（23）可见，等效阻尼只与变量相角有关。将等效阻尼代入系统模型，得到系统动力学方程为：

（24）

添加归一化参数：

（25）

得到有阻尼范围内各部分归一化振幅分别为：

（26）

（27）

（28）

观察式（21）和（23）可见等效阻尼与归一化振幅，有关，即与频率比有关，所以在不同频率下系统的等效线性阻尼是不一样的。若将式（21）代入等效阻尼式（23），并将含有反三角函数的等效阻尼代入式（28）来反解归一化的激振频率，再将和等效阻尼代入式（26）中求主系统稳态振幅，整个计算过程将十分复杂。式（23）中等效阻尼只与归一化振幅有关，且在已知的情况下，可由式（28）反解出等效线性阻尼下对应的频率。将得到的参数和代入式（23），即可解出对应频率和相对振幅下的主系统归一化振幅。由图4可知，当归一化相对稳态振幅大于阻尼产生位置归一化振幅时，系统的稳态振动才会有阻尼参与。所以从开始，取系列归一化相对稳态振幅，形成。利用式（21）和（23）获得对应变阻尼相角和等效线性阻尼：

（29）

式中 内部元素为所取的不同归一化相对稳态振幅的值，和各参数内部元素如下：

（30）

（31）

由等效阻尼可得到等效阻尼比为：

（32）

式中 结构形式与相同，为便于后文说明，定义内部元素为。

通过式（28）求解等效线性系统下相对稳态振幅和等效阻尼比对应的激振频率比为：

（33）

经计算，频率中每个元素包含四个解：

（34）

引入参数：

解得式（34）中各元素分别为：

（35）

（36）

（37）

（38）

将结果代入式（26）中，可得到与和对应的主系统振幅为：

（39）

与形式相同，每个元素包含四个解：

（40）

式中 中各元素解分别为：

（41）

（42）

（43）

（44）

3 数值解验证及主系统幅频特性

3.1 数值解仿真验证

取参数，，，，， 。由式（14）确定阻尼产生位置归一化振幅，并利用第2，3节所述方法可以得到主系统归一化振幅。计算无阻尼参与的频率范围内解析解和有阻尼频率范围内的近似解析解，并将有阻尼频率范围内的数值解与解析解对比，得到结果如图6所示。图6表明，除振幅较大的峰值处略有不同外，解析解和数值解基本重合，说明本文对分段阻尼的处理方法是有效可行的。

3.2 主系统幅频特性

如图7所示，固定刚度为1120 N/m，并在一定范围内调节线性阻尼可改变两振幅的自身高度。如图8所示，固定阻尼并调节刚度可以有效调节两峰值的相对高度，这种情况与线性系统相似。同时改变吸振器的刚度和阻尼，不会对在反共振点频率处主系统振幅为0这一特性产生影响。

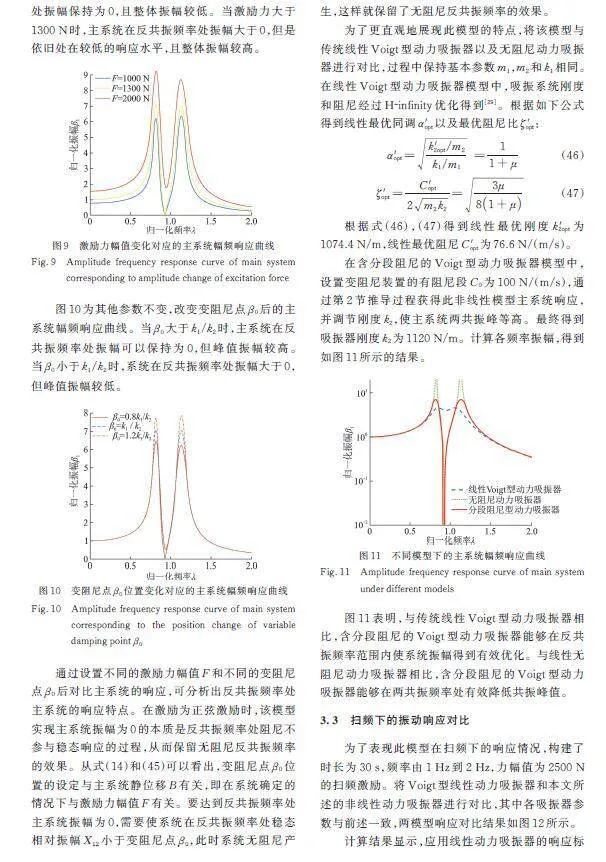
图9为其他参数不变，只改变激励力幅值后的主系统幅频响应曲线。分别设置激励力为1000，1300和2000 N。其中变阻尼点为激励力为1300 N时无阻尼反共振点相对振幅，即

（45）

当激励力小于1300 N时，主系统在反共振频率处振幅保持为0，且整体振幅较低。当激励力大于1300 N时，主系统在反共振频率处振幅大于0，但是依旧处在较低的响应水平，且整体振幅较高。

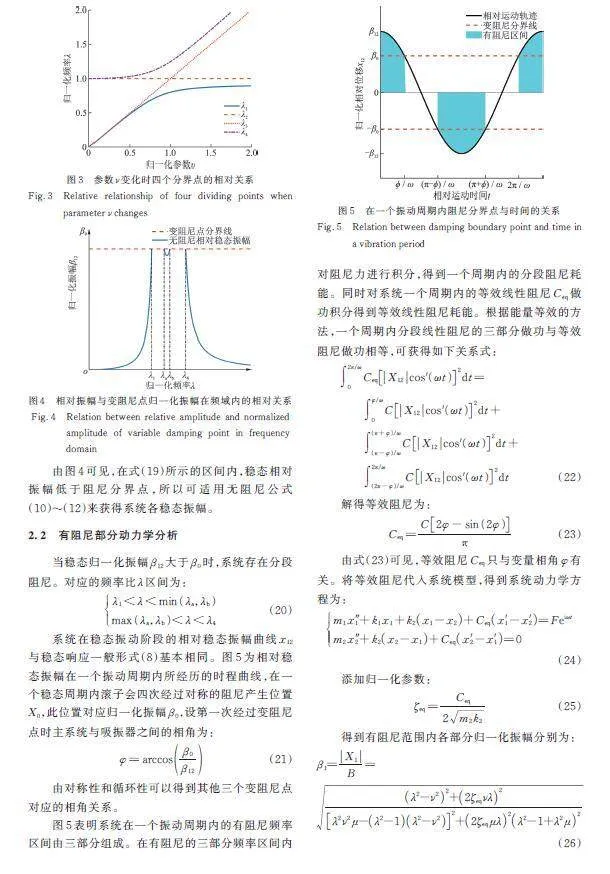
图10为其他参数不变，改变变阻尼点后的主系统幅频响应曲线。当大于时，主系统在反共振频率处振幅可以保持为0，但峰值振幅较高。当小于时，系统在反共振频率处振幅大于0，但峰值振幅较低。

通过设置不同的激励力幅值和不同的变阻尼点后对比主系统的响应，可分析出反共振频率处主系统的响应特点。在激励为正弦激励时，该模型实现主系统振幅为0的本质是反共振频率处阻尼不参与稳态响应的过程，从而保留无阻尼反共振频率的效果。从式（14）和（45）可以看出，变阻尼点位置的设定与主系统静位移有关，即在系统确定的情况下与激励力幅值有关。要达到反共振频率处主系统振幅为0，需要使系统在反共振频率处稳态相对振幅小于变阻尼点，此时系统无阻尼产生，这样就保留了无阻尼反共振频率的效果。

为了更直观地展现此模型的特点，将该模型与传统线性Voigt型动力吸振器以及无阻尼动力吸振器进行对比，过程中保持基本参数，和相同。在线性Voigt型动力吸振器模型中，吸振系统刚度和阻尼经过H‑infinity优化得到［29］。根据如下公式得到线性最优同调以及最优阻尼比：

（46）

（47）

根据式（46），（47）得到线性最优刚度为1074.4 N/m，线性最优阻尼为76.6 N/（m/s）。

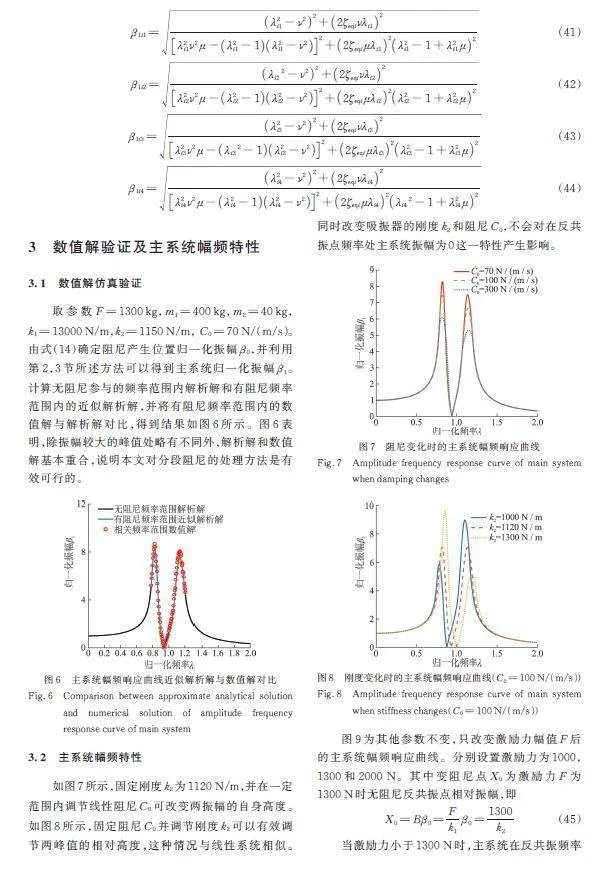
在含分段阻尼的Voigt型动力吸振器模型中，设置变阻尼装置的有阻尼段为100 N/（m/s），通过第2节推导过程获得此非线性模型主系统响应，并调节刚度，使主系统两共振峰等高。最终得到吸振器刚度为1120 N/m。计算各频率振幅，得到如图11所示的结果。

图11表明，与传统线性Voigt型动力吸振器相比，含分段阻尼的Voigt型动力吸振器能够在反共振频率范围内使系统振幅得到有效优化。与线性无阻尼动力吸振器相比，含分段阻尼的Voigt型动力吸振器能够在两共振频率处有效降低共振峰值。

3.3 扫频下的振动响应对比

为了表现此模型在扫频下的响应情况，构建了时长为30 s，频率由1 Hz到2 Hz，力幅值为2500 N的扫频激励。将Voigt型线性动力吸振器和本文所述的非线性动力吸振器进行对比，其中各吸振器参数与前述一致，两模型响应对比结果如图12所示。

计算结果显示，应用线性动力吸振器的响应标准差为1.4024×10-1，非线性动力吸振器的响应标准差为2.6356×10-1。可见，非线性动力吸振器扫频激励下整体响应没有明显改善。

4 结 论

基于移动凸轮和线性阻尼器设计了分段阻尼装置，并将该装置应用于动力吸振器，分析了含分段阻尼特性动力吸振器的吸振特性，得到结论如下：

（1）当激励幅值不大时，本文提出的动力吸振器在反共振点处的振幅为0，振动控制效果等同于无阻尼动力吸振器，但共振点附近主系统的振幅得到有效抑制，特性明显优于无阻尼动力吸振器。

（2）当激励幅值较大时，主系统反共点处的幅值不为0，但振幅远小于有阻尼动力吸振器的振幅。

（3）传统无阻尼动力吸振器能够在反共振频率处使主系统振幅为0，但抑振频带狭窄，尤其在共振点处，主系统的振幅为无限大；传统线性Voigt型动力吸振器能够很好地抑制共振振幅，却在反共振频率处大大增加了主系统振幅。本文提出的分段阻尼装置仍然适用于反共振点处较窄的吸振频带，其吸振效果明显优于传统线性阻尼器，且当激振频率偏离吸振频带，尤其是共振点处时，仍能有效抑制主系统的振动。

参考文献：

［1］ 清华大学力学系工程力学教研组振动组. 机械振动［M］. 北京： 机械工业出版社， 1980.

［2］ Frahm H. Device for damping vibrations of bodies： US989958A［P］.1911-04-18.

［3］ Ormondroyd J， Den Hartog J P. The theory of the dynamic vibration absorber［J］. Journal of Fluids Engineering， 1928， 49-50（2）： 021007.

［4］ Den Hartog J P. Mechanical Vibrations［M］.3rd ed. New York： McGraw-Hall Inc.， 1947： 112-132.

［5］ Nishihara O， Asami T. Closed-form solutions to the exact optimizations of dynamic vibration absorbers （minimizations of the maximum amplitude magnification factors）［J］. Journal of Vibration and Acoustics， 2002， 124（4）： 576-582.

［6］ Nishihara O， Asami T. Closed-form exact solution to H-infinity optimization of dynamic vibration absorber： Ⅱ. development of an algebraic approach and its application to a standard problem［C］//Proceedings of SPIE-the International Society for Optical Engineering. 2000， 3989： 500-511.

［7］ Crandall S H， Mark W D. Random Vibration in Mechanical Systems［M］. 2nd ed. Pittsburgh， USA： Academic Press， 1963.

［8］ Yamaguchi H. Damping of transient vibration by a dynamic absorber［J］. Transactions of the Japan Society of Mechanical Engineers， 1988， 54（499）： 561-568.

［9］ Asami T， Nishihara O， Baz A M. Analytical solutions to H∞ and H2 optimization of dynamic vibration absorbers attached to damped linear systems［J］. Journal of Vibration and Acoustics， 2002， 124（2）： 284-295.

［10］ Asami T， Nishihara O. Analytical and experimental evaluation of an air damped dynamic vibration absorber： design optimizations of the three-element type model［J］. Journal of Vibration and Acoustics， 1999， 121（3）： 334-342.

［11］ Ren M Z. A variant design of the dynamic vibration absorber［J］. Journal of Sound and Vibration， 2001， 245（4）： 762-770.

［12］ Liu K F， Liu J. The damped dynamic vibration absorbers： revisited and new result［J］. Journal of Sound and Vibration， 2005， 284（3-5）： 1181-1189.

［13］ Liu K F， Coppola G. Optimal design of damped dynamic vibration absorber for damped primary systems［J］. Transactions of the Canadian Society for Mechanical Engineering， 2010， 34（1）： 119-135.

［14］ 背户一登. 动力吸振器及其应用［M］. 北京： 机械工业出版社， 2013.

［15］ 胡海岩. 论线性系统的反共振问题［J］. 动力学与控制学报， 2018， 16（5）： 385-390.

Hu Haiyan. On anti-resonance problem of a linear system［J］. Journal of Dynamics and Control， 2018， 16（5）：385-390.

［16］ 刘耀宗， 郁殿龙， 赵宏刚，等. 被动式动力吸振技术研究进展［J］. 机械工程学报， 2007， 43（3）： 14-21.

Liu Yaozong， Yu Dianlong， Zhao Honggang，et al. Review of passive dynamic vibration absorbers［J］. Journal of Mechanical Engineering， 2007， 43（3）： 14-21.

［17］ Bellizzi S，Chung K W. Vibration reduction using a nonlinear attachment including an active damper with delay［C］//Proceeding of the ASME 2015 International Mechanical Engineering Congress and Exposition. Houston， Texa， USA： ASME， 2015.

［18］ 鲁正， 王自欣， 吕西林. 非线性能量阱技术研究综述［J］. 振动与冲击， 2020， 39（4）： 1-16.

Lu Zheng， Wang Zixin， Lü Xilin. A review on nonlinear energy sink technology［J］. Journal of Vibration and Shock， 2020， 39（4）： 1-16.

［19］ 刘丽兰， 任博林， 朱国栋，等. 考虑非线性阻尼的双稳态电磁式吸振器的动力学特性研究［J］. 振动与冲击， 2017， 36（17）： 91-96.

Liu Lilan，Ren Bolin，Zhu Guodong，et al. Dynamic characteristics of a bi-stable state electromagnetic vibration absorber considering nonlinear damping［J］. Journal of Vibration and Shock， 2017， 36（17）： 91-96.

［20］ Milovanovic Z， Kovacic I，Brennan M J. On the displacement transmissibility of a base excited viscously damped nonlinear vibration isolator［J］. Journal of Vibration and Acoustics， 2009，131（5）： 054502.

［21］ Jing X J. Nonlinear characteristic output spectrum for nonlinear analysis and design［J］. IEEE/ASME Transactions on Mechatronics， 2014， 19（1）： 171-183.

［22］ Koo J H， Ahmadian M， Setareh M， et al. In search of suitable control methods for semi-active tuned vibration absorbers［J］. Journal of Vibration and Control， 2004，10（2）： 163-174.

［23］ Shen Y J， Ahmadian M. Nonlinear dynamical analysis on four semi-active dynamic vibration absorbers with time delay［J］. Shock and Vibration， 2013， 20：649-663.

［24］ Shen Y J， Wang L， Yang S P， et al. Nonlinear dynamical analysis and parameters optimization of four semi-active on-off dynamic vibration absorbers［J］. Journal of Vibration and Control， 2012， 19（1）： 143-160.

［25］ 郎君， 申永军， 杨绍普. 一种半主动动力吸振器参数优化及性能比较［J］. 振动与冲击， 2019， 38（17）：172-177.

Lang Jun， Shen Yongjun， Yang Shaopu. Parametric optimization and performance comparison for 2 semi-active Voigt DVAs［J］. Journal of Vibration and Shock， 2019， 38（17）： 172-177.

［26］ 郎君， 申永军， 杨绍普. 半主动控制接地式动力吸振器参数优化及性能比较［J］. 动力学与控制学报， 2019， 17（2）： 168-177.

Lang Jun， Shen Yongjun， Yang Shaopu. Parameter optimization and performance comparison of semi-active ground-hook control DVAs［J］. Journal of Dynamics and Control， 2019， 17（2）： 168-177.

［27］ 刘中坡， 乌建中， 王菁菁，等. 轨道型非线性能量阱对高层结构脉动风振的控制仿真［J］. 振动工程学报， 2016， 29（6）： 1088-1096.

Liu Zhongpo， Wu Jianzhong， Wang Jingjing， et al. Simulation of track nonlinear energy sink for wind-induced vibration control in high-rise building［J］. Journal of Vibration Engineering， 2016， 29（6）： 1088-1096.

［28］ 刘中坡， 吕西林， 鲁正， 等. 轨道型非线性能量阱振动控制的振动台试验研究［J］. 建筑结构学报， 2016， 37（11）： 1-9.

Liu Zhongpo， Lü Xilin， Lu Zheng， et al. Experimental investigation on vibration control effect of track nonlinear energy sink［J］. Journal of Building Structures， 2016， 37（11）： 1-9.

［29］ 盛美萍， 王敏庆， 马建刚. 噪声与振动控制技术基础［M］. 三版. 北京： 科学出版社， 2017.

Vibration absorption characteristics of dynamic vibration absorber with piecewise damping characteristics

LU Xue-li， XING Hai-jun， RUAN Zi-yue

（School of Mechanical Engineering， Shijiazhuang Tiedao University， Shijiazhuang 050043， China）

Abstract： A segmented damping device is designed using a cam mechanism in this study. Based on the traditional Voigt dynamic vibration absorber， this device is installed between the main system and subsystem of the dynamic vibration absorber， and the dynamic equation of the vibration absorber is established. Using the principle of equivalent damping energy dissipation within one vibration period， the equivalent damping coefficient of the segmented damping device at the same vibration frequency is obtained. The theoretical solution of a dynamic vibration absorber with piecewise damping characteristic is derived and verified by numerical solution. The vibration absorption characteristics of undamped， traditional linear damping， and dynamic absorber with piecewise damping are compared and analyzed. The results show that the amplitude frequency characteristics of the dynamic vibration absorber with piecewise damping characteristics integrate the characteristics of undamped and traditional linear damping dynamic vibration absorbers. This ensures that the amplitude of the main system at the anti-resonance point is very low， and the suppression effect of the resonance amplitude of the main system is close to that of the traditional linear damping dynamic vibration absorber.

Key words： dynamic vibration absorber；piecewise damping；resonance；anti-resonance；energy equivalence principle

作者简介： 卢学礼（1997—），男，硕士研究生。 E-mail： 2093728776@qq.com。

通讯作者： 邢海军（1967—），男，博士，教授，博士生导师。 E-mail： 412261035@qq.com。