含裂纹缺陷的预扭壳结构非线性振动特性研究

摘要： 基于扩展等几何方法和一阶壳体剪切变形理论建立了含裂纹缺陷的功能梯度预扭壳结构的非线性振动控制方程。控制方程中考虑了预扭壳结构的预扭角度及几何非线性，应用扩展等几何方法，采用反映位移变化的富集函数来描述裂纹的位置及长度，一方面可以提高计算精度，另一方面可以避免在裂纹处的网格加密，提高计算效率。采用了直接迭代法求解非线性振动控制方程。通过与现有文献结果对比，证明了本文方法的正确性和稳定性。在此基础上，探究裂纹对功能梯度预扭壳结构非线性振动频率的影响，研究了预扭角度、裂纹位置及长度和材料的功能梯度指数等参数对预扭壳非线性振动特性的影响规律。

关键词： 非线性振动； 功能梯度材料； 裂纹预扭壳结构； 扩展等几何方法； 一阶壳体剪切变形理论

中图分类号： O322 文献标志码： A 文章编号： 1004-4523（2024）06-0937-08

DOI：10.16385/j.cnki.issn.1004-4523.2024.06.004

引 言

旋转机械在工业中普遍存在，其主要部件叶片在长期运行过程中可能会出现裂纹的产生及扩展，影响机械的正常运行。因此，判断裂纹的产生位置和长度显得尤为重要，其中通过叶片振动频率的变化来识别裂纹参数是一种重要的判断手段。而在利用振动特征识别裂纹参数的过程中，对含裂纹缺陷的叶片结构进行精确振动建模十分重要。功能梯度材料（FGMs）［1］的使用，为叶片在复杂环境中运行提供了更多的可能性。为了探究裂纹对于同性材料及功能梯度材料叶片振动频率的影响规律，学者们提出了多种裂纹叶片模型。

徐可君等［2］采用等效刚度法表示裂纹效应，将叶片等效为无扭曲的悬臂梁，探究了单面和双面裂纹对于叶片第一阶固有频率的影响。赵迪等［3］应用了传递矩阵法和有限元法计算了含裂纹悬臂梁模型的固有频率，证明了传递矩阵法可以较好地描述裂纹结构的固有振动特征。诸多学者使用无质量弹性旋转弹簧模拟裂纹产生的附加刚度［4‑6］，探究裂纹参数对于裂纹梁动力响应的影响。张俊红等［7］建立了航空发动机叶片的有限元模型，分析了裂纹的存在对于叶片自由振动和强迫振动的影响。Panigrahi等［8］探索了在单频和多频激励下功能梯度裂纹梁的非线性振动响应。

由于方法的局限性，以上文献所研究的含有裂纹的叶片模型大多是基于一维梁理论来建立的，适用于大展弦比类型的叶片结构。但是对于很多旋转机械，其叶片的长度与宽度的比值并不是很大，此时一维梁理论便不再适用，而应采用二维的板壳变形理论。另外，叶片（特别是含有裂纹的叶片）在复杂的工作环境中，受到多种载荷的影响，往往会发生大变形，从而产生非线性应变，进而发生非线性振动。因此探究含裂纹缺陷的功能梯度（FG）叶片的非线性振动特性是极为重要的。

扩展等几何方法（XIGA）是一种在扩展有限元方法（XFEM）的基础上发展起来的用于解决非连续区域问题的方法［9］。由于其在含间断面子域中采用反映局部位移特征的富集函数，既可以提高计算精度，又可以避免过密的网格划分，并且对不连续面的描述是完全独立于计算网格的，使其在裂纹扩展后无需进行传统有限元的网格重构。近年来，诸多学者将XIGA应用于求解含裂纹板壳的静态和动态特性［10‑12］。

针对含裂纹缺陷的叶片建模难度较大及其非线性振动特性不明确的问题，本文基于XIGA、一阶壳体剪切变形理论和von Kármán几何非线性理论，将小展弦比叶片等效为考虑预扭角的二维壳模型，探究FG裂纹预扭壳的非线性振动特性。基于von Kármán几何非线性理论，得到非线性应变项，采用直接迭代法求解非线性控制方程。通过与其他方法的对比，验证XIGA求解方法的正确性。在此基础上，探究预扭角度、裂纹位置及长度和材料的功能梯度指数对FG预扭壳结构非线性振动特性的影响规律，为旋转机械叶片的裂纹识别及疲劳机理研究提供一定的理论依据。

1 基本原理

1.1 FG裂纹预扭壳模型

本文考虑的FG裂纹预扭壳结构，基本形状参数如图1所示。壳体的长、宽和高分别用L， b和h表示，假设预扭角度沿x方向线性变化，预扭角的变化率kth=θ0/L，θ0为x=L时的预扭角度。裂纹和根部x=0之间的距离用cl表示，裂纹的长度为cd。

图2所示为扩展等几何方法描述的裂纹预扭壳模型，其中红色直线表示裂纹存在的位置及长度，斜线表示固支边界条件。

1.2 一阶壳体剪切变形理论

本文将预扭壳结构等效为具有双曲率的二维壳模型。根据一阶壳体剪切变形理论，预扭壳上任意一点的位移变量可以表示为：

（1）

式中 u，v，w为中面上任意一点的位移；φx和φy分别表示y‑z和x‑z方向的转角。

根据von Kármán几何非线性理论，当大变形存在时，预扭壳的位移与应变的关系表达式为：

（2）

（3）

（4）

式中 下标“，x”和“，y”分别表示对x和y变量进行求导；和分别为线性应变和非线性应变；A为拉梅系数；Rx， Ry和Rxy分别表示预扭壳结构x，y两个方向的曲率和扭转曲率，则扭转曲率［13］为：

（5）

式中 表示扩展等几何方法中y方向节点向量的变量。

应变的非线性部分可以进一步表示为如下形式：

（6）

式中 Aθ部分与振动位移向量q有关；为非线性应变矩阵。

由广义胡克定律，应力与应变的关系可表示为：

（7）

其中：

（8）

本文中剪切修正系数kn取5/6。

本文考虑的功能梯度材料沿厚度方向呈指数函数变化，具体表达式为：

（9）

式中 P表示各种材料参数，下标“c”和“m”分别表示陶瓷和金属材料；h为预扭壳的厚度；n为材料的功能梯度指数。材料参数P在本文中指材料的弹性模量E（z）、泊松比μ（z）和密度ρ（z）。

1.3 扩展等几何方法（XIGA）

XIGA是在等几何方法的基础上，依据扩展有限元（XFEM）思想发展起来的一种用于解决非连续区域问题的方法。本文中，在裂纹预扭壳结构的连续区域采用标准的等几何方法构造计算使用的基函数，而在裂纹存在区域及裂尖位置所对应的参数单元内，对标准的计算基函数进行修正，增加能够描述裂纹处间断特性及裂尖处奇异性的富集函数，从而提高计算精度。XIGA采用水平集方法［14］来描述裂纹，使得对于裂纹的描述可以独立于等几何单元，在裂纹扩展时，不需要进行网格的重新构造，提高计算效率。

裂纹预扭壳上任意一点的位移向量可以表示为：

（10）

式中 M为所有控制点的个数；H为裂纹贯穿单元内的控制点个数；G为裂尖单元内的控制点个数；，和分别表示标准单元、裂纹贯穿单元和裂尖单元的位移；u=［u， v， w， φx， φy］；为等几何单元基函数，其具体表达式为：

（11）

式中 ωi，j为每个控制点所对应的权值；，分别为，两个方向节点向量E和H建立的B样条基函数；p， q为基函数的阶数。由于篇幅限制，这里B样条基函数的具体表达式并没有展开，对此感兴趣的读者可以参阅文献［15］。

Heaviside阶跃函数的表达式为：

（12）

式中 xl为距离坐标x最近且位于裂纹上的某一点；en为沿着裂纹方向的法向量。

裂尖单元的富集函数Gl（x）本身是裂尖局部极坐标的函数Gl（r， θ），当u=［u， v， w］时，Gl（r， θ）MuwtHH8X6a6kYBtmCKqmvScVylHPDl+ojwU5qAlZOJ8=的表达式［16］为：

（13）

当u=［φx， φy］时，Gl （r， θ）的表达式［16］为：

（14）

在进行计算时，利用水平集方法判断不同的参数单元类型。在标准单元中，u=ui，应变矩阵只包括标准线性应变矩阵和标准非线性应变矩阵；在裂纹贯穿单元中，u=［ui， uh］，应变矩阵中包含加强项；在裂尖单元中，u=［ui，u1t， u2t，u3t，u4t］，应变矩阵中包含加强项；其中和分别为裂纹单元的加强线性应变和非线性应变矩阵，和分别表示裂尖单元的加强线性应变和非线性应变矩阵。

另外，构建基函数的参数域（，）到实际模型坐标域（x， y）之间的转换雅可比矩阵可表示为：

（15）

关于坐标x和y的一阶偏导数可以写为以下形式：

（16）

1.4 裂纹预扭壳的非线性振动方程

通过上述的推导，可以得到裂纹预扭壳的势能和动能表达式为：

（17）

（18）

基于哈密顿原理，得到以下表达式：

（19）

式中 为变分符号。

进一步得到在考虑大变形的情况下，裂纹预扭壳的控制方程为：

（20）

考虑谐波运动，控制方程还可以改写成：

（21）

为了消除时间参数t，使用加权残数法，并在内积分［17］，得到：

（22）

其中：

，

（23）

本文采用直接迭代法求解上述裂纹预扭壳的非线性振动方程（22），从而得到非线性振动频率，具体求解步骤如下：

（1） 首先忽略非线性刚度矩阵KNL1和KNL2，利用方程（22）求解初始线性频率和基频对应的振型向量。

（2） 将得到的初始振型向量进行归一化后，再乘以一定的放大倍数Wmax以此达到相应的大变形振动幅值。Wmax是假设的最大位移变形幅值，通常取与变形板壳结构厚度h成比例的数值。

（3） 以放大后的振动向量为基础得到非线性矩阵KNL1和KNL2，然后根据方程（22），得到新的频率和振动位移向量。

（4） 重复步骤（2）和（3），直到相邻两次迭代得到的第一阶频率误差小于0.1%，迭代结束，得到非线性频率值。

本文采用第一阶非线性频率和第一阶线性频率的比值γ=ωNL/ωL来表示裂纹预扭壳的非线性振动强弱［17］。频率比越大，非线性频率与线性频率的差值越大，即频率比表示控制方程的非线性项对振动行为的影响。当频率比接近1时，表明非线性频率和线性频率几乎具有相同的值，且非线性项对振动行为的影响相当小，可以忽略不计。随着频率比的增加，振动行为变为非线性，此时进行线性分析是不恰当的。

2 数值结果和讨论

2.1 收敛性和准确性验证

首先考虑一个纯钢材料的裂纹预扭壳结构，其形状参数为：L=0.4 m， b=0.2 m， h=0.01 m， θ0=30°， cl=0.5L，考虑有裂纹存在和无裂纹的两种情况。具体材料参数如表1所示。本文方法中基函数的阶次p=q=3，取不同的控制点得到的3组结果与ANSYS有限元分析软件得到的结果进行对比。需要注意的是，在ANSYS有限元分析软件中，分析裂纹预扭壳模型时，预扭角本身增加了模型建模的难度；由于裂纹的存在，在裂纹尖端位置需要采用ANSYS自带的2D裂纹奇异单元PLANE183模拟裂纹尖端处的奇异性；在裂纹贯穿处还需进行网格加密处理，用以保证裂纹贯穿处的计算精度，这些操作都会使得有限元的计算成本增加，降低其计算效率。通过表2的数据对比可以看出，本文方法随着控制点数量的增加，结果呈收敛的趋势，考虑到计算效率，在计算裂纹预扭壳结构时，可采用36×18控制点组合形式。具体参数单元和控制点的分布如图3所示。

为了验证本文非线性振动方程求解方法的正确性，考虑了简支边界条件下（当x=0， L时，v=w=φy=0且当y=-b/2， b/2时，u=w=φx=0）无裂纹Al/Al2O3功能梯度板模型的非线性振动，板的几何形状数据为：L=0.2 m， b=0.2 m， h=0.02 m。如图4所示，与参考文献［18］相比，不同的功能梯度指数n下结果吻合较好，证明了等几何方法和直接迭代法求解本文中非线性问题的适用性和准确性。

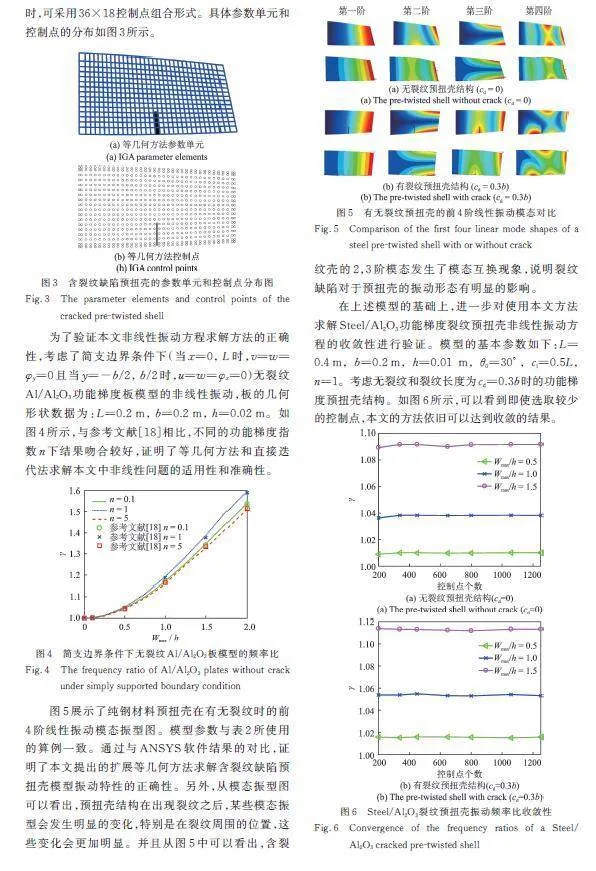
图5展示了纯钢材料预扭壳在有无裂纹时的前4阶线性振动模态振型图。模型参数与表2所使用的算例一致。通过与ANSYS软件结果的对比，证明了本文提出的扩展等几何方法求解含裂纹缺陷预扭壳模型振动特性的正确性。另外，从模态振型图可以看出，预扭壳结构在出现裂纹之后，某些模态振型会发生明显的变化，特别是在裂纹周围的位置，这些变化会更加明显。并且从图5中可以看出，含裂纹壳的2，3阶模态发生了模态互换现象，说明裂纹缺陷对于预扭壳的振动形态有明显的影响。

在上述模型的基础上，进一步对使用本文方法求解Steel/Al2O3功能梯度裂纹预扭壳非线性振动方程的收敛性进行验证。模型的基本参数如下：L=0.4 m， b=0.2 m， h=0.01 m， θ0=30°， cl=0.5L， n=1。考虑无裂纹和裂纹长度为cd=0.3b时的功能梯度预扭壳结构。如图6所示，可以看到即使选取较少的控制点，本文的方法依旧可以达到收敛的结果。

2.2 参数分析

接下来，本文通过求解非线性振动方程（22），讨论功能梯度指数、预扭角度、裂纹位置和长度对裂纹预扭壳模型非线性振动的影响。除非特别说明，模型参数均与图6相同。首先，本文研究了功能梯度指数对于裂纹预扭壳的第1阶线性频率和非线性频率比的影响。表3给出了裂纹预扭壳的第1阶线性频率和频率比随着振动幅值比例及n的变化。可以明显地看出，频率比受振动幅值的影响较大，随着振动幅值的增大而增大。随着n的增大，裂纹预扭壳结构的线性频率减小，这是因为随着n的增大，金属材料的比例增加，陶瓷材料所占比重减小，导致模型的整体刚度减小、质量增加，所以线性频率降低。但是材料对于频率比的影响并不是单调的，在振动幅值较小时，材料对于频率比的影响较小，随着振动幅值的增大，频率比随着功能梯度指数的增加呈现出先增大后减小的趋势。说明了在大变形振动的情况下，考虑裂纹预扭壳非线性振动频率的必要性。

紧接着，分析了裂纹长度对于裂纹预扭壳频率比的影响。图7给出了考虑三种不同的裂纹长度时，非线性频率比随着振动幅值比例变化的曲线。从图7中可以看出，当裂纹位于壳体中间位置时，频率比随着裂纹长度的增加而增加，这是因为随着裂纹长度的增加，壳体刚度减小，使得线性频率减小。而且裂纹长度对于频率比的影响随着振动幅值的增大更加明显。表4展示了当壳体裂纹位置不同时，含有不同长度裂纹的功能梯度预扭壳的频率比。由表4中数据可知，当裂纹位于不同位置时，裂纹对预扭壳结构的非线性频率的影响程度不同。在表4考虑的两个裂纹位置中，当幅值比例小于3，裂纹位于0.5L位置时，裂纹对功能梯度预扭壳的频率比影响更大；而当幅值比例等于3，裂纹位于0.2L位置时，对功能梯度预扭壳的频率比影响更大。数据表明，裂纹对预扭壳结构非线性振动的影响规律还与大变形振动发生的幅值有关。

表5给出了裂纹预扭壳的第一阶线性频率和非线性频率比随着裂纹位置变化的数据。由表5中数据可知，当裂纹远离固定端（x=0）时，壳体的线性频率逐渐增大，也就是说裂纹出现在叶片固定端时，对于线性频率的影响是最大的。然而频率比随裂纹位置的变化与线性频率不同，当裂纹靠近根部（cl/L=0.4）时，频率比达到最大，然后随着裂纹向自由端靠近，频率比略有减小。

最后，本文探究了壳体预扭角对于有/无裂纹预扭壳频率比的影响。如表6中数据所示，在本文考虑的预扭角变化范围之内，随着预扭角的增大，有/无裂纹预扭壳的非线性频率比都会减小。而在线性振动中，线性频率同样是随着预扭角的增大而减小的。根据频率比γ=ωNL/ωL，可知非线性频率必然也是随着预扭角角度的增大而减小。裂纹的存在并没有改变预扭角对线性频率和频率比的影响规律。

3 结 论

本文利用von Kármán几何非线性理论，探究在大振幅振动的情况下含裂纹缺陷预扭壳结构的非线性振动特性。基于扩展等几何的方法建立了含有裂纹的预扭壳模型，利用富集函数和水平集方法描述裂纹的存在，通过与有限元结果对比，证明了本文方法应用于功能梯度裂纹预扭壳结构的准确性和稳定性。扩展了等几何方法的应用，避免了有限元方法在裂纹处的网格加密，在裂纹扩展时，不需要进行网格重构，可以极大地提高分析含裂纹壳结构的效率。最后探讨了裂纹的长度及位置，预扭角度及功能梯度指数对于大振幅振动时裂纹预扭壳频率比的影响规律。针对本文研究的预扭壳模型，功能梯度指数对于线性频率的影响是单调的，而对于频率比的影响是相对复杂的。裂纹长度越大，频率比越大；当裂纹位于壳体靠近根部cl/L=0.4处，频率比最大。裂纹的存在不会改变预扭角对本文模型线性频率和非线性频率的影响。本文在扩展等几何方法的基础上，只研究了裂纹缺陷对含裂纹预扭壳结构静频的影响，接下来会继续探究考虑旋转速度的情况下，裂纹对于预扭壳结构动频的影响规律。

参考文献：

［1］ Miyamoto Y， Kaysser W A， Rabin B H， et al. Functionally graded materials： design， processing and applications［M］. Berlin， Germany： Springer Science & Business Media， 2013.

［2］ 徐可君，江龙平.裂纹对叶片固有频率影响的分析［J］. 推进技术， 1997， 18（6）： 68‑71.

XU Kejun， JIANG Longping. Analysis of effect of crack on the natural frequency of blade［J］.Journal of Propulsion Technology， 1997， 18（6）： 68‑71．

［3］ 赵迪， 尚新春. 含裂纹旋转叶片结构的振动特征分析［J］. 武汉大学学报（工学版）， 2011， 44（4）： 487‑491.

ZHAO Di， SHANG Xinchun. Analysis of vibration characteristics of rotating blade with cracks［J］. Engineering Journal of Wuhan University， 2011， 44（4）： 487‑491.

［4］ Kitipornchai S， Ke L L， Yang J， et al. Nonlinear vibration of edge cracked functionally graded Timoshenko beams［J］. Journal of Sound and Vibration， 2009， 324（3‑5）： 962‑982.

［5］ Panigrahi B， Pohit G. Effect of cracks on nonlinear flexural vibration of rotating Timoshenko functionally graded material beam having large amplitude motion［J］. Proceedings of the Institution of Mechanical Engineers， Part C： Journal of Mechanical Engineering Science， 2018， 232（6）： 930‑940.

［6］ 戴缘， 王天宇， 杨骁. 基于裂纹等效扭转弹簧模型的裂纹梁振动分析［J］. 上海大学学报（自然科学版）， 2019， 25（6）： 965‑977.

DAI Yuan， WANG Tianyu， YANG Xiao. Vibration analysis of cracked beam based on crack’s equivalent rotational spring model［J］. Journal of Shanghai University （Natural Science）， 2019， 25（6）： 965‑977.

［7］ 张俊红， 杨硕， 刘海， 等. 裂纹参数对航空发动机叶片频率转向特性影响研究［J］. 振动与冲击， 2014， 33（20）： 7‑11.

ZHANG Junhong， YANG Shuo， LIU Hai， et al. Influence of crack parameters on frequency veering characteristic of aero‑engine blade［J］. Journal of Vibration and Shock， 2014， 33（20）： 7‑11.

［8］ Panigrahi B， Pohit G. Nonlinear dynamic response of open and breathing cracked functionally graded beam under single and multi‑frequency excitation［J］. Engineering Structures， 2021， 242： 112437.

［9］ Nguyen V P， Anitescu C， Bordas S P A， et al. Isogeometric analysis： an overview and computer implementation aspects［J］. Mathematics and Computers in Simulation， 2015， 117： 89‑116.

［10］ Singh S K， Singh I V， Mishra B K， et al. Analysis of cracked functionally graded material plates using XIGA based on generalized higher‑order shear deformation theory［J］. Composite Structures， 2019， 225： 111038.

［11］ Zhang J， Yu T， Bui T Q. An adaptive XIGA with locally refined NURBS for modeling cracked composite FG Mindlin‑Reissner plates［J］. Engineering with Computers， 2021，38（4）： 3639‑3661.

［12］ 尹硕辉. 面向 CAD/CAE 集成的等几何分析和有限胞元法研究及应用［D］. 南京： 河海大学， 2016.

YIN Shuohui. Research on isogeometric analysis and finite cell method toward CAD/CAE integration and their applications［D］. Nanjing： Hohai University， 2016.

［13］ Sun J， Arteaga I L， Kari L. General shell model for a rotating pretwisted blade［J］. Journal of Sound and Vibration， 2013， 332（22）： 5804‑5820.

［14］ Shi J， Chopp D， Lua J， et al. Abaqus implementation of extended finite element method using a level set representation for three‑dimensional fatigue crack growth and life predictions［J］. Engineering Fracture Mechanics， 2010， 77（14）：2840‑2863.

［15］ Hughes T， Cottrell J A， Bazilevs Y. Isogeometric analysis： CAD， finite elements， NURBS， exact geometry and mesh refinement［J］. Computer Methods in Applied Mechanics & Engineering， 2005， 194（39‑41）： 4135‑4195.

［16］ Liu P， Bui T Q， Zhu D， et al. Buckling failure analysis of cracked functionally graded plates by a stabilized discrete shear gap extended 3‑node triangular plate element［J］. Composites Part B： Engineering， 2015， 77： 179‑193.

［17］ Kiani Y. Isogeometric large amplitude free vibration of graphene reinforced laminated plates in thermal environment using NURBS formulation［J］. Computer Methods in Applied Mechanics and Engineering， 2018， 332： 86‑101.

［18］ Chaudhari V K， Gupta A， Talha M. Nonlinear Vibration response of shear deformable functionally graded plate using finite element method［J］. Procedia Technology， 2016， 23： 201‑208.

Nonlinear vibration characteristic analysis of a cracked pre-twisted shell

ZHONG Sai‑feng1， JIN Guo‑yong1， HE Tao2， YE Tian‑gui1

（1.College of Power and Energy Engineering， Harbin Engineering University， Harbin 150001， China；2.Wuhan Second Ship Design and Research Institute， Wuhan 430205， China）

Abstract： This paper establishes the governing equations of the nonlinear vibration of a functionally graded shell with a crack， based on the extended isogeometric analysis （XIGA） and the first-order shear deformation theory. The study investigates the effects of the crack on the nonlinear vibrational frequency ratio of the model， taking into account large amplitude vibrations. Enriched functions， which represent displacement changes， are used to describe the position and length of the crack. This approach enhances calculation accuracy and avoids mesh refinement at the crack. The nonlinear governing equation is solved using the direct iteration method， and its correctness is validated by comparing the results with existing literature. The study further explores the effects of the pre-twisted angle， crack location， crack length and material variation parameters on the nonlinear vibration characteristics of the pre-twisted shells with cracks.

Key words： nonlinear vibration；functionally graded materials；cracked pre‑twisted shell structure；extended isogeometric analysis；first‑order shear deformation theory

作者简介： 仲赛凤（1995―），女，博士研究生。E‑mail： saifengzhong@hrbeu.edu.cn。

通讯作者： 靳国永（1980―），男，博士，教授。电话： （0451）82588822；E‑mail： guoyongjin@hrbeu.edu.cn。