TMD对人行桥疲劳寿命的影响研究

摘要： 针对人群运动导致人行结构振动过大而日益突出的疲劳破坏问题，可供参考的研究成果甚少。本文以钢⁃玻璃人行桥为试验平台开展关于安装TMD前后人致人行桥疲劳性能的研究，采用APS400电子激振器激励模拟人行荷载，通过长期应变监测数据，分析得出了该结构下的疲劳应力谱以及日平均损伤度，进而预估其疲劳寿命。结果表明：安装TMD后，结构1/2处的加速度峰值由0.15 m/s²减少到0.084 m/s²，减振率达44.0%；位移峰值由2.98 mm减少到0.92 mm，减振率达69.1%；应变幅值由40 减少到13 ，减振率达67.5%。结构跨中处等效应力幅值最大，疲劳寿命最短，为74年；安装TMD后，结构跨中处疲劳寿命为2880年，延长近39倍，其他测点处依次延长了3.95倍、7.41倍。

关键词： 钢⁃玻璃人行桥； 疲劳破坏； 应变监测； 疲劳应力谱； 疲劳寿命

中图分类号： U448.11； O346.2 文献标志码： A 文章编号： 1004-4523（2024）06-0928-09

DOI： 10.16385/j.cnki.issn.1004-4523.2024.06.003

引 言

近年来，伴随着旅游资源开发项目在全国各地的兴起，许多名胜景点修建了大量的人行景观桥，而柔性的人行钢⁃玻璃组合桥以其强大的跨越能力、独特的造型以及与景区环境的协调性，也得到了广泛青睐与应用。此类桥梁较一般车行桥更为纤细、质量更轻、自振频率更低、阻尼更小。在人行荷载作用下，因人行步频与人行桥基频接近而易产生共振，造成人行桥振动过大的问题［1⁃2］，当振动超出一定范围时，会对桥梁构件造成累积疲劳损伤，影响人行桥的安全性，甚至造成人行桥垮塌。因此开展人致振动人行桥疲劳寿命及振动控制的研究显得尤为重要。

目前，国内外学者主要围绕人行桥在人行荷载作用下的动力响应和振动舒适度［3⁃6］进行了大量研究。曹玉贵等［7］利用有限元软件ANSYS建立了某人行悬索桥的有限元模型，模拟人行悬索桥在不同人行荷载作用下的动力响应，并进行了振动舒适度评估。何勇等［8］针对多跨柔性人行桥在人行荷载作用下的振动舒适度验算问题，提出了基于振动均方根加速度响应谱的计算方法。Tubino等［9］把人行桥看作Euler梁模型，利用振型叠加法计算了人行桥的动力响应，并基于不同的TMD模型对其振动进行控制。陈舟等［10］根据交通流和生物力学的研究成果，将人体视为具有质量、刚度、阻尼的两自由度系统，建立了人群过桥时人群⁃桥梁耦合系统的动力学模型，分析了人群作用下人行桥的动力响应。Venuti等［11］提出考虑人群⁃人行桥竖向动力相互作用的建模框架，框架由两部分组成，一部分是由社会力模型模拟出人行桥任意时刻每个人的位置和速度，另一部分是人行桥模型和人群运动动力耦合，最后仿真出了人行荷载作用下人行桥的振动。朱前坤等［12］把人行桥看作Euler梁模型，基于振型叠加法计算了不同行走步速下人行桥的动力响应。关于桥梁疲劳的研究大多集中在车行桥疲劳方面。文献［13⁃14］利用青马大桥结构健康监测系统数据，综合考虑交通荷载、台风影响以及钢材锈蚀等因素，通过统计分析长期应变监测数据建立了标准日应力谱；比较分析了应力集中效应和钢材锈蚀因素对焊接节点的疲劳寿命失效概率和可靠度指标的影响规律。Saberi等［15］对位于马萨诸塞州的一座钢桥设计安装了健康监测系统，并进行了连续6个月的监测，监测到了1225辆卡车作用下桥梁的应变响应，进而得到疲劳危险关键部位的疲劳应力谱。Fu等［16］建立了世界上首座千米级三塔悬索桥泰州大桥的三维全桥模型，通过简化的车辆荷载模型，将随机车流加载于大桥有限元模型上，计算了其关键构件的动力响应。文献［17⁃19］建立了基于车桥耦合振动的桥梁动应力分析方法，探讨了列车速度、轨道不平顺、横向振动、交通演变等对桥梁疲劳应力的影响。文献［20⁃21］基于包含车辆多参数的概率统计特征随机车流模型，计算得到悬索桥结构细节在随机车流作用下的疲劳应力。王滢等［22］根据结构健康监测系统记录的钢箱梁在交通和环境载荷下的应变时程曲线，研究了润扬大桥的钢箱梁结构在正常交通载荷、重车过桥和台风经过时的疲劳应力谱特征。吉伯海等［23］以江阴长江大桥钢箱梁上记录的应变数据为基础，研究钢箱梁在运营荷载作用下的疲劳应力特征。刘建等［24］以国内最大跨度的独塔自锚式悬索桥为工程背景，用桥梁健康监测系统实测数据，得到了钢箱梁的疲劳应力谱。

综上所述，目前关于人致振动的研究主要集中于结构振动舒适度、动力响应以及振动控制方面；同时结构疲劳方面的研究也以车行桥疲劳为主，而针对人行荷载下的人行桥振动疲劳性能研究则鲜有涉及。基于此，本文以钢⁃玻璃人行桥为试验对象，进行为期20天的现场应力⁃应变试验，研究安装TMD前后结构疲劳寿命变化规律以及结构疲劳损伤性能。

1 疲劳试验

1.1 试验模型及动力特性

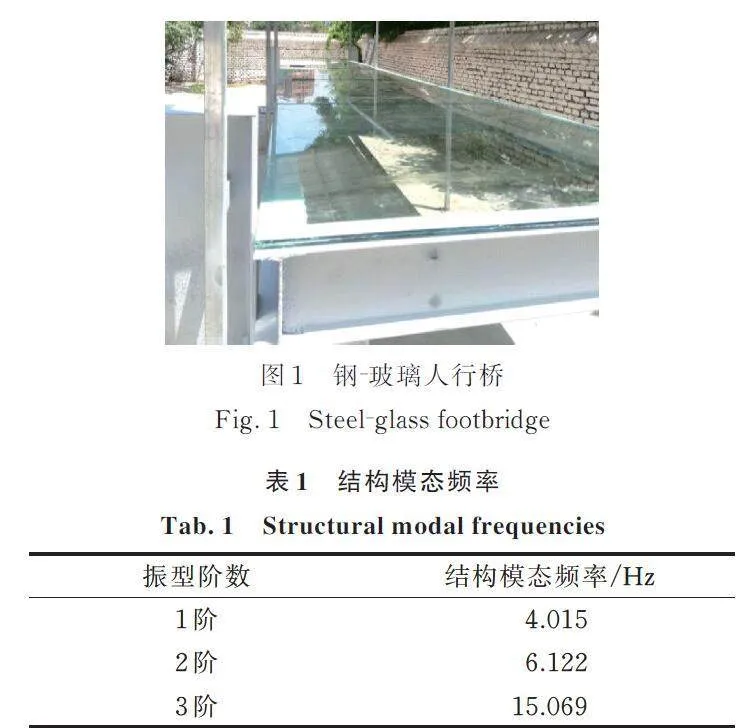
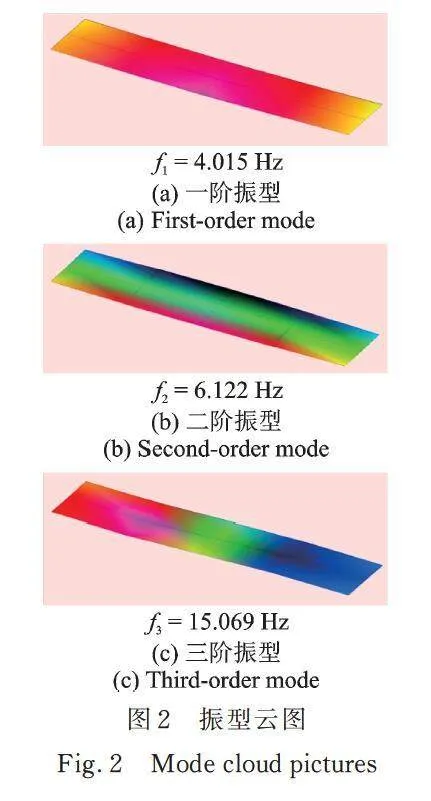
选用本课题组自制钢⁃玻璃人行桥为试验对象，如图1所示。桥梁全长10 m，宽1.6 m，钢框架主体由2根10 m长的20a型工字钢和6根1.6 m的20a型工字钢焊接而成，桥面由5块双层夹胶玻璃（10 mm+2.28 PVB+10 mm）与钢框架采用粘接连接，钢框架搭接在支座上，支座与地面采用地脚螺栓锚固连接。环境激励下结构动力特性参数如表1所示，振型云图如图2所示。

1.2 试验设备

EY501工具式表面应变计，如图3所示，具有输出灵敏度极高、线性好、稳定性好、构造简单、安装使用方便等优点。应变采集设备采用东华DH⁃5921型智能应变采集系统，如图4所示。德国APS400低频模态电子激振器：频率范围为0～200 Hz，冲程为158 mm，推力可达445 N，如图5所示。

1.3 试验方案

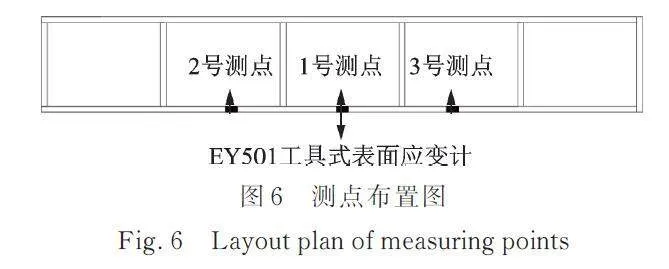
根据《美国道路通行能力手册HCM 2000》人行道服务水平标准［25］，按准自由状态活动进行取值，取单位面积的人数小于0.5人，故该桥上行走人数应取小于8人。在桥梁正常运营状态下采用东华DH⁃5921型智能应变采集系统对钢⁃玻璃人行桥进行为期10天的疲劳应变监测，采样频率为50 Hz。采集测点位置按应变最大处、最容易发生疲劳破坏的部位进行选取，共3个测点，应变计布置图如图6所示。

1.4 应变响应分析

1.4.1 激振器模拟人行激励可行性分析

为验证激振器激励模拟人行激励的可行性，图7（a）和（b）为分别开展激振器参数设定为定频2 Hz、定幅10 Vpp的激励试验和行人在1号测点处以2 Hz跳跃的激励试验，试验结果如图7（c）所示。在1号测点处采集两种工况下的应变曲线，曲线重合度很高，幅值大小均近似78 με；故激振器激励可很好地模拟人行荷载并代替人行荷载对结构进行激励以开展疲劳试验。

APS400电子激振器模拟人行荷载的参数设定依据如下：由《美国道路通行能力手册HCM 2000》人行道服务水平标准［25］可知，行走人数取为7人，行人重量为750 N/人，人行荷载动载因子DLF（Dynamic Load Factor）取为0.036；则7人同步行走时的激振力；故激振器产生的力，激振器自重m1为73 kg，计算得加速度a=2.589 m/s²；又由公式可知，频率f=4 Hz时，激振器悬臂位移s=0.16 m；经查APS400电子激振器说明书可知，s=161 mm时，幅值为10 Vpp。故激振器模激励模拟人行荷载激励的参数值设定为4 Hz，10 Vpp。

1.4.2 结构应变响应分析

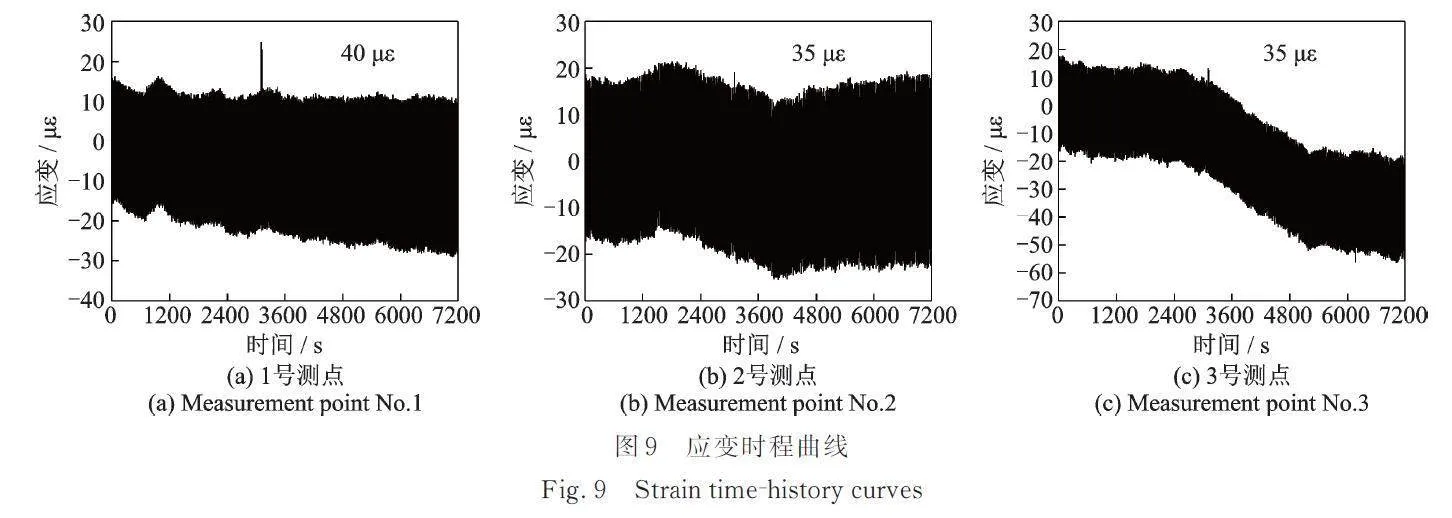
为了更加精确地得出结构在最不利情况下的结构疲劳损伤度和结构疲劳寿命。现设计试验方案如下：将APS400电子激振器放置在结构响应最大处，采用定频、定幅激励模式，为期10天，现场测试如图8所示。试验采集得到了3个测点的应变时程曲线，如图9所示。

综合图9（a）～（c）可知，激振器激励下，各测点应变幅值基本相似；1号测点应变峰值为40 ，2号测点应变峰值为35 ；3号测点应变偏移量较大，但应变幅值基本不变，也保持在35 ；由此可见该结构下跨中处应变响应较大。

2 疲劳应力谱获取

2.1 雨流计数法

雨流计数法是目前在疲劳设计和疲劳试验中应用最广泛的一种计数方法，是变程计数法的一种，可根据所研究材料的应力⁃应变之间的非线性关系进行计数。雨流计数法是建立在对封闭的应力⁃应变迟滞回线逐个计数的基础上，因此该方法能够比较全面地反映随机荷载的全过程。由荷载⁃时间历程得到的应力⁃应变迟滞回线与造成的疲劳损伤是等效的。

2.2 疲劳应力谱

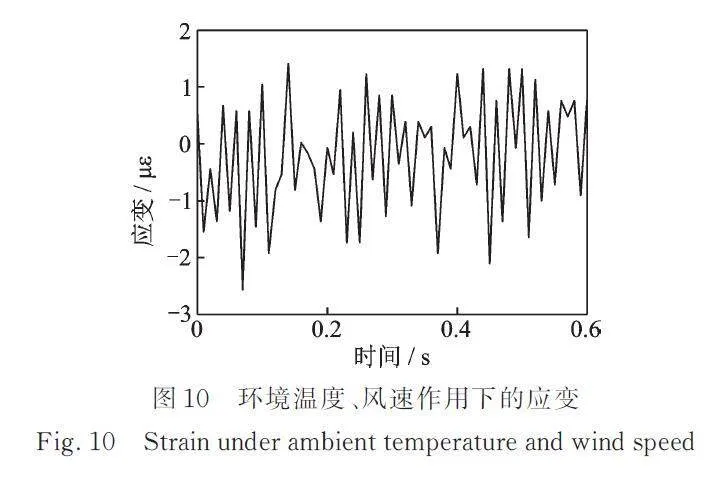
人行桥在正常运营状态下，主要受人行荷载数量，人行步频、步长、步速，环境温度以及风速等一系列综合因素的影响。其中环境温度和风速相对于人行荷载影响甚微，但对等效应力幅值有影响，故应予以剔除，只保留人行荷载作用下的应力幅值。

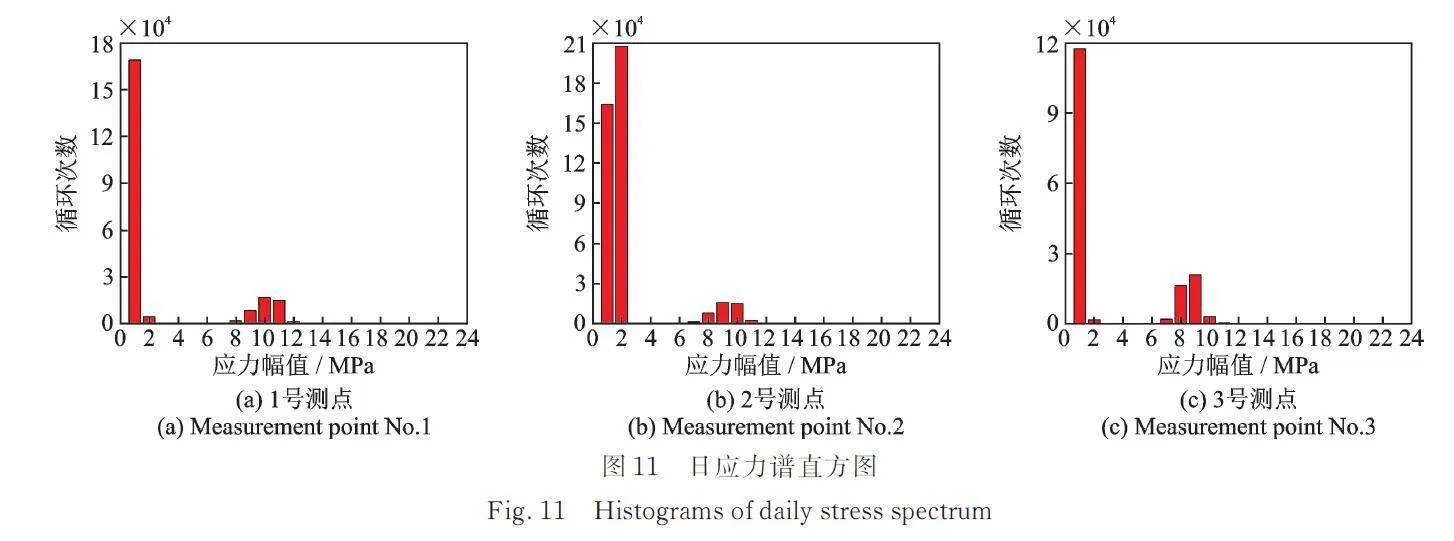
图10为环境激励下得到的结构应变时程曲线。由图10可知，应变传感器的有效量程下限值为5 με，应舍弃应力谱中小于2 MPa的应力幅值。APS400激振器激励下结构的日应力谱直方图如图11所示。

由图11可知，APS400电子激振器激励下，1，2，3号测点处的应力幅值都在24 MPa以内，高次应力循环数集中在7～12 MPa范围内。

3 基于BS 5400规范的疲劳寿命预估

3.1 等效应力幅值计算

国内外研究表明，变幅疲劳问题可换算成一个等效常幅疲劳进行计算；基于疲劳强度S⁃N（正应力幅值⁃应力循环次数）曲线和Miner损伤定律，可将试验中变应力幅值转化为一个等效的常应力幅值，使得等效常应力幅值作用下的疲劳损伤等效于变应力幅值下的疲劳损伤，转化公式如下：

（1）

式中 为变应力幅值所对应的等效常应力幅值；为循环次数，取值范围为103～104；为各级变应力幅值；为各级变应力幅值下的循环次数；m为特定连接构造细节下S⁃N曲线的斜率。

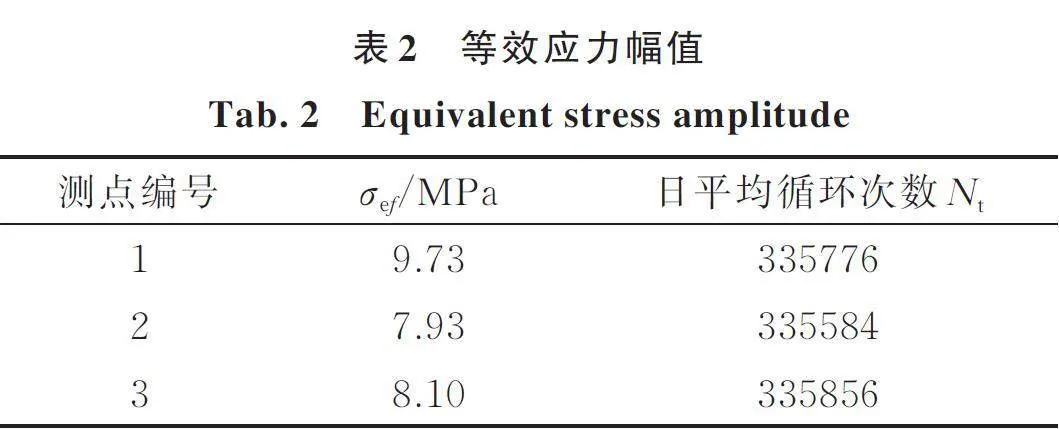
由式（1）计算的人行荷载激励和APS400激振器激励下各测点的等效应力幅值如表2所示。由表2可知，APS400电子激振器激励下3个测点处的日平均循环次数非常接近，都在3.35×105次附近；说明激振器作为激励源时输出的能量具有稳定性和一致性，可较好地替代人行荷载激励进行结构疲劳试验。其中1号测点等效应力幅值最大，为9.73 MPa；2，3号测点的等效应力幅值分别为7.93，8.10 MPa。

3.2 不同失效概率下结构疲劳寿命计算

3.2.1 Miner线性损伤定律

基于Miner线性损伤定律和疲劳强度S⁃N曲线关系的指数模型对该桥梁各测点做损伤计算，原理如下：测试部位在某应力幅值作用下有ni次循环，由S⁃N曲线计算得到作用下对应的疲劳寿命为Ni，则作用下的疲劳损伤率为ni/Ni，各级应力幅值作用下的累计损伤度计算公式为：

（2）

从工程应用的角度，粗略地认为当时，结构发生疲劳破坏。

3.2.2 疲劳寿命经验计算公式

根据BS 5400规范［26］确定各构件细节的连接类型，从而获取相应的疲劳极限计算参数K0，Δ，等。日平均损伤度Nd经验计算公式如下：

（3）

式中 Nd为日平均损伤度，d为各失效概率下的系数值，取值见表3。

经查BS 5400规范［26］可知，1，2，3号测点所对应的构件连接类型都为C型，为非焊接构件下无连接处的母材轧制型钢，对应公式（3）中的构建连接细节参数为：K0=1.08×1014，Δ=0.625，u=3.5。

3.2.3 不同失效概率下的疲劳寿命预估

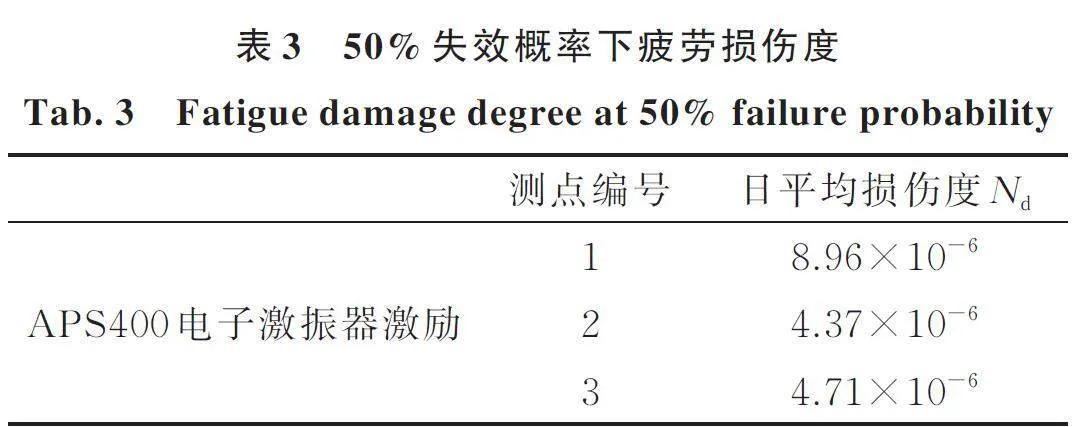
由公式（3）计算得出表3中各测点在50%失效概率下的日平均疲劳损伤度。由表3可知，APS400电子激振器激励下1号测点处的日平均损伤度最大，为8.96×10-6；2，3号测点处的损伤度分别为4.37×10-6，4.71×10-6。

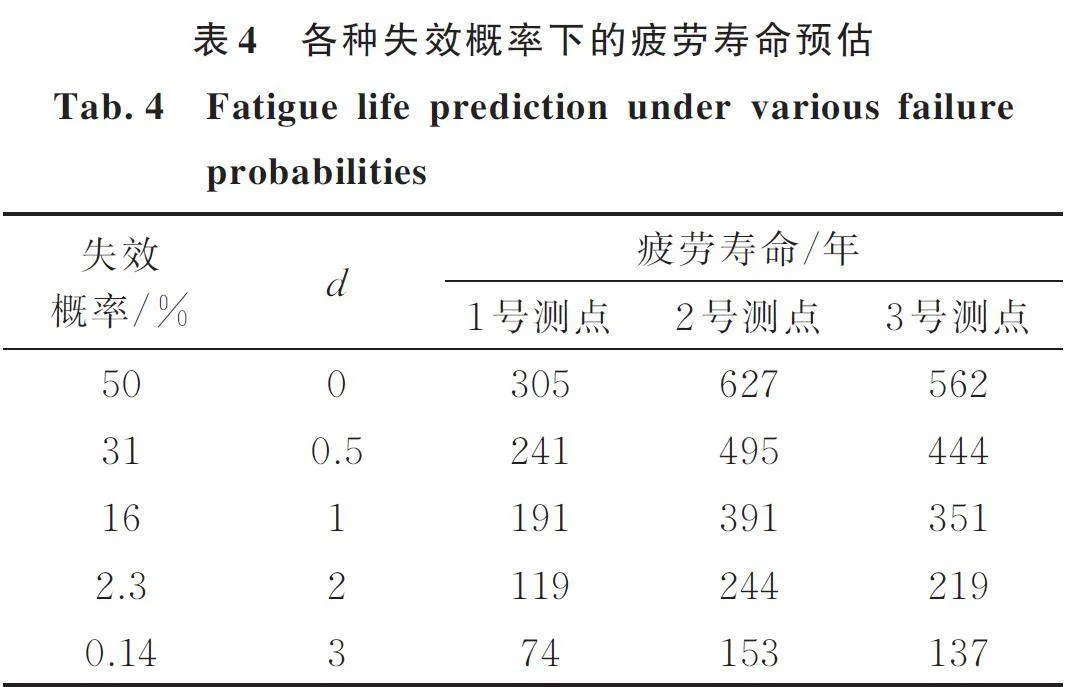
代入公式（2）计算结构疲劳寿命，表4为各种失效概率下的疲劳寿命预估。由表4可知，各测点的疲劳寿命均大于100年，仅当失效概率为0.14%时，1号测点处的疲劳预估寿命为74年；对比各测点疲劳预估寿命可知，对于简支梁桥，跨中处抗疲劳性能最差，最容易发生疲劳破坏，在实际工程中应做加固处理。

4 TMD作用下结构疲劳寿命预估

4.1 TMD减振系统

本试验所设计的TMD减振装置是由4根弹簧、电涡流阻尼原件（铜板和磁铁组成）以及质量块组成的振动系统。根据文献［27］中的Den Hartog模型最优频率比和TMD阻尼比，TMD设计参数如下：质量md=15.9 kg，刚度kd=11.4 kN/m，阻尼cd=0.052 kN∙s∙m-1，如图12所示。具体参数设计见文献［28］。

TMD在结构上的安装位置为一阶模态振型位置处（桥梁1/2跨），如图13所示。阻尼器频率调整为接近桥梁基频（4.06 Hz），减振原理如下：结构在外力作用下引起共振，调谐质量阻尼器通过振动惯性力反作用于结构本身，进而达到减小结构振动响应、位移响应、应变响应的目的，从而延长结构疲劳寿命。

4.2 试验方案

为了更好地对比安装TMD前后结构疲劳寿命的变化，试验测试方案同1.3节。在一阶模态振型最大处放置TMD，同图13。利用APS400电子激振器在跨中处以4.0 Hz，10 Vpp的定频、定幅参数进行为期10天的激励，测点布置同图6。采集不同测点处的结构应变时程曲线，同时利用位移计和加速度传感器采集安装TMD前后结构的位移时程曲线和加速度时程曲线。

4.3 响应分析

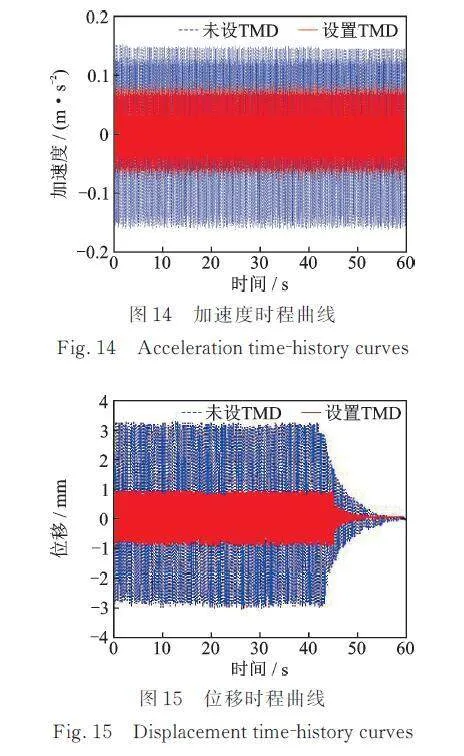
图14为APS400电子激振器激励下安装TMD前后结构的加速度时程曲线。由图14可知，安装TMD后结构加速度峰值由0.15 m/s²减少到0.084 m/s²，加速度峰值降低了0.066 m/s²，减振率为44.0%。图15为安装TMD前后结构的位移时程曲线，结构位移峰值由3.15 mm减少到0.92 mm，减振率为70.8%。因此综合图14和15可知，TMD对结构响应控制较好，减振效果明显。

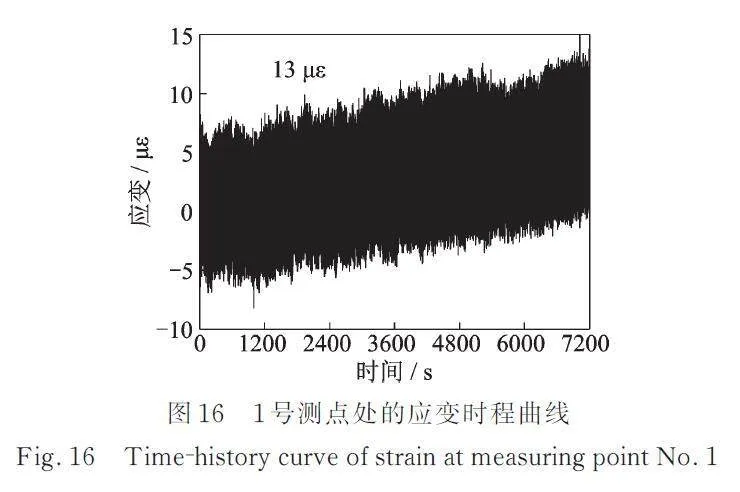
图16为安装TMD后1号测点处的应变时程曲线。由图16可知，安装TMD后1号测点应变幅值在13 以内，相较于图9中未安装TMD时的40 με，结构应变幅值大大降低；安装TMD后结构的应变减振率可达近67.5%。

4.4 疲劳寿命预估

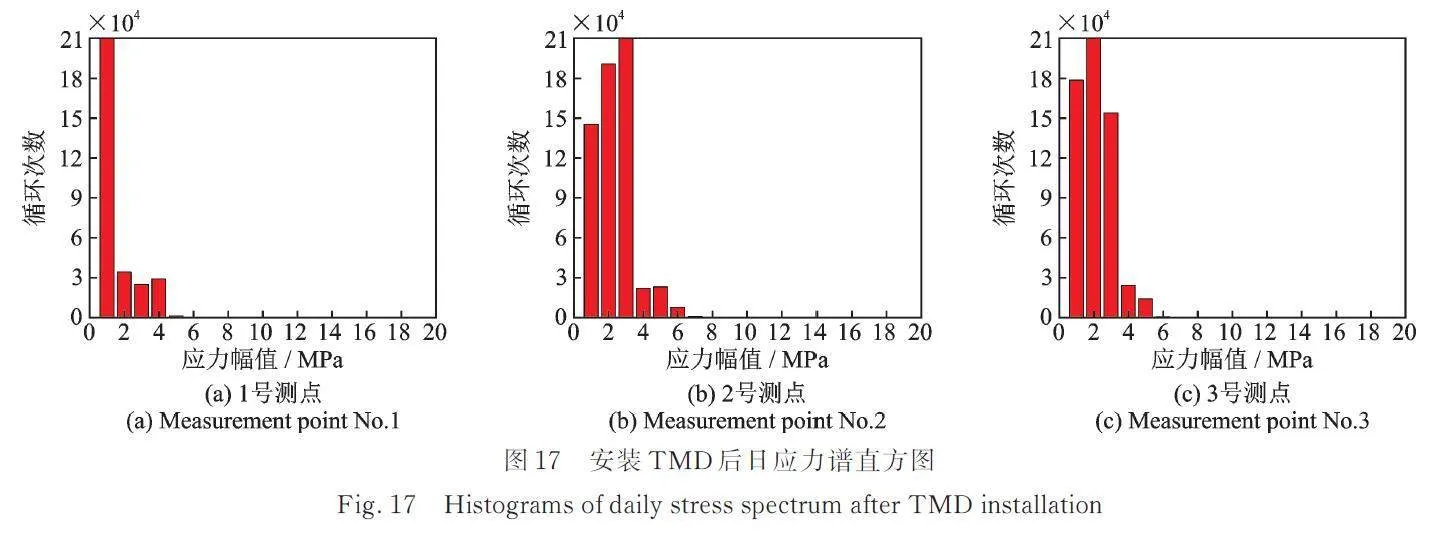
图17为安装TMD后APS400电子激振器激励下结构各测点的日应力谱直方图。由图17可知，安装TMD后，1号测点处大于2 MPa的总应力循环次数远小于2，3号测点处的值。3个测点处的高次应力幅值大多集中在3～6 MPa，远小于未安装TMD时的应力幅值7～12 MPa，说明TMD对结构的应变减振效果较好。

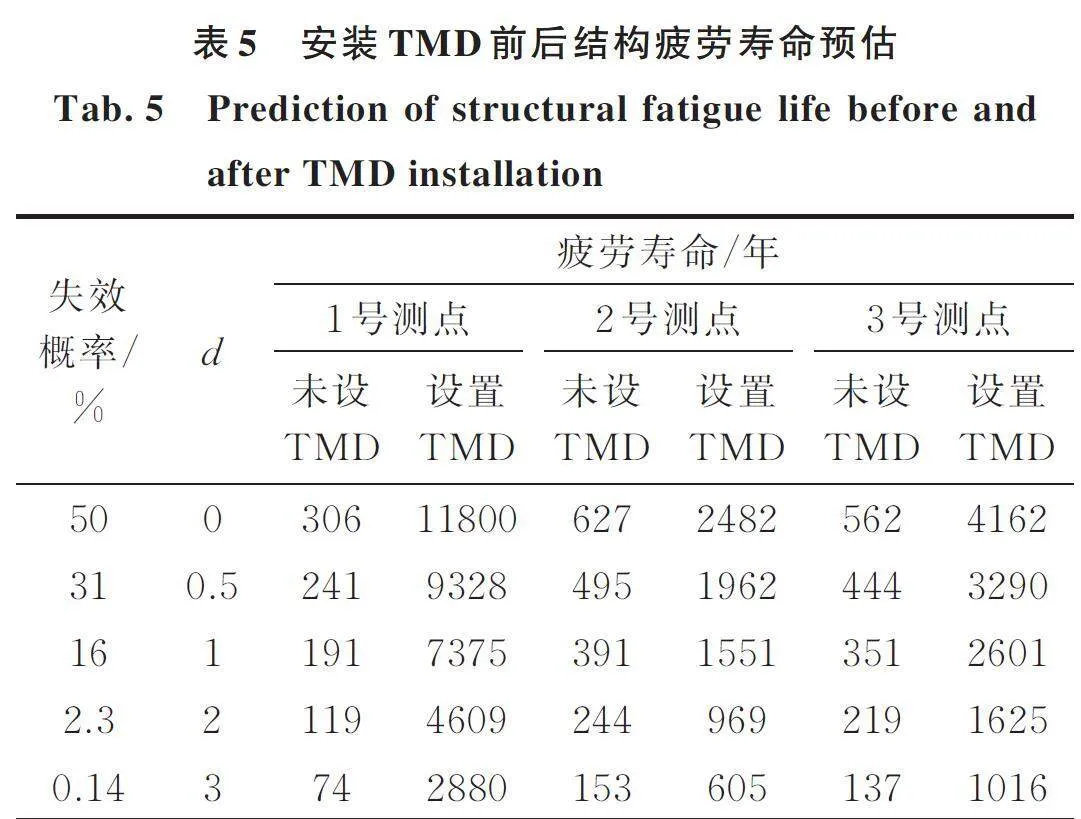
同理按公式（2）～（3）进行结构疲劳寿命预估，得到各种失效概率下的结构疲劳寿命如表5所示。

由表5可知，安装TMD后，失效概率为0.14%时，1号测点处的疲劳寿命为2880年，相较于未安装TMD增加了近39倍，结构疲劳寿命延长效果显著；而2，3号测点处的疲劳寿命依次增加了3.95倍、7.41倍，增加幅度较小。这是因为此TMD的设计主要用于控制结构的一阶模态振型处的振动，对其他位置处的振型控制较弱。假设在2，3号测点处也增设TMD，此两点处的疲劳预估寿命也将显著提升，该假设也将在后续研究中继续完善。

5 结 论

基于实验室钢⁃玻璃人行桥现场应变测试，分析了TMD对人行桥疲劳寿命的影响，得到以下结论：

（1）对于简支梁桥，跨中处应变响应最大，最容易发生疲劳破坏，结构设计时应在跨中做加固处理。

（2）失效概率为0.14%时，结构安装TMD位置处疲劳寿命增加了近39倍，其他位置处依次增加了3.95倍、7.41倍；因此在实际工程结构疲劳修复时可考虑在振动敏感区安装TMD以延长结构疲劳寿命。

（3）此外本文安装TMD后的结构疲劳寿命较大的原因是只考虑了荷载作用下结构的疲劳寿命，而未考虑环境腐蚀下的疲劳损伤，实际情况下钢结构更容易受环境腐蚀发生疲劳破坏，疲劳寿命将会大幅降低，需进一步作全面研究。

参考文献：

［1］ Živanović S， Pavić A， Ingólfsson E T. Modeling spatially unrestricted pedestrian traffic on footbridges［J］. Journal of Structural Engineering， 2010， 136（10）： 1296-1308.

［2］ 朱前坤， 蒲兴龙， 惠晓丽， 等. 基于人群-结构耦合作用甘肃省体育馆悬挂结构振动舒适度评估及控制［J］. 工程力学， 2018， 35（增刊1）： 46-52.

Zhu Qiankun， Pu Xinglong， Hui Xiaoli， et al. Serviceability evaluation and control of suspension structure of Gansu gymnasium based on pedestrian-structure coupled vibration［J］. Engineering Mechanics， 2018， 35（Sup1）： 46-52.

［3］ 闫畅， 陈建兵， 李新生. 大跨度人行钢桥动力性能测试及舒适度评估［J］. 苏州科技大学学报 （工程技术版）， 2019， 32（3）： 15-19.

Yan Chang， Chen Jianbing， Li Xinsheng. Dynamic performance test and comfort evaluation of large-span pedestrian steel girder bridges［J］. Journal of Suzhou University of Science and Technology （Engineering and Technology）， 2019， 32（3）： 15-19.

［4］ 崔又文， 李睿， 徐征， 等. 抗风缆对玻璃桥面人行悬索桥动力特性和舒适度影响分析［J］. 钢结构 （中英文）， 2019， 34（11）： 86-90.

Cui Youwen， Li Rui， Xu Zheng， et al. Analysis of wind resistant cable on dynamic characteristics and comfort of pedestrian suspension bridge with glass deck［J］. Steel Construction （Chinese and English）， 2019， 34（11）： 86-90.

［5］ Abdeljaber Osama， Hussein Mohammed， Avci Onur， et al. A novel video-vibration monitoring system for walking pattern identification on floors［J］. Advances in Engineering Software， 2020， 139： 102710.

［6］ 朱前坤， 蒲兴龙， 惠晓丽， 等. 考虑人-结构相互作用装配式轻质楼盖振动舒适度评估［J］. 建筑结构学报， 2019， 40（11）： 220-229.

Zhu Qiankun， Pu Xinglong， Hui Xiaoli， et al. Assessment of vibration serviceability of precast lightweight floor considering human-structure interaction［J］. Journal of Building Structures， 2019， 40（11）： 220-229.

［7］ 曹玉贵， 胡隽， 李小青， 等. 人行索桁桥振动分析及舒适度评价［J］. 江苏大学学报 （自然科学版）， 2014， 35（5）： 605-610.

Cao Yugui， Hu Jun， Li Xiaoqing， et al. Comfort evaluation and dynamic performance of suspension footbridge［J］. Journal of Jiangsu University （Natural Science Edition）， 2014， 35（5）： 605-610.

［8］ 何勇， 金伟良， 宋志刚. 多跨人行桥振动均方根加速度响应谱法［J］. 浙江大学学报 （工学版）， 2008， 42（1）： 48-53.

He Yong， Jin Weiliang， Song Zhigang. RMS acceleration response spectrum method of multi-span footbridge under pedestrian excitation［J］. Journal of Zhejiang University （Engineering Science）， 2008， 42（1）： 48-53.

［9］ Tubino F， Piccardo G. Tuned mass damper optimization for the mitigation of human-induced vibrations of pedestrian bridges［J］. Meccanica， 2015， 50（3）： 809-824.

［10］ 陈舟， 颜全胜， 胡俊亮， 等. 人群-桥梁耦合振动研究及参数分析［J］. 华南理工大学学报 （自然科学版）， 2014， 42（5）： 75-83.

Chen Zhou， Yan Quansheng， Hu Junliang， et al. Coupling vibration investigation and parameter analysis of crowd-bridge system［J］. Journal of South China University of Technology （Natural Science Edition）， 2014， 42（5）： 75-83.

［11］ Venuti F， Racic V， Corbetta A. Modelling framework for dynamic interaction between multiple pedestrians and vertical vibrations of footbridges［J］. Journal of Sound and Vibration， 2016， 379： 245-263.

［12］ 朱前坤， 李宏男， 杜永峰， 等. 不同行走步速下人行桥振动舒适度定量化评估［J］. 工程力学， 2016， 33（10）： 97-104.

Zhu Qiankun， Li Hongnan， Du Yongfeng， et al. Quantitative evaluation of vibration serviceability of pedestrian bridge under different walking speed［J］. Engineering Mechanics， 2016， 33（10）： 97-104.

［13］ Ye X W， Ni Y Q， Wong K Y， et al. Statistical analysis of stress spectra for fatigue life assessment of steel bridges with structural health monitoring data［J］. Engineering Structures， 2012， 45： 166-176.

［14］ 叶肖伟， 傅大宝， 倪一清， 等. 考虑多因素共同作用的钢桥焊接节点疲劳可靠度评估［J］. 土木工程学报， 2013， 46（10）： 89-99.

Ye Xiaowei， Fu Dabao， Ni Yiqing， et al. Fatigue reliability assessment of welding joints in steel bridges considering multiple effects［J］. China Civil Engineering Journal， 2013， 46（10）： 89-99.

［15］ Saberi M R， Rahai A R， Sanayei M， et al. Bridge fatigue service-life estimation using operational strain measurements［J］. Journal of Bridge Engineering， 2016， 21（5）： 04016005.

［16］ Fu Z Q， Ji B H， Ye Z， et al. Fatigue evaluation of cable-stayed bridge steel deck based on predicted traffic flow growth［J］. KSCE Journal of Civil Engineering， 2017， 21（4）： 1400-1409.

［17］ Li H L， Frangopol D M， Soliman M， et al. Fatigue reliability assessment of railway bridges based on probabilistic dynamic analysis of a coupled train-bridge system［J］. Journal of Structural Engineering， 2016， 142（3）： 04015158.

［18］ 李慧乐， 夏禾. 基于车桥耦合随机振动分析的钢桥疲劳可靠度评估［J］. 工程力学， 2017， 34（2）： 69-77.

Li Huile， Xia He. Fatigue reliability evaluation of steel bridges based on coupling random vibration analysis of train and bridge［J］. Engineering Mechanics， 2017， 34（2）： 69-77.

［19］ Li H L， Soliman M， Frangopol D M， et al. Fatigue damage in railway steel bridges： approach based on a dynamic train-bridge coupled model［J］. Journal of Bridge Engineering， 2017， 22（11）： 06017006.

［20］ 鲁乃唯， 刘扬， 邓扬. 随机车流作用下悬索桥钢桥面板疲劳损伤与寿命评估［J］. 中南大学学报 （自然科学版）， 2015， 46（11）： 4300-4306.

Lu Naiwei， Liu Yang， Deng Yang. Fatigue damage and life assessment for steel decks of suspension bridge under stochastic traffic flow［J］. Journal of Central South University （Science and Technology）， 2015， 46（11）： 4300-4306.

［21］ 刘扬， 李明， 邓扬， 等. 基于随机车辆模拟的钢桥面板焊接细节疲劳可靠度研究［J］. 中国公路学报， 2017， 30（11）： 89-98.

Liu Y， Li M， Deng Y， et al. Research on fatigue reliability of steel bridge deck welding details based on random vehicle simulation［J］. Chinese Journal of Highway and Transport， 2017， 30（11）： 89-98.

［22］ 王滢， 李兆霞， 吴佰建. 润扬悬索桥钢箱梁结构疲劳应力监测及其分析［J］. 东南大学学报 （自然科学版）， 2007， 37（2）： 280-286.

Wang Ying， Li Zhaoxia， Wu Baijian. Fatigue stress monitoring and analysis for steel box girder of Runyang suspension bridge［J］. Journal of Southeast University （Natural Science Edition）， 2007， 37（2）： 280-286.

［23］ 吉伯海， 叶枝， 傅中秋， 等. 江阴长江大桥钢箱梁疲劳应力特征分析［J］. 世界桥梁， 2016， 44（2）： 30-36.

Ji Bohai， Ye Zhi， Fu Zhongqiu， et al. Analysis of fatigue stress property of steel box girder of Jiangyin Changjiang river bridge［J］. World Bridges， 2016， 44（2）： 30-36.

［24］ 刘建， 桂勋， 李传习. 基于健康监测的自锚式悬索桥钢箱梁细节疲劳可靠度研究［J］. 公路交通科技， 2015， 32（1）： 69-75.

Liu Jian， Gui Xun， Li Chuanxi. Study on fatigue reliability of details of steel box girders of a self-anchored suspension bridge based on health monitoring［J］. Journal of Highway and Transportation Research and Development， 2015， 32（1）： 69-75.

［25］ Transportation Research Board. Highway Capacity Manual 2000［M］. 4th ed. Washington D. C.， USA： Transportation Research Board， 2000.

［26］ 钢， 混凝土和组合材料桥梁. 疲劳的详细分类图： BS 5400-10C―1999［S］. 伦敦： 英国标准学会， 1999.

Steel， concrete and composite bridges. Charts for classification of details for fatigue： BS 5400-10C―1999［S］. London： British Standard Institute， 1999.

［27］ 李晓玮， 何斌， 施卫星. TMD减振系统在人行桥结构中的应用［J］. 土木工程学报， 2013， 46（增刊1）： 245-250.

Li Xiaowei， He Bin， Shi Weixing. Application of TMD seismic vibration control system in the bridge structures［J］. China Civil Engineering Journal， 2013， 46（Sup1）： 245-250.

［28］ 朱前坤， 马齐飞， 张琼， 等. 新型竖向电涡流-磁力混合阻尼装置试验研究［J］. 振动与冲击， 2022， 41（3）： 62-72.

Zhu Qiankun， Ma Qifei， Zhang Qiong， et al. Test of a new vertical eddy current magnetic hybrid damping device［J］. Journal of Vibration and Shock， 2022， 41（3）： 62-72.

Effect of TMD on fatigue life of steel-glass footbridge model

Ma Fa-rong1，2， Zhu Qian-kun2， Pu Xing-long1，2， Du Yong-feng2

（1. School of Civil Engineering， Hexi University， Zhangye 734000， China；2. Institute of Earthquake Prevention and Disaster Reduction， Lanzhou University of Technology， Lanzhou 730050， China）

Abstract： Research on the increasingly significant issue of fatigue failure in pedestrian structures due to crowd-induced vibrations is limited. This paper uses a steel-glass footbridge as a test platform to study the fatigue performance of the footbridge before and after the installation of a Tuned Mass Damper （TMD）. The APS400 electronic shaker is used to simulate pedestrian load， and long-term strain monitoring data is analyzed to determine the fatigue stress spectrum and daily average damage degree of the structure， which is then used to estimate its fatigue life. The results show that the installation of the TMD reduced the peak acceleration at half of the structure from 0.15 m/s² to 0.084 m/s²， a vibration reduction rate of 44.0%. The peak displacement was reduced from 2.98 mm to 0.92 mm， a vibration reduction rate of 69.1%； and the strain amplitude was reduced from 40 to 13， a vibration reduction rate of 67.5%. The amplitude of the equivalent effect force across the middle of the structure is the largest， and the fatigue life is the shortest， at 74 years. After the installation of the TMD， the fatigue life of the structure span increased to 2880 years， nearly 39 times longer， and the fatigue life at other measurement points extended by 3.95 times and 7.41 times.

Key words： steel-glass footbridge； fatigue damage； strain monitoring； fatigue stress spectrum； fatigue life

作者简介： 马法荣（1996—），男，博士研究生，助教。E-mail： 1778142275@qq.com。

通讯作者： 朱前坤（1981—），男，博士，教授，博士生导师。电话： （0931）2976789； E-mail： zhuqklut@qq.com。