非平稳随机激励下高维非线性系统可靠度分析的概率密度全局演化方法

摘要： 实际工程结构遭受的灾害性动力作用（如强风、地震等）往往具有显著的随机性和非平稳性。对复杂随机激励下高维非线性系统的动力可靠度进行精细化分析，对于实际工程结构的抗灾设计和优化具有重要意义。基于一般连续随机过程的降维概率密度演化方程，给出了一类非平稳随机激励下的高维非线性系统动力可靠度分析方法。具体地，若仅针对系统某一感兴趣物理量在给定安全域下的首次超越问题，则可以构造该物理量在安全域内的吸收边界过程，并建立其瞬时概率密度函数满足的二维偏微分方程，即降维概率密度演化方程。方程中的本征漂移系数是驱动概率密度演化的全局性物理驱动力，可以通过对原系统有限次代表性确定性动力分析获取的数据进行数值构造。采用数值方法求解降维概率密度演化方程，即可获得系统的动力可靠度解答。文中通过两个算例验证了该方法的有效性，并讨论了需要进一步研究的问题。

关键词： 降维概率密度演化方程； 高维非线性随机动力系统； 非平稳随机激励； 动力可靠度分析； 物理驱动

中图分类号： O324； TU318 文献标志码： A 文章编号： 1004-4523（2024）06-0903-12

DOI：10.16385/j.cnki.issn.1004-4523.2024.06.001

引 言

实际工程结构在服役过程中，不可避免地会受到各类外部激励的作用，如强风、地震等［1］。这些外部激励往往具有很强的随机性和非平稳特征，可能导致结构不同部位的损伤、乃至不同模式的破坏［2‑3］。因而，灾害性随机动力作用下复杂工程结构的可靠性分析一直是人们所关心的重要问题［4‑5］。

基于首次超越失效准则的结构动力可靠性理论经历了长期的发展［6‑7］，但是对复杂工程结构的精确求解依然存在局限［4］。事实上，传统的首次超越可靠度理论主要包括三类：跨越过程理论、扩散过程理论和极值分布理论。跨越过程理论基于Rice公式［8］，进而引入关于跨越事件性质的假设来估计动力可靠度［9］。然而对于复杂工程系统，其响应及速度的联合概率密度很难准确获得，且难以消除由对跨越事件性质的假定引起的误差［10］。扩散过程理论通过求解Chapman‑Kolmogorov方程或Kolmogorov后向方程获得动力可靠度［11］，但同样面临高维系统难以求解的困难［6］。极值分布理论最早始于对独立随机变量序列极值的研究［12］，虽然此后对不同情形下随机抽样极值或渐近极值的研究逐渐成熟［13］，但对于随机过程极值分布的解析或数值研究迄今仍不成熟。最近，针对Markov过程发展了增广Markov系统方法［14‑16］和概率分布演化积分方程［17］等确定时变极值分布的系统性方法，但目前仍难以突破维数对计算成本的限制。

在上述理论的基础上，若考虑高维系统的可靠度评估问题，往往需要借助一定数量的系统观测或动力分析样本数据。直接通过样本数据估计可靠度的思想就是随机模拟方法，包括直接蒙特卡罗模拟及其各类改进方法，如重要性抽样［18］、子集模拟［19］、线抽样［20］等。这类方法是随机收敛的，且对蒙特卡罗的各类改进往往以牺牲其适用性为代价。各类低偏差点集方法（有时又称拟蒙特卡罗模拟）［21］原则上是确定性收敛的，依然难以应用于高维问题。另一类应用广泛的方法是矩方法，即先由样本数据估计响应极值或极限状态函数的几阶矩，进而由矩信息估计极值分布或可靠度，这方面的代表性研究包括高阶矩法［22‑23］、分数阶矩法［24‑25］、线性矩法［26］等。矩方法采用响应的矩估计信息、结合既定的响应尾部或极值分布形式，往往对可靠度分析具有较高的计算效率，但由于从根本上对概率密度函数的反映是不完全的，因此其适用性在一定程度上取决于问题本身的性质。

21世纪初提出的概率密度演化理论［4，27］揭示了系统物理本质对随机性传播的驱动规律，从而为高维系统的可靠度分析提供了新的视角。根据概率守恒原理的随机事件描述［28］，可以通过对降维概率密度演化方程设置吸收边界条件［29］、构造等价极值事件［30‑31］或采用物理综合法［3，32］等，实现对高维非线性系统的动力可靠度、乃至整体可靠度的评估。近年来，在概率密度演化理论的点演化实现途径基础上［33］，进一步发展出了数值求解稳健性和尾部精度更高的概率密度全局演化方法，在此方法下建立起的方程称为降维概率密度演化方程。全局演化方法最初只应用于白噪声激励下各类高维非线性随机动力系统的响应分析［34‑35］和可靠度分析［36］，随着一般连续随机过程的降维概率密度演化方程统一理论框架的建立［37］，该方法可以用于随机波浪场激励［38］、分数阶系统［39］等更具一般性的复杂工程随机动力问题。

在降维概率密度演化方程的理论基础上，本文尝试将其拓展至一般非平稳随机激励下高维非线性系统的可靠度分析。对非平稳激励下系统感兴趣量的吸收边界过程建立了降维概率密度演化方程，并发展了相应的数值实现方法。

1 高维系统吸收边界过程的降维概率密度演化方程

1.1 非平稳Gauss白噪声激励下的高维非线性系统

首先考虑非平稳Gauss白噪声激励下的自由度非线性系统，其动力方程为：

（1）

式中 ，和分别为系统的维位移、速度和加速度列向量过程；为表征系统阻尼力和恢复力的维函数列向量；为非平稳调制函数；为表征激励作用位置的维矩阵；为维Gauss白噪声列向量过程，其维强度矩阵为，即有且，其中，为期望算子，为Dirac函数，表示元素全为零的维列向量。系统的初值和均为维确定性列向量。

由于外部激励是随机过程，因此系统的所有响应过程也都是随机的。若仅关心系统第个自由度的位移响应， 在某一给定安全域下的首次超越破坏问题，则系统的动力可靠度可以定义为：

（2）

式中 为实数域上边界记为的任意开集；表示事件的发生概率。

由于系统各个响应分量在动力方程中的耦合性，若采用经典的随机振动方法分析系统的首次超越可靠度，则需要求解吸收边界条件下所有响应量（位移和速度）的联合概率密度函数所满足的高维FPK方程或Kolmogorov后向方程，这对于自由度数很大的情形（如），计算成本往往难以接受［6］。此时，一个可行的途径是构造感兴趣量及其速度响应关于安全域的吸收边界过程，建立并求解吸收边界过程的概率密度函数所满足的降维概率密度演化方程。

具体地，定义和关于安全域的吸收边界过程为：

（3）

式中 为关于安全域的首次超越时间，其中表示变量的下确界。过程和及其吸收边界过程和的样本路径之间的关系如图1所示。

显然，若吸收边界过程在时刻的值位于安全域内，则说明感兴趣量在时间段内一直位于内，即系统尚未失效；若在时刻的值位于安全域边界上，则说明在时间段内至少发生了一次超越安全域的事件，即系统已经失效。因此，时刻的动力可靠度即等于吸收边界过程的概率密度函数在安全域内的积分，即

（4）

一旦获得了吸收边界过程的瞬时概率密度函数解答，即等价于解得了系统的动力可靠度。

一般地，系统的位移和速度响应均为样本连续的随机过程，由此易知其吸收边界过程必然也是样本连续的随机过程。根据样本连续过程的降维概率密度演化方程［37］可得，吸收边界过程和的联合概率密度满足如下二阶偏微分方程：

（5）

式中 系数和 分别称为本征漂移系数和本征扩散系数［37］，它们分别是和的前两阶条件导出矩，即

（6）

根据动力方程（1）的第个分量以及式（3），可知和满足如下微分关系：

（7）

式中 ；表示矩阵的第行向量；为向量的第l个分量；是与对应的维Wiener列向量过程，即有且。

将式（7）代入式（6），可得：

（8）

式中 为矩阵中的第个元素； 为示性泛函。而式（6）中只有本征漂移系数无法给出解析表达，但可以将其表达为：

（9）

于是，式（5）化简为：

（10）

式（10）即称为关于吸收边界过程和的降维概率密度演化方程。方程的初始条件可由动力方程（1）的初值确定，即

（11）

式中 和分别为位移初值和速度初值。

由以上推导过程可知，降维概率密度演化方程（10）是精确成立的。在实际中，对一些系统，如能量等分的碰撞振子，可获取其表达的待定函数形式［34］。对于更一般的情况，本征漂移系数，即式（9）的条件期望函数形式难以解析地给出。若可以采用适当的数值方法构造，并将其代入降维概率密度演化方程（10）求解得到和的联合概率密度函数，即可积分获得的瞬时概率密度函数，最终由式（4）计算动力可靠度。

注记1：应指出，不论系统的自由度数多大，若仅关心系统某一关键的响应过程及其速度过程，那么获得的降维概率密度演化方程就只是二维偏微分方程，即不会受到系统维数的限制，数值求解将十分方便。此外，降维概率密度演化方程原则上对于任意维数的连续随机过程均成立，因此在理论上，也可以只建立关于自身的一维偏微分方程，但是由于自身未直接受到白噪声激励的作用，这样建立起来的一维方程将是不含二阶扩散项的双曲型偏微分方程，这将对其数值求解带来不便。因此，上述推导过程中选择将和直接被白噪声激励的速度过程联立，建立其吸收边界过程的联合概率密度所满足的二维偏微分方程，使得方程成为包含精确二阶扩散项的抛物型偏微分方程，更便于后文的数值求解。

1.2 非平稳非白噪声激励下的高维非线性系统

再考虑非平稳非白噪声激励下的自由度非线性系统，其动力方程可以写为：

（12）

式中 为维非平稳非白噪声列向量过程，可以用来表征随机地震动加速度、随机脉动风速等一般工程激励。

一般地，可以表征为非平稳调制函数和某一给定功率谱密度矩阵的平稳向量过程的乘积，或直接由演变功率谱密度矩阵刻画。根据线性滤波理论［40］，可以表征为Gauss白噪声激励下某个维线性滤波系统的输出响应的函数（），即

（13）

式中 为维滤波响应列向量过程；为维函数列向量；和分别为维和维矩阵。若具有有理功率谱密度，则这里的，和可以直接由谱参数确定；否则，它们需要由非有理谱采用非线性最小二乘拟合最优值［38］。此外，若直接由演变功率谱密度矩阵刻画，则不显含，而和是时变的；而若表征为非平稳调制函数和某个平稳过程的乘积，则需显含，而和是时不变的。

对于动力方程（12）控制的自由度非线性系统，仍关心系统第个自由度的位移响应， 在某一给定安全域下的首次超越可靠度，则可以构建和某个扩散项不为零的滤波响应过程（）关于安全域的吸收边界过程，即

（14）

一般地，Gauss白噪声激励下的线性滤波响应是一个时间上连续的随机过程，则其吸收边界过程必然也是时间上连续的随机过程。故而和的联合概率密度满足降维概率密度演化方程［37］。经过与1.1节类似的推导，可得降维概率密度演化方程为：

（15）

式中 为矩阵中的第个元素；和为本征漂移系数，有：

（16）

式中 为的第k列构成的向量。

若采用适当的数值方法构造和，并将其代入降维概率密度演化方程（15）求解得到和的联合概率密度函数，即可积分获得的瞬时概率密度函数，最终由式（4）计算动力可靠度。

注记2：应指出，对于非白噪声激励问题，这里并没有与1.1节一样选择相应速度过程作为辅助过程构建降维概率密度演化方程，而是选择了某个扩散项不为零的滤波响应过程。这是因为对于有限功率谱密度的非白噪声激励，系统速度响应的本征扩散系数为零，而滤波响应过程由于受Gauss白噪声的直接激励，其扩散项不为零［37］。

2 非平稳随机激励下高维系统可靠度计算的数值方法

基于降维概率密度演化方程的动力可靠度分析通常可分为两个步骤：（1） 基于物理驱动的本征漂移系数数值构造；（2） 吸收边界过程的降维概率密度演化方程数值求解。下面以非平稳Gauss白噪声激励下的高维系统为例（即本征漂移系数式（9）的构造和降维概率密度演化方程（10）的求解）阐述该方法的数值实现流程，而对于非平稳非白噪声激励下的高维系统（即本征漂移系数式（16）的构造和降维概率密度演化方程（15）的求解），则可以类似地处理。

2.1 基于物理驱动的本征漂移系数数值构造

尽管对于一些特殊的高维系统，目前已经可以给出本征漂移系数的解析表达或稳态解析表达［34］，但是对于一般的高维非线性随机动力系统，降维概率密度演化方程中的本征漂移系数通常难以解析地获得，因此需要基于原系统动力方程的演化特性，采用适当的数值方法加以构造。

式（9）的本征漂移系数可以表达为：

（17）

式中 是和与均相关的随机过程。

根据式（17）所表达的作为条件期望的物理意义，对其进行数值构造的一个可行途径是：

（1） 对原系统的动力方程（1）进行有限次代表性确定性动力分析（分析次数记为），可获得系统响应和的个时程数据。其中有限次确定性动力分析是指对激励进行随机模拟（如采用线性滤波法［40］、谱表达法［41］或随机谐和函数法［42］），进而以随机激励样本作为输入求解系统的动力方程，获得分析数据。

（2） 对某一时刻， （为数值离散时间步数），记录满足“时段内时程从未失效”这一条件的，和的数据值分别为，和， ，其中为所有个数据中满足这一条件的数据个数，注意此处应有。

（3） 根据三维状态量空间Oxva内的数据点， ，估计某一给定状态点处的本征漂移系数值， ； （和为估计本征漂移系数时在安全域内划分的网格数）。这一步有多种可行的参数化或非参数化数值方法，例如采用局部加权回归的思想［43］，可将本征漂移系数构造为：

（18）

其中，回归系数对每一状态点是不同的，可以根据当前状态点与所有数据点， 的距离选取合适的权函数，采用加权最小二乘方法估计。

2.2 吸收边界过程的降维概率密度演化方程数值求解

在已知本征漂移系数的解答后，可以选用适当的数值方法，在初值条件式（11）下，求解降维概率密度演化方程（10）。本节阐述该方程的路径积分求解格式。

根据随机微分方程理论［6］，若存在二维Markov扩散向量过程，其初值为和，且其样本路径满足如下Itô随机微分方程：

（19）

式中 为标准Wiener过程，则该二维过程的联合概率密度也满足式（10）的二维偏微分方程。亦即，此处构造的二维Markov过程和二维（非Markov的）吸收边界过程，二者在任意单一时点处的瞬时概率密度函数是相等的。故而，可以直接采用路径积分格式求解的瞬时概率密度函数，也就同时获得了吸收边界过程的瞬时概率密度函数。而根据Itô随机微分方程（19），二维Markov过程的转移概率密度函数在时间步很小时可以由短时Gauss假定［44］给出解析表达，即

（20）

故而，若已知吸收边界过程在时刻的联合概率密度函数的解，则其在， 时刻的联合概率密度函数可由如下路径积分格式计算：

（1） 对于，有：

（21）

（2） 对于，有：

（22）

由此，可以逐时间步地计算的联合概率密度函数，进而根据式（4），可以给出系统的时变动力可靠度以及相应的时变失效概率解答：

（23）

在上述降维概率密度演化方程的数值求解中，本征漂移系数作为原高维系统物理方程中的感兴趣量所在低维状态空间内物理力的反映，通过决定式（20）中转移概率密度函数在每一时间步的表达，驱动着吸收边界过程的概率密度演化，因而它本质上是概率密度全局演化的本征物理驱动力。这一物理关系的反映如图2所示，图中，表示安全域内的概率总和，即可靠度。（注：为了更直观，图中省略了所在维度，仅表现了一维情形下本征漂移系数对概率密度演化的物理驱动，对于二维情形是类似的。图2中左边表示本征漂移系数与有限次确定性分析数据之间的条件期望关系；右边表示概率密度函数随时间演化过程中的平均漂移趋势与局部涨落规律。）

3 数值算例

3.1 非平稳Gauss白噪声激励下的10层滞回非线性框架结构

非平稳Gauss白噪声激励下自由度滞回非线性框架结构的动力方程可以写为：

（24）

式中 和分别为维集中质量矩阵和Rayleigh阻尼矩阵；为维非线性恢复力函数列向量；为维滞回位移列向量过程；为元素全为1的m维列向量；是强度为的Gauss白噪声过程。

本例中非线性恢复力采用Bouc‑Wen模型［45‑47］刻画，即结构第层层间恢复力取为：

（25）

式中 为结构屈服刚度与初始刚度之比；为结构第层层间初始刚度；为结构第层层间位移过程。

结构第层滞回位移过程和滞回耗能过程的演化由如下微分方程控制：

（26）

式中 为符号函数；和为基本滞回形状控制参数；和分别为强度和刚度退化系数；为总滑移量；，，，和分别为控制捏拢初值、坡度、幅值、速率和强度的参数。

本例中取结构自由度数，结构各层集中质量均为2.6×105 kg、初始弹性模量均为3×1010 Pa；结构底层高4 m、柱截面0.5 m × 0.5 m，其余各层高3 m、柱截面0.4 m × 0.4 m；结构前二阶阻尼比均为0.05；Bouc‑Wen模型各参数取值为：，，，，，，，，。结构所受的白噪声激励强度，非平稳调制函数为［48］：

（27）

式中 ，，。

结构在非平稳Gauss白噪声激励下底层层间恢复力‑位移曲线的典型样本如图3所示。由图3可以看出恢复力具有很强的滞回非线性特性。

取结构的底层位移作为感兴趣的物理量，考察底层位移响应在安全域下的首次超越可靠度（其中阈值为常数），则可以建立底层位移和底层速度的吸收边界过程的联合概率密度函数满足的降维概率密度演化方程（如式（10）所示）。对原系统的动力方程（24）进行800次代表性确定性分析，并根据分析数据构造本征漂移系数的数值解，即可数值求解降维概率密度演化方程获得时变可靠度或失效概率的解答。同时，若直接建立和的联合概率密度函数满足的降维概率密度演化方程，则可数值求解获得二者的响应概率分布信息（具体可参见文献［37］）。

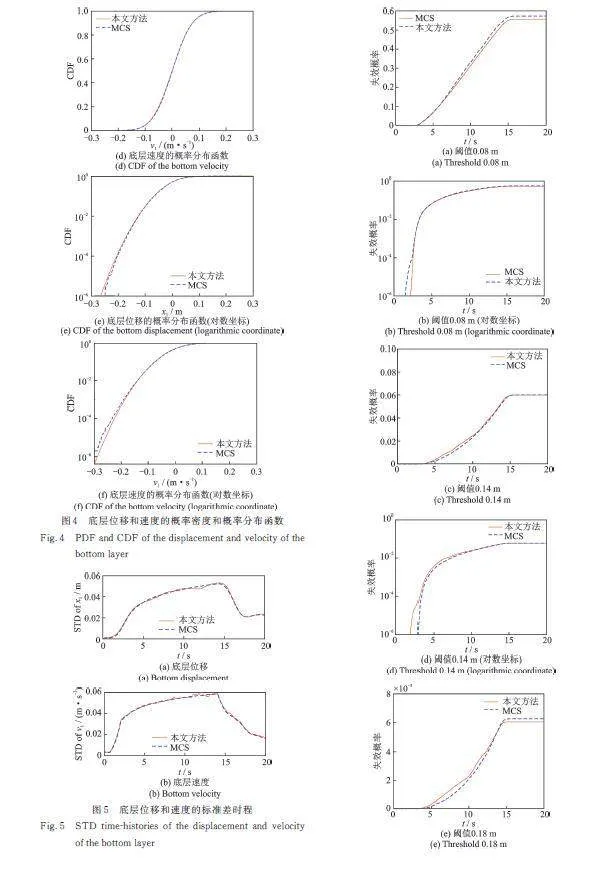
本例给出该结构随机响应分析和可靠度分析的数值结果与106次蒙特卡罗模拟（MCS）结果的对比，以验证本文方法的精度和有效性：在14 s时刻结构底层位移和速度的概率密度函数（PDF）和概率分布函数（CDF）如图4所示；结构底层位移和速度的标准差（STD）时程如图5所示；结构底层位移在不同阈值下的时变失效概率如图6所示；地震动衰减阶段（20 s时刻）结构的失效概率数值结果与蒙特卡罗模拟的相对误差比较如表1所示。从图6中可以看出，概率密度全局演化方法获得的响应分析和可靠度结果与蒙特卡罗模拟的结果完全一致。当14 s之后，随着外部激励进入衰减段，响应的标准差迅速下降，结构的失效概率也趋于平缓不再升高，在随机激励下，结构的这些物理随机特性都可以通过求解降维概率密度演化方程精确地捕捉到。

3.2 非平稳随机地震动作用下的10层滞回非线性框架结构

仍考虑算例3.1中的10层滞回非线性框架结构，但外部激励采用非平稳随机地震动激励。结构所受的地震动激励的加速度由非平稳时间调制下的Kanai‑Tajimi模型［49‑50］给出，其功率谱密度函数为：

（28）

式中 为强度；为圆频率；和分别为场地的特征圆频率和阻尼比。

根据线性滤波理论，地震动加速度可以表达为如下Gauss白噪声激励下的单自由度线性滤波系统：

（29）

式中 为系统的位移响应。

其相对加速度响应［51］，即

（30）

本例中取，，。生成的非平稳随机地震动加速度的典型时程样本如图7所示。

取结构的顶层位移作为感兴趣的物理量，考察顶层位移响应在安全域下的首次超越可靠度（其中阈值为常数），则可以建立顶层位移和滤波速度的吸收边界过程的联合概率密度函数满足的降维概率密度演化方程（如式（15）所示）。对原系统的动力方程和滤波系统进行800次代表性确定性分析，并根据分析数据构造本征漂移系数的数值解，即可数值求解降维概率密度演化方程获得时变可靠度或失效概率的解答。

结构顶层位移在不同阈值下的时变失效概率如图8所示。从图8中可以看出，概率密度全局演化方法获得的响应分析和可靠度结果与蒙特卡罗模拟的结果完全一致。

4 结 论

（1） 对于一般的非平稳随机激励下的高维系统，通过构造感兴趣响应量以及某个辅助过程的吸收边界过程，并建立其瞬时概率密度满足的降维概率密度演化方程（一个二维偏微分方程），可以实现系统给定阈值下的首次超越可靠度分析。

（2） 降维概率密度演化方程中的本征漂移系数是驱动概率密度演化的本征物理驱动力。对于一般非线性问题，本征漂移系数难以给出解析表达，需要根据原始高维系统的有限次代表性确定性动力分析数据，通过合适的数值方法构造。

（3） 降维概率密度演化方程对于高维随机动力系统的可靠度分析具有较高的精度和计算效率。数值算例表明，仅需要几百次确定性分析结果构造本征漂移系数，即可实现罕遇事件下的小失效概率精细化评估。

在上述研究的基础上，本文所提出的理论框架可进一步应用于实际工程结构的抗震可靠度分析。此外，不同本征漂移系数的数值构造方法对降维概率密度演化方程数值精度的影响也有待进一步研究。本文主要讨论了降维概率密度演化方程在非平稳Gauss白噪声或非白噪声激励下高维系统的可靠度分析，该方法对于非Gauss噪声激励问题［52‑56］的适用性值得深入研究。

参考文献：

［1］ 刘章军， 陈建兵， 彭勇波. 结构动力学［M］. 北京： 中国建筑工业出版社， 2022.

［2］ 李杰. 论第三代结构设计理论［J］. 同济大学学报 （自然科学版）， 2017， 45 （5）： 617‑624.

Li J. On the third generation of structural design theory［J］. Journal of Tongji University （Natural Science）， 2017， 45 （5）： 617‑624.

［3］ 李杰. 工程结构整体可靠性分析研究进展［J］. 土木工程学报， 2018， 51 （8）： 1‑10.

Li J. Advances in global reliability analysis of engineering structures［J］. China Civil Engineering Journal， 2018， 51 （8）： 1‑10.

［4］ Li J， Chen J B. Stochastic Dynamics of Structures ［M］. Singapore：John Wiley & Sons，Inc.， 2009.

［5］ 李杰. 工程结构可靠性分析原理［M］. 北京： 科学出版社， 2021.

Li J. Fundamental of Structural Reliability Analysis［M］. Beijing： Science Press， 2021.

［6］ 朱位秋. 随机振动［M］. 北京： 科学出版社， 1992.

［7］ 李桂青， 曹宏， 李秋胜， 等. 结构动力可靠性理论及其应用［M］. 北京： 地震出版社， 1993.

［8］ Rice S O. Mathematical analysis of random noise［J］. Bell System Technical Journal， 1944， 23（3）： 282‑332.

［9］ Yang J N， Shinozuka M. On the first excursion probability in stationary narrow‑band random vibration［J］. Journal of Applied Mechanics， 1971， 38 （4）： 1017‑1022.

［10］ Vanmarcke E. 随机场： 分析与综合［M］.修订扩展版. 陈朝晖， 范文亮，译. 北京： 高等教育出版社， 2017.

［11］ Roberts J B. First‑passage probabilities for randomly excited systems： diffusion methods［J］. Probabilistic Engineering Mechanics， 1986， 1： 66‑81.

［12］ Gumbel E J. Statistics of Extremes［M］. New York， USA： Columbia University Press， 1958.

［13］ 洪华生， 邓汉忠. 工程中的概率概念——在土木与环境工程中的应用［M］. 2版. 陈建兵， 彭勇波， 刘威， 等，译. 北京： 中国建筑工业出版社， 2017.

［14］ 陈建兵， 律梦泽. 一类Markov过程的最大绝对值过程概率密度求解的新方法［J］. 力学学报， 2019， 51 （5）： 1437‑1447.

Chen J B， Lü M Z. A new method for the probability density of maximum absolute value of a Markov process［J］. Chinese Journal of Theoretical and Applied Mechanics， 2019， 51 （5）： 1437‑1447.

［15］ Chen J B， Lü M Z. A new approach for time‑variant probability density function of the maximal value of stochastic dynamical systems［J］. Journal of Computational Physics， 2020， 415： 109525.

［16］ Lü M Z， Chen J B， Pirrotta A. A novel method based on augmented Markov vector process for the time‑variant extreme value distribution of stochastic dynamical systems enforced by Poisson white noise［J］. Communications in Nonlinear Science and Numerical Simulation， 2020， 80： 104974.

［17］ Lü M Z， Wang J M， Chen J B. Closed‑form solutions for the probability distribution of time‑variant maximal value processes for some classes of Markov processes［J］. Communications in Nonlinear Science and Numerical Simulation， 2021， 99： 105803.

［18］ Harbitz A. An accurate probability‑of‑failure calculation method［J］. IEEE Transactions on Reliability， 1983， 32 （5）： 458‑460.

［19］ Au S K， Beck J L. Estimation of small failure probabilities in high dimensions by subset simulation［J］. Probabilistic Engineering Mechanics， 2001， 16 （4）： 263‑277.

［20］ Koutsourelakis P S， Pradlwarter H J， Schuëller G I. Reliability of structures in high dimensions， Part Ⅰ： algorithms and applications［J］. Probabilistic Engineering Mechanics， 2004， 19 （4）： 409‑417.

［21］ Xu J， Kong F. A new unequal‑weighted sampling method for efficient reliability analysis［J］. Reliability Engineering & System Safety， 2018， 172： 94‑102.

［22］ Zhao Y G， Lu Z H. Fourth moment standardization for structural reliability assessment［J］. Journal of Structural Engineering， 2007， 133（7）： 916‑924.

［23］ Zhao Y G， Zhang X Y， Lu Z H. Complete monotonic expression of the fourth‑moment normal transformation for structural reliability［J］. Computers & Structures， 2018， 196： 186‑199.

［24］ Xu J. A new method for reliability assessment of structural dynamic systems with random parameters［J］. Structural Safety， 2016， 60： 130‑143.

［25］ Xu J， Dang C. A new bivariate dimension reduction method for efficient structural reliability analysis［J］. Mechanical Systems and Signal Processing， 2019， 115： 281‑300.

［26］ Zhang L W， Lu Z H， Zhao Y G. Dynamic reliability assessment of nonlinear structures using extreme value distribution based on L‑moments［J］. Mechanical Systems and Signal Processing， 2021， 159： 107832.

［27］ Li J， Chen J B. Probability density evolution method for dynamic response analysis of structures with uncertain parameters［J］. Computational Mechanics， 2004， 34： 400‑409.

［28］ Li J， Chen J B. The principle of preservation of probability and the generalized density evolution equation［J］. Structural Safety， 2008， 30 （1）： 65‑77.

［29］ Chen J B， Li J. Dynamic response and reliability analysis of non‑linear stochastic structures［J］. Probabilistic Engineering Mechanics， 2005， 20 （1）： 33‑44.

［30］ Li J， Chen J B， Fan W L. The equivalent extreme‑value event and evaluation of the structural system reliability［J］. Structural Safety， 2007， 29 （2）： 112‑131.

［31］ Wang D， Li J. An efficient load effect combination method based on probability density evolution method［J］. Structural Safety， 2022， 97： 102217.

［32］ Li J， Gao R F. Fatigue reliability analysis of concrete structures based on physical synthesis method［J］. Probabilistic Engineering Mechanics， 2019， 56： 14‑26.

［33］ Li J， Chen J B， Sun W L， et al. Advances of the probability density evolution method for nonlinear stochastic systems［J］. Probabilistic Engineering Mechanics， 2012， 28： 132‑142.

［34］ Sun T T， Chen J B. Physically driven exact dimension reduction of a class of nonlinear multi‑dimensional systems subjected to additive white noise［J］. Journal of Risk and Uncertainty in Engineering Systems， Part A： Civil Engineering， 2022， 8 （2）： 04022012.

［35］ Chen J B， Lü M Z. Globally‑evolving‑based generalized density evolution equation for nonlinear systems involving randomness from both system parameters and excitations［J］. Proceedings of the Royal Society A， 2022， 478（2264）： 20220356.

［36］ Lü M Z， Chen J B. First‑passage reliability of high‑dimensional nonlinear systems under additive excitation by the ensemble‑evolving‑based generalized density evolution equation［J］. Probabilistic Engineering Mechanics， 2021， 63： 103119.

［37］ Lü M Z， Chen J B. A unified formalism of the GE‑GDEE for generic continuous responses and first‑passage reliability analysis of multi‑dimensional nonlinear systems subjected to non‑white‑noise excitations［J］. Structural Safety， 2022， 98： 102233.

［38］ Luo Y， Chen J B， Spanos P D. Determination of monopile offshore structure response to stochastic wave loads via analog filter approximation and GV‑GDEE procedure［J］. Probabilistic Engineering Mechanics， 2022， 67： 103197.

［39］ Luo Y， Spanos P D， Chen J B. Stochastic response determination of multi‑dimensional nonlinear systems endowed with fractional derivative elements by the GE‑GDEE［J］. International Journal of Non‑Linear Mechanics， 2022，147： 104247.

［40］ Spanos P D， Mignolet M P. ARMA Monte Carlo simulation in probabilistic structural analysis［J］. The Shock & Vibration Digest， 1989， 21 （11）： 3‑14.

［41］ Shinozuka M， Deodatis G. Simulation of stochastic processes by spectral representation［J］. Applied Mechanics Reviews， 1991， 44 （4）： 191‑204.

［42］ Chen J B， Sun W L， Li J， et al. Stochastic harmonic function representation of stochastic processes［J］. Journal of Applied Mechanics， 2013， 80（1）： 011001.

［43］ Cleveland W S. Robust locally weighted regression and smoothing scatterplots［J］. Journal of the American Statistical Association， 1979， 74 （368）： 829‑836.

［44］ Risken H. The Fokker‑Planck Equation：Methods of Solution and Applications［M］.2nd ed. Berlin， Germany： Springer‑Verlag， 1989.

［45］ Bouc R. Modèle mathématique d'hystérésis： application aux systèmesàun degréde liberté［J］. Acustica， 1971， 24 （1）： 16‑25.

［46］ Wen Y K. Method for random vibration of hysteretic systems［J］. Journal of Engineering Mechanics， 1976， 102： 249‑263.

［47］ Ma F， Zhang H， Bockstedte A， et al. Parameter analysis of the differential model of hysteresis［J］. Journal of Engineering Mechanics， 2004， 71（3）： 342‑349.

［48］ Amin M， Ang A H S. Nonstationary stochastic models of earthquake motions［J］. Journal of the Engineering Mechanics Division， 1968， 94 （2）： 559‑583.

［49］ Kanai K. Semi‑empirical formula for the seismic characteristics of the ground［J］. Bulletin of the Earthquake Research Institute， 1957， 35 （2）： 309‑325.

［50］ Tajimi H. A statistical method of determining the maximum response of a building structure during an earthquake［C］∥ Proceedings of the 2nd World Conference on Earthquake Engineering. Tokyo， Japan， 1960： 781‑797.

［51］ Clough R， Penzien J. Dynamics of Structures［M］. 3rd ed. Berkeley， USA： Computers & Structures Inc.， 2003.

［52］ Xu Y， Li H， Wang H Y， et al. The estimates of the mean first exit time of a bistable system excited by Poisson white noise［J］. Journal of Applied Mechanics， 2017， 84（9）： 091004.

［53］ Li Y G， Xu Y， Kurths J. First‑passage‑time distribution in a moving parabolic potential with spatial roughness ［J］. Physical Review E， 2019， 99： 052203.

［54］ Li Y G， Xu Y， Kurths J， et al. The influences of correlated spatially random perturbations on first passage time in a linear‑cubic potential［J］. Chaos， 2019， 29： 101102.

［55］ Zan W R， Xu Y， Metzler R， et al. First‑passage problem for stochastic differential equations with combined parametric Gaussian and Lévy white noises via path integral method［J］. Journal of Computational Physics， 2021， 435： 110264.

［56］ Zan W R， Jia W T， Xu Y. Reliability of dynamical systems with combined Gaussian and Poisson white noise via path integral method［J］. Probabilistic Engineering Mechanics， 2022， 68： 103252.

GE‑GDEE for reliability analysis of high‑dimensional nonlinear systems enforced by non‑stationary stochastic excitations

LÜ Meng‑ze1，2， CHEN Jian‑bing1，2

（1.State Key Laboratory of Disaster Reduction in Civil Engineering， Tongji University， Shanghai 200092， China；

2.College of Civil Engineering， Tongji University， Shanghai 200092， China）

Abstract： Dynamic actions such as strong winds and earthquakes often have significant randomness and non-stationarity， which can have disastrous effects on practical engineering structures. Therefore， accurately evaluating the dynamic reliability of high-dimensional nonlinear systems under non-stationary stochastic excitations is crucial for the disaster-resistant design and optimizatio1M824I6wONc1+/Ycw8lFBcVBLRwwWJ37+dUrsm9Fn3U=n of these structures. This paper presents a numerical method for solving the high-dimensional nonlinear dynamic reliability under non-stationary noises， based on the globally-evolving-based generalized density evolution equation （GE-GDEE） for generic continuous processes. Specifically， if we are concerned with the first-passage reliability of a quantity of interest within a specified safe domain， an absorbing boundary process （ABP） of the quantity of interest can be constructed. This leads to a two-dimensional partial differential equation for its transient probability density function （PDF）， known as the GE-GDEE for ABPs. The effective drift coefficient in the GE-GDEE， which serves as the global physical driving force for evolution of the PDF， can be identified using data from representative deterministic dynamic analyses. The solution for dynamic reliability can be obtained by solving the GE-GDEE. This paper includes two numerical examples to verify the efficiency and accuracy of the proposed method and discusses areas that require further study.

Key words： globally‑evolving‑based generalized density evolution equation （GE‑GDEE）；high‑dimensional nonlinear stochastic dynamic system；non‑stationary stochastic excitation；dynamic reliability analysis；physically driven

作者简介： 律梦泽 （1994—），男，博士，博士后。 E‑mail： lyumz@tongji.edu.cn。

通讯作者： 陈建兵 （1975—），男，博士，教授。电话： （021） 65981505； E‑mail： chenjb@tongji.edu.cn。