勾股定理的图形证明

哪里有数学，哪里就有美，勾股定理也不例外。作为几何学中的一颗璀璨明珠，千百年来，它吸引了无数人乐此不疲地进行证明，贡献了许多数学证明中的优美案例。让我们跟随数学家们的脚步，通过拼图的方式来验证勾股定理。

《周髀算经》与赵爽“弦图”

据《周髀算经》记载，公元前11世纪，我们的祖先就在生产实践中发现了“勾三股四弦五”的结论。三国时期，赵爽注解《周髀算经》时，创制了“弦图”，并用数形结合的方法给出了勾股定理的证明。

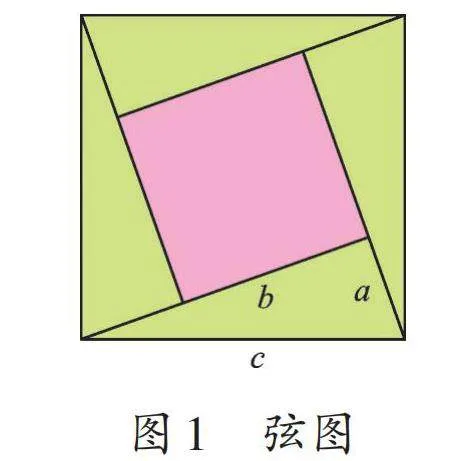
如图1，用4个全等的直角边长分别为a、b，斜边长为c的直角三角形拼成一个边长为c的大正方形。

一方面，大正方形的边长为c，因此大正方形的面积为c2。另一方面，大正方形的面积又等于4个直角三角形的面积之和再加上中间边长为b-a的小正方形的面积，因此大正方形也可以表示为4×½ab+（b-a）2。由等面积法可得4×½ab+（b-a）2=c2，化简即得a2+b2=c2。

《九章算术注》中的“青朱出入图”

魏晋时期数学家刘徽在写《九章算术注》时，利用“青朱出入图”，证明了勾股定理。图虽失传，但根据割补法原理，参照书中类似方法，后人还原了此图。

如图2，使用割补法，将S1平移至S1′，将S2平移至S2′，将S3平移至S3′，我们不难发现：以a为边长的正方形与以b为边长的正方形的面积之和等于以c为边长的正方形的面积，即a2+b2=c2。

加菲尔德的“总统证法”

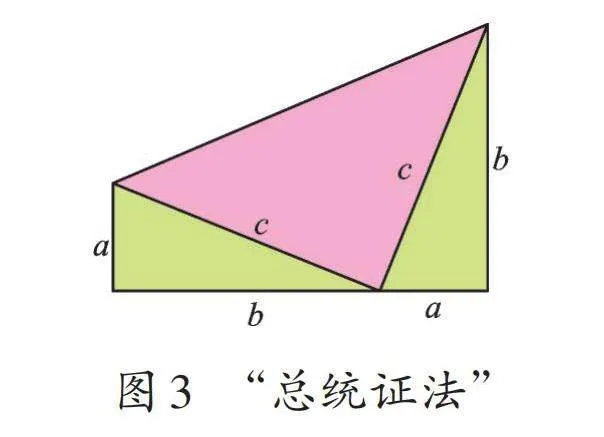
时任美国俄亥俄州共和党议员的加菲尔德，通过构造直角梯形证明了勾股定理，其证法构思独特、图形直观、步骤简洁，轰动了当时的数学界。5年后，加菲尔德就任美国第二十任总统，此证法因此被称为“总统证法”。

如图3，直角梯形的面积可以表示为两个直角三角形的面积之和再加上等腰直角三角形的面积，即½（a+b）（a+b）=½ab×2+½c2，化简可得a2+b2=c2。

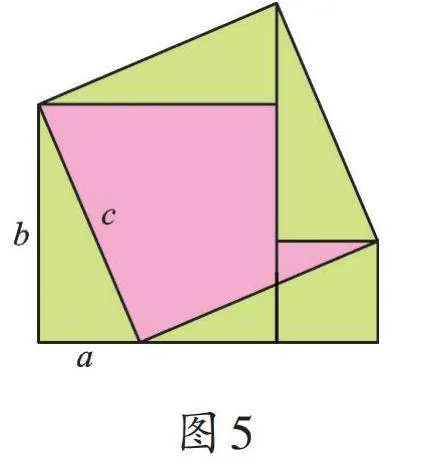
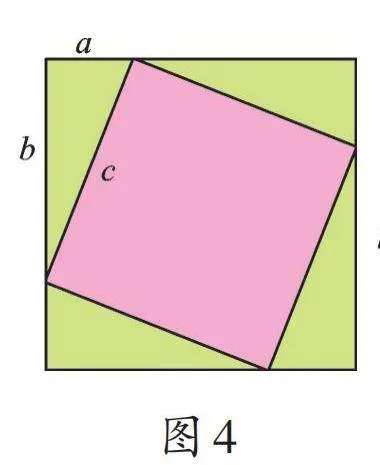
我们不难发现，以上证明方法都运用了图形的割补，进行面积的转化和计算。其实，我们还可以继续，例如给你图4、图5，你能自行验证勾股定理吗？

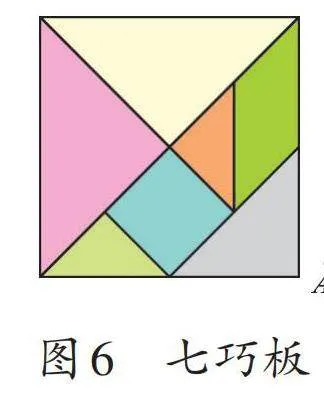
其实，除了上述用直角边长分别为a、b，斜边长为c的直角三角形来验证之外，传统的七巧板也可以用来演示两条直角边长度相等情况下的勾股定理（如图6、图7）。

设图6中的小正方形面积为1，则一副七巧板的总面积为8。图7中等腰直角三角形ABC的面积为4，等腰直角三角形CDE和等腰直角三角形BEF的面积均为2，那么这三个等腰直角三角形的面积存在如下的数量关系：等腰直角三角形ABC的面积=等腰直角三角形CDE的面积+等腰直角三角形BEF的面积，即½BC2=½CE2+½BE2，所以BC2=CE2+BE2，这个等式说明在等腰直角三角形BCE中，直角边CE和BE的平方和等于斜边BC的平方。

有资料表明，关于勾股定理的证明方法已有500余种，仅我国清末数学家华蘅芳就提供了二十多种精彩的证法，淋漓尽致地展现了数学的趣味和美感，这是其他定理无法比拟的。

（作者单位：江苏省昆山市石牌中学）