基于深度元学习的固体发动机性能预测方法研究

摘 要： 针对飞行器动力系统中固体发动机性能实验的诸多限制， 如高成本、 专业设备需求、 特定实验环境、 高风险性等问题， 本文提出了一种基于深度元学习的人工智能方法， 用于发动机性能预测。 该方法采用模型不可知元学习（Model-Agnostic Meta-Learning， MAML）和深度卷积神经网络（Deep Convolutional Neural Networks， DCNN）模型， 首先根据不同实验条件划分推力-时间数据为不同训练任务， 通过内循环训练得到各任务最佳模型参数， 在外循环中更新模型初始化参数， 内外循环迭代优化后， 获得了能够高精度预测固体发动机总冲的模型， 最后用新任务进行测试。 测试结果显示， 相较于无元学习的DCNN， 该方法在测试集上的误差显著下降， 百分比误差最大为2.27%。 证明了元学习模型在小样本条件下对固体发动机性能的高精度预测能力。

关键词： 固体发动机； 发动机性能； 元学习； 模型不可知元学习； 深度卷积神经网络

中图分类号： TJ760; V23

文献标识码： A

文章编号： 1673-5048（2024）05-0110-05

DOI： 10.12132/ISSN.1673-5048.2024.0089

0 引 言

固体发动机作为飞行器动力系统的重要组成部分， 为飞行器提供了强大的推力， 确保了飞行器的稳定飞行和高效性能。 固体发动机具有操作简单、 存储方便、 可靠性高等优点， 广泛应用于火箭、 导弹以及宇宙飞船等领域。 固体发动机的总冲是衡量其性能的一个关键指标［1］， 总冲是指发动机在一个工作循环中所做的功， 是提供给飞行器的总动量， 从而影响到整个飞行器的飞行性能和射程。 通常情况下， 对发动机进行推力实验， 由传感器采集发动机推力数据， 再将其处理成推力-时间曲线， 推力对工作时间进行积分， 从而得到发动机总冲。

由于固体发动机地面实验的成本较高， 在实验中很难采集到足量有用的推力数据， 所以难以通过推力-时间数据得到总冲。 传统的深度学习对数据量依赖较大， 导致采用深度学习模型的效果并不理想。 为能得到泛化能力较好的人工智能模型以及更准确的预测性能， 引入深度元学习方法， 开展了基于深度元学习的人工智能发动机性能预测方法。

元学习也称“学会学习”（Learning to learn）， 是一种基于任务的学习方式， 目的是发现并合理利用已有的先验知识， 在面对新任务时能取得良好表现。 相对于元学习， 传统的深度神经网络虽然在拥有大量数据集和足够的计算资源时， 能够取得很好的效果， 但是其可扩展能力差、 对新任务处理困难、 需要大量数据训练模型， 在快速学习新概念方面的能力很有限。 而元学习模型能够较好地推广到训练新环境上， 并且在小样本数据的任务上也有很好的表现［2-4］， 能够将深度神经网络与具有自我学习能力的元学习联系起来， 使网络学会怎样去学习。 Luo等［5］提出了一种三元组关系网络（TRNet）， 通过迭代学习几个相关的元任务进行跨组件的小样本故障诊断。 Rivas-Posada等［6］提出了XC8XK1cOoS7fa7jxwjRdkg==一种元无监督算法， 通过解决任务来获取知识， 以此推荐初始参数来解决其他新任务。 Vettoruzzo等［7］提出了一种新的元学习框架， 该框架可以通过当前任务调节模型来处理多模态任务， 从而更快地适应新任务。 万鹏等［8］提出了一种基于元学习的刀具磨损预测方法， 采用元学习算法来优化融合模型的损失函数以最大化利用数据和机理所提供的信息。 结果表明，

所采用方法能有效提高在不同工况下的刀具磨损预测精度和稳定性。 Wang等［9］引入了元学习来增强所采用模型

收稿日期： 2024-05-24

基金项目： 辽宁省属本科高校基本科研业务费专项资金资助

作者简介： 崔研（1998-）， 女， 辽宁大连人， 硕士研究生。

*通信作者： 杨慧欣（1985-）， 女， 辽宁沈阳人， 博士， 副教授。

在多任务领域的泛化能力， 实验结果表明， 元学习方法能够有效适应多任务， 并提高了刀具磨损的预测结果值。 Huang等［10］将元学习引入到工业的视觉检测中以解决异物数据难以采集和积累的问题， 同时通过参数优化策略更新模型权重， 使得元学习模型在面对样本较少的新任务时也能够更有效地学习。 夏鹏程等［11］将元学习引入到故障诊断领域以解决难以获取充足故障数据样本的问题。 结果表明， 在所有故障中， 仅仅提供非常少的样本（如1个、 5个）均能达到较高的准确率。 Minot等［12］利用元学习方法来克服蛋白质工程中嘈杂和标记不足的数据， 并加快抗体工程的工作流程。 航空兵器 2024年第31卷第5期

崔 研， 等： 基于深度元学习的固体发动机性能预测方法研究

由此可知， 元学习方法适合于难以用深度学习直接解决的小样本问题。 具体的方法主要有三类： 基于度量的元学习、 基于模型的元学习、 基于优化的元学习。 基于度量的元学习是一种通过度量来学习不同新旧任务之间的相似性以达到模型快速适应新任务的目标。 其主要代表模型是Vinyals等［13］开发的MatchingNet模型。 主要通过在嵌入特征空间时利用余弦距离进行度量相似度来实现， 使得在特征空间中， 相似的数据点靠得更近， 不相似的数据点离得更远。 基于模型的元学习的核心思想是能够快速将模型收敛到适用于每个任务的最优结构， 其中代表模型是Ravi等［14］开发的Meta-Learner LSTM模型， 主要通过LSTM模型学习一个用于更新另一个神经网络模型内部结构的优化算法。 基于优化的元学习的核心思想是学习一种优化策略， 从而帮助模型在新任务上更快速地收敛到最优解。 其主要代表模型是Finn等［2］开发的MAML模型。 主要通过寻找对所有任务都较为敏感的初始化模型参数， 使模型能够在新任务上快速适应， 提高学习效果。

然而， 到目前为止， 元学习还没有被用于预测固体发动机的总冲问题。 传统的总冲预测方法通常需要大量的标记数据来进行训练和参数调整， 以及大量的数据样本来实现最佳的网络预测性能， 同时还需要大量的计算资源。 本文提出了一种基于元学习深度卷积神经网络（Meta-learning Deep Convolutional Neural Networks， MDCNN）的人工智能方法， 能够有效解决飞行器动力系统由于实验成本较高而无法采集到大量有效数据的问题， 同时可以在不需要额外数据采集的情况下， 减少在面对新任务时训练模型所需的时间， 有效提高模型的性能、 泛化能力以及鲁棒性。

1 基本原理

1.1 MAML的基本原理

模型不可知元学习方式（Model Agnostic Meta- Learning， MAML）是一种与模型无关的元学习算法。 它适用于任何使用梯度下降法更新参数的模型， 通过从多个相关任务中快速学习并适应新任务来优化模型的性能。 与传统的机器学习方法相比， MAML更注重利用不同任务间的共性知识， 以加速新任务的学习过程。 MAML算法不是针对特定任务进行训练， 而是通过对多个相关任务的学习， 不断更新模型参数， 优化模型性能， 使得模型在面对新任务时， 能够迅速适应并表现出良好的性能。

MAML 的关键思想是得到最优的模型初始化参数。 MAML训练过程中， 通过对大量任务进行训练， 对每一个任务都进行参数更新， 最终得到一个最优的初始化参数， 使得模型在新任务上通过少量的梯度下降步骤就能快速适应， 并在新任务上表现出最好的性能。 MAML的训练流程如图1所示。

MAML算法通常由内循环与外循环构成。 内循环中先初始化模型参数， 然后在每个任务的支持集上对模型进行训练， 更新模型参数， 最后在查询集测试， 计算损失， 检测模型在新的样本上的性能。 外循环中MAML根据所有任务的查询集损失的平均值或总和， 使用梯度下降法更新模型初始化参数。

对于几个训练任务进行元训练， 在内循环上的参数更新过程如下：

θ′i=θ－αΔθLTi（fθ）（1）

式中： θ′i是任务； Ti的最优参数； θ为初始化参数； α为内循环学习率； ΔθLTi（fθ）为任务Ti的梯度。

在外循环上的参数更新过程如下：

θ=θ－βΔθ∑Ti－p（T）LTi（fθ′i） （2）

式中： θ为适合所有任务的最优初始化参数； β为外循环学习率； Δθ∑Ti－p（T）LTi（fθ′i）为所有任务累计的梯度。

1.2 DCNN模型

深度卷积神经网络（Deep Convolutional Neural Networks， DCNN）是人工智能领域中一种重要的前馈神经网络。 DCNN通常由多个卷积层、 激活函数层、 池化层以及全连接层组成。 卷积层负责提取数据的局部特征； 激活函数层引入非线性因素， 增强模型的表达能力； 池化层则进行下采样操作， 降低数据的维度和计算复杂度； 全连接层通常位于网络的末端， 用于整合前面层提取到的特征并进行最终的分类或回归任务。

DCNN的工作原理可以概括为前向传播和反向传播两个过程。 在前向传播阶段， 输入数据经过多个卷积层、 激活函数层和池化层的处理， 逐层提取出从低级到高级的特征表示； 在反向传播阶段， 通过计算损失函数对模型参数的梯度， 利用优化算法更新网络权重， 以最小化预测输出与实际标签之间的差异。

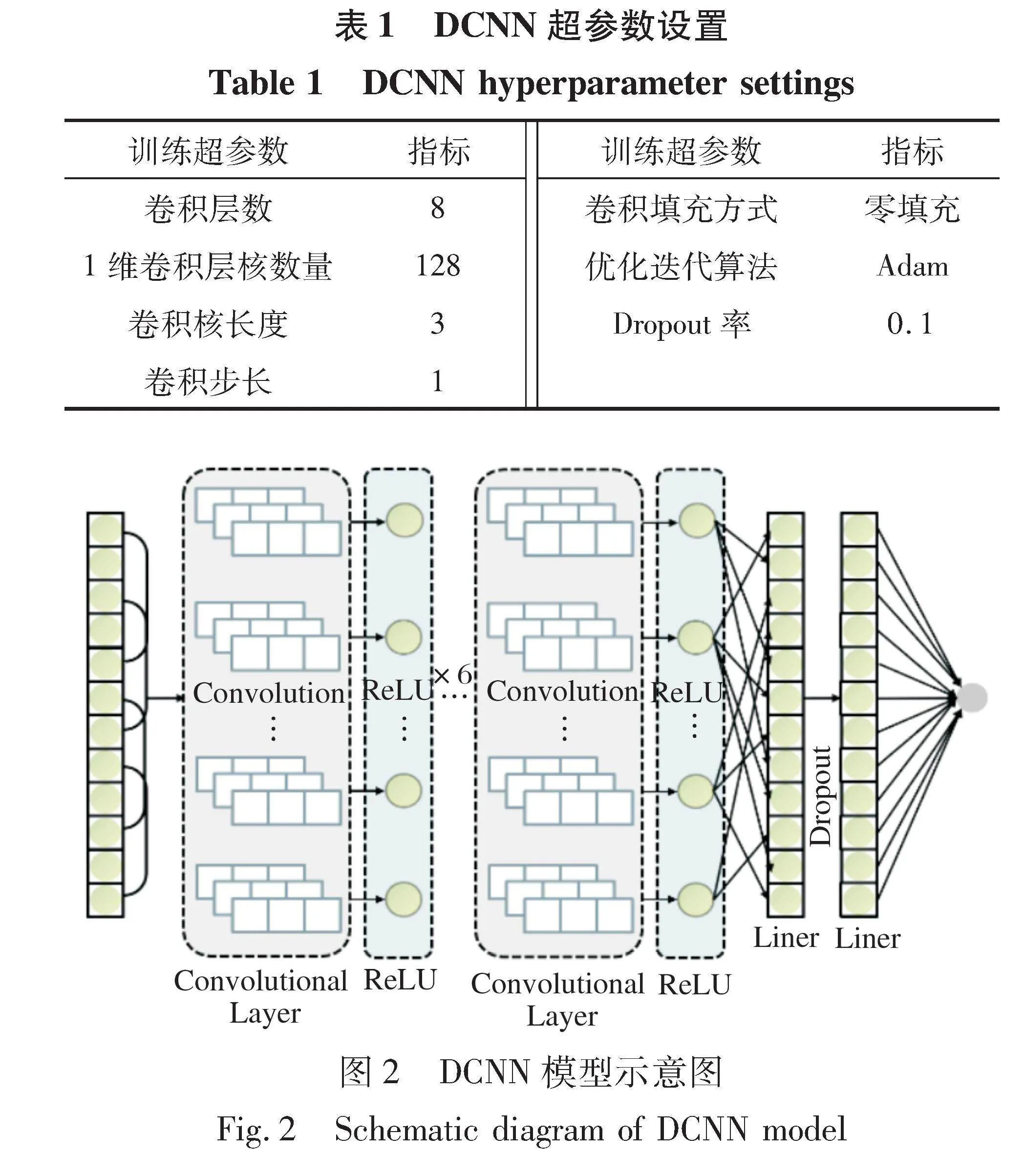
模型的超参数设置会影响其性能表现， 并决定了模型在训练过程中的学习行为以及最终的预测能力。 本文模型的超参数设置如表1所示， 采用的DCNN模型示意如图2所示。 本文采用的DCNN模型加入了Dropout层， 这一策略在训练过程中随机地将网络中的一部分神经元置为不活跃状态， 有效减少了网络中的参数数量， 降低了模型的复杂度， 从而有助于防止过拟合现象的发生， 并且增加了模型的多样性， 有助于提升模型的泛化能力。

1.3 MDCNN模型训练流程

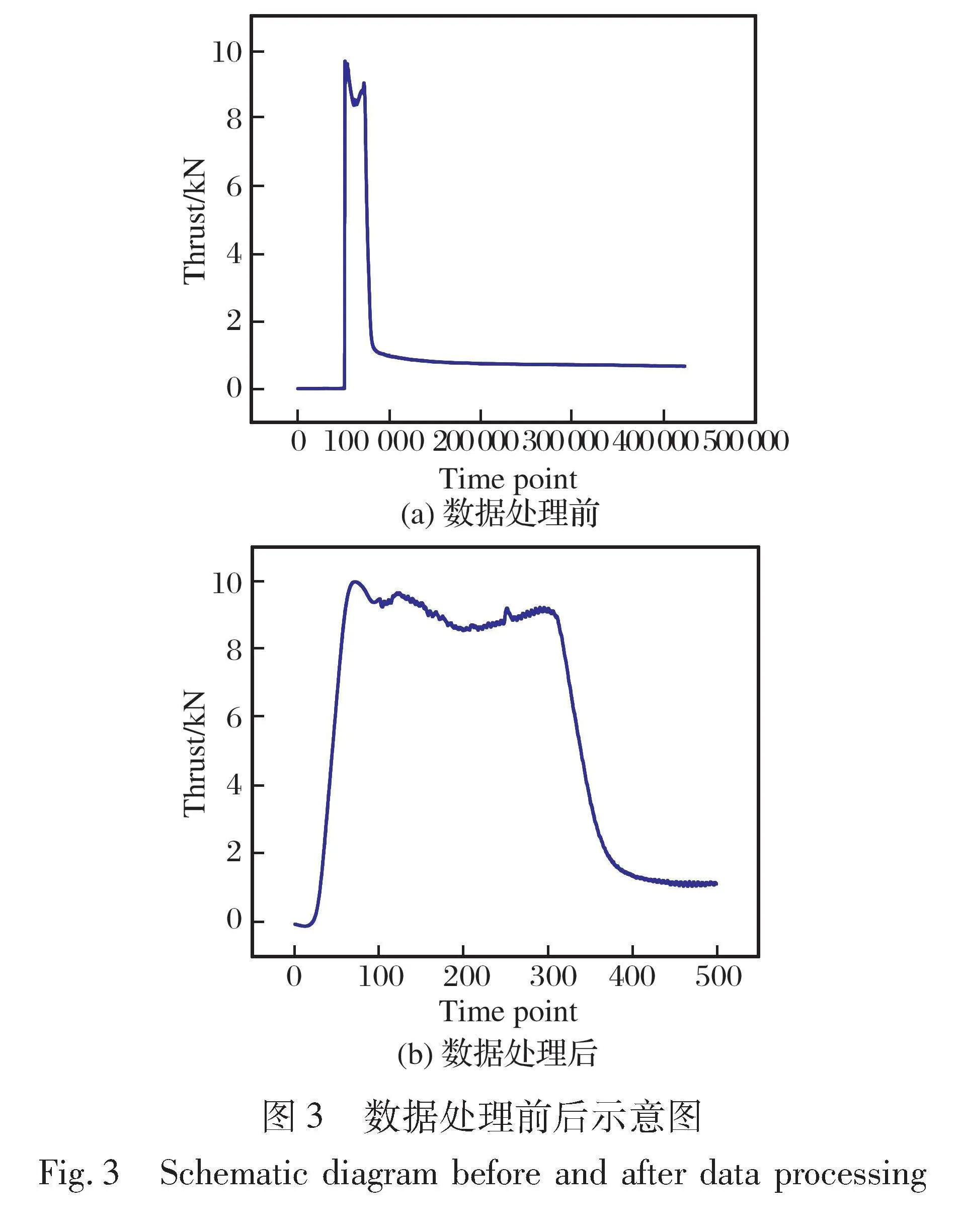
本文以DCNN模型作为预测器搭建了元学习的框架， 所使用的数据集来自不同温度条件下的固体发动机地面试车实验， 这些数据通过传感器测量并经过后处理得到推力-时间曲线。 该数据集由90组高温实验数据、 80组低温实验数据以及25组常温实验数据所构成。 为了优化模型训练过程， 通过降低采样减少数据集大小， 降低模型对计算资源的依赖， 减少计算所需的时间， 以此去除大量难以提取特征和信息的相似数据， 降低模型过拟合的风险， 数据处理前后如图3所示。 本文将高温与低温实验数据设为元训练任务， 并将其按照9∶1的比例随机划分为支持集与查询集， 以供元训练阶段的模型训练与性能评估。 同时， 将常温实验数据设为元测试任务， 以4∶1的比例划分为支持集与查询集， 用于元测试阶段的模型训练与性能测试。

元训练阶段， 在内循环中， 输入训练任务中的支持集并使用DCNN模型来进行训练， 以此对DCNN模型的参数进行第一次更新， 更新之后在每个任务查询集进行测试， 计算查询集的误差。 在外循环中， 通过查询集误差的梯度， 并使用梯度下降法对没有MDCNN模型的参数进行二次更新， 直到得到在不同任务中共同的最优MDCNN模型参数。

在元测试阶段， 利用MDCNN模型对测试任务的支持集进行训练并更新MDCNN模型参数， 训练完毕后， 利用5组查询集进行测试， 评估MDCNN模型的性能。

2 结果分析

2.1 收敛速度分析

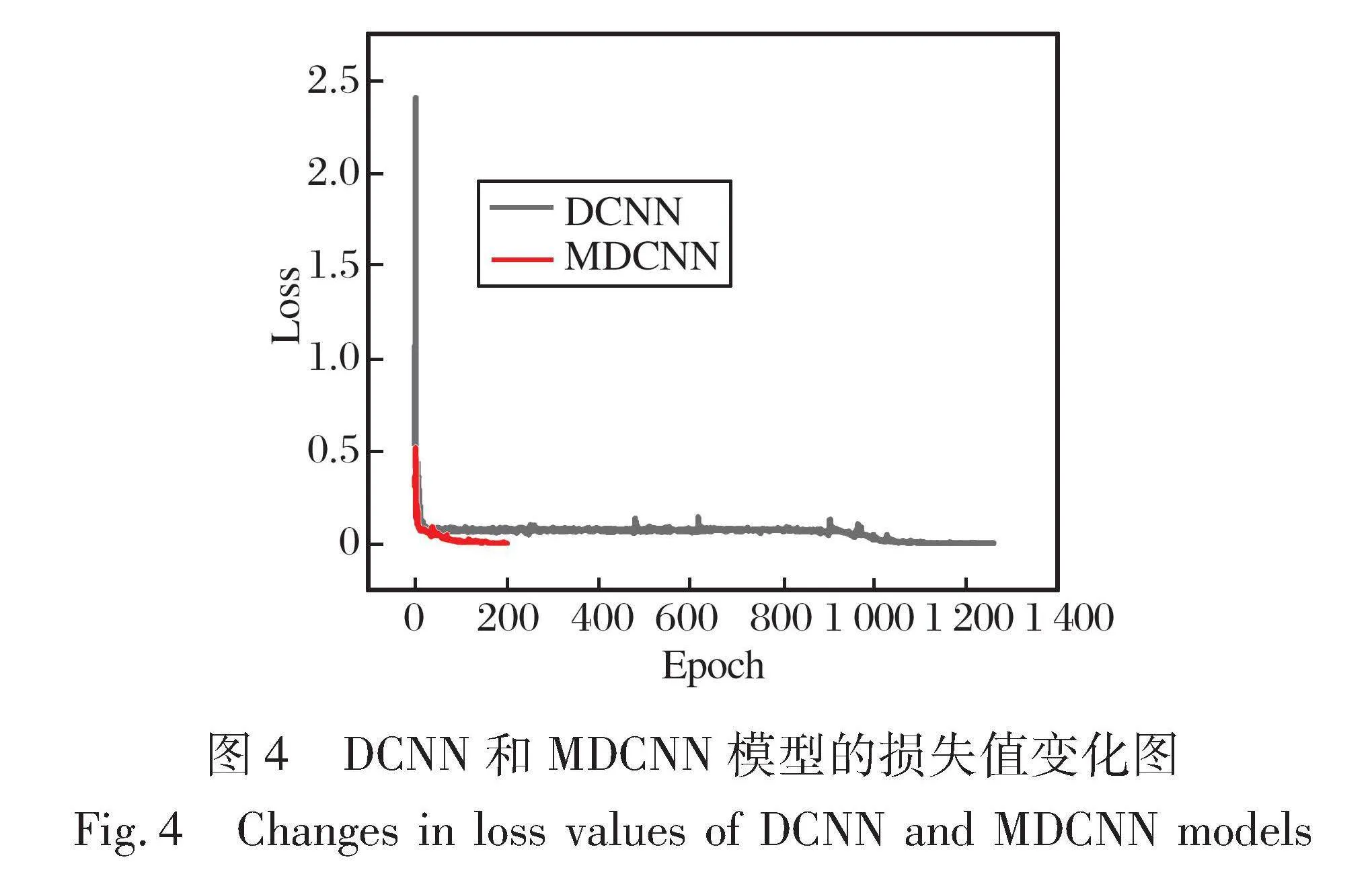
通过比较DCNN模型在训练过程中以及MDCNN模型在元测试阶段支持集训练过程中的损失函数值Loss的变化趋势， 分析使用元学习方法前后对固体发动机性能预测的收敛速度。 损失值变化如图4所示。

如图4所示， 相比于未采用元学习的DCNN模型， 所提出的MDCNN模型更快地达到了收敛状态。 同时， 所提出模型在训练200步时， 误差降低至1×10-3。 而传统DCNN则需要将近1 300步才能达到相同的精度。 由此可见， MDCNN在训练到相同精度所需的步数远远小于传统DCNN模型。 结果表明， 通过元学习模型可以从最优模型参数出发， 使用更少的梯度步骤达到收敛。

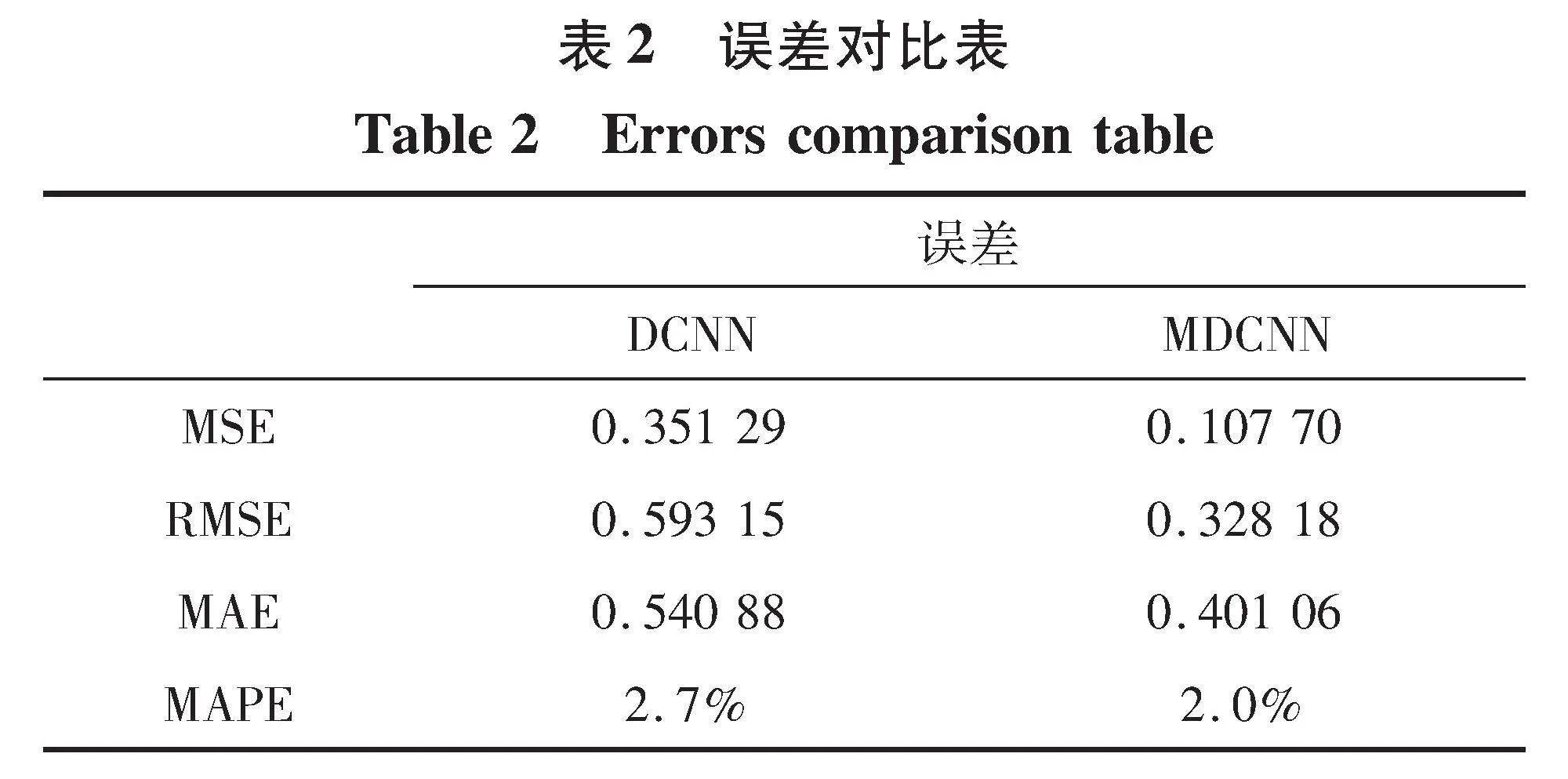
2.2 误差对比

通过比较百分比误差、 均方误差（Mean Square Error， MSE）、 均方根误差（Root Mean Square Error， RMSE）、 平均绝对误差（Mean Absolute Error， MAE）以及平均绝对百分比误差（Mean Absolute Percentage Error， MAPE）， 分析使用元学习方法前后的预测效果。

DCNN与MDCNN误差对比如表2所示。

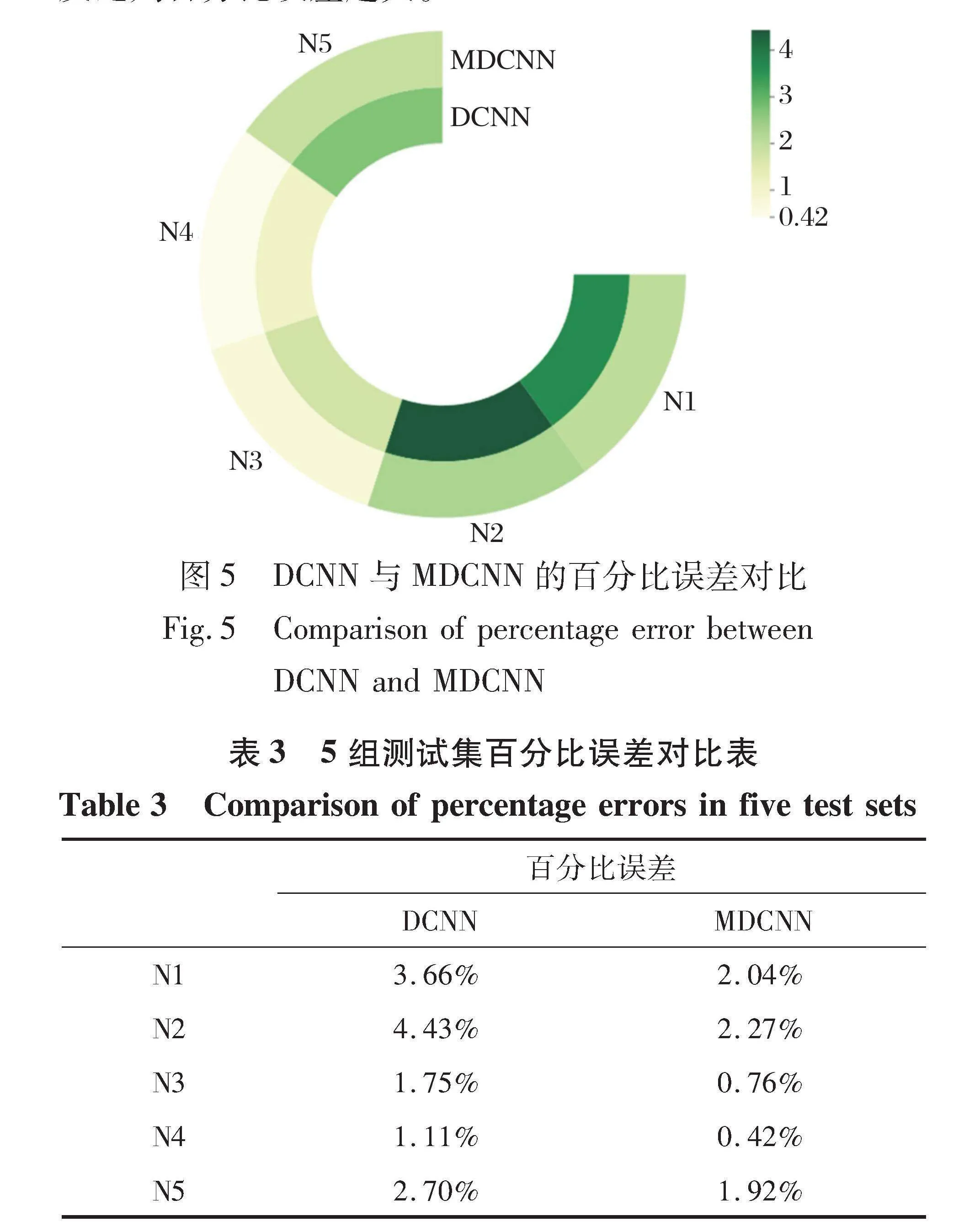
由图表可以看出， 在5组测试集上MDCNN的百分比误差都要小于DCNN。 其中， DCNN最大的百分比误差为4.43%， 而MDCNN模型最大百分比误差仅为2.27%。 表明元学习方法在预测结果的准确性上远远高于传统的DCNN模型。

2.3 预测结果分析

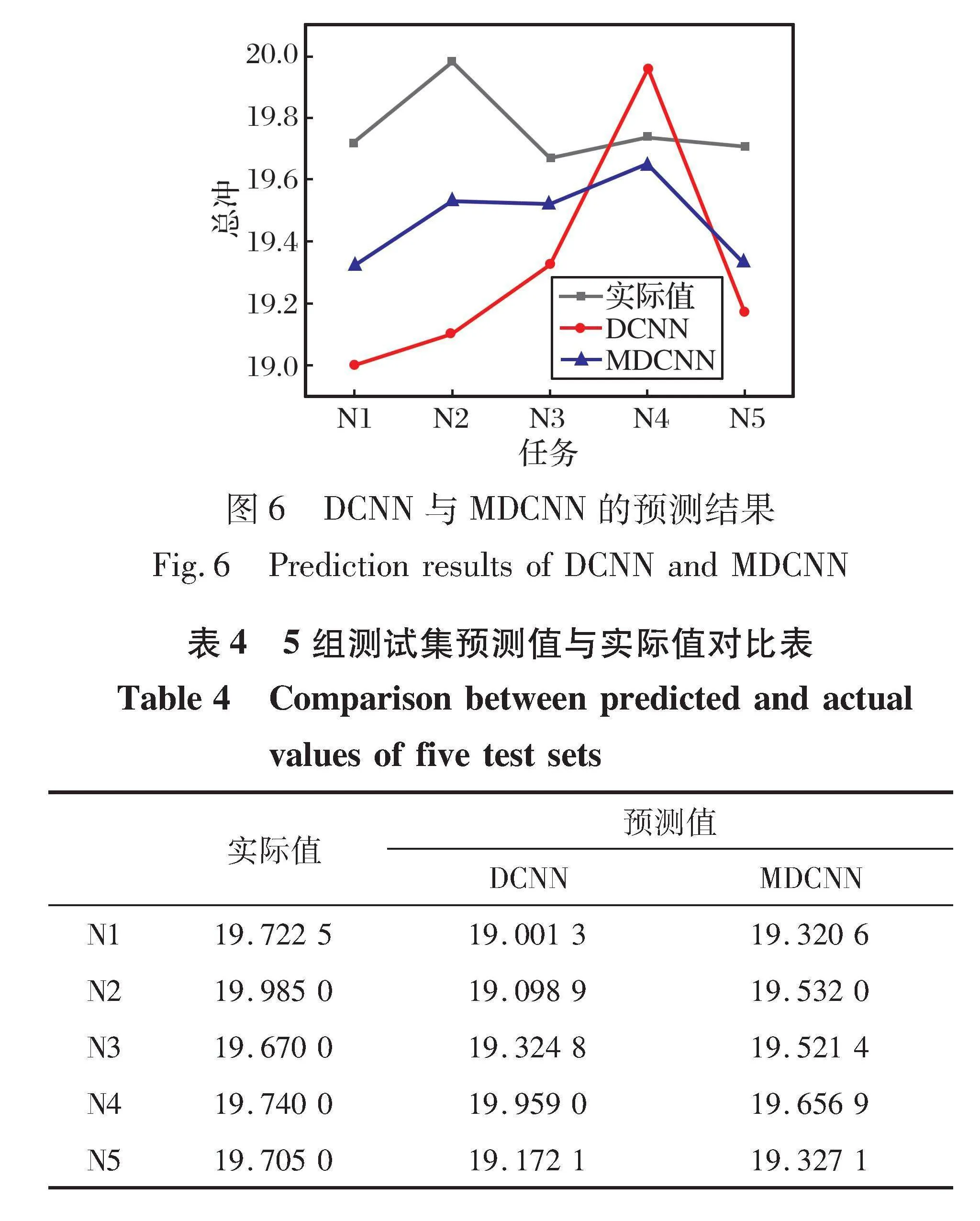
在5组测试集上的预测结果如图6和表4所示， MDCNN模型的预测值明显要比DCNN模型更逼近实际值。 结果表明， MDCNN模型在不同测试集上预测结果的准确性上远远高于传统的DCNN模型， 从而证明了MDCNN在面对复杂数据时更强的适应性和鲁棒性， 不仅能够更有效地从训练数据中学习、 提取出关键特征， 还能更好地适应新的、 未见过的数据。

3 结 论

通过搭建元学习框架， 开发了一种基于深度元学习的人工智能方法， 该方法采用了MDCNN模型对飞行器动力系统中的发动机性能进行预测， 解决了传统发动机性能计算的固有复杂性以及传统人工智能方法数据依赖性大、 泛化能力差等问题， 为未来固体发动机性能预测提供了新方向， 不仅有助于提升发动机本身的效能， 同时也将为飞行器动力系统的整体优化和设计提供有力的支持。 利用MDCNN通过内外循环从不同的推力-时间数据上学习元知识， 并利用新的任务对MDCNN模型进行测试。 与未采用元学习的DCNN模型进行对比， 得出以下结论：

（1） 通过元学习模型， 可以使模型从最优模型参数出发， 使用更少的梯度步骤达到收敛， 并提高模型的收敛速度。

（2） 相对于传统的DCNN模型， MDCNN模型展现出了更高的准确性和稳定性， 在5种误差的比较中都全面小于DCNN模型。

（3） 在5组测试集上， MDCNN的曲线明显要比DCNN模型更逼近实际值， 证明了MDCNN在面对复杂数据时的有效性和鲁棒性， 能更好地适应新的、 未见过的数据。

参考文献：

［1］ 蔡淑芬， 张玉成， 胡克娴， 等. 固体火箭发动机总冲精度预示与分析［J］. 推进技术， 1996（2）： 27-31.

Cai Shufen， Zhang Yucheng， Hu Kexian， et al. Accuracy Prediction and Analysis of Totnj4DsFwE+34/RE9VUh1GOw==al Impulse for Solid Rocket Motor［J］. Journal of Propulsion Technology， 1996（2）： 27-31.（in Chinese）

［2］ Finn C， Abbeel P， Levine S. Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks［C］∥International Conference on Machine Learning， 2017.

［3］ Mahalakshmi V， Sandhu M， Shabaz M， et al. Few-Shot Learning-Based Human Behavior Recognition Model［J］. Computers in Human Behavior， 2024， 151： 108038.

［4］ Liao R， Zhai J， Zhang F. Optimization Model Based on Attention Mechanism for Few-Shot Image Classification［J］. Machine Vision and Applications， 2024， 35（2）： 1-14.

［5］ Luo M C， Xu J， Fan Y Q， et al. TRNet： A Cross-Component Few-Shot Mechanical Fault Diagnosis［J］. IEEE Transactions on Industrial Informatics， 2023， 19（5）： 6883-6894.

［6］ Rivas-Posada E， Chacon-Murguia M I. Meta-Learning Methodology Based on Meta-Unsupervised Algorithm for Meta-Model Selection to Solve Few-Shot Base-Tasks［J］. Neural Computing and Applications， 2024， 36（15）： 9073-9094.

［7］ Vettoruzzo A， Bouguelia M R， Rgnvaldsson T. Multimodal Meta-Learning through Meta-Learned Task Representations［J］. Neural Computing and Applications， 2024， 36（15）： 8519-8529.

［8］ 万鹏， 李迎光， 华家玘， 等. 基于元学习和PINN的变工况刀具磨损精确预测方法［J］. 南京航空航天大学学报， 2022， 54（3）： 387-396.

Wan Peng， Li Yingguang， Hua Jiaqi， et al. Accurate Prediction Method of Tool Wear Under Varying Cutting Conditions Based on Meta Learning and PINN［J］. Journal of Nanjing University of Aeronautics and Astronautics， 2022， 54（3）： 387-396. （in Chinese）

［9］ Wang D D， Liu Q Y， Wu D Z， et al. Meta Domain Generalization for Smart Manufacturing： Tool Wear Prediction with Small Data［J］. Journal of Manufacturing Systems， 2022， 62： 441-449.

［10］ Huang H， Luo X， Yang C. Industrial Few-Shot Fractal Object Detection［J］. Neural Computing and Applications， 2023， 35（28）： 21055-21069.

［11］ 夏鹏程， 黄亦翔， 王誉翔， 等. 基于数据增强的判别元学习方法在跨设备少样本故障诊断中的应用［J］. 中国科学： 技术科学， 2023， 53（11）： 2003-2004.

Xia Pengcheng， Huang Yixiang， Wang Yuxiang， et al. Augmentation-based Discriminative Meta-Learning for Cross-Machine Few-Shot Fault Diagnosis［J］. Scientia Sinica： Technologica， 2023， 53（11）： 2003-2004.（in Chinese）

［12］ Minot M， Reddy S T. Meta Learning Addresses Noisy and Under-Labeled Data in Machine Learning-Guided Antibody Engineering［J］. Cell Systems， 2024， 15（1）： 4-18.

［13］ Vinyals O， Blundell C， Lillicrap T， et al. Matching Networks for One Shot Learning［C］∥ Proceedings of the 30th International Conference on Neural Information Processing Systems， 2016： 3637-3645.

［14］ Ravi S， Larochelle H. Optimization as a Model for Few-Shot Learning［C］∥International Conference on Learning Representations， 2017.

Research on Solid Motor Performance Prediction Method

Based on Deep Meta-Learning

Cui Yan， Lou Bixuan， Yu Pengcheng， Yang Huixin*

（College of Aerospace Engineering， Shenyang Aerospace University， Shenyang 110136， China）

Abstract： Addressing the numerous limitations in solid motor performance experiments for aircraft power systems， such as high costs， specialized equipment requirements， specific experimental environments， and high risks， this paper proposes an artificial intelligence method based on deep meta-learning for engine performance prediction. This method employs model-agnostic meta-learning （MAML） and deep convolutional neural networks （DCNN） models. Firstly， thrust-time data is divided into different training tasks according to varying experimental conditions. The optimal model parameters for each task are obtained through inner-loop training， and the model initialization parameters are updated in the outer-loop. After iterative optimization of the inner-loop and the outer-loop， a model predicted the total impulse of solid engines with high accuracy is obtained， and finally it is tested for new tasks. The test results demonstrate that compared to DCNN without meta-learning， this method reduces the error on the test set significantly， with a maximum percentage error of 2.27%. This verifies the high-precision prediction ability of the meta-learning model for solid motor perfor-mance under small sample conditions.

Key words： solid motor； motor performance； meta-learning； model-agnostic meta-learning； deep convolutional neural networks