梯度风场滑翔仿生飞行器设计与仿真

摘 要： 将信天翁从梯度风场中获取能量滑翔数千英里的飞行策略应用在飞行器上是突破飞行器续航瓶颈的重要方法之一。 本文结合信天翁身体特性和飞行策略， 设计了一种具有信天翁仿生外形、 气动布局和控制方式的仿信天翁飞行器， 巡航时升阻比为梯形翼飞行器的1.13倍， 最大可达梯形翼飞行器升阻比的1.31倍， 通过翼尖变形阻力最高可减小12%， 翼根载荷减小35%。 根据信天翁在滑翔时不时扑动翅膀的行为提出了间歇动力梯度风滑翔方法， 对仿信天翁飞行器进行了风梯度滑翔操控性能仿真。 结果表明实际飞行路径与风梯度滑翔路径的误差小于5%， 能量消耗为匀速飞行的51.5%， 验证了间歇动力梯度风滑翔策略的合理性。

关键词： 梯度风场； 飞行策略； 仿生无人机； 变形机翼； 操控性能

中图分类号： TJ760； V221

文献标识码： A

文章编号： 1673-5048（2024）05-0103-07

DOI： 10.12132/ISSN.1673-5048.2023.0248

0 引 言

在自然界中， 许多大型海鸟可以利用海面上垂直分布的水平梯度风场进行远距离滑翔飞行， 如信天翁可以飞行数千英里并且几乎不拍动翅膀。 所以， 将信天翁从梯度风场中获取能量的飞行策略应用到飞行器上， 可以改善飞行器的巡航时间甚至做到无动力飞行。

目前， 国内的无人机风梯度滑翔策略研究较少， 且主要为滑翔机理、 路径优化等理论分析， 对操控方面的研究很有必要。 2001年， Kicenuik提出滑翔机在水平层流和垂直层流中的最佳操控方式［1-2］。 2011年， Lawrance等总结了信天翁远距离滑翔飞行的策略和方法， 并分析其应用于飞行器动态滑翔的可行性［3-6］。 2012年， Sachs等研究了信天翁的飞行轨迹， 公布了一些关于信天翁风梯度滑翔的实验数据［7］。 2014～2017年， 高显忠等对梯度风获取能量的运动特征进行了分析， 建立了自主梯度风动态滑翔飞行的简化方法［8-10］。 2018年， Stempeck等根据信天翁等多种鸟类翼翅设计了平面机翼并与标准几何翼形进行对比［11］。 2021年， Mathew等模拟了信天翁和猎鹰的空气动力学特性， 可以作为进一步设计具有最佳空气动力学特性和低能耗的仿生无人机的基础［12］。 同年， An等建立了信天翁仿生机翼， 并分析了该机翼的气动性能［13］。 2022年， Wang等提出一种动态滑翔轨迹， 为深入研究动态滑翔机理提供飞行试验基础［14］。 以上研究表明， 信天翁的翼翅结构和滑翔策略可以极大地延长飞行器的巡航时间， 但目前的研究所用的飞行器属于传统飞行器， 没有适用于风梯度滑翔的特殊飞行器。 其次， 目前的研究主要集中在运动学分析和对航迹进行分析优化上， 虽然这表明风梯度滑翔可以延长飞行器巡航时间， 但缺少操控性方面的研究。

本文从信天翁的外形中提取了仿生机翼和机身的几何参数， 建立了仿生飞行器的三维模型， 并对飞行器进行气动计算和分析； 根据信天翁姿态控制方式设计变形机翼来控制飞行器的俯仰、 滚转和偏航运动并且实现减阻减载的效果； 建立虚拟海上梯度风场， 对仿信天翁飞

行器从海面上梯度风场中获取能量进行滑翔飞行进行操控仿真分析， 验证了仿生飞行器间歇动力风梯度滑翔策略。

1 飞行器总体设计

1.1 机翼仿生外形设计

信天翁由于性别、 种群、 年龄的差异， 身体参数也有

所不同。 本文选取一种中等体型的信天翁——黑背信天

收稿日期： 2023-12-26

作者简介： 刘建河（1976-）， 男， 河南叶县人， 副研究员， 硕士生导师。

*通信作者： 李加东（1980-）， 男， 山东临沂人， 博士， 研究员， 博士生导师。

翁为仿生对象， 据密歇根大学动物博物馆介绍， 该信天翁身长为80 cm， 体重为2 210～2 800 g， 是一种有极长翼羽的大鸟， 翼展为195～215 cm。 本文以黑背信天翁直线滑翔状态为拟合对象， 建立翼展为2 m、 平均弦长为218 mm、 根弦长为260 mm的仿生机翼模型（总体参数指标如表1所示）， 并对其进行优化。

航空兵器 2024年第31卷第5期

刘建河， 等： 梯度风场滑翔仿生飞行器设计与仿真

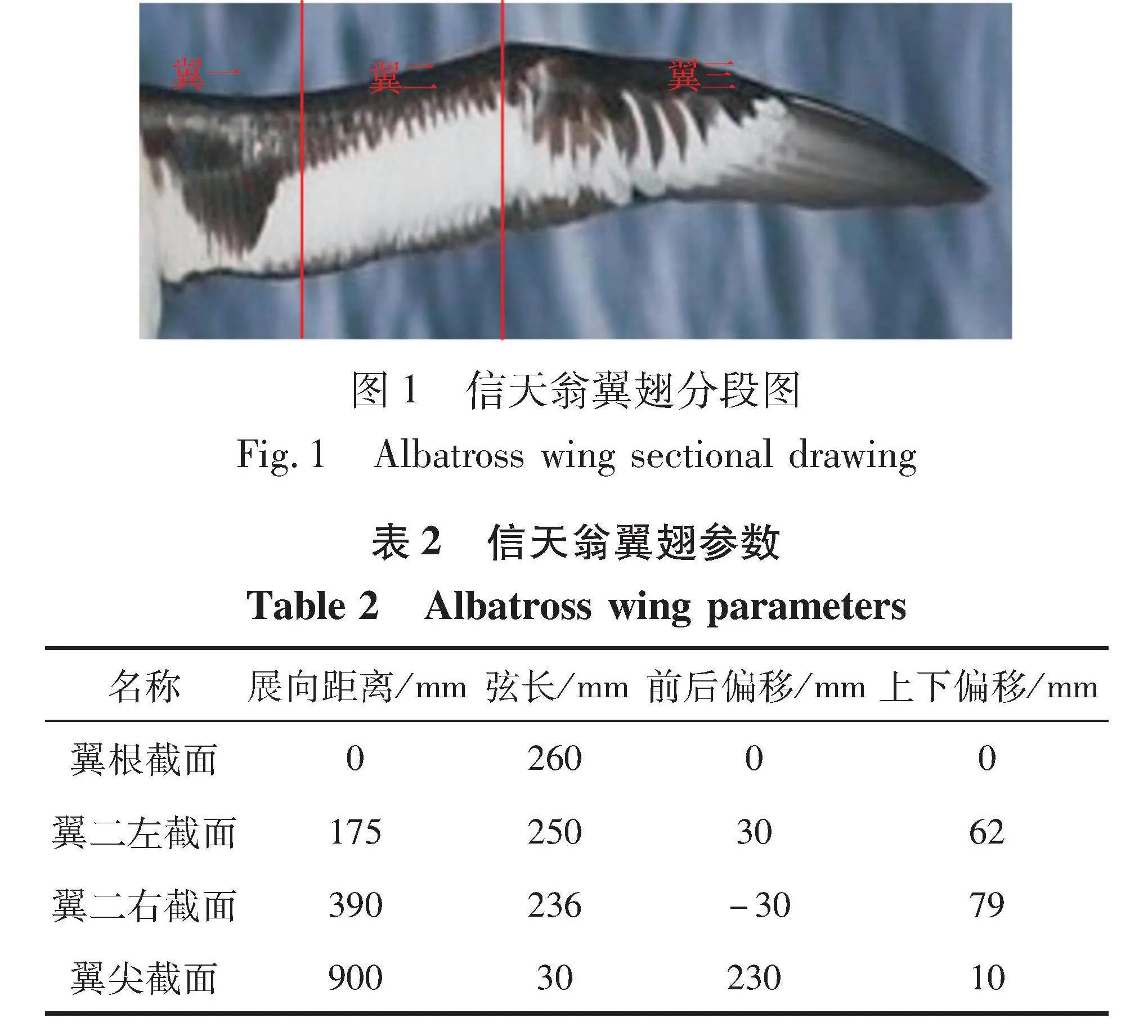
机翼制作通常需要知道展长、 弦长、 后掠角和二面角， 为了方便建模， 本文用当前截面翼型的前缘点相对翼根翼型的前缘点的前后偏移表达后掠角， 用上下偏移表达二面角。 为了收集信天翁翼翅的参数， 通过大量信天翁水平滑翔时的腹部仰视图和尾部视图进行对比测量［10-11］。 首先， 根据信天翁滑翔时翼翅的后掠角、 二面角对其进行分段， 如图1所示， 翼一具有较大的上反角和后掠角， 翼二上反角逐渐减小为零且机翼前掠， 翼三机翼下反后掠。 然后， 以展长为比例因子， 计算每个翼段断面的弦长、 偏移量（上下偏移和前后偏移）， 结果记录在表2中。 表中前后偏移和上下偏移指当前截面翼型的前缘点距翼根翼型前缘点的竖直和水平距离。

1.2 翼型确定及优化

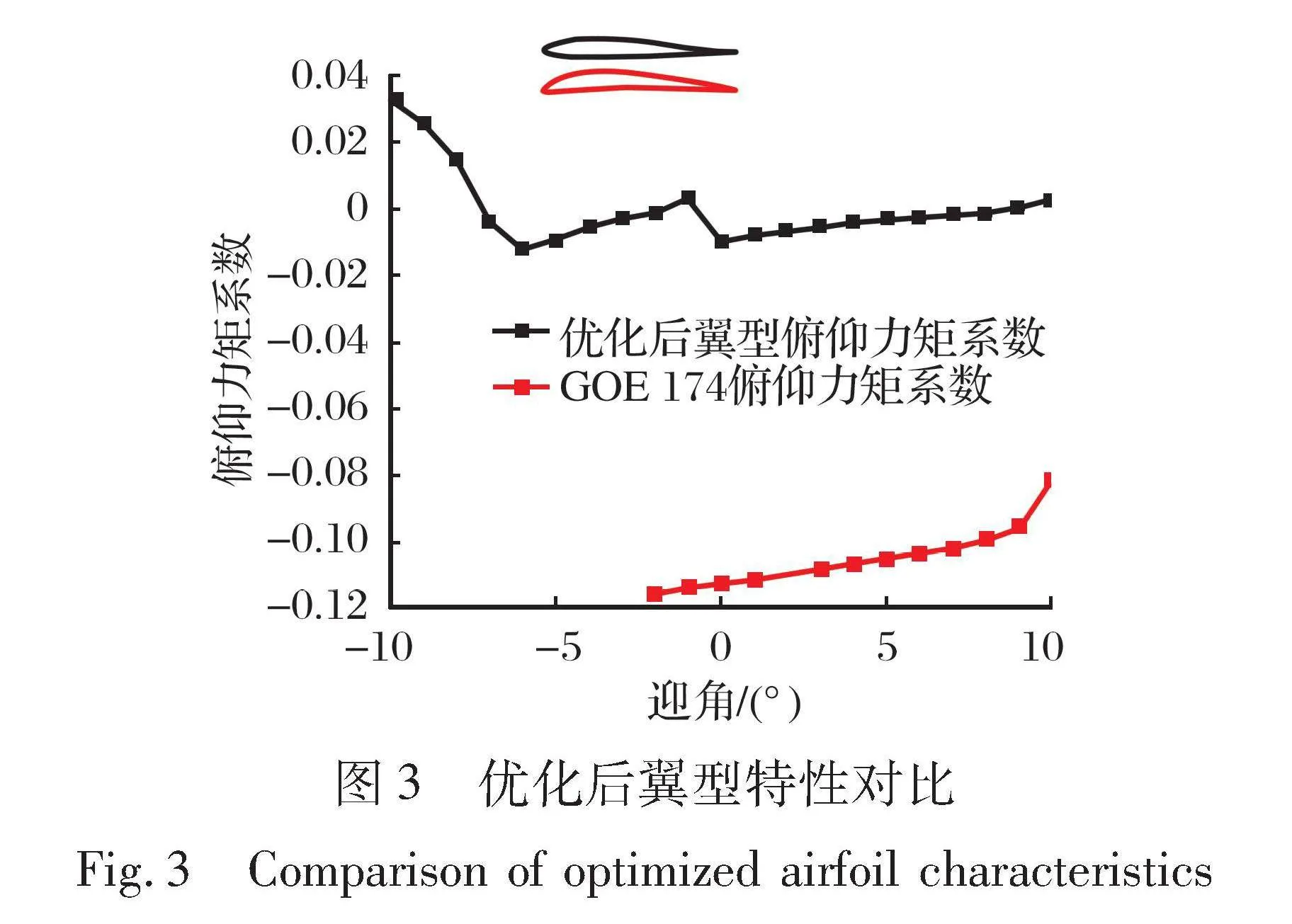
信天翁翼翅的尺寸参数确定后， 需要选择合适的翼型建立机翼三维模型。 翼型设计软件中的GOE 174是基于信天翁翼翅截面创建出的翼型， 具有高升阻比的特点， 然而信天翁在飞行中几乎看不到尾巴， 在实际应用中仿照鸟类的无尾布局要求机翼自身具有较强的俯仰稳定性， 所以需要对GOE 174翼型进行俯仰力矩系数方面的优化。

本节使用遗传算法结合有限元分析软件对翼型进行优化计算。 使用Hicks-Henne型函数对翼型上下表面各关键点形状的影响平滑均衡， 根据优化软件提供的邻域培植遗传算法NCGA对翼型进行优化［15］。

首先使用Hicks-Henne型函数对翼型上下曲线进行调整， 然后对翼型进行网格划分， 结果如图2所示。 翼型弦长为1 m， 网格数目为86 366， 最大网格质量为0.427。 解算器设置： 采用标准k-ε模型， 经验常数取默认值， 二阶迎风格式控制方程， 边界条件为速度入口， 迎角为4°， 来流速度为15 m/s， 求出4°迎角时的升阻比和俯仰力矩系数。 多目标优化器优化方法参数为每代个体6， 共8代， 其余参数采用默认值。 设计要求如下：

（1） 4°迎角， 标准SST k-omega模型进行有限元计算。

（2） 约束条件为： 优化后的翼型最大厚度为8.6%～9.8%， 俯仰力矩系数Cm范围为-0.3～0， 4°迎角时的升阻比k范围为65～85。

（3） 要求减小俯仰力矩系数， 同时尽可能保持较大的升阻比。

优化前后翼型对比如图3所示。 可以看出优化后的翼型在俯仰力矩系数方面的表现很好， 保持在0附近， 并且在大迎角情况下也可以稳定在0左右。

1.3 飞行器总体布局

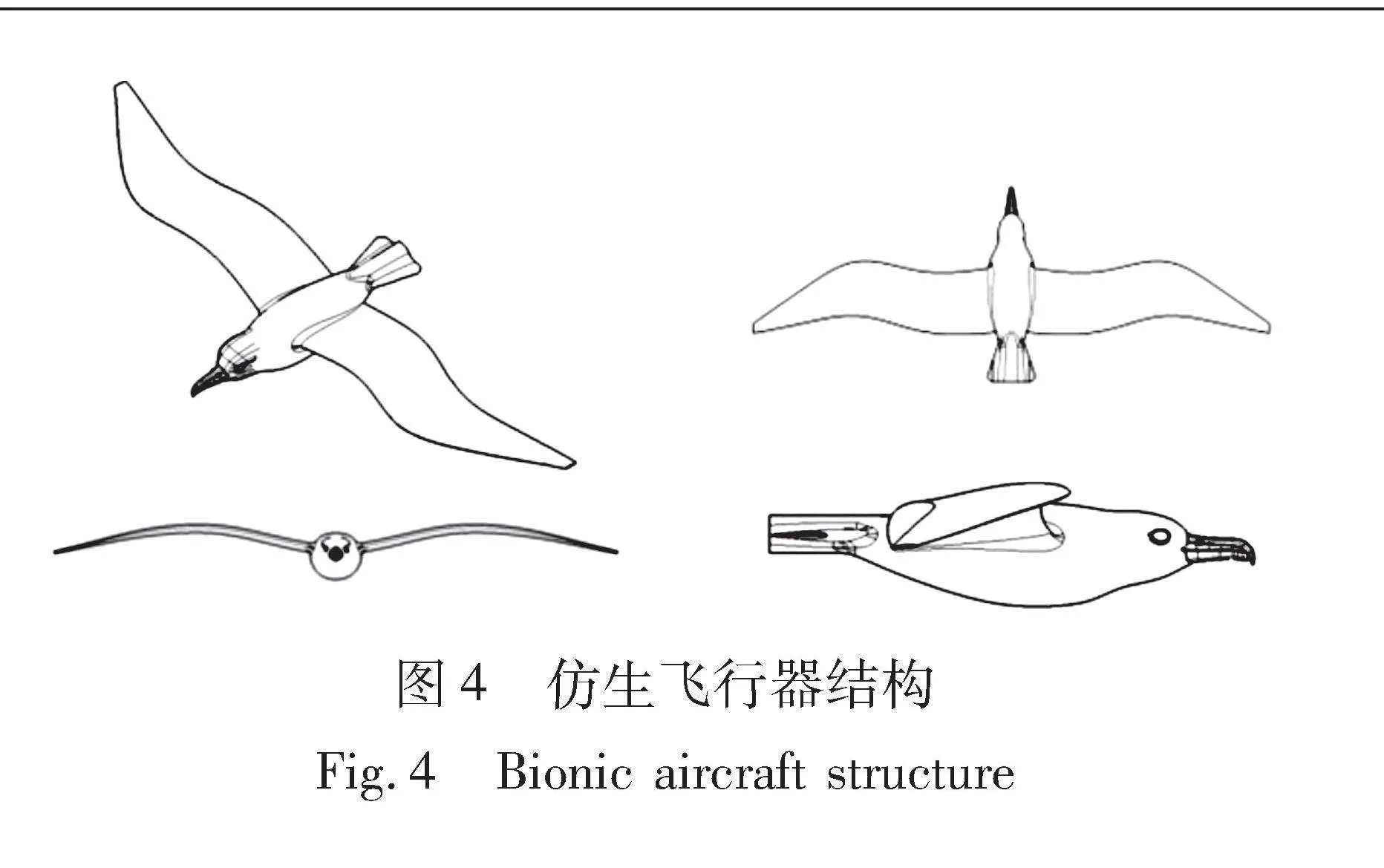
根据优化后的翼型和表2参数， 建立仿生机翼模型， 再根据信天翁身体建立机身模型， 信天翁滑翔时为飞翼布局， 所以本文所设计的飞行器为尾推式飞翼布局， 如图4所示。

2 空气动力学分析

2.1 飞行器性能分析

使用仿真软件对二维翼型分析或者对整个飞机进行气动分析， 基于升力线理论、 涡格法、 三维面元法对机翼进行求解。 对整机进行定速分析， 机翼参数为： 投影面积为0.4 m2， 展弦比为10， 平均气动弦长为218 mm， 翼展为2 m。 速度为15 m/s， 机翼安装角为4°， 尾翼翼型为NACA0012， 由信天翁翼翅在身体上的分布情况确定尾翼前缘与机翼前缘的距离为290 mm， 平尾面积为197 cm2， 平尾力臂为262.5 mm， 重心位置到机翼前缘距离为72.5 mm， 位于机翼三分之一处且在气动中心之前。 仿生飞行器网格划分如图5所示。

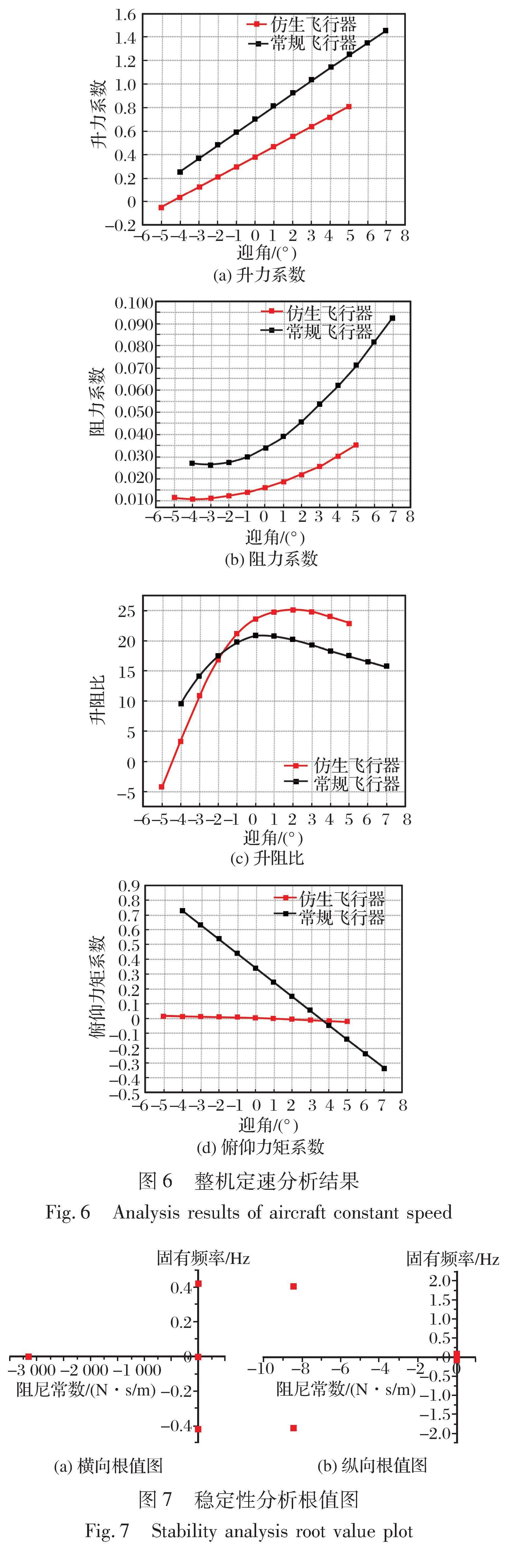
飞行器定速分析结果如图6所示。 可以看出， 当俯仰力矩系数为0时， 仿生飞行器迎角为0.4°， 表明飞行器稳定飞行时的迎角为0.4°， 机翼自身迎角等于安装角+飞行器迎角=4.4°， 此时飞行器升力系数0.416， 根据升力公式， 此时机翼提供的升力为22 N， 阻力系数为0.017 2。 仿生飞行器在正迎角下升阻比大于矩形翼飞行器， 0°迎角巡航时升阻比为梯形翼飞行器的1.13倍， 迎角越大仿生飞行器的升阻比相对梯形翼飞行器的倍数越大， 5°时为梯形翼飞行器升阻比的1.31倍， 所以仿生飞行器在爬升时具有较大优势。

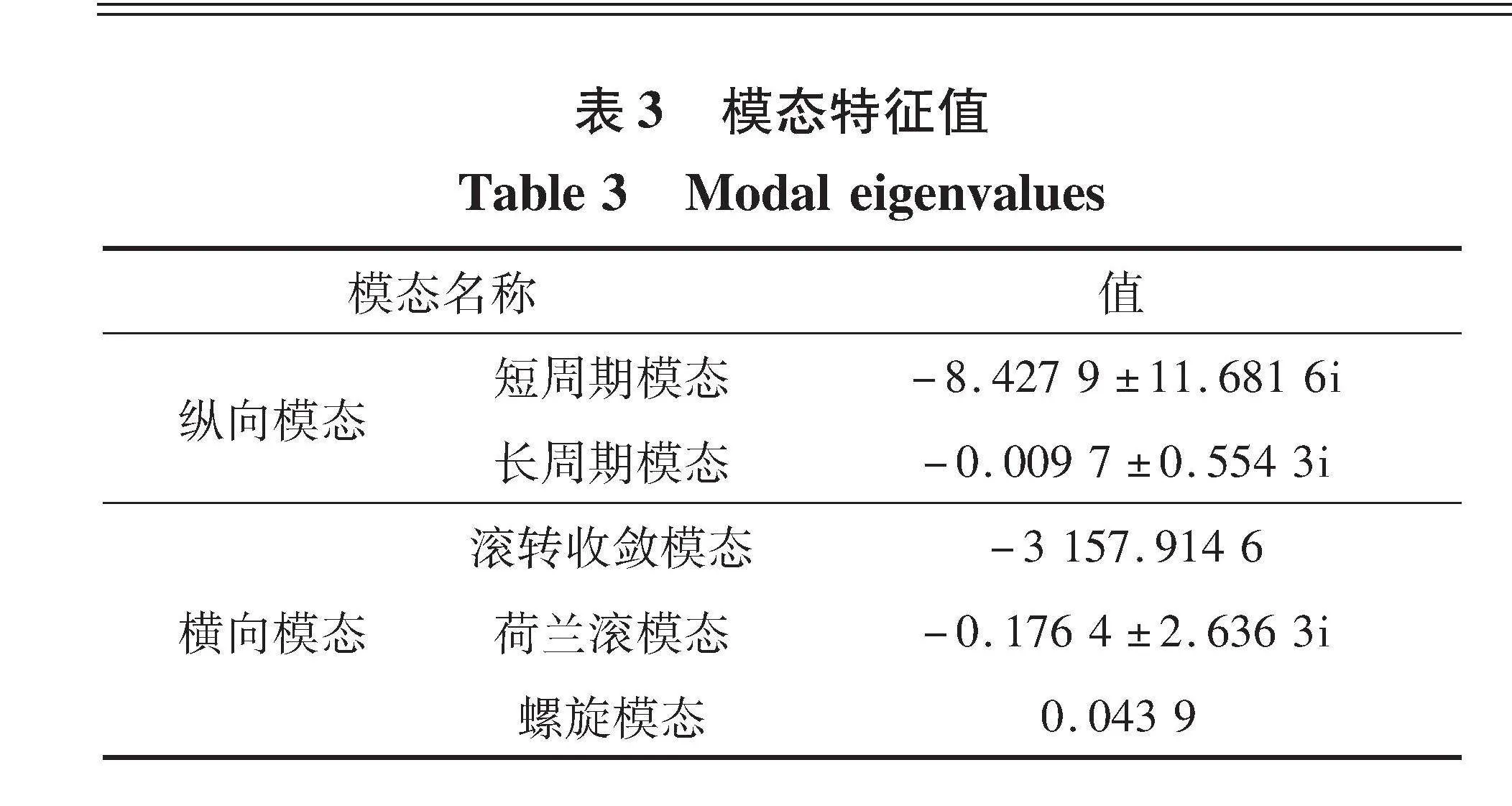
稳定性分析结果如图7和表3所示。 从表3数据中可以看出， 纵向模态频率ω12=8.427 92+11.681 62=14.4， ω34=0.55 ； 阻尼比ξ12=0.59， ξ34=0.018； 周期T12=0.44， T34=11.4。 前四个模态是稳定的， 而螺旋模态为不稳定状态， 这是由于飞行器没有方向舵， 无法控制飞行器的偏航姿态。 针对这种情况， 模仿信天翁飞行时翼翅上下折叠控制自身姿态的行为设计了转折变形机翼， 此模态可以通过控制翼尖的折叠运动进行控制。

2.2 翼尖设计

信天翁使用翼翅就可以控制滚转、 俯仰和偏航运动。 图8（a）为机翼初始位置， 在飞行器控制方面以信天翁为蓝本设计了转折翼尖， 如图8（b）所示， 俯仰和滚转运动

均由翼尖进行控制， 增大了舵面积； 另一方面信天翁在滑翔时需要面临不断变化的阵风冲击， 这对机翼的强度和抗疲劳性能具有一定的要求。 为了更好地应对阵风冲击［16］并延长机翼的使用寿命， 本文设计了一种具有转折翼尖机构的变形机翼， 如图8（c）所示。

转折翼尖的展向长度直接影响飞行器的偏航运动， 对不同翼尖展长进行偏航力矩分析， 翼尖转动角度均为20°， 来流速度15 m/s， 得出的结果如图9所示。 当翼尖展长为480 mm时产生的偏航力矩最大为0.43 N·m， 所以翼尖展长选为480 mm。

对两侧翼尖做对称折叠运动进行仿真。 翼尖初始位置如图8（a）所示， 水平向下8°即-8°， 设置翼尖角度每0.5 s增加4°， 结果如图10～11所示。 在翼尖从下反到上反的运动过程中， 阻力最大减少12%， 翼根载荷减少35%。 当翼尖位于初始位置时阻力最大， 翼尖水平时翼根载荷达到最大。

3 梯度风场飞行仿真

信天翁滑翔过程中大部分时间不用拍动翅膀， 只有

在自身动能不足时会扑动翅膀。 基于这种飞行方式， 本文提出了间歇动力梯度风滑翔策略， 即在每个滑翔周期初始阶段进行逆风爬升时， 飞行器继承自上一周期的能量不足以使飞行器爬升到指定高度的情况下需要启动螺旋桨对飞行器进行能量补充， 当飞行器速度达到周期滑翔的标准时再关闭螺旋桨， 一般会在逆风爬升阶段提供动力， 到顶点转弯阶段关闭动力。 下面通过操控仿真对该方法进行验证。

信天翁进行梯度风滑翔的必要条件是该区域存在梯度风场， 为了方便计算， 假设梯度风场为沿水平方向垂直分布的风速快速变化的风场， 风速大小仅与高度相关。 文中梯度风场使用美军标准MIL-F-8785C［17］， 风速与高度的关系可表示为

W=W0ln（z/z0）ln（z1/z0） （1）

式中： W为飞行器所在高度z处的风速； W0为飞行器最高飞行高度处的风速； z0为修正因子。

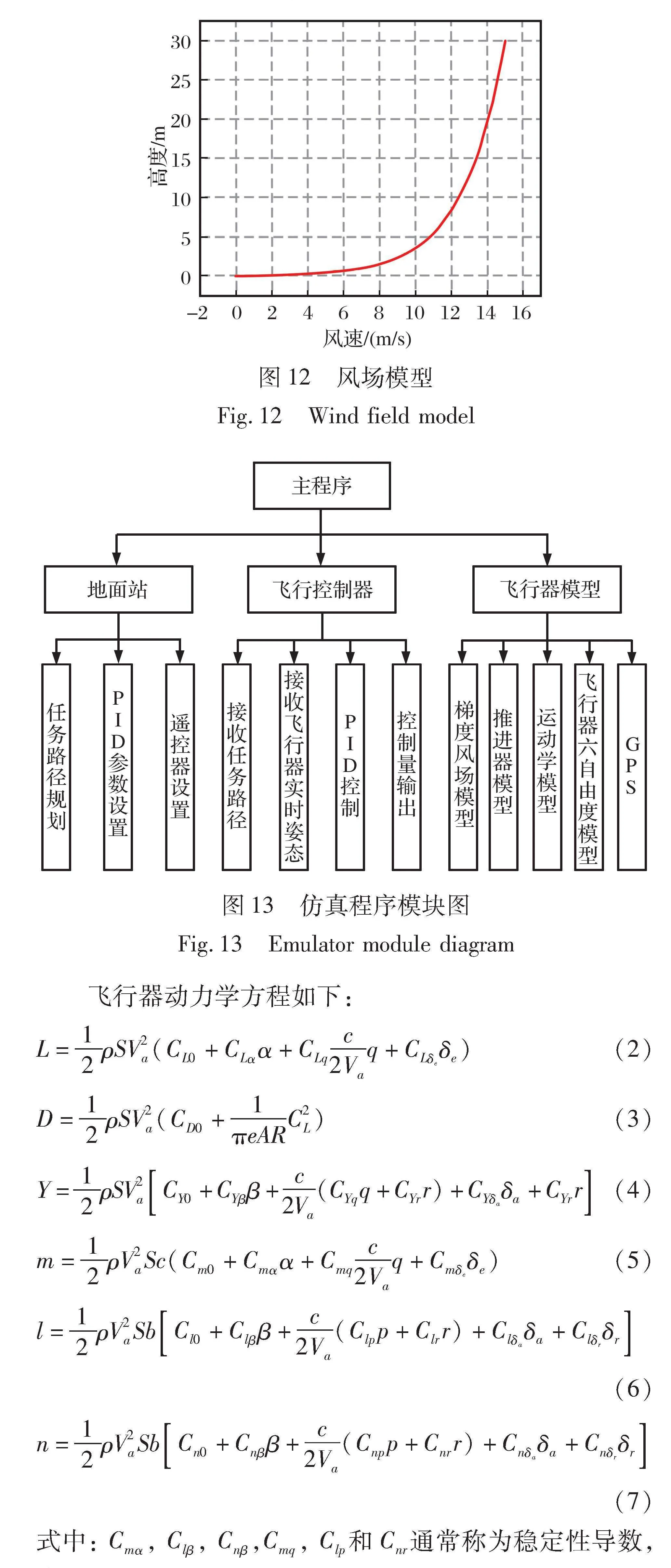
图12为模拟落差30 m之内的梯度风场模型， W0取15 m/s， z0取0.5 m， z1取30 m。

风场模型确定后， 接下来从仿生飞行器操控性能方面入手， 使用可视化仿真工具进行飞行器操控性仿真， 在一个飞行周期结束后又进行了逆风爬升。

仿真程序主要分为地面站、 飞行控制器、 飞行器模型3部分。 地面站部分包括任务路径、 PID参数设置和模拟遥控器； 飞行控制器部分负责接收飞行器实时数据（位置、 欧拉角、 空速）并与任务路径对比， 实现对方向舵、 副翼和油门控制量的PID控制， 将控制量输出到飞行器模型部分； 飞行器模型部分包括梯度风场设置、 推进器设置、 六自由度模型、 运动学模型和GPS数据收集， 负责对飞行器的位置、 受力和空速解算并反馈给飞行控制器部分。 仿真程序模块图如图13所示。

飞行器动力学方程如下：

L=12ρSV2a（CL0+CLαα+CLqc2Vaq+CLδeδe） （2）

D=12ρSV2a（CD0+1πeARC2L） （3）

Y=12ρSV2aCY0+CYββ+c2Va（CYqq+CYrr）+CYδaδa+CYrr （4）

m=12ρV2aSc（Cm0+Cmαα+Cmqc2Vaq+Cmδeδe） （5）

l=12ρV2aSbCl0+Clββ+c2Va（Clpp+Clrr）+Clδaδa+Clδrδr（6）

n=12ρV2aSbCn0+Cnββ+c2Va（Cnpp+Cnrr）+Cnδaδa+Cnδrδr （7）

式中： Cmα， Clβ， Cnβ，Cmq， Clp和Cnr通常称为稳定性导数， 决定了MAV的静态和动态稳定性； Cmδe， Clδa为主控制导数， 与控制面的变化有关； Cnδa为交叉控制导数， 反应了当控制面变化后所产生的离轴力矩； δe为副翼舵量， 在此为扭转翼扭转量； e为奥斯瓦尔德效率因素， 其值在0.8～1.0范围变化； AR为机翼展弦比。 在仿真软件中对转折翼尖进行襟翼设置： 角度为10°， 铰链位置X为1%弦长， 铰链位置Y为0%厚度。 并对飞行器进行稳定性分析， 在稳定性分析设置时分别使翼尖进行对称转动和差动， 将设计点特性导出得到无量纲操控导数和稳定性导数。 表4为求解得到的空气动力学系数。

仿真程序初始参数设置如式下：

（， θ， ψ）=（0， 0， 0）（Vx， Vy， Vz）=（25， 0， 0）（x， y， z）=（0， 0， 2） （8）

抛飞时飞行器距地约2 m， 所以飞行器初始高度为2 m。 首先， 将梯度风滑翔路径转化为离散的点并提取到任务路径中。 在飞行时会依次提取任务点， 每0.5 s对飞行器当前位置和任务路径点进行误差比较。 当飞行器位置与第一个路径点坐标的误差没有超出预设的精度范围， 则提取下一个路径点， 通过飞行器坐标和路径坐标的差值估计出控制面运动量控制飞行器向下一个路径点飞行， 重复该过程直至到达最终路径点。 对飞行结果进行平滑处理， 如图14所示。

从图14（a）中可以看出， 实际飞行路径与任务路径在横航向上基本吻合， 飞行器的横向操控性能满足滑翔轨迹的要求； 由图14（c）可以得出， 飞行高度与任务路径误差小于5%。 飞行器可以实现梯度风滑翔的周期性飞行。

图15（a）～（b）分别为仿生飞行器梯度风滑翔模式和匀速飞行模式（速度为14 m/s）的油门随时间变化曲线图。 对于梯度风滑翔模式0～55 s为一个周期， 前12 s为

逆风爬升阶段， 12～16 s顶点转弯， 16～55 s顺风滑翔。 对于匀速飞行模式， 前15 s进行爬升飞行， 15～18 s顶点转弯， 18～55 s顺风滑翔。

使用无人机动力系统测试台测试油门量和能耗关系， 如图16所示。 该测试台通过脉宽信号控制电机转速。 脉冲信号范围为1 100～1 700 Hz， 脉冲信号增量为50 Hz， 得出脉冲信号对应的电流、 功率参数如表5所示。

根据表5得出功率和油门量关系如下：

P=1 624.4t5－3 391.6t4+2 359t3－

428.818 8t2+46.792 2t（9）

式中： t为油门量。

根据式（9）和图15可得一个周期内功率随时间的变化关系。 对于梯度风滑翔方式， 一个周期内只有前12 s提供动力， 选取0～55 s时间段内的功率积分变换得出一个周期所消耗的能量为1 204.3 J； 对于匀速飞行模式， 一个周期所消耗的能量为2 338.61 J。 由此可知， 一个周期内梯度风滑翔所消耗的能量是匀速飞行模式的51.5%， 飞行时间可提高1.941 9倍。

4 结 论

通过遗传算法对信天翁翼型GOE 174进行优化， 将俯仰力矩系数控制在0附近， 降低飞行器在纵向稳定性方面对平尾的依赖， 减小了平尾面积， 进一步减小了阻力。 结合信天翁飞行、 控制方式和身体结构设计了仿信天翁变体飞行器， 并在气动特性方面与常规梯形翼飞行器进行比较， 仿生飞行器在巡航和爬升时具有优势。 通过对比不同展长翼尖在飞行时产生的偏航力矩， 确定了折叠翼尖展长尺寸为480 mm， 在机翼展长中占比48%， 通过翼尖变形最高可减少12%的阻力和35%的翼根载荷。 根据此减载减阻特点， 仿生飞行器还可减少阵风对飞行器的影响， 使飞行器在阵风中更轻松地飞行。 根据信天翁飞行方式提出了间歇动力梯度风滑翔策略， 在一个飞行周期内除爬升阶段外， 其他飞行阶段可进行无动力飞行。 由操控仿真结果可知， 所设计的飞行器可以沿梯度风滑翔路径飞行， 航向基本吻合， 飞行高度误差小于5%。 与匀速飞行相比， 梯度风滑翔飞行所消耗的能量更少， 为匀速飞行的51.5%， 可使飞行时间延长约1倍。

参考文献：

［1］ Kiceniuk T. Dynamic Soaring and Sailplane Energetics［J］. Technical Soaring， 2001， 25（4）： 221-227.

［2］ Kiceniuk T. Calculations on Soaring Sink［J］. Technical Soaring， 2001， 25（4）： 228-230.

［3］ Lawrance N R J， Sukkarieh S. Autonomous Exploration of a Wind Field with a Gliding Aircraft［J］. Journal of Guidance， Control， and Dynamics， 2011， 34（3）： 719-733.

［4］ Lawrance N R J， Sukkarieh S. Path Planning for Autonomous Soaring Flight in Dynamic Wind Fields［C］∥ IEEE International Conference on Robotics and Automation， 2011： 2499-2505.

［5］ Lawrance N R J， Sukkarieh S. A Guidance and Control Strategy for Dynamic Soaring with a Gliding UAV［C］∥ IEEE International Conference on Robotics and Automation， 2009： 1649-1654.

［6］ Lawrance N R J. Autonomous Soaring Flight for Unmanned Aerial Vehicles［D］. Sydney： The University of Sydney， 2011.

［7］ Sachs G， Traugott J， Nesterova A P， et al. Flying at no Mechanical Energy Cost： Disclosing the Secret of Wandering Albatrosses［J］. PLoS One， 2012， 7（9）： e41449.

［8］ Gao X Z， Hou Z X， Guo Z， et al. Analysis and Design of Gui-dance-Strategy for Dynamic Soaring with UAVs［J］. Control Engineering Practice， 2014， 32： 218-226.

［9］ Zhu B J， Hou Z X， Ouyang H J. Trajectory Optimization of Unmanned Aerial Vehicle in Dynamic Soaring［J］. Proceedings of the Institution of Mechanical Engineers， Part G： Journal of Aerospace Engineering， 2017， 231（10）： 1779-1793.

［10］ Zhu B J， Hou Z X， Lu Y F， et al. The Direction Zone of Engineless UAVs in Dynamic Soaring［J］. Computer Modeling in Engineering and Sciences， 2015， 105（6）： 467-490.

［11］ Stempeck A， Hassanalian M， Abdelkefi A. Aerodynamic Perfor-mance of Albatross-Inspired Wing Shape for Marine Unmanned Air Vehicles［C］∥ Aviation Technology， Integration， and Operations Conference， 2018.

［12］ Mathew B C， Sahu S K， Dutta P， et al. Albatross and Falcon Inspired Bionic UAV： An Aerodynamic Analysis［J］. International Journal of Aviation， Aeronautics， and Aerospace， 2021， 8（3）： 1-22.

［13］ An W G， Shi F Z， He S B， et al. Aerodynamic Design and Optimization of Bionic Wing Based on Wandering Albatross［C］∥International Conference on Aerospace System Science and Engineering， 2021： 517-535.

［14］ Wang W， An W G， Song B F. Modeling and Application of Dynamic Soaring by Unmanned Aerial Vehicle［J］. Applied Sciences， 2022， 12（11）： 5411.

［15］ 马艳， 庞永杰， 范亚丽. 基于iSIGHT平台的翼型水动力优化［J］. 船舶力学， 2011， 15（8）： 867-873.

Ma Yan， Pang Yongjie， Fan Yali. Hydrodynamic Optimization of 2D Airfoil Based on iSIGHT Platform［J］. Journal of Ship Mechanics， 2011， 15（8）： 867-873.（in Chinese）

［16］ Wilson T， Kirk J， Hobday J， et al. Small Scale Flying Demonstration of Semi Aeroelastic Hinged Wing Tips［C］∥International Forum on Aeroelasticity and Structural Dynamics， 2019： 1-19.

［17］ Moorhouse D， Woodcock R. US Military Specification， MIL-F-8785C ［R］. Washington DC： US Department of Defense， 1980.

Design and Simulation of Gradient Wind Gliding Bionic Vehicle

Liu Jianhe1， Wang Mengshuo1， Liu Kun2， 3， Li Renshu2， 3， Huang Wei2， 3， Li Jiadong1， 2， 3*

（1. School of Mechanical and Electrical Engineering， Changchun University of Science and Technology，

Changchun 130022， China; 2. Suzhou Institute of Nano-Tech and Nano-Bionic， Chinese Academy of Science，

Suzhou 215123， China; 3. Key Laboratory of Multifunctional Nanomaterials and Smart Systems，

Chinese Academy of Science， Suzhou 215123， China）

Abstract： One of the important ways to break the endurance bottleneck of aircraft is to apply the flight strategy of albatrosses obtaining energy from gradient wind fields to glide thousands of miles on aircraft. Based on the body characteristics and flight strategy of albatross， a bionic albatross aircraft with bionic shape， aerodynamic layout and control mode is designed. The lift-drag ratio during cruise is 1.13 times that of conventional aircraft， and the maximum lift-drag ratio is 1.31 times that of conventional aircraft. The maximum drag is reduced by 12% and the wing root load is reduced by 35% through wing tip deformation. According to the behavior of albatross flapping its wings from time to time during gliding， the intermittent dynamic gradient wind gliding method is proposed， and the control performance simulation of bionic albatross aircraft is carried out. The results show that the error between the actual flight path and the gradient wind gliding path is less than 5%， and the energy consumption is 51.5% of uniform flight， which verifies the rationality of the intermittent dynamic gradient wind gliding strategy.

Key words： gradient wind field; flight strategy; bionic drone; deformed wing; control performance