基于中末制导交班点识别的高速高机动飞行器轨迹预测方法

摘 要： 针对高速高机动滑翔飞行器轨迹预测过程中任务场景定义不明确、 意图先验信息利用不充分等问题， 提出了一种基于中末制导交班点识别的轨迹预测方法。 首先， 构建高速高机动飞行器滑翔至多个典型中末制导交班点的任务场景， 利用准平衡滑翔制导方法生成轨迹数据集。 然后， 提出了一种基于长短期记忆（Long Short-Term Memory， LSTM）网络的中末制导交班点识别方法， 利用跟踪数据构造特征序列， 对滑翔轨迹进行初步分类。 最后， 引入自注意力机制提升序列到序列（Sequence-to-Sequence， Seq2Seq）预测网络的特征提取性能， 利用编码-解码的方式对分类后的滑翔轨迹进行长时预测。 仿真结果表明， 所提出的基于中末制导交班点识别的轨迹预测方法具有较高精度， 预测时长为120 s， 180 s和240 s时， 轨迹误差分别在18.77 km， 36.91 km和57.75 km以内； 相比于直接利用深度学习模型预测的方法， 所提出的预测方法在240 s的预测时长内平均预测误差降低了37.61%， 最大预测误差降低了37.34%。

关键词： 高速高机动飞行器; 长短期记忆网络; 中末制导交班点识别; 轨迹预测

中图分类号： TJ765； V249

文献标识码： A

文章编号： IfVExVONvMOwdnfl+JDn9w==; 1673-5048（2024）05-0074-08

DOI： 10.12132/ISSN.1673-5048.2024.0058

0 引 言

高速高机动滑翔飞行器是一种利用自身高升阻比气动外形提供升力， 在高度位于20～100 km范围内的临近空间以马赫数大于5的速度进行长时间、 远距离滑翔的飞行器［1］。 该类飞行器凭借强大的纵深穿透能力、 精确打击能力， 打破了传统的战略攻防平衡体系， 成为世界各军事大国竞争博弈的焦点。 可以预见， 未来几年高速高机动技术领域的竞争将越发激烈， 各国空天安全将面临新的威胁［2］。 高速高机动飞行器的轨迹预测是实施拦截防御的前提条件， 不但可以为防御方尽早制定拦截方案提供数据支撑， 也可为拦截弹发射决策、 遭遇点解算提供依据， 是目前防御方研究的重要方向之一［3-4］。

从高速高机动飞行器轨迹预测技术的构建方法来看， 目前研究重点可分为两方面。 一是基于模型驱动的轨迹预测， 此类方法一般应用于典型控制模式下， 通过特征参数辨识进行轨迹预测， 需要辨识的特征参数包括气动参数、 总体参数和控制参数等。 这类方法的基本思路是利用高精度跟踪数据估计上述特征参数和其变化规律， 并基于运动模型外推状态实现轨迹预测。 李广华［5］在假设高超声速飞行器控制变量服从一定规律的条件下， 通过对攻角和倾侧角滤波辨识， 研究了跳跃弹道和非跳跃弹道的预测问题； 张洪波等［6］将攻角和倾侧角建模成一阶Gauss-Markov过程， 联合半速度坐标系下的运动方程组成扩展状态变量实现了预测。 由于直接对攻角和倾侧角建模会导致跟踪和预测模型过于复杂， 并且难以提前获取非合作目标的本体参数， 部分学者转而求解其他包含控制量信息的参量。 李世杰等［7］提取了与目标攻角和倾侧角有关且易于建模及预测的控制参数， 构建了新的等效控制量； 王路等［8］通过分析高超声速目标

收稿日期： 2024-04-01

基金项目： 国家自然科学基金项目（12072027）； 河南省通用航空技术重点实验室开放基金项目（ZH-KF-230201）

作者简介： 马康康（1995-）， 男， 甘肃华亭人， 硕士研究生。

*通信作者： 胡星志（1988-）， 男， 湖南永州人， 副研究员。

的升阻比变化规律， 拟合得到升阻比函数， 依据升阻比的预测积分完成轨迹预测；翟岱亮等［9］定义了

一组新的气动参数， 通过对该参数的历史数据进行拟合并预测其未来状态； 陈南华等［10］利用自回归集成滑动平均模型预测变机动高超声速目标的加速度， 结合无迹卡尔曼滤波（Unscented Kalman Filter， UKF）算法对目标轨迹进行了预测。 基于模型驱动的预测方法具有较强的理论基础和良好的可解释性， 但现有的研究成果中并未明确定义此类方法适用的任务场景， 这导致实际预测过程中当任务场景不匹配时该方法的预测精度较低。

航空兵器 2024年第31卷第5期

马康康， 等： 基于中末制导交班点识别的高速高机动飞行器轨迹预测方法

另一方面是基于数据驱动的轨迹预测， 此类方法主要是将高速高机动飞行器的历史轨迹视为包含时间和空间特征的特殊时间序列， 通过神经网络对数据进行特征提取、 统计分析， 最终实现对数据变化趋势的预测。 胡星志等［11］将高斯过程回归分析引入预测任务当中， 建立了含噪声输入条件下的不确定轨迹预测模型， 能够给出高精度预测结果及其概率分布； 李青勇等［12］研究了多步预测过程中模型的性能变化， 提出一种基于长短期记忆（Long Short-Term Memory， LSTM）网络的Encode-Decoder轨迹预测技术， 能够从历史数据中提取更多的轨迹特征； 杨春伟等［13］针对滑翔式和跳跃式飞行轨迹预测问题， 利用LSTM网络设计编码器和解码器， 提出一种基于注意力机制的序列到序列（Sequence-to-Sequence， Seq2Seq）轨迹预测模型， 可以对目标的多种飞行轨迹进行有效预测； Zhang等［14］利用卷积运算代替了全连接运算， 提出一种基于卷积长短时记忆网络（ConvLSTM）的轨迹预测方法， 可以更好地处理目标的时空特征数据。 LSTM网络有效缓解了循环神经网络在训练过程中梯度消失或梯度爆炸的问题， 广泛应用于轨迹预测问题， 但随预测时长增长， 其性能会不断下降。 为进一步提高轨迹预测精度， 李明杰等［15］结合LSTM网络提出一种基于控制参数估计的智能轨迹预测算法， 通过对控制参数变化规律的学习， 积分外推实现了轨迹预测； 蔡远利等［16］、 宋波涛等［17］利用深度学习网络提出一种弹道分类器和预测器， 先对目标再入类型进行分类， 而后再对目标轨迹进行预测， 为高速高机动飞行器的轨迹预测提供了新思路。 基于数据驱动的预测方法需要丰富的轨迹数据集训练模型， 但现有的研究成果在构建轨迹数据集时对目标的意图先验信息利用不充分， 这导致此类方法在目标具有多种位置意图时难以取得良好的预测效果。

高速高机动飞行器的轨迹是“设计、 优化和控制”的结果， 其在滑翔段具有一定的目的性， 统计意义上存在规律， 可通过深度学习方法对其未来运动轨迹做出预测。 此外， 从目标飞行器全程制导的角度来看， 当目标具有位置意图时， 必然存在明确的中末制导交班点， 可以根据目标的位置意图推断出其可能位置。 对于滑翔段准平衡制导方法， 该交班点的位置作为终端约束， 直接参与制导算法运行， 可以通过识别中末制导交班点对准平衡滑翔轨迹初步分类。 因此， 本文开展基于中末制导交班点识别的高速高机动飞行器轨迹预测方法研究。 为简化问题， 暂不考虑禁飞区和主动博弈策略对飞行轨迹的影响， 构建高速高机动飞行器在不同再入条件下以准平衡滑翔弹道制导至多个典型交班点的任务场景， 生成目标轨迹数据集。 然后， 基于中末制导交班点识别网络， 对目标轨迹进行分类。 最后， 基于Seq2Seq预测网络， 在编码器中引入自注意力机制提升特征提取性能， 通过编码-解码的结构实现了目标轨迹的多步预测。 仿真结果表明， 本文提出的基于中末制导交班点识别的预测方法优于直接利用深度学习模型预测的方法， 可进一步提升轨迹预测精度。

1 高速高机动飞行器动力学模型及制导方法

1.1 动力学模型

忽略地球自转， 在半速度坐标系中建立飞行器三自由度运动方程［18］：

V·=－CDρV2Sm2m－μMr2sinθ

θ·=CLρVSm2mcosυ－μMr2cosθV

σ·=－CDρVSm2mcosθsinυ+Vtanφcos2θsinσrcosθr·=Vsinθ

λ·=－Vcosθsinσ/（rcosφ）

φ·=Vcosθcosσ/r （1）

式中： V为飞行器相对地球速度； θ为航迹倾角； σ为航迹偏角； r为地心距； λ和φ分别为经度、 纬度； ρ为大气密度； m为飞行器质量； Sm为飞行器参考面积； μM为地球引力常数； CD与CL分别为阻力系数和升力系数， 控制参数攻角α隐含其中， 另一控制参数为倾侧角υ。

1.2 准平衡滑翔制导

相对于跳跃滑翔弹道， 准平衡滑翔弹道具有高度变化平缓、 热流密度和动压峰值小等优点， 攻角和倾侧角曲线光滑， 易于姿态控制回路的跟踪实现， 对飞行器的制导控制能力要求低， 被广泛用于高超声速飞行器滑翔段制导［19］。 本文利用准平衡滑翔制导方法生成轨迹数据集， 具体分为基于航迹偏差角控制的侧向制导和基于航程控制的纵向制导， 均是由中末制导交班点的状态参数进行驱动， 这也为基于识别中末制导交班点进行预测提供了可行性。

1.2.1 侧向航迹偏差角控制

航迹偏差角定义为从飞行器当前位置到目标的视线方向与当前水平面内速度方向的夹角：

Δσ=σLOS－σ（2）

式中： σLOS为视线角， 通过球面三角理论求得。 为了消除该航迹偏差角， 采用比例型误差增益反馈的方式， 即

υ=－kσΔσ（3）

式中： υ为由航迹偏差角误差反馈获得的倾侧角； kσ为设定的正增益系数。

1.2.2 纵向航程控制

根据准平衡滑翔条件， 可推导出航迹倾角和航程解析关系式：

LR=RetanθlnRe+hRe+h1（4）

式中： h1为起始高度； h为当前高度； LR表示从起始高度到当前高度覆盖的航程； Re为地球平均半径。

基于式（4）， 根据航程要求可实时确定所需的航迹倾角， 并通过调整攻角进行准平衡滑翔纵向轨迹控制：

tanθref=RelnRe+hfRe+h/LRtogo（5）

式中： LRtogo为待飞航程； hf为期望的终端高度； θref为所需的参考航迹倾角。

采用反馈线性化控制理论设计轨迹控制律， 经推导可得

CLcmd=2mρVScosυgV－VRe+hcosθref+

2mρVScosυθ·ref－1τ（θ－θref）（6）

式中： CLcmd为升力系数指令； τ为时间常数。 据此可通过气动参数插值获得攻角α。

2 任务场景及轨迹数据集构建

非合作高速高机动目标的运动通常符合一定的运动规律或特定的任务场景， 因此， 首先对高速高机动飞行器滑翔段的任务场景进行明确定义。 假定根据目标再入和防御方要地位置推断出的中末制导交班点的位置如图1所示。

定义的任务场景具体描述为： 高速高机动飞行器从某确定点O再入， 采用1.2节所述的准平衡滑翔制导方法， 无动力滑翔至A， B， C三个典型的中末制导交班点。 在此任务场景下， 改变不同的初始再入状态， 生成丰富的轨迹数据， 构建轨迹数据集， 开展中末制导交班点识别及轨迹预测方法研究。 此任务场景中， 预设定的高速高机动飞行器再入点和典型中末制导交班点的位置参数如表1所示。

3 中末制导交班点识别模型

3.1 特征序列

中末制导交班点的识别属于时间序列分类问题， 首

先应当确定能够识别中末制导交班点的特征序列。 在本文所提任务场景中， 根据雷达跟踪获得的高速高机动飞行器轨迹信息， 防御方可持续计算目标与预设的3个中末制导交班点间的剩余航程和航迹偏差角， 生成相应的时间序列数据。 另外， 考虑速度特征反映了目标飞行器当前的能量状态， 当目标滑翔至不同剩余航程交班点时， 速度变化也必然不同。 因此， 将目标飞行器的速度也作为一个关键特征序列， 共获得7个特征序列， 以此对中末制导交班点进行识别。 跟踪过程中特征序列的生成示意图如图2所示。

目标飞行器与中末制导交班点间的剩余航程为

L=arccos（sinφTsinφ+cosφTcosφcos（λT－λ））（7）

目标飞行器与中末制导交班点的位置视线角为

σLOS=arctansin（λT－λ）cosφtanφT－sinφcos（λT－λ）（8）

式中： λT和φT为中末制导交班点的经度和纬度。 由此根据式（2）可计算目标飞行器和典型中末制导交班点的航迹偏差角。

3.2 LSTM识别网络

循环神经网络（Recurrent Neural Network， RNN）常用于时间序列分类问题。 LSTM网络作为RNN的改进网络， 其主要思想是通过引入三个门， 即遗忘门、 输入门、 输出门， 来处理记忆单元的信息， 具备保存长期信息的能力， 可以较好地对信息的时间变化规律进行挖掘。 LSTM网络单元结构如图3所示［20］。 图中， Ct－1表示上一时刻的单元状态； ht－1表示上一单元的输出； xt表示当前时刻的输入； Ct与ht表示当前时刻的单元状态与输出。

在前向传播过程中， 遗忘门决定了当前时刻的单元状态Ct可以保留多少上一时刻单元状态Ct－1的信息， 计算公式为

Ft=σ（Wf·［ht－1， xt］+bf）（9）

式中： σ（·）表示Sigmoid激活函数； Wf表示遗忘门的权重； bf表示遗忘门的偏置。 遗忘门通过Sigmoid函数将输入与上一时刻的状态映射为0～1之间的值来决定上一时刻状态的保留情况， 1表示完全保留， 0表示舍弃。

然后由输入门决定当前时刻的单元状态Ct可以保留多少当前时刻的输入xt。 输入门首先通过tanh函数构建候选向量C～t， 再通过Sigmoid函数选择其遗忘的比例， 计算公式为

C～t=tanh（Wc·［ht－1， xt］+bc）（10）

it=σ（Wi·［ht－1， xt］+bi）（11）

式中： Wc与bc表示构造候选向量时的权重与偏置； Wi与bi表示输入门的权重与偏置。

最后， 由输出门决定当前时刻的单元状态Ct有多少可以传送到输出ht， 计算公式为

Ct=Ft·Ct－1+it·C～t（12）

Ot=σ（Wo·［ht－1， xt］+bo）（13）

ht=Ot·tanh（Ct）（14）

式中： Ct为当前时刻的单元状态； Wo与bo分别表示输出门权值和偏置； 当前时刻的输出ht为当前状态Ct经过tanh后与Singmoid层的输出Ot相乘后的结果。

基于LSTM的分类网络结构如图4所示， 包含一个序列输入层（Sequence Input Layer）、 两个全连接层（Fully Connected Layer）、 一个双向长短期记忆网络层（BiLSTM Layer）、 一个Softmax层和一个Classification层， 网络的输入为目标飞行器的特征序列， 输出为目标飞行器滑翔至典型中末制导交班点的分类结果。

4 Seq2Seq轨迹预测模型

高速高机动飞行器的轨迹预测可视为时间序列预测问题。 基于LSTM网络设计的Seq2Seq轨迹预测模型［12］， 建立了输入序列和输出序列的函数映射关系。 编码器将跟踪获得的高速高机动飞行器轨迹作为输入序列转化为固定长度的上下文向量， 解码器将这个固定长度的向量滚动解码为可变长度的输出序列作为预测的飞行轨迹。

4.1 编 码 器

编码器主要使用LSTM网络， 将跟踪的经纬高轨迹数据xi作为输入， 映射到状态向量Ci和输出向量hi当中， 同时为了减少对不重要信息的关注， 引入自注意力机制， 通过对每一时刻LSTM层的输出序列进行动态加权， 得到编码网络的输出结果h～n， 这使得编码网络的输出与LSTM层每一步的输出直接相关， 可提升网络特征提取性能。 引入自注意力机制的编码网络结构如图5所示。

将LSTM网络输出向量hi作为Attention机制层的输入， 根据不同时刻信息的重要性程度确定影响权重， 第i个输入向量的得分计算公式为

ei=Φ（WThi+b） i=1， 2， …， n（15）

式中： W和b分别为权重矩阵和偏置向量; Φ（·）为得分函数， 可设置为神经网络中的激活函数， 如sigmoid函数。

通过softmax函数对式（15）进行标准化， 计算公式为

αi=softmax（ei）=exp（ei）∑ni=1exp（ei）（16）

注意力机制层最后的输出结果表示为

h～n=∑ni=1αihi（17）

最终， 编码器将LSTM最后的状态cn和注意力机制层的输出h～n合并为上下文向量V， 表示为

V=（h～n， cn）（18）

4.2 解 码 器

解码器主要是将固定长度的上下文向量V解码成不定长度的输出序列， 解码器的结构如图6所示。

解码器主要由LSTM层和全连接层组成。 LSTM层首先接收从编码器传下的上下文向量V和初始状态y0， 然后输出新的隐藏状态， 通过滚动预测的原理， 不断利用上一时刻的输出yt－1与更新的隐藏状态Vt－1实现多步轨迹预测。

4.3 轨迹预测方法

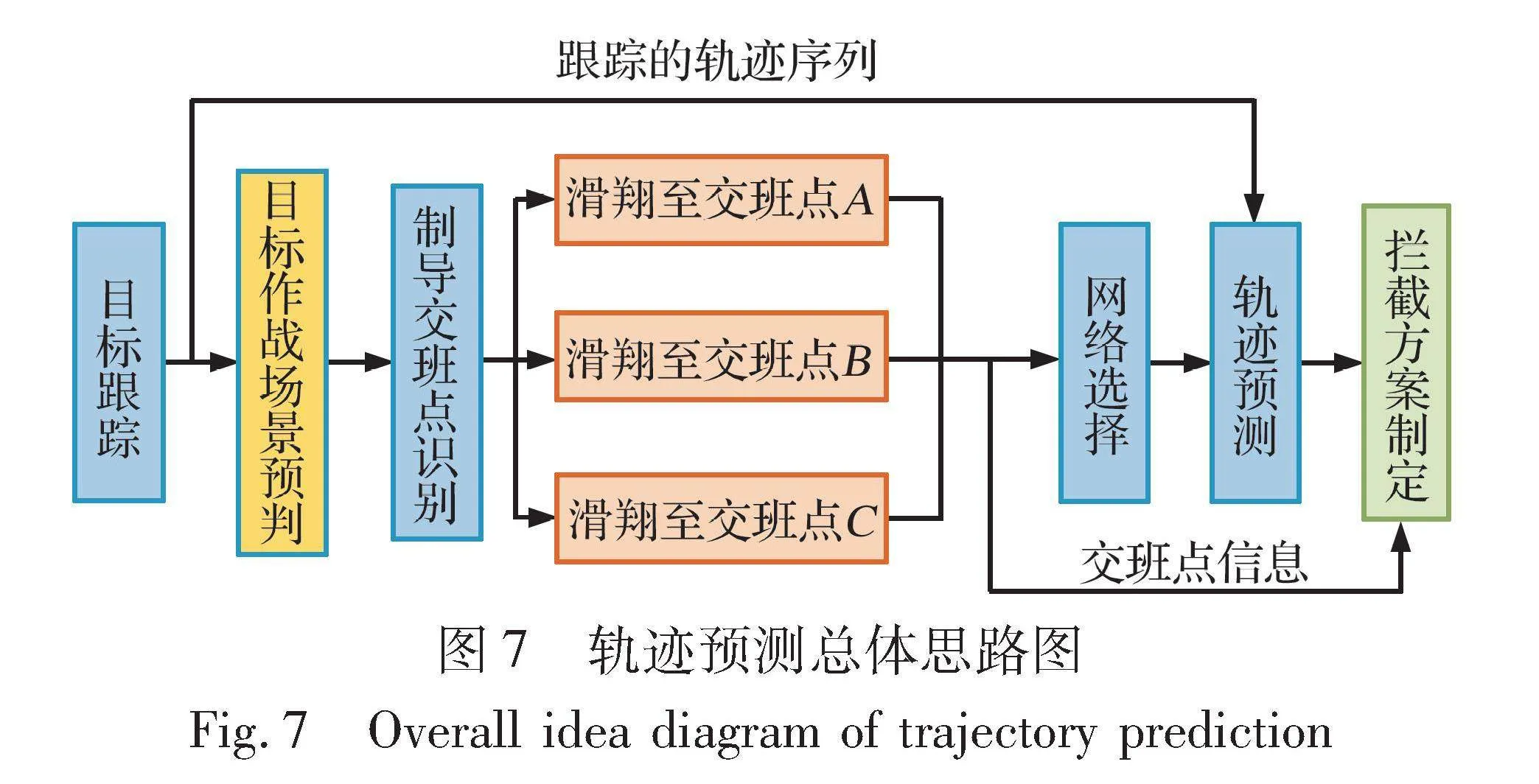
高速高机动飞行器在不同的任务场景当中， 滑翔至不同的中末制导交班点生成的轨迹形状不同， 如果使用统一的深度学习模型对目标轨迹进行预测， 可能会增加网络的训练难度， 难以取得良好的预测效果［17］。 因此， 根据探测系统的跟踪数据和防御方重点保护目标的信息， 对目标可能的任务场景做出预判， 基于提出的中末制导交班点识别方法可对目标轨迹进行分类。 同时， 识别到的中末制导交班点也可对拦截方案制定提供初步参考信息。 然后， 根据分类后的轨迹， 选择相应预训练好的轨迹预测模型， 对目标轨迹进行预测， 为拦截弹发射决策、 遭遇点解算提供依据。 本文所提出的高速高机动飞行器轨迹预测方法总体思路如图7所示。

5 仿真结果

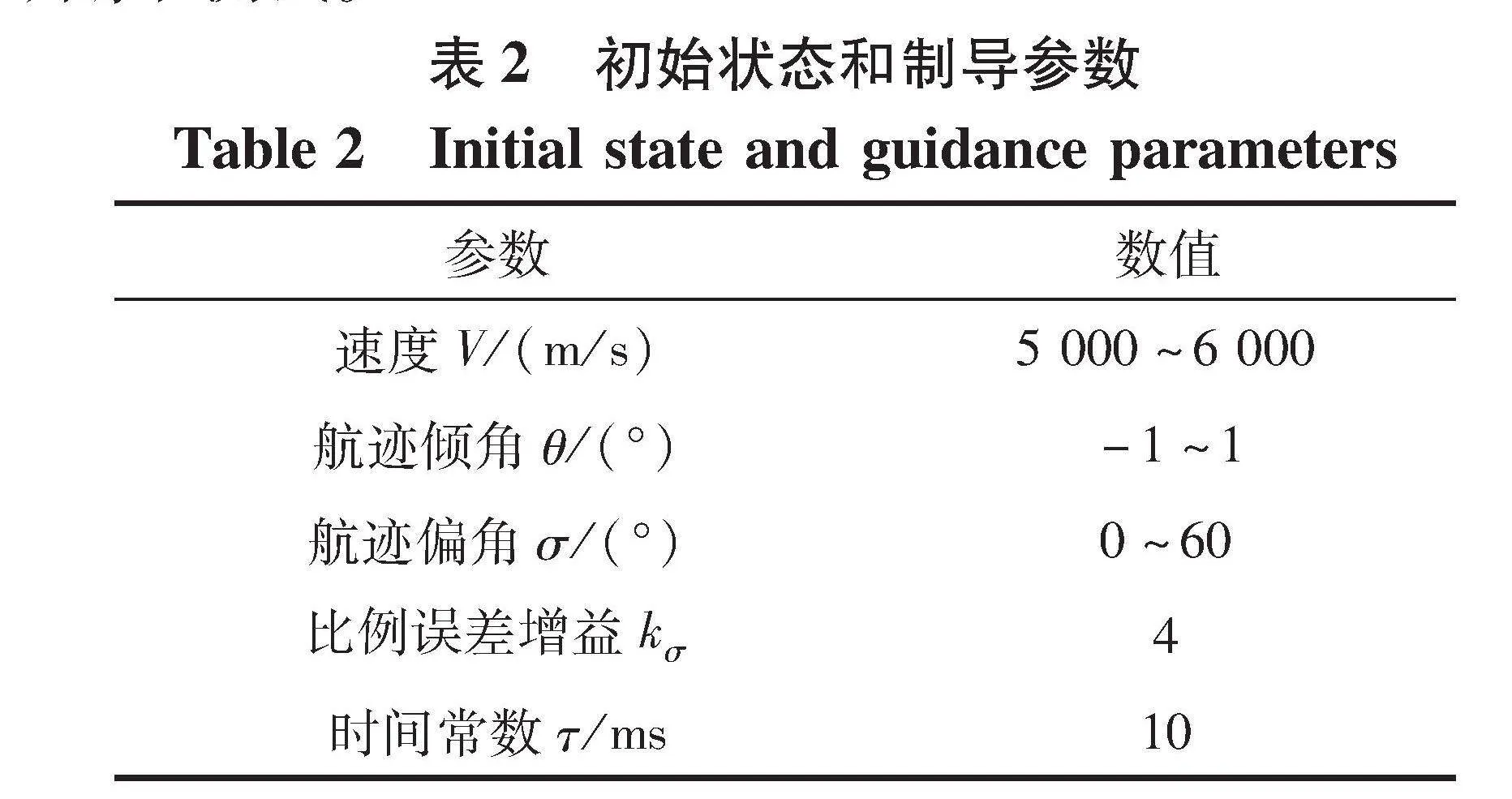
本节通过数值仿真验证所提出的基于中末制导交班点识别的轨迹预测算法性能。 采用文献［21］中讨论的高超声速飞行器为具体研究对象， 利用其相应的气动参数和结构参数进行三自由度准平衡滑翔制导仿真。 再入点的初始状态和准平衡制导算法中的参数如表2所示， 通过交叉组合不同的初始状态参数， 在目标飞行器准平衡滑翔至3个典型制导交班点的任务场景下， 共生成1 440条轨迹数据， 构成轨迹数据集。 将数据集中的轨迹样本按照8∶2划分为训练集（Training Set）和测试集（Test Set）， 对中末制导交班点识别网络和轨迹预测网络进行训练和测试。

5.1 中末交班点识别结果

根据跟踪过程中计算的特征序列对中末制导交班点进行识别， 图8～10展示了从再入点准平衡滑翔到3个典型制导交班点过程中800～1 200 s内各特征序列变化趋势。 因为目标飞行器是以准平衡滑翔弹道飞行至交班点， 所以各特征序列均为单调变化， 速度特征反映了飞行器的当前剩余能量状态， 航迹偏差角和剩余航程特征反映了飞行器准平衡滑翔的制导意图。 对比图8～10可以看出， 当目标制导到不同交班点时， 其速度变化大小不同； 表征航迹偏差角的特征序列在目标轨迹对应到相应交班点时逐渐收敛到0， 而与其他交班点的航迹偏差逐渐发散； 表征剩余航程的特征序列均在逐渐减小， 但滑翔至不同交班点的变化大小不同。 从长期来看， 当目标滑翔至某交班点时， 相对应的速度和剩余航程变化会下降更快。 综合以上特征序列可对目标滑翔轨迹做初步分类。

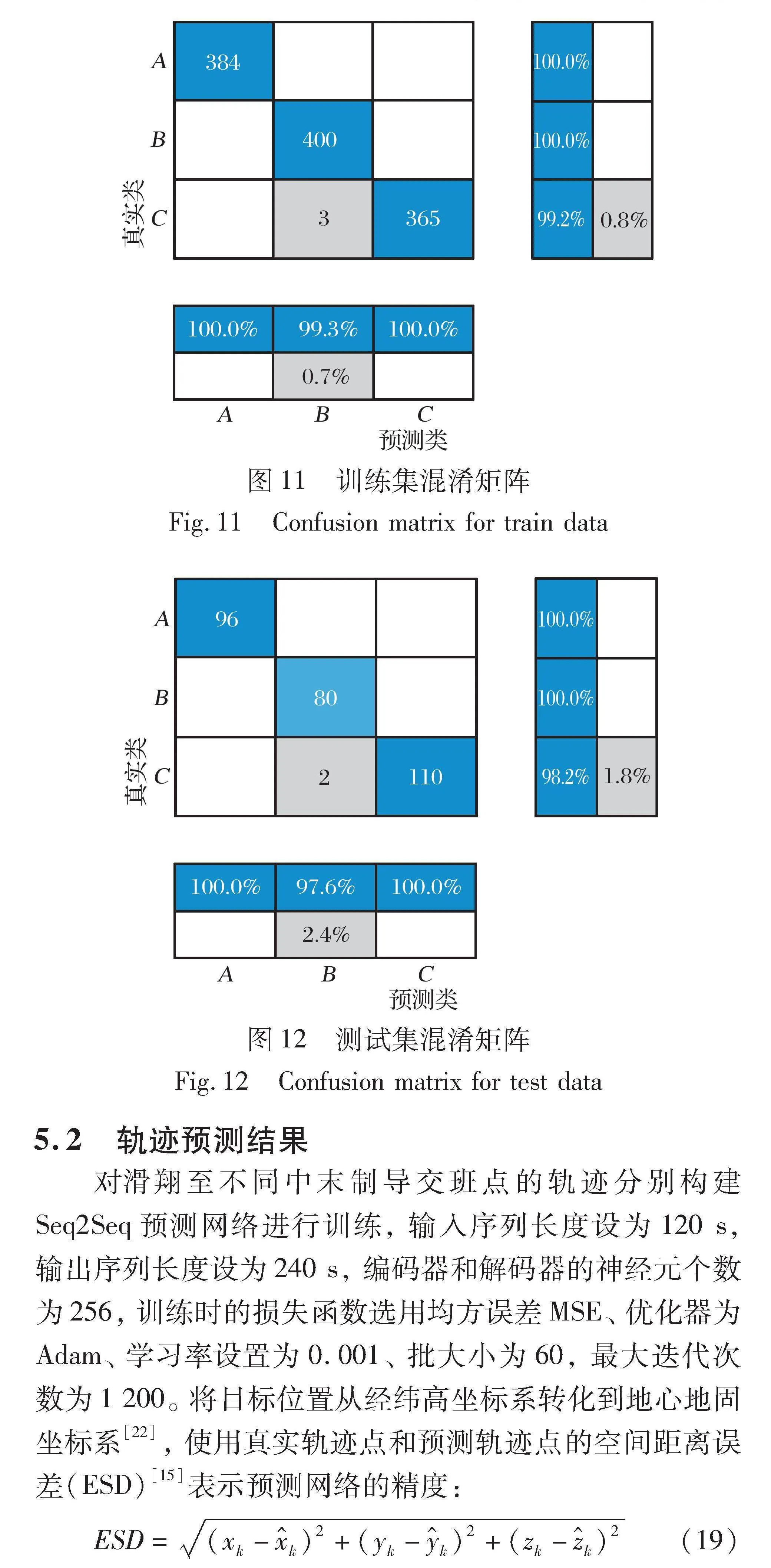
LSTM识别网络输入的特征序列长度设为120 s， Bi-LSTM层中神经单元个数为200， 训练时使用交叉熵损失函数、 优化器为Adam、 学习率设置为0.001、 批大小为60， 最大迭代次数为500。 采用分类准确率（ACC）作为交班点识别网络度量指标， 网络的分类性能用混淆矩阵表示。 从图11～12可以看出， 在此任务场景下， 网络分类效果显著， 在测试集中准确率达到98%以上， 可以有效识别场景中的中末制导交班点位置， 实现预测轨迹分类。

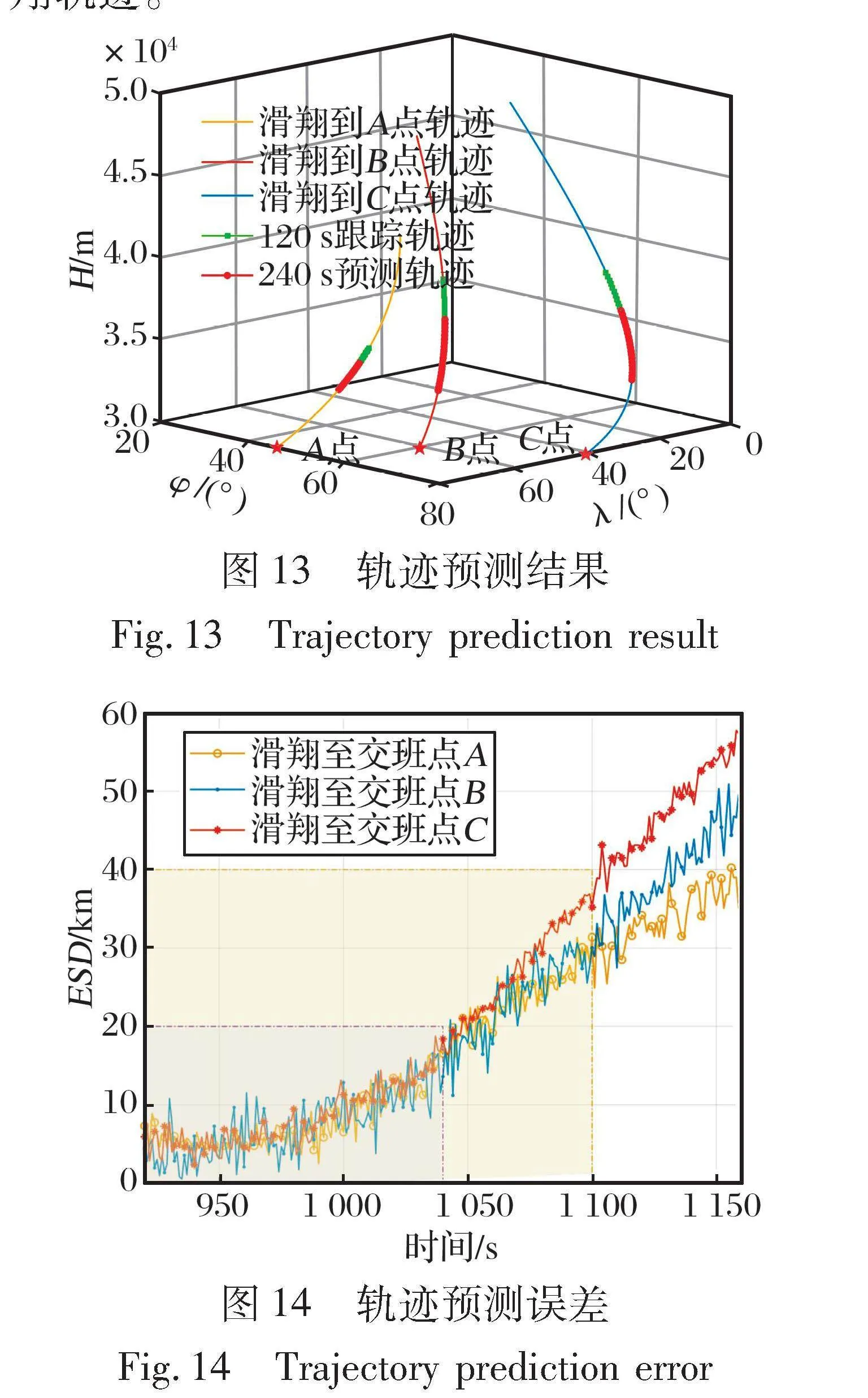
5.2 轨迹预测结果

对滑翔至不同中末制导交班点的轨迹分别构建Seq2Seq预测网络进行训练， 输入序列长度设为120 s， 输出序列长度设为240 s， 编码器和解码器的神经元个数为256， 训练时的损失函数选用均方误差MSE、 优化器为Adam、 学习率设置为0.001、 批大小为60， 最大迭代次数为1 200。 将目标位置从经纬高坐标系转化到地心地固坐标系［22］， 使用真实轨迹点和预测轨迹点的空间距离误差（ESD）［15］表示预测网络的精度：

ESD=（xk－x^k）2+（yk－y^k）2+（zk－z^k）2（19）

式中： （xk， yk， zk）和（x^k， y^k， z^k）分别为k时刻飞行器在地心地固坐标系下的真实轨迹坐标和预测轨迹坐标。

在对目标中末制导交班点位置准确识别的情况下， 目标飞行器的轨迹预测结果如图13～14所示。 从图14可以看出， 预测时间越短， 预测精度越高。 预测时长为120 s时， 轨迹误差均在18.77 km以内； 预测时长为180 s时， 轨迹误差在均36.91 km以内； 预测时长为240 s时， 轨迹误差均在57.75 km以内。 所提出的基于中末制导交班点识别的轨迹预测方法可以有效预测目标飞行器的准平衡滑翔轨迹。

5.3 与直接预测方法对比结果

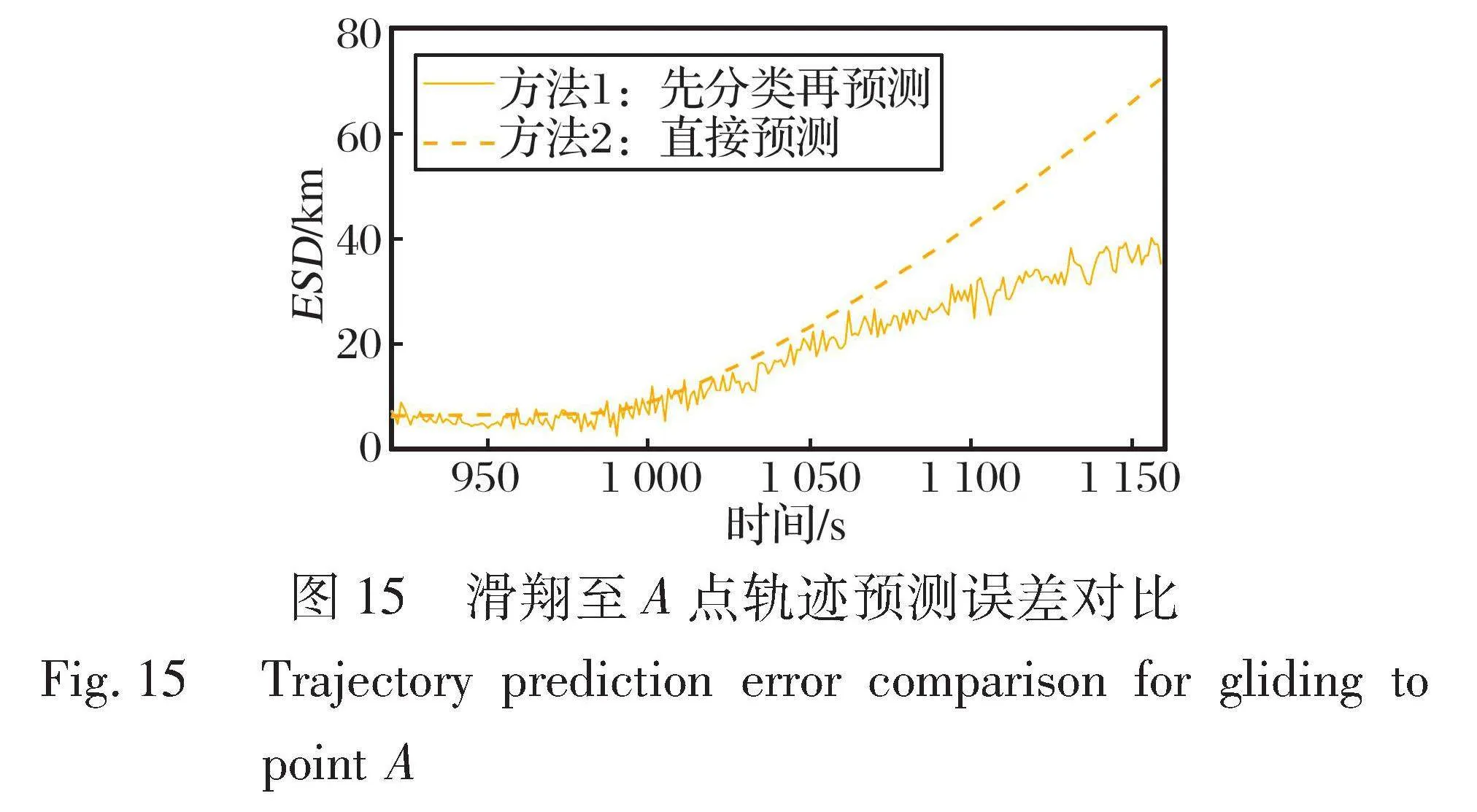
为验证中末交班点识别网络对后续轨迹预测精度的影响， 在不分类的情况下直接构建Seq2Seq预测网络进行训练， 网络的输入序列长度仍为120 s， 输出长度仍为240 s， 网络的结构参数和训练参数与5.2节设置相同。 在本文所构建的任务场景下， 基于中末制导交班点识别先分类再预测（方法1）的测试结果和直接预测（方法2）的测试结果对比如图15～17所示， 预测时长为120 s， 180 s和240 s时的平均预测误差（AESD）和最大预测误差（MESD）对比如表3所示。

从图15～17可以看出， 基于中末制导交班点识别先分类再预测的方法轨迹预测误差曲线存在波动， 而直接预测的方法由于利用目标飞行器准平衡滑翔至3个典型中末制导交班点的所有轨迹训练集训练深度学习网络， 其预测误差曲线较平滑。 相比于直接利用深度学习模型进行轨迹预测， 基于中末制导交班点识别先分类再预测的方法显著降低了轨迹预测误差， 且随预测时间增长， 先分类再预测的方法优势愈加明显。

从表3可以看出， 预测时长为120 s， 180 s和240 s时， 先分类再预测的方法使得平均轨迹预测误差降低了39.43%， 36.81%和37.61%， 最大预测误差降低了32.48%， 33.03%和37.34%。

6 结 论

针对高速高机动滑翔飞行器轨迹预测过程中任务场景定义不明确、 意图先验信息利用不充分等问题， 开展了基于中末制导交班点识别的轨迹预测方法研究。

（1） 提出一种基于中末制导交班点识别的滑翔轨迹分类方法， 分类准确率在98%以上， 可以有效识别典型任务场景下目标的制导意图。

（2） 基于中末制导交班点识别结果， 利用Seq2Seq网络实现了滑翔轨迹的长时预测。 预测时长为120 s， 180 s和240 s时， 轨迹误差分别在18.77 km， 36.91 km和57.75 km以内。 相比于直接预测的方法， 基于中末制导交班点识别的预测方法平均预测误差分别降低了39.43%， 36.81%和37.61%， 最大预测误差分别降低了32.48%， 33.03%和37.34%。

参考文献：

［1］ 兰旭辉， 熊家军， 张君彪， 等. 临近空间高超声速飞行器轨迹预测技术［M］. 武汉： 华中科技大学出版社， 2022： 1-5.

Lan Xuhui， Xiong Jiajun， Zhang Junbiao， et al. Trajectory Prediction Technology of Near Space Hypersonic Vehicle［M］. Wuhan： Huazhong University of Science and Technology Press， 2022： 1-5.（in Chinese）

［2］ 赵良玉， 雍恩米， 王波兰. 反临近空间高超声速飞行器若干研究进展［J］. 宇航学报， 2020， 41（10）： 1239-1250.

Zhao Liangyu， Yong Enmi， Wang Bolan. Some Achievements on Interception of Near Space Hypersonic Vehicles［J］. Journal of Astronautics， 2020， 41（10）： 1239-1250.（in Chinese）

［3］ 周池军， 李明杰， 雷虎民. 临近空间再入滑翔目标轨迹预测研究进展综述［J］. 飞航导弹， 2021（6）： 127-132.

Zhou Chijun， Li Mingjie， Lei Humin. Review on Research Progress in Trajectory Prediction for Near Space Reentry Gliding Target ［J］. Aerodynamic Missile Journal， 2021（6）： 127-132.（in Chinese）

［4］ 邵雷， 雷虎民， 赵锦. 临近空间高超声速飞行器轨迹预测方法研究进展［J］. 航空兵器， 2021， 28（2）： 34-39.

Shao Lei， Lei Humin， Zhao Jin. Research Progress in Trajectory Prediction for Near Space Hypersonic Vehicle［J］. Aero Weaponry， 2021， 28（2）： 34-39.（in Chinese）

［5］ 李广华. 高超声速滑翔飞行器运动特性分析及弹道跟踪预报方法研究［D］. 长沙： 国防科学技术大学， 2016.

Li Guanghua. Motion Characteristics Analysis and Trajectory Prediction for Hypersonic Glide Vehicles［D］.Changsha： National University of Defense Technology， 2016. （in Chinese）

［6］ 张洪波， 黄景帅， 李广华， 等. 典型控制规律滑翔飞行器的轨迹预测方法［J］. 现代防御技术， 2017， 45（4）： 112-118.

Zhang Hongbo， Huang Jingshuai， Li Guanghua， et al. Trajectory Prediction of Glide Vehicle Based on Typical Control Law［J］. Modern Defence Technology， 2017， 45（4）： 112-118.（in Chinese）

［7］ 李世杰， 雷虎民， 周池军， 等. 基于控制变量估计的高超声速再入滑翔目标轨迹预测算法［J］. 系统工程与电子技术， 2020， 42（10）： 2320-2327.

Li Shijie， Lei Humin， Zhou Chijun， et al. Trajectory Prediction Algorithm for Hypersonic Reentry Gliding Target Based on Control Variables Estimation［J］. Systems Engineering and Electronics， 2020， 42（10）： 2320-2327.（in Chinese）

［8］ 王路， 邢清华， 毛艺帆. 基于升阻比变化规律的再入高超声速滑翔飞行器轨迹预测算法［J］. 系统工程与电子技术， 2015， 37（10）： 2335-2340.

Wang Lu， Xing Qinghua， Mao Yifan. Trajectory Prediction of Reentry Hypersonic Glide Vehicle Based on Changing Rule of Lift-Drag Ratio［J］. Systems Engineering and Electronics， 2015， 37（10）： 2335-2340.（in Chinese）

［9］ 翟岱亮， 雷虎民， 李海宁， 等. 面向轨迹预测的高超声速飞行器气动性能分析［J］. 固体火箭技术， 2017， 40（1）： 115-120.

Zhai Dailiang， Lei Humin， Li Haining， et al. Trajectory Prediction Oriented Aerodynamic Performances Analysis of Hypersonic Vehicles［J］. Journal of Solid Rocket Technology， 2017， 40（1）： 115-120.（in Chinese）

［10］ 陈南华， 赵良玉， 雍恩米， 等. 变机动高超声速滑翔目标的轨迹序列预测算法［J］. 航空兵器， 2021， 28（2）： 40-48.

Chen Nanhua， Zhao Liangyu， Yong Enmi， et al. Trajectory Sequence Prediction Algorithm for Hypersonic Gliding Target with Variable Maneuver［J］. Aero Weaponry， 2021， 28（2）： 40-48.（in Chinese）

［11］ 胡星志， 王旭， 江雄， 等. 基于高斯过程回归的高超声速飞行器不确定轨迹预测［J］. 空天技术， 2022（4）： 49-61.

Hu Xingzhi， Wang Xu， Jiang Xiong， et al. Uncertain Trajectory Prediction of Hypersonic Flight Vehicles Based on Gaussian Process Regression［J］. Aerospace Technology， 2022（4）： 49-61.（in Chinese）

［12］ 李青勇， 何兵， 张显炀， 等. 基于LSTM的Encoder-Decoder多步轨迹预测技术［J］. 航空兵器， 2021， 28（2）： 49-54.

Li Qingyong， He Bing， Zhang Xianyang， et al. Encoder-Decoder Multi-Step Trajectory Prediction Technology Based on LSTM［J］. Aero Weaponry， 2021， 28（2）： 49-54.（in Chinese）

［13］ 杨春伟， 刘炳琪， 王继平， 等. 基于注意力机制的高超声速飞行器LSTM智能轨迹预测［J］. 兵工学报， 2022， 43（S2）： 78-86.

Yang Chunwei， Liu Bingqi， Wang Jiping， et al. LSTM Intelligent Trajectory Prediction for Hypersonic Vehicles Based on Attention Mechanism［J］. Acta Armamentarii， 2022， 43（S2）： 78-86.（in Chinese）

［14］ Zhang J B， Xiong J J， Lan X H， et al. Trajectory Prediction of Hypersonic Glide Vehicle Based on Empirical Wavelet Transform and Attention Convolutional Long Short-Term Memory Network［J］. IEEE Sensors Journal， 2022， 22（5）： 4601-4615.

［15］ 李明杰， 周池军， 雷虎民， 等. 基于控制参数估计的再入滑翔目标智能轨迹预测算法［J］. 系统工程与电子技术， 2023， 45（1）： 221-233.

Li Mingjie， Zhou Chijun， Lei Humin， et al. An Intelligent Tra-jectory Prediction Algorithm of Reentry Glide Target Based on Control Parameter Estimation［J］. Systems Engineering and Electro-nics， 2023， 45（1）： 221-233.（in Chinese）

［16］ 蔡远利， 邓逸凡， 苏悦华. 高超声速飞行器LSTM弹道分类与预报方法［C］∥ 第21届中国系统仿真技术及其应用学术年会， 2020： 311-315.

Cai Yuanli， Deng Yifan， Su Yuehua. LSTM Based Trajectory Classification and Prediction for Hypersonic Vehicle［C］∥ 21th China Conference on System Simulation Technology and its Application， 2020： 311-315.（in Chinese）

［17］ 宋波涛， 许广亮. 基于LSTM与1DCNN的导弹轨迹预测方法［J］. 系统工程与电子技术， 2023， 45（2）： 504-512.

Song Botao， Xu Guangliang. Missile Trajectory Prediction Method Based on LSTM and 1DCNN［J］. Systems Engineering and Electronics， 2023， 45（2）： 504-512.（in Chinese）

［18］ Li G H， Zhang H B， Tang G J. Maneuver Characteristics Analysis for Hypersonic Glide Vehicles［J］. Aerospace Science and Technology， 2015， 43： 321-328.

［19］ 包为民， 朱建文， 张洪波， 等. 高超声速飞行器全程制导方法［M］. 北京： 科学出版社， 2021.

Bao Weimin， Zhu Jianwen， Zhang Hongbo， et al. Full-Course Guidance Method for Hypersonic Vehicle［M］. Beijing： Science Press， 2021.（in Chinese）

［20］ Graves A. Supervised Sequence Labelling with Recurrent Neural Networks［M］. Berlin： Springer， 2012： 37-45.

［21］ Keshmiri S， Colgren R， Mirmirani M. Six DoF Nonlinear Equations of Motion for a Generic Hypersonic Vehicle［C］∥AIAA Atmospheric Flight Mechanics Conference and Exhibit， 2007.

［22］ 吴德伟. 导航原理［M］. 2版. 北京： 电子工业出版社， 2020.

Wu Dewei. Navigation Principle［M］. 2nd ed. Beijing： Publishing House of Electronics Industry， 2020.（in Chinese）

A Trajectory Prediction Method for High-Speed and

High-Maneuverability Glide Vehicle Based on Mid-Terminal

Guidance Handover Point Identification

Ma Kangkang1， Zhao Liangyu1， Hu Xingzhi2*， Li Mingjie2

（1. School of Aerospace Engineering， Beijing Institute of Technology， Beijing 100081， China；

2. Beijing Aerohydrodynamic Research Center， Beijing 100120， China）

Abstract： Addressing the challenges of unclear mission scenario definition and insufficient intent prior information utilization in the trajectory prediction process for high-speed and high-maneuverability glide vehicle， a trajectory prediction method for high-speed and high-maneuverability glide vehicle based on mid-terminal guidance handover point identification is proposed. Firstly， a mission scenario involving the gliding of high-speed and high-maneuverability vehicle towards multiple typical guidance handover points is constructed. A quasi-equilibrium glide guidance method is employed to generate trajectory datasets. Secondly， a guidance handover point recognition method based on long short-term memory network is proposed， utilizing tracking data to construct feature sequences for preliminary classification of glide trajectory. Finally， the self-attention mechanism is introduced to improve the feature extraction performance of sequence-to-sequence prediction networks， and encoder-decoder method is employd to predict the classified glide trajectory in the long term. Simulation results show that the trajectory prediction method based on mid-terminal guidance handover point identification exhibits high accuracy. For prediction times of 120 s， 180 s， and 240 s， the trajectory errors remain within 18.77 km， 36.91 km， and 57.75 km， respectively. Compared to directly utilizing a deep learning mo-del for prediction， the proposed prediction method demonstrates a reduction of 37.61% in average prediction error and 37.34% in maximum prediction error within a prediction time of 240 s.

Key words： high-speed and high-maneuverability vehicle; long short-term memory network; mid-terminal gui-dance handover point identification; trajectory prediction