基于深度强化学习的来袭导弹智能拦截与平台机动策略优化技术

摘 要： 目前空中作战环境日益复杂， 新作战方式对空中平台生存能力提出了巨大挑战， 需要采用新型硬杀伤手段来防御先进的空空导弹。 为了提升发射空空导弹拦截来袭导弹这一硬杀伤手段的胜率和效率， 提出了一种基于强化学习的载机平台智能机动策略和拦截弹发射策略。 首先， 设计了导弹威胁评估技术， 构建了仿真环境， 并确定了策略模型的状态和奖励函数； 其次， 通过设定不同的来袭空空导弹攻击角度和位置， 在不同载机平台姿态下， 训练了机动与拦截策略， 实现了对来袭目标的主动拦截和载机平台的有效机动。 实验表明， 相较于运筹学博弈策略5.8%的平均逃离概率， 使用基于强化学习的机动、 拦截策略后， 逃离概率可提升至56.8%； 同时， 拦截弹利用率提高了约13.3%， 且响应时间始终保持在24 ms以内。 设计的策略能够自适应不同数量的来袭导弹， 显著提高了载机平台的生存能力和对来袭导弹的拦截成功率， 并支持在空战多维状态空间中的持续优化。

关键词： 拦截弹； 机动策略； 强化学习； 拦截策略； 逃离概率； 响应时间； 空空导弹

中图分类号： TJ760

文献标识码： A

文章编号： 1673-5048（2024）05-0056-11

DOI： 10.12132/ISSN.1673-5048.2024.0045

0 引 言

随着新型战斗机、 新型空空导弹等空战武器装备技术的迅速发展， 以及远中近距等作战模式的不断涌现， 空中平台的防御难度大幅增加， 生存能力遭到了严峻的考验。 伴随空空导弹的机动能力和抗干扰能力的不断提升， 以干扰、 机动逃逸等为主要自卫手段的战斗机传统软防御手段的有效性大打折扣， 甚至面临失效风险， 故需要通过直接拦截来袭导弹等硬杀伤式防御来提升载机的生存能力。 在防御过程中， 来袭导弹的攻击空间运动受我方载机平台运动方式的制约， 载机平台、 来袭导弹、 拦截弹三分空间运动相互强耦合， 载机平台的机动策略将对主动拦截效果产生直接的影响。 因此， 载机平台需要采取智能博弈机动策略， 产生及时且高效的机动， 可以有效改变来袭导弹攻击弹道， 同时在博弈过程中， 载机平台采取智能化拦截弹发射策略， 适时发射一枚或多枚拦截弹进行硬式杀伤防御， 能够大幅提升载机平台的生存能力。

为持续优化机动与发射策略， 相关研究建模策略的优化模型， 采用动态规划与强化学习相结合的方式运行得到优化求解结果， 具体包括以下2个方面：

动态规划算法。 通过自适应动态规划（Adaptive Dynamic Programming， ADP）［1］、 神经动态规划（Neural Dynamic Programming， NDP）［2］等算法， 可用于贝尔曼方程求解［3］、 序贯决策［4］、 连续时间线性系统决策［5］、 未知非线性系统稳定决策［6］、 导弹制导决策［7］等。

强化学习算法。 通过基于模型的强化学习［8］、 基于高效扩散策略的离线强化学习［9］、 密集型强化学习［10］等算法， 可用于机器人连续高效控制［11-12］、 优化导弹的末端制导策略［13］、 整合和适应性制导及控制［14-15］、 空战目标分配决策［16-17］、 飞机路径规划［18］等。

虽然上述优化算法能在一定程度上解决特定场景的

收稿日期： 2024-03-12

作者简介： 吕振瑞（1987-）， 男， 宁夏吴忠人， 硕士， 高级工程师。

*通信作者： 司迎利（1985-）， 男， 甘肃静宁人， 硕士， 高级工程师。

优化问题， 但在面向策略优化的动态规划、 强化学习等算法设计中仍存在明显不足： 一方面， 这些算法难以在空战中直接使用， 如当前使用的最优控制策略［19］、 策略迭代方法［20］等均属于间接控制， 其实际优化效果依赖于预置的专家先验知识及其复杂的预处理过程， 由于策略需要多次迭代以收敛至最优策略， 在空战等复杂、 动态决策场景下面临高昂的计算成本， 同时也难以获得精确、 全面的空战专家知识； 另一方面， 这些算法在空战中的实际优化效果不足， 泛化性有限， 如当前使用的自适应PID［21］、 模型参考自适应［22］、 随机生成动作向量优化［23］、 在线自适应优化强化学习［24-26］、 非线性系统的实时优化［27］、 仿射非线性连续系统优化［28］、 ADP方法［29］、 改进型Actor-Critic网络和奖励函数［30］等均可提升动态规划、 强化学习算法性能， 但需要持续的在线学习和实时性能。 在处理高维度和连续动作空间时， 通常面临样本效率低和探索不足的挑战， 其优化效果和泛化能力会受到数据质量和多样性的限制， 难以有效应对新空战场景， 也难以在复杂、 动态空战场景下保障决策鲁棒性。

航空兵器 2024年第31卷第5期

吕振瑞， 等： 基于深度强化学习的来袭导弹智能拦截与平台机动策略优化技术

综上， 将动态规划、 强化学习等算法应用于空中平台防御尤其是硬杀伤式防御手段， 仍然面临许多挑战。 本文针对上述问题， 探索一种基于深度强化学习的智能化空中平台防御策略。 通过对策略迭代、 学习算法和奖励函数的改进， 提高载机平台的防御效果， 并在空战仿真环境中实验验证拦截的有效性。

1 载机平台动力学方程

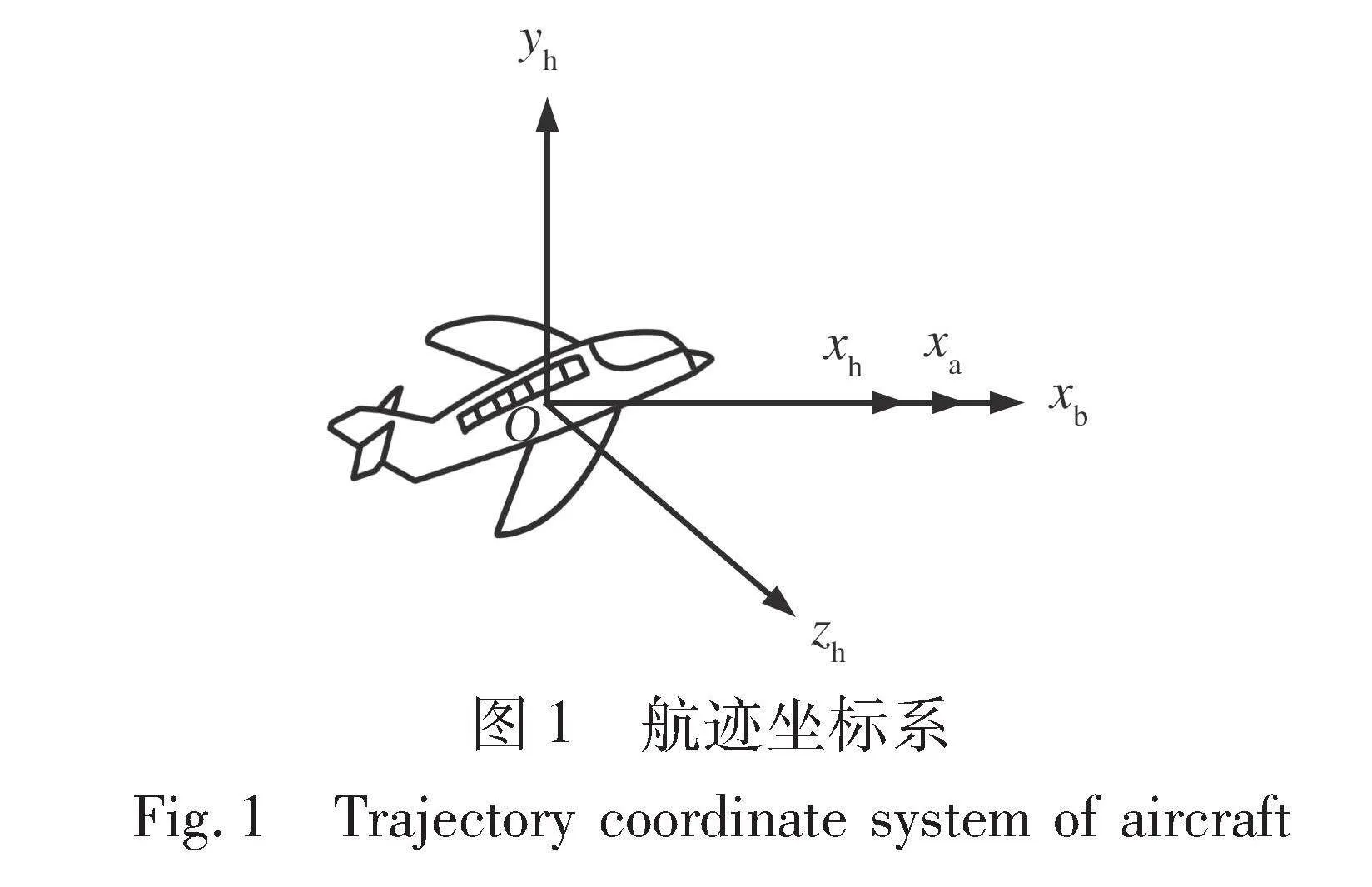
航迹坐标系的原点O固连于飞机的质心处。 Oxh轴沿飞机飞行速度方向， 向前为正； Oyh轴在通过Oxh的铅垂面内与Oxh轴垂直， 向上为正； Ozh轴垂直于Oxhyh平面， 指向飞机右向为正， 构成右手系。

切向过载nx： 角标x表示Oxh轴方向， 沿载机的飞行速度方向， 用于控制载机的水平轴向加速度， 取nxmax=2。

法向过载nf： 角标f代表法向， 表示垂直于飞机机翼平面和飞机飞行方向， 由速度方向垂直的ny与nz共同确定， nf=ny+nz， 取nfmax=Nmax， Nmax代表飞机的法向过载最大值。

载机的转弯坡度角： γs=arccos1nf， 角标s代表侧倾含义。

在载机航迹坐标系Oxhyhzh（见图1）下建立的载机3自由度质点动力学方程如式（1）所示。

V·=g（nx－sinθ）

θ·=gV（nfcosγs-cosθ）

ψ·s=－gVcosθnfsinγs（1）

假设载机做无侧滑运动， 忽略载机侧滑角的影响， 则侧滑角β为零， 侧力F为零。

忽略载机迎角的影响， 则迎角α为零， 俯仰角等于航迹倾斜角θ与迎角α之和， 则θ =。

假设载机运动时不计风速， 则航迹坐标系的Oxh轴、 速度坐标系的Oxa轴与机体坐标系的Oxb轴一致， 即γs=γ， ψs=ψ。

假设载机质量m为常数， 且重力加速度g不随飞行高度的变化而变化。

2 来袭导弹威胁能力评估

来袭空空导弹目标威胁评估的目的是明确来袭空空导弹目标对载机是否构成威胁， 以及威胁程度的大小， 然后按威胁程度排序。 针对拦截来袭导弹的空战场景， 来袭导弹包括角度、 距离和速度3方面威胁， 并对这些威胁进行量化计算， 通过模糊理论［31］进行加权平均， 计算出最终的威胁系数。

2.1 威胁模型建模

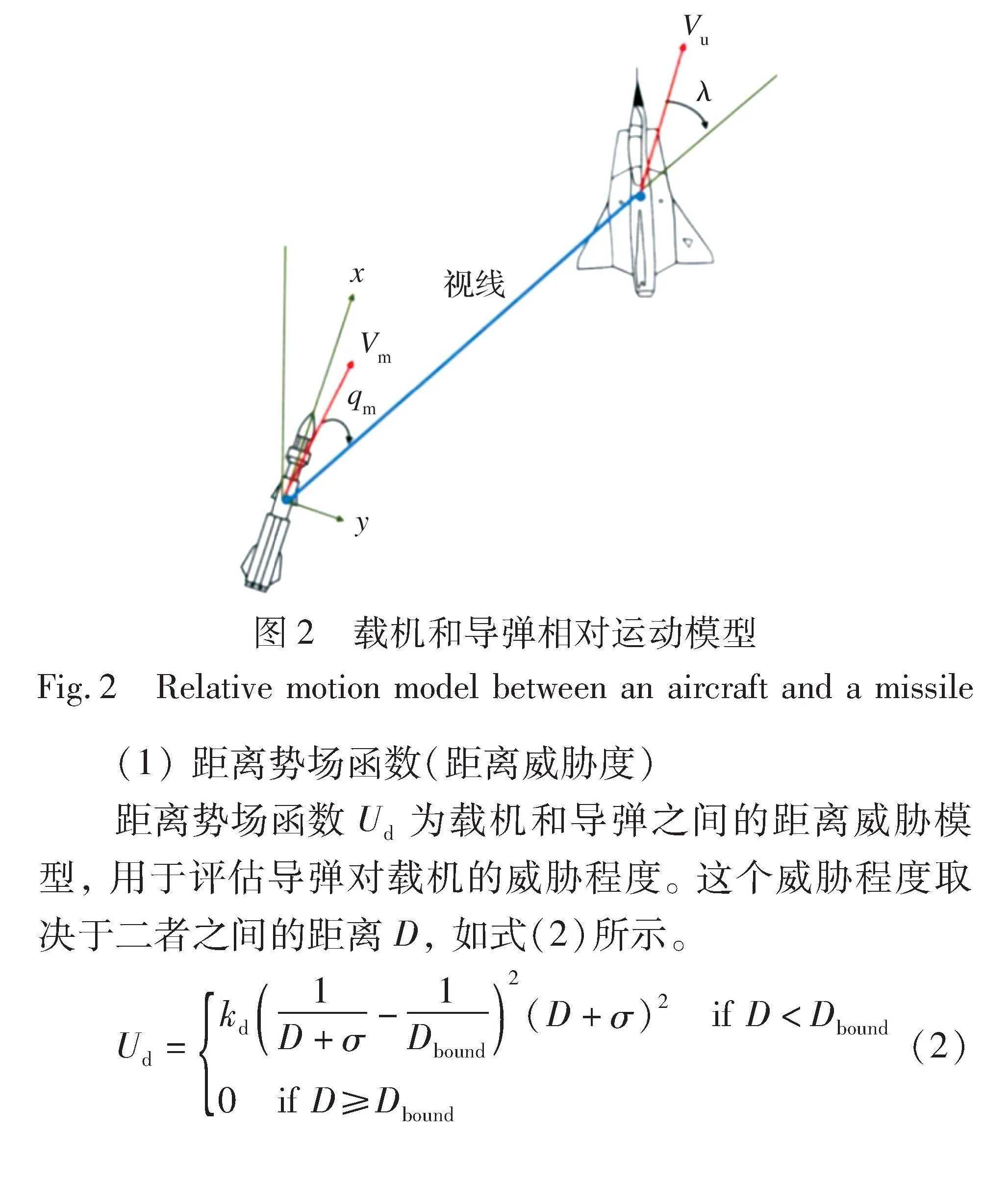
来袭导弹威胁度超实时评估模型的建模依赖于载机和来袭导弹的相对运动模型， 本文采用距离-角度-速度势场函数。 如图2所示， 来袭导弹弹体的重心与载机重心的连线定义为视线； 来袭导弹弹体的正方向与视线的夹角称为来袭导弹的进入角qm； 来袭导弹的速度矢量为Vm； 载机的速度矢量为Vu。

（1） 距离势场函数（距离威胁度）

距离势场函数Ud为载机和导弹之间的距离威胁模型， 用于评估导弹对载机的威胁程度。 这个威胁程度取决于二者之间的距离D， 如式（2）所示。

Ud=kd1D+σ－1Dbound2（D+σ）2 if D<Dbound

0 if D≥Dbound （2）

D=x2+y2+z2（3）

式中： kd为正的系数； D为导弹与载机的距离； x， y， z为分别表示载机与导弹在x， y， z三维坐标轴上的坐标差； σ为小量（防止分母为0和乘数为0， 造成（0， 0）点突变）； Dbound为距离边界， 即导弹最大攻击范围， 大于此值， 威胁度为0。

距离威胁值随载机与来袭导弹相对距离变化的函数如图3所示， 红色线条表示D<Dbound条件下的距离威胁值， 绿色线条表示D≥Dbound条件下的距离威胁值， 即我方载机在来袭导弹攻击区外的范围， 此时威胁值为0。

在载机规避导弹问题中， 由于距离势场函数考虑高度的影响， 而载机爬升性能并没有导弹强， 来袭导弹在发射后， 急速提高速度， 短期速度增加能力比载机高。 因此， 使用距离势场函数时， 可以去掉高度的影响， 即D=x2+y2。

（2） 进入角的势场函数（角度威胁度）

来袭导弹对载机的威胁不仅可以从距离角度考虑， 也可以从导弹进入角（导弹速度方向与视线方向的夹角）考虑。 设导弹进入角为qm， 导弹速度为vx， vy， vz， 下标x， y， z表示导弹速度矢量在三维坐标轴x， y， z轴上的分解。 同样不考虑高度的影响， 导弹进入角计算公式如下：

cosqm=Vm·P|Vm|·|P|=xvx+yvyx2+y2·v2x+v2y（4）

式中： Vm为导弹速度矢量； P为载机与导弹的视线矢量。

导弹进入角的势场函数如式（5）所示。

Ua=ka·1qm+σ－11802·（qm+σ）2 if D<Dbound

0 if D≥Dbound（5）

式中： ka为正的系数， 下标a表示“角度”。 角度威胁值随载机与来袭导弹相对角度变化的函数如图4所示， 图中绿色线条表示式（5）在D<Dbound条件下的角度威胁值， 黄色线条表示D≥Dbound条件下的角度威胁值。 随着进入角变小， 角度威胁值呈对数趋势下降。 当进入角大于来袭导弹的最大攻击范围时， 角度威胁值为0。

（3） 速度威胁度

速度威胁度是一个根据导弹相对于载机的速度计算得到的值， 它用来量化导弹的速度对载机的威胁程度。 速度威胁度的计算根据相对速度的不同区间而变化， 具体定义如式（6）所示。

TS=

1 if vivj>1.5

-0.5+vivj if 0.6<vivj≤1.5

0.1 ifvivj≤0.6 （6）

式中： vi为来袭导弹的预估速度； vj为我方载机的预估速度。 我方载机相对于来袭导弹的运动速度越大， 则受威胁程度越低。 速度威胁值随载机与来袭导弹相对速度变化的函数如图5所示， 图中绿色线条表示vivj≤0.6条件下的速度威胁值， 紫色线条表示0.6<vivj≤1.5条件下的速度威胁值， 红色线条表示vivj>1.5条件下的速度威胁值。

2.2 威胁值计算

本文使用实时环境数据计算出的三个威胁值， 通过层次分析法（AHP）输出的权重矩阵完成综合威胁值的计算， 然后， 根据专家经验设立置信区间， 从而为飞行员实时提供威胁值的等级评价。

综合威胁值的计算公式如式（7）所示。

T=ρ1Ua+ρ2Ud+ρ3TS（7）

式中： ρ1+ρ2+ρ3=1。

式（7）表示我方载机的总体受威胁态势为角度威胁态势、 距离威胁态势与速度威胁态势的加权求和。 总体受威胁态势越大， 则我方载机被来袭导弹击中的几率越大； 反之， 总体受威胁态势越小， 我方载机被来袭导弹击中的几率越小。

AHP方法通过将威胁值中的角度威胁、 速度威胁和距离威胁进行两两比较， 建立成对比较矩阵的方法， 进行比较。 矩阵中的一个值表示行列两个因子对某因素的影响大小， 称为成对比较判断矩阵， 简称判断矩阵。

本文使用的判断矩阵如表1所示。

在层次分析法中， 判断矩阵经归一化处理后， 生成的权重即表示同一层次内不同因素对于上一层次某因素的相对重要性， 这个过程称为层次单排序。 为确保模型的准确性， 进行一致性检验。 一致性检验是为了验证判断矩阵的合理性。 如果判断矩阵未通过一致性检验， 则需要返回上一步重新构建判断矩阵， 直到通过一致性检验为止。 一致性指标和随机一致性比率的计算依赖于AHP中的随机一致性指标表［31］。

在实际的实验仿真中， 根据所提供的判断矩阵并通过一致性检验后， 本文确定的权重值如下： 角度威胁态势的权重ρ1为0.085， 速度威胁态势的权重ρ2为0.148， 距离威胁态势的权重ρ3为0.767。 这些权重反映了综合威胁值计算中各因素的相对重要性。

将ρ1， ρ2， ρ3作为权重矩阵的输出， 将其与3个威胁值Ua， Ud， TS点乘， 即可得到综合威胁值。

3 载机平台机动与拦截策略优化

深度强化学习可以自动提取高效特征， 便于实现端到端的策略生成。 机动策略模块和拦截策略模块都使用深度强化学习的方法来生成策略。

3.1 强化学习

强化学习的输入数据为环境向量和动作向量， 对于一般问题， 每一个时刻选取的动作可以是任意的， 每个动作间没有强关联的信息。 但对载机平台， 后一刻的动作和前一刻的动作是相关的， 在前一刻使用的动作， 后一刻许多动作就不能立即使用， 需要通过其他中间机动进行过渡。 例如， 将俯仰角或过载降为一个合适的数值， 才能满足机动的要求。 在利用强化学习生成载机平台机动策略过程中， 需首先将动作库的限制全部实现， 才能保证学习过程合理高效， 防止无效动作的产生。

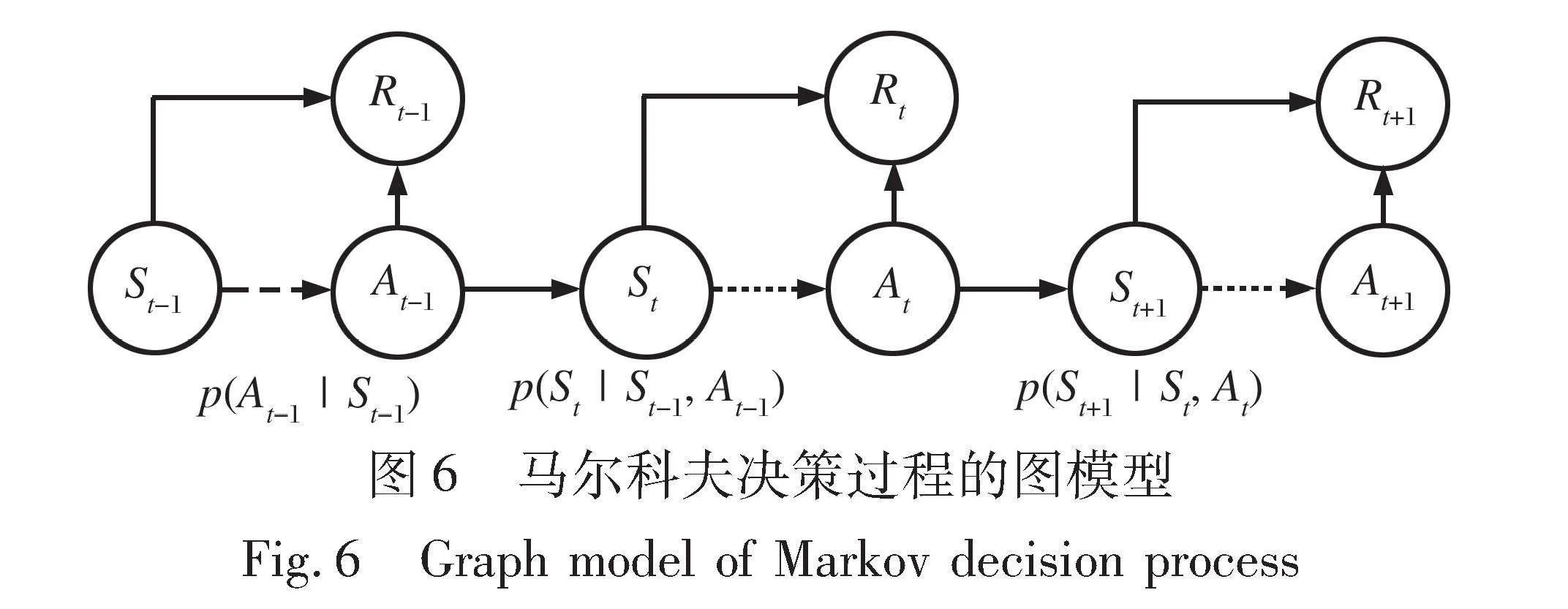
实现载机平台机动策略和智能化拦截策略的强化学习过程， 都基于马尔科夫决策过程（Markov Decision Process， MDP）， 其立即奖励与状态和动作都有关， 如图6所示。 给定一个状态下的一个动作， 马尔可夫决策过程的下一个状态不固定唯一。

作为空中机动策略的动作空间具有高维、 连续性强的特征， 使用传统的表格式强化学习难以设计高质量、 高效的特征进行学习。 使用深度强化学习方法， 利用人工神经网络对空战环境的向量进行特征提取， 并根据奖励函数提供的TD-target信息进行梯度的更新。

基于值函数的DRL是采用了深度神经网络（Deep Neural Network， DNN）的逼近奖励值函数。 类似地， 用DNN逼近策略并利用策略梯度方法求得最优策略， 被称为基于策略梯度的DRL。

值函数是RL中的基本概念， 时间差分学习（TD Learning）和Q学习 （Q-learning）则分别是学习状态值函数和动作值函数的经典算法。 本文的载机平台机动与智能拦截策略基于值函数的强化学习算法， Q-learning是经典的值强化学习算法。

Q-learning运用历史存放的经验来学习。 如果状态和动作空间是离散而有限的， 学习趋近于无限次（即学习率的和趋近于无穷大）， 此时可以收敛到最优策略Q（学习率的二次和趋近于无穷大）。 对于单步的SARSA （state- action-reward-state′-action′）算法， 不管采用epsilon贪婪策略还是贪心策略， 都证明能收敛到Q， 即

Q^（s， a）←Q^（s， a）+α［（r+γmaxa′Q^（s′， a′））－Q^（s， a）］（8）

式中： 左侧取值表示当前状态-动作对的Q值， 代表在状态s下采取动作a的预期效用； 右侧表示Q^（s′， a′）下一个状态-动作对的Q值， 这是在下一个状态s′采取动作a′的效用； α是学习率， 它决定了新信息取代旧信息的程度， 其值为0意味着智能体不学习任何东西， 而其值为1则意味着智能体仅考虑最新的信息； γ表示折扣因子， 它量化了对未来奖励的重视程度， 其值为0会使智能体短视， 只考虑当前奖励， 而接近1的值会使其追求长期的高额奖励。

估计准确的值函数是基于值的强化学习算法的核心。 时间差分（Temporal Difference， TD）是强化学习中估计值函数的一个核心方法， 它结合了动态规划和蒙特卡洛方法的思想。 与动态规划相似， 时间差分在估算的过程中使用了自举法， 但它和蒙特卡洛一样， 不需要在学习过程中了解环境的全部信息。

时间差分利用差异值学习， 即目标值和估计值在不同时间步上的差异。 使用自举法的原因是它需要从观察到的回报和对下一个状态的估值中来构造目标。 具体来说， 最基本的时间差分使用式（9）进行更新。

V（St）←V（St）+α［Rt+1+γV（St+1）－V（St）］（9）

该方法称为TD（0）， 或者是单步TD。 也可以通过将目标值改为在N步未来中的折扣回报和N步过后的估计状态价值来实现N步TD。 时间差分的目标值可以在每一步都算出， 也就意味着它每一步都可以学习。 由于学习是来自状态转移的信息， 而不需要具体动作信息， 其在实践中往往收敛得更快。

与直接使用真实Reward估计作为值函数的优化目标相比， 时间差分算法在每一步都可以学习， 进行实时的机动动作选取， 并预测下一刻的近似空战博弈状态。 根据预测结果和真实结果， 更新网络参数， 从而完成对更高奖励动作的更准确估计。 整个过程递归执行。

在此基础上， 本文设计了深度神经网络用于拟合值函数， 并使用时间差分法构造神经网络的损失函数。

3.2 奖励函数设计

距离奖励： 在规避过程中， 导弹与载机的距离越大， 载机获得的奖励就越高， 鼓励载机向远离导弹的方向机动。 距离优势分两部分进行整合， 包括相对距离的改变与初始距离相比所带来的优势奖励， 以及相对距离改变得到的绝对奖励。 初始距离奖励定义如式（10）所示。

rd0=C1×D/D0（10）

式中： D0为载机与导弹的初始距离； D为初始距离奖励函数自变量， 表示来袭导弹和载机之间的距离； C1为初始距离奖励的权重系数， 用于调整初始距离奖励在整体奖励函数中的重要性， 本文的实验中选取C1=10。

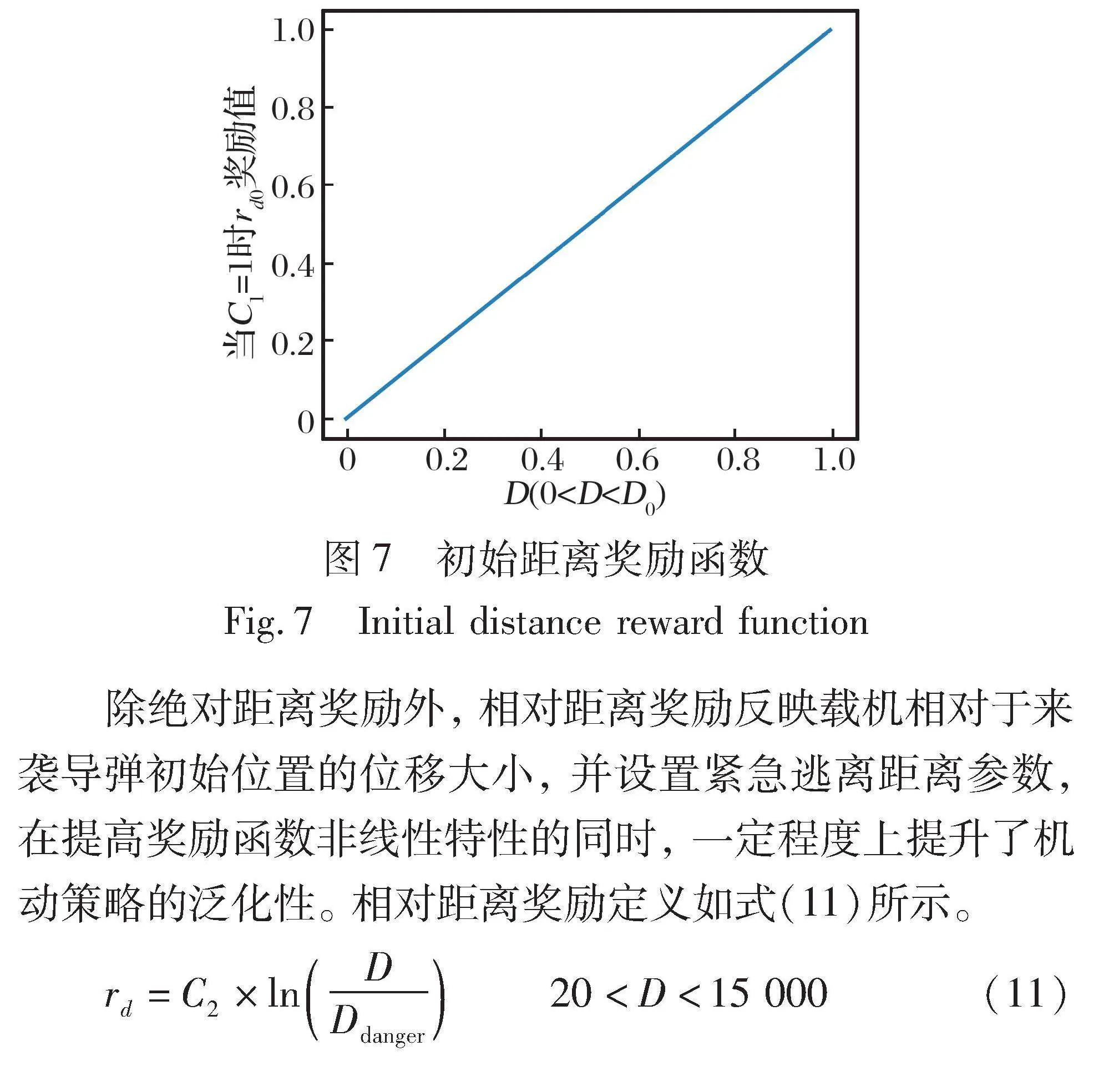
初始距离奖励值随载机与来袭导弹的距离变化函数如图7所示。 由于载机平台的机动能力与来袭导弹间存在差距， 所以本文只考虑博弈过程中来袭导弹与载机之间相对距离D， 相对于初始距离D0， 初始距离始终较大， 即0<D<D0， 表明载机平台一定被导弹追踪并且接近的情况。 初始距离奖励反映一个单位时间内， 载机位置的危险程度。 在其他环境条件不变的情况下， 若载机与来袭导弹的初始距离大， 则说明载机处于一种相对安全的状态。

除绝对距离奖励外， 相对距离奖励反映载机相对于来袭导弹初始位置的位移大小， 并设置紧急逃离距离参数， 在提高奖励函数非线性特性的同时， 一定程度上提升了机动策略的泛化性。 相对距离奖励定义如式（11）所示。

rd=C2×lnDDdanger 20<D<15 000（11）

式中： Ddanger为来袭导弹距离载机呈危险态势的经验值， 设置为2 000 m； C2为相对距离奖励的权重系数， 用于调整相对距离奖励在整体奖励函数中的重要性， 本文实验中选取C2=10。 相对距离奖励的函数如图8所示。

威胁度奖励： 在规避过程中， 选取威胁度最大的导弹作为当前的威胁值奖励， 威胁越大， 惩罚（负奖励）就越大。 因为威胁度是综合评价标准， 载机的机动策略主要的目标就是要在一定时间内降低威胁度， 所以利用威胁度对载机机动的趋势进行指引， 具体如式（12）所示。

rT=C3×max（Ti） i∈index（missiles） if Tit>Ti（t－1）

C4×max（Ti） i∈index（missiles） if Tit≤Ti（t－1） （12）

式中： 当前时刻下的威胁值Tit比上一时刻的威胁值Ti（t－1）小时， 可获得一个正的奖励； 反之则给一个负的奖励（惩罚）； C3为威胁度惩罚权重系数， 值小于0， 用于调整威胁度惩罚在整体奖励函数中的重要性， 本文的实验中选取C3=－20； C4为威胁度奖励的权重系数， 用于调整威胁度奖励在整体奖励函数中的重要性， 本文的实验中选取C4=5。

机动不合规惩罚： 在机动策略的训练中， 由于经验是通过随机动作选取的， 所以不可避免地会出现与限制条件相冲突的动作， 在这种情况下， 需要给一个惩罚（负奖励）， 降低机动不合规出现的概率。

rp=C5（13）

式中： C5为机动不合规惩罚， 作为一个可以调整的超参数， 调整C5可以调整机动不合规惩罚对于整体奖励函数而言的重要性， 本文中取C5=－100。

稀疏奖励： 当博弈结束时， 查看结束标志， 如果机动躲避成功， 则获得一个正的大奖励， 如果被击中， 则获得一个负的大惩罚。

rs=C6 if escapeFlag=1

-C6 if escapeFlag=0（14）

式中： C6为稀疏奖励的绝对值， 作为一个可以调整的超参数， 调整C6可以调整稀疏奖励对于整体奖励函数的重要程度。

智能化拦截弹发射策略的奖励函数需要在机动策略的基础上， 增加与拦截弹相关的奖励与惩罚， 能够激励拦截弹正确发射， 同时避免拦截弹不必要的浪费。

拦截弹威胁奖励： 通过计算拦截弹对其锁定的来袭导弹的威胁度来计算一个奖励值， 拦截弹对其锁定的来袭导弹的威胁度越高， 总的奖励值越大。 当拦截弹试图拦截发射范围之外的来袭导弹时， 发射奖励为0。 此奖励随着拦截过程的进行， 实时计算威胁度并更新， 以此实现拦截弹发射策略根据上一刻打击效果自适应推演能力。 定义如式（15）所示。

rI.T=C7∑i∈I， j∈MTi（mj） if d（I.T）<Ibound and I.T=j

0 if d（I.T）≥Ibound and I.T=j （15）

式中： Ibound表示拦截弹的拦截边界， 即最大距离； 对于每个拦截弹I（Interceptor）， I.T为拦截弹I锁定导弹的索引， d（I.T）为拦截弹I与I.T号来袭导弹的距离。 式（15）表示当拦截弹锁定的来袭目标距离d（I.T）小于拦截弹的最大拦截距离且I.T=j时， 给予奖励。 C7为拦截弹威胁奖励的权重系数， 用于调整拦截弹威胁奖励在整体奖励函数中的重要性， 本文的实验中选取C7=10。

拦截威胁度奖励的函数如图9所示， 图中蓝色线条表示d（I.T）<Ibound以及 I.T=j条件下的拦截弹威胁奖励值， 黑色线条表示d（I.T）≥Ibound以及I.T=j条件下的拦截弹威胁奖励值。

剩余拦截弹奖励： 载机的载弹量是评价战机性能的重要指标， 由于携带的导弹过多会影响载机的机动性能。 在空战中， 携带的导弹是重要的战斗资源， 所以在拦截过程中， 需要节约拦截弹资源， 在成功拦截来袭目标基础上， 发射尽量少的拦截弹。 随着拦截过程的进行， 实时更新拦截弹总体的数量状态， 以此实现智能拦截弹发射过程， 在与来袭导弹的博弈过程中不断调整更新能力， 如式（16）所示。

rIR=C8∑i∈I1 if I.Attacking=－1（16）

式中： 拦截弹的Attacking标志位为-1， 即式中的I.Attacking=－1， 表示随载机飞行， 即挂载在载机上。 载机当前挂载的拦截弹越多， 剩余拦截弹奖励越大。 C8代表剩余拦截弹奖励的超参数， 用于调整剩余拦截弹奖励在总体奖励中的权值比例， 本文中取C8=0.5。

对于每个拦截弹， I.Attacking表示拦截弹I的随机飞行标志。 I.Attacking=-1， 表示随载机飞行； I.Attacking=0表示已经发射， 用于拦截来袭导弹。

表2展示了所有奖励的取值范围。

3.3 策略训练过程

训练参数初始化： 初始化两个完全相同的人工神经网络， 一个人工神经网络代表动作选取的在线人工神经网络， 另一个用于平滑训练的目标网络。 每隔一段时间， 将在线网络的参数全部赋值给目标网络。

智能化机动与拦截策略训练结构如图10所示， 使用目标网络技术降低DQN的估计误差。 目标网络实现打乱

相关性的机制， 会使DQN中出现两个结构完全相同但参数不同的网络， 预测Q估计的网络在线人工神经网络使用的是最新的参数， 而预测Q现实的神经网络目标网络参数使用的是旧参数， 表示当前网络在线人工神经网络的输出， 用来评估当前状态动作对的值函数。 引入目标网络后， 在一段时间里目标Q值保持不变， 可在一定程度降低当前Q值和目标Q值的相关性， 提高了算法稳定性。

3.4 算法改进

均方差裁剪机制： 为了避免训练过程中的梯度爆炸现象， 对平方误差进行裁剪， 这等同于将均方误差替换成δ=1情况下的Huber损失。 Huber损失如式（17）所示。

Lδ（x）=12x2 x≤δδx－12δ 其他 （17）

鼓励探索机制： 使用Noisy DQN向动作价值函数中引入一种噪声， 以一种可控的方式来探索更多的动作。 Noisy DQN通过在神经网络的输出层中引入一个随机噪声变量， 训练时生成具有一定随机性的动作价值函数。 噪声变量是可学习的参数， 其值由神经网络自适应地学习和更新， 而噪声在预测时被去除， 从而提升策略的鲁棒性。 Noisy DQN能够在保持动作价值函数的确定性和准确性的同时， 探索更多的动作， 从而提高算法的稳定性。 训练伪代码如算法1所示。

算法1： Noisy Double DQN算法

输入： Env为博弈环境； Nf为列表x的最大长度； ε为网络随机变量的集合； B为经验回放缓存； ζ为初始化网络参数； ζ－为初始化目标网络参数； NB为经验回放缓存大小； NT为训练的小批量大小； N－为更新目标网络的频率。

输出： Q（.， ε; ζ）为状态-动作价值函数

1： For episode e∈{1， 2， …， M}do

2： x←［］ /* x为状态向量列表

3： 初始化状态序列x0～Env

4： x［0］←x0

5： For t∈{1， 2， …}do/*l［－1］为列表l的最后一个元素

6： Set x←x［－1］

7： 从噪声网络中采样ξ～ε

8： 选取一个动作a←arg maxb∈A Q（x， b， ξ; ζ-）

9： 抽样下一状态y～P（·|x， a）， 获取奖励r←R（x， a）， 给x增添元素x：x［－1］←y

10： if |x|>Nf then

11： 删除x中最旧的元素

12： end if

13： 将元组（x， a， r， y）加入回放缓存B［－1］←（x， a， r， y）

14： if |B|>NB then

15： 删除B中最旧的元素

16： end if

17： 从回放记忆中均匀随机采样一个batch的转换样本数据（（xj， aj， rj， yj）～D）NTj=1

18： for j∈{1， 2， …， NT} do

19： 从噪声网络中采样ξj～ε

20： 从目标噪声网络中采样ξ′j～ε

21： if y是一个终止状态then

22： yj←rj

23： else

24： yj←rj+maxb∈AQ（yj， b， ξ′j～ε）

25： 以（yj－Q（xj， aj， ξj; ζ））2作为损失函数进行梯度下降

26： end if

27： if t≡0（mod N－）then

28： 更新目标网络： ζ－←ζ

29： end if

4 仿真分析

4.1 强化学习算法结果分析

训练深度策略模型的超参数如表3所示。

机动与拦截策略步均Reward值如图11所示， 其横坐标表示训练的迭代序号， 纵坐标表示当代模型在一局博弈中获取的步均奖励值。 在训练初期处于低位， 随着训练的进行逐渐处于高位且平稳， 并保持每一步的回报基本在10左右。 步均Reward的曲线用滑动平均值进行平滑， 实验中的滑动窗口取值为20。 阴影部分表示滑动值与真实值的差距。

步均Reward反映的是智能体每一步对整个博弈过程的影响程度， 主要是对普通奖励（即过程奖励）的效果反映。 在训练初期， 步均Reward处于低位， 并且震荡很大， 说明此时模型的状态不稳定， 效果不佳， 主要原因在于经验回放缓存获取的数据量不够。 当数据量达到一定数量时， 模型效果显著提升， 反映在曲线上的10 000次迭代， 此时经验回放缓存获取的数据量已经可以使模型获得比较好的效果。 但是， 由于训练量不够， 此时模型参数还不稳定； 当继续训练到50 000次迭代， 模型的震荡明显下降， 此时的步均Reward也趋于一个高的稳定位置， 说明模型训练取得了好的结果， 策略使得智能体每一步都能获取到一个相对稳定且较高的奖励。

机动与拦截策略每局评估的Reward值如图12所示。 与平均Reward值类似， 横坐标表示训练的迭代序号， 纵坐标表示当代模型在一局博弈中获取的奖励值。 局均Reward值比步均Reward过渡得更平滑， 每一局的Reward平均在8 000～9 000左右。

局均Reward反映的是智能体每一局（即每一次博弈）的整体效果， 包括普通奖励（即过程奖励）和稀疏奖励。 使用了与步均Reward曲线相同的滑动平均方法。 相对于步均Reward， 在训练初期， 局均Reward处于低位， 并且震荡更大， 说明此时模型的状态不稳定， 每次博弈产生的结果随机性很大； 当达到一定数据量时， 模型效果显著提升， 反映在曲线上的10 000次迭代， 此时经验回放缓存获取的数据量可以使模型获得比较好的效果， 但主要是改进了过程奖励的效果， 而对于稀疏奖励而言， 模型还不够稳定； 当继续训练到50 000次迭代， 模型的震荡明显下降， 所得到的局均Reward也趋于一个高的稳定位置， 证明此时模型的稀疏奖励也回归到一个相对稳定的值上， 说明模型训练取得了好的结果， 策略使得智能体每一局都能获取到一个稳定的奖励， 并且使智能体在博弈过程中能够取得一个相对大的奖励。

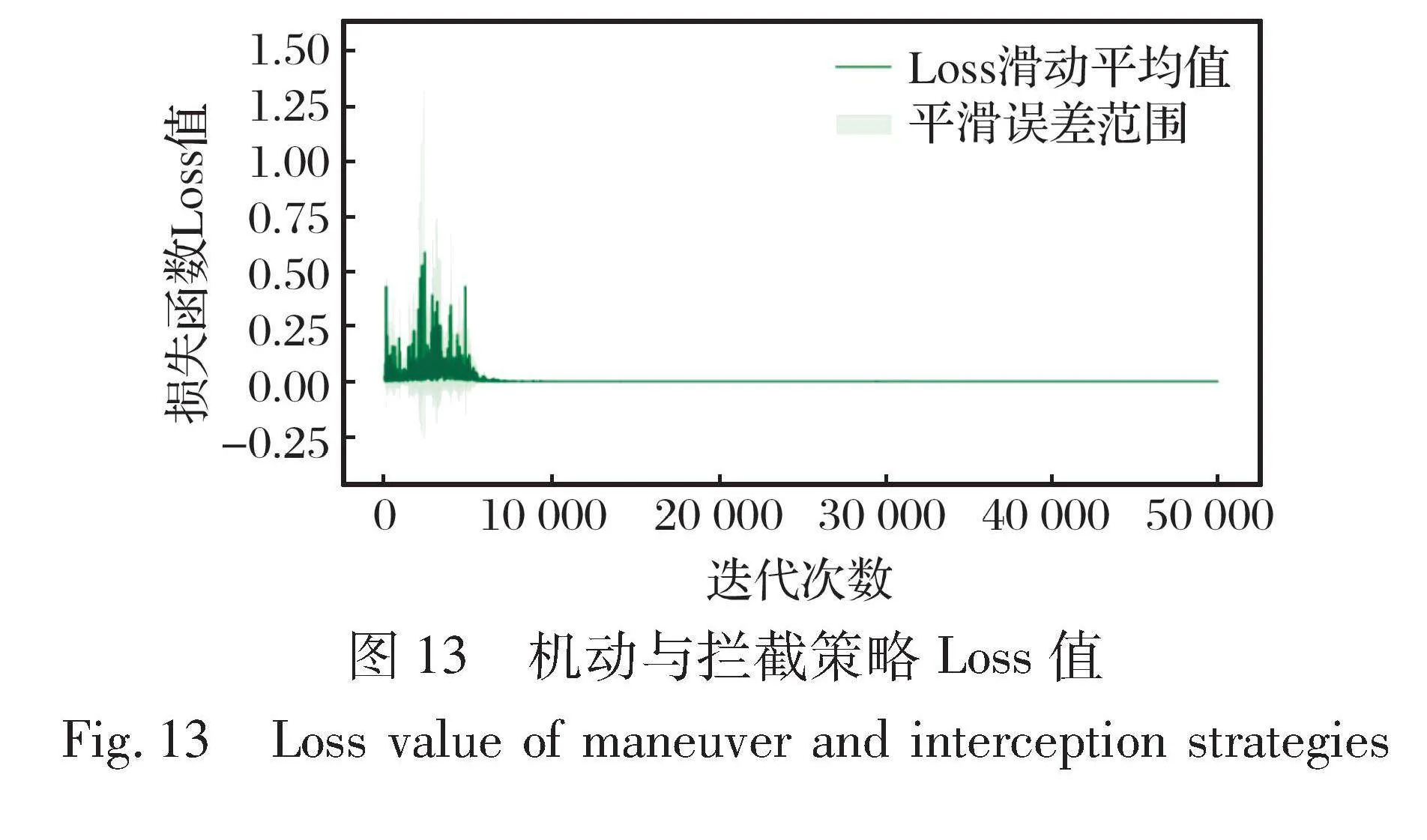
策略模型训练时的Loss值变化如图13所示， 横坐标表示训练的迭代序号， 纵坐标表示当代模型的时间差

分损失， 时间差分的计算遵循第3.1节的方法。 在训练初期， Loss值比较大， 且震荡严重， 随着训练迭代次数的增加逐渐处于低位并且平稳， 证明模型收敛。

4.2 仿真结果分析

4.2.1 拦截率测试

本研究通过与传统的基于固定规则的运筹博弈策略进行多方面的比较， 全面评估基于强化学习的智能机动与拦截策略的有效性。

运筹学博弈策略： 基于一套既定的决策规则及威胁度评估， 其综合考量了来袭导弹的距离、 角度和速度。 该策略源于超视距空战的运筹学与博弈理论， 采用if-then规则实施适应性决策， 以最大化载机平台的逃逸概率。

强化学习智能拦截策略（本文方法）： 依靠持续的环境互动和学习过程， 自动调整其行动策略以达成最佳决策。 这一策略并不基于预设规则， 而是利用算法在广泛的模拟战斗中学习评估威胁并作出响应， 从而增强了其在复杂战场环境中的适应性和泛化能力。

为了确保研究结果的可靠性和适用性， 本文统计和分析10 000局空空博弈的仿真实验结果， 每处理100局来袭导弹场景进行一次统计， 共完成100次重复实验。

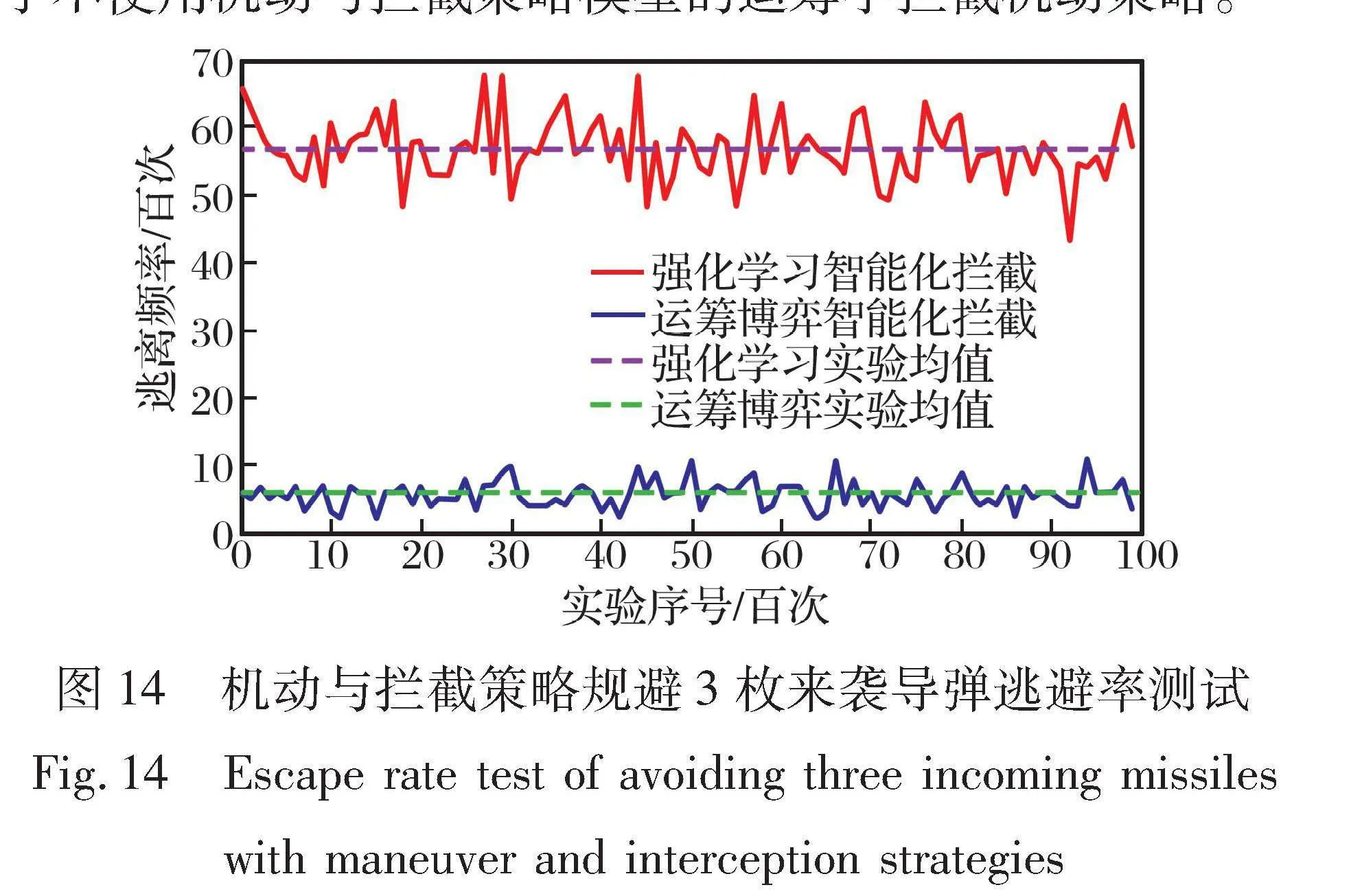
对于3枚来袭导弹， 每100局统计一次逃避的次数， 共进行100次实验。 10 000局空空博弈中载机平台的逃逸率统计实验结果如图14所示。 可以看出， 使用运筹学博弈策略， 载机平台平均逃离的概率在5.8%左右。 使用机动与拦截策略， 载机平台平均逃离的概率在56.8%左右。 使用机动与拦截策略模型在每100局中的逃避率均优于不使用机动与拦截策略模型的运筹学拦截机动策略。

因此， 机动与拦截策略模型对于3枚来袭导弹的情况有指导意义， 可以有效提升载机平台的生存率。 对于被3枚来袭导弹锁定的情况， 载机平台自身的危险系数非常高， 在实际中逃离的概率比较低， 而且每局使用的环境完全随机， 使用机动与拦截策略模型所带来的效果在56.8%左右， 证明所得到的策略模型有着很好的泛化性， 可以根据环境或者来袭导弹的攻击态势不同， 提供有效的策略。 在躲避拦截的同时， 还能够保留一定的打击力量， 确保飞行员夺取空战对抗的优势， 可以提升载机平台在空空导弹规避博弈时的安全性， 提高载机平台的生存能力。

4.2.2 拦截效率测试

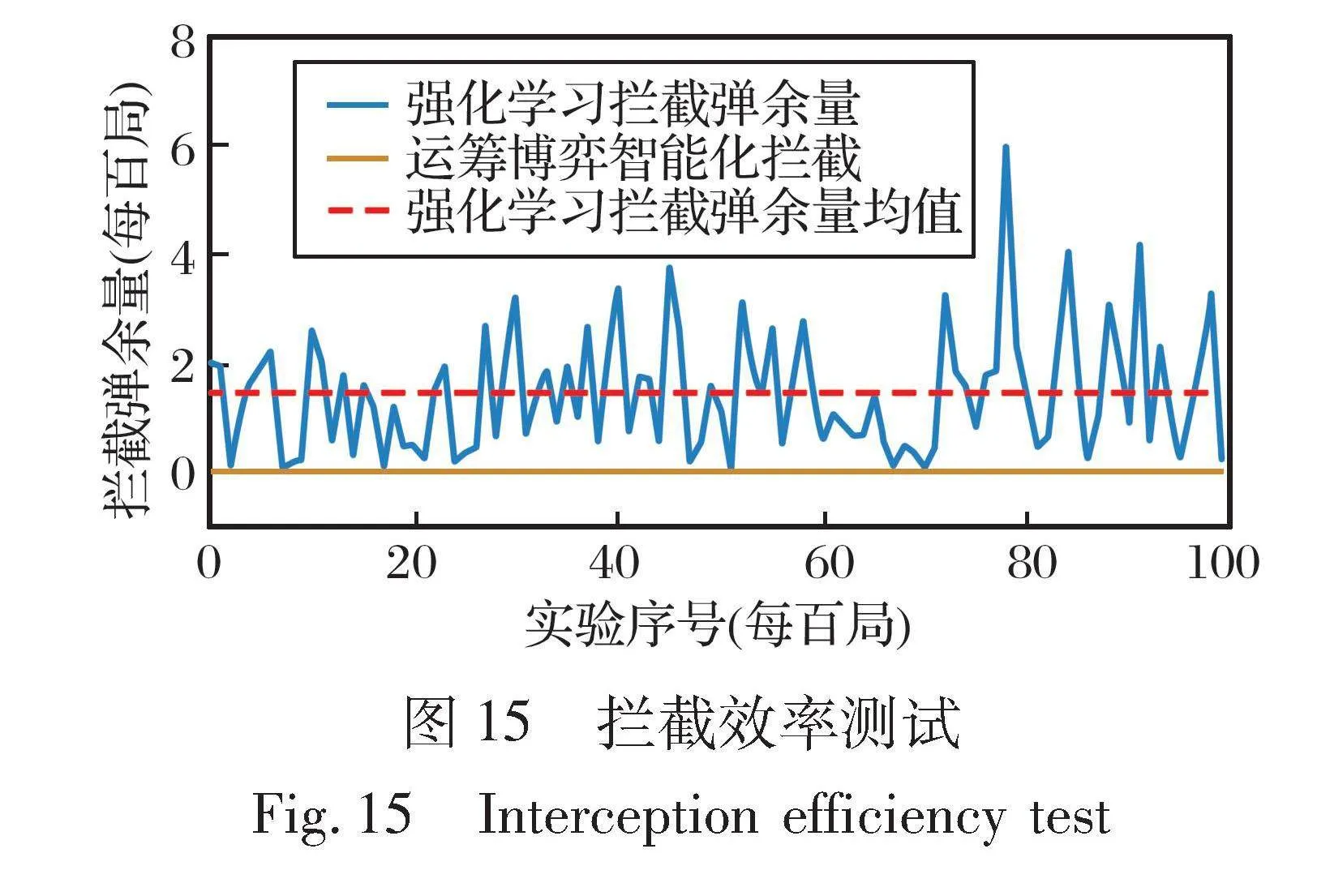
为展示基于强化学习的智能机动与拦截策略对拦截弹利用率的提升效果， 在仿真环境中， 设定载机每局携带6枚拦截弹， 通过统计博弈后剩余的拦截弹数量， 分析策略在实际操作中节省拦截弹的效能。

进行10 000次实验， 输出每100次的平均剩余拦截弹量， 如图15所示。 对比运筹学博弈策略和使用智能化机动与拦截策略的效果可以看出： 3枚来袭导弹情况下， 基于相同空空博弈场景， 智能化拦截或机动逃离的耗弹量在5个左右， 而运筹学博弈策略的剩余导弹量基本归零。 在10 000局的测试中， 每一局平均节省0.8枚拦截弹， 证明智能化拦截弹发射策略具有更优的拦截效率。

在机载智能化拦截模型中， 拦截成功时使用拦截弹数量不多于5枚， 而运筹学博弈方法则每次实验基本都需要全部发射6枚导弹才能拦截到其中一部分来袭导弹。 说明机载智能化拦截模型在大规模的拦截场景下拦截目标时， 可以节约一定成本， 减少拦截弹的发射量。

4.2.3 响应效率测试

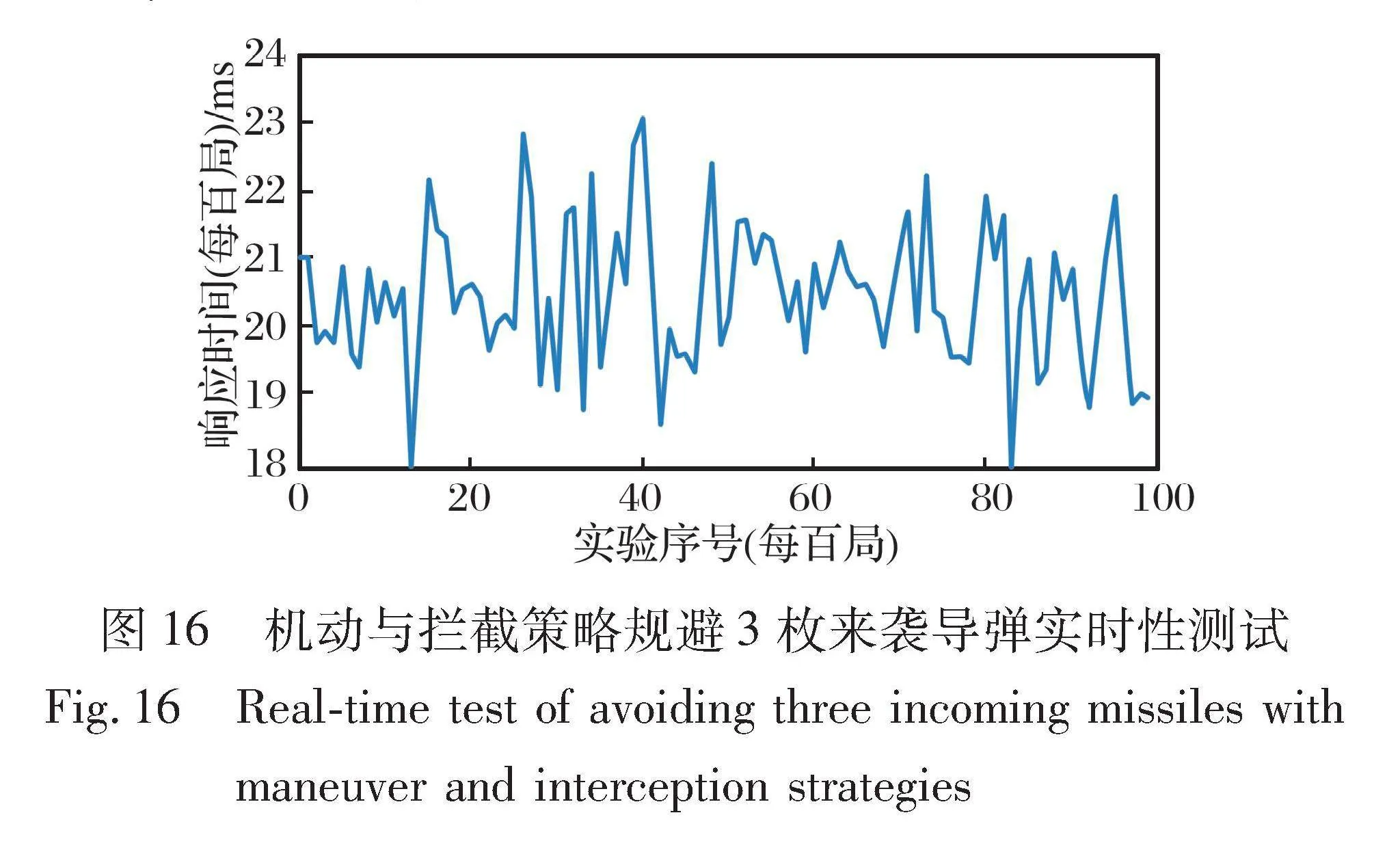
进行10 000次实验， 每100次输出一个平均响应时长， 如图16所示， 测试环境使用AMD Ryzen 5 5600G CPU， 16G RAM。

对于2枚来袭导弹， 可以看出， 每回合的平均响应时间在24 ms以下， 在通用计算机上运行的响应速度在300 ms以内。 通过10 000次的响应测试可以看出， 响应速度都在正常范围内， 没有异常数据产生， 即通过DDQN或N3D训练出的载机平台机动与拦截策略， 响应速度快， 模型稳定且效率高。

综上， 使用深度强化学习方法训练出的机载智能化拦截模型相对于传统的运筹博弈方法， 能够在实际应用中取得更好的效果， 具有更高的逃离率（逃离率是指目标成功逃脱的概率）， 并且使用更少的导弹就能完成拦截任务。 该方法具有以下优势：

（1） 相对于运筹博弈方法， 深度强化学习显著提升了逃离率。 在实际应用中， 目标往往具有一定的逃避能力， 需要拦截模型具备一定的适应性和灵活性。 深度强化学习通过不断学习和优化， 能够逐渐适应不同的目标逃避策略， 提高拦截成功率， 显著降低来袭导弹对载机带来的风险。

（2） 使用更少的导弹能够降低拦截成本， 在空空对抗中尤其重要。 在保证战斗力的前提下， 尽可能地节省导弹的使用量对于载机来说非常重要。 使用深度强化学习方法训练出的机载智能化拦截模型能够显著减少导弹的使用量， 从而大大降低拦截成本， 提高战斗效益。

（3） 在实际应用中， 拦截模型需要能够快速响应不同的目标和环境变化， 以保障飞行安全。 机载智能化拦截模型能够通过实时的状态观测和决策反馈， 快速做出适应性的调整和优化， 保证模型的实时性和可靠性。

5 结 论

采用深度强化学习方法， 实现对空空博弈环境的特征提取、 经验缓存和策略优化， 能有效地训练和测试拦截和机动算法模型， 实现载机平台有效逃离和对来袭导弹的有效拦截。 在载机平台机动限制和拦截弹类型与发射角度限制下， 根据来袭导弹弹道和平台机动策略， 构建基于拦截导弹发射目标及数量的博弈策略快速生成算法， 结合具体的作战场景， 对多种不同打击效果的博弈策略进行深度融合， 形成最优策略模型， 通过基于法则分析和强化学习计算， 证明拦截弹发射策略的有效性。 通过设计拦截弹的相关属性和参数， 可以实现不同拦截弹参数下的策略生成。 利用仿真分析对载机平台机动与拦截模型进行收敛性能、 机动与拦截性能、 实时性指标的测评， 证明所提出的机动与拦截模型可以有效拦截威胁目标， 同时提高了拦截与机动策略的效率和鲁棒性。

参考文献：

［1］ Prokhorov D V， Wunsch D C. Adaptive Critic Designs ［J］. IEEE Transactions on Neural Networks， 1997， 8（5）： 997-1007.

［2］ Nobleheart W， Shivanapura L G， Chakravarthy A， et al. Single Network Adaptive Critic （SNAC） Architecture for Optimal Tracking Control of a Morphing Aircraft during a Pull-up Maneuver［C］∥Proceedings of the AIAA Guidance， Navigation， and Control （GNC） Conference， 2013.

［3］ Wang Y， O’Donoghue B， Boyd S. Approximate Dynamic Programming via Iterated Bellman Inequalities［J］. International Journal of Robust and Nonlinear Control， 2015， 25（10）： 1472-1496.

［4］ Bertsekas D P， Tsitsiklis J N. Neuro-Dynamic Programming： An Overview［C］∥Proceedings of 34th IEEE Conference on Decision and Control， 1995.

［5］ Zhu L M， Modares H， Peen G O， et al. Adaptive Suboptimal Output-Feedback Control for Linear Systems Using Integral Reinforcement Learning［J］. IEEE Transactions on Control Systems Techno-logy， 2015， 23（1）： 264-273.

［6］ Bhasin S. Reinforcement Learning and Optimal Control Methods for Uncertain Nonlinear Systems［D］. Gainesville： University of Florida， 2011.

［7］ 孙景亮， 刘春生. 基于自适应动态规划的导弹制导律研究综述［J］. 自动化学报， 2017， 43（7）： 1101-1113.

Sun Jingliang， Liu Chunsheng. An Overview on the Adaptive Dynamic Programming Based Missile Guidance Law［J］. Acta Automatica Sinica， 2017， 43（7）： 1101-1113.（in Chinese）

［8］ Moerland T M， Broekens J， Plaat A， et al. Model-Based Reinforcement Learning： A Survey［J］. Foundations and Trends in Machine Learning， 2023， 16（1）： 1-118.

［9］ Kang B， Ma X， Du C， et al. Efficient Diffusion Policies for Offline Reinforcement Learning［EB/OL］. （2023-05-31） ［2024-03-11］. https：∥arxiv.org/abs/2305.20081.

［10］ Feng S， Sun H W， Yan X T， et al. Dense Reinforcement Learning for Safety Validation of Autonomous Vehicles［J］. Nature， 2023， 615： 620-627.

［11］ Rosete-Beas E， Mees O， Kalweit G， et al. Latent Plans for Task-Agnostic Offline Reinforcement Learning［EB/OL］. （2022-09-19） ［2024-03-11］. https：∥arxiv.org/abs/2209. 08959.

［12］ Luo J L， Dong P， Wu J， et al. Action-Quantized Offline Reinforcement Learning for Robotic Skill Learning［EB/OL］. （2023-10-18） ［2024-03-11］. https：∥ arxiv.org/pdf/2310.11731.pdf.

［13］ Deng T B， Huang H， Fang Y W， et al. Reinforcement Learning-Based Missile Terminal Guidance of Maneuvering Targets with Decoys［J］. Chinese Journal of Aeronautics， 2023， 36（12）： 309-324.

［14］ Gaudet B， Furfaro R. Integrated and Adaptive Guidance and Control for Endoatmospheric Missiles via Reinforcement Meta-Learning［C］∥Proceedings of the AIAA SCITECH 2023 Forum， 2023.

［15］ Gaudet B， Furfaro R. Line of Sight Curvature for Missile Guidance using Reinforcement Meta-Learning［C］∥AIAA SCITECH 2023 Forum， 2023.

［16］ Wang Z， Hao Y T. Reinforcement Learning Adaptive Risk-Sensitive Fault-Tolerant IGC Method for a Class of STT Missile with Non-Affine Characteristics， Stochastic Disturbance and Unknown Uncertainties［J/OL］.Nonlinear Dynamics， doi：10.1007/s11071-024-09776-5.

［17］ Merkulov G， Iceland E， Michaeli S， et al. Reinforcement Learning Based Decentralized Weapon-Target Assignment and Guidance［C］∥Proceedings of the AIAA SCITECH 2024 Forum， 2024.

［18］ Alpdemir M N. A Hierarchical Reinforcement Learning Framework for UAV Path Planning in Tactical Environments［J］. Turkish Journal of Science and Technology， 2023， 18（1）： 243-259.

［19］ Dierks T， Jagannthan S. Optimal Control of Affine Nonlinear Discrete-Time Systems［C］∥17th Mediterranean Conference on Control and Automation， 2009.

［20］ Liu D R， Wei Q L. Policy Iteration Adaptive Dynamic Programming Algorithm for Discrete-Time Nonlinear Systems［J］. IEEE Transactions on Neural Networks and Learning Systems， 2014， 25（3）： 621-634.

［21］ He P G， Jagannathan S. Reinforcement Learning Neural-Network-Based Controller for Nonlinear Discrete-Time Systems with Input Constraints［J］. IEEE Transactions on Systems， Man and Cybernetics， Part B （Cybernetics）， 2007， 37（2）： 425-436.

［22］ 郭红霞， 吴捷， 王春茹. 基于强化学习的模型参考自适应控制［J］. 控制理论与应用， 2005， 22（2）： 291-294.

Guo Hongxia， Wu Jie， Wang Chunru. Model Reference Adaptive Control Based on Reinforcement Learning［J］. Control Theory & Applications， 2005， 22（2）： 291-294.（in Chinese）

［23］ 高瑞娟， 吴梅. 基于改进强化学习的PID参数整定原理及应用［J］. 现代电子技术，11555a921fb0fc25916d5ccf1f9d2fd81258f4412e866a329e828e33f9371c2e 2014， 37（4）： 1-4.

Gao Ruijuan， Wu Mei. Principle and Application of PID Parameter Tuning Based on Improved Reinforcement Learning［J］. Mo-dern Electronics Technique， 2014， 37（4）： 1-4.（in Chinese）

［24］ Jagannathan S， He P G. Neural-Network-Based State Feedback Control of a Nonlinear Discrete-Time System in Nonstrict Feedback Form［J］. IEEE Transactions on Neural Networks， 2008， 19（12）： 2073-2087.

［25］ Vrabie D， Lewis F. Neural Network Approach to Continuous-Time Direct Adaptive Optimal Control for Partially Unknown Nonlinear Systems［J］. Neural Networks， 2009， 22（3）： 237-246.

［26］ Vamvoudakis K G， Lewis F L. Online Actor-Critic Algorithm to Solve the Continuous-Time Infinite Horizon Optimal Control Pro-blem［J］. Automatica， 2010， 46（5）： 878-888.

［27］ Han D C， Balakrishnan S N. State-Constrained Agile Missile Control with Adaptive-Critic-Based Neural Networks［J］. IEEE Tran-sactions on Control Systems Technology， 2002， 10（4）： 481-489.

［28］ Milovanovic M B， Antic D S， Milojkovic M T， et al. Adaptive Control of Nonlinear MIMO System with Orthogonal Endocrine Intelligent Controller［J］. IEEE Transactions on Cybernetics， 2022， 52（2）： 1221-1232.

［29］ Chen K L. Intelligent Control Using Neural Networks［J］. IEEE Control Systems， 1992， 12（2）： 11-18.

［30］ 陈宇轩， 王国强， 罗贺， 等. 基于Actor-Critic算法的多无人机协同空战目标重分配方法［J］. 无线电工程， 2022， 52（7）： 1266-1275.

Chen Yuxuan， Wang Guoqiang， Luo He， et al. Target Re-Assignment Method for Multi-UAV Cooperative Air Combat Based on Actor-Critic Algorithm［J］. Radio Engineering， 2022， 52（7）： 1266-1275.（in Chinese）

［31］ Vaidya O S， Kumar S. Analytic Hierarchy Process： An Overview of Applications［J］. European Journal of Operational Research， 2006， 169（1）： 1-29.

Optimization Technology for Intelligent Interception of

Incoming Missiles and Platform Maneuvering Strategies

Based on Deep Reinforcement Learning

Lü Zhenrui1， 2， Shen Xin3， Li Shaobo4， Tian Peng1， 2， Si Yingli1， 2*

（1. China Airborne Missile Academy， Luoyang 471009， China；

2. National Key Laboratory of Air-based Information Perception and Fusion， Luoyang 471009， China；

3. The First Military Representative Office of Air Force Equipment Department in Luoyang， Luoyang 471009， China；

4. Xi’an Jiaotong University， Xi’an 710049， China）

Abstract： Facing the increasing complexity of aerial combat environments and challenges to the survivability of air platforms from new combat methods， it is necessary to adopt new hard-kill methods to counter advanced air-to-air missiles. In order to improve the success rate and efficiency of launching air-to-air missiles to intercept incoming missiles as a hard kill method， this study proposes intelligent maneuvering strategies for aircraft platforms and missile interception strategies based on reinforcement learning. Firstly， this paper designs the missile threat assessment technology， constructs the simulation environments， and determines the strategy model state and reward function. By setting various attack angles and positions of incoming air-to-air missiles and training maneuvering and intelligent interception strategies under different aircraft platform postures， this paper achieves active interception of incoming targets and effective maneuvering of the aircraft platform. Experiments show that compared to the average escape probability of 5.8% in operations research game strategies， after using maneuver and interception strategies based on reinforcement learning， the average escape probability can increase to 56.8%; Meanwhile， the utilization rate of interceptors has increased by approximately 13.3%， and the response time has remained within 24 ms. The designed strategy can adapt to different numbers of incoming missiles， can significantly improve the survival ability of the carrier platform and the success rate of intercepting incoming missiles. This study can support continuous optimization in a high-dimensional state space of air combat.

Key words： interception missile； maneuvering strategy； reinforcement learning； interception strategy; escape probability; response time; air-to-air missile