基于复杂网络中心性理论的典型海上杀伤链节点重要度评估研究

摘 要： 海上杀伤链是当今海上联合作战体系运转的核心， 是信息化战争形态下OODA环的实践运用， 体现了联合作战体系信息流主导能量流进行闭环运转的运行机理。 如何研判对方海上杀伤链的关键节点是当前海上综合制权的前提。 目前海上杀伤链关键节点的研判问题， 主要应用理论分析与复杂网络分析等方法， 其中复杂网络分析法大多利用逐个节点删除的方法评估节点的重要性， 存在搜索效率低、 适用规模小等问题。 本文以NIFC-CA系统为例， 构建了海上典型杀伤链模型， 利用融合中心性的复杂网络评估方法， 对杀伤链节点重要性进行排序， 找到了关键节点。 同时， 在评估过程中运用Python的Network库中图论与网络分析工具， 显著提高了计算效率。

关键词： 作战体系； 复杂网络； 建模； 关键节点； 杀伤链

中图分类号： TJ760

文献标识码： A

文章编号： 1673-5048（2024）05-0050-06

DOI： 10.12132/ISSN.1673-5048.2024.0051

0 引 言

杀伤链是在打击目标的过程中各个相互依赖的环节构成的有序链条。 在信息化战争时代， 杀伤链通常指探测目标、 瞄准目标、 交战并评估交战结果的闭环过程。

杀伤链是一个描述攻击过程的模型， 它包括多个节点， 不同的节点对攻击的成败有着意义不等的作用。 发现对手的杀伤链关键节点， 并针对性地进行打击是取得战斗优势的关键， 如何分析评估杀伤链的关键点一直是研究的热点问题。

杀伤链的传统分析方法有理论分析与建模后利用复杂网络进行分析等方法， 其中复杂网络的分析方法主要结合OODA环（观察、 判断、 决策、 行动）理论和杀伤链概念建模， 再利用节点删除法评估杀伤链节点的重要性。 这种方法通过观察网络作战能力及网络循环效率的下降程度来确定关键节点［1］， 但这种方法需要逐个删除节点， 在面对大型杀伤链时， 此方法效率非常低。

在此基础上， 衍生出了使用算法和人工智能等对杀伤链进行分析的方法， 相比节点删除法有着更高的效率与准确性。 本文采用复杂网络的中心性算法对以NIFC-CA系统为蓝本构造的典型海上杀伤链进行分析。

1 典型海上杀伤链的作战流程

“海军一体化火控-制空”（Naval Integrated Fire Control-Counter Air， NIFC-CA）系统， 是一种典型的分布式网络化的空中火力控制系统， 也是以远程交战和超地平线防空拦截为目标设计出的典型海上杀伤链体系。 该海上杀伤链以基础的“F2T2EA（发现（Find）、 定位（Fix）、 跟踪（Track）、 决策（Target）、 交战（Engage）、 评估（Assess））”杀伤链作战概念为蓝本， 结合了海军装备的特点， 于20世纪90年代提出概念， 2002年正式命名为NIFC-CA。 2014年， E-2D预警机正式服役， 使NIFC-CA系统具备初始作战状态。 2015年通过了“罗斯福”号航空母舰打击群认证测试， 标志其具备作战能力［2］。

在NIFC-CA杀伤链中， 基于Link-16/22战术数据链的高速数据传输网络和协同作战系统（Cooperative Engagement Capability， CEC）， 可以整合各个节点上的传感

器信息， 将海基/空基平台探测感知装备、 防空反导武器

收稿日期： 2024-03-26

作者简介： 潘长鹏（1977-）， 男， 山东莱州人， 教授， 博士。

*通信作者： 张雨晨（1994-）， 男， 辽宁开原人， 硕士研究生。

以及指挥系统相互连接起来， 构成了一套具有威胁探测识别、 高效决策分析、 目标实时跟踪、 精确瞄准打击、 快速毁伤判断能力的全能型海上杀伤链。

NIFC-CA海上杀伤链中所有单元可以分为“感知平台（及其下辖的感知单元）”“发射平台”“指挥控制单元”“拦截武器”等， 如表1所示。

航空兵器 2024年第31卷第5期

潘长鹏， 等： 基于复杂网络中心性理论的典型海上杀伤链节点重要度评估研究

首先， 感知平台探测到来袭目标信息， 立刻传送给“宙斯盾”舰MK1指挥决策系统， 系统完成威胁评估和交火作战决策， 协同运用作战资源， 系统内各要素子系统均与指挥控制单元连接， 由其统一进行火力分配和下达指令［3］。

武器发射后， 根据感知平台不断传送的目标最新信息， 指挥控制单元根据具体情况选择中段制导的最优单元进行接力制导， 直至武器命中目标［4］， 如图1所示。

2 基于复杂网络理论的典型海上杀伤链体系构建与评估

NIFC-CA杀伤链的结构非常适合使用复杂网络建模分析， 本文以NIFC-CA的运转流程为基础， 构建防御反舰导弹突袭为场景假定的海上典型杀伤链， 并通过复杂网络进行分析。

2.1 典型海上杀伤链体系建模

复杂网络可以表示多种多样的复杂系统，其中， 节点代表网络中的实体， 边表示实体之间的关系［5］。 这些节点和边的组合构成了网络的基本结构， 是复杂网络模型的基础。

2.1.1 典型海上杀伤链的节点构建

场景假定： 红方海空平台依托体系支撑对蓝方“宙斯盾”驱逐舰发射反舰导弹。 蓝方MQ-4C无人机、 F-35C①战斗机、 E-2D预警机、 E/A-18G电子战飞机各1架隐蔽探测来袭目标， 同时， E-2D预警机、 F-35C②战斗机担负“宙斯盾”舰发射的“标准”-6导弹中继制导任务。 基于场景假定， 编制网络节点组成如表2所示。

2.1.2 典型海上杀伤链的边构建

网络中的边表示节点之间的关系。 基于假定场景， 本文拟给定一个有向无权网络G=（V， E）， V=（M， v1， v2， …， v7）为表2中的节点， E代表节点间的边， E={（vi， vj）|vi， vj∈V}， |E|=20， 分别代表各节点探测到导弹来袭、 传递导弹坐标、 中继制导等过程中的信息流转的20条边［6］。 同时， 对典型杀伤链系统内部节点的边作如下规定［7］：

（1） 初始状态下不存在孤立节点， 即海上防空反导作战开始时一切节点都在可控范围内。

（2） 边的连接可以表示物质、 能量和信息的交互关系， 本网络以作战节点之间信息交互为主。

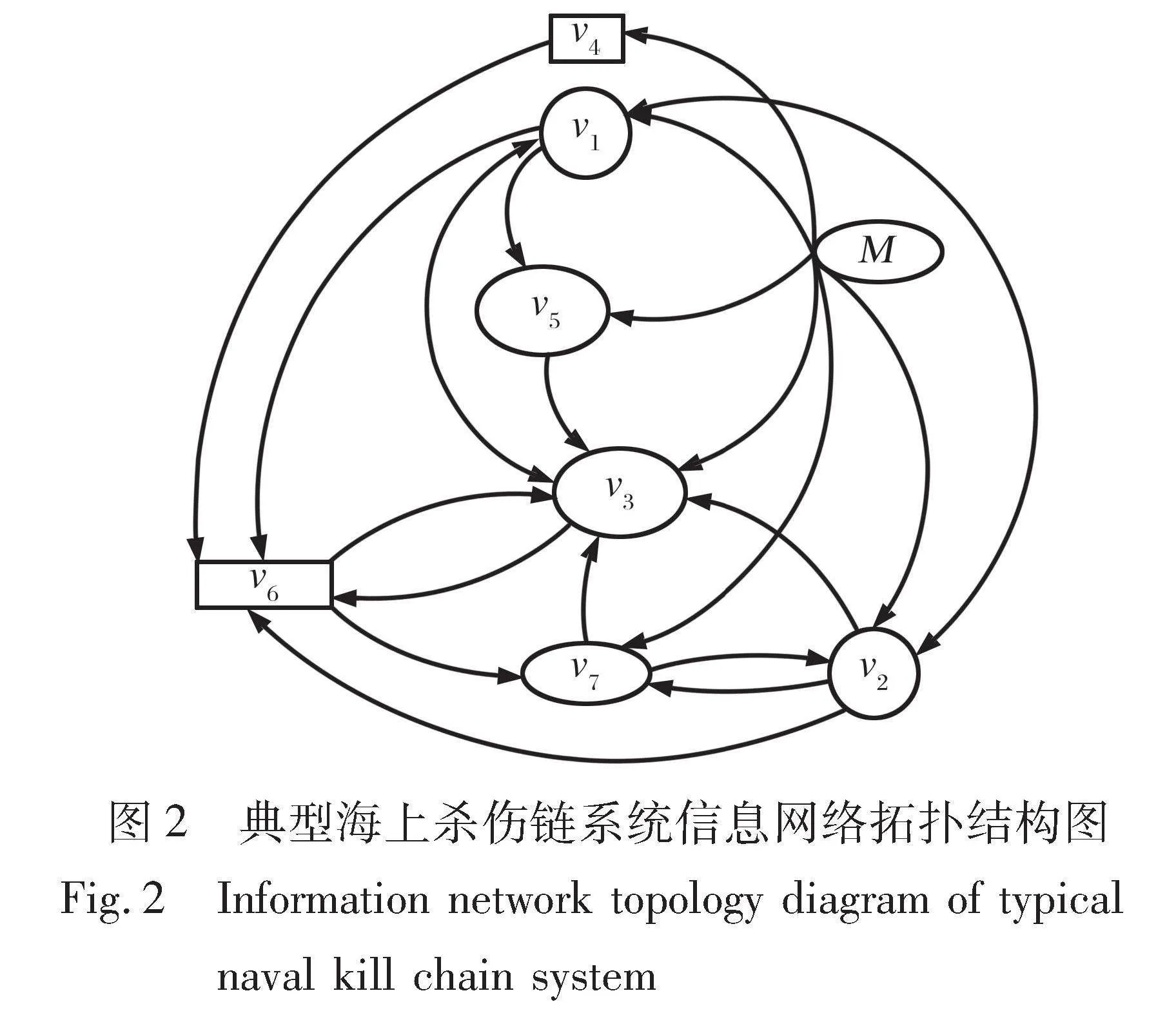
绘制复杂网络拓扑结构图如图2所示（交叉线不存在信息交互）。

naval kill chain system

2.2 典型海上杀伤链节点重要度的评估方法选择

复杂网络中， 网络节点的重要性是通过节点的中心性（Centrality）进行度量的［8］， 节点的中心性越高， 通常意味着该节点在网络中的地位越重要， 其影响力也越大［9］。 中心性评估的方法通常包括度中心性、 介数中心性、 接近中心性等。 这些度量方式从不同角度反映了节点在网络中的重要性和影响力［10］。

（1） 度中心性

度中心性是衡量节点重要性的最直接的指标， 是其他中心性指标的基础， 它仅考虑与该节点直接相连的边的数量， 计算简便。

（2） 介数中心性

介数中心性关注的是节点在所有最短路径上出现的频率， 揭示了节点在网络中的结构位置。 一个节点如果具有很高的介数中心性， 说明它在网络中起到了重要的桥梁作用， 控制着信息或资源的流动。

（3） 接近中心性

接近中心性反映的是节点在网络中的中心程度或可达性。 如果一个节点到其他所有节点的平均距离越短， 那么该节点的接近中心性就越高， 意味着这个节点在网络中的位置越靠近中心， 信息传播或资源流动的效率可能越高。

这3个中心性分析方法各有利弊。 在实际战场环境中， 单一的中心性计算方法难以适应多变的战况， 因此本文选取融合中心性（Compromise Centrality Measure）作为分析方式。

融合中心性是将度中心性、 介数中心性、 特征向量中心性得出的结果进行综合处理所得。 度中心性、 介数中心性、 接近中心性的注重范围从局部到全体， 从不同角度量化了节点在网络中的重要性和影响力， 而在处理为融合中心性之后， 能够利用各自的优点弥补单一算法的局限性， 能更有效地识别复杂网络节点的重要度［7］ 。

2.3 典型海上杀伤链节点重要度的评估方法

在计算融合中心性之前， 首先需要计算组成融合中心性的3个基础中心性。

2.3.1 度中心性的计算

在有向网络中， 节点的度分为入度和出度。 节点的入度是指有向网络中从其他节点指向该节点的边的数目。 节点的出度是指有向网络中从节点指向其他节点的边的数目［11］。 节点i的度可以表示为

ki=∑j∈Naij（1）

式中： N为该有向网络中节点的总数； aij为该网络邻接的矩阵元数量。

Python软件中的Network库是一个用Python语言开发的图论与复杂网络建模工具， 它内置了常用的图与复杂网络分析算法， 能够方便地进行复杂网络数据分析与仿真建模工作， 可以快速地计算各节点的各种中心性数据。 利用该库求得每个节点的出度和入度， 得到结果如表3所示。

2.3.2 介数中心性的计算

介数中心性的研究基础是图论中的最短路径问题， 最短路径在有向图中定义为路径的权重求和， 无赋权时默认权重值为1。 用BC表示一个节点介数中心性，定义为经过该节点的最短路径数占最短路径总数的比， 用dst表示s到t的最短路径数量， dst（）表示s到t的最短路径中经过节点vi的路径数量［13］， 则节点vi介数中心性的计算公式为

BCi=1（N－1）（N－2）∑dst（）dst（3）

以图2中节点v1为例， 其介数中心性计算过程如下：

BCv1=（0+0+0+0+14+0）+（0+0+0+1+0+0）+（0+0+0+1+0+0）+（0+0+0+1+0+0）（8－1）（8－2）+（0+0+0+0+0+0）+（0+0+0+0+1+0）+（0+0+0+0+1+0）（8－1）（8－2）=0.125（4）

式中： 分子中的第一个括号表示从节点M出发， 经过节点v1到其他节点的最短距离数量除以从节点M到其他节点的最短距离数量， 即

M到v2， 不经过v1， 为0；

M到v3， 不经过v1， 为0；

M到v4， 不经过v1， 为0；

M到v5， 不经过v1， 为0；

M到v6， 有4条最短距离， 只有1条经过v1， 为1/4；

M到v7， 不经过v1， 为0。

以此类推， 可以计算出其余节点的介数中心性， 求得各个节点介数中心性如表5所示。

2.3.3 接近中心性的计算

接近中心性算法用于发现可通过图高效传播信息的节点［14］。 对于每个节点， 接近中心性算法在计算所有节点对之间最短路径的基础上， 还要计算它到其他各节点的距离之和， 然后求倒数， 以确定该节点的接近中心性得分［15］。

节点i到其他节点的最短距离之和为di， 公式为

di=∑Nj=1dij（5）

式中： dij代表当前所求节点i到其他所有节点j的最短距离， dij越小， 代表节点i越接近网络的中心位置。 节点i的接近中心性可以理解为， 除节点i之外所有节点的总数与最短距离之和的比重。 节点的接近中心性计算公式为［16］

CCi=N－1di（6）

将各个节点代入式（5）可求得其接近中心性如表6。

在接近中心性的计算中， 有着非联通图无法计算的问题， 由于在本文的假设场景中所有节点不存在孤立的节点， 因此不做讨论。

2.3.4 融合中心性的计算

节点i的融合中心性用CEDi表示， DCi、 BCi、 CCi分别表示节点i的度中心性、 介数中心性和接近中心性。

首先， 需要将3个中心性的计算结果进行归一化处理， 其目的是将数据规范化为标准范围内的数值（本文为0到1）， 去除数据的单位限制， 便于不同单位或量级的指标能够进行比较和加权， 平衡不同特征的权重。

归一化处理的计算方法为

C～i=Ci∑Ni=1C2i ， i=1， 2， …， N（7）

其中， C～i表示节点i的归一化中心值 ， N为复杂网络节点数， 将DCi、 BCi、 CCi代入式（6）运算， 得到DC～i、 BC～i、 CC～i， 分别为节点i的度中心性、 接近中心性和介数中心性归一化中心值， 利用欧拉公式得到的融合中心性的值定义为［10］

CEDi=1N（DC～i2+BC～i2+CC～i2）（8）

可以得到各节点融合中心性如表7所示。

2.4 计算结果与分析

根据结果分析可以得出， 典型的海上杀伤链并不是完全的“去中心化”， 仍然存在着薄弱的点， 如图3所示。

综上可以得出结论， 在典型海上杀伤链中， v3节点即E-2D的中心性最高， v6节点“宙斯盾”舰和负责中继制导的F-35C②次之， 在复杂网络的中心性越高， 代表节点的重要性越高， 这3个节点在整个杀伤链系统中起到了至关重要的作用， 即是整个系统信息流转的中心， 也是整个网络中最关键的节点， 对这些节点进行干扰将迫使蓝方的杀伤链效能下降甚至中断， 需要花费更多的时间进行重组， 无法正常完成反导任务， 在实际的战争中使红方取得优势。

其他节点的重要排序依次是： SM-6防空导弹、 负责探测的F-35C①、 E/A-18G、 MQ-4C无人机。 在条件允许的情况下， 根据重要度排名对目标进行干扰或攻击， 可以更有效地破坏蓝方杀伤链的运行。

从分析结果可以得出， 最关键的两个单元是E-2D与“宙斯盾”舰， 它们都属于杀伤链中的感知平台， 感知单元作为信息获取的重要手段， 能够快速形成网络信息体系闭环， 推动感知、 决策、 指挥控制等各环节产生量变与质变， 是整个杀伤链最为薄弱的环节， 也是战争胜负的关键点。

因此在破击蓝方典型海上杀伤链的行动中， 配合反舰导弹攻击的过程， 可以通过对蓝方的感知平台施加干扰或者首先破坏感知平台， 有效地阻塞甚至瘫痪杀伤链的运行， 达到“破点”“断链”的效果， 大大提高反舰导弹的突防能力。

3 对杀伤链建设的启示

根据本文对典型海上杀伤链分析可以看出， 杀伤链的建设是一个复杂的系统工程， 其中暴露出的弱点对新一代杀伤链的建设过程有着很深刻的启示意义。 随着大量新技术的投入使用， 这些杀伤链中的弱点也可以针对性的改善。

3.1 强化冗余快速重组， 保证杀伤链不中断

在现代战争中， 防御远比攻击更加困难， 如果仅仅选择增强感知平台的防御， 不仅会对战术的选择造成较大的局限， 也会在感知平台因为各种原因失能后陷入被动。 最好的方式是通过强化冗余重组能力来防止单一平台被破坏。 如果在杀伤链系统中加入多个预警机和“宙斯盾”舰， 使其能够在干扰后快速动态重组， 迅速替代受破坏节点的工作， 则反舰导弹突防的成功率会大幅下降。

3.2 无人平台功能多元化， 增强杀伤链抗毁能力

根据图3可以得出， MQ-4C作为感知平台， 是整个杀伤链体系中中心性最小的， 其中一个很重要的原因是其功能单一， 仅能提供侦察能力， 无法在SM-6发射后提供中继制导等功能。 如果能够升级MQ-4C型平台， 使其具有和E-2D相近的功能性， 那么， 即使作为杀伤链中心的E-2D被毁， MQ-4C仍能协同其他节点工作， 提供全面的战场态势感知与通信中继， 可以有效地增强杀伤链的抗毁能力。

同时， MQ-4C型无人机作为无人装备， 可以低成本大量部署， 多个感知单元的加入会使整个杀伤链变得更加难以阻断， 也可以减少杀伤链中高价值高风险的有人节点部署数量， 避免可能造成的人员损失。

3.3 多样化信息来源， 推动杀伤链向杀伤网转化升级

杀伤链的抗毁能力很大程度取决于整个杀伤链的大小， 即链内的节点数量。 如果能够融合信息来源， 加入来自战场外的电子侦察、 卫星图像等， 形成多元化的情报收集体系， 将多个杀伤链凝结为杀伤网， 那么就可以扩充整个杀伤链体系， 提供海量的高价值节点， 使整个杀伤链的运行变得高效， 抗毁性能得到显著增强， 在未来的攻防作战中将取得决定性的优势。

4 结 论

本文对以NIFC-CA为蓝本建模的典型海上杀伤链进行建模分析， 与以往使用单一的中心性进行分析不同， 采用了融合中心性， 以多种中心性的数据进行融合后获得最终结果， 减少了单一方法的局限性， 提高了准确度。 根据结果得出， 典型杀伤链中最关键的节点是E-2D与“宙斯盾”舰， 皆属于感知平台， 并给出破击的建议与杀伤链建设的启示， 为杀伤链重要度分析提供了一种解题思路， 也为改善杀伤链弱点与破坏敌方杀伤链、 降低其作战效能提供了决策依据。

此外， 使用不同的融合方式（TOPSIS中心性等）或者将更多的中心性评价方式（PageRank中心性等）加入后对杀伤链评估的影响是下一步需要研究的问题。

参考文献：

［1］ 陈登， 陈楚湘， 周春华. 基于OODA环的杀伤网节点重要性评估［J］.兵工学报， 2024， 45（2）： 363-372.

Chen Deng， Chen Chuxiang， Zhou Chunhua. Importance Evaluation of Kill Network Nodes Based on OODA Loop ［J］.Acta Armamentarii， 2024， 45（2）： 363-372.（in Chinese）

［2］ 任淼， 刘琪， 刘晶晶. 2019年国外空空导弹发展动态研究［J］. 航空兵器， 2020， 27（4）： 17-24.

Ren Miao， Liu Qi， Liu Jingjing. Research on Foreign Air-to-Air Missiles’ Development in 2019［J］. Aero Weaponry， 2020， 27（4）： 17-24.（in Chinese）

［3］ 熊海峰. 浅析NIFC-CA系统在美军杀伤网构建中发挥的作用［J］. 军事文摘， 2021（3）： 13-18.

Xiong Haifeng. Analysis on the Role of NIFC-CA System in the Construction of US Military Kill Net［J］. Military Digest， 2021（3）： 13-18.（in Chinese）

［4］ 宫尚玉， 陈亮， 王月悦. 美“海上一体化防空火控” 体系发展及对抗思路分析［J］. 电讯技术， 2022， 62（12）： 1859-1864.

Gong Shangyu， Chen Liang， Wang Yueyue. Analysis of U.S. Navy NIFC-CA System-of-System Development and Countermeasures［J］. Telecommunication Engineering， 2022， 62（12）： 1859-1864.（in Chinese）

［5］ 艾均. 复杂网络中目标节点分析技术研究［D］. 沈阳： 东北大学， 2013.

Ai Jun. Research on Techniques of Target-Node Analysis in Complex Networks［D］. Shenyang： Northeastern University， 2013. （in Chinese）

［6］ 崔雪莲， 董海涛. 基于关键节点识别的社交网络舆情控制策略研究［J/OL］. 计算机工程与应用， doi： 10.3778/j.issn.1002-8331.2310-0208.

Cui Xuelian， Dong Haitao. Research on Social Network Public Opinion Control Strategy Based on Key Node Identification［J/OL］. Computer Engineering and Applications， doi： 10.3778/j.issn.1002-8331.2310-0208.（in Chinese）

［7］ 卞泓斐， 张千宇. 基于复杂网络的舰艇编队防空作战模型研究［J］. 舰船电子工程， 2015， 35（4）： 29-32.

Bian Hongfei， Zhang Qianyu. Warship Formation Air Defense Mo-del Based on Complex Network［J］. Ship Electronic Engineering， 2015， 35（4）： 29-32.（in Chinese）

［8］ 罗春蕾. 基于复杂网络中心性的关键种识别研究［D］. 北京： 华北电力大学， 2019.

Luo Chunlei. Identifying Keystone Species Based on Centrality of Complex Networks［D］. Beijing： North China Electric Power University， 2019. （in Chinese）

［9］ 冯朗荣. 海上交通复杂网络节点识别研究［D］.大连： 大连海事大学， 2023.

Feng Langrong. Research on Node Identification in Complex Maritime Traffic Networks［D］. Dalian： Dalian Maritime University， 2023. （in Chinese）

［10］ 张希康. 复杂网络的链路预测算法研究［D］. 贵阳： 贵州大学， 2023.

Zhang Xikang. Research on Link Prediction Algorithm for Complex Networks［D］. Guiyang： Guizhou University， 2023. （in Chinese）

［11］ 张廷萍. 浅议几种复杂网络节点重要度分析的中心性方法［J］. 价值工程， 2016， 35（14）： 209-210.

Zhang Tingping. Centrality Measures to Identify Influential Nodes in Complex Networks［J］. Value Engineering， 2016， 35（14）： 209-210.（in Chinese）

［12］ 杨隽豪. 基于复杂网络理论的高速公路网络节点重要度评价及连通可靠性研究［D］. 成都： 西华大学， 2022.

Yang Junhao. Research on Importance Evaluation of Node and Connectivity Reliability in Expressway Network Based on Complex Network Theory［D］. Chengdu： Xihua University， 2022. （in Chinese）

［13］ 朱庆存. 基于网络中心性算法的关键节点识别方法研究［D］. 济南： 齐鲁工业大学， 2021.

Zhu Qingcun. RXcksWPJNiZFIbXR4BfoKth088WxafSkAr9DsLcGA+eE=esearch on Key Node Recognition Method Based on Network Centrality Algorithm［D］. Jinan： Qilu University of Technology， 2021. （in Chinese）

［14］ 涂敏， 韩雨濛. 改进TOPSIS法的武汉城市轨道交通节点重要度评估［J］. 重庆交通大学学报： 自然科学版， 2023， 42（9）： 113-121.

Tu Min， Han Yumeng. Importance Evaluation of Wuhan Rail Transit Nodes Based on Improved TOPSIS Method［J］. Journal of Chongqing Jiaotong University： Natural Science， 2023， 42（9）： 113-121.（in Chinese）

［15］ 陈妤， 秦威. 基于排序学习的复杂网络节点接近中心性近似排序［J］. 计算机系统应用， 2022， 31（11）： 387-392.

Chen Yu， Qin Wei. Approximate Rank of Closeness Centrality of Complex Network Nodes Based on Learning to Rank［J］. Compu-ter Systems and Applications， 2022， 31（11）： 387-392.（in Chinese）

［16］ 陈静， 田晓杰， 曾兴善， 等. 基于复杂网络的军事通信建模及关键节点评估［J］. 指挥控制与仿真， 2021， 43（5）： 55-59.

Chen Jing， Tian Xiaojie， Zeng Xingshan， et al. Research on Military Communication Modeling and Key Node Evaluation Based on Complex Network［J］. Command Control & Simulation， 2021， 43（5）： 55-59.（in Chinese）

Research on Node Importance Assessment in Maritime Kill Chain

Based on Complex Network Centrality Theory

Pan Changpeng， Zhang Yuchen*， Li Chaobo

（Naval Aeronautical University， Yantai 264001， China）

Abstract： The maritime kill chain constitutes the core of the current joint maritime combat system， representing the practical application of the OODA loop in the context of informationized warfare. It embodies the operational mechanism of the joint combat system， where information flow dominates energy flow in a closed-loop operation. Determining the critical nodes of the maritime kill chain is the prerequisite for achieving comprehensive maritime dominance. Currently， the assessment of key nodes within maritime kill chains employs theoretical analysis and complex network methods. Complex network analysis techniques， which often utilize a node-by-node deletion approach to evaluate node importance， suffer from issues such as low search efficiency and limited applicability to small-scale systems. This paper takes the NIFC-CA system as an example to construct a typical maritime kill chain model. The importance of kill chain nodes is ranked using a complex network assessment method of integration centrality， and key nodes are identified. Additionally， graph theory and network analysis tools from Python’s Network library are utilized during the assessment to significantly enhance the computational efficiency.

Key words： combat system; complex network; modeling; key node; kill chain