基于ARCH族模型的股票超高频数据的波动性研究

【摘 要】论文基于浦发银行股票的逐笔交易数据，利用ARCH族模型对其超高频数据中的波动性进行了研究。论文首先通过对数据的预处理和单位根检验，确保了数据的平稳性，随后应用多种ARCH族模型对波动性进行建模与比较，最终选择TGARCH（2，1，1）模型作为最优模型。该模型不仅能够捕捉数据中的波动集聚效应，还揭示了显著的波动非对称性。研究结果表明，浦发银行的股票收益波动性具有显著的持久性和杠杆效应，负面冲击对波动的影响大于正面冲击。基于这些发现，论文提出了加强高频交易监管、优化投资策略和强化风险管理等政策启示。

【关键词】超高频数据；ARCH族模型；波动性；浦发银行

【中图分类号】F832.5 【文献标志码】A 【文章编号】1673-1069（2024）08-0056-03

1 引言

金融市场研究中，时间序列分析尤重，高频数据尤其超高频数据为股市微观结构和波动性研究带来新视角。市场波动性作为监管核心，影响投资决策及市场稳定[1]。逐笔交易数据作为超高频数据源，详尽记录交易信息，揭示市场瞬时动态，助力高频交易分析与市场微观结构探索[2]。但其海量与复杂性要求严格的数据预处理。本研究采用ARCH族模型，针对浦发银行股票超高频数据，旨在精确量化其波动性特征，为市场动态提供量化分析。此研究不仅深化了对市场风险的理解，也为投资者与监管者提供宝贵洞见，助力有效市场监管与决策。

2 ARCH族模型

2.1 ARCH模型

rt为因变量，xt为自变量，εt为误差项，ht为时间t的条件方差。且vt独立同分布，均值为0，方差为1，则称误差序列εt服从阶数为m的ARCH过程，简记为εt～ARCH（m），此时vt为一个白噪声序列。

2.2 GARCH模型

其中，vt独立同分布，满足均值为0，方差为1。

2.3 EGARCH模型

EGARCH模型在20世纪90年代提出，EGARCH（p，r，q）模型可表示为：

2.4 TGARCH模型

国外学者提出了以下的TGARCH（m，s，q）模型：

其中，dt-k是一个虚拟变量，θi为非负参数。

3 实证分析

本文选取浦发银行2024年5月20日的逐笔交易_{I0H42YR/RHSjs8a7L7AXGw==}数据，研究其波动性。作为中国主要的股份制商业银行之一，浦发银行在证券市场上流动性高、交易活跃，其数据能够代表中国证券市场的特征。

3.1 模型构建

3.1.1 数据预处理及基本信息

对搜集到的超高频数据进行复合对数收益率处理：rt=ln（pt）-ln（pt-1）。其中，rt和pt分别表示t时slK6dwImp6vRsuDN3A1c4g==刻的收益率和收盘价，未详细展示64 015笔交易的波动情况。

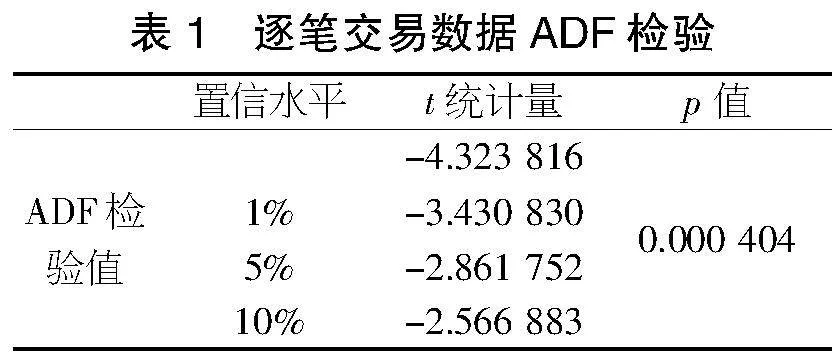
通过统计基本信息，发现对数收益率序列的均值和标准差非常小，表明股市收益率在5月20日整体接近0，且波动不大。偏度为-0.048，说明存在左拖尾；峰度为5.237，体现尖峰厚尾特征。JB统计量表明该序列不服从正态分布。单位根检验结果显示t统计量为-4.32，小于1%显著水平，p值接近0，拒绝原假设，表明数据平稳。

之后进行单位根检验，结果如表1所示。其中t统计量为-4.32，小于1%的置信水平下对应的临界值-3.43。其对应的p值与0非常接近，小于0.05的显著性概率，拒绝原假设，即对数收益率数据是平稳的。

3.1.2 均值模型构建

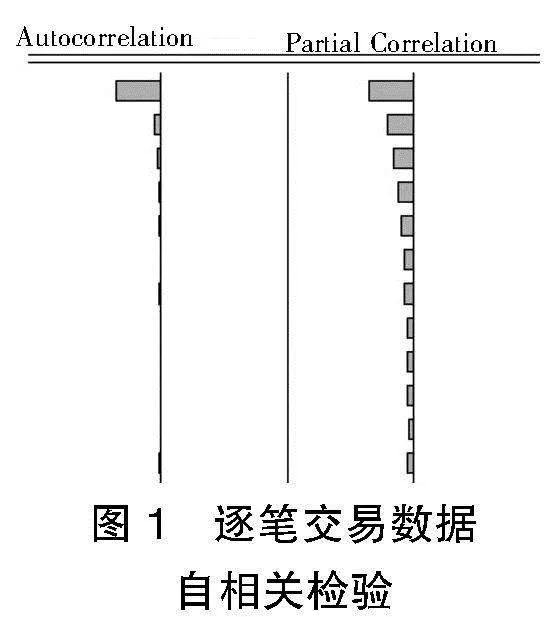
在构建ARCH模型前，需建立均值方程以剔除序列中的线性依赖，所以先进行自相关（ACF）和偏自相关（PACF）检验，结果如图1所示。

通过序列的自相关（ACF）和偏自相关（PACF）检验，发现滞后1期显著自相关，表明序列中存在短期依赖关系，但在更长的滞后期，序列趋于独立。偏自相关显示滞后1至3期与当前期存在明显关联，适用AR（1）和AR（3）模型。

表2给出滞后5阶数据的Ljung-Box Q统计量及其对应的p值，残差序列在滞后1期到5期均具有显著的自回归条件异方差性（ARCH效应）。这种效应表明，序列波动性具有时间上的依赖性，因此需要进一步通过ARCH族模型来捕捉波动集聚性。

为选择最佳均值方程，尝试多种ARMA模型并比较AIC值，最终确认ARMA（3，2）模型最优，且所有参数通过显著性检验（p值<0.05），显示模型拟合效果良好（见表3）。在ARMA（3，2）模型中，自回归项和移动平均项的系数均通过了显著性检验，表明收益率序列在滞后3期内具有显著的自回归特征，而滞后2期的移动平均项对当前期的波动也产生了显著影响。整体来看，模型较好地捕捉了序列中的短期波动性和结构性依赖特征。

3.1.3 ARCH族模型构建

为了捕捉收益率序列的波动性，本研究选用了ARCH、GARCH、EGARCH和TGARCH等模型，考虑了不同分布假设，并通过AIC和SC准则选择最优模型。

在模型构建过程中，首先选择了不同的GARCH族模型，包括ARCH（1）、ARCH（2）、GARCH（1，1）、GARCH（1，2）、GARCH（2，1）、EGARCH以及TGARCH等模型。通过t分布假设，估计了各模型的参数，结果显示大部分模型中的参数均具有统计显著性（见表4）。

对于ARCH（1）和ARCH（2）模型，残差平方项的系数均显著为正，表明过去期的波动性对当前波动性具有显著影响。然而，随着模型阶数的增加，如在GARCH（1，1）和GARCH（2，1）模型中，GARCH项的系数依然显著且接近1，显示出时间序列中的波动性具有较强的持久性。

在EGARCH模型的估计中，非对称性效应得到了较好的刻画。EGARCH（1，1，1）模型中的非对称项显著为负，表明负面冲击对波动性的影响大于正面冲击，这与金融市场中的“杠杆效应”一致。同样地，TGARCH模型通过引入门限项，进一步证实了市场波动中的非对称性特征。

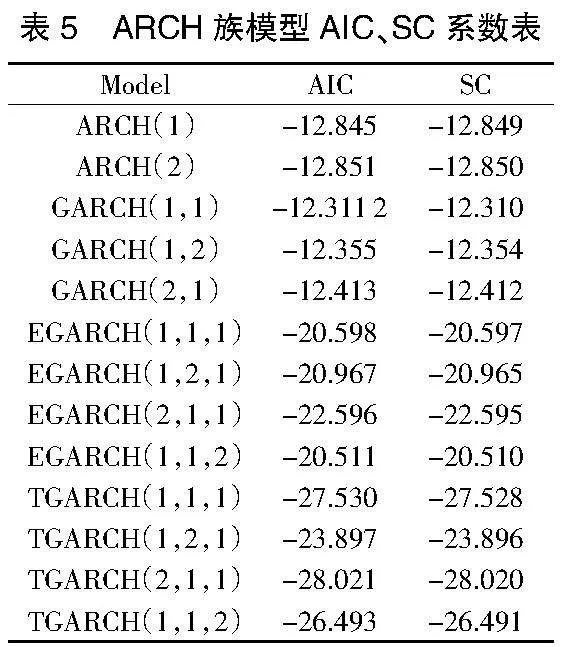
为了确定最优的模型，本研究依据AIC和SC信息准则对不同模型进行了比较，如表5所示。AIC值和SC值越小，表明模型对数据的拟合程度越高。

TGARCH（2，1，1）模型的AIC和SC值最低，因此可以认为TGARCH（2，1，1）模型最佳。

此外，EGARCH模型也表现出较为优良的拟合效果，尤其在处理金融市场波动的非对称性方面具有独特优势。相比之下，ARCH和GARCH模型虽然能够捕捉波动集聚性，但在处理复杂的非对称波动时存在局限。

3.2 TGARCH（2，1，1）模型的结果分析

在构建多种ARCH族模型后，通过比较AIC、SC等信息准则，发现TGARCH（2，1，1）模型在处理收益率波动非对称性方面表现最佳。该模型不仅能够解释超高频数据中的波动集聚现象，还能捕捉市场波动中的杠杆效应。因此，我们最终选择此模型进行详细的分析与解释（见表6）。

模型的均值方程中AR（1）和AR（2）显著为负，表明收益率存在负相关性，MA（1）和MA（2）为正，显示过去收益率对当前波动有正向影响。

TGARCH（2，1，1）模型表明：①波动集聚性。滞后残差的平方项和条件方差项均为正且显著，表明股票收益率的波动存在明显的集聚性。②杠杆效应。通过非对称项的显著性检验，TGARCH模型显示了负向冲击对波动的放大效应，验证了市场上的杠杆效应。③持久性。方差方程中的GARCH项接近1，表明波动具有较强的持久性。说明短期内波动不会迅速减弱。4 结论与政策启示

4.1 结论

本文基于浦发银行2024年5月20日的逐笔交易数据，采用ARCH族模型对其超高频数据的波动性进行了分析。通过单位根检验确定数据的平稳性后，比较了多种ARCH族模型，最终选取TGARCH（2，1，1）模型作为最优模型，该模型捕捉了波动集聚效应和非对称性特征。

实证结果显示，浦发银行股票的波动性具有显著的集聚性，过去的波动性对当前波动具有持续影响，且波动不会迅速衰减。通过引入t分布假设，模型捕捉了超高频数据中的非对称效应，验证了负面冲击对市场波动的放大效应，即当股市面临不利消息时，波动性显著上升，而正面冲击的影响则相对较弱。这一结果与金融市场中的杠杆效应相吻合，反映了负面消息对市场情绪和交易行为的强烈冲击。

4.2 政策启示

基于研究，提出以下政策建议：首先，监管者应加强对超高频交易的监控，防止市场过度波动，确保市场稳定；其次，投资者应重视负面冲击对市场波动的放大效应，制定更保守的投资策略，并利用对冲工具应对极端波动；最后，市场参与者应加强波动性分析与风险管理，利用ARCH模型实时监测波动，优化投资组合，提升风险管理能力，以适应市场开放和国际化的需求。

【参考文献】

【1】潘斯，许天仁.融资融券对我国股票市场价格波动性的影响研究[J].全国流通经济，2021（24）：148-150.

【2】杨科，张洲深，田凤平.高频数据环境下我国股票市场的波动率预测——基于机器学习和HAR模型的融合研究[J].计量经济学报，2023，3（03）：886-904.