“双减”背景下初中数学单元作业整体设计初探

［ 摘 要 ］随着“双减”政策的实施和“五项管理”的落地，作业问题再次引起人们的广泛关注.以“认识三角形”为例，通过“单元课标分析、单元教材分析、单元学情分析、单元目标制定、单元整体规划”等环节的系统分析，给出其单元整体视域下第一课时的作业设计，并结合案例给出初步思考：单元作业整体设计-调控数量，提高质量；单元作业整体设计-分层呈现，面向全体；单元作业整体设计-一以贯之，一脉相承.

［ 关键词 ］单元作业；整体设计；认识三角形；“双减”

缘起

随着“双减”政策的实施和“五项管理”的落地，作业问题再次引起了人们的广泛关注 . 那么，如何以作业为切入点，切实减轻学生过重的课业负担？如何确保在作业数量减少的情况下提高教学质量？对作业进行单元整体设计成为实现上述目的的有效途径 . 本文依托对“认识三角形”一章的整体分析，给出“减负高效优质”的“认识三角形 （第1课时） ”的作业设计，以期抛砖引玉，不当之处，敬请指正.

案例呈现

为更好地进行单元视角下课时作业的设计，我们构建了基本流程：单元课标分析、单元教材分析、单元学情分析、单元目标制定、单元整体规划、具体课时作业.下面，分别进行简单介绍.

1.单元课标分析

《义务教育数学课程标准（2022年版）》（以下简称“新课标”）对本章提出了明确要求：“1.理解三角形及其内角、外角、中线、高线、角平分线等概念，了解三角形的稳定性；2.探索并证明三角形的内角和定理.掌握它的推论：三角形的外角等于与它不相邻的两个内角的和；3.证明三角形的任意两边之和大于第三边；4.理解全等三角形的概念，能识别全等三角形中的对应边、对应角，等等.”

以上课标要求中的第2、4条，涉及定理与定理证明的内容属于学段终9VexXkycOUmLh+yO+0SfTPV3SUs4oGKVLf+hj6iQqEk=极目标，本套教材的编写将分阶段实施，现阶段关于演绎推理的要求以“教学目标”为准，相关内容的学段终极目标的实现安排在七年级下册.

2.单元教材分析

初中阶段图形与几何领域包括“图形的性质”“图形的变化”和“图形与坐标”三个主题.本单元选自山东教育出版社《义务教育教科书（五四学制）数学七年级上册》第一章，隶属于图形与几何中的图形性质部分.本单元主要包含五部分内容：认识三角形、图形的全等、探索三角形全等的条件、三角形的尺规作图和利用三角形全等测距离.

本单元是在认识了三角形的特征、三角形的分类、通过度量和操作知道了三角形的内角和为 180°，三角形的两边之和大于第三边；通过六下“相交线与平行线”学习了平行线的性质和判定方法，会用尺规作一条线段等于已知线段、作一个角等于已知角的基础上，对三角形进一步深入和拓展.它是图形与几何部分的基础内容，为后续学习研究轴对称、等腰三角形、平行四边形和圆等几何图形奠定了基础.

3.单元学情分析

认知基础：学生在前一阶段的学习过程中，积累了观察、度量、计算、拼图等数学活动经验，空间观念、几何直观、推理能力也得到了初步的培养和锻炼.

活动经验：七年级学生的思维活跃，接受能力强，具备了一定的数学探究活动经验和应用数学的意识.薄弱之处：

1.图形语言、文字语言和数学符号语言的相互转换是一个循序渐进的过程，在学习的初始阶段用数学符号语言表达推理过程是一个难点；

2. 探索三角形全等的条件时，运用分类讨论的思想方法、转化的思想方法是难点.以上教学以及作业设计时应该重点关注，特别是在作业设计中应有针对性地进行“补偿”呈现，体现“教学评”一致性.

4.单元目标制定

基于课标、学情及教材、单元大概念对单元教学所要达成的目标进行细化，分为知识目标和素养目标.

（1）知识目标

①研读文本，结合生活实例说出对全等形与全等三角形的理解，探究全等三角形的性质，进行边与角的转化.

②通过画图、叠合、探究、观察等活动，分析三角形全等所需要素，探索三角形全等的四种判定方法并初步运用，说出判定两个三角形全等的思路.

③用尺规作三角形，并说出理论依据，探究全等三角形的应用价值，同时初步了解尺规作图的依据.

④围绕全等三角形的概念、性质、判定进行重构过关，灵活应用全等三角形模型、转化思想解决综合问题.

（2）素养目标

①在探索图形性质的过程中，经历观察、操作、想象、推理、交流等环节，积累数学活动经验，进一步发展空间观念和推理能力.

②尝试用多种方式表达自己的想法，表述问题解决的理由，培养初步的演绎推理能力和条理表达的能力.

③感受数学与现实世界的密切联系，引导学生体会“数学来源于生活，又服务于生活”，形成“三会”.

（3）重点难点

①重点：三角形的基本要素及其基本性质和三角形的全等.

②难点：三角形基本性质及三角形全等的应用.

5.单元整体规划

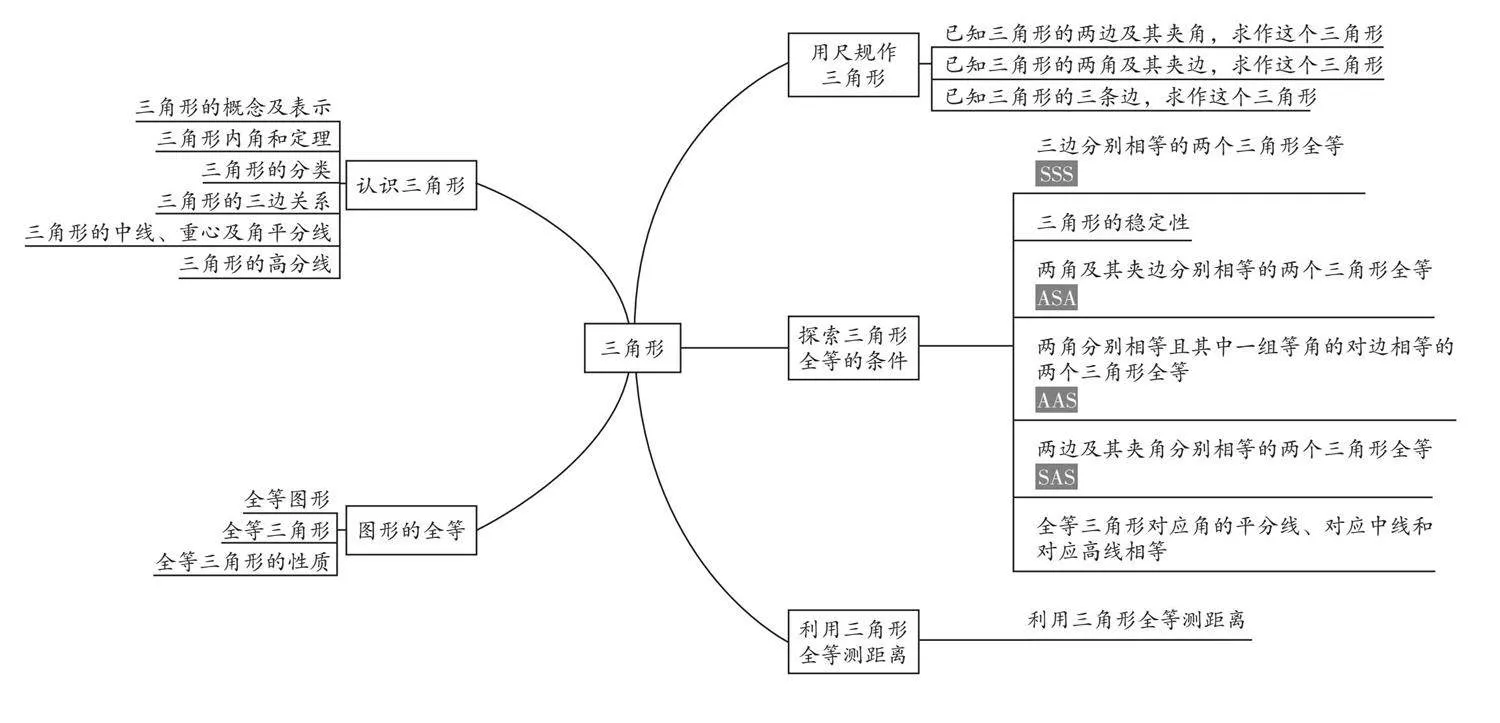
（1）构建单元知识网络

（2）单元作业设计思路

①单元整体规划：三角形是图形与几何部分的基础内容，为后续学习研究轴对称、等腰三角形、平行四边形和圆等几何图形奠定了基础.作业设计重在兴趣引导，以帮助学生理解基础内容为主，题量不宜过多，难度适中，但是作业批改和讲评要及时、规范等.

②课时分层呈现：每课时均设计“基础性作业”（面向全体，体现课标，要求学生必做）和“发展性作业”（体现个性化、探究性、实践性，要求学生有选择地完成），具体设计体系如下.

6.具体课时作业——以第一课时为例

第一部分：课堂练习作业

基础达标：

1.（原创）△ABC的三角之比

是1：2：3，则△ABC是（

A.锐角三角形

B.直角三角形

C.钝角三角形

D.无法确定

2.（原创）图中以AB为边的三 角形共有______个.

3. （引 用） 如 图 ， AB∥CD，AC⊥BC，∠BAC = 65°，则∠BCD =_______.

4. （原创） 如图，线段 AC 与BD相交于点E，连接AD，AB，BC.

（1） 指出图中有几个三角形，并分别用字母表示出来；

（2） ∠AED是哪个三角形的角？∠DBC呢？

（3） AE是哪两个三角形的公共边？AB是哪几个三角形的公共边？

（4） ∠D 是哪两个三角形的公共角？

第二部分：课后延伸作业 （针对A、B、C层学生设计）

基础达标：

5. （原创） 如图是钝角三角形的是（ ）

6. （改编） 已知△ABC 的周长是 24 cm，若三边 a，b，c 满足 b∶c = 3∶4，且a = 2c - b，则边a的长度是__________.

7. （原创） 如图，共有______个三角形.

8. （改编） 如图，已知 D 是△ABC 的边 BC 延长线上的一点，DF⊥AB，交 AB 于点 F，交e3a68a4d807755cb03c0d6e40e3bcb00 AC 于点E，∠A = 55°，∠D = 30°，求∠ACB的度数.

能力提升：

9. （引用） 过 A，B，C，D，E五个点中任意三点画三角形.

（1） 其中以 AB 为一边可以画出_________个三角形；

（2） 其中以 C 为顶点可以画出________个三角形.拓展延伸：

10.（引用）观察图形规律：

（1） 图①中共有_________个三角形，图②中共有_________个三角形，图③中共有________个三角形；

（2） 由以上规律进行猜想，第n个图形共有_______个三角形.

几点思考

1.单元作业整体设计：调控 数量，提高质量

严格按照“双减”要求，合理 调控学生书面作业总量，建立数学 作业布置协商机制，每天由数学教 师负责协调，控制书面作业量，确 保学生每天书面作业平衡，实现调 控数量、提高质量的初衷.

同时，提高单元作业整体设计， 聚焦关键环节，围绕重点、难点和核 心考点，从知识、思想和素养等角度 进行作业设计，螺旋上升，逐步增加 难度，起到事半功倍的效果.

2.单元作业整体设计：分层 呈现，面向全体

依据课标、教材、学情，面向全 体，实行分类、分层布置作业，比如 上述作业设计中的基础达标、能力提 升、延伸拓展等环节；同时布置弹性 和个性化作业，比如在课时作业的基 础上，还可以设计单元检测作业、单 元实践作业、单元项目作业、单元写 作作业等多种长周期作业.

3.单元作业整体设计：一以贯之，一脉相承

单元整体作业设计还可以通过体例上的“一以贯之”与情境上的“一脉相承”来体现其整体性.比如在“认识三角形”一章的每个课时的作业设计中采用统一的体例，在数量上一致，每个课时 10个题目；在结构上一致，分为基础达标、能力提升、延伸拓展等三类；此外还可以在情境设计上体现“一脉相承”，比如对上述作业设计的第 10题，在后续课时中可以继续出现，可以让学生判断三角形的形状、画出三角形的高等，以此提升效率，提高质量.

总之，单元视角下的作业整体设计具有调控数量，提高质量；分层呈现，面向全体；一以贯之，一脉相承等优点，值得一线教师在教学中积极践行，为落实“双减”政策贡献数学力量.