“不变性”作为十二音系统的逻辑链

摘 要：不变性，是十二音序列在变化时保持不变的音乐特征或关系。文章提出米尔顿·巴比特的“不变性”理论——包括移位不变性与倒影不变性，对他的十二音系统创作起到决定性逻辑作用。同时，在巴比特的晚期创作中，尤其在大型矩阵复合式作品中也对音高组织的细节处理表现出不同的“不变性”的结构思维。

关键词：不变性；十二音；米尔顿·巴比特；矩阵

中图分类号：J614 文献标识码： A 文章编号：1004 - 2172（2024）04-0123-10

DOI：10.15929/j.cnki.1004 - 2172.2024.04.016

十二音作曲系统在性质和含义上是真正具有“革命性”程度的，就如同任何抽象模型完满的公式化系统一样，十二音系统可以通过要素的陈述、内部的关系来完整地描述音乐特征，并对相关音乐元素设定相应操作。在这个作曲程序中，作曲家使用这种“公式化系统”进行非公式化处理，所得到的某种“不变性”，是本文分析研究的重要焦点。约瑟夫·施特劳斯 （Joseph Straus）在教科书《后调性理论导论》（An Introduction to Post-Tonal Theory） 中这样定义“不变性”：十二音作品中的序列不管进行何种移位变型组合排列，总能辨识出一些保持不变的音乐特征或关系[1]。米尔顿·巴比特（Milton Babbitt）更是认为“不变性”是十二音作品的决定性作曲技术。

一、“不变性”的决定性因素

巴比特在对“不变性”理论的研究文章《不变性是十二音作曲的决定性因素》[2]中，围绕勋伯格《第三弦乐四重奏》（Op.30）及韦伯恩《钢琴变奏曲》（Op.27，第二乐章）两个例子，分别说明原型序列与移位序列间，以及互为倒影形式序列间的不变性特征及产生的逻辑关系。这种逻辑关系，正是“不变性”的决定性因素，即移位不变性与倒影不变性。

（一）移位不变性

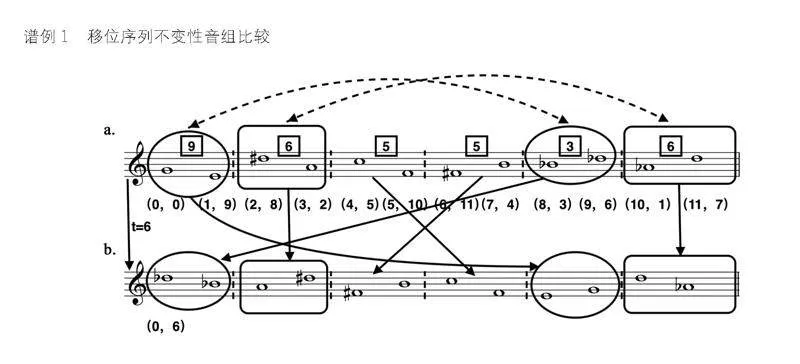
十二音系统中首先需要考虑的是排列性质，移位会导致原始序列中不存在的音高相邻，从而建立一个新的子集并导致元素的置换。“传统”作曲意义上的移位，即移调，意味着基本轮廓的保留。从字面上讲，将移位定义为十二音系统内的一项变化形式是毫无意义的，因为轮廓是音乐元素独特音区的表现功能，音区与音长、音强、音色或与作曲表现必然相关的任何其他属性一样不受集合结构的定义。由于这种限定很容易导致十二音系统原理与作曲容许性（即“一个序列可以用任何八度表示”）之间的混淆，因此，更有效的方法是用数字符号、有序数对的标记来体现移位变化：数对中的第一个成员表示该音所处序列中的位置，第二个成员表示音高级的“音高号”。巴比特正是利用这种方式定义了勋伯格《第三弦乐四重奏》（Op.30）的原型序列（见谱例1）。

任何序列的移位可以通过将整数0 —11添加到集合的每个音高数来表示。如果 （a，b） 是表示P序列的某一元素，则移位t后该元素变为 （a，b+t） ，其中t为“移位数”。 因此，序列的移位值则被视为对音高数的操作与排列。与给定P序列相关的十二个移位序列的总和构成一个组合群，凭借生成的群结构，以及源自该组群的交换和传递性质，可以推导出与序列移位相关的附加属性。由于每个t值都会导致序列元素的完全紊乱，却又有着相同的音程顺序，因此在寻找移位组合层次化标准时，这些属性都不能作为区分的基础。同样，移位的每一个值都定义了一个常规置换，但随着互补t（和为0的数字，模12）与只有这样的t产生相同顺序的倒影置换，区分的不变性基础出现了。这些属性其中的不变量（在移位操作下保留的集合属性，以及集合之间的某些关系），可以视为十二音系统中的“不变性”结构，需要在音高集合以及音程集合上具有同一性的能力。互补的移位算子对原型序列来说，会产生相同数量的音级邻接，包括有序邻接和反向邻接。如果一个序列的a和b、c和d表示处于连续序号位置的音集，如果移位算子为t，而a+t=c，b+t=d，那么在t的移位下，a和b与处于原型序列位置中的c和d相关联；在12-t的移位下，c和d与处于原型序列位置的a和b相关联。原型序列的音程结构决定了在特定移位算子及其补码下保留的不变邻接组，这个数字来源于原型序列中具有功能性与多重性的互补音程数。

例如，将谱例1a的序列按照相邻关系两两一组，分成六个相邻二音组：（0，0）与（1，9）；（2，8）与（3，2）；（4，5）与（5，10）；（6，11）与（7，4）；（8，3）与（9，6）；（10，1）与（11，7），这六个二音组的内部音程关系（半音数）为[965536]。由此，第三组与第四组各自内部的音程距离均为5，而两组之间的音程距离是6；第一组和第五组各自内部的音程距离为互补的9和3，而两组之间的音程距离也是6；除此之外，第二组和第六组各自内部的音程距离均为6。因而，将该序列进行t=6的移位操作（见谱例1b），同样进行相邻二音组的划分，这六个音组分别与原型序列保持了相应的不变性。以原型序列二音组为参照，T6序列出现的六个音组顺序为第五组、第二组、第四组、第三组、第一组、第六组，音程距离为6的两组在t=6的移位下互换，而本身内部音程距离为6的音组保持不变。这体现了利用序列移位形式扩展到序列元素保持不变性的有效手段。

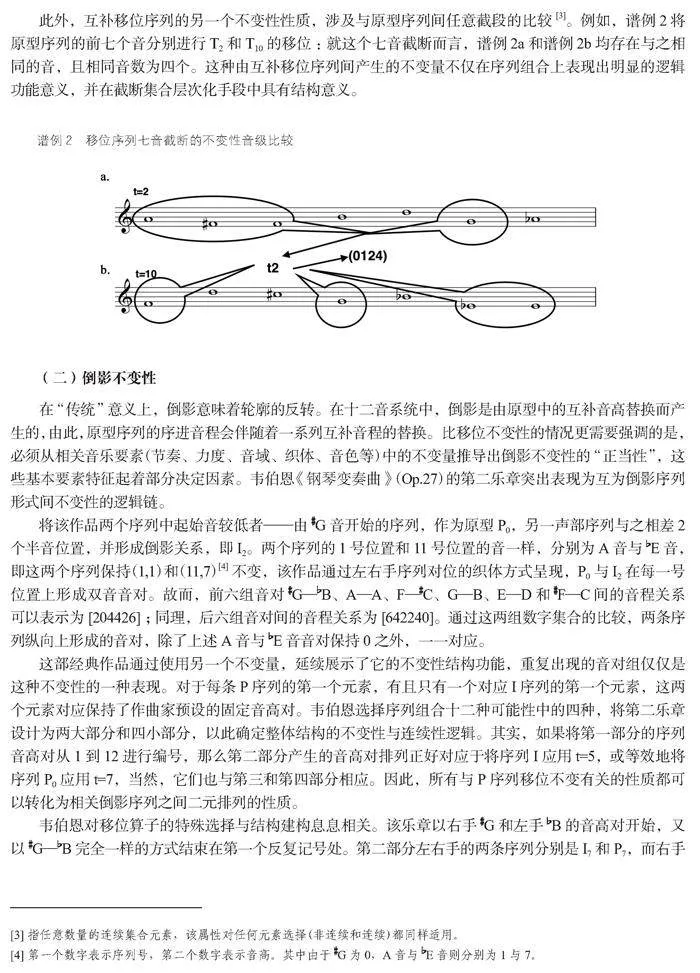
此外，互补移位序列的另一个不变性性质，涉及与原型序列间任意截段的比较[3]。例如，谱例2将原型序列的前七个音分别进行T2和T10的移位：就这个七音截断而言，谱例2a和谱例2b均存在与之相同的音，且相同音数为四个。这种由互补移位序列间产生的不变量不仅在序列组合上表现出明显的逻辑功能意义，并在截断集合层次化手段中具有结构意义。

（二）倒影不变性

在“传统”意义上，倒影意味着轮廓的反转。在十二音系统中，倒影是由原型中的互补音高替换而产生的，由此，原型序列的序进音程会伴随着一系列互补音程的替换。比移位不变性的情况更需要强调的是，必须从相关音乐要素（节奏、力度、音域、织体、音色等）中的不变量推导出倒影不变性的“正当性”，这些基本要素特征起着部分决定因素。韦伯恩《钢琴变奏曲》（Op.27）的第二乐章突出表现为互为倒影序列形式间不变性的逻辑链。

将该作品两个序列中起始音较低者——由G音开始的序列，作为原型P0，另一声部序列与之相差2个半音位置，并形成倒影关系，即I2。两个序列的1号位置和11号位置的音一样，分别为A音与E音，即这两个序列保持（1，1）和（11，7）[4]不变，该作品通过左右手序列对位的织体方式呈现，P0与I2在每一号位置上形成双音音对。故而，前六组音对G—B、A—A、F—C、G—B、E—D和F—C间的音程关系可以表示为[204426]；同理，后六组音对间的音程关系为[642240]。通过这两组数字集合的比较，两条序列纵向上形成的音对，除了上述A音与E音音对保持0之外，一一对应。

这部经典作品通过使用另一个不变量，延续展示了它的不变性结构功能，重复出现的音对组仅仅是这种不变性的一种表现。对于每条P序列的第一个元素，有且只有一个对应I序列的第一个元素，这两个元素对应保持了作曲家预设的固定音高对。韦伯恩选择序列组合十二种可能性中的四种，将第二乐章设计为两大部分和四小部分，以此确定整体结构的不变性与连续性逻辑。其实，如果将第一部分的序列音高对从1到12进行编号，那么第二部分产生的音高对排列正好对应于将序列I应用t=5，或等效地将序列P0应用t=7，当然，它们也与第三和第四部分相应。因此，所有与P序列移位不变有关的性质都可以转化为相关倒影序列之间二元排列的性质。

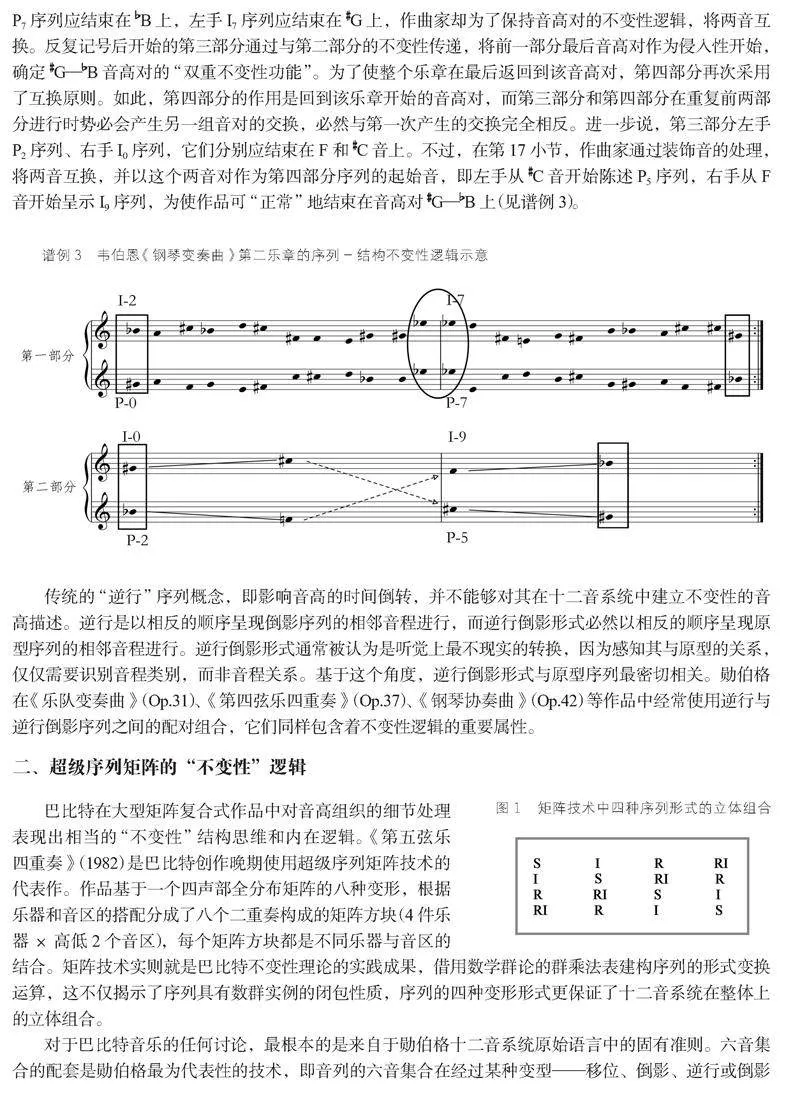
韦伯恩对移位算子的特殊选择与结构建构息息相关。该乐章以右手G和左手B的音高对开始，又以G—B完全一样的方式结束在第一个反复记号处。第二部分左右手的两条序列分别是I7和P7，而右手P7序列应结束在B上，左手I7序列应结束在G上，作曲家却为了保持音高对的不变性逻辑，将两音互换。反复记号后开始的第三部分通过与第二部分的不变性传递，将前一部分最后音高对作为侵入性开始，确定G—B音高对的“双重不变性功能”。为了使整个乐章在最后返回到该音高对，第四部分再次采用了互换原则。如此，第四部分的作用是回到该乐章开始的音高对，而第三部分和第四部分在重复前两部分进行时势必会产生另一组音对的交换，必然与第一次产生的交换完全相反。进一步说，第三部分左手P2序列、右手I0序列，它们分别应结束在F和C音上。不过，在第17小节，作曲家通过装饰音的处理，将两音互换，并以这个两音对作为第四部分序列的起始音，即左手从C音开始陈述P5序列，右手从F音开始呈示I9序列，为使作品可“正常”地结束在音高对G—B上（见谱例3）。

传统的“逆行”序列概念，即影响音高的时间倒转，并不能够对其在十二音系统中建立不变性的音高描述。逆行是以相反的顺序呈现倒影序列的相邻音程进行，而逆行倒影形式必然以相反的顺序呈现原型_{2029b2f7e36b20342acd6e7ebce05e98}序列的相邻音程进行。逆行倒影形式通常被认为是听觉上最不现实的转换，因为感知其与原型的关系，仅仅需要识别音程类别，而非音程关系。基于这个角度，逆行倒影形式与原型序列最密切相关。勋伯格在《乐队变奏曲》（Op.31）、《第四弦乐四重奏》（Op.37）、《钢琴协奏曲》（Op.42）等作品中经常使用逆行与逆行倒影序列之间的配对组合，它们同样包含着不变性逻辑的重要属性。

二、超级序列矩阵的“不变性”逻辑

巴比特在大型矩阵复合式作品中对音高组织的细节处理表现出相当的“不变性”结构思维和内在逻辑。《第五弦乐四重奏》（1982）是巴比特创作晚期使用超级序列矩阵技术的代表作。作品基于一个四声部全分布矩阵的八种变形，根据乐器和音区的搭配分成了八个二重奏构成的矩阵方块（4件乐

器×高低2个音区），每个矩阵方块都是不同乐器与音区的结合。矩阵技术实则就是巴比特不变性理论的实践成果，借用数学群论的群乘法表建构序列的形式变换运算，这不仅揭示了序列具有数群实例的闭包性质，序列的四种变形形式更保证了十二音系统在整体上的立体组合。

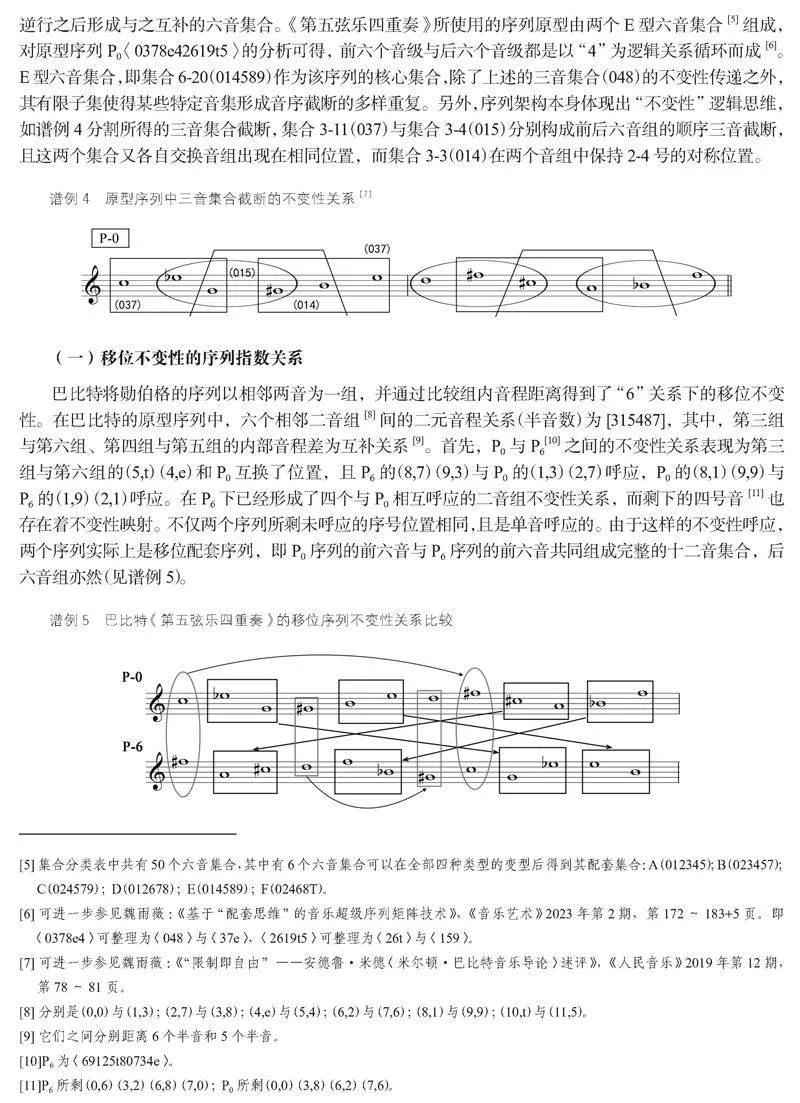
对于巴比特音乐的任何讨论，最根本的是来自于勋伯格十二音系统原始语言中的固有准则。六音集合的配套是勋伯格最为代表性的技术，即音列的六音集合在经过某种变型——移位、倒影、逆行或倒影逆行之后形成与之互补的六音集合。《第五弦乐四重奏》所使用的序列原型由两个E型六音集合[5]组成，对原型序列P0〈0378e42619t5〉的分析可得，前六个音级与后六个音级都是以“4”为逻辑关系循环而成[6]。E型六音集合，即集合6-20（014589）作为该序列的核心集合，除了上述的三音集合（048）的不变性传递之外，其有限子集使得某些特定音集形成音序截断的多样重复。另外，序列架构本身体现出“不变性”逻辑思维，如谱例4分割所得的三音集合截断，集合3-11（037）与集合3-4（015）分别构成前后六音组的顺序三音截断，且这两个集合又各自交换音组出现在相同位置，而集合3-3（014）在两个音组中保持2-4号的对称位置。

（一）移位不变性的序列指数关系

巴比特将勋伯格的序列以相邻两音为一组，并通过比较组内音程距离得到了“6”关系下的移位不变性。在巴比特的原型序列中，六个相邻二音组[8]间的二元音程关系（半音数）为[315487]，其中，第三组与第六组、第四组与第五组的内部音程差为互补关系[9]。首先，P0与P6[10]之间的不变性关系表现为第三组与第六组的（5，t）（4，e）和P0互换了位置，且P6的（8，7）（9，3）与P0的（1，3）（2，7）呼应，P0的（8，1）（9，9）与P6的（1，9）（2，1）呼应。在P6下已经形成了四个与P0相互呼应的二音组不变性关系，而剩下的四号音[11]也存在着不变性映射。不仅两个序列所剩未呼应的序号位置相同，且是单音呼应的。由于这样的不变性呼应，两个序列实际上是移位配套序列，即P0序列的前六音与P6序列的前六音共同组成完整的十二音集合，后六音组亦然（见谱例5）。

P2与Pt均为P0的移位配套序列，另也存在一种“不变性”序列，它们的前后六音组相同，即P4与P8序列是P0的“相同”序列。移位序列可分为两组：配套组和相同组，观察两组序列的指数，配套组的P2-6-t与相同组的P0-4-8均建立在以“4”为基数的循环关系。这种“4”的循环关系不仅是巴比特架构序列的逻辑核心，还成了一种不变性的序列选择逻辑链，即公式化表示为Invariant[P0-Px] →[Px=Px+4n]（n为1，2，3）。

（二）倒影不变性的序列指数关系

《第五弦乐四重奏》原型序列的核心三音集合3-3（014）、3-4（015）和3-11（037）分别作为非离散三音集合出现在序列前后两个六音截断中各一次。集合（014）分别在P2与Pt下互相映射，集合（015）与（037）则是通过倒影关系呈现不变性。而序列前后六音组中分别出现的三个核心四音集合4-17（0347）、4-19（0148）与4-20（0158）也同样在倒影I5与I9关系中体现着不变性。这里，I5与I9的指数又出现了“4”关系，按照此逻辑链推理，I1势必与P0存在某种倒影等同关系，或I1一定与I5、I9存在某种不变性关系。

根据巴比特对韦伯恩作品倒影序列不变性的研究，两条互为倒影关系的序列以纵向上形成的二音对作为不变性形态贯穿。如果将指数“4”关系代入巴比特的P0序列，I7、Ie序列与其在相同序号位置上形成的纵向二音对在其他位置上保持不变性，构成倒影不变性序列关系。按照移位不变性序列的指数公式带入，与P序列形成如此关系的倒影序列间的指数关系可以类比为公式Px=Ix+3+4n（n=0，1，2）。因而，倒影序列间同样存在指数为“4”循环的不变性逻辑链。

序列I5、I9与P0除了上述的音列局部不变性之外，它们还是P0的倒影配套序列，即它们的前后六音组与P0为配套关系，P1亦然。因此，与P序列形成配套关系的倒影序列间的指数关系可以类比为Px=

Ix+1+4n（n=0，1，2）。该作品序列选择逻辑除了以上分析所得的“4”循环之外，最核心的“不变性”逻辑链是利用互为倒影配套的序列进行，这也是巴比特矩阵技术的灵魂所在，由此形成横向上两条互为倒影关系的音列有序呈示，纵向上两个互补六音集合“块状”呈示的音响效果。

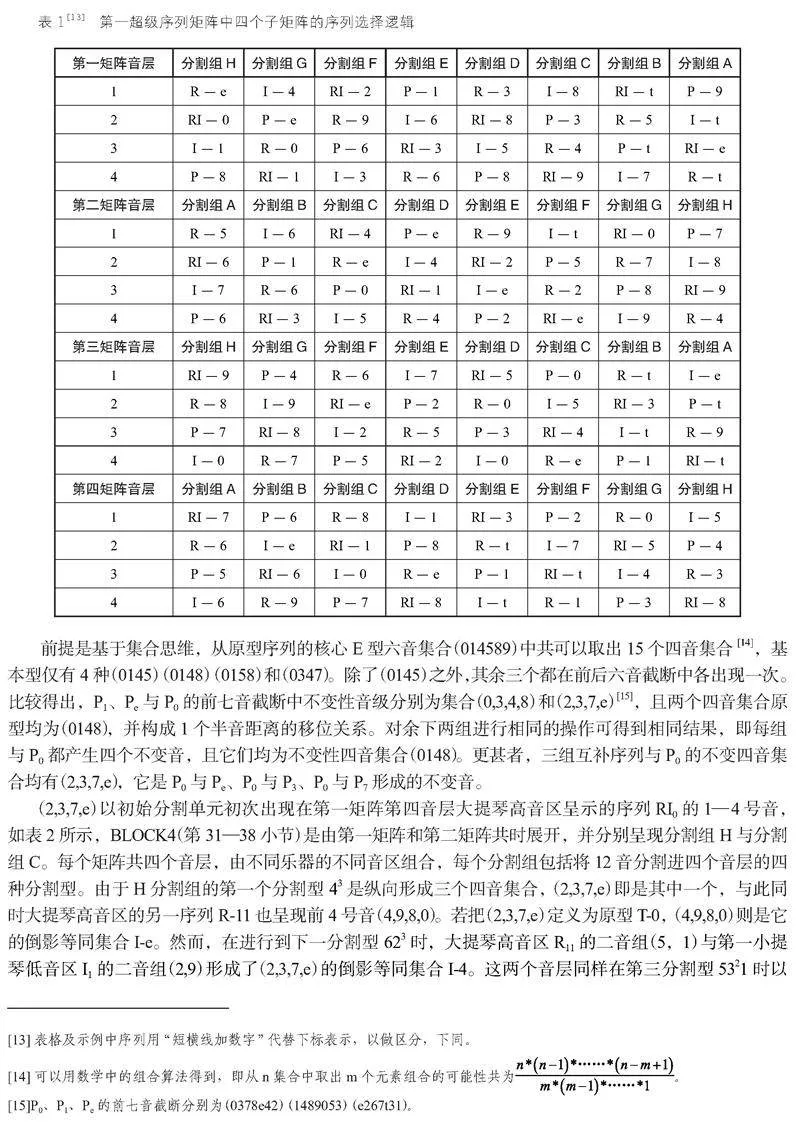
以第一超级序列矩阵呈示的四个矩阵为例来研究序列指数关系，四个音层在呈示八个分割组下的序列进行可以分为两组配套关系：音层1-2的一对序列指数间关系为（+1，+5，+5，+5，+5，+5，+5，+1）；而音层3-4的一对序列指数间关系为（+1，+9，+5，+9，+9，+9，+1，+5）。因此，纵向音层对之间的一对倒影配套序列，可以用公式表示指数Px=Ix+1+4n（n=0，1，2）关系。且在每个音层的横向呈示上，同时仍存在着序列形式的循环以及指数“4”循环的逻辑不变性。如以第一矩阵第一音层为例，分割组H-E分别陈述四种序列形式：R-e、I-4、RI-2和P-1，之后，在分割组D-A再次以这四种序列形式出现顺序依次为R-3、I-8、RI-t和P-9，相同序列形式间的指数关系均为“4”关系。因而，由此实现Invariant（不变）→Non-Invariant（非不变）之“以不变应万变，然不变即万变”。（见表1）

（三）四音集合的不变性关系

巴比特在其另一代表性文章《集合结构作为作曲的一个决定要素》[12]中指出，在任何作曲系统技术中保留的集合形式及衍生关系会架构起作品的独特逻辑结构。根据巴比特对互补序列不变性的研究，同样将原型序列与某个移位序列及它的互补序列的前七音截断集合进行比较，选择哪些互补序列做参考系成为了首要问题。根据上文对移位序列不变性的研究，已知相同形式的序列，在其指数差为4时的两个序列是保持“不变的”，如P0与P4、P8；而在指数差为2+4n时（n=0，1，2）时，两个序列为相同形式的配套序列，如P0与P2、P6和Pt。因此，以下将比较恰好剩下的3组互补序列：P0、Pe，P3、P9和P5、P7之间的不变性。

前提是基于集合思维，从原型序列的核心E型六音集合（014589）中共可以取出15个四音集合[14]，基本型仅有4种（0145）（0148）（0158）和（0347）。除了（0145）之外，其余三个都在前后六音截断中各出现一次。比较得出，P1、Pe与P0的前七音截断中不变性音级分别为集合（0，3，4，8）和（2，3，7，e）[15]，且两个四音集合原型均为（0148），并构成1个半音距离的移位关系。对余下两组进行相同的操作可得到相同结果，即每组与P0都产生四个不变音，且它们均为不变性四音集合（0148）。更甚者，三组互补序列与P0的不变四音集合均有（2，3，7，e），它是P0与Pe、P0与P3、P0与P7形成的不变音。

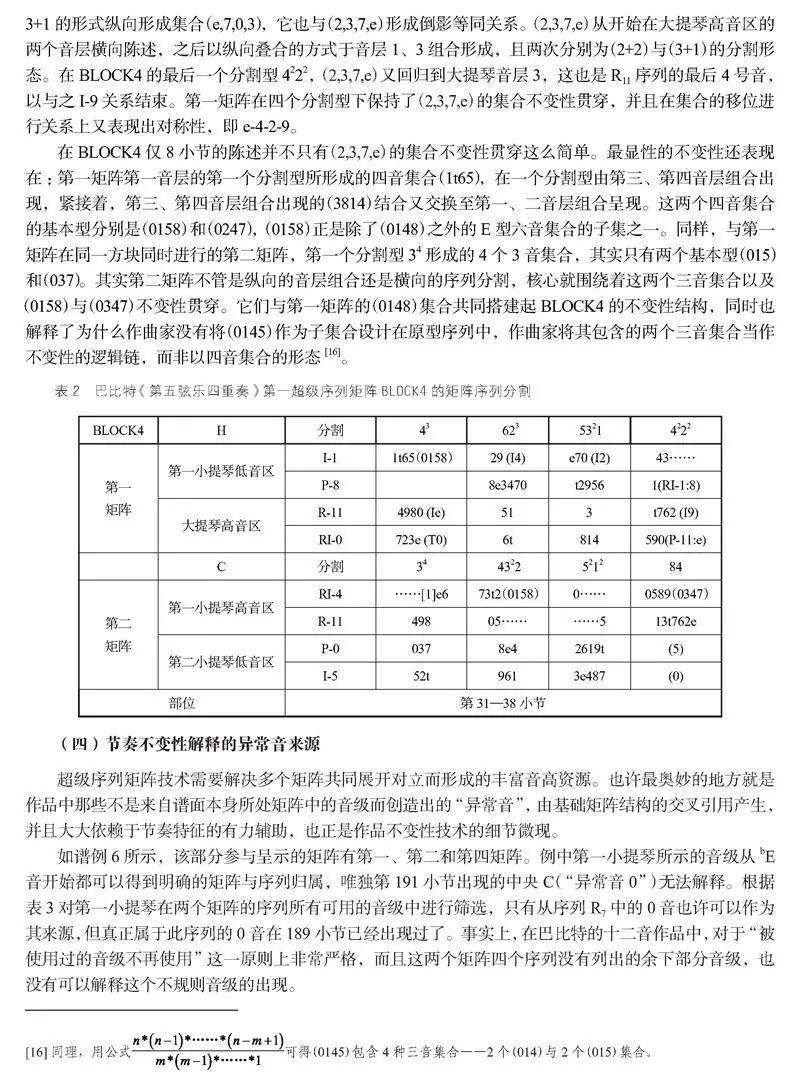
（2，3，7，e）以初始分割单元初次出现在第一矩阵第四音层大提琴高音区呈示的序列RI0的1—4号音，如表2所示，BLOCK4（第31—38小节）是由第一矩阵和第二矩阵共时展开，并分别呈现分割组H与分割组C。每kdA5ycQfpct5pjw25dhdOPexHbR3F+rUa8pJOC25eo0=个矩阵共四个音层，由不同乐器的不同音区组合，每个分割组包括将12音分割进四个音层的四种分割型。由于H分割组的第一个分割型 43是纵向形成三个四音集合，（2，3，7，e）即是其中一个，与此同时大提琴高音区的另一序列R-11也呈现前4号音（4，9，8，0）。若把（2，3，7，e）定义为原型T-0，（4，9，8，0）则是它的倒影等同集合I-e。然而，在进行到下一分割型 623时，大提琴高音区R11的二音组（5，1）与第一小提琴低音区I1的二音组（2，9）形成了（2，3，7，e）的倒影等同集合I-4。这两个音层同样在第三分割型5321时以3+1的形式纵向形成集合（e，7，0，3），它也与（2，3，7，e）形成倒影等同关系。（2，3，7，e）从开始在大提琴高音区的两个音层横向陈述，之后以纵向叠合的方式于音层1、3组合形成，且两次分别为（2+2）与（3+1）的分割形态。在BLOCK4的最后一个分割型4222，（2，3，7，e）又回归到大提琴音层3，这也是R11序列的最后4号音，以与之I-9关系结束。第一矩阵在四个分割型下保持了（2，3，7，e）的集合不变性贯穿，并且在集合的移位进行关系上又表现出对称性，即e-4-2-9。

在BLOCK4仅8小节的陈述并不只有（2，3，7，e）的集合不变性贯穿这么简单。最显性的不变性还表现在：第一矩阵第一音层的第一个分割型所形成的四音集合（1t65），在一个分割型由第三、第四音层组合出现，紧接着，第三、第四音层组合出现的（3814）结合又交换至第一、二音层组合呈现。这两个四音集合的基本型分别是（0158）和（0247），（0158）正是除了（0148）之外的E型六音集合的子集之一。同样，与第一矩阵在同一方块同时进行的第二矩阵，第一个分割型34形成的4个3音集合，其实只有两个基本型（015）和（037）。其实第二矩阵不管是纵向的音层组合还是横向的序列分割，核心就围绕着这两个三音集合以及（0158）与（0347）不变性贯穿。它们与第一矩阵的（0148）集合共同搭建起BLOCK4的不变性结构，同时也解释了为什么作曲家没有将（0145）作为子集合设计在原型序列中，作曲家将其包含的两个三音集合当作不变性的逻辑链，而非以四音集合的形态[16]。

（四）节奏不变性解释的异常音来源

超级序列矩阵技术需要解决多个矩阵共同展开对立而形成的丰富音高资源。也许最奥妙的地方就是作品中那些不是来自谱面本身所处矩阵中的音级而创造出的“异常音”，由基础矩阵结构的交叉引用产生，并且大大依赖于节奏特征的有力辅助，也正是作品不变性技术的细节微现。

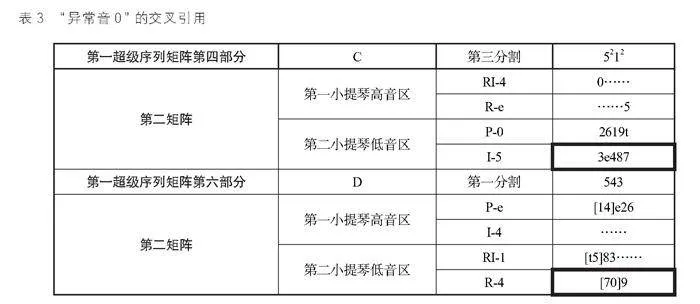
如谱例6所示，该部分参与呈示的矩阵有第一、第二和第四矩阵。例中第一小提琴所示的音级从bE音开始都可以得到明确的矩阵与序列归属，唯独第191小节出现的中央C（“异常音0”）无法解释。根据表3对第一小提琴在两个矩阵的序列所有可用的音级中进行筛选，只有从序列R7中的0音也许可以作为其来源，但真正属于此序列的0音在189小节已经出现过了。事实上，在巴比特的十二音作品中，对于“被使用过的音级不再使用”这一原则上非常严格，而且这两个矩阵四个序列没有列出的余下部分音级，也没有可以解释这个不规则音级的出现。

通过对第一小提琴横向上形成的旋律截断分析来看，第190小节由连音线划分的三音截断（4，8，7）以及“异常音0”与重复7音组成的二音截断（7，0）是破解来源的重要线索。通过在序列阵中找寻这两个截断，序列I5是异常音有力的来源候补者，它的最后四号音就是（4，8，7，0）。因此，该“异常音0”就是对第四部分第二矩阵第二小提琴低音音层4序列I5特定位置的引用。首先，关于上述两个截断的来源分别是第二矩阵音层4在第四部分第三分割处形成了五音的分割I5（3，e，4，8，7）以及在第六部分第一分割处形成的三音分割I5（7，0）与R4（9）。若没有节奏特征的辅助，上述解释可能是对于总体引用的错误判断，正是节奏使得这种特定区域的来源变得确定而清晰。第190小节的（4，8，7）是五连音的第三、四、五部分，在引用的第四部分第二矩阵音层4的第三分割处形成的五音分割中，这三个音级相应的同样是在第三、四、五部分。（0，7）是191小节三连音的第一、二部分，它们也同样是引用部分实现三音分割的第一、二部分。而且，音级7的音高不变性在结构表面也同样以重复形式表现出来。

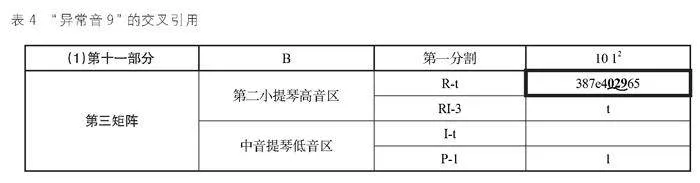
另一个这样的引用发生在201－202小节，也是第一超级序列矩阵的第十四部分，大提琴分为高、低音区分别属于第一矩阵和第四矩阵。如谱例7a所示，0音和2音的来源分别是RI8和R3，而9音（“异常音9”）不规则出现了。序列RI8确实有9音，但在 201小节出现过了，且是在与“异常音9”不同的八度上。巴比特避免呈现来源相同的音级在同一位置的两个八度上，因此RI8不可能是“异常音9”的来源。实际上这里的引用是来自第一超级序列矩阵第十一部分第三矩阵第二小提琴高音声部音层1的序列Rt。音层1在该部分第一分割处形成了一个十音的分割，而（0，2，9）出现在第六、七、八号位置上。第201小节，这三个音在五音组的第一、二、三部分代替一个八分音符。巴比特对于节奏的设计使得一切合理又巧妙。五连音的前面有两个十六分休止，所以休止和五连音按时值可以被理解为十音组代替一个四分音符，而这个十音组的第六、七、八部分是音级（0，2，9）。并且第137小节第三矩阵第二小提琴高音声部音层1的（0，2，9）三音进行在轮廓上（见谱例7b）与201小节大提琴声部的进行相似，但通过节奏和其他因素削弱了这种关联，实现了不变性的呼应。

三、结语

任何关于“自由”十二音系统的创作都必须面对这样一个问题：这种所谓的“自由”是否会导致“不变性”的数量和范围的维持、增加或减少，以及这种广义化的表面“自由”在更深层意义上是否会减少而不是增加结构性资源。同样地，将十二音系统运行于不变性结构逻辑中的一个必要条件是，不变量是系统音高性质的必要结果。十二音系统中的“不变性”技术就如同数学中的不变量，是在一系列变换或运算下保持不变的属性或值。它是系统的一个不变的特征，可以用来对系统的行为做出一般的陈述和预测。“不变性”的基本思想是不管十二音系统如何变化，它都具有恒定的属性，通过识别和理解这些保持不变的特征，对整个十二音系统做出有效分析。

对于巴比特的超级序列矩阵而言，音高组织的“不变性”属性来自矩阵音集间界限垂直分割而形成的复合音集。在这种大型复合矩阵结构中，巴比特一直在追求某种不变性，既是技术层面，也是继承着勋伯格最具有机性的发明——配套性的不变思维。十二音系统的音高资源不会也不可能被“耗尽”，其结构手段的广泛性、灵活性和精确性，从不逊色于任何过去或现在的作曲系统，因为它的不变性一直吸引着音乐创作者的思想。

作者简介：魏雨薇，博士，上海音乐学院教师。

[1]参见[美]约瑟夫·内森·施特劳斯：《后调性理论导论》（第三版），齐研译，人民音乐出版社，2014，第204页。“Any musical quality or relationship preserved when the series transformed called an invariant. As we hear our way through a piece， our ear often led via chain of invariants.”

[2]Milton Babbitt， “Twelve-Tone Invariants as Compositional Determinants，” The Musical Quarterly 46/2 （1960）：246-259.

[3]指任意数量的连续集合元素，该属性对任何元素选择（非连续和连续）都同样适用。

[4]第一个数字表示序列号，第二个数字表示音高。其中由于G为0，A音与E音则分别为1与7。

[5]集合分类表中共有50个六音集合，其中有6个六音集合可以在全部四种类型的变型后得到其配套集合：A（012345）；B（023457）；C（024579）；D（012678）；E（014589）；F（02468T）。

[6]可进一步参见魏雨薇：《基于“配套思维”的音乐超级序列矩阵技术》，《音乐艺术》2023年第2期，第172～183+5页。即〈0378e4〉可整理为〈048〉与〈37e〉，〈2619t5〉可整理为〈26t〉与〈159〉。

[7]可进一步参见魏雨薇：《“限制即自由”——安德鲁·米德〈米尔顿·巴比特音乐导论〉述评》，《人民音乐》2019年第12期，第78～81页。

[8]分别是（0，0）与（1，3）；（2，7）与（3，8）；（4，e）与（5，4）；（6，2）与（7，6）；（8，1）与（9，9）；（10，t）与（11，5）。

[9]它们之间分别距离6个半音和5个半音。

[10]P6为〈69125t80734e〉。

[11]P6所剩（0，6）（3，2）（6，8）（7，0）；P0所剩（0，0）（3，8）（6，2）（7，6）。

[12]Milton Babbitt， “Set Structure as a Compositional Determinant，” Journal of Music Theory 5/1 （1961）：72-94.

[13]表格及示例中序列用“短横线加数字”代替下标表示，以做区分，下同。

[14]可以用数学中的组合算法得到，即从n集合中取出m个元素组合的可能性共为。

[15]P0、P1、Pe的前七音截断分别为（0378e42）（1489053）（e267t31）。

[16]同理，用公式可得（0145）包含4种三音集合——2个（014）与2个（015）集合。