基于工况识别与预测的纯电动汽车剩余里程估算研究
2024-11-01李方舟钟勇邱煌乐范周慧李少伟

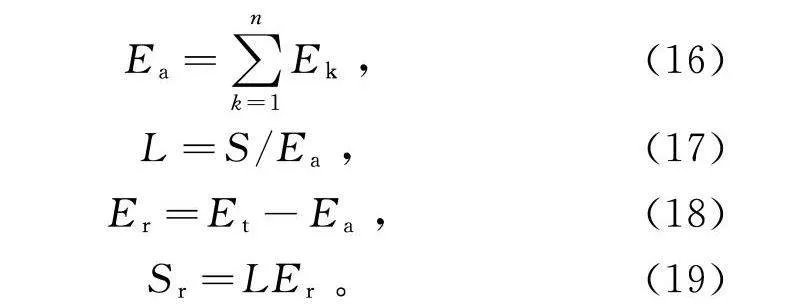
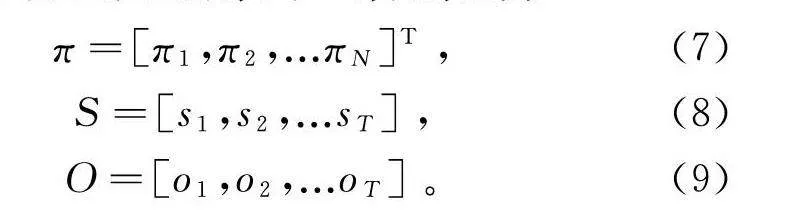

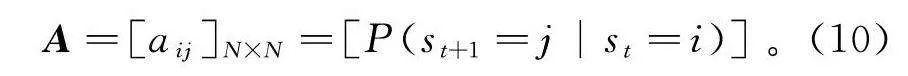


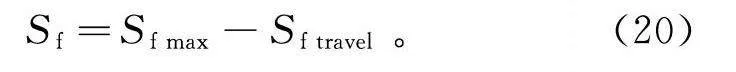
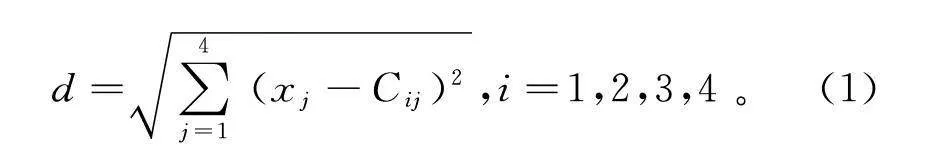
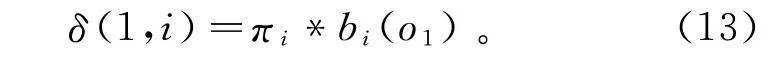
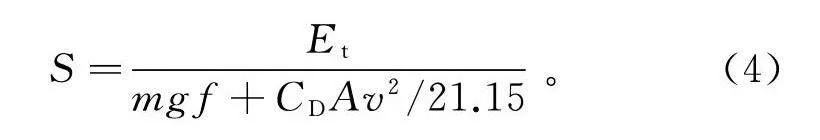

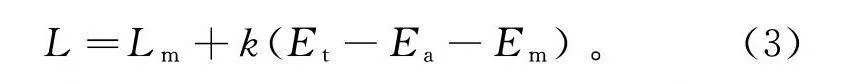
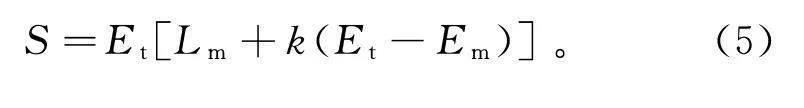



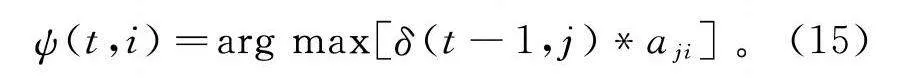
摘要:为了提升纯电动汽车剩余里程估算方法的准确度,在汽车行驶工况识别与预测的基础上,提出了一种新的剩余里程估算模型。通过采集实际汽车行驶工况数据,利用模糊聚类等方法对工况进行状态识别和分析,并建立了车辆能耗与工况特征参数之间的模糊规则库。同时,应用隐马尔可夫模型对行驶工况进行预测,通过将工况识别与工况预测相结合的方法,构建了基于工况识别与预测的纯电动汽车剩余里程估算方法。在AVL CRUISE中对纯电动汽车进行整车剩余里程仿真,选取了综合CLTC与WLTC的混合工况,以更贴近实际汽车行驶情况,详细比较了工况识别和工况识别与预测两种估算方法。研究结果表明,对于基于工况识别的剩余里程方法,其估算值随着时间的增加与仿真值间的误差逐渐增大,而工况预测方法的引入能有效减小误差。通过对比发现,工况识别与预测方法的最大绝对误差和绝对误差平均值相比仅采用工况识别的方法分别降低了34.04%和55.79%,标准偏差也减小至1.44 km,表明其具有更好的估算精度,为纯电动汽车续驶里程的预测提供了一种新途径。
关键词:纯电动汽车;剩余里程;估计;模糊聚类;隐马尔可夫模型
DOI:10.3969/j.issn.1001-2222.2024.05.012
中图分类号:U467.11 文献标志码:B 文章编号:1001-2222(2024)05-0086-07
随着纯电动汽车认可程度的不断提升,以及绿色环保理念的深入推广和油价上涨等因素的影响,在整体乘用车销售出现下滑的情况下,纯电动汽车的销量却持续逐年增长,其在市场销售中所占份额也越来越大[1]。尽管目前大多数电动汽车已经配备了剩余里程估算功能,但由于估算算法不同,导致估算准确度存在一定差异。若估算里程高于实际可行驶里程,这可能会误导用户产生盲目乐观的心态,造成车辆行驶中途因电量耗尽而抛锚。相反,若估算里程过低,用户可能会担心现有电量不足以支持车辆到达预定目的地,陷入不必要的“里程焦虑”。这两种情况最终都会对用户的实际体验产生负面影响。
车辆在实际行驶工况中的复杂性,使得纯电动汽车的剩余里程估算受到多方面因素的影响。当前国内外学者们已从不同角度展开了相关研究,并取得了一定的成果。王炯[2]从电池荷电状态SOC的角度进行了深入分析,采用了开路电压、安时积分和无迹卡尔曼滤波等三种方法的融合对SOC进行估计,并利用二阶RC等效电路模型和带有遗忘因子的递推最小二乘法来辨识模型参数,最终通过ADVISOR仿真软件进行了续驶里程的仿真估算。然而这类模型的建立需要准确的车辆和动力电池参数,并且有些参数会随着车辆使用发生较大变化,因此建立准确的模型比较困难。J. Bi等[3]采用稳健的非线性回归方法来确定模型参数,重点研究了车辆速度与单位电量行驶距离之间的非线性关系,且运用数据驱动方法建立了剩余行驶里程的非线性估计模型,综合考虑了荷电状态、速度和温度等因素对剩余行驶里程的影响。魏恒等[4]通过主成分分析和聚类分析确定了工况识别的特征参数,并将行驶工况分为四类,而后针对每一类工况选择了固定的能耗模型,以实现对当前车辆能耗的预测,这一方法不再仅仅依赖于电池等参数。晏玖江等[5]针对监控数据进行挖掘,对大批量车辆、长时间跨度的实际运行数据进行挖掘,计算出大量真实的道路状况运行数据集,从而实现车辆工况的识别,进而对行驶工况进行预测,估算出更加精确的行驶工况,提高剩余里程的估算精度。这类方法实现了行驶工况的识别与预测,但需要大量数据支撑,且计算更为复杂,难以实现工程应用。
本研究以某型号纯电动汽车为研究对象,采用模糊聚类方法进行行驶工况识别,并构建了车辆能耗与不同行驶工况之间的模糊规则库。在此基础上,运用隐马尔可夫模型实现行驶工况的预测,从而提出了一种基于工况识别与预测的在线剩余里程估算模型。最后通过仿真验证的方式验证了该估算方法的可行性,由此得到一种能相对精确估算纯电动汽车剩余里程的方法。
1 仿真平台搭建及数据分析
1.1 动力参数匹配与整车建模
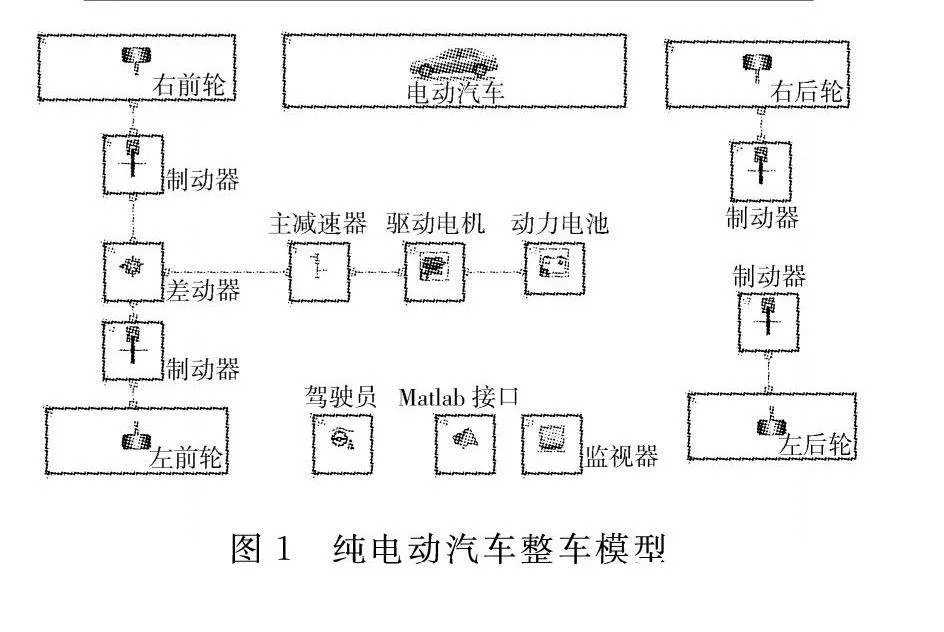
本研究聚焦于某款纯电动汽车,以其为基准对象进行剩余里程估算方法的研究。首先进行动力参数的匹配,整车参数如表1所示,动力性指标如表2所示。通过使用AVL CRUISE进行仿真,构建了整车模型,主要由车身模块、车轮模块、驱动电机模块、主减速器模块、动力电池模块、联合仿真模块等多模块组成,其模型如图1所示。
1.2 行驶数据获取与划分
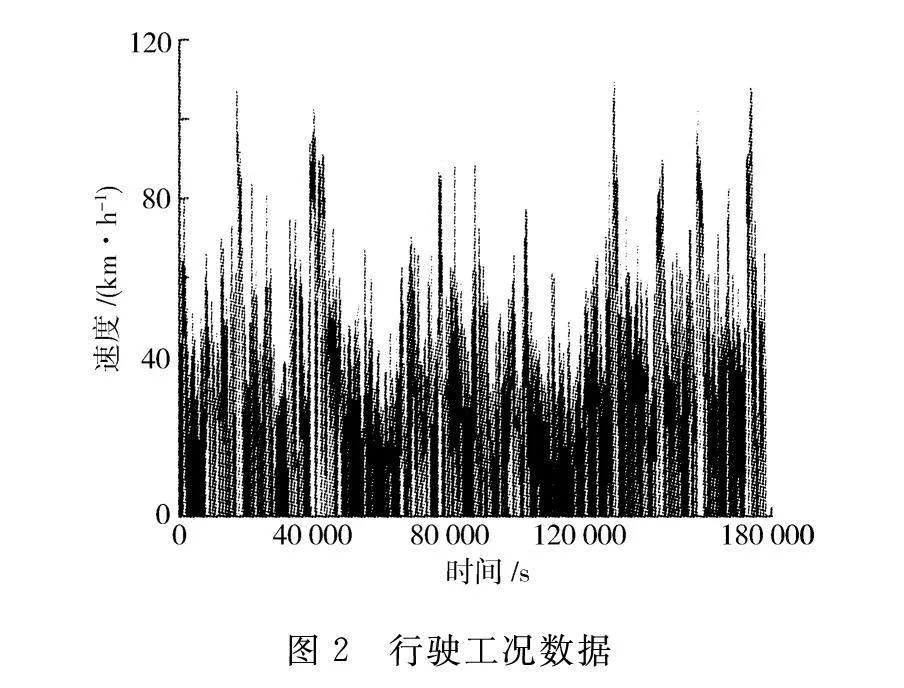
识别和预测汽车的行驶工况都不可或缺地需要可靠的数据支持,因此必须进行汽车行驶工况数据的采集。行驶工况数据来自某公司,包括了市区拥堵工况、市区正常行驶工况和高速工况等。对获取的数据进行处理,剔除明显异常值,得到的行驶工况数据可通过速度-时间曲线表示,如图2所示。
综合考虑到后续研究的计算量与估算准确度等问题,采用定步长划分法[6]对行驶工况数据进行划分,以120 s为一个片段共得到3 948个行驶工况片段。为了保证行驶工况片段所包含信息的完整性,根据现有研究[7-8]选择了平均速度、驻车时间比、减速时间比、加速时间比等4个特征参数,用以描述划分得到的工况片段。
1.3 工况片段的聚类分析
聚类算法是一种常用的技术,其主要目的在于将一组数据对象划分为多个类别或簇,使同一类别内的数据对象相似,而不同类别之间的数据对象具有较大的差异。模糊C均值聚类(fuzzy C-means clustering, FCM)作为一种基于聚类分析的无监督学习算法,是对传统的K均值聚类算法的扩展和改进。模糊C均值聚类在每个数据点与各个簇中心的关联上引入了隶属度,用于度量数据点属于不同簇的可能性,而不同于K均值聚类直接将数据点分配到某个簇中[9]。
模糊C均值聚类的基本原理步骤可概括如下。
1) 首先确定聚类的数量K,并为每个数据点随机分配初始的隶属度值,同时随机选择K个数据点作为初始聚类中心。
2) 对于每个样本和每个聚类中心,需要基于样本与各个聚类中心之间的距离,计算该样本属于该聚类中心的隶属度值。
3) 根据当前的隶属度值,重新计算每个聚类的中心点,对于每个簇,根据隶属度加权平均计算聚类中心。
4) 重复步骤2和步骤3,直到满足达到最大迭代次数或聚类中心不再明显变化等停止条件。最终,根据最后一次迭代得到的隶属度值,确定每个数据点所属的聚类簇。
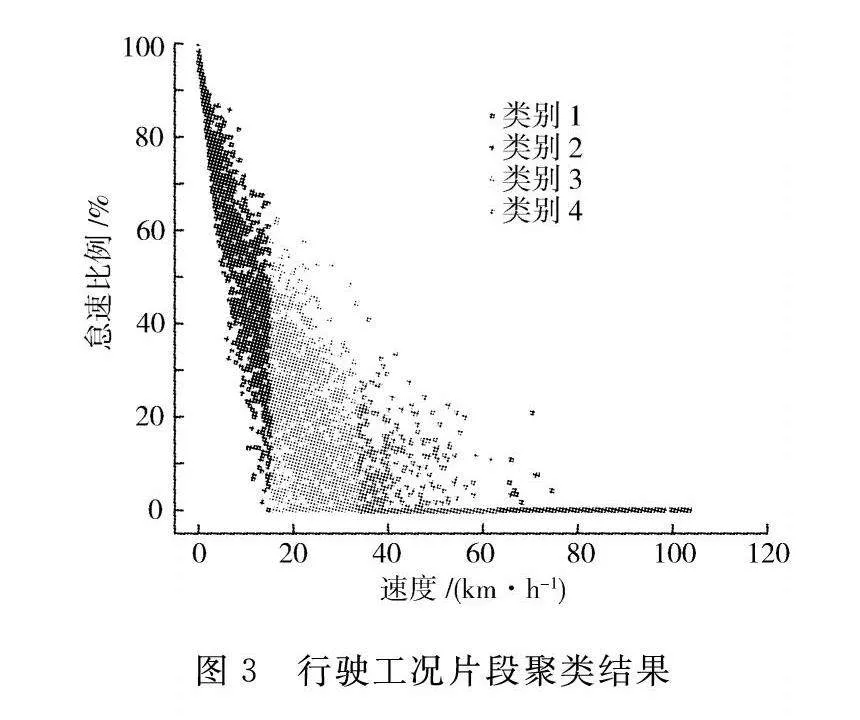
模糊C均值聚类中聚类数量K的取值范围一般大于2且小于样本总数n,结合文献[10-13],设定聚类个数K的取值为4。聚类结果如图3所示。
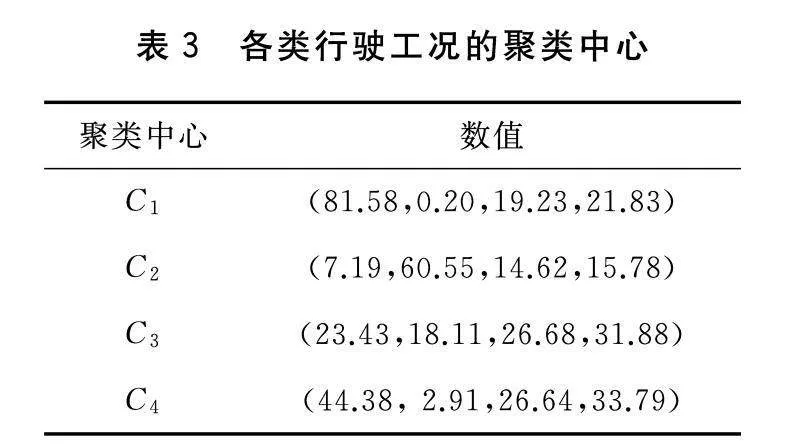
将上述行驶工况片段进行模糊C均值聚类,最终可得到4个聚类中心,如表3所示。
对数据进行分析可知:第一类工况属于交通畅通的高速工况,其平均速度较高,停驻比例较低;第二类工况表现为拥堵的低速工况,交通堵塞,平均速度最低,同时停驻时间也最长;第三类工况为交通比较畅通的市区工况,其速度较低,且停驻比例相对较高;第四类工况的特点是停驻时间较短,平均速度相对较高,这一类工况多见于城市快速路。
1.4 工况片段的识别
在车辆的实际行驶过程中,需要对实际行驶工况进行在线识别。首先将连续的行驶数据按照时间划分为长度120 s的片段,每个片段代表一个特定时段的行驶情况。而后从每个工况片段中提取关键特征参数,包括平均速度、停车时间比、减速时间比和加速时间比等,并计算与预先得到的各个聚类中心之间的欧氏距离。最后通过最小欧氏距离的原则,可将每个工况片段识别为对应的工况类别。距离计算公式为
d=∑4j=1(x-C)2,i=1,2,3,4。(1)
式中:d为当前识别的工况片段与第i类行驶工况聚类中心距离;x为当前工况片段的4个特征参数中第j个特征参数值;C为第i类工况的第j个特征参数的聚类中心值。
2 剩余里程估算方法
2.1 行驶工况片段能耗计算
通过建立的AVL CRUISE整车模型,结合Matlab平台仿真,计算划分得到的3 948个行驶工况片段能耗。各行驶工况片段的能量消耗见图4。
已经由模糊C均值聚类方法对行驶工况进行了分类,基于分类结果可以计算每个聚类的平均能耗:
E=1n∑nj=1E,i=1,2,3,4。(2)
式中:E为第i类聚类的平均能耗;n为第i类聚类的片段数量;E为第i类聚类的第j个片段能耗。经由上式对各类工况的平均能耗计算可得,第一类工况的平均能耗为0.114 8 kW·h,第二类工况的平均能耗为0.043 61 kW·h,第三类工况的平均能耗为0.061 30 kW·h,第四类工况的平均能耗为0.071 48 kW·h。
2.2 基于工况识别的剩余里程估算
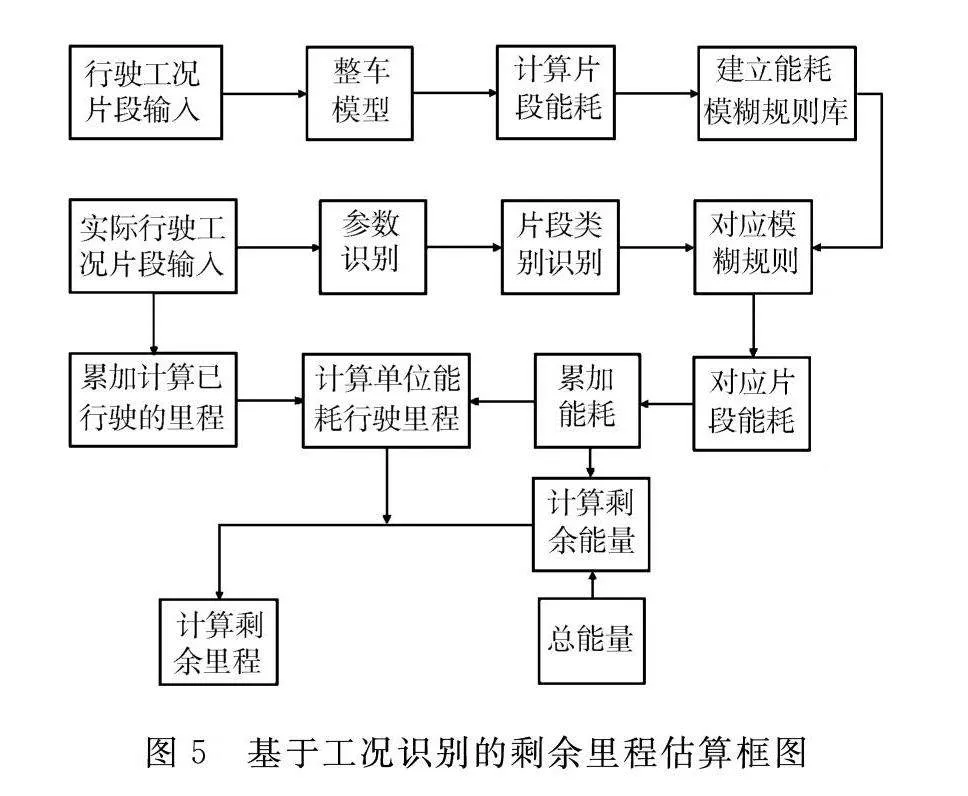
在进行剩余里程的估算过程中,可以借助计算模糊聚类方法得出的四种行驶工况的平均能耗,从而进行剩余里程的估算。而实际行驶过程中,车辆的能耗变化范围相当宽泛,不仅局限于这四种预定义的能耗情况。为了更准确地将行驶能耗与工况特征参数相联系,建立了二者之间的模糊规则库,以实现对当前能耗情况的自适应辨识,并在此基础上估算剩余里程。具体流程如图5所示。
该估算方法通过模糊聚类,将所有实际采集的行驶工况片段分为四个聚类,而后对每个聚类分别根据模糊规则库建立能耗与特征参数之间的关系。首先,在Matlab中为每个类别的行驶工况建立模糊规则库,输入参数为平均速度V、加速时间比P、减速时间比P和驻车时间比P,输出为片段能耗E,这些规则库是根据实际数据和经验构建的,以尽可能准确地描述能耗与特征参数之间的关系;其次,提取当前工况片段的平均速度、加速时间比、减速时间比和驻车时间比等4个特征参数;再次,根据片段的参数判断当前工况片段的片段类别;最后,由当前工况片段的类别和特征参数,通过对应类别的模糊规则库得到待识别片段的能耗。
通过这个流程,能够根据车辆当前的行驶特征参数,灵活地适应不同的行驶工况,进而估算出更准确的剩余里程。整个过程充分利用了模糊聚类和模糊规则库的优势,以提高能耗估算的精度和可靠性。而为了满足剩余里程呈线性递减趋势,建立了单位能耗与剩余能耗的线性关系:
L=L+k(E-E-E)。(3)
式中:L为单位能耗行驶里程;L为根据先前片段得到的单位能耗行驶里程最小值,根据分析取2.1 km;E为已消耗的能量;E为总能量;E为保守最低电量,此处取6.4 kW·h;k为线性预估计量。
车辆行驶过程中行驶里程和行驶阻力关系如下[14]:
S=Emgf+CAv2/21.15。(4)
式中:v为车速,取50 km/h;E取32 kW·h。
车辆最大行驶里程和电池总电量关系为
S=E[L+k(E-E)]。(5)
联立可得k=0.408 1。
最终剩余续驶里程为
S=L(E-E)。(6)
2.3 基于工况识别与预测的剩余里程估算
准确的工况预测可以让驾驶员更好地规划行程和充电计划,从而避免电量不足导致无法按时到达目的地或中途耗尽电量的情况发生[15]。因此在工况识别的基础上,引入行驶工况预测,可以更精准地对纯电动汽车剩余行驶里程进行估算。
目前能够对未来行驶工况进行准确预测的模型并不多,主要方法是基于统计学原理,通过对历史工况进行大量统计,以最大概率确定未来可能出现的工况。这种基于统计学的方法对计算量的要求并不高。前文已经将车辆行驶工况分为四类,这些工况之间的状态转换可以由近期数据分析推导得出,与历史数据无关,该过程具有马尔可夫性[16]。
隐马尔可夫模型(hidden Markov model,HMM)是对马尔可夫链的一种扩展。隐马尔可夫模型的基本原理是设定有一个系统,其中包含隐藏状态和可见状态,隐藏状态之间可以通过转移概率矩阵相互转换。与马尔可夫链类似,隐马尔可夫模型中的转移概率仅由当前数据决定,而与历史数据无关。然而HMM在处理非线性的离散时间序列时,例如行驶工况类别,相比马尔可夫链表现更优越。
设定Q={q,q,…q}是所有可能隐藏状态的集合,V={v,v,…v}是所有可能观测状态的集合。同时引入隐藏状态初始向量π,隐藏状态序列S以及其对应的观测序列O,分别记为
π=[π,π,...π]T,(7)
S=[s,s,...s],(8)
O=[o,o,...o]。(9)
从上一时刻到下一时刻不同状态之间转换的概率,即隐藏状态转移概率矩阵A表示为
A=[a]=[P(s=j|s=i)]。(10)
在某个状态下各种观测出现的概率,即观测状态转移概率矩阵B表示为
B=[b]=[P(o=j|s=i)]。(11)
隐马尔可夫模型由以上三个分布决定,因此可以用一个三元符号表示,即
λ=(A,B,π)。(12)
为了对模型参数π,A和B进行估计,采用Baum-Welch算法通过迭代优化来使得观测序列的似然概率最大化。Baum-Welch算法是基于Expectation-Maximization(EM)算法,其中E步骤用于计算前向概率α(t,i)和后向概率β(t,i)。前向概率α(t,i)表示在时刻t处于隐藏状态s,并且观测到序列O的概率;后向概率β(t,i)表示在时刻t处于隐藏状态s的前提下,从t+1到T时刻观测到序列O的概率。M步骤则用于更新模型参数π,A和B,利用E步骤计算得到的前向概率和后向概率,使得似然概率最大化。通过E步骤和M步骤的交替迭代,使模型参数达到收敛。
最后在预测过程中,使用动态规划的维特比算法寻找最大概率路径,从而确定最可能的隐藏状态序列,即代表行驶工况类别的序列。首先初始化,设置回溯指针为零,在初始时刻初始路径概率δ为
δ(1,i)=π*b(o)。(13)
式中:π为初始状态概率;b(o)为在状态s下观测到观测值o的概率。
而后从t=2开始进行递推,计算每个时间点的最大概率δ(t,i):
δ(t,i)=max[δ(t-1,j)*a]*b(o)。(14)
式中:a为从状态s转移到状态s的概率;b(o)为在状态s下观测到观测值o的概率。
同时记录对应的回溯指针ψ(t,i):
ψ(t,i)=arg max[δ(t-1,j)*a]。(15)
在递推完成后,通过回溯指针ψ可以从最后一个时间点T开始回溯,找出最可能的隐藏状态序列。
根据车辆历史行驶数据,将行驶工况片段的特征参数,即平均速度和驻车时间比等作为隐马尔可夫模型的观测状态,而行驶工况类别作为隐藏状态。基于训练数据,通过Baum-Welch算法估计模型的转移概率矩阵、观测概率分布以及初始状态概率。在得到最近工况片段的特征参数后,利用维特比算法来确定最可能的隐藏状态序列,即为预测的工况结果。由预测得到的行驶工况类型,可以利用对应工况的平均能耗进行剩余里程估算,即
E=∑nk=1E,(16)
L=S/E,(17)
E=E-E,(18)
S=LE。(19)
式中:E为一段时间内所有片段能耗累加的总能耗;E为第k个工况片段的能耗;L为单位能耗行驶里程;S为已行驶的里程;E为剩余能量;E为总电量;S为剩余里程。
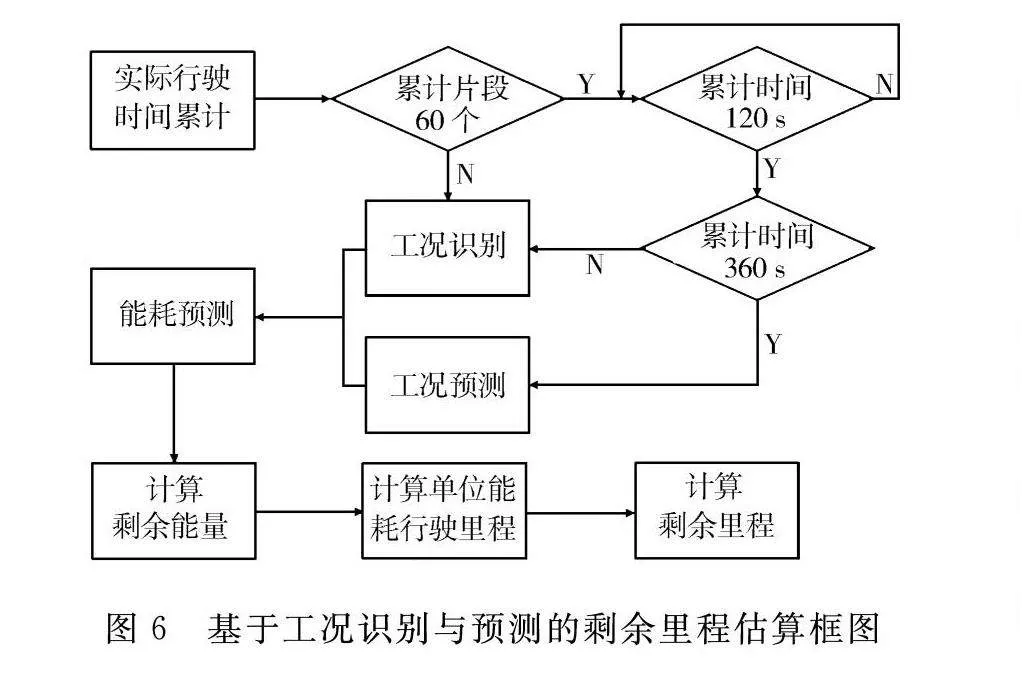
结合工况识别和工况预测对纯电动汽车的剩余里程进行估算,具体流程如图6所示。车辆当前总电量在上电时进行初始化,并随着时间的累计,每120 s累计为一个实际行驶工况片段,然后进行剩余里程估算。在前60个片段中仍然采用工况识别法,根据当前行驶工况片段,利用模糊能耗规则进行能耗预测,得出当前消耗的能量,计算单位能耗行驶里程并结合剩余能量估算剩余里程。而在累计了60个行驶工况片段后,每累计360 s即3个行驶工况片段,进行一次工况预测。借助预测得到的行驶工况片段类别以及每类工况的平均能耗,可以计算得到单位能耗行驶里程,由此估算剩余里程;若累计时间达到120 s但不足360 s,则依然使用工况识别法进行估算。
3 剩余里程估算仿真
对纯电动汽车剩余续驶里程估算方法进行仿真验证。为了更好地模拟车辆实际行驶情境,仿真工况的选择应涵盖多种不同的行驶工况。因此采用了多种工况进行仿真验证,包括中国轻型汽车行驶工况 (China light vehicle test cycle,CLTC),全球统一轻型车辆测试循环 (worldwide harmonized light vehicles test cycle,WLTC),以及CLTC和WLTC的混合工况,涵盖了拥堵低速、城市快速、高速等多种典型工况。在仿真过程中,将车辆的初始电池电量即SOC设置为100%,并设定当电池电量降至20%时停止仿真。CLTC工况累计时长为50 288 s,行驶距离为403.31 km;WLTC工况累计时长为25 109 s,行驶距离为323.65 km;CLTC和WLTC的混合工况累计时长为34 079 s,行驶距离为352.39 km。
在所设定的工况下,初始设定的SOC对应着一个最大仿真续驶里程值,而在AVL CRUISE仿真过程中会实时记录车辆的已行驶里程,则仿真剩余里程可表示为
S=S-S。(20)
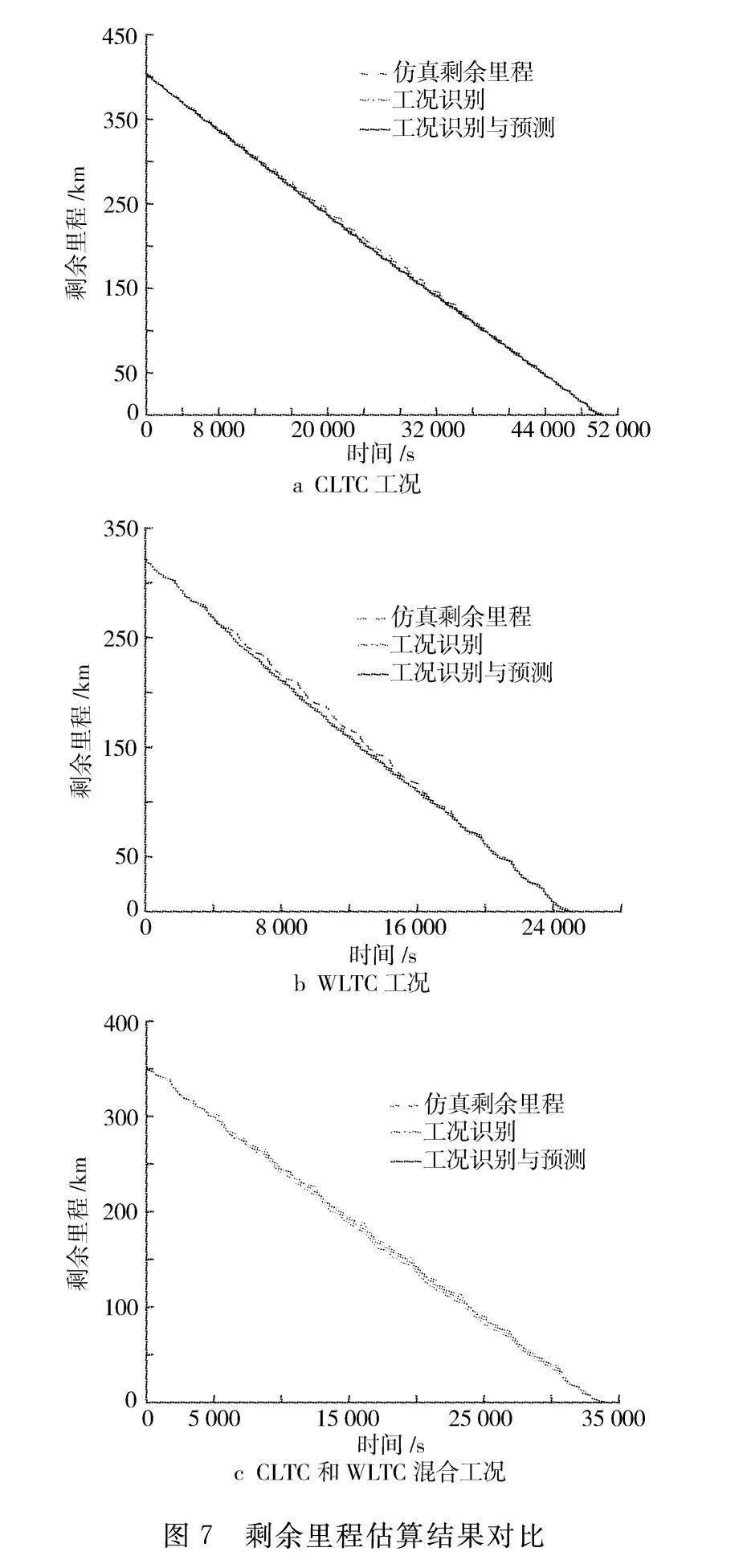
将基于工况识别方法和基于工况识别与预测方法得到的剩余里程估算结果进行滤波处理后与仿真剩余里程进行了对比,结果如图7所示。
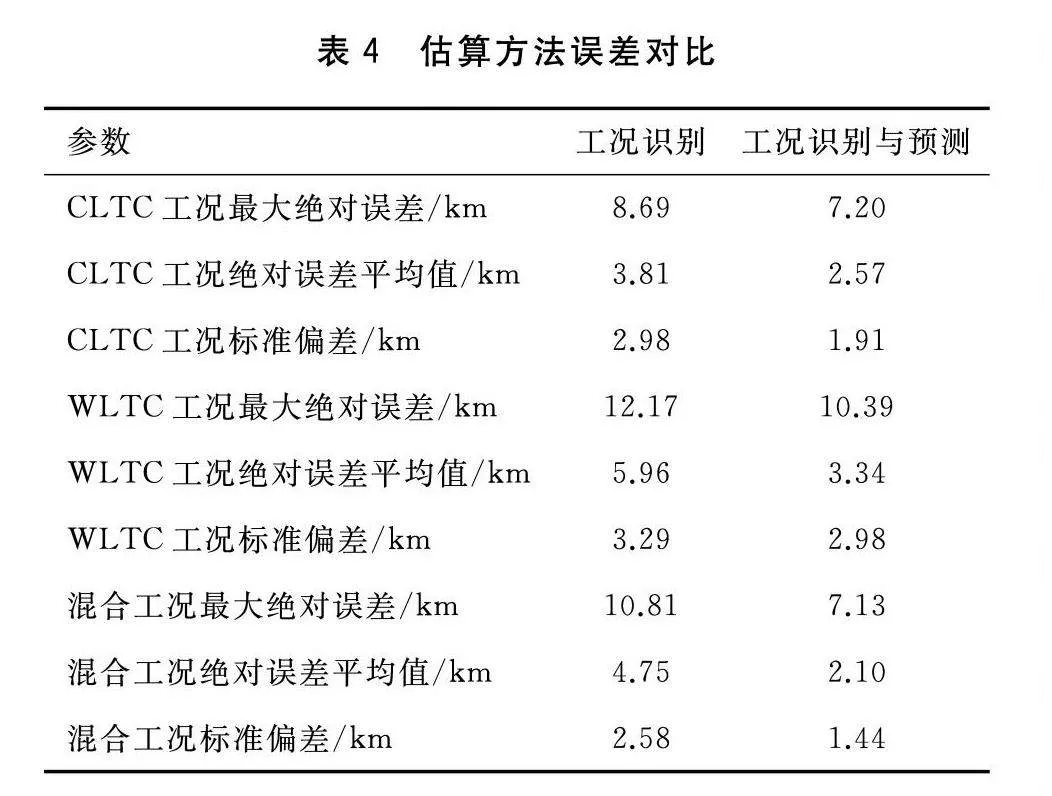
从图7可知,在7 200 s之前,两种方法的估算结果与仿真值的拟合度较好,且误差相近,这是因为在该段时间内所采用的是相同估算方法。然而随着时间的增加,基于工况识别法的估算结果与仿真剩余里程之间的误差逐步增大,尤其是在仿真时间的中段,误差达到了最大值。相反,工况识别与预测方法在时间推移中逐渐展现出其优势,其估算误差相较于单一的工况识别方法来说更小。
将两种估算方法的剩余里程估算值与仿真值进行了进一步比较分析,相关数据列于表4。值得注意的是,在不同工况下,工况识别与预测方法所得到的剩余里程估算值与仿真值间的误差均更小。特别是在混合工况下,工况识别与预测方法的所得到的剩余里程估算值与仿真值之间最大绝对误差为7.13 km,绝对误差的平均值为2.10 km,相较于仅工况识别方法分别减少了34.04%和55.79%。此外,从标准偏差的角度来看,工况识别与预测方法的标准偏差值为1.44 km,也小于工况识别法的2.58 km。这意味着工况识别与预测的估算值更接近于仿真值,相较于单一的工况识别方法更为稳定,误差较小,整体精确度更高。
4 结束语
提高纯电动汽车续航里程估算的准确性对纯电动汽车的发展至关重要。利用模糊聚类等方法对汽车工况进行状态识别和分析,建立了车辆能耗与工况特征参数之间的模糊规则库。同时,采用隐马尔可夫模型对行驶工况进行预测,将工况识别与工况预测相结合,提出了基于工况识别与预测的剩余里程估算方法。通过AVL CRUISE对纯电动汽车进行剩余里程仿真,在不同工况下,基于工况识别与预测方法的剩余估算值与仿真值之间的最大绝对误差、绝对误差的平均值和标准偏差值,均小于单一的工况识别方法。结果表明了基于工况识别与预测的纯电动汽车剩余里程估算方法的可行性和优越性,为新能源汽车的续驶里程预测提供了一个新途径。
参考文献:
[1] 曹镇杭,胡延明,刘洋,等.我国纯电动汽车发展及对策[J].时代汽车,2021(10):84-86.
[2] 王炯.基于电池SOC估计的汽车续航里程预测算法研究[D].石家庄:石家庄铁道大学,2022.
[3] Bi J,Wang Y,Sai Q,et al.Estimating remaining driving range of battery electric vehicles based on real-world data:A case study of Beijing, China[J].Energy,2019,169:833-843.
[4] 魏恒,何超,李加强,等.基于实际行驶工况的纯电动汽车续驶里程在线估算方法研究[J].公路交通科技,2020,37(12):149-158.
[5] 晏玖江,肖伟,贾俊,等.基于能耗参数辨识和路况预测的剩余续驶里程数据驱动算法[J].重庆理工大学学报(自然科学),2020,34(10):83-90.
[6] 郑宁安.纯电动汽车能耗预测与续驶里程估算[D].大连:大连理工大学,2016.
[7] 连静,郑宁安,周雅夫,等.基于电池荷电状态和行驶工况辨识的电动汽车续驶里程估算[J].科学技术与工程,2016,16(13):113-117.
[8] 徐宗煌,林瑶.基于主成分和聚类分析的汽车行驶工况构建[J].宁夏大学学报(自然科学版),2021,42(3):270-276.
[9] 谢中华.MATLAB统计分析与应用[M].北京:北京航空航天大学出版社,2010.
[10] 高建平,高小杰,郗建国.融合车、路、人信息的电动汽车续驶里程估算[J].中国机械工程,2018,29(15):1854-1862.
[11] 尹安东,赵韩,周斌,等.基于行驶工况识别的纯电动汽车续驶里程估算[J].汽车工程,2014,36(11):1310-1315.
[12] 石琴,郑与波,姜平.基于运动学片段的城市道路行驶工况的研究[J].汽车工程,2011,33(3):256-261.
[13] 乔慧敏,靳博文,储亚楠.一种电动汽车续航里程估算算法的研究与应用[C]//第十五届河南省汽车工程科技学术研讨会论文集.[出版地不详]:河南省汽车工程学会,2018:347-350.
[14] 余志生.汽车理论[M].6版.北京:机械工业出版社,2018.
[15] 曹磊,陈长文,孙强.基于马尔可夫链的汽车行驶工况预测[J].内燃机与动力装置,2017,34(3):13-17.
[16] 宋鹏翔.插电式混合动力公交车工况预测与智能能量管理策略研究[D].长春:吉林大学,2021.
Estimation of Remaining Mileage for Pure Electric Vehicle Based on Condition Identification and Prediction
LI Fangzhou,ZHONG Yong,QIU Huangle,FAN Zhouhui,LI Shaowei
(Fujian Key Laboratory of Automotive Electronics and Electric Drive(Fujian University of Technology),Fuzhou 350118,China)
Abstract: To enhance the accuracy of remaining mileage estimation method for pure electric vehicles, a novel model centered on the identification and prediction of vehicle driving conditions was put forward. By gathering real-world vehicle driving condition data, the techniques such as fuzzy clustering were used to discern and analyze condition states. Furthermore, a fuzzy rule base correlating vehicle energy consumption with condition-specific parameters was established. Concurrently, the Hidden Markov model was employed to forecast driving conditions. By combining condition identification and prediction, a methodology for estimating the remaining mileage of pure electric vehicles was developed. During the simulation of entire vehicle remaining mileage in AVL CRUISE, the hybrid working conditions which integrate CLTC and WLTC were used to closely mimic real-world driving conditions. Two estimation methods of condition identification alone and condition identification with prediction were compared in detail. The results reveal that the estimation error increases gradually with the increase of time based on the identification of working conditions, and decreases effectively after the introduction of working condition prediction method. Specifically, the maximum absolute error and mean absolute error for the condition identification and prediction methods reduce by 34.04% and 55.79% respectively. Moreover, the standard deviation decreases to 1.44 km. These results prove the superior accuracy of the proposed method, which presents a new perspective on forecasting the range of pure electric vehicles.
Key words: pure electric vehicle;remaining mileage;estimation;fuzzy clustering;Hidden Markov model
[编辑:袁晓燕]
