基于CGOA-MAM-TCN算法的车用锂电池荷电状态估计
2024-11-01王鸿彬
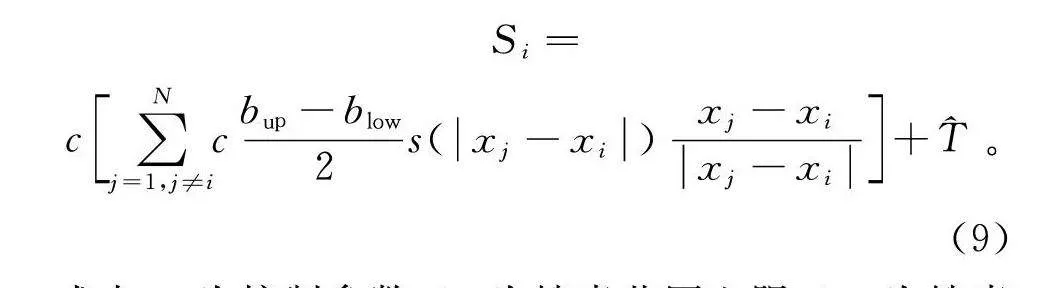
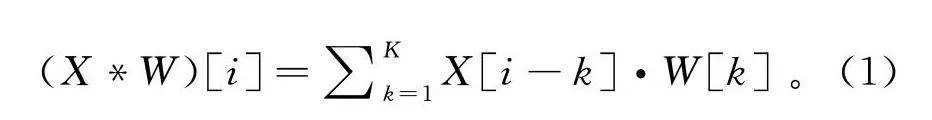



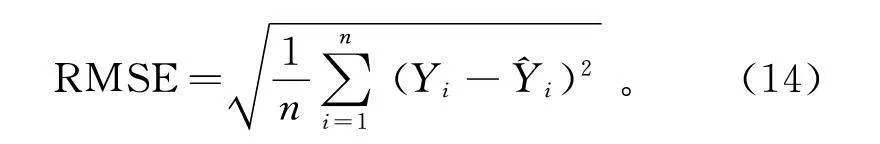
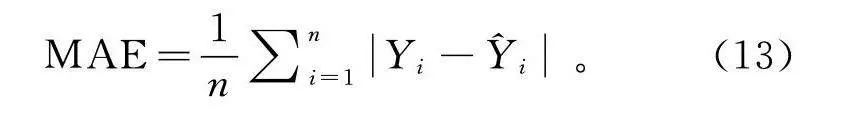

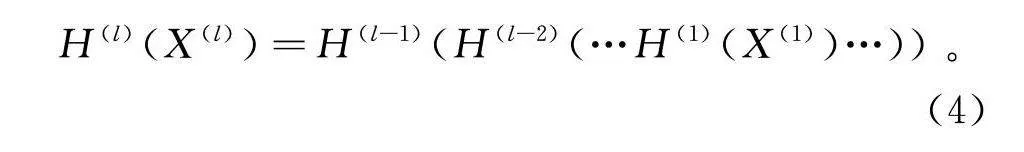
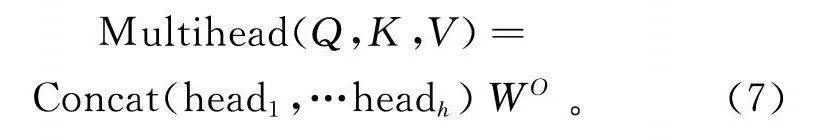
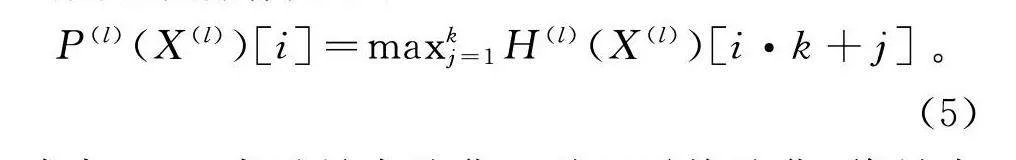


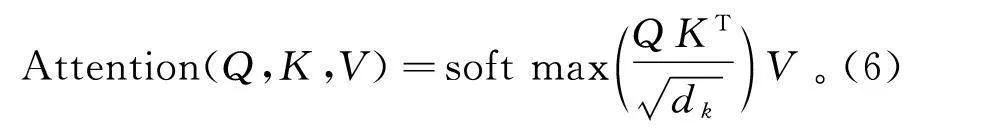


摘要:针对数据驱动的锂电池荷电状态估计方法仍然存在对大量标定数据的依赖、同时应对动态变化和复杂运行状况时表现不佳等问题,提出了改进蝗虫算法优化结合时域卷积网络和多头注意力机制的锂电池荷电状态估计方法。首先利用时域卷积网络对锂电池荷电时间序列数据中的长期依赖关系进行建模,同时采用多头注意力机制学习数据特征长期依赖关系,利用每个注意力头去计算序列中不同张量的依赖关系,辅助时域卷积神经网络增强对依赖关系的捕获,降低其对大量标定数据的依赖;另外为使模型发挥出最佳性能,改进了混沌蝗虫算法优化模型的超参数。试验结果表明:在不同温度条件下,相较于其他方法,优化模型在锂电池荷电状态估计任务中表现出更好的准确率和稳定性。
关键词:锂电池;荷电状态;估计;时域卷积;多头注意力;蝗虫优化算法
DOI:10.3969/j.issn.1001-2222.2024.05.011
中图分类号:TM912 文献标志码:B 文章编号:1001-2222(2024)05-0078-08
新能源动力车辆广泛使用锂电池,当前车用锂电池管理中,至关重要的部分是对锂电池剩余电量(state-of-charge,SOC)的估计预测。精确的SOC估计能确保系统的安全和性能稳定性。此外,精确的SOC估计还可以提高能源管理效率、优化能源分配、提高能源利用率,从而让电池组的工作时间和续航时间最大程度地延长[1-3]。总而言之,针对锂电池准确可靠的SOC估计方法对于推动电池技术的发展具有重要意义。
锂电池SOC的估计方法可以分为模型法和数据驱动法两类。模型法基于建立电池动力学模型,通过对电池内部物理过程的建模来推断其SOC。这种方法的优点在于可以提供对电池内部状态的物理解释,有较高的准确性和可解释性[4-5]。然而,模型法需要准确的电池参数和工作条件,且要求模型有较高的精确性,基于模型法进行SOC估计时通常采用等效电路模型(equivalent circuit model, ECM)。M. K. Tran等[6]研究了电池管理系统中常用的ECM,通过试验证明了电池健康状态对ECM参数的影响,提出了一个包含SOC、温度的经验模型,该模型具有低复杂性,但未详细探讨模型的适用范围和稳定性。X. Lai等[7]研究了在电池健康状态和SOC变化时,通过粒子群优化确定2RC模型的关键参数,随后通过敏感性分析提出一个简化模型,仅更新高灵敏性的参数以降低计算复杂性,在保持模型准确性的同时有效降低了计算负担。黄凯等[8]提出了一种基于观测方程重组的增强拓展卡尔曼滤波器,通过误差修正策略减少信息,提高SOC估计准确性,试验证实该算法适应不同温度和工况,并具有较高的SOC估计精度。
数据驱动法则是基于电池的输入输出数据,通过统计学或机器学习方法来建立SOC估计模型。这种方法不需要对电池内部物理过程进行建模,因此更加灵活,并且可以适应不同工况和电池类型。数据驱动法可以通过大量的标定数据来提高估计精度,且对实时性和鲁棒性的要求较低。I. Babaeiyazdi等[9]进行锂离子电池SOC估计运用的是机器学习模型结合电化学阻抗谱的方法,试验结果显示高斯过程回归模型的误差小于3.8%。该方法有嵌入电池管理系统的潜力,可确保电池的高效运行。C. Hu等[10]提出了一种TCN-LSTM(temporal convolutional neural network-long short term memory)模型用于锂离子电池SOC估计,同时提取空间和时间特征,实现了准确和鲁棒的SOC估计;该模型在多种条件下表现良好,优于独立使用的LSTM、TCN和CNN-LSTM网络。D. N. T. How等[11]提出一种改进的深度神经网络SOC估计模型,通过试验证明增加隐藏层数(最多4个)能够提高SOC估计准确性,研究显示在动态应力测试驾驶循环上训练的4个隐藏层深度神经网络,能准确预测其他未见驾驶循环的SOC值。然而,目前的数据驱动方法也存在一些缺点,例如对大量标定数据的依赖、对实时性和鲁棒性要求等问题[12]。当前数据驱动方法的缺点之一是对大量标定数据的依赖,虽然大量标定数据可以提高估计精度,但数据采集和标定过程需要耗费大量时间和资源。此外,对实时性和鲁棒性要求较低也意味着当前方法在应对动态变化和复杂工况时可能表现不佳。因此,需要改进的重点在于提高估计精度的同时,降低对大量标定数据的依赖,并提高模型对动态变化和复杂工况的适应能力。
为了解决这些问题,本研究将时域卷积网络和多头注意力机制相结合,以实现对空间和时间特征的同时提取。其中时域卷积网络有效识别长期依赖关系的时间序列数据,提高了模型对长期依赖关系的建模能力,并且时域卷积网络有效解决了梯度消失与爆炸等缺陷;而多头注意力机制能更好地辅助时域卷积网络有效识别序列中的长期依赖关系,且对模型的表征能力和泛化能力有较大的提升。融合时域卷积网络和多头注意力机制各自的独特优势,并且通过改进蝗虫算法对整体算法进行参数优化,从而得到准确、鲁棒的锂电池SOC估计算法。该SOC估计方法具备较低的计算复杂度和良好的泛化能力,为新能源汽车、储能设备等工程领域提供高效可靠的电池管理解决方案,促进相关技术的发展应用。
1 算法设计
1.1 时域卷积网络TCN
时域卷积网络(temporal convolutional network,TCN)是一种在时序数据上进行建模和学习的深度学习架构[13-14]。TCN的基本原理涉及到卷积操作、残差连接以及因果卷积,其设计灵感来自于经典的卷积神经网络和残差网络,通过引入因果卷积,TCN能够有效地捕捉时序数据中的长期依赖关系进行数据预测。
TCN的核心在于使用卷积操作来对时序数据进行特征提取。给定输入序列X,卷积操作可以表示为
(X*W)[i]=∑KX[i-k]·W[k]。(1)
式中:(X*W)为卷积的结果;X[i]为输入序列的第i个元素;W[k]为卷积核第k个权重;K为卷积核尺寸。因果卷积的实现方式是通过将卷积核的未来部分置零,确保在进行卷积操作时只能使用当前时刻及之前的信息。对于长度为K的卷积核,因果卷积可以表示为
(X*W)[i]=∑KX[i-k]·W[k],i≥K-1。(2)
即只有在时刻i大于等于卷积核大小减1时,才会对输入序列进行卷积操作。
残差连接的残差块是输入直接与卷积层的输出相加而形成的。输入给定的X,卷积层的输出为H(X),残差连接可以表示为
output=H(X)+X。(3)
这种结构使得网络能够更容易学习残差,从而更好地适应时序数据中的长期依赖关系。
为了增加模型的表达能力,TCN通常采用多层堆叠的结构。每一层都可以具有不同的卷积核大小,捕捉不同尺度的时序模式。设X(l)为第l层的输入,H(l)为第l层的输出,则
H(l)(X(l))=H(l-1)(H(l-2)(…H(1)(X(1))…))。(4)
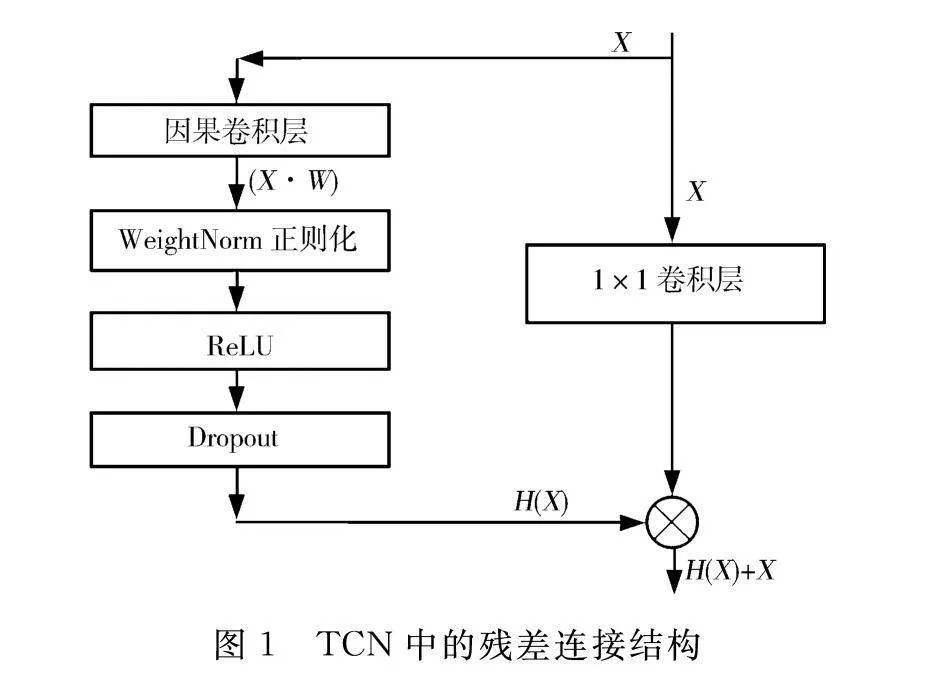
式中:H(l)(·)为第l层的卷积操作。其具体连接结构如图1所示。
在TCN中,池化层用于降低序列的长度,减少计算复杂度。平均化或最大化均可应用于池化操作。假设第l层的池化操作为P(l),池化的大小为k,则池化操作如下:
P(l)(X(l))[i]=maxkH(l)(X(l))[i·k+j]。(5)
式中:max表示最大池化。对于平均池化,将最大值替换为平均值即可。
1.2 多头注意力机制MAM
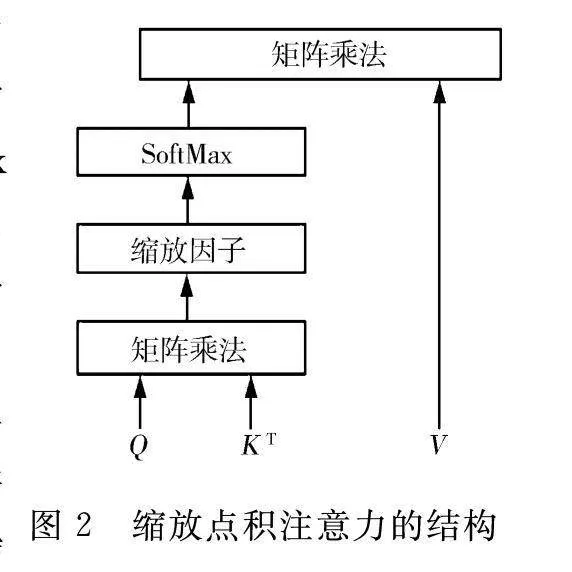
多头注意力机制(multi-head attention mechanism,MAM)是一种用于序列建模的机制,它可以计算同一批次中不同张量之间的依赖关系,从而更好地捕获序列中的长期依赖关系[15],其基本单元是缩放点积:
Attention(Q,K,V)=soft maxQKTdV。(6)
式中:Q,K和V分别为查询、键和值矩阵;d为K的距离维度;softmax运算的相似度得到权重,如图2所示输出结果为该权重的值矩阵。
首先进行矩阵乘法变换处理(如图3所示),处理结果再独立缩放点积,随后将结果拼接矩阵乘法输出,并行多头注意力机制,显著提升序列数据不同依赖关系的建模能力,更有效地捕捉序列数据的复杂依赖关系。
那么多头注意力算式为
Multihead(Q,K,V)=Concat(head,…head)WO。(7)
式中:head=Attention(QWQ,KWK,VWV)为第i个注意力头的计算结果;WQ,WK和WV分别为线性变换的投影矩阵;WO表示最终的输出变换矩阵。
1.3 多头注意力机制-时域卷积模型MAM-TCN
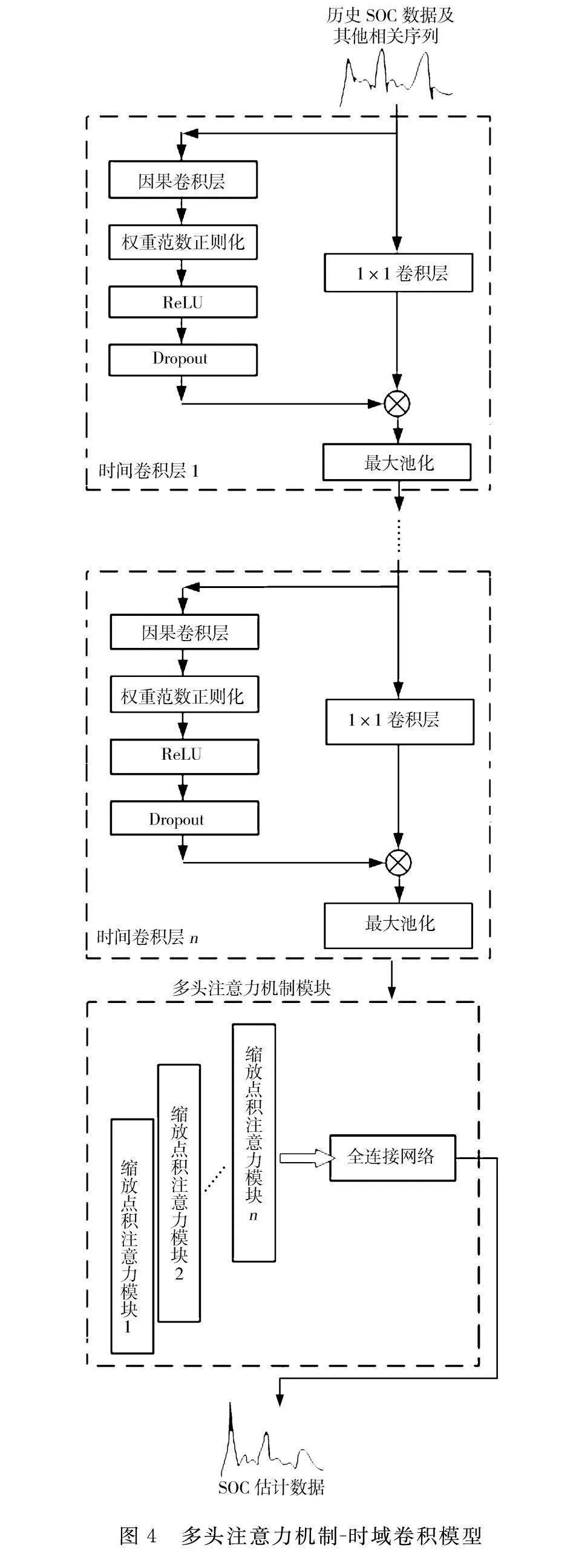
时域卷积网络通过多个不同尺寸和维度的卷积核提取多维信息进行数据预测,而多头注意力机制提取信号数据长期依赖影响,多头注意力-时域卷积的总体结构见图4,其中每个时间步之间的依赖关系用多个并行的注意力头来计算,然后拼接变换。采用多头注意力机制对时间序列数据的长期依赖关系进行增强学习,利用每个注意力头去计算序列中不同张量的依赖关系,辅助时域卷积神经网络增强对依赖关系的捕获,降低对大量标定数据的依赖。
1.4 CGOA-MAM-TCN算法
蝗虫优化算法(grasshopper optimization algorithm,GOA)是受自然界中蝗虫表现启发而来的优化算法,用于解决数值求解优化问题[17-18]。该算法模拟了蝗虫群体的迁徙和协作行为,通过蝗虫个体的位置更新和信息共享来搜索潜在的最优解。另外为了增加算法的探索性,引入了混沌Logistic映射,提高解的多样性,混沌蝗虫优化算法的计算步骤如下。
首先随机初始蝗虫种群,初始蝗虫总数为N,每个蝗虫表示一个潜在的解决方案。每个蝗虫的位置由问题的搜索空间Ω内的随机值确定,蝗虫i的位置记为x,则有x=(nk,nl,nh),式中x∈Ω。另外蝗虫个体适应度值f(x)反映了该超参数下模型表现的优劣,并且使用模型在验证集的损失函数作为适应度值。蝗虫算法的迭代由彼此吸引力S、重力G、风力A决定,位置迭代更新规则数学模型如下:
x=S+G+A。(8)
相互作用力S的计算方法如下:
S=c∑Nj=1,j≠icb-b2s(x-x)x-xx-x+。(9)
式中:c为控制参数;b为搜索范围上限;b为搜索范围下限;为当前种群的最优解;s()为蝗虫之间的相互作用力函数,将蝗虫之间的距离定为排斥、吸引和舒适区。而当蝗虫在舒适区时就不会改变状态了。具体计算方法如下:
s(r)=f·exp-rl-exp-r。(10)
式中:r为到最近个体的距离;f与l分别为吸引力的力度和尺度。在位置更新过程中,利用Logistic映射引入混沌性。Logistic映射的公式如下:
x=μ·x·(1-x)。(11)
式中:x是当前时刻的位置;μ是映射调整变量。x的取值范围为[0, 1],需要根据搜索空间上下限进行归一化处理,而μ值范围通常为[2, 4],这样可以确保产生混沌行为。按照式(8)至式(11)更新种群内所有个体,完成一轮迭代。判断若收敛,则算法完成,否则再次迭代,并且不断循环达到收敛或预设最多迭代数为止。在优化过程的初始阶段,采用加入混沌扰动的更新策略能够较好地权衡全局探索和局部开采的平衡关系,这一算法的设计使得蝗虫个体能够快速向最优区域靠拢,从而提升了算法的收敛速率。随着迭代推进,算法使单个蝗虫在临近最优解完成细致探索,增强了算法对最优解的捕捉效果。
另外多头注意力-时域卷积网络需要优化对模型性能影响最大的3个超参数:TCN卷积核大小nk,TCN层数nl以及注意力头数nh。而混沌蝗虫优化-多头注意力-时域卷积网络(CGOA-MAM-TCN)是非常有效的方法,整体算法的流程如图5所示。该方法中,多头注意力机制-时域卷积网络模型用于直接对锂电池的SOC进行估计,而混沌蝗虫优化(CGOA)算法则对多头注意力-时域卷积网络的超参数进行优化,实现最佳的模型自适应性能。
2 试验及结果分析
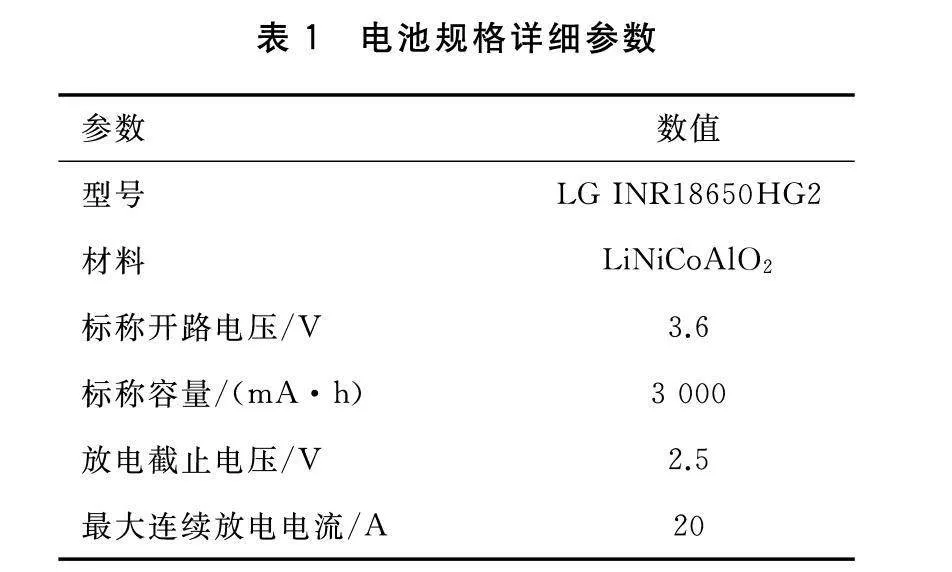
2.1 试验数据
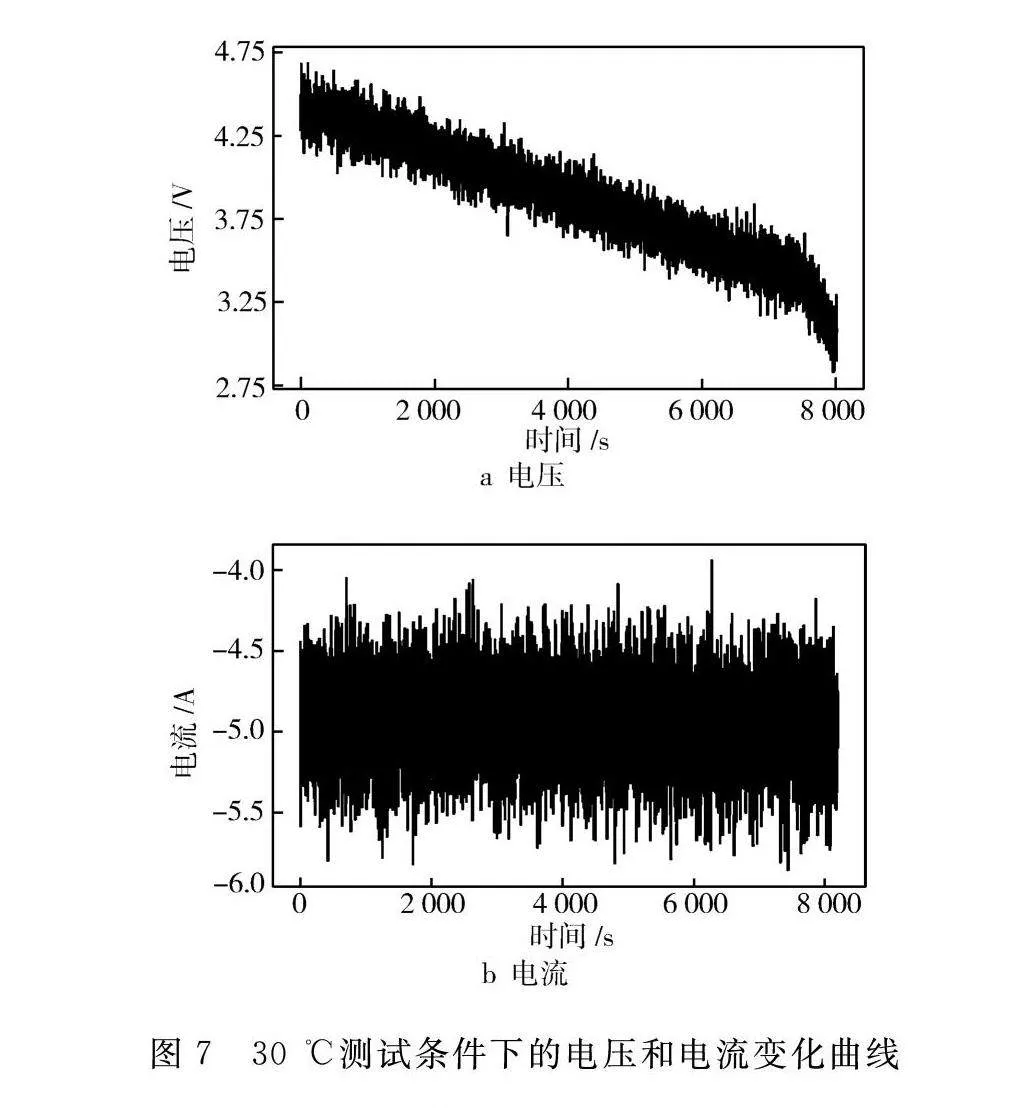
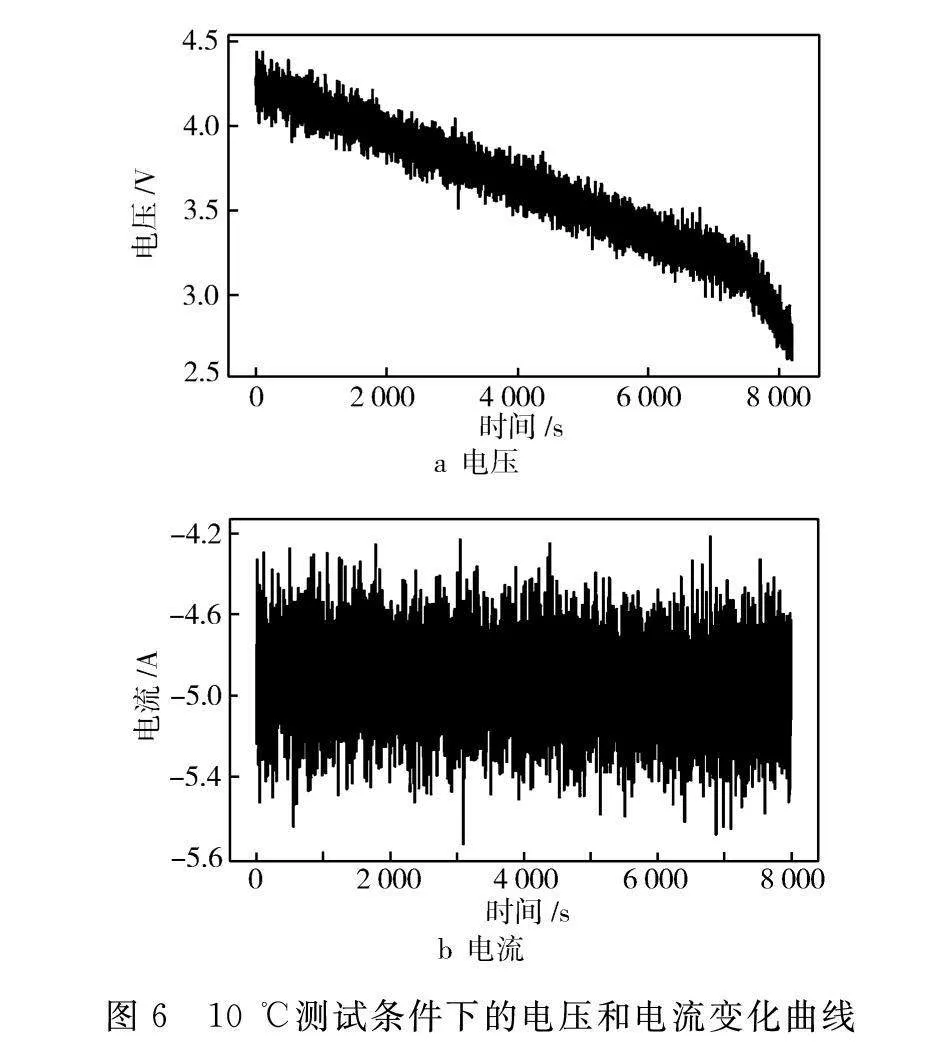
选用常用的车用锂离子电池(参数见表1)的数据集,使用加速老化测试的试验设置,电池被放置在热舱中,以确保其温度能够实时精确测量。主机用于数据监测和存储,测试在不同条件下电池的放电性能,并将实时温度、电流和电压数据回传。电压、电流和单体温度的数据采样时间为1 s。通过计算得到真实的SOC数据。首先,在每轮测试结束后对总体电功率进行时间上的积分,则某一时刻的SOC可由从测试开始到当前时刻电功率的积分值占总体电功率积分值的比例来确定。锂电池系统在复杂、多变的温度和工况下运行,因此在试验室环境中应全面考虑和尽可能覆盖所有温度和工况。数据集涵盖了整个SOC范围,从100%开始,消耗到0%为止,在2个温度(10 ℃和30 ℃)下测取。
用5组完整的数据作为模型的训练集,并用第6组数据作为模型的验证集。其中,训练集数据的选择原则首先是要覆盖全SOC范围,以确保模型能够学习到电池在不同SOC状态下的特征,其次要包含多种温度工况,因为温度是影响电池性能的重要因素。另外还要确保数据丰富多样,每种温度工况下使用5组完整放电数据作为训练集,以增加训练数据的多样性,避免过度拟合某一工况。最后使用第6组数据作为验证集,用于模型在训练过程中的性能评估和调优,验证集数据与训练集有同样的分布。图6和图7示出在10 ℃和30 ℃温度条件下的测量数据。训练模型时,输入为Tk,Uk,IkT,Tk,Uk和Ik分别为t时刻前k个时刻的温度、电压和电流向量。输出为下一个时刻的SOC值S。本研究中,所有的时间窗口k的长度取10。
数据处理方法为最大-最小归一化法,该方法用于将数据缩放到[0,1]内,确保各种特征或变量的数值范围一致,有助于避免量纲差异而引起的不同特征权重的问题。具体如下式:
X=X-XX-X。(12)
式中:X为样本数据;X和X分别为样本历史最低值、最高值。
2.2 模型配置
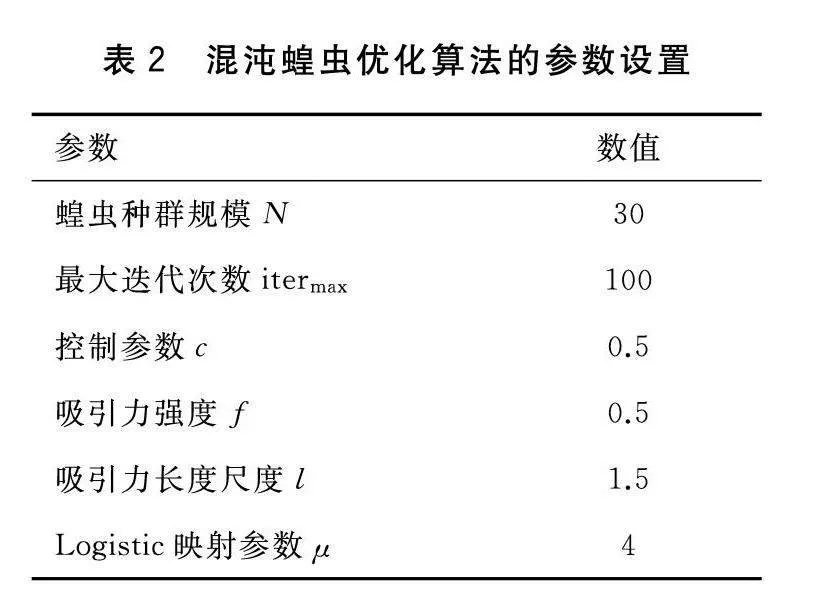
时间卷积-多头注意力模型的初始配置如下:时域卷积网络(TCN)的卷积核大小nk=3,层数nl=4;多头注意力的头数量nh=4。搜索范围上界为b=(9,8,16),下界为b=(3,2,4)。考虑到这3个超参数对模型性能的显著影响,采用了基于Logistic映射的混沌蝗虫优化算法对它们进行优化。由于以上超参数只能取整,所以在计算时,将所有可行解的结果进行四舍五入取整后代入模型进行训练、测试,并获得测试集的损失函数值作为适应度值参与混沌蝗虫优化算法进行迭代计算。混沌蝗虫优化算法的参数设置如表2所示。
模型输入滑动窗口的长度为100,输出长度为1,学习率为0.001(初始),批量大小为64,迭代轮数为30,采用Xavier初始化权重,采用Adam优化器,并采用L2正则化。对比组为LSTM和RNN模型,为了平衡模型的复杂性和表达能力,LSTM与RNN都是3层,每层都有128节点,激活函数都是tanh,采用与TCN同样的优化和训练配置。
2.3 评价方法
锂电池的SOC估计算法常使用平均绝对误差(MAE)和均方根误差(RMSE)进行评价。MAE计算公式如下:
MAE=1n∑nY-。(13)
式中:n为观测值的数量;Y为实际观测值;为对应的模型预测值。MAE的值越小,表示模型越接近真实观测。
均方根误差(RMSE)的公式为
RMSE=1n∑ni=1(Y-)2。(14)
与MAE相比,RMSE对大误差的惩罚更重。RMSE的值越小,表示有越好的模型预测效果,跟真实情况较为接近。
2.4 结果分析
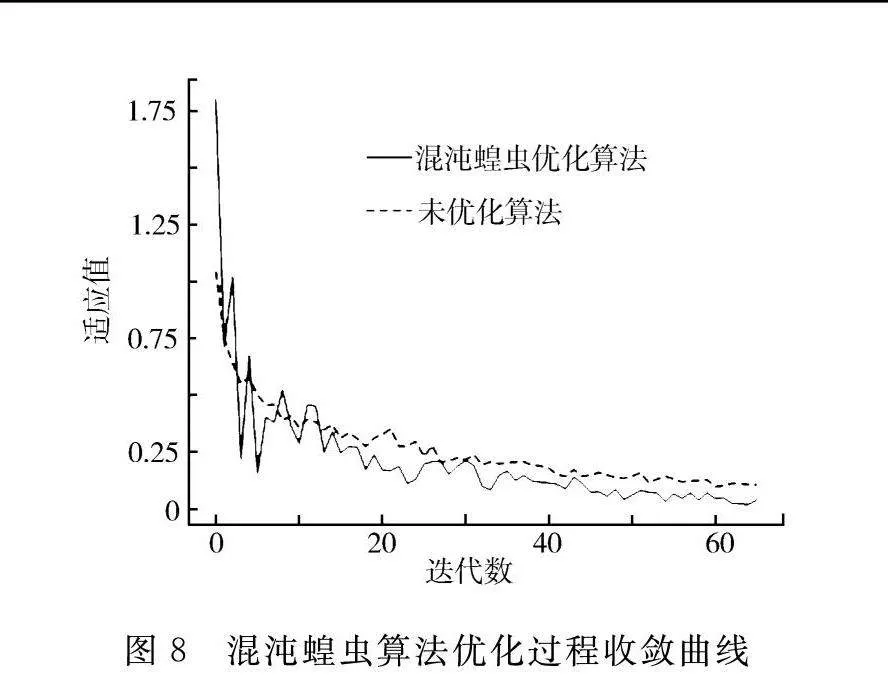
为了直观地观察混沌蝗虫优化算法优化过程,分别绘制了混沌蝗虫优化算法和未加入优化算法的迭代代数-适应值曲线(见图8)。由图可知,由于Logistic映射的混沌扰动,混沌蝗虫优化算法前期波动较原始算法更大,在66代迭代后曲线收敛(适应值变化小于0.01时自动停止)。曲线在前10代左右,目标函数值的验证集损失出现了较大幅度的下降,说明算法初期较快地接近了最优区域;随后的10~47代间,曲线下降趋势变缓,表明算法已接近最优解;在46代之后,曲线进入了一个波动收敛的阶段,这是由于引入的Logistic映射的混沌扰动机制所致。而此时原始优化算法已经陷入局部最优,适应值未能进一步改善。当算法接近全局最优时,混沌扰动使得种群个体能够在最优解附近小范围内振荡搜索,进一步提高了解的精度,避免过早收敛于次优解。最后算法搜索获得最优解卷积核大小nk=5、层数nl=6、注意力头数量nh=12。
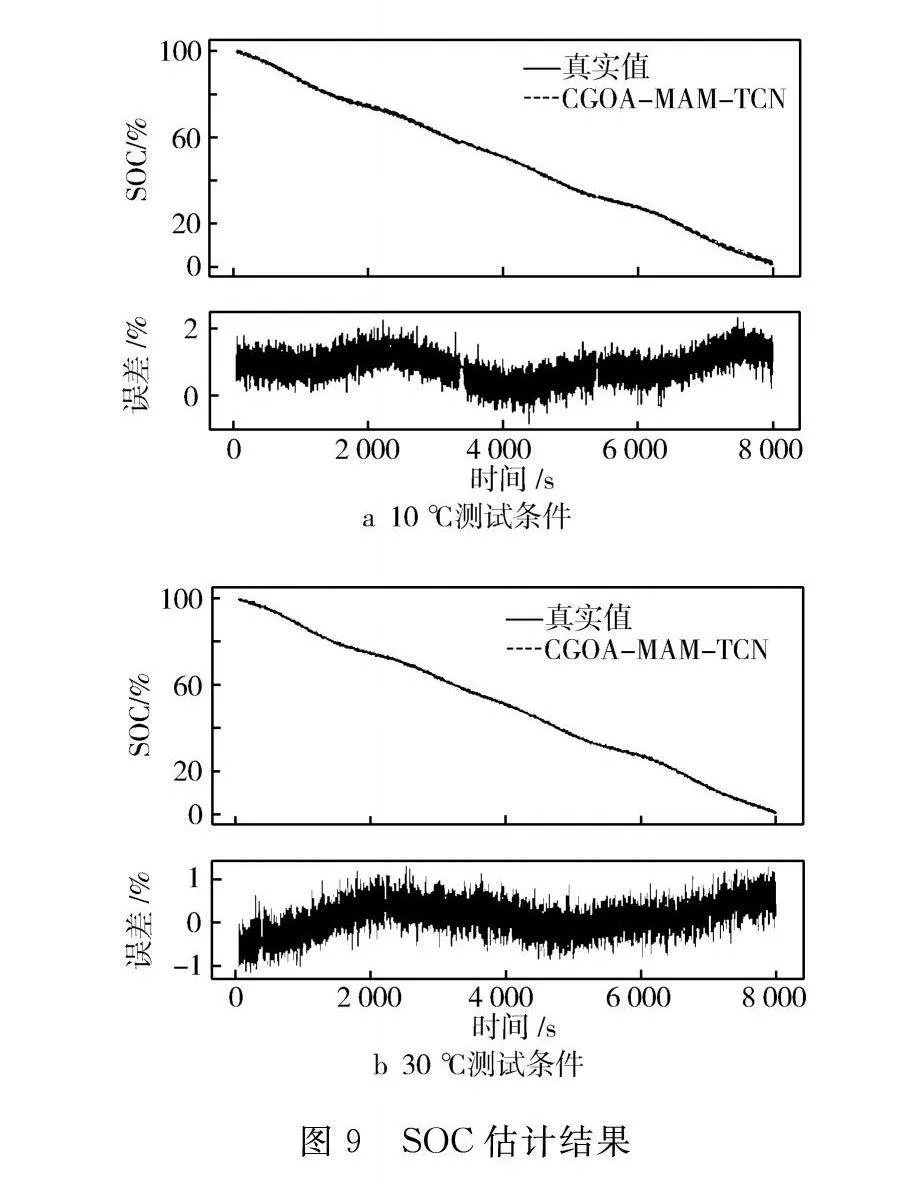
算法超参数经混沌蝗虫算法优化后模型的预测结果与误差曲线见图9。通过观察图9中的曲线,可以初步了解模型在不同温度条件下的性能。
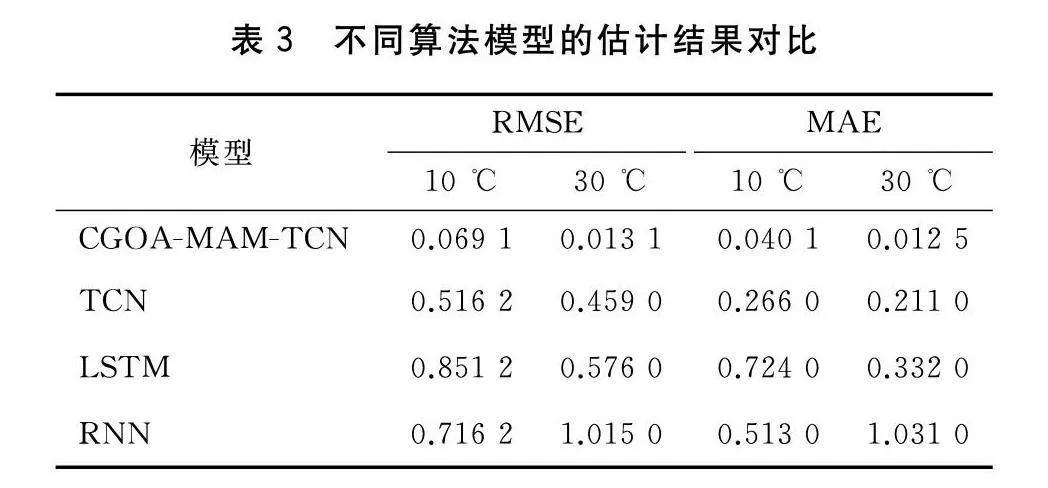
为了更全面地评估时域卷积-多头注意力模型与其他预测模型的性能差异,表3对比了不同模型在10 ℃和30 ℃两种温度条件下的预测结果。不同温度下模型的预测结果略有不同,如表3所示,当电池温度为10 ℃时,CGOA-MAM-TCN模型的RMSE为0.069 1 ,MAE为0.040 1;而在30 ℃的条件下,CGOA-MAM-TCN模型的RMSE降低为0.013 1,MAE为0.012 5。相较于低温条件,在接近常温条件下模型的预测效果更佳。多种算法相比之下,CGOA-MAM-TCN模型对比TCN、LSTM和RNN在这两个温度条件下的表现最佳。
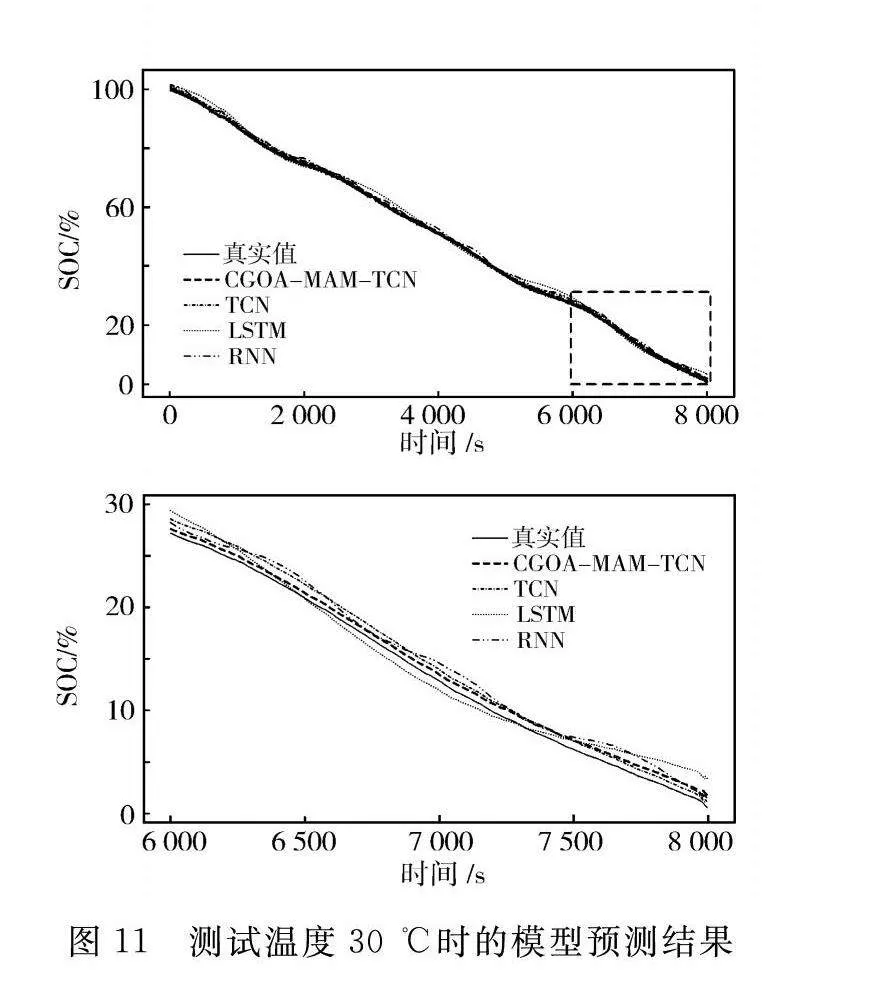
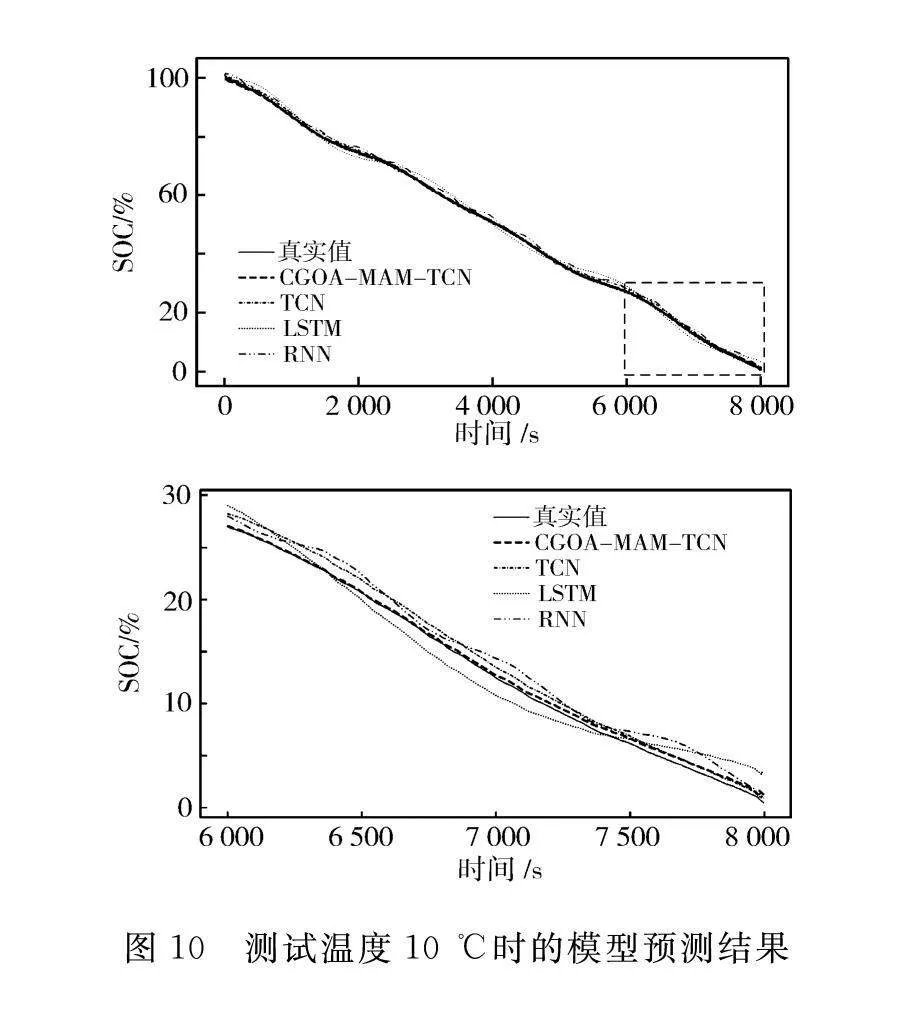
在30 ℃条件下,CGOA-MAM-TCN模型相较于其他模型具有更低的MAE和RMSE,表现出更为准确的SOC预测能力。而在10 ℃条件下,CGOA-MAM-TCN模型在MAE和RMSE方面同样有最优表现。图10和图11表明,CGOA-MAM-TCN模型在处理锂电池SOC估计任务时,在不同温度条件下都明显表现出了更为优越的性能。
3 结束语
提出了一种基于CGOA-MAM-TCN的SOC估计模型,旨在解决锂电池SOC准确估计和对大量标定数据的依赖等问题。时域卷积网络通过卷积操作和残差连接提高了对时序数据中长期依赖关系的建模能力,使用了混沌蝗虫优化算法对MAM-TCN算法的超参数进行优化,使得提出的SOC估计模型在空间和时间特征的提取上表现出较好的性能。试验结果表明,在不同温度条件下,提出的CGOA-MAM-TCN模型相较于其他模型具有更低的MAE和RMSE,表现出更为准确和稳定的SOC估计能力。
未来将从以下三个方面持续改进和拓展所提算法。首先是扩展数据集范围。本研究试验所用数据集主要覆盖10 ℃和30 ℃两种温度条件,未来将获取更多极端温度(如0 ℃以下)以及复杂工况下的实测数据,以进一步评估和提高算法的适用性。同时,也会考虑收集不同电池老化程度(SOH)下的数据,使算法能够适应电池健康状态的变化。其次是优化算法结构。将在现有CGOA-MAM-TCN模型的基础上,探索更高效的特征提取方法和注意力机制变体,以期进一步提升模型对复杂时序模式的捕获能力。此外,研究新的超参数优化策略,替代或结合当前的混沌蝗虫优化算法,追求更精准的参数调优效果。最后是拓展应用场景。本研究工作主要针对新能源汽车的锂电池SOC估计问题,但所提出的数据驱动建模思路和算法框架也可推广应用于其他储能领域,如非车用电池组、电网储能系统等。未来将该算法推广至更广阔的场景,为相关领域的能源管理提供有力支持。
参考文献:
[1] Adaikkappan M,Sathiyamoorthy N.Modeling,state of charge estimation,and charging of lithium-ion battery in electric vehicle:a review[J].International Journal of Energy Research,2022,46(3):2141-2165.
[2] Hannan M A,Lipu M S H,Hussain A,et al.A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications:Challenges and recommendations[J].Renewable and Sustainable Energy Reviews,2017,78:834-854.
[3] Cui Z,Wang L,Li Q,et al.A comprehensive review on the state of charge estimation for lithium-ion battery based on neural network[J].International Journal of Energy Research,2022,46(5):5423-5440.
[4] Jiang C,Wang S,Wu B,et al.A state-of-charge estimation method of the power lithium-ion battery in complex conditions based on adaptive square root extended Kalman filter[J].Energy,2021,219:119603.
[5] Wang S,Fernandez C,Yu C,et al.A novel charged state prediction method of the lithium ion battery packs based on the composite equivalent modeling and improved splice Kalman filtering algorithm[J].Journal of power sources,2020,471:228450.
[6] Tran M K,Mathew M,Janhunen S,et al.A comprehensive equivalent circuit model for lithium-ion batteries,incorporating the effects of state of health,state of charge,and temperature on model parameters[J].Journal of Energy Storage,2021,43:103252.
[7] Lai X,Wang S,Ma S,et al.Parameter sensitivity analysis and simplification of equivalent circuit model for the state of charge of lithium-ion batteries[J].Electrochimica Acta,2020,330:135239.
[8] 黄凯,孙恺,郭永芳,等.基于观测方程重构滤波算法的锂离子电池荷电状态估计[J].电工技术学报,2024,39(7):2214-2224.
[9] Babaeiyazdi I,Rezaei-Zare A,Shokrzadeh S.State of charge prediction of EV Li-ion batteries using EIS:A machine learning approach[J].Energy,2021,223:120116.
[10] Hu C,Cheng F,Ma L,et al.State of charge estimation for lithium-ion batteries based on TCN-LSTM neural networks[J].Journal of the Electrochemical Society,2022,169(3):030544.
[11] How D N T,Hannan M A,Lipu M S H,et al.State-of-charge estimation of li-ion battery in electric vehicles:A deep neural network approach[J].IEEE Transactions on Industry Applications,2020,56(5):5565-5574.
[12] Zhang C,Zhu Y,Dong G,et al.Data-driven lithiumion battery states estimation using neural networks and particle filtering[J].International Journal of Energy Research,2019,43(14):8230-8241.
[13] Zhou D,Li Z,Zhu J,et al.State of health monitoring and remaining useful life prediction of lithium-ion batteries based on temporal convolutional network[J].IEEE Access,2020,8:53307-53320.
[14] Hewage P,Behera A,Trovati M,et al.Temporal convolutional neural(TCN) network for an effective weather forecasting using time-series data from the local weather station[J].Soft Computing,2020,24:16453-16482.
[15] Zeng P,Hu G,Zhou X,et al.Muformer:A long sequence time-series forecasting model based on modified multi-head attention[J].Knowledge-Based Systems,2022,254:109584.
[16] Li Z,Li L,Chen J,et al.A multi-head attention mechanism aided hybrid network for identifying batteries’ state of charge[J].Energy,2024,286:129504.
[17] Mirjalili S Z,Mirjalili S,Saremi S,et al.Grasshopper optimization algorithm for multi-objective optimization problems[J].Applied Intelligence,2018,48:805-820.
[18] Meraihi Y,Gabis A B,Mirjalili S,et al.Grasshopper optimization algorithm:theory,variants,and applications[J].IEEE Access,2021,9:50001-50024.
Estimation for SOC of Vehicle Lithium-Ion Battery Based on CGOA-MAM-TCN Algorithm
WANG Hongbin
(Tianjin Coastal Polytechnic,Tianjin 300459,China)
Abstract: Data-driven estimation method for the state of charge(SOC) of lithium batteries still relies on a large amount of calibration data and shows poor performance in dealing with dynamic changes and complex operating conditions. Therefore, an improved locust algorithm optimization combined with time-domain convolutional networks and multi-head attention mechanisms was proposed to estimate the SOC of lithium battery. A time-domain convolutional network was first used to model the long-term dependency relationships in the time series data of lithium battery charging. Meanwhile, multi-head attention was used to learn the long-term dependency relationships of data features, and each attention head was used to calculate the dependency relationships of different tensors in the sequence to assist the time-domain convolutional neural network in enhancing the capture of dependency relationships and reducing its dependence on a large amount of calibration data. In addition, the chaotic locust algorithm was improved to optimize the hyperparameters of model to maximize the performance of model. The experimental results show that, compared with other methods, the optimized model can exhibit better accuracy and stability in the task of estimating the SOC of lithium battery under different temperature conditions.
Key words: lithium battery;state of charge(SOC);estimation;time-domain convolution;multi-head attention;locust optimization algorithm
[编辑:袁晓燕]
