基于模型预测框架的燃料电池汽车混合动力系统能量管理
2024-11-01王金环宋占伟

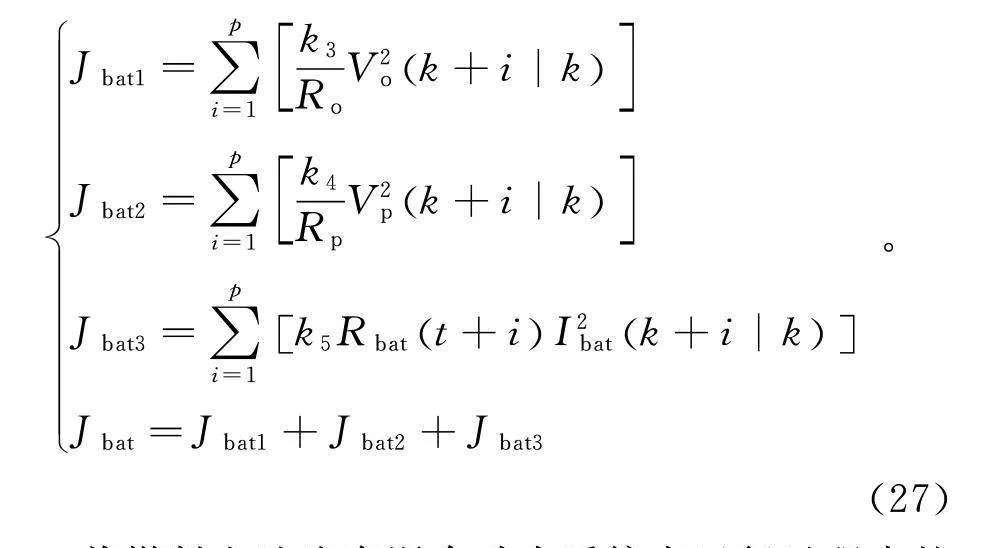


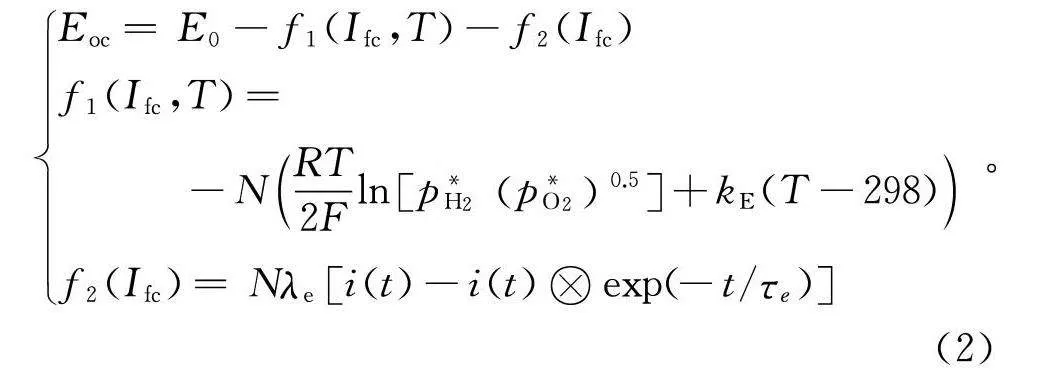


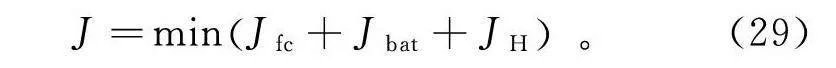
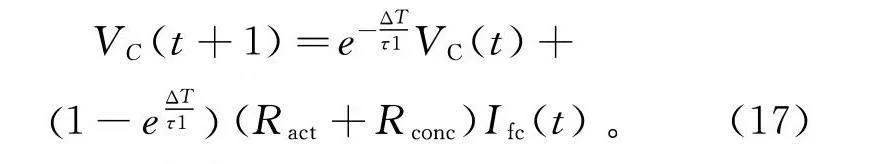
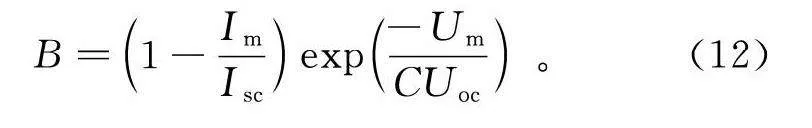
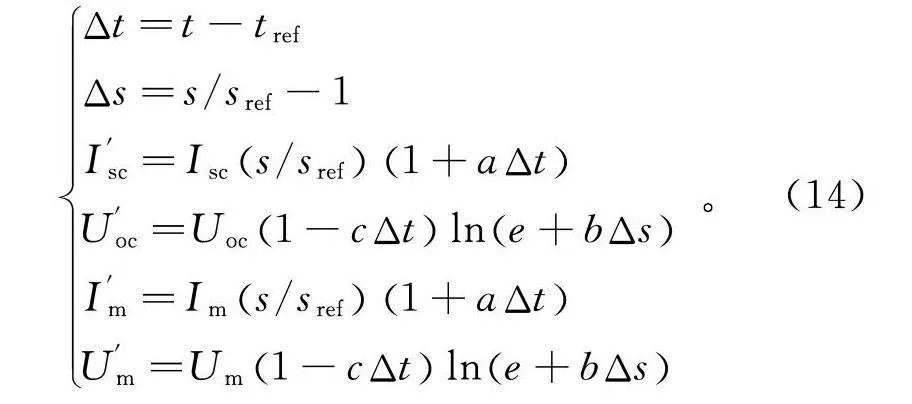
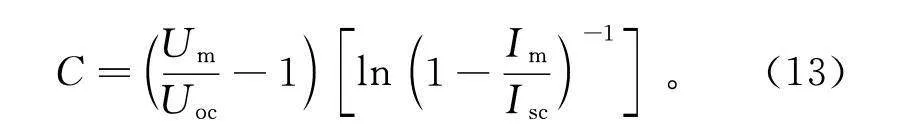

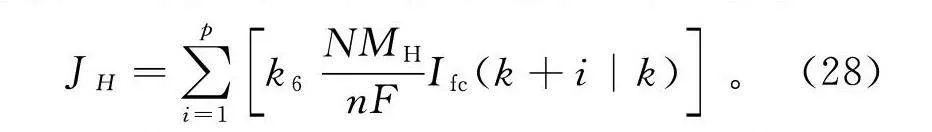




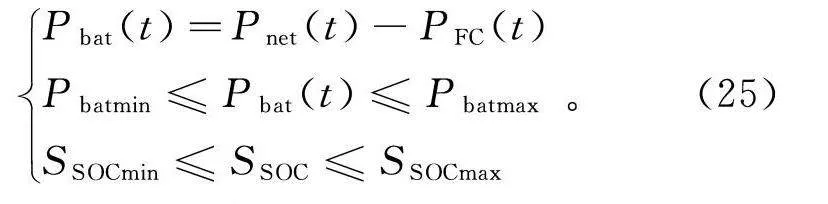


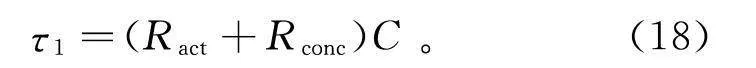

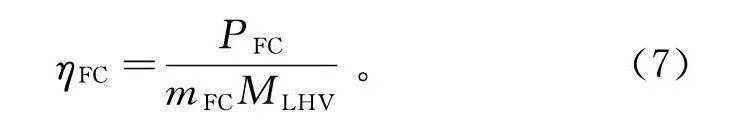

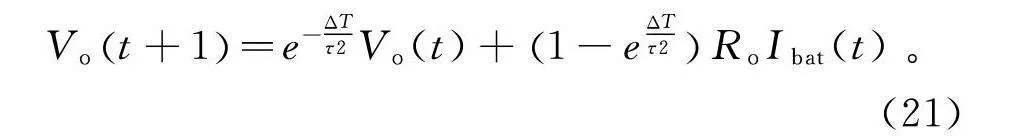
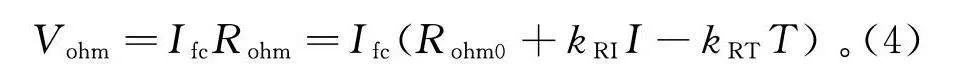
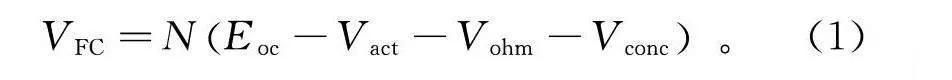

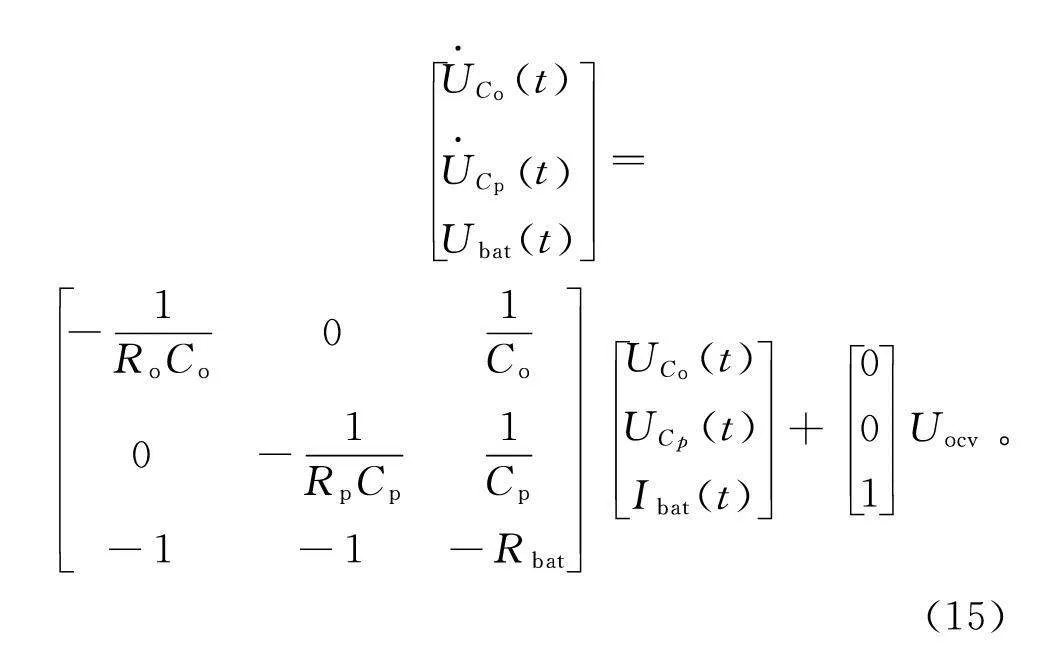
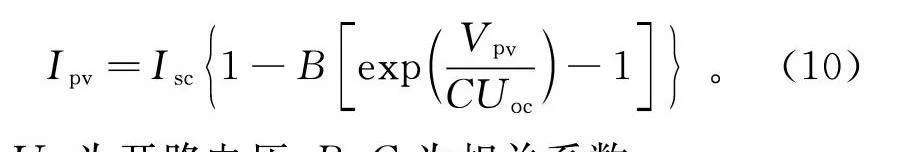
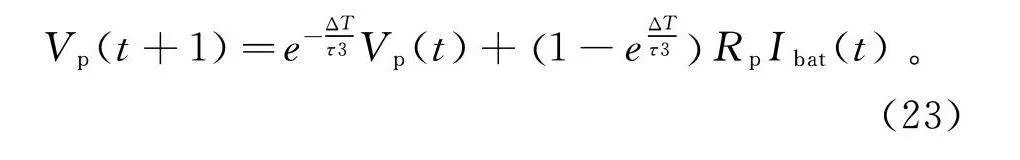
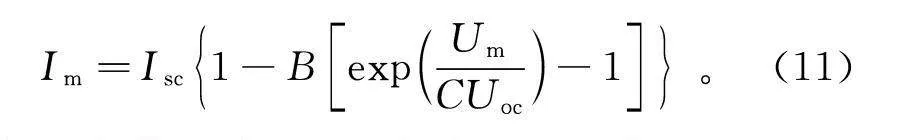

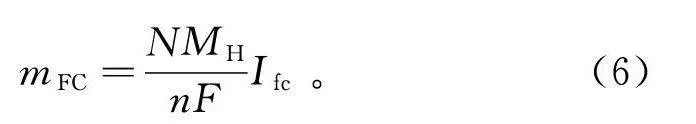
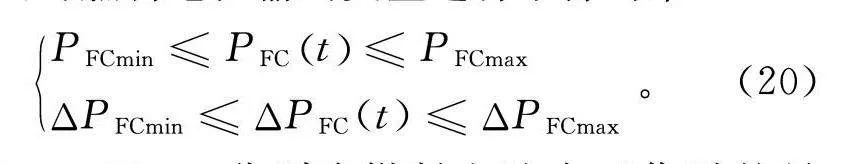
摘要:混合动力系统作为燃料电池汽车的关键组成部分,系统的能耗与寿命优化是推动其进一步商业化发展的关键,而能量管理策略(EMS)在提高燃料电池汽车混合动力系统的效率和燃料经济性方面发挥着重要作用。为有效降低混合动力系统的内部损耗,进一步提高系统经济性,提出了一种基于模型预测框架的混合动力系统能耗优化能量管理控制方法。首先构建包含动力系统内部损耗与氢气消耗的目标函数,然后利用模型预测架构求解目标函数来控制燃料电池的输出电流,以实现合理的能量分配,最后在Matlab中进行仿真,验证所制定方法的合理性和有效性。与应用较为广泛的等效氢耗最小策略(ECMS)相比,结果表明所提方法可以显著降低动力系统的内部损耗和氢气消耗。此外,该策略还可以有效保持蓄电池的荷电状态(SOC),延长动力系统的使用寿命。
关键词:燃料电池汽车;混合动力系统;能量管理;模型预测控制
DOI:10.3969/j.issn.1001-2222.2024.05.009
中图分类号:TM911.4 文献标志码:B 文章编号:1001-2222(2024)05-0061-10
随着十四五规划与“双碳”目标的提出,电动汽车因其无污染、可持续发展等综合优势在交通运输行业具有更高的利用价值[1-2]。以燃料电池为主电源、锂电池为辅助电源,同时结合光伏构成的混合动力系统,已成为电动汽车的未来发展趋势。但目前混合动力系统面临着损耗大、效率低、经济性差等问题,同时在不可预测的驾驶环境中,动力系统存在加速时的瞬时高功率和制动再生时的高功率等情况,会使蓄电池过充或过放,从而加速电池寿命的衰减[3-4]。为了突破上述技术瓶颈,混合动力系统的功率分配问题成为目前的研究热点,即如何平衡多个电源之间的配电与发电成为必须要考虑的问题,因此,合理的能量管理方法设计尤为重要[5-6]。
对于混合储能系统,现有的能量管理策略主要分为基于规则和基于优化两种类型。基于规则的算法不需要提前熟悉驾驶信息,对硬件的要求较低,被广泛实际应用,包括逻辑阈值算法[7]、模糊逻辑算法[8-9]、过滤方法[10]、滑动模式控制[11]等类型。在文献[11]中,平坦控制和基于模糊逻辑的能量管理算法被应用于由燃料电池、电池和UC组成的混合动力系统中,研究表明,所设计的EMS适用于不同的混合操作模式。Q. Zhao等[12]评估了针对电池-UC组成的HESS的三模式规则策略,仿真结果表明,该方法可以最大化储能系统容量,并最大程度地减少系统的能源消耗。但是,在车辆控制过程中,这些驱动状态不可能像基于优化的控制策略一样准确。同时,当设置驾驶状态的边界条件时,需要大量的先验知识。由于上述缺陷,基于规则的控制策略具有较低的鲁棒性和较差的控制效果。基于优化的策略由于其可以更好地匹配汽车工况,提升控制策略的稳定性和鲁棒性,在电动汽车能量管理方面得到了更多的应用。
基于优化的策略可以分为离线策略和在线策略。常用的离线算法包括动态规划算法(DP)[13]、庞特里亚金极小值原理算法[14]、遗传算法[15]、凸优化[16]、粒子群优化[17]等。动力系统关于能量消耗、系统效率等目标的最佳全局解决方案可以通过这些离线策略获得。基于离线的策略存在必须事先知道全局负载功率信息等缺陷,使得其在动力系统的实时管理应用中受到限制。A. Fathy等[17]通过从动态规划的结果中提取相关规则,在线控制混合储能系统的功率分配来解决DP算法的实时性问题。这在实时操作过程中需要存储大量数据,将占用大量计算资源。模型预测控制算法因具有可以在线预测驾驶工况、实现滚动优化等优异性能,在现有的基于优化的在线策略中得到了更为广泛的应用。D. Zhou等[18]使用模型预测控制(MPC)来实现以蓄电池组和超级电容组合的混合储能系统功率分配,系统的结构和复杂性得以完全体现,并通过试验证明MPC在实际系统中的可操作性。M. Sellali等[19]提出了一种使用模型预测控制框架控制每个转换器参考电流的方法,并以磁滞控制作为底层,以跟踪燃料电池-电池-燃料电池混合动力源的电流。通过DSPACE系统试验验证了混合动力源MPC的可靠性和有效性。Y. Yan等[20]在混合电动汽车的动态功率分配中采用了显示模型预测控制算法,并通过试验与隐式模型预测控制方法做了对比,结果证明,就微处理器硬件要求而言,显式MPC低于MPC。
然而,电动汽车动力系统作为实时动态系统,在模型预测算法建立过程中需要对储能系统进行详细建模,而多数算法仅关注其时变特性来均衡蓄电池的荷电状态与混合动力系统的能量消耗与效率等,其寿命情况以及动力系统的负载端特性被忽略。因此本研究提出了一种基于模型预测框架的电动汽车混合储能系统寿命优化控制方法,该算法考虑混合储能系统寿命与负载端特性,实现了动力系统在快速变载下的寿命成本优化,并有效减少了控制系统的计算负担,降低了其在处理器中的计算时间,增强了该算法在系统控制方法中的实际应用性。
1 混合动力系统模型
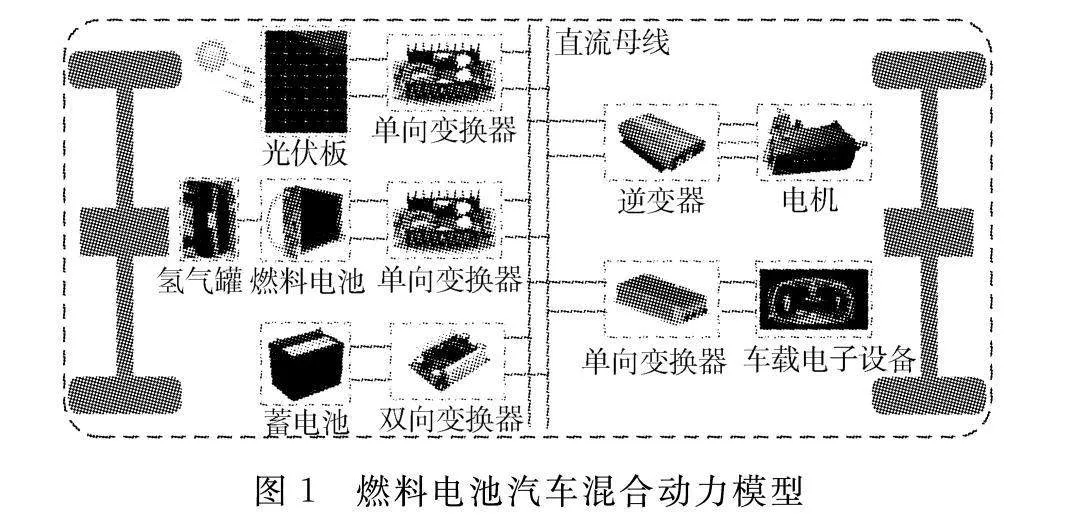
燃料电池汽车混合动力系统拓扑如图1所示。燃料电池作为系统主要供给电源,承担负载的多数功率需求。为提升燃料电池汽车的续航能力,通常会在汽车车顶搭建光伏面板来为其他辅助负载(如电动天窗、遮阳帘、空调等)提供能量,或者在汽车爬坡、加速时为动力系统提供缺额能量,在光照充足时可以弥补部分功率缺额,在功率需求不高或者制动时,可以给蓄电池供给能量。蓄电池作为辅助能源用来补充负载功率迅速变化所造成的能量缺口,与燃料电池共同支撑汽车的动力需求。燃料电池和光伏面板分别经单向Boost DC-DC变换器连接至母线,蓄电池经双向Buck-Boost DC-DC变换器连接直流母线。母线能量经由逆变器控制永磁电机驱动传动轴使汽车获得动力,为考虑负载端特性,将负载端视为恒流源,可等效为阻感性负载;母线经单向Buck DC-DC变换器向车内其他车载设备供电。
1.1 燃料电池模型
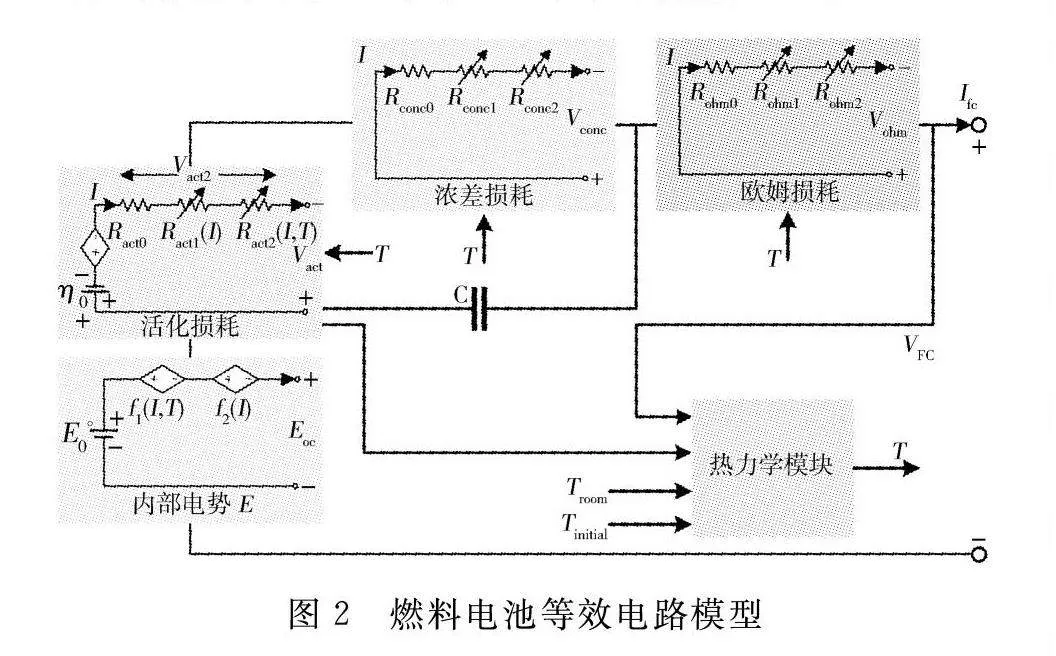
燃料电池是一个非线性、强耦合、多输入的复杂动态系统,其动态特性涉及流体力学、热力学及电化学等众多学科门类,工作过程是固液气三相混合的流体流动、传质、传热和电化学动态过程。本研究经过对燃料电池工作原理与参数模型的分析,针对其电气特性制定简化模型,所建立等效电路模型见图2[21]。
将燃料电池欧姆损失等效为由电阻R造成的内部损耗,将电池内部的活化损失等效为活化电阻R,将燃料电池内部的浓差损耗等效为浓差损失电阻R,将双层电荷效应视为电容C。得到的燃料电池等效电路输出电压表达式为
V=NE-V-V-V。(1)
式中:N为燃料电池单体数量;E为燃料电池内部电势;V为燃料电池活化反应引起的电压降;V为燃料电池的总欧姆电压降;V为燃料电池的浓差电压降。
根据等效电路模型,燃料电池内部电势可表示为
{E=E-f(I,T)-f(I)f(I,T)= -NRT2Flnp*p*0.5+k(T-298)f(I)=Nλi(t)-i(t)Uexp(-t/τ)。(2)
式中:E为标准状态下的参考电位;I为燃料电池输出电流;T为燃料电池反应温度;F为法拉第常数;i(t)为单体电池电流;τ表示总流量延迟;k,λ,R为常数。
根据等效电路,燃料电池活化损耗电压降V可表示为
V=η+a(T-298)+bTln(I)。(3)
式中:η,a,b都为常数。
欧姆损失电动势V是由电子通过电极材料和质子流过交换膜的阻力引起的,可以表示为
V=IR=I(R+kI-kT)。(4)
式中:R为电流和温度的函数;R为常数部分;k,k均为经验常数。
根据等效电路,燃料电池浓度损耗电压降V可表示为
V=RT2Fln1-IAj。(5)
式中:A为薄膜面积;j为极限电流密度。
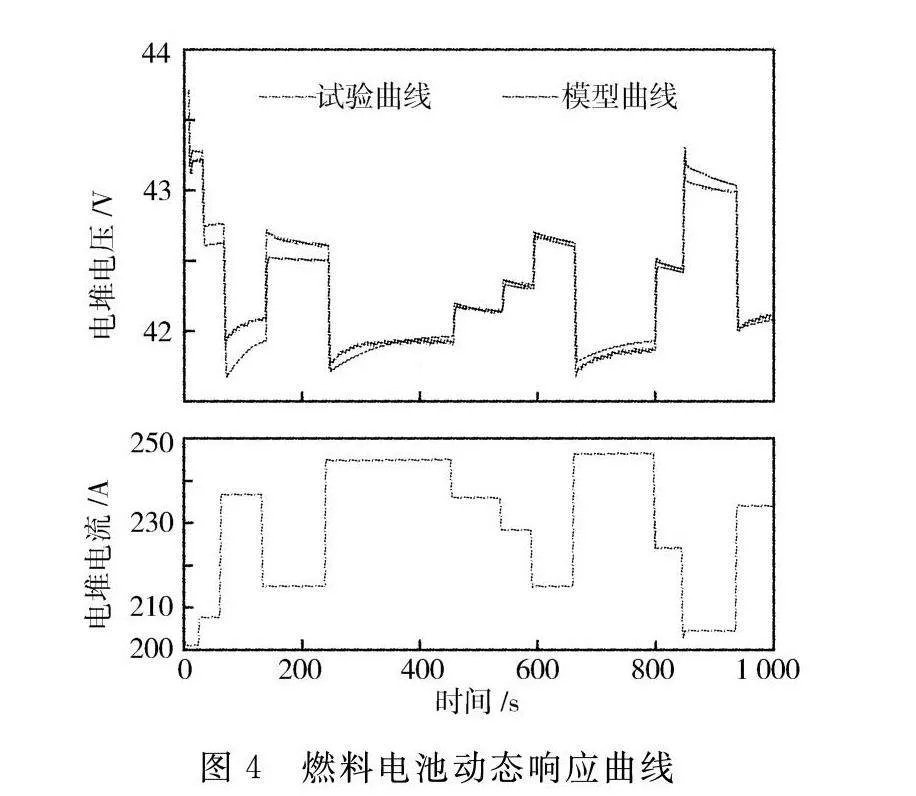
燃料电池系统仿真模型相关参数如表1所示,其极化特性曲线如图3所示。为验证模型精确性,对燃料电池模型的动态响应进行了测试,试验与仿真结果对比如图4所示。由图4可以看出,仿真模型具有较高的精确性,其动态响应能力符合误差要求。
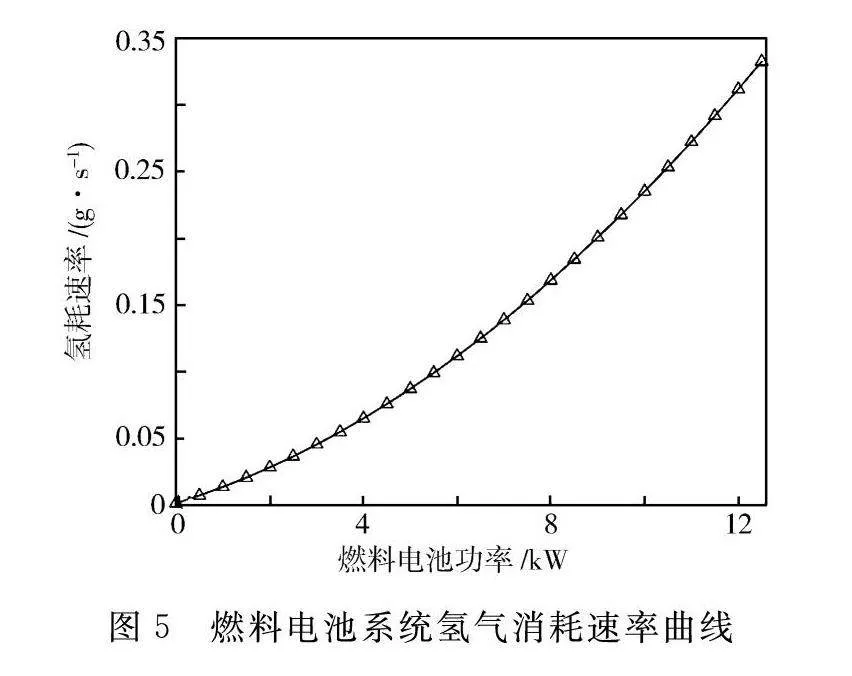
燃料电池系统的净输出功率可以通过电堆的总输出功率减去辅助系统消耗的功率得到。系统单位时间内的氢气消耗量可以表示为
m=NMnFI。(6)
式中:M为氢气的摩尔质量;n为参与反应的电子数。根据模型得到的氢耗曲线见图5。
而燃料电池系统效率可以通过下式计算:
η=PmM。(7)
式中:P为燃料电池功率;M为氢气低热值。得到的效率曲线如图6所示。
1.2 光伏模型
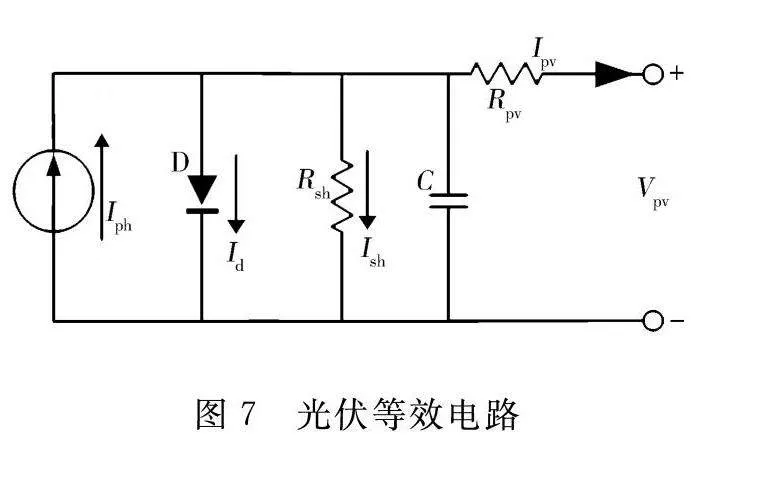
太阳能光伏发电的原理是利用半导体材料接收光照时所产生的光生伏打效应,在持续光照下,部分光以光子的形式与PN结的原子价电子发生碰撞,产生电子和空穴,然后在PN结势垒区内建电场的作用下,电子和空穴分别驱向N区和P区两个不同的区域,若在P区和N区之间焊接上金属引线,并接上负载,则可形成闭合电流回路。太阳能光伏电池输出特性受太阳辐射强度S与电池表面温度T的影响,光伏输出电压等效电路模型如图7所示。
图7中:I为光电效应产生的电流;I为流经二极管的电流;R为旁漏电阻;I为流经旁漏电阻的电流;C为光伏自身所含的等效电容;R为光伏内阻;I为光伏输出电流;V为光伏输出电压。
根据光伏等效电路,结合基尔霍夫电流定律得:
I=I-I-I。(8)
P-N结电流和电压关系满足下式:
I=I{expqV+IRAkT-1}。(9)
式中:I为二极管反向饱和电流;q为电子电荷量;A为P-N结理想因子;K为玻尔兹曼常数;T为环境绝对温度。
通常情况下旁漏电阻R的取值较大,导致I较小,故可将其忽略不计。同时内阻R的值也较小,故设定I=I,可以得到:
I=I{1-BexpVCU-1}。(10)
式中:U为开路电压;B,C为相关系数。
设定光伏在开路状态下有V=U,I=0,在最大功率点处有V=U,I=I。当光伏处于最大功率点时,将已知条件代入上式得到:
I=I{1-BexpUCU-1}。(11)
由于光伏一般工作在常温下,有exp(U/CU)>>1,可求得系数B:
B=1-IIexp-UCU。(12)
在光伏正常工作状态下,有exp1/C>>0,可求得系数C:
C=UU-1ln1-II-1。(13)
由于光伏正常工作过程中会受到诸多环境因素的影响,具有随机性与不确定性,因此,本研究引入修正系数对环境因素进行一定的修正,以便更加准确表示光伏的实际工作状态。制定的修正方案如下:
{Δt=t-tΔs=s/s-1I′=Is/s1+aΔtU′=U1-cΔtlne+bΔsI′=Is/s1+aΔtU′=U1-cΔtlne+bΔs。(14)
式中的各项参数设定值如表2所示。
1.3 蓄电池模型
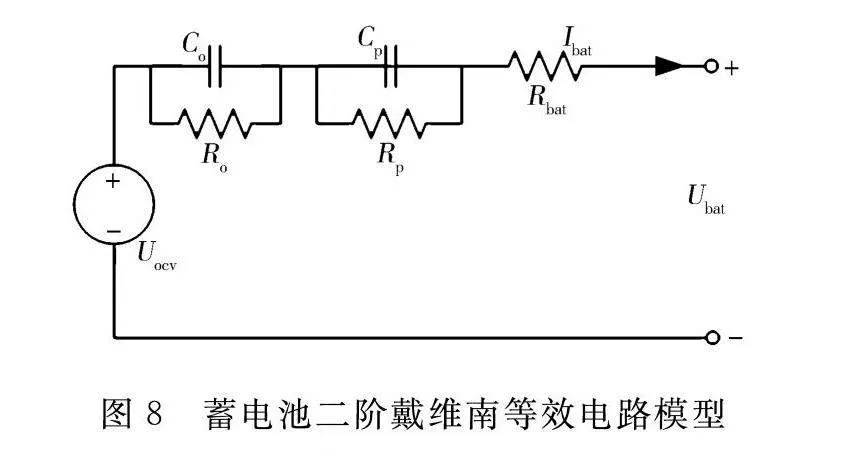
蓄电池的充放电过程实质上是一个由众多复杂随机变量构成的非线性函数。建立二阶戴维南等效模型,利用电压源、电阻、电容进行等值电路计算,不但可以较为准确地表达阻容特性,还能反映蓄电池的动态和静态特性,具有计算分析简单、适用性强的特点[22]。蓄电池等效电路模型如图8所示。
图8中:两个RC电路都表示电池内部的极化反应,R,C分别为欧姆极化反应的极化电阻和电容;R,C分别为浓差极化反应的极化电阻和电容;R为蓄电池的内阻;U为蓄电池输出电压;I为蓄电池输出电流;U为蓄电池开路电压。
由二阶戴维南等效电路模型建立状态方程组:
U·(t)U·tU(t)=-1RC01C0-1RC1C-1-1-RU(t)U(t)I(t)+001U。(15)
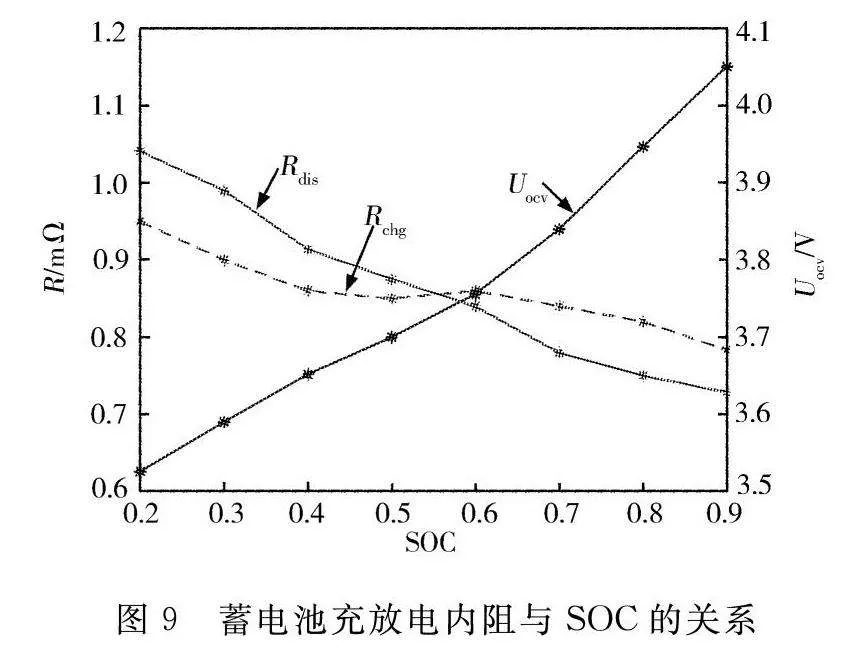
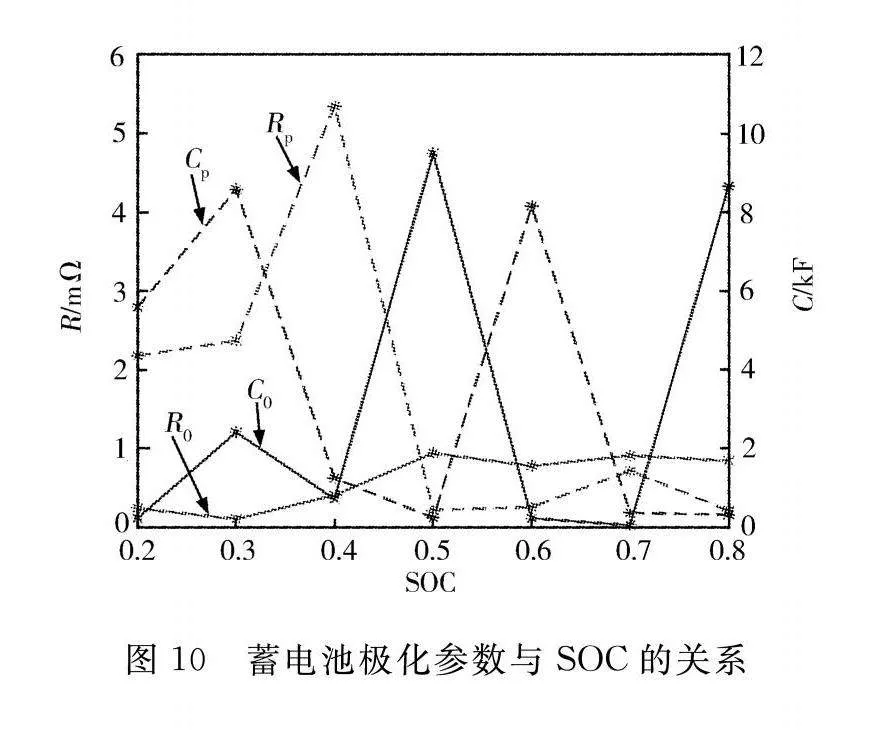
根据等效电路模型,对蓄电池的相关特性参数进行了试验测试。蓄电池充放电内阻和开路电压与荷电状态(SOC)关系曲线如图9所示。据图9可知,蓄电池充放电内阻都随SOC的增大而逐渐非线性减小,开路电压随SOC增大而逐渐增大;欧姆极化与浓差极化所对应的电阻和电容与SOC关系曲线见图10,据图10可知关系曲线并无明显规律。
2 能量管理方法构建
以模型预测控制算法为框架,提出一种考虑系统内部损耗与氢气消耗的能量管理方法,实现降低动力系统内部损耗、提高燃料经济性的目标。由于太阳能光伏系统的能量输出与外界环境中的光照强度和温度有关,不在所考虑的内部损耗优化和经济优化目标之内,而且负载需求功率远大于光伏最大输出功率,只需制定MPPT算法保证光伏电池持续最大功率输出即可,其内部损耗将不予考虑。因此定义直流母线的净需求功率为
P=P-P。(16)
式中:P为负载总需求功率;P为光伏系统输出功率。
根据燃料电池等效电路模型,其内部损耗包含欧姆损耗、活化损耗和浓差损耗。为简化计算,降低模型复杂度,用电容C来表征双层电荷效应,对电容两端电压V进行前向欧拉离散处理可得到:
V(t+1)=e-ΔTτV(t)+1-eΔTτ(R+R)I(t)。(17)
式中:τ为时间常数;ΔT为采样时间。
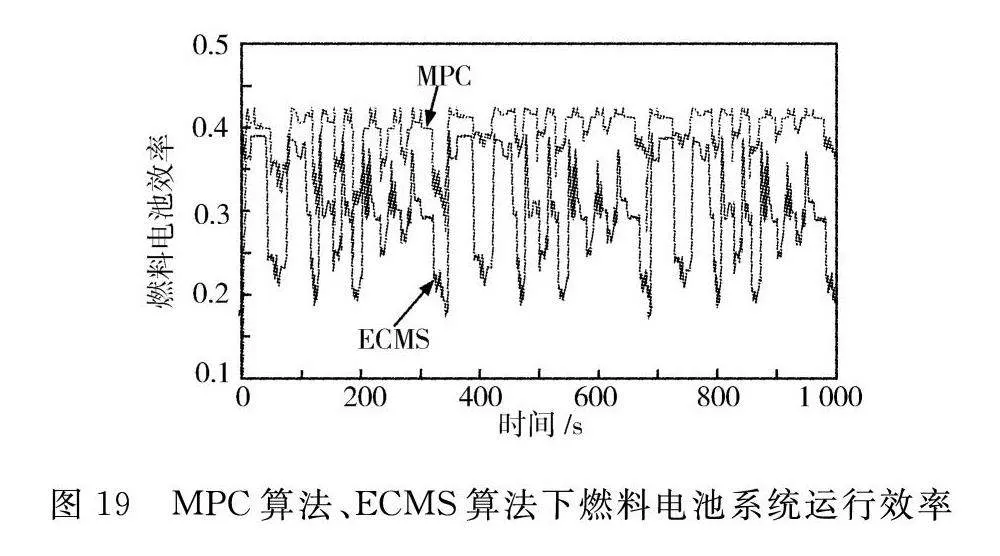
τ=(R+R)C。(18)
对欧姆内阻进行前向欧拉离散处理可得到:
R(t+1)=R+k(1-ΔT)I(t)-kT(t)。(19)
同时,为保证燃料电池可以更加高效安全稳定地运行,延长燃料电池的使用寿命,在大幅度变载工况下需要对燃料电池输出变量进行条件约束:
{P≤Pt≤PΔP≤ΔP(t)≤ΔP。(20)
式中:P,P分别为燃料电池在工作时的最小和最大输出功率;ΔP,ΔP为燃料电池在系统运行时输出功率变化率的最小值和最大值,分别对应的值为-100 W/s,100 W/s。
蓄电池内部损耗主要来源于欧姆损耗与浓差损耗,欧姆极化反应压降V的前向欧拉离散结果可以表示为
Vt+1=e-ΔTτV(t)+1-eΔTτRI(t)。(21)
对应的时间常数τ表示为
τ=RC。(22)
浓差极化反应压降V的前向欧拉离散结果可以表示为
V(t+1)=e-ΔTτV(t)+1-eΔTτRI(t)。(23)
对应的时间常数τ表示为
τ=RC。(24)
同理,为了使蓄电池始终工作在安全高效率区间,需确保SOC在动力系统运行过程中处于合理区间,蓄电池的输出需满足如下约束条件:
{P(t)=P(t)-P(t)P≤P(t)≤PS≤S≤S。(25)
式中:P为蓄电池功率;P,P分别为蓄电池在工作过程中的最小和最大功率;S,S分别为蓄电SOC的安全运行区间的最小值和最大值。
根据以上分析,将燃料电池的内部损耗分别添加到目标函数中,构建目标函数如下:
{J=∑pi=1kR+RV2(k+i|k)J=∑pi=1kRt+iI2(k+i|k)J=J+J。(26)
将蓄电池的内部损耗分别添加到目标函数中,构建目标函数如下:
{J=∑pi=1kRV2k+i|kJ=∑pi=1kRV2k+i|kJ=∑pi=1kRt+iI2k+i|kJ=J+J+J。(27)
将燃料电池汽车混合动力系统在运行过程中的氢气消耗量添加到目标函数中,构建目标函数如下:
J=∑pi=1kNMnFI(k+i|k)。(28)
基于上述目标函数,构建出系统内部总损耗优化目标函数,相应的最小化目标表示为
J=minJ+J+J。(29)
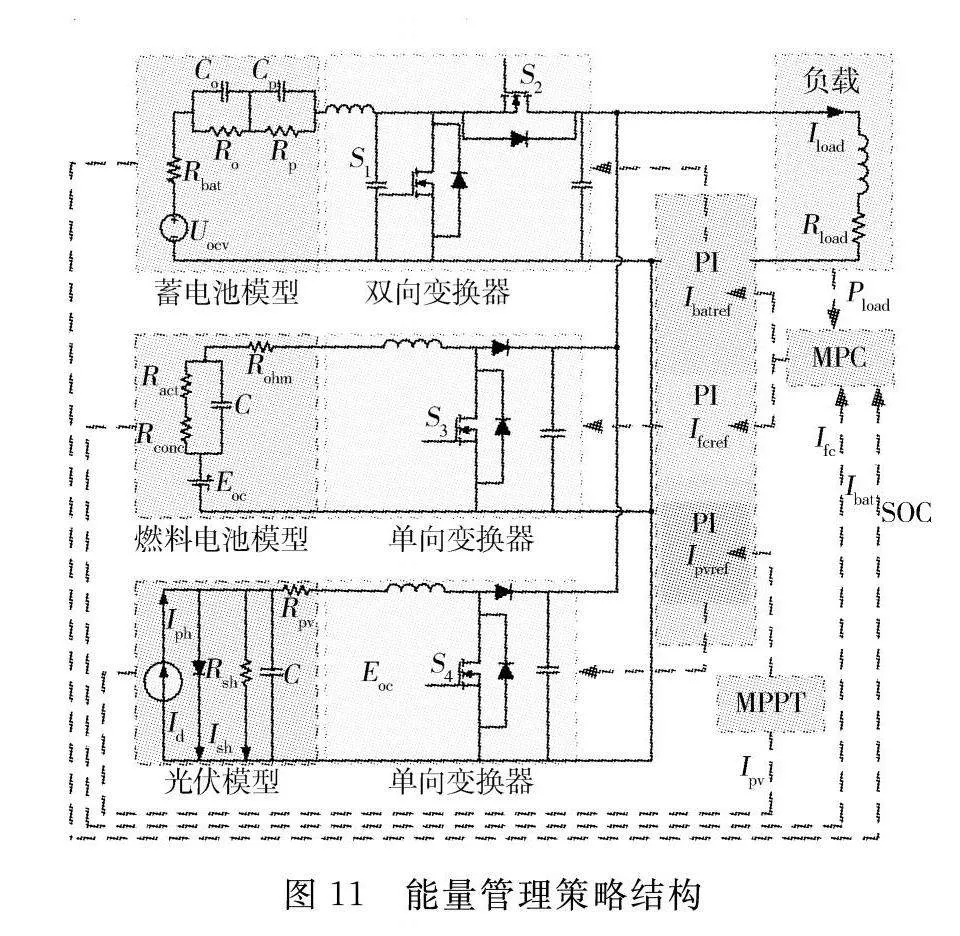
式中:p为预测步长;J,J,J为各部分能耗量;k~k为权重系数,如表3所示。本研究所提出的能量管理策略结构如图11所示。
3 仿真结果分析
为验证策略的有效性,在Matlab/Simulink平台上基于各单元模型对所提策略进行验证,系统参数设定如表4所示。
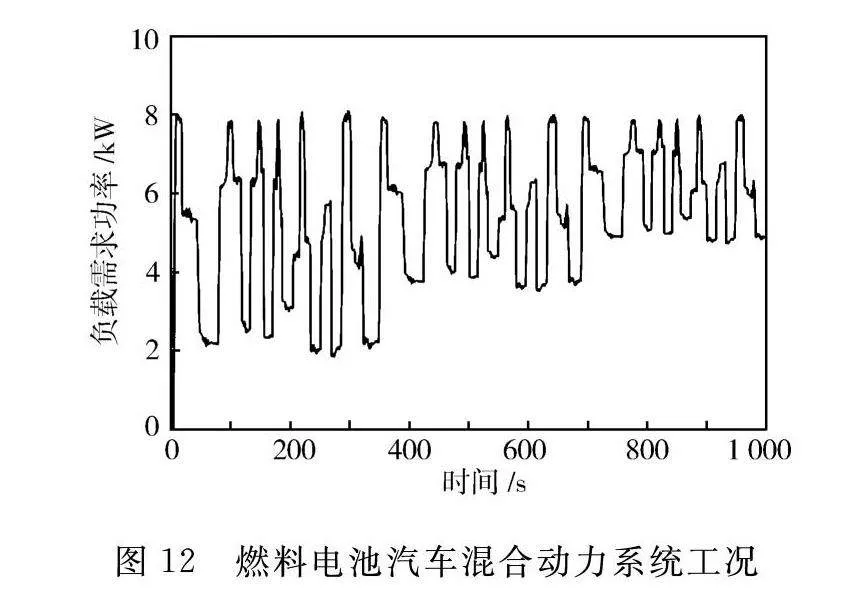
在燃料电池汽车运行过程中,负载需求功率波动很大,存在诸多急剧变载的情况。为了更加准确模拟车辆实际工况,设定负载总需求功率如图12所示,工况时间为1 000 s,负载需求功率范围为2~8 kW,蓄电池SOC初始状态为60%。
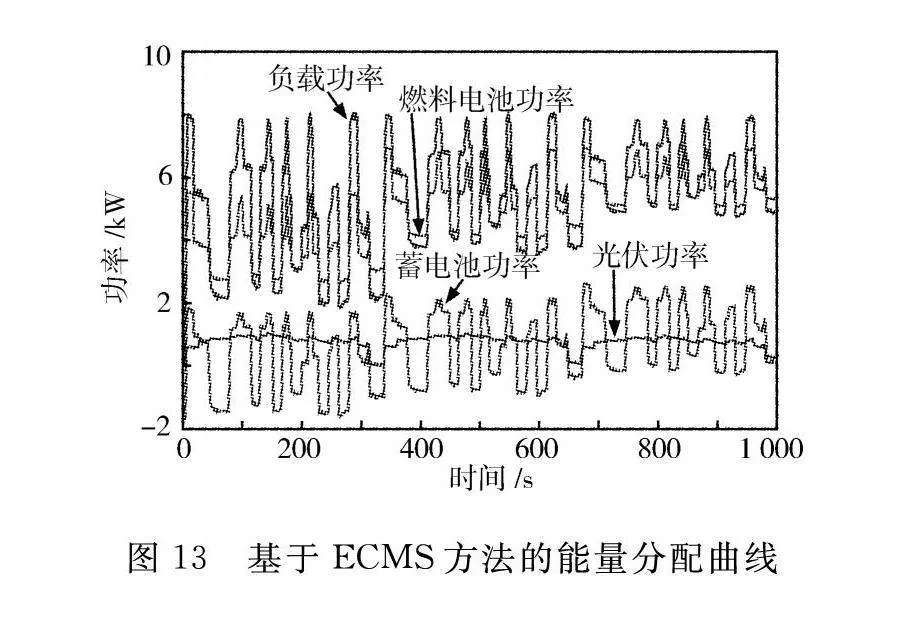
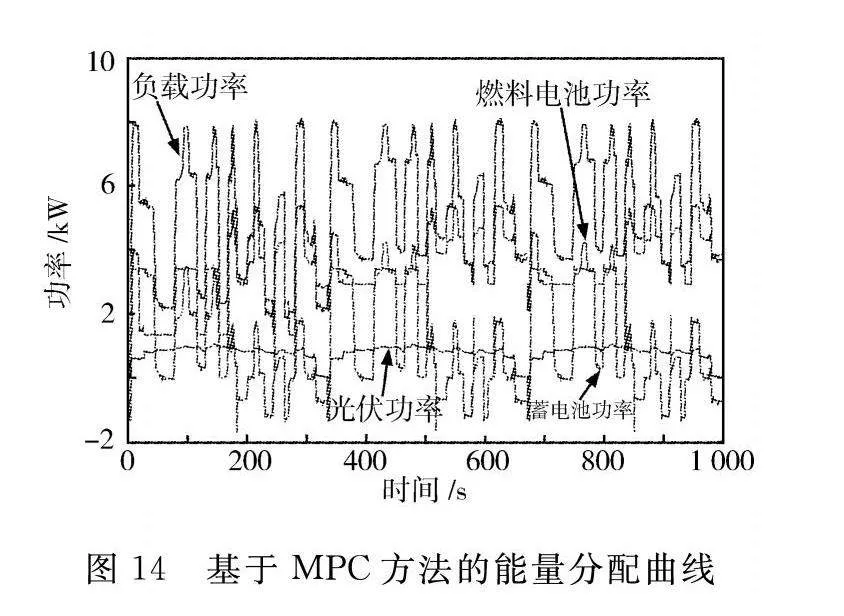
依据负载需求工况,分别进行基于等效氢耗最小方法和所制定的基于模型预测框架方法的仿真验证,测试得到基于ECMS算法和MPC算法的功率分配曲线,如图13和图14所示。可以看出,在运行过程中,光伏始终通过MPPT控制保持最大功率输出状态。
由图13可知,在系统运行初始阶段,燃料电池急剧提高输出功率,蓄电池无法及时响应负载需求,功率输出较低;此外,在整个运行期间,燃料电池的输出功率随着负载的变化存在较大的波动,对系统稳定性极其不利。由图14可知,蓄电池在运行初始阶段具有快速和高功率的输出,有效地补偿了燃料电池的缓慢动态特性,同时显著降低了氢消耗;在之后运行过程中,燃料电池和蓄电池随着负载的变化波动较小,对延长混合动力系统的寿命有积极作用,同时系统的内部能量损失和氢气消耗也会受到配电结果的影响。
混合动力系统运行过程中蓄电池的SOC变化曲线如图15所示。在运行结束时,基于ECMS方法的蓄电池SOC为55.43%,下降幅度为4.57%;而基于MPC方法的蓄电池最终荷电状态为59.76%,下降幅度仅为0.24%。因此,所制定的基于模型预测框架方法可有效保持蓄电池SOC。
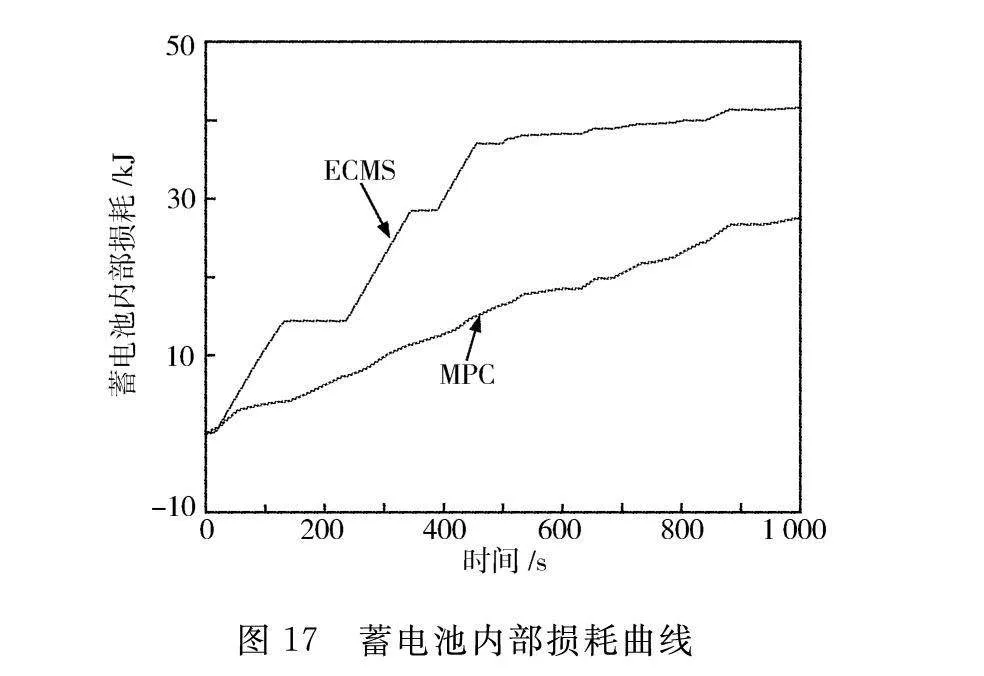
图16和图17分别示出燃料电池和蓄电池内部能量损耗曲线。由图16可知,在运行结束时,基于ECMS方法的燃料电池内部损耗量为150.65 kJ,而基于MPC方法的内部损耗量为97.85 kJ,相较于ECMS方法减少35.05%。由图17可知,在运行结束时,基于ECMS方法的蓄电池内部损耗量为43.25 kJ,而基于MPC方法的内部损耗量为28.34 kJ,相较于ECMS方法减少34.47%。通过对比数据得出,所制定的策略可以显著降低燃料电池和蓄电池内部损耗,提高混合动力系统经济性。
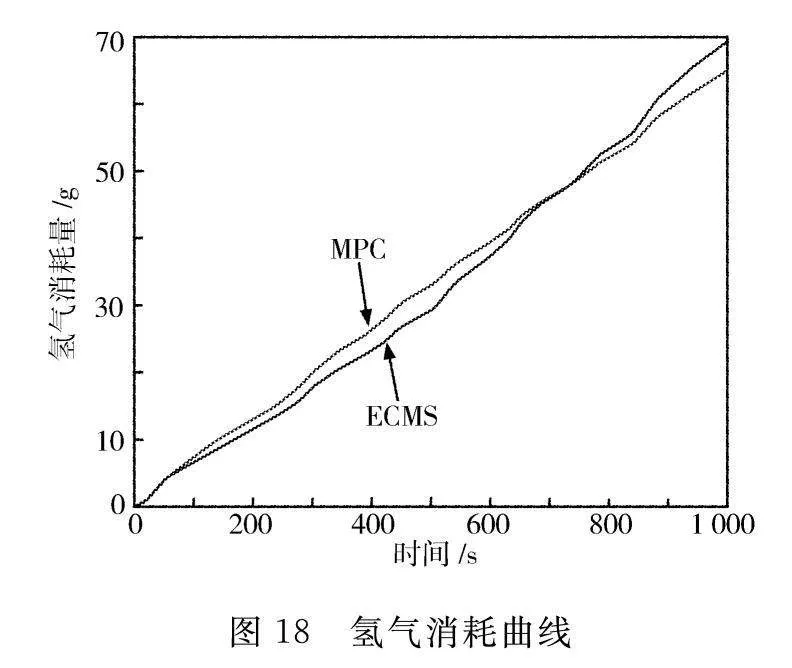
图18示出动力系统在工作过程中燃料电池的氢气消耗曲线。由图18可知,在结束时刻ECMS方法所对应的氢气消耗量为69.18 g,MPC架构方法下氢气消耗量为64.93 g,氢耗降低6.14%。因此,基于模型预测框架方法能明显降低系统氢气消耗。
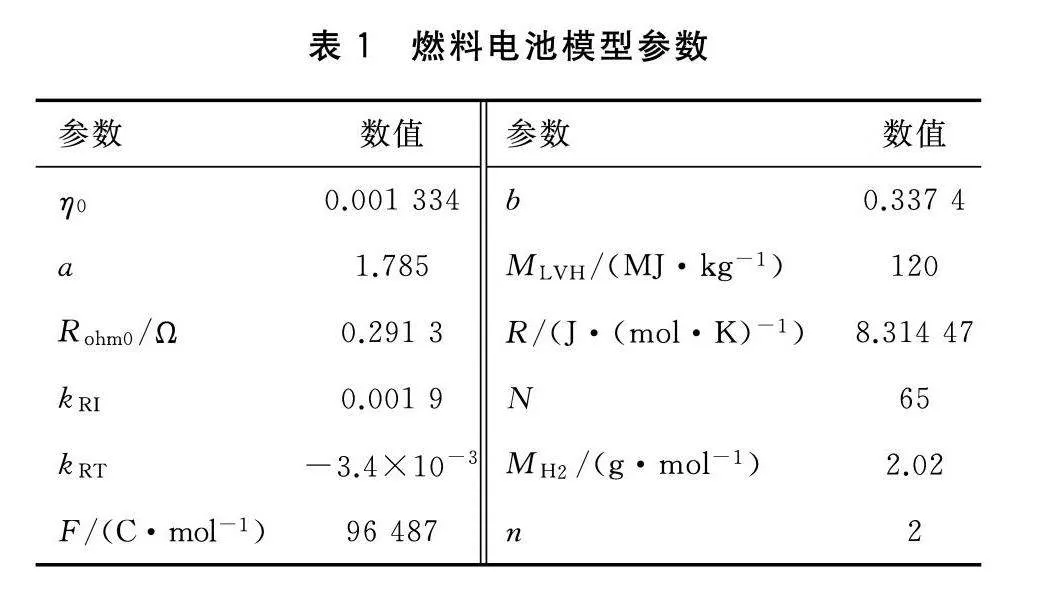
在某一系统运行时刻,燃料电池运行效率越高,燃料电池的内部损耗越小。燃料电池的运行效率曲线如图19所示。由图19可以看出,在MPC算法下燃料电池系统的运行效率高于ECMS算法,MPC算法的燃料电池系统平均效率为38.2%,而ECMS算法的燃料电池系统平均效率为35.9%,因此可以得出,MPC算法可以有效地降低内部损耗。
动力系统的电源应力是指动力系统负载工况变化过程中供电源输出电能改变的频率和幅值。通常情况下,其频率和幅值越小,供电源在动力系统运行过程中受到的运行应力越低[24]。对于燃料电池混合动力系统而言,其运行应力与使用寿命相关联。本研究通过波尔小波变换将燃料电池和蓄电池在运行过程中的瞬时功率信号分解成高频和低频分量,其高频分量的标准差可以更好地反映能量源的运行应力,其标准差越小,所受的运行应力越小。为此,本研究对燃料电池和蓄电池的输出功率进行波尔小波变换,得到燃料电池和蓄电池在各算法下的运行应力(如图20所示)。在系统运行过程中,MPC算法中燃料电池的标准差σ=21.63,蓄电池的标准差σ=55.60, ECMS算法中燃料电池的标准差σ=33.89,蓄电池的标准差σ=63.57。可以看出,在系统运行过程中, MPC算法中各能量源的运行应力均明显低于ECMS,表明其在运行过程中可以更加合理地分配功率,使每个能量源都可以承受着较轻的运行应力,进一步改善系统寿命。
4 结束语
本研究建立了燃料电池汽车混合动力系统中的燃料电池、光伏、蓄电池等效模型,在模型预测算法框架的基础上,将动力系统内部损耗与氢气消耗最小化作为目标函数,提出基于模型预测的能量管理策略以实现系统能量的高效合理分配。在仿真平台上对所制定方法进行了验证,结果表明,与ECMS算法相比,MPC算法能显著降低变载工况下燃料电池输出功率与蓄电池SOC波动频率,提高系统稳定性与使用寿命;其次,燃料电池与蓄电池内部损耗也明显降低,有效提高系统效率;相应地氢气消耗也降低了6.14%,提高了燃料经济性。试验分析结果充分体现了所制定方法在将内部损耗与氢耗最小化作为目标函数时的优越性,保证了系统的运行稳定性与燃料经济性,适宜运用在燃料电池车辆混合动力系统。
参考文献:
[1] 陈达.论国际能源合作背景下的中国能源安全[J].中国集体经济, 2021(32):5-6.
[2] 高吉喜,侯鹏,翟俊,等.以实现“双碳目标”和提升双循环为契机,大力推动我国经济高质量发展[J].中国发展,2021,21(增Ⅰ):47-52.
[3] Wu X,Tian Z,Guo J.A review of the theoretical research and practical progress of carbon neutrality[J].Sustainable Operations and Computers,2022,3:54-66.
[4] Huang M T,Zhai P M.Achieving Paris Agreement temperature goals requires carbon neutrality by middle century with far-reaching transitions in the whole society[J].Advances in Climate Change Research,2021,12(2):281-286.
[5] 陈家一,高帷韬,贾璐,等.燃料电池汽车动力系统及能量管理策略研究进展[J].中南大学学报(自然科学版),2024,55(1):80-92.
[6] 栾怡萱.混合动力汽车能量管理策略研究进展[J].汽车实用技术,2023,48(24):178-182.
[7] Pan C,Peters G P,Andrew R M,et al.Emissions embodied in global trade have plateaued due to structural changes in China[J].Earth’s Future,2017,5(9):934-946.
[8] Savvaris A,Malandrakis K.Development of a fuel cell hybrid-powered unmanned aerial vehicle[C]//2016 24th mediterranean conference on control and automation(MED).[S.l.]:IEEE,2016:1242-1247.
[9] Boukoberine M N,Zhou Z,Benbouzid M.A critical review on unmanned aerial vehicles power supply and energy management:Solutions,strategies,and prospects[J].Applied Energy,2019,255:113823.
[10] Hu D,Wang Y,Li J,et al.Investigation of optimal operating temperature for the PEMFC and its tracking control for energy saving in vehicle applications[J].Energy Conversion and Management,2021,249:114842.
[11] Wilailak S,Yang J H,Heo C G,et al.Thermo-economic analysis of phosphoric acid fuel-cell(PAFC) integrated with organic ranking cycle(ORC)[J].Energy,2021,220:119744.
[12] Zhao Q,Zhang H,Hu Z,et al.An alkaline fuel cell/direct contact membrane distillation hybrid system for cogenerating electricity and freshwater[J].Energy,2021,225:120303.
[13] Jienkulsawad P,Patcharavorachot Y,Chen Y S,et al.Energy and exergy analyses of a hybrid system containing solid oxide and molten carbonate fuel cells,a gas turbine,and a compressed air energy storage unit[J].International Journal of Hydrogen Energy,2021,46(70):34883-34895.
[14] Peng J,Huang J,Wu X,et al.Solid oxide fuel cell (SOFC) performance evaluation,fault diagnosis and health control:A review[J].Journal of Power Sources,2021,505:230058.
[15] Dou H,Zhang Y,Fan L.Design of optimized energy management strategy for all-wheel-drive electric vehicles[J].Applied Sciences,2021,11(17):8218.
[16] Liu C,Liu L.Optimal power source sizing of fuel cell hybrid vehicles based on Pontryagin’s minimum principle[J].International journal of hydrogen energy,2015,40(26):8454-8464.
[17] Fathy A,Yousri D,Alanazi T,et al.Minimum hydrogen consumption based control strategy of fuel cell/PV/battery/supercapacitor hybrid system using recent approach based parasitism-predation algorithm[J].Energy,2021,225:120316.
[18] Zhou D,Gao F,Ravey A,et al.Online energy management strategy of fuel cell hybrid electric vehicles based on time series prediction[C]//2017 IEEE Transportation Electrification Conference and Expo (ITEC).[S.l.]:IEEE,2017:113-118.
[19] Sellali M,Ravey A,Betka A,et al.Multi-objective optimization-based health-conscious predictive energy management strategy for fuel cell hybrid electric vehicles[J].Energies,2022,15(4):1318.
[20] Yan Y,Li Q,Huang W,et al.Operation optimization and control method based on optimal energy and hydrogen consumption for the fuel cell/supercapacitor hybrid tram[J].IEEE Transactions on Industrial Electronics,2020,68(2):1342-1352.
[21] Liu S,Song Z,Dong Z,et al.Generic carrier-based PWM solution for series-end winding PMSM traction system with adaptative overmodulation scheme[J].IEEE Transactions on Transportation Electrification,2022,9(1):712-726.
[22] Deng K,Peng H,Dirkes S,et al.An adaptive PMP-based model predictive energy management strategy for fuel cell hybrid railway vehicles[J].ETransportation,2021,7:100094.
[23] Liu S,Liu C,Zhao H,et al.Improved flux weakening control strategy for five-phase PMSM considering harmonic voltage vectors[J].IEEE Transactions on Power Electronics,2022,37(9):10967-10980.
[24] 马睿,宋剑,王宇昂,等.计及飞行任务与能耗分析的航空燃料电池推进系统能量管理策略[J].中国电机工程学报,2023,43(1):221-236.
Energy Management Method for Hybrid Power System of FuelCell Vehicle Based on Model Prediction Framework
WANG Jinhuan1,SONG Zhanwei2
(1.Changchun University of Architecture,Changchun 130607,China;
2.Jilin University,Changchun 130012,China)
Abstract: As a key component of fuel cell vehicles, the optimization of energy consumption and lifespan is crucial for the further commercial development of hybrid power system. Energy management strategy(EMS) plays an important role in improving the system performance and fuel economy of hybrid power system in fuel cell vehicles. To effectively reduce the internal loss of hybrid power system and further improve system economy, an optimized energy management control method for internal loss of hybrid power system was proposed based on a model prediction framework. An objective function that included the internal loss of power system and hydrogen consumption was first constructed. A model prediction architecture was then used to solve the objective function to control the output current of fuel cell so as to achieve reasonable energy distribution. Finally, the simulation was conducted in Matlab to verify the rationality and effectiveness of the proposed method. Compared with the widely-used equivalent hydrogen consumption minimization strategy(ECMS), the proposed method can significantly reduce the internal loss and hydrogen consumption of power system according to the results. In addition, this strategy can effectively maintain the state of charge(SOC) of battery and extend the service life of power system.
Key words: fuel cell vehicle;hybrid power system;energy management;model prediction control
[编辑:袁晓燕]
