费曼学习法在数学分析课程教学改革中的现状及实践研究

摘 要：数学分析是高校数学专业的一门专业基础课程，它的教学效果对整个数学专业学习具有决定性影响。然而在现实的数学分析教学中，学生往往只是被动地学习，学习效果不佳。因此有必要对传统教师以讲授为主的学习方法进行改革。费曼学习法作为一种新型输出式教学方法，已经被广泛应用到各理工类课程教学中，取得很好的教学效果。受此启发，该文研究将费曼学习法应用于数学分析教学中。通过专访和问卷调查相结合的方式，了解大学数学分析课程教学及学生学情现状，即数学分析课堂上大多以讲授法为主，学生参与感低，学习缺乏主动性，兴趣泛泛。基于这一现状，以“函数列极限交换定理”为例，具体来探讨如何将费曼学习法应用于数学分析课堂教学中，充分发挥学生的自觉能动性，提高数学分析的学习效率。

关键词：数学分析；费曼学习法；教学改革；极限交换；问卷调查；教学效果

中图分类号：G642 文献标志码：A 文章编号：2096-000X（2024）32-0130-06

Abstract： Mathematical Analysis is a fundamental course for mathematics majors in universities， and its teaching effectiveness has a decisive impact on the learning of the entire mathematics major. However， in practical mathematical analysis teaching， students often only passively learn， resulting in poor learning outcomes. Therefore， it is necessary to reform the traditional teacher centered learning method. The Feynman learning method， as a new type of output based teaching method， has been widely applied in the teaching of various science and engineering courses， achieving good teaching results. Inspired by this， this article studies the application of Feynman learning method in mathematical analysis teaching. Through a combination of interviews and questionnaire surveys， we aim to understand the teaching and student learning situation of university mathematics analysis courses. Specifically， in mathematics analysis classes， teaching methods are mainly used， resulting in low student participation， lack of initiative in learning， and broad interests. Based on this situation， taking the "limit exchange theorem of function sequences" as an example， this article specifically explores how to apply Feynman learning method to mathematical analysis classroom teaching， fully tap into students' conscious initiative， and improve the learning efficiency of mathematical analysis.

Keywords： Mathematical Analysis; Feynman learning method; teaching reform; limit exchange; questionnaire survey; teaching effectiveness

基金项目：山西省高等学校教学改革创新项目“基于费曼学习法的数学分析课堂教学改革实践与策略研究”（J20220471）；山西省留学人员科技活动择优资助项目“统一框架下的时间驱动型切换系统的稳定性研究”（20220023）

第一作者简介：玉强（1979-），男，汉族，河北邯郸人，博士，教授，硕士研究生导师。研究方向为非线性动力系统稳定性。

数学分析是普通高等学校数学专业的一门重要基础课，其内容十分抽象，且前后知识关联性较大，如柯西收敛准则贯穿于整个知识体系，遍布在实数完备性、极限、积分和级数等方面。数学分析的学习对于提升学生的逻辑思维能力以及解决问题能力等方面有很大的帮助，并且在整个大学学习生涯占有很大的课时量，所以学好数学分析是极为重要的[1-4]。然而很多学生认为其晦涩难懂，特别是刚开始接触数学分析的大学一年级新生，面对一些抽象的知识无从下手，这不仅会严重影响学生对于数学分析这门课的学习，也会大大削弱他们对后继专业课程学习的激情与兴趣。

对于数学分析的学习，多数高校选择了传统的教学方法，即以老师讲授为主，常见的课堂画面：教师滔滔不绝地讲，学生死气沉沉地听。这种教学方法的优点在于教师可以很快将所需知识传授给学生，大大节约教学时间，但这种教学方法也有其局限性，那就是它仅仅对理解能力强、逻辑思维能力优秀的学生有用，大多学生仍无法从中获得更深的理解从而内化为自己的知识，这导致学生的课堂参与感弱，而且这种教学方式也比较单一，容易让学生感到乏味，降低学习兴致。一方面是数学分析课程的极端重要性，另一方面是低效的被动教学模式，这形成了当前该课程教学的最大矛盾之处。相关的专家和学者对数学分析课程进行教学改革的必要性已达成共识，主要将注意力和研究重点放在如何教改以便更好地提升教学效果上。文献[5]从师资角度提出“一厚二强三优”的课程建设理念；文献[6]分析了数学分析课程分层教学问题；以线上线下混合式一流本科数学分析课程为对象，文献[7]对该课程教学改革与创新进行有意的探索；文献[8]探讨了BOPPPS模式下数学分析课程的可行性及实践；文献[9]调研了财经类院校数学分析课程学习中一些现状，研究表明多数学生对该课程兴趣泛泛、教学方式单一、缺乏学习主动性和学习效果差等问题。

一 数学分析教学及学生学习现状调查

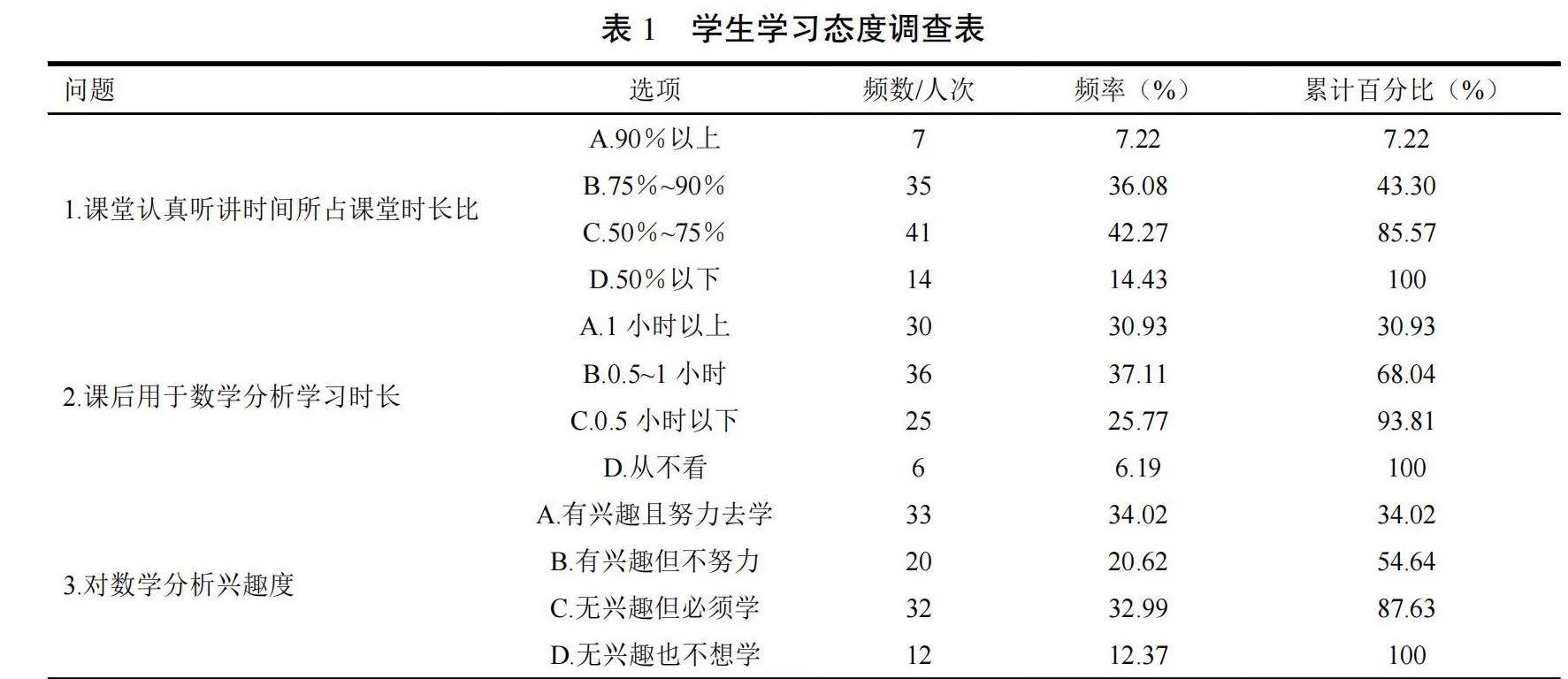
为了更好地了解师范类高校数学分析课程（以下简称“本课程”）教学与学生学习现状，笔者利用微信小程序在相关班级开展匿名问卷调查[10]，最后收回有效问卷97份。分别针对学生学习态度（表1）、知识掌握情况（表2），数学分析课堂开展情况（表3）以及学生对本课程的建议（表4）展开调查，具体结果如下。

表1调查显示，数学分析作为大学数学专业的必修课程之一，学生们的学习态度还是相对积极的。有40%以上的学生能做到上课专心听讲，课下认真复习课上所学知识，另有约40%学生少部分时间会出小差，基本做到上课耐心听讲，课下也会抽出一些时间用来复习。少部分（不到15%）的学生课上大部分时间都在做一些与本课程无关的事情，且课后基本不对课上的知识回顾与复习。由此可得出：大部分学生上课态度还是比较积极和端正的，但值得注意的是近一半的学生对本课程缺乏足够的兴趣。

表2调查显示，不足四分之一同学能掌握知识点并灵活运用，超过40%的同学掌握了知识点的内容但不能合理的应用，超过五分之一的同学部分掌握知识点，近10%的同学甚至对知识点完全不掌握。关于测试成绩，大部分学生成绩集中在“75～90分”和“60～75分”分数段。由此可得出：目前学生对知识有一定掌握但存在不少问题。

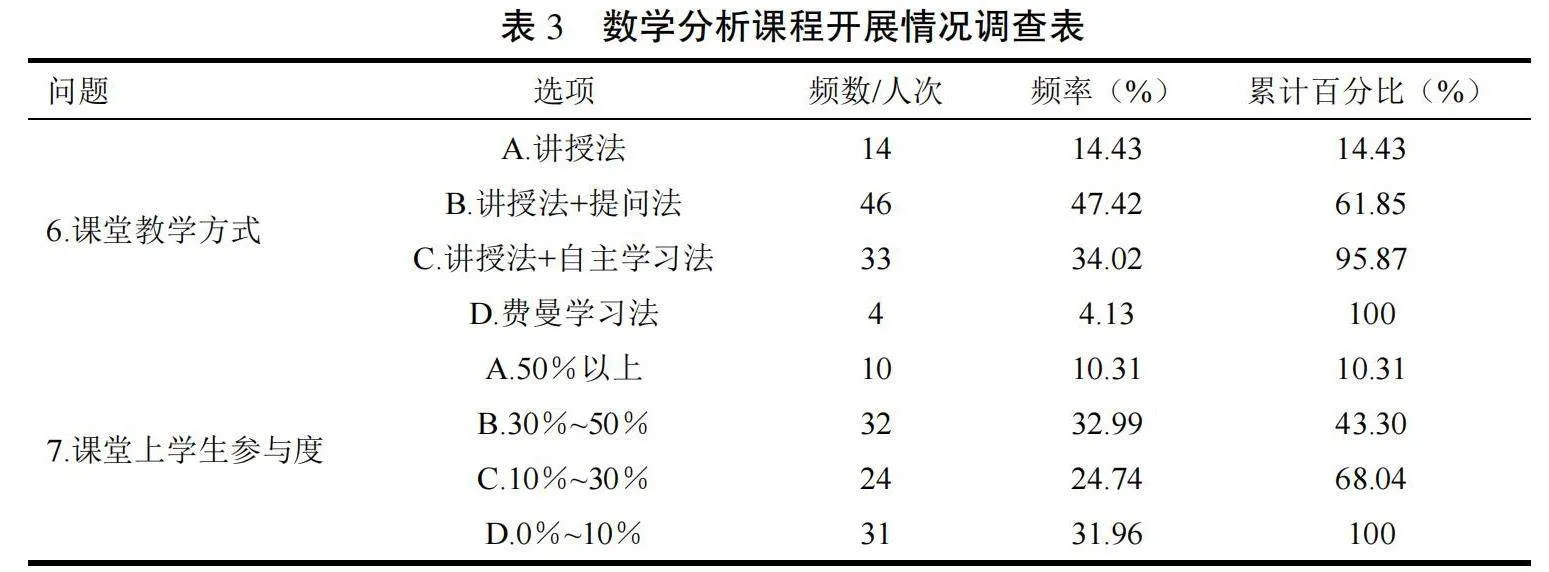
表3调查显示，教师在课堂上主要以“讲授法+提问法”为主，课堂上只用“讲授法”一种形式的占14.43%，“讲授法+提问法”的课堂教学模式占比近一半，“讲授法+自主学习法”的课堂模式约占三分之一，费曼学习法的课堂模式不足二十分之一。总体上课上学生参与度极低。由此可得出：目前学校的教学方法大多还是以“讲授法+提问法”为主，学生的参与度低，学生容易产生依赖心理，抑制了学生学习的独立性、主动性和创造性。

从以上数据可得出，同学们刚从中学过渡到大学，学习的自觉性还是挺高的，虽然很多同学对数学分析这门课程的兴趣并没有很大，但依旧在很认真地学习。尽管如此，学生们的成绩却并不很理想。主要有以下几点原因：首先，中学知识与大学知识在内容上有很大的不同，中学知识比较形象易懂但大学知识就相对更加抽象，学生接受起来相对困难。其次，课堂上老师多以“讲授法+提问法”为主，学生参与感较低，整堂课都在被动地学习，看似会了，但实际应用到题目中只是一知半解，没有做题的思路。由此得出，当前最需要解决的是提高学生学习的兴趣，增强学生的课堂参与感，更多关注“学生的学”。

二 费曼学习法

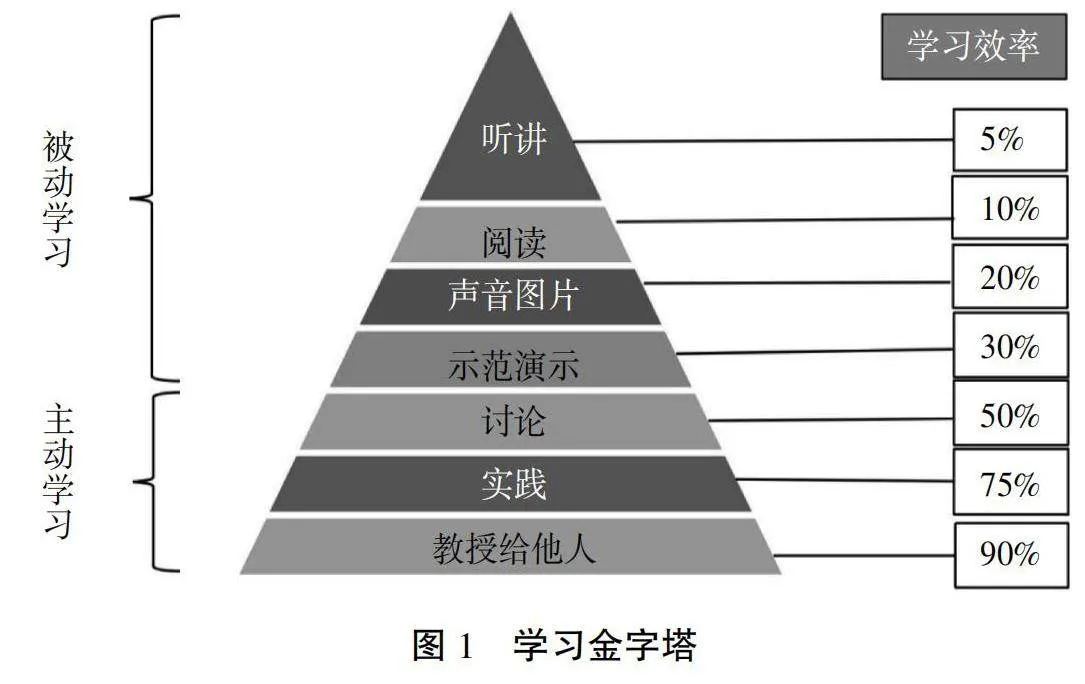
不同于传统教学法的被动学习，由理查德·菲利普斯·费曼提出的费曼学习法更注重学生学习的主体地位，能充分激发他们学习的主动性和兴趣，其在思考性及互动性方面有其独特的价值，且这种学习方法符合学习金字塔原理[11]（图1）。

费曼学习法[12]强调“以教促学”的学习方式，这种方法是让学习者变成教学者，并且把要学习的知识教授给其他人，无论如何要让其他人学会，从而达到自己熟练掌握的程度。这种学习方法可以增强学生的学习兴趣，从而为之后的学习打下良好基础。

费曼学习法的基本要求是，首先需要明确学习目标，精确定位学习内容，并且消化知识点；其次以小组为单位进行模拟教学，即学生以讲授身份者讲解知识点；接着在讲解中更深层次理解知识点，并与讲解前进行比较，查看是否有出入，进而巩固知识点；最后将知识点的概念简化，得出核心要点（图2）。

三 费曼学习法在数学分析课程教学改革中的应用探究

函数列/项级数极限交换定理，也称为极限交换定理，是数学分析中的一个重要定理。该定理指出，在函数列/项级数一致收敛的条件下，两个独立变量x与n在分别求极限时其求极限的顺序可以交换。该定理在函数列/项级数性质的学习中扮演重要角色，它的证明具有一定的抽象性和典型性，其推导过程涉及对函数列/项级数的一致收敛性和解析性质（连续性、可积性、可微性）等概念的深入理解。例如，若各项都连续的函数列fn（x）在区间I上一致收敛，则其极限函数f（x）在I上也连续。这些推论进一步扩展了极限交换定理的应用范围，使得在一致收敛的条件下，极限运算与积分运算的顺序可以交换。根据以往传统讲授法教学经验，学生在该定理证明的理解和掌握方面存在较大误区，教学效果常常事倍功半。这里探讨用费曼学习法来进行该极限交换定理的教学，不仅发挥了学生的主导作用，而且在教学过程中，学生也能够积极讨论、发表意见，从而调动起来学生学习的主观能动性。

优质的课程学习可以提高数学分析的学习质量。结合学生掌握知识的现状，基于费曼学习法的“极限交换定理”的课堂教学内容安排如下：①回顾ε-N、ε-δ、柯西收敛准则、函数列/项级数一致收敛等概念，确立目标；②分析该“极限交换定理”的条件和需要证明的结论，引导学生寻找条件与结论的差距，逐步引导学生搭建起两者之间的桥梁；③学生分组讨论后，各组组内及各组代表之间模拟教学，重复回顾、对比；④最终代表完成讲授，教师点评总结，知识凝练、升华。

（一） 课前设计

1 基本情况

实践班级为笔者任教的2021和2023级的数学与应用数学专业的两个标准班级。实践课题为函数列/项级数的极限交换定理的学习，重点是对定理的理解和证明方法、技巧的掌握。

2 实践目标

基本目标：深刻理解极限交换定理，掌握该定理的推导过程，理解其对函数列/项级数的一致收敛性、连续性、可积性、可微性作用及意义。

能力目标：通过该定理的学习，更深入地理解函数项级数的一致收敛性质及其对极限、积分、导数等数学运算的影响，体会其在数学分析中有着重要的应用。进一步扩展了解极限交换定理的应用范围，以及在其他学科如物理学、工程学等领域中发挥的关键作用。

深层目标：增加学生对数学分析的学习兴趣，激发学生的求知欲，为以后的数学学习打下良好的基础。

3 分组合作

针对任教的2021级学生（共48人），根据疫情期间的客观情况进行分组，主要以宿舍为单位分组，方便学生之间交流，每6人一组，共8组。

针对任教的2023级学生（共50人），主要根据学生成绩，知识基础、智力水平和心态心境等个体的不同，采取互补、均衡分组，方便组内团结协作，组内成员之间尽可能既有互相讨论的基础，又有相互补充的特长，从而促进个体成长和教学任务的达成，10人一组，共5组。老师根据教学大纲确定学习内容和目标后，指导和监督小组学习过程，及时解决出现的问题。

（二） 课堂模拟实践

证明如下极限交换定理。

定理：设函数列{fn}在（a，x0）∪（x0，b）上一致收敛于f（x），且对每个n， fn（x）=an，则an和 f（x）均存在且相等.

鉴于需要证明数列和函数极限存在问题，首先引导学生回顾，数列极限的ε-N、函数极限的ε-δ、柯西收敛准则等。

设{an}为数列，a为定数.若对任给的正数ε，总存在正整数N，使得当n>N时有an-a<ε，则称数列{an}收敛于a，定数a称为数列{an}的极限，并记作an=a.

设函数f在点x0的某个空心邻域U0（x0；δ′）内有定义，A为定数.若对任给的ε>0，存在正数δ（<δ′），使得当0<x-x0<δ时有f（x）-A<ε，则称函数f当x趋于x0时以A为极限，记作 f（x）=A.

设函数f在U0（x0；δ′）上有定义. f（x）存在的充要条件是：任给ε>0，存在正数δ（<δ′），使得对任何x′，x″∈U0（x0；δ）有f（x′）-（x″）<ε.

证明思路（分两步）：①先证an存在；②再设an=A，证明 f（x）=A即可。

先证an存在。

引导学生思考证明极限存在常用方法，主要包括定义法和柯西收敛准则等。

分析：本例中证明极限的存在性由于题目中没有出现该数列极限可能的极限值，无法直接使用定义等来证明；因柯西收敛准则的优点是仅依赖这个数列本身就可判断数列收敛性，故需选用柯西收敛准则来证明它的存在性。

要证∀ε>0，∃N∈N+，p∈N+，n>N时，an-an+p<ε.引导学生思考：由于 fn（x）=an，则可考虑用fn（x）-fn+p（x）代替an-an+p.虽然近似代替会产生误差，但当x→x0时，这个误差趋于零， 故可用 fn（x）-fn+p（x）<ε来代替an-an+p<ε.这可以结合图3直观来获得.

引导学生给出具体证明：由{fn}在（a，x0）∪（x0，b）上一致收敛，故∀ε>0，∃N∈N+，使得∀x∈（a，x0）∪（x0，b），n>N，p∈N+，fn（x）-fn+p（x）<ε.就有fn（x）-fn+p（x）≤ε，从而有an-an+p≤ε，故由柯西准则可得an存在.

设an=A.接下来只需证明 f（x）=A即可.

分析：由于出现了极限值，故可以选用定义法来证明.要证 f（x）=A，即证∀ε>0，存在正数δ（<δ′=min{x0-a，b-x0}），使得当0<x-x0<δ时有fn（x）-A<ε.

（引导学生思考）由于题目中对极限函数f（x）和A的信息较少，因此难以获得f（x）-A的直接信息，考虑到{fn}一致收敛于f（x）和 fn（x）=an，则f（x）可以用fn（x）来近似代替，A可以用an来近似代替（当n足够大时）. 产生的误差分别为f（x）-fn（x）和A-an.从而给出f（x）-A的估计式：f（x）-A≤f（x）-fn（x）+fn（x）-an+an-A.这也可以结合图3直观来获得.

引导学生给出具体证明：由于fn（x）一致收敛于f（x）及an收敛于A，因此对任意ε>0，存在正数N，当n>N时，对任意x∈（a，x0）∪（x0，b），

fn（x）-f（x）<和an-A<，

同时成立，特别取n=N+1，有

fN+1（x）-f（x）<，aN+1-A<。

又 fN+1（x）=aN+1，故存在δ>0，当0<x-x0<δ时，

fN+1（x）-aN+1<。

这样，当x满足0<x-x0<δ时，

f（x）-A≤ f（x）- fN+1（x）+ fN+1（x）-aN+1+ aN+1-A<++=ε，

即 f（x）=A.

引导学生总结：在掌握数学分析的基本概念等基础上，对于定理及其抽象证明都有其内在的逻辑，一般总能通过数形结合来直观理解定理的意义及获得证明的思路。

四 教学改革成效

基于对山西师范大学2021级和2023级数学专业本科生的教改实践，费曼学习法下的数学分析课堂改革成效显著，获得学生一致好评。教改课程出现了满分成绩，学生课堂参与度、学习积极性、期末优良和及格率均明显高于传统授课班级。2021—2024年，任教课程在学生评教中始终名列前茅，个人总体教学评价排名位居学院前5%，其中2023—2024年度学院教学评价排名第一（1/75）。

针对2021级教改学生，由于已完成教学实验，主要从后继发展说明教改成效：指导教改班级学生在第14、15届全国大学生数学竞赛中多人次获省一、二等奖；作为指导教师指导教改班级学生获批2024年国家级大学生创新创业训练计划项目、2024年山西省首届大学生职业规划大赛二等奖、2024年山西省创新创业大赛省优秀奖、2024年山西师范大学未来教师素质大赛二等奖及单项奖和中国国际大学生创新大赛（2024）校赛一等奖（排名学校第一，已推荐省赛）。

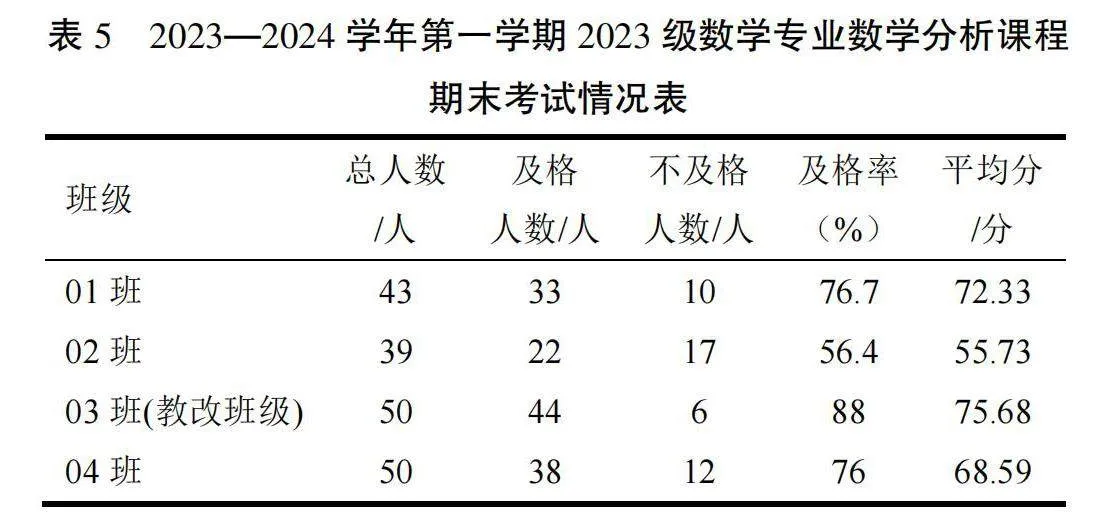
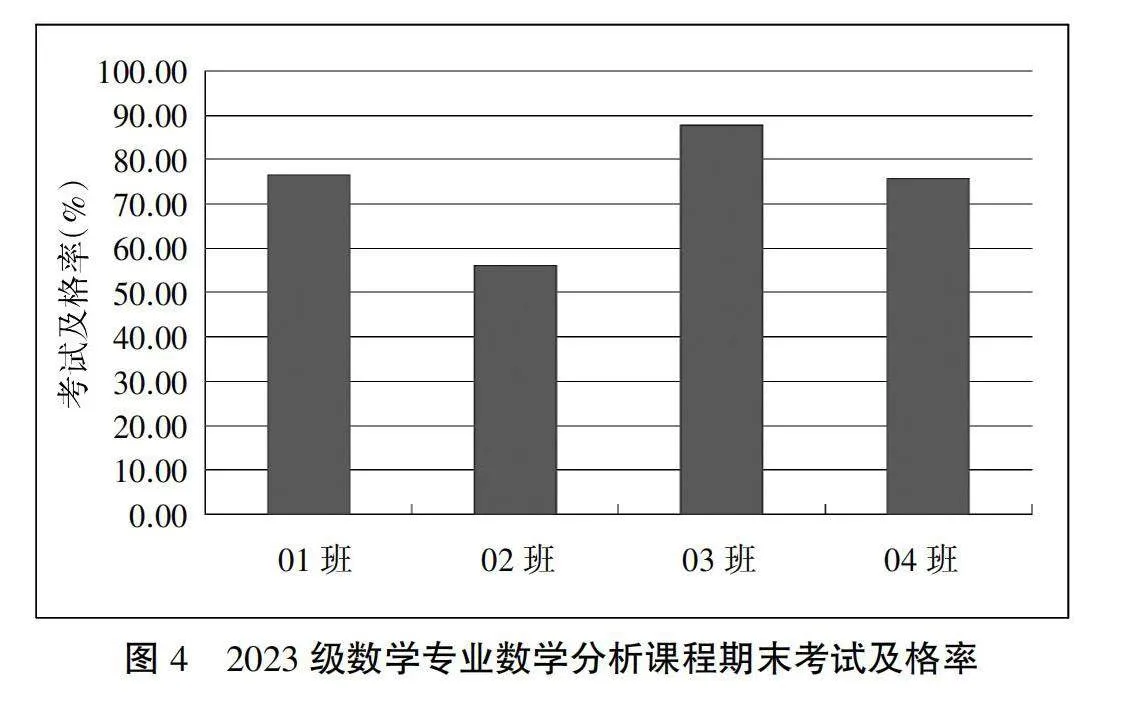
针对2023级学生，由于仍是一年级新生且尚处于教改实验中，只能从同级成绩对比的角度来说明教改成效。作为最重要的专业基础课，学校对数学分析的考核实行委托校外同类院校专家命题的教考分离政策，保证考试的保密性和教学评价的客观性。以下以2023—2024学年第一学期数学专业四个平行班级期末考试成绩来说明教改成效。从图4、图5及表5可以清晰看到执行教改的03班的平均分和及格率均明显高于对比班级。

五 结束语

本文基于教学经验和问卷调查探讨了数学分析课程的教学现状，分析了传统讲授教学法在数学分析教学中的优缺点。简要介绍了费曼学习法，并研究了基于该方法的数学分析课堂教学改革的可行性。最后以极限交换定理为例演示费曼学习法在数学分析课堂教学中的具体运用与策略实施。

参考文献：

[1] 华东师范大学数学系编.数学分析[M].5版.北京：高等教育出版社，2019.

[2] 拉菲·格林贝格.普林斯顿数学分析读本[M].李馨，译.北京：人民邮电出版社，2020.

[3] 李傅山.数学分析中的问题与方法[M].北京：科学出版社，2016.

[4] 陈纪修，於崇华，金路.数学分析[M].3版.北京：高等教育出版社，2019.

[5] 石少广，傅尊伟，郭政，等.地方大学数学类一流课程建设与实践——以临沂大学数学分析课程为例[J].高教学刊，2024，10（1）：8-12.

[6] 段雅丽，程艺.数学分析课程分层教学探索与实践[J].大学数学，2023，39（5）：5-9.

[7] 张冕，张杰.一流课程建设背景下课程教学创新探索——以“数学分析”课程为例[J].教育教学论坛，2023（45）：105-108.

[8] 王海燕，王林，刘颖.“数学分析”课程教学创新探索与实践[J].科技风，2024（6）：143-145.

[9] 罗清君.财经类院校《数学分析》课程学习现状的调查分析——以西安财经学院为例[J].高教学刊，2018（4）：86-88.

[10] 庞安彤.费曼学习法在中职学校地理教学中的应用研究[D].济南：山东师范大学，2021.

[11] DALE E. Audio-Visual Methods in Teaching. Holt[M].Rinehart & Winston， New York： Dryden Press，1969.

[12] 尹红心，李伟.费曼学习法（用输出倒逼输入）[M].南京：江苏凤凰文艺出版社，2021.