基于DE-SVM算法的淘洗机选矿过程优化研究

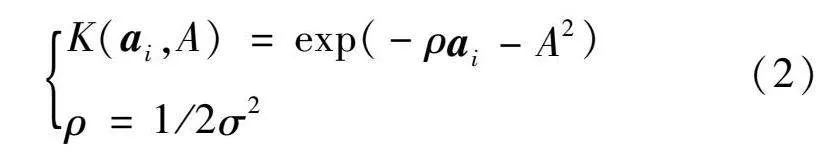
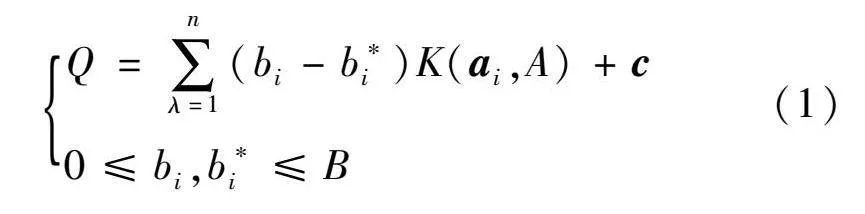
摘要：研究了基于差分进化算法（DE）和支持向量机（SVM）的混合算法在淘洗机选矿过程中的应用。针对选矿过程中淘洗机选矿质量差、效率低等问题，提出了DE-SVM算法，并构建了相应的选矿质量预测模型。试验结果表明，DE-SVM算法的平均预测准确率和预测精准率分别为93.7 %和95.6 %，基于该算法的淘洗机选矿质量预测模型的预测精矿回收率和预测精矿品位绝对误差分别为98.4 %和0.309 %。相较于其他算法和模型，DE-SVM算法和基于该算法的淘洗机选矿质量预测模型表现出显著优势，为提高淘洗机选矿质量和效率提供了有效方法。

关键词：DE算法；SVM；选矿；淘洗机；过程优化

中图分类号：TD457文章编号：1001-1277（2024）10-0080-04

文献标志码：Adoi：10.11792/hj20241013

引言

选矿作为一种将有用矿物与脉石矿物分离的工艺，在矿产品生产过程中扮演着重要角色［1］。选矿过程中，淘洗机的选矿质量和效率，决定着整体选别质量［2］。淘洗机选矿存在选矿质量差、效率低等问题［3］。因此，寻找一种提高淘洗机选矿质量和效率的方法对保障选别品位和回收率具有重要意义。支持向量机（Support Vector Machine，SVM）是一种二分类模型，具有鲁棒性强和计算效率高等特点，被广泛应用于预测和识别等领域［4］。然而，SVM具有易发生过拟合和欠拟合等缺点。差分进化算法（Differential Evolution，DE）是一种高效的全局优化算法，具有结构简单、收敛速度快等优势，能有效弥补SVM的缺陷［5］。因此，研究将DE算法引入SVM，构建DE-SVM算法，并将该算法应用于淘洗机选矿过程优化，以期提高淘洗机选矿质量和效率，为选矿过程优化提供一定的理论依据。

1DE-SVM算法构建

SVM是一种基于统计学理论的监督学习模型，其原理是在一个超平面中寻找最大化类之间的间隔，从而求解出二次规划的最优化算法，具有鲁棒性强和计算效率高等特点，被广泛应用于预测和识别等领域［6］。SVM预测计算公式如式（1）所示。

Q=∑nλ=1（bi－b*i）K（ai，A）+c0≤bi，b*i≤B （1）

式中：Q为SVM的预测回归；b*i和bi分别为拉格朗日乘子和常数；n为样本数；K（ai，A）为径向基核函数，ai和A分别为支持向量和核函数中心；c为偏置向量；B为惩罚函因子。

SVM在处理非线性问题时通常采用径向基（Radial Basis Function，RBF）核函数代替非线性的变化，其计算公式如式（2）所示。

K（ai，A）=exp（－ρai－A2）ρ=1/2σ2 （2）

式中：ρ为核函数；σ为函数的宽度参数。

由式（1）、式（2）可知：SVM在处理非线性时会受到惩罚因子和核函数的影响。其中，核函数为数据映射到新的特征空间后的分布，其大小影响SVM的预测速度，且核函数与支持向量的数量呈负相关关系，即核函数越大，支持向量越少，核函数越小，则支持向量越多；惩罚因子决定了SVM的复杂度和泛化能力，惩罚因子过大容易发生过拟合，过小则容易发生欠拟合。寻找一种方法为SVM选择出最优核函数和惩罚因子对提高SVM性能具有重要意义。DE算法是一种高效的全局优化算法，具有结构简单、收敛速度快等优势［7］，借助其强大的全局搜索特性，能够为SVM高效率地搜寻最优参数。DE算法计算流程［8］如图1所示。

由图1可知：DE算法基本计算流程为，随机生成种群并对各个初始化个体进行适应度值计算。对个体的适应度值进行判断，以确定其是否满足条件或判断是否迭代次数已用完，如果满足则终止；反之，采用变异、交叉和选择操作24P+D3L9YJQtnIc5dS+npH+V/MxZ4hN0MxZPoZqU0PM=对种群进行迭代和重组，从而得到新一代种群，然后再进入迭代，直至满足终止条件。其中，初始化种群中的个体由设定在解空间中随机均匀生成的M个N维个体表示，且wLλ，j≤wλ，j（0）≤wPλ，j，则第λ个个体的第j维wλ，j（0）数学表达式如式（3）所示。

wλ，j（0）=wLλ，j+r（0，1）·（wPλ，j－wLλ，j）（3）

式中：wLλ，j、wPλ，j分别为N维向量的下限、上限，且i=1，2，…，M;j=1，2，…，N。

变异操作的作用是将即将变异的个体合体，采用变异因子和差分向量对个体与个体间的差异进行变异操作。设定在第f代的个体中，选取3个个体，其变异向量vλ（f+1）计算公式如式（4）所示。

vλ（f+1）=db1（f）+FΔb2，b3（f）（4）

2024年第10期/第45卷矿业工程矿业工程黄金

式中：b1，b2，b3分别为个体1，2，3，且b1≠b2≠b3；F为变异因子且为0～2；db1为个体1的输入向量；Δb2，b3（f）为差分向量；f为个体代数。

交叉操作的作用是利用交叉算子通过1对1的方式与其父代进行杂交，在保留父代较好信息的同时生成下一代，进而保留种群多样性。保留父代信息的新种群Tλ，j（f+1）计算公式如式（5）所示。

Tλ，j（f+1）=vλ，j（f+1）r（0，1）≤τCRdλ，j（f）otherwise （5）

式中：τCR为交叉算子且其值属于0到1，其值越趋于0，则收敛速度越快；vλ，j（f+1）为变异个体向量。

选择操作的作用是将通过交叉操作得到的新一代种群与其对应的父代进行比较，选择适应度高的个体保存到下一代种群中，其计算公式如式（6）所示。

φi（f+1）=Ti（f+1）φ［Ti（f+1）］<φ［di（f）］di（f）else （6）

式中：φ为适应度函数；φi（f+1）为适应度更高的下一代个体。

基于上述公式，研究将DE算法融入SVM中构建了DE-SVM算法，该算法旨在为SVM寻找最优参数，DE-SVM算法参数寻优流程如图2所示。

由图2可知：DE-SVM算法首先将经标准化处理后的特征数据按照2∶1随机抽取一部分作为训练集，剩下的作为测试集。利用核函数和惩罚因子对DE算法进行初始化操作，生成初始化种群。随后，在利用训练集对SVM进行训练的同时计算目标函数值，通过设定条件判断是否满足条件或者迭代是否完成，如果该函数值不满足条件则进入DE算法进行下一代进化。对不满足条件的个体进行交叉、选择和变异操作后产生新一代的核函数和惩罚因子，重新作为SVM的训练集对SVM进行训练，直至满足条件后作为最优的核函数和惩罚因子进行输出。

2基于DE-SVM算法的淘洗机选矿质量预测模型

研究将DE-SVM算法应用于淘洗机选矿质量预测，并构建基于DE-SVM算法的淘洗机选矿质量预测模型，达到优化淘洗机选矿过程，提高选矿质量的目的。

选矿工艺流程主要由磨碎、筛分、脱泥和淘洗等组成［9］。其中，淘洗机起到分离矿粉与尾矿、提升矿石品位的作用。淘洗机底阀开度、主水开度和给矿品位等都会影响精矿品位及回收率，因此，研究将淘洗机中与精矿品位有相关性的因素作为选矿质量特征值，并将这些特征值作为DE-SVM算法的输入值，预测精矿品位及回收率。对_{2l2RYGvOllbEA5pfIYOKo2emNjj+8rmE4gL4Chny8vk=}数据进行标准化处理有利于剔除重复和冗杂等数据，提高数据质量［10-11］，标准化公式如式（7）所示。

Zx=xi－xs（7）

式中：Zx为标准化后数据；xi为原始数据；x为该组数据的平均值；s为该组数据的标准方差。

为确保数据的有效性，采用抽样合适性检验（Kaiser-Meyer-Olkin，KMO）和巴特利特球度检验对标准化数据进行验证，将KMO值大于0.5和巴特利特球度检验小于0.05的值进行保留。为使预测更加准确，使用主因子提取法对特征值进行提取，选取主因子累计方差大于75 %的特征值。主因子计算表达式如式（8）所示。

Hε=αε1F1+αε1F2+…+αεoFo+λε（8）

式中：Hε为主因子；αε1，αε2，…，αεo为输入的特征；F1，F2…，Fo为公共因子；λε为不被解释的因子，ε=1，2，…，4，o=1，2，3且ε≤4。

将式（8）进行线性变换，得到主成分计算公式如式（9）所示。

Fo=αε1H1+αε2H2+…+αε4H4（9）

将提取出符合贡献率的特征值输入DE-SVM算法中，对淘洗机选矿质量进行预测，由此，构建基于DE-SVM算法的淘洗机选矿质量预测模型。该模型的具体计算流程为：选取一部分经标准化和主因子提取的特征值数据集，随机抽取一部分作为测试集，剩下的作为训练集；输入一部分经标准化和主因子提取的特征值作为训练集，通过DE算法对SVM进行参数寻优训练；训练完成后，将测试集输入DE-SVM算法进行选矿质量预测，若选矿质量与实际相同则表示训练效果良好，如果不同则重新训练。

3基于DE-SVM算法的性能分析

3.1DE-SVM算法性能分析

为验证DE-SVM算法性能的优越性，研究将其与其他算法进行对比试验分析。试验对比算法包括PSO-SVM算法和VtVGG-f算法，试验对比指标为预测准确率、预测精准率。试验结果如图3所示。

由图3-a）可知：DE-SVM算法的平均预测准确率为93.7 %，PSO-SVM算法的平均预测准确率为88.9 %，VtVGG-f算法的平均预测准确率为81.2 %，DE-SVM算法的平均预测准确率最高。由图3-b）可知：DE-SVM算法的平均预测精准率为95.6 %，PSO-SVM算法的平均预测精准率为90.8 %，VtVGG-f算法的平均预测精准率为83.7 %，DE-SVM算法的平均预测精准率最高。从精准率和准确率2个维度来看，DE-SVM算法的性能显著优于其他算法，具有有效性。

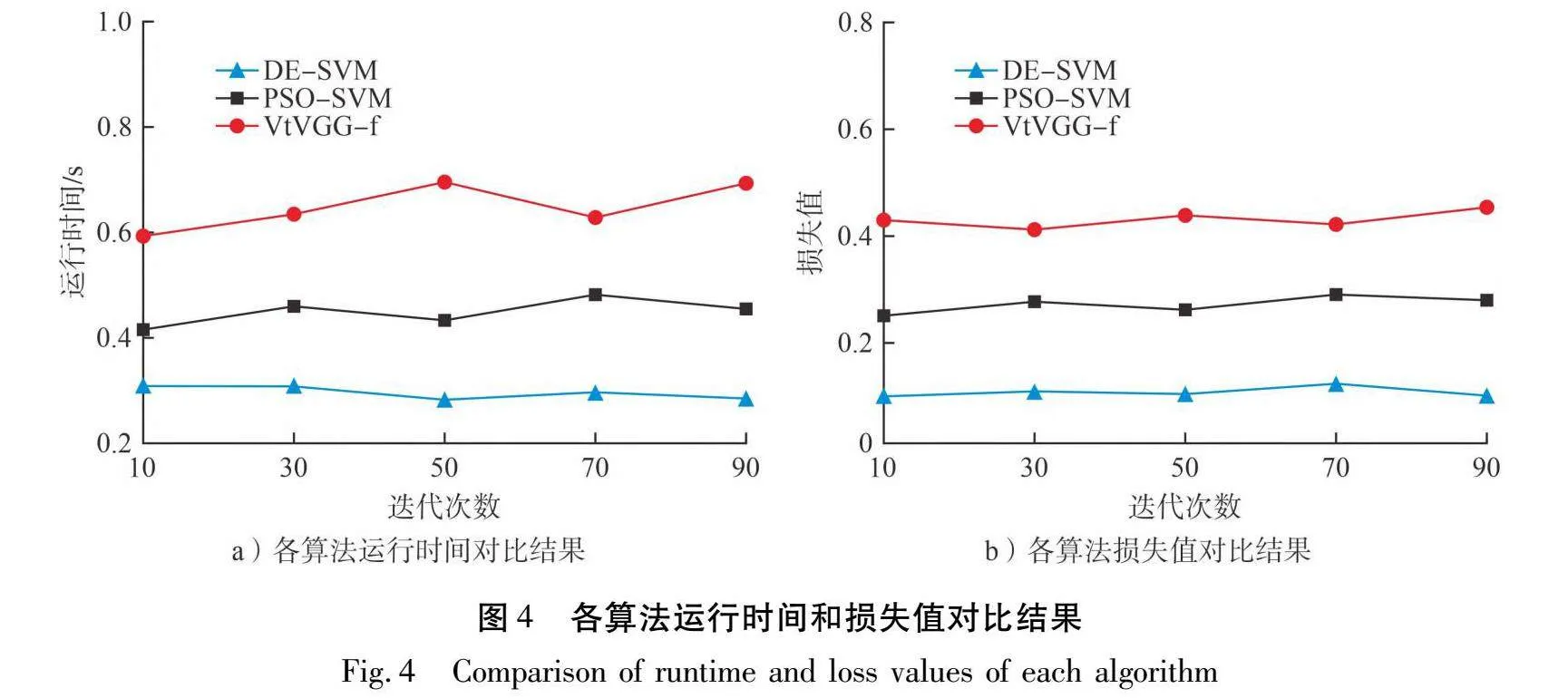
各算法的运行时间和损失值对比结果如图4所示。

由图4-a）可知：DE-SVM算法的平均运行时间为0.37 s，PSO-SVM算法的平均运行时间为0.42 s，VtVGG-f算法的平均运行时间为0.63 s，DE-SVM算法平均运行时间最低。由图4-b）可知：DE-SVM算法的平均损失值为0.12，PSO-SVM算法的平均损失值为0.23，VtVGG-f算法的平均损失值为0.41，DE-SVM算法平均损失值最低。从运行时间和损失值2个维度来看，DE-SVM算法性能优于对比算法。

3.2淘洗机选矿质量预测模型性能分析

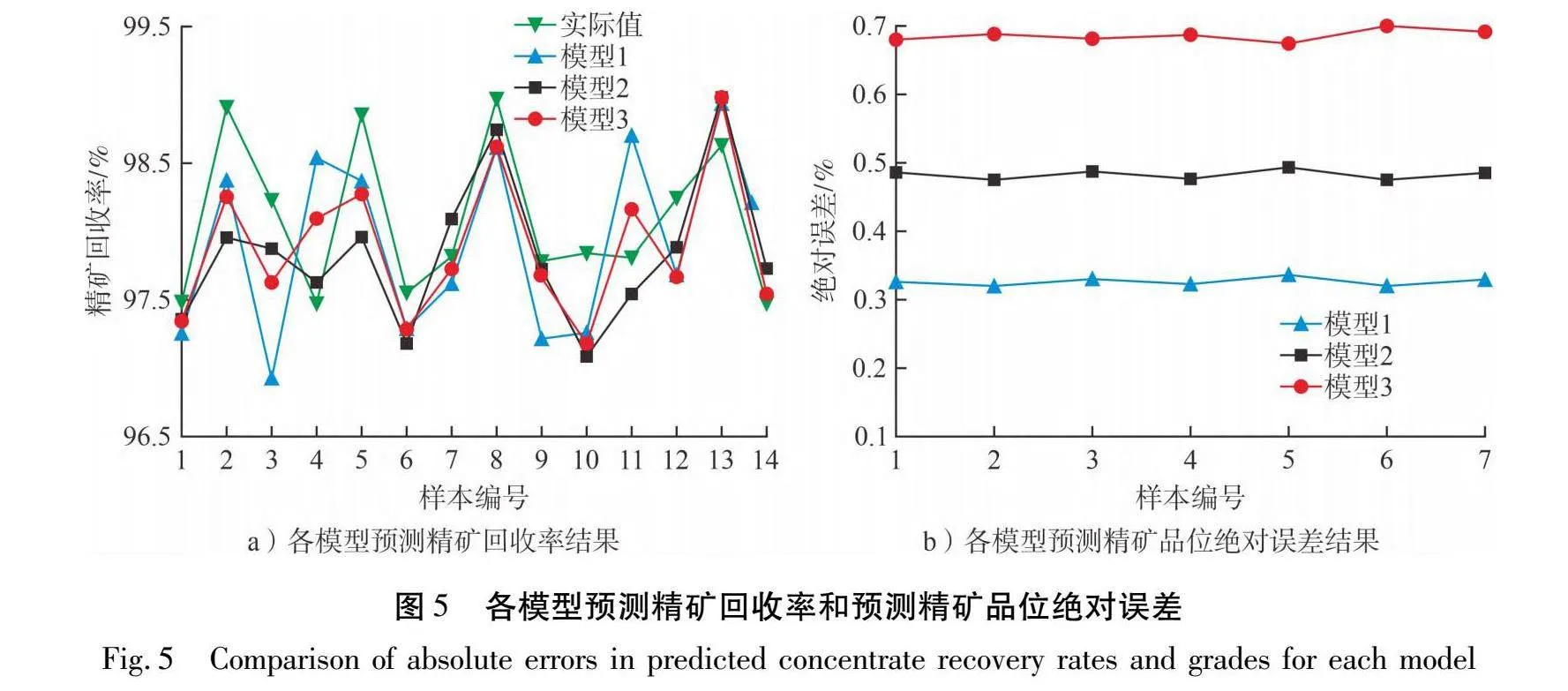
为验证基于DE-SVM算法的淘洗机选矿质量预测模型（模型1）性能的优越性，将其与基于PSO-SVM算法的淘洗机选矿质量预测模型（模型2）和基于VtVGG-f算法的淘洗机选矿质量预测模型（模型3）进行对比试验分析。试验指标为预测精矿回收率和预测精矿品位绝对误差。试验结果如图5所示。

由图5-a）可知：各模型预测精矿回收率在实际值上下浮动，其中，模型1的平均预测精矿回收率为98.4 %，模型2平均预测精矿回收率为97.3 %，模型3平均预测精矿回收率为97.1 %，模型1的平均预测精矿回收率最高。由图5-b）可知：模型1的平均预测精矿品位绝对误差为0.309 %，模型2的平均预测精矿品位绝对误差为0.486 %，模型3的平均预测精矿品位绝对误差为0.687 %，模型1的平均预测精矿品位绝对误差最低。结果表明，基于DE-SVM算法的淘洗机选矿质量预测模型性能优于对比模型，具有实用性。

4结论

1）为解决选矿过程中淘洗机选矿质量差、效率低等问题，研究将DE算法引入SVM，利用DE算法对SVM的参数选择进行优化，构建DE-SVM算法，并将该算法应用于淘洗机选矿质量预测模型，构建了基于DE-SVM的淘洗机选矿质量预测模型。将该算法与其他算法对比分析发现，DE-SVM算法性能优于对比算法，具有有效性。

2）将基于DE-SVM算法的淘洗机选矿质量预测模型与基于PSO-SVM算法的淘洗机选矿质量预测模型和基于VtVGG-f算法的淘洗机选矿质量预测模型进行精矿回收率和预测精矿品位绝对误差维度的性能对比分析，结果发现，基于DE-SVM算法的淘洗机选矿质量预测模型的平均预测精矿回收率为98.4 %，平均预测精矿品位绝对误差为0.309 %，相较于其他对比模型，研究提出的基于DE-SVM算法的淘洗机选矿质量预测模型性能优越，具有实用性，有助于提高淘洗机选矿质量和效率。但是，实际的选矿过程更为复杂，对实际环境中复杂选矿过程进行优化是进一步研究方向。

［参 考 文 献］

［1］殷博，朱继华，徐海东，等.基于贵金属纳米颗粒生长的比色传感研究进展［J］.化学通报，2023，86（6）：690-698.

［2］龙冰，谢加文，黄伟生，等.柿竹园磁铁矿粗精矿提质选矿实验［J］.矿产综合利用，2022（4）：41-47.

［3］吴鹏.新疆哈密某选厂利用淘洗机提质降杂的应用［J］.冶金与材料，2024，44（7）：34-36.

［4］WANG S，MU M.Exploring online intelligent teaching method with machine learning and SVM algorithm［J］.Neural Computing and Applications，2021，34：2 583-2 596.

［5］丁学振，李卓轩，李予国，等.基于差分进化算法的磁梯度张量系统误差校正［J］.地球物理学报，2022，65（12）：4 930-4 943.

［6］SAMANTARAY S，SAHOO A.Prediction of suspended sediment concentration using hybrid SVM-WOA approaches［J］.Geocarto International，2022，37（19）：5 609-5 635.

［7］王波，陈川辉，于竞宇.基于差分进化算法的智能化预制厂房设备资源配置优化［J］.科学技术与工程，2023，23（25）：10 941-10 947.

［8］高颖，夏斌，张立晔，等.差分进化协同定位算法研究［J］.无线电工程，2023，53（9）：2 151-2 157.

［9］米子军，罗良飞，李宗蔚，等.峨口铁矿二磁精矿制备高品质铁精矿粉试验研究［J］.矿冶工程，2023，43（6）：88-91.

［10］许洪峰，牛艳萍.阳离子浮选体系中蓝晶石族矿物与石英的交互影响［J］.矿冶工程，2023，43（3）：56-60.

［11］王斌，王业，孙齐振，等.基于增量支持向量机算法的大数据网络安全系统检测技术_{JfjXEclQ+ExiS1MhQOS+o1245qVUaxWfBK5K1DzZh90=}［J］.自动化与仪器仪表，2024（8）：9-13.

Optimization study of mineral processing in elutriation machine using DE-SVM algorithm

Xiong Yang，Dong Kebin

（Civil-Military Integration Center of China Geological Survey）

Abstract：This study explores the application of a hybrid algorithm based on Differential Evolution （DE） and Support Vector Machine （SVM） in the mineral processing of elutriation machine.To address the problems of low quality and efficiency in metal beneficiation during elutriation，the DE-SVM algorithm was proposed，and a corresponding beneficiation quality prediction model was constructed.Experimental results showed that the average prediction accuracy and precision of the DE-SVM algorithm were 93.7 % and 95.6 %，respectively.The predicted concentrate recovery rate and the absolute error of predicted concentrate grade using the model were 98.4 % and 0.309 %，respectively.Compared with other algorithms and models，the DE-SVM algorithm and its associated elutriation machine beneficiation quality prediction model demonstrated significant advantages，providing an effective method to improve the quality and efficiency of precious metal beneficiation.

Keywords：DE algorithm;SVM;beneficiation;elutriation machine;process optimization