基于数学核心素养的中学数学批判性思维能力的培养

摘 要：学生在有逻辑地表达以及探索解决数学问题时，必须运用批判性思维.数学批判性思维能力的培养要以数学知识为基础，学生不仅要关注数学中结论的正确与否，而且要关注结论得出的原因.学生要以批判性的思维去思考数学，去把握数学知识的脉络，从而真正做到数学答案合乎逻辑、严谨、准确且合理.

关键词：核心素养；逻辑思维；批判性思维

在中学数学学习中，学生应当具有独立思考的能力.在课程的学习以及教师的教学中，学生的数学逻辑思维得到锻炼以及发展，数学批判性思维在数学逻辑思维的基础上得到了升华，这也体现了思维水平的进一步发展.学生具备的数学素养，应当与现实世界的知识相结合，他们不只是掌握书本上的数学知识，更重要的是思维能力的培养.随着21世纪信息技术不断发展进步，新时代的学生应该具有探索事物本原的基本素养，以批判性的视角去看待问题，进而综合运用知识解决实际问题.本文旨在分析数学批判性思维的价值，并提出培养批判性思维的策略，为发展学生数学核心素养提供助力.1 数学批判性思维的基本阐述批判性思维是心理学术语，是指通过一定的评价思维，进而改善思维，是合理的反思性思维.批判性思维的萌芽来自古希腊哲学家苏格拉底（Socrates）对批判性思维的实践，进而被众多学者如柏拉图（Plato）、亚里士多德（Aristotle）等继承发展，从而透过表面，看清内在本质.虽然说批判性思维由来已久，但是并未有系统的阐述.在20世纪中叶，国外心理学界对此给出了定义，但概念的界定仍然有分歧，一种观点认为批判性思维是一种能力；另一种观点认为批判性思维是一种思维过程，但二者都有一个共识，即批判性思维是有目的性及自我调节的判断.

在我国，对于批判性思维的认识，不同的哲学流派或者心理学派以不同的角度探索、研究、阐述过，因此各有不同的侧重点，并不矛盾.例如，从个体角度看，批判性思维就是一种个体存在的能力；从认知角度来看，批判性思维就是一种认知过程.国内外研究者们基本达成的一致观点是批判性思维包含三个维度：批判性思维知识、批判性思维技能、批判性思维倾向.［1］

数学批判性思维是批判性思维所涵盖的一部分，二者之间是包含关系，是批判性思维在数学学习中的体现.关成志教授研究论述了数学思维具有批判性品质的观点.［2］在此基础上，数学特级教师孙联荣提出了数学教育维度的批判性思维的定义.［3］数学批判性思维是指对已有数学表述和论证提出自己的见解，敢于质疑，独立思考，不轻信，不盲从.反映到学生身上来说就是学生发现自己和他人认知方面的错误认识以及不足，独立思考，与教师讨论，并加以完善总结，唯“知识”，但不唯“教师”.

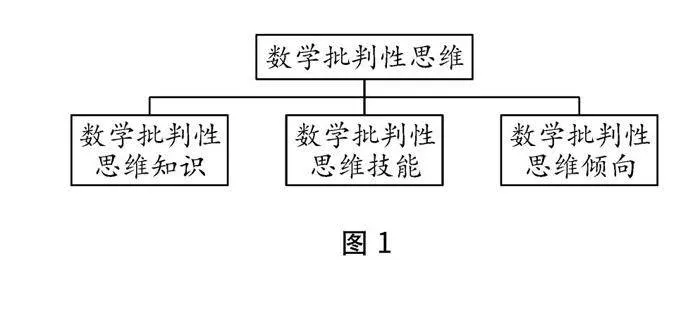
按照批判性思维所涵盖的三个维度，我们认为数学批判性思维也应当涵盖三个维度：数学批判性思维知识、数学批判性思维技能、数学批判性思维倾向.［4］如图1所示，三个维度有机结合，共同发挥着作用.

数学批判性思维知识包括以下三点：①数学批判陈述性知识.它是指在描述数学批判性思维的特点以及关系时，起到描述作用的知识.如对已有的数学命题或结论的批判性描述，是外显表达的第一步.它所代表的是“是什么”的问题.②数学批判程序性知识.它是指关于数学批判性思维的带有完整操作步骤的知识.如对数学对象进行辨别差异、比较、分析.它所代表的是“做什么”和“怎么做”的问题.③数学批判元认知知识.它是指对数学批判性思维知识认识的知识，以及认识主体对自身知识认识的知识.如自己对数学知识的掌握情况以及薄弱情况的了解，哪些是清晰明确的，哪些是模糊不清的.

数学批判性思维技能包括以下七点：①观察理解能力，即对数学知识进行观察，以及对数学命题结论的外在理解.②分析思考能力，即有逻辑地对数学知识进行分析，独立地进行思考，富有内涵的逻辑论断，进而分析出正确结论.③判断评价能力，即对数学问题，有根据地进行判断，在思考的基础上进行反思，根据具体问题进行评价，判断其是否正确，进而发现其中不足.④假设推理能力，即在判断评价的基础上，运用头脑中已有的数学知识和技能，进行归纳、演绎，进而提出自己的假设，正确地进行推理.⑤证实推导能力，即整体的框架已经显现，当前这一环节在于将已经假设推理出的数学问题，运用有逻辑的方式方法进行反复验证推导，进而形成一个完整的逻辑闭环.⑥验证监控能力，即以数学的方式进行验证新提出的假设正确与否，亦即对整个系列过程进行证明，在此之上，还对其进行整体的环节进行监控，为的是使整个过程更加合理、准确、严谨，没有遗漏.⑦反思总结能力，即对整体的把握，需要进行综合的复盘，一方面，在原有的问题上，对数学知识的综合把握；另一方面，在后续问题上，不断探索完善，进而进行创新.综上所述，各个技能并非独立于数学批判性思维之外，而是各个技能之间相互协调、多元化形式作用的结果，而且它们也并不是单一存在的，之间也还存在着联系，是以所学的数学知识作为其核心，各种技能相互协调联系的总和.其中分析思考、判断评价、提出质疑，是数学批判性思维体现的核心，直接影响着数学批判性思维的产生.此外，这些技能并非按照以上的顺序进行下去的，而是构成数学批判性思维的一系列要素.

批判性思维倾向是指有意识地进行评判的心理准备状态、意愿和情感，是一种根据心理状态而产生的能动性思想.［5］对于数学批判性思维倾向，笔者认为是运用数学的整体思维去能动性地评判数学问题的意向.数学批判性思维倾向主要包括以下五点：①思想的求真性，即对数学知识存在着一种执着的精神，探求数学真理与知识，不人云亦云，冷静求真，唯“真理”，不唯“教师”.②思想的开放性，即在数学的学习中，对某一数学知识，出现了不同的看法时，采取宽容的处理方式，积极讨论，防止出现偏见的可能.③求知与好奇心，即个体在数学学习中，所产生的自我内驱力，促进其求知好奇的进一步发展，也就是好奇心的产生，驱使个体自我探索，发现新问题，做出更进一步的尝试.④公正性的思考，即数学中更应该注重这种公正性的思考形式.错误或者是不同数学知识点之间的讨论，尤其需要这种公正性的思考，只有这样才更能迸发出批判性的讨论，从而完善思维过程.⑤情感的发展，即数学学习中所蕴含的情感发展之一是自信心.自信是学生在学习过程中以及在日常生活中进行良好互动时必须具备的一种态度.良好的自信心不仅为数学学习提供动力，而且还有助于塑造学生的良好品格.2 数学批判性思维的价值数学批判性思维是正确的反思性思维方式，其核心在于选择认识到数学所蕴含的知识是什么，为什么这样，怎么才能成为这样.这样的思维，首先要通过提出数学问题，清晰明确地表达数学观点，其次要利用自己头脑中原有的数学知识储备来分析数学问题，最后从各种数学观点中发现不同，敢于质疑否定，因此自信在此过程中也尤为重要.学生要勇于坚持自己的观点，不断验证假设猜想，进而解决数学问题，得出结论.数学的某些问题需要反复的论证讨论，才能辨伪求真，达到数学严谨的目的.

2.1 数学批判性思维可以提升提出数学问题的能力

提出数学问题是解决一切数学问题的前提条件，只有敢于提出不同的问题，才能有数学问题的后续发展.学生一旦具备了数学批判性思维，并能够合理地进行运用，那么在进行数学问题的思考时，就能够快速地发现其中的问题，并能够提出富有建设性意义的意见和看法.例如，试证明无理数加上无理数，还是无理数，并写出证明过程.如果这一道数学证明题摆在学生面前，在进行提问时，学生首先会想到的是什么呢？大部分学生会在看到题目的第一眼，首先进行思考，认为这是一道证明题，应该按照常规的步骤进行证明，于是逻辑混乱地对题目进行尝试解答，为了使结论看起来更“像”结论，盲目给它找出一个合理的“解释”，不敢去质疑题目是有问题的.如部分学生认为无限不循环小数加无限不循环小数还是无限不循环小数，所以上述结论成立.但是殊不知，这道题的本身就是有问题的.但还是会有一部分的学生，能够大胆地举出反例，进行质疑，这说明这部分的学生初步具备了数学批判性的思维，进而外显地进行了表达，提出了这个数学问题.由此可见，数学批判性思维能让学生更擅于以自己的思维去评价知识真伪，进而促进数学批判性思维的提升.

2.2 数学批判性思维可以提升分析数学问题的能力

分析数学问题的能力主要表现在能够分析、推理、辩证性讨论、交流数学知识和技能，其中最重要的环节在于辩证性地交流讨论.分析数学问题时所必备的思维情感就是数学批判性思维的自信心.

在分析数学问题中，自信心的重要性体现在以下三个方面.

（1）数学问题分析过程中的自信心建立.

（2）数学问题分析过程中的自信心表达.

（3）数学问题分析过程中的自信心保持.

以下面这一道题目为例.判断命题真假并证明你的结论.对于一切自然数n，1≤n≤19，n2-n+11都是质数.学生提交的答卷中呈现两种结果.

一部分学生认为是真命题，证明结果如下.

当n=1时，12-1+11=11，结果为质数，命题成立.

当n=2时，22-2+11=13，结果为质数，命题成立.

当n=3时，32-3+11=17，结果为质数，命题成立.

……

同理，当n=19时，192-19+11=353，结果仍为质数，则命题成立.

另一部分学生认为是假命题，证明结果如下.

当n=11时，112-11+11=121，121不是质数，是假命题.

从这样的一道题目的解答过程中，我们能够了解到，在面对一道题的时候，分析的整个过程，离不开批判性思维的思考以及自信心的整体运用，不能拘泥刻板地以一种思考形式去分析多种问题.

2.3 数学批判性思维可以提升解决数学问题的能力

解决数学问题的能力主要表现在两方面：一方面，在清晰表达观点的基础上，根据头脑中原有的认知去解决问题，从各种观点中发现不同，反思性思考，质疑式提问，在现有问题的前提下得出富有建设性意义的结论；另一方面，在抑制数学问题解决中思维定式的迁移.思维定式的迁移是指将头脑中原有的固定习惯或者方法应用到新问题解决上，以达到快速解决问题的目的.因此数学批判性思维在问题解决中尤为重要.因为有思维定式的存在，学生很难改变原有的思维方式，不能够另辟蹊径，从不同角度去解决问题，所以在数学学习的整个过程中，批判性思维水平高的学生，则具有良好的思路，更善于从正、反两个方面去评判，更能多角度地排除思维定式迁移的干扰.3 数学批判性思维的培养从数学教育角度研究数学批判性思维的培养是尤为重要的.在培养学生96V0JiD2wz+QWULvRn3N/Q==数学批判性思维的时候，教师应当从数学和教育两个角度来看，这样有助于教师将批判性思维的生成机制，运用到实际的数学教学当中.数学批判性思维的培养主要体现在以下几个方面中.

3.1 夯实“四基”

整个数学大厦的框架是由基本的数学概念、数学公理构成的，是数学批判性思维的起点，也是最终数学批判性思维的落脚点.只有扎实的数学基础知识和基本技能，才能够稳固地支撑数学的发展.在数学批判性思维的形成过程中，有各种各样的方式方法，不同的方式方法适用于不同的条件，而且也适用于不同的思维主体.基本思想在其中也发挥着重要的作用，数学批判性思维中蕴含着反思性的思考.在数学中对于数学条件的分析以及整体思考，教师往往以常规的思维去分析，但是这种思想往往会在过程中遇到阻碍，如果教师能够用好数学中的基本思想，就能开拓思路逆向推导还原，进而解决问题.学生的基本数学活动经验也尤为重要，数学经验来源于日常数学活动，但高于日常数学活动，它有目标、有内容、有思维.数学的经验如果与生活相互贴近，那么将会超越数学学习，进而达到数学现实，这是一种理性认识升华的过程.

3.2 提升“四能”

发现问题的能力是基础，提出问题的能力是关键，分析问题的能力是核心，解决问题的能力是目标.数学批判性思维蕴含在整个问题解决的过程中，各个环节之间互相联系、协调发展，共同组成了整个问题解决的过程.有意识地进行提升能力的训练，对于数学批判性思维发展有着十分重要的意义.根据数学知识的发展规律，特别是一些关键或者薄弱的环节，有意识地、有针对性地进行训练，以便数学批判性思维的整体提升，克服一切外界因素的阻碍，从而达到最终的目的.学生可以通过在不同的环境中体验解决问题的过程，有效地发挥自己的能力，也可以经常练习数学批判性思维能力来发展和提高数学素养.参考文献

［1］李文婧.数学批判性思维及其教学研究［D］.济南：山东师范大学，2004.

［2］［5］关成志，王前.数学思维三题［J］.数学教育学报，1992（1）：70-76.

［3］孙联荣.数学教育中培养批判性思维的探讨［J］.数学教育学报，1995（4）：16-20.

［4］刘其知.数学批判性思维与试误教学的探索［D］.石家庄：河北师范大学，2007.