引导聚焦基本图形，变式追问成果扩大

摘 要：九年级相似三角形学习之后的复习课或习题课往往涉及与圆有关的相似问题.与其零星出现一两道圆的问题，教师不如安排“相似学后再看圆”的专题课，带领学生从相似的角度研究圆相关的基本图形，进行变式设问，生成一系列与相似有关的同类问题，切实提升解题教学效益.

关键词：基本图形；相似；圆

《义务教育数学课程标准（2011年版）》和《义务教育数学课程标准（2022年版）》对“相似”“圆”的学习要求都不高，很多知识或定理的教学要求都是“了解”或“选学”级别.不少版本的初中数学教材将“圆”安排在九年级上册，将“相似”安排在九年级下册，这样就使得九上学习圆时不会涉及与圆有关的相似问题，而九下学习相似时，又很少与圆结合起来.笔者曾检索过人教版《义务教育教科书数学九年级下册》，在“相似”一章中，仅章末练习中出现一道与圆的相交弦性质有关的相似习题；苏科版《义务教育教科书数学九年级下册》，在“相似”一章中，也只是在习题部分出现了两道与圆有关的相似习题.为了引导学生从相似的视角看圆的一些基本图形问题，笔者设计了一节“相似学后再看圆”的专题课，本文整理该课的教学设计，为广大教师提供课例研讨.

1 “相似学后再看圆”专题课教学设计@@教学环节1：从“垂径定理”基本图形出发.##

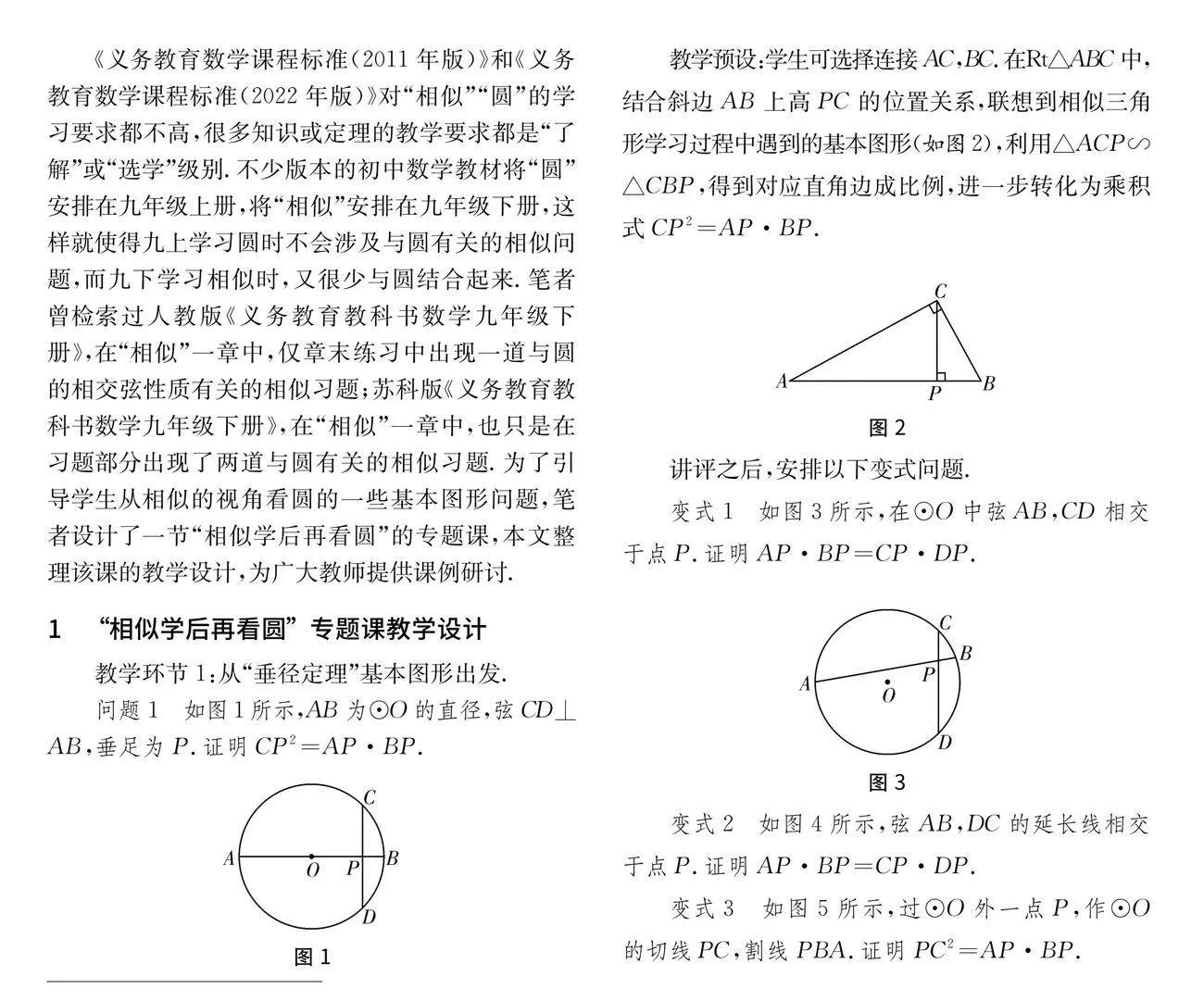
问题1 如图1所示，AB为⊙O的直径，弦CD⊥AB，垂足为P.证明CP2＝AP·BP.

教学预设：学生可选择连接AC，BC.在Rt△ABC中，结合斜边AB上高PC的位置关系，联想到相似三角形学习过程中遇到的基本图形（如图2），利用△ACP∽△CBP，得到对应直角边成比例，进一步转化为乘积式CP2＝AP·BP.

讲评之后，安排以下变式问题.

变式1 如图3所示，在⊙O中弦AB，CD相交于点P.证明AP·BP＝CP·DP.

变式2 如图4所示，弦AB，DC的延长线相交于点P.证明AP·BP＝CP·DP.

变式3 如图5所示，过⊙O外一点P，作⊙O的切线PC，割线PBA.证明PC2＝AP·BP.

教学预设：这组变式立意体现了从特殊到一般再到特殊的过程.证明思路都是构造相似三角形.三道变式题讲评之后，教师可在图5的基础上，作射线PO与⊙O相交于M，N两点（如图6），连接OC，设⊙O的半径为r，点P到圆心O的距离为d，容易得到d2-r2＝PC2.同理，在图4中，也可得到AP·BP＝CP·DP＝d2-r2.问题1及其变式的证明体现了“数学上统一的精神”

@@教学环节2：研究“垂径定理”基本图形.##

问题2 如图7所示，AB为⊙O的直径，弦CD⊥AB，垂足为P.连接AC，BC，BD，AD.证明AC·BD＋AD·BC＝AB·CD.

教学预设：考虑到垂径定理基本图形中具有很多轴对称性质的线段，可以将相等的线段进行等量代换.待证等式的左边AC·BD＋AD·BC＝AC·BC＋AC·BC＝2AC·BC.待证等式的右边＝AB·CD＝AB·2CP＝2AB·CP.由△ABC∽△CBP，可得AC·BC＝AB·CP.可得，等式左边=等式右边，接通证明思路.另外，如果从四边形ACBD是特殊的四边形“筝形”来看，基于面积的角度“算两次”也可证明.在讲评上述方法之后，教师出示以下不同的证法，安排学生“阅读理解”.

阅读理解：如图8所示，在AB上取一点E，连接EC，使∠ACE＝∠DCB，结合∠CAE＝∠CDB，可证△AEC∽△DBC，得比例式ACDC＝AEDB，化为乘积式AC·DB＝AE·CD①.

由∠ACE＝∠DCB，可得∠ACD＝∠ECB，结合∠ADC＝∠EBC，可证△ADC∽△EBC，得比例式 ADEB＝CDBC，化为乘积式AD·BC＝BE·CD②.

将①＋②，可得AC·DB＋AD·BC＝（AE＋BE）·CD，即AC·BD＋AD·BC＝AB·CD.

教学组织：学生在“阅读理解”之后，教师可安排学生在小组内交流，简述这种证明思路，然后每个小组推荐一名代表在组内详细讲解，教师抽一两名学生上台讲解上述解法.讲评之后，教师引导学生回顾反思，发现这种证明思路并不需要垂径定理的特殊图形，没有使用直径、垂径弦等“强化条件”.教师引导学生猜测上述结论是否可以一般化，进而提出如下的挑战问题.

教学环节3：拓展挑战与同类再练.##

挑战问题 如图9所示，四边形ABCD的四个顶点在同一个圆上，连接对角线AC，BD.证明AB·CD＋BC·AD＝AC·BD.

教学预设：学生结合上面的“阅读理解”证明过程，发现挑战问题的证明思路与其完全相同.在AC上取一点E，连接EB，使∠ABE＝∠DBC，分别“证两次相似三角形”，得到两组比例式转化为对应的乘积式后再相加即可.教师鼓励最先获得思路的学生上台展示交流自己的证明思路.教师总结归纳该问题的结论就是著名的“托勒密定理”.

同类练习1 如图10所示，点P在等边三角形ABC的外接圆上，连接PA，PB，PC.证明PB＋PC＝PA.

教学预设：根据“挑战问题”的结论可知AB·CP＋AC·BP＝AP·BC.结合等边三角形ABC的三边相等，化简可得PB＋PC＝PA.

同类练习2 如图11所示，AB是⊙O的直径，点C在圆上，CD平分∠ACB，交⊙O于点D，分析线段AC，BC，CD之间的数量关系，并说明理由.

教学预设：连接AD，BD，可先证出△ABD是等腰直角三角形，有AB＝2AD＝2BD.结合“挑战问题”的结论可知AC·BD＋AD·BC＝AB·CD，简化为AC＋BC＝2CD.

@@教学环节4：课堂小结，布置作业.##

教师引导学生总结发现本课是学习相似之后对与圆有关基本图形的再认识，引导学生总结问题中涉及的基本图形性质.

教师布置如下作业.

（1）题干条件同课上“问题1后的变式3”，当PC＝4，PB＝2时，求AB的长.

（2）题干条件同课上训练的“同类练习2”，当⊙O的半径为2，∠BAC＝30°时，求CD的长.（用两种不同的方法）

（3）围绕本课所学内容，选取某一个基本图形问题的思路探究及“成果扩大”，整理成一篇解题随笔.

2 教学立意的进一步解读

2.1 精心选取基本图形，变式追问成果扩大

李善良教授曾就“问题情境设计”提醒教师要“注重一境多用，让学生形成整体的认识，防止出现一个内容一个情境、情境遍地开花的现象.”［1］在上文课例中，教师选取圆中“垂径定理”基本图形，从相似的角度探究基本图形性质，并通过变式追问促进学生对该图形的深刻理解，达到研究一个图形，学会一类问题的教学目标.

2.2 深刻理解问题本质，概括性质应用巩固

日本数学家、教育家米山国藏在《数学的精神、思想和方法》中曾提到“充满在整个数学中的统一建设的精神”，并指出很多同类问题“无论表面上看来多么不同，都可用同样的方法处理”.［2］在上文课例中，笔者基于圆的“垂径定理”基本图形提出一个圆内接四边形的两组对边乘积之和等于两条对角线之积的命题，先安排学生从相似或面积法的思路进行证明，随后给出一个不同方法的“阅读理解”，引导学生理解这种证明思路，并将命题概括为“一般化”的结论（即“托勒密定理”）.进一步安排两个经典问题巩固所学性质，并理解这类“形异质同”问题的解法具有一致性.

参考文献

［1］李善良.高中数学课程改革：探索与实践［M］.南京：江苏教育出版社，2012.

［2］米山国藏.数学的精神、思想和方法［M］.上海：华东师范大学出版社，1986.