动量定理在流体模型中的应用

动量定理是高中物理中的重要知识，不仅可以处理恒力问题，也可处理变力问题，还可以处理流体问题，本文谈动量定理在流体模型中的应用．

１ 流体运动模型

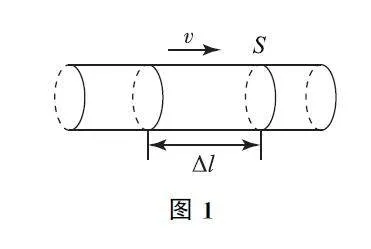
对于运动流体，可沿流速v 的方向选取一段柱形流体，设在极短的时间Δt 内通过某一横截面S 的流体柱的长度为Δl，如图１所示．设流体的密度为ρ，在Δt时间内流过该截面的流体质量Δm ＝ρSΔl＝ρSvΔt，根据动量定理知，流体微元所受的合外力的冲量等于该微元动量的增量，即FΔt＝ΔmΔv．

流体作用过程分两种情况：１）吸收模型，作用后流体元停止，有Δv＝－v，代入上式有F ＝－ρSv２;２）反射模型，作用后流体元以速率v 反弹，有Δv＝－２v，代入上式有F＝－２ρSv２．

２ 动量定理在流体模型中的应用

２.１ 解决气体类流动问题

通常气体流等被广义地视为“流体”，质量具有连续性，设密度为ρ，解题思路如下：

１）建立“柱状模型”，沿流速v 的方向选取一段柱形流体，其横截面积为S．

２）微元研究，在极短的作用时间Δt 内的一段柱形流体的长度为Δl，对应的质量为Δm ＝ρSvΔt．

３）建立方程，应用动量定理研究这段柱状气流．

例１ 台风对沿海地区的破坏力非常巨大，１２级台风登陆时中心附近最大风力约为３５m·s－１．已知小明站立时，在垂直于风速方向的受力面积约为０.５m２，空气的密度约为１.２９kg·m－３．假设空气吹到人身体上后速度减为零，则小明站在１２级台风中心附近，所受的风力大小约为（ ）．

A．７９０N B．７９N

C．２３０N D．２３N

解析 单位时间Δt 吹到人身体上的空气质量m ＝ρV＝ρSvΔt，根据动量定理有－FΔt＝０－mv，所以小明所受的风力大小约为F ＝ρSv２ ＝１.２９×０.５×３５２ N≈７９０N，故选A．

点评 本题用微元法，利用动量定理求风力的大小，考查了动量定理的应用，体现了学科素养中的模型建构能力．

２．２ 解决微粒类流动问题

通常电子流、光子流、尘埃等被广义地视为“微粒”，质量具有独立性，通常给出单位体积内粒子数n，解题思路如下：

１）建立“柱状”模型，沿运动的方向选取一段微元，柱体的横截面积为S．

２）微元研究，极短作用时间Δt 内一段柱形流体的长度为Δl＝v０Δt，对应的体积为ΔV＝Sv０Δt，则微元内的粒子数N ＝nv０SΔt （n 为单位体积内的粒子数）

３）先应用动量定理研究单个粒子，建立方程，再乘以N 研究整体．

例２ 一宇宙飞船的横截面积为S，以v０ 的恒定速率航行，当进入有宇宙尘埃的区域时，设在该区域单位体积内有n 颗尘埃，每颗尘埃的质量为m ，若尘埃碰到飞船前是静止的，且碰到飞船后就粘在飞船上，不计其他阻力，为保持飞船匀速航行，飞船发动机的牵引力功率为（ ）．

A．Snmv２０ B．２Snmv２０

C．Snmv３０ D．２Snmv３０

解析 时间Δt 内粘在飞船上的尘埃质量为M ＝v０ΔtSnm ，对粘在飞船上的尘埃，由动量定理得FΔt＝Mv０－０，解得飞船对这些尘埃的作用力为F＝nmv２０S;根据牛顿第三定律及平衡条件，可知为保持飞船匀速航行，飞船发动机的牵引力F′＝F，牵引力的功率为P ＝F′v０＝nmv３０S，故选项C正确，A、B、D错误．

点评 本题考查了微粒类流体问题，利用微元法求得作用力，进一步求得发动机的牵引力功率．建构起正确的物理模型是解题的关键．

例３ 如图２所示为放在水平桌面上的沙漏计时器，从里面的沙子全部在上部容器里开始计时，沙子均匀地自由下落，到沙子全部落到下部容器里时计时结束，不计空气阻力和沙子间的影响．对计时过程取两个时刻：时刻１，下部容器底部没有沙子，部分沙子正在做自由落体运动;时刻２，上、下容器内都有沙子，部分沙子正在做自由落体运动．下列说法正确的是（ ）．

A．时刻１，桌面对沙漏的支持力大小等于沙漏的总重力大小

B．时刻１，桌面对沙漏的支持力大小大于沙漏的总重力大小

C．时刻２，桌面对沙漏的支持力大小等于沙漏的总重力大小

D．时刻２，桌面对沙漏的支持力大小小于沙漏的总重力大小

解析 时刻１，下部容器内没有沙子，部分沙子正在做自由落体运动，对整体分析，有一部分沙子有向下的加速度，则总重力大于支持力，合力向下，故A、B错误;对时刻２，部分沙子做自由落体运动，设沙漏的总质量为m ，空中正在下落的沙子质量为m１，沙漏中部细孔到底部静止沙子表面的高度为h，因细孔处速度很小，可视为零，故下落的沙子冲击底部静止沙子表面的速度v＝根号下２gh ，沙子下落的时间为t，有v＝gt，解得t＝根号下２h／g ．设下落的沙子对底部静止沙子的冲击力为F１，在极短时间Δt 内，撞击在底部静止沙子表面的沙子质量为Δm ，由动量定理有F１Δt＝Δmv＝Δm根号下２gh ，解得F１＝ΔmΔt根号下２gh ．空中的沙子质量为m１，有m１t ＝Δm／Δt ，解得m１＝ΔmΔtt＝ΔmΔt根号下 ２h／g ，则F１＝m１g，对沙漏受力分析，可知桌面对沙漏的支持力FN＝（m －m１）g＋F１＝mg，故C正确，D错误．

点评 当下部容器底部没有沙子时，只有失重现象，桌面对沙漏的支持力大小小于沙漏的总重力大小;当上、下容器内都有沙子，空中沙子处于失重状态，导致桌面对沙漏的支持力减小，落到容器底部的沙子由于受冲击力作用，致使桌面对沙漏的支持力增大，两种作用力的效果相抵，定量分析得到桌面对沙漏的支持力大小等于沙漏的总重力大小．

２．３ 解决液体类流动问题

对于液体类流动问题，基本的解题思路与前两种情况的解题思路相同．

例４ 国产水刀———超高压数控万能水切割机，以其神奇的切割性能引起轰动．它能切割４０mm 厚的钢板、５０mm 厚的大理石及其他材料．水刀就是将普通的水加压，使其从口径为０.２ mm 的喷嘴中以４００～１０００m·s－１的速度射出的水射流．我们知道，任何材料承受的压强都有一定的限度，表１列出了几种材料所能承受的压强限度．

设想有一水刀的水射流横截面积为S，垂直入射的速度为４００m·s－１，水射流与材料接触后以原速率反弹，水的密度ρ＝１×１０３ kg··m－３，则此水刀不能切割的上述材料是（ ）．

A．铸铁和工具钢 B．花岗岩和工具钢

C．花岗岩、铸铁和工具钢D．都不能切割

解析 以射到材料上的质量为Δm 的水为研究对象，取极短的时间Δt，则Δm ＝ρSvΔt．设水对材料表面的压强为p，则材料对水的压强p′＝p，取水反弹的方向为正方向，根据动量定理有pSΔt＝Δmv－Δm （－v），解得p ＝２ρv２，解得p ＝３.２×１０８Pa，故水刀不能切割的表中材料是铸铁和工具钢，选项A 正确．

点评 本题属于反弹模型，抓住流体的特点，建立柱体模型，化无形为有形，本题即可迎刃而解．

本题的研究对象为“变质量”的“连续”流体．处理这类问题时，一般要假设一段极短时间Δt 内的流体，其长度为vΔt，流体横截面积为S，得流体体积V＝SvΔt，故流体质量为Δm ＝ρV ＝ρSvΔt，再对质量为Δm 的流体应用动量定理求解．

（完）