成本摊销式单服务器私人情报检索方法

摘要：私人情报检索旨在保护用户的查询内容和隐私，是情报检索领域内隐私保护的重要技术扩展。基于成本摊销的思想设计了一种高度可配置、有状态的、单服务器私人情报检索方案。在一个包含100万个1 kB元素的数据库上进行的实验表明，该方法能够在不到1 s的时间内响应客户端的查询请求，同时服务器的响应数据仅放大不到3.6倍。值得注意的是，实验分析基于一个简单的、未经过优化的Rust实现，说明该方法在涉及大量客户端的部署环境中特别适用。综上，结果表明该方法在私人情报检索领域具有显著的潜力，并且可以为处理大规模情报检索任务提供高效、经济实惠的解决方案。

关键词：情报检索；单服务器；在线开销；摊销成本；隐私保护

中图分类号：G354文献标志码：A文章编号：1002-4026（2024）05-0122-09

开放科学（资源服务）标志码（OSID）：

Cost amortization-based single-server private information retrieval method

CAI Xinyan1， YU Xiao2

（1.Shandong Institute of Scientific and Technical Information，Jinan 250101，China；2.School of Computer Science and Technology，

Shandong University of Finance and Economics， Jinan 250014，China）

Abstract∶Private information retrieval aims to protect users’ query content and privacy， serving as an important extension of privacy protection in the field of information retrieval. A highly configurable， stateful， single-server private information retrieval scheme was designed based on the concept of cost amortization. Experiments conducted on a database containing 1 million 1 kB elements showed that this method delivered superior performance， being able to respond to client queries in less than 1 s， with the server’s response data being increased by less than 3.6 times. It is noteworthy that the experimental analysis was based on a simple， unoptimized Rust implementation， suggesting that this method is particularly suitable for deployment environments involving a large number of clients. Experimental results indicate that this method holds significant potential in the field of private information retrieval and can provide an efficient and cost-effective solution for handling large-scale retrieval tasks.

Key words∶information retrieval; single-server; online overhead; amortized cost; privacy protection

私人情报检索专注于在保护用户隐私的同时，允许用户从存储在可能不可信服务器上的数据中检索信息。传统的情报检索方法通常要求用户将查询明文发送给服务器，这可能导致用户的查询内容暴露给第三方或中介者。相比之下，私人情报检索使用加密技术和安全协议，使用户能够在不泄露查询内容的情况下从服务器中获取所需信息［1-4］。例如使用私人情报检索方案，学生可以从数字图书馆取书，而不必向图书馆透露她取的是哪本书。

在现有的研究中，私人情报检索主要分为有状态和无状态两种方案。在无状态的私人情报检索中，使用了加性同态加密技术来隐藏客户端的查询内容［5-7］，这种模式被称为无状态，因为客户端无需在本地存储任何信息就能发起查询。然而，Sion等［8］研究表明，当网络带宽只有

每秒几百千比特时，这种方案实际上比简单地让客户端下载整个服务器数据库要差得多［9］，每个客户机查询都要执行O（m）个运算。此后，研究人员提出了各种方法进行优化［10-11］。不幸的是，无状态方法仍然需要处理计算开销，这在大规模部署中变得很具挑战性。例如，对于一个包含一百万个每条记录大小为256字节的数据库，响应一个客户端的查询可能需要超过1 s的时间。这种方法在大量客户端或需要及时响应的情况下并不适用。

最近的研究表明，将昂贵且与查询无关的计算移至初始的离线阶段可以提升在线性能。这种策略可以减少在线成本，并将离线阶段的费用分摊到多个客户端查询中［8］。这种模式被称为有状态私人情报检索。例如，Aguilar-Melchor等［12］使用基于格的密码学设计高效的单服务器私人情报检索方法。在他们的方法中，对于m=220个元素的数据库，服务器计算时间大约为5 s。Corrigan-Gibbs等［5］提出了一个次线性查询方法。具体来说，当客户端进行m次查询时，成本为O（m），而之前的方法则需要O（m）的计算开销。与之前的方案相比，最近的研究进一步降低了在线成本，但离线阶段的成本与之前的研究相似［13-15］。因此，改进私人信息检索算法以降低计算成本是当前研究中一个亟待解决的问题。

最近研究采用构造具有次线性服务器端平摊代价的方法。然而，现有实现次线性平摊时间的方法存在局限性，需要多个非串通服务器的方案，需要许多业务实体之间的仔细协调。此外，这些方案的安全性相对脆弱，因为它依赖于攻击者无法破坏多个服务器，而不是依赖于加密的硬度。最近的批处理方法要求客户端在单个非自适应批处理中立即完成所有查询，但不适用于许多自然应用程序（例如，数字图书馆、网页浏览）。

为了解决上述问题，本文旨在提出一项方案来提高私人情报检索的技术水平：它们只需要一个数据库服务器，有次线性的服务器时间，允许客户端自适应地发出数据库查询。本文的方案进一步依赖于标准的加密原语，即使当许多客户端查询单个数据库时，也具有很好的性能。

1研究方法

1.1数学符号与定理定义

对于一组向量x1，…，x，用［x1‖…‖x］来表示这些向量组成的矩阵。x表示将向量x中的每个数四舍五入到最近的整数。类似地，使用「x表示将x中的每个数四舍五入到下一个最高的整数。对于x∈mq，使用xp表示计算 （p/q）x，其中四舍五入适用于x的每个条目。对于某个集合χ，使用x←$χ 表示从χ中均匀地采样x，而x←$（χ）m表示从m维向量中进行采样，每个条目均匀地从χ中采样。此外，本文14a99431fc3683cfe7a13cfe0b4428f8用log（x）表示取x的以2为底的对数。使用λ表示安全参数，并称算法在λ的条件下是概率多项式时间可解的。

本文使用LWE问题的决策版本［16-18］，LWE能够支持构建安全的加密算法和协议，为保护信息安全提供有力理论支持，具有如下几个定义：

定义1.1设χ是某个分布，而q，n，m>0 依赖于λ。决策性 LWE 问题（LWEq，n，m，χ）是要区分以下两种情况：

（A，sT·A+eT）∈n×mq×mq

（A，μ）∈n×mq×mq，（1）

其中A←n×mq，sT←（χ）n，eT←（χ）m，μ←$mq。

假设1.2当χ是三元值（即{-1，0，1}）上的均匀分布时，LWEq，n，m，χ问题仍然难以解决。

定义1.3设χ为某个分布，设q，n，m>0依赖于λ。MatLWEq，n，m，χ是为了区分：（A，S·A+E）∈n×mq××mq（A，U）∈n×mq××mq，（2）

其中A←n×mq，S←（χ）×n，E←（χ）×m，U←$×mq。

推论1.4假设A是对MatLWEq，n，m，χ具有优势ε的PPT对手，则我们可以构造一个对 LWEq，n，m，χ具有优势ε/的 PPT 对手 B。

推论1.5对于足够大的m=poly（λ），从均匀三元值分布（即 {-1， 0， 1}）中抽取的m个样本的总和不超过4m。

1.2私人情报检索方案的性质

本文使用有状态检索方案，一个优异的有状态方案必须保证以下内容：

（1）正确性。下面的正确性定义确保客户端以非常大的概率接收到正确响应。

定义1.6给定一个数据库DB，对于查询 xt∈{0，1，…，n－1}，正确的答案是数据库的第x位。为了保证正确性，要求对于任意的q和n，这些量都在多项式级别受到λ的限制，存在一个可以忽略的函数negl（·），使得对于任意的数据库DB和任意的查询序列xt∈{0，1，…，n－1}，在使用数据库DB和查询xt∈{0，1，…，n－1}的诚实执行下，检索方案以概率 1－negl（·）返回所有正确的答案。

（2）安全性。本文使用安全的标准定义来强制执行客户端查询的不可区分性。

定义1.7设DB为服务器数据库。能够通过运行服务器设置生成参数，服务器预处理生成公共参数，同时能够运行客户端预处理生成客户端状态，则说该方案是安全的。上述定义可以扩展为指定查询不可区分性，即两个大小为r的客户端查询集彼此是不可区分的［19］。

（3）效率。保证所需的通信开销比让客户机下载整个服务器数据库的开销要小。在有状态的情况下，当将成本分摊到客户端查询的数量上时，它应该成立。

定义1.8对于启动c条查询的单个客户端，如果客户端通信开销小于|DB|/c，则该方案是有效的。对于有状态方案，总客户端通信成本计算公式为：comms（离线）+ c·comms（在线）。

1.3方法的具体流程与性质满足

1.3.1加密设置

加密设置是保证私人情报检索中检索方和服务器方信息不被泄露的关键所在，是整个方法的第一步。具体来讲，假设DB是一个包含m个元素的数组，每个元素由w位组成。索引i对应于它在数组中的位置。现在，假设有C个客户端，每个客户端将对DB发起最多c个查询。对于所使用的LWE实例化：设n和q分别为LWE维数和模量;令0<ρ<q;设χ为{-1，0，1}上的均匀分布;λ代表具体的安全参数。最后，我们使用PRG（μ，x，y，q）表示伪随机生成器，该生成器将种子μ←${0，1}λ扩展为x×yq的矩阵。

在定义1.3中，我们给出了LWEq，n，m，χ的一个变体，称为矩阵LWE问题（用MatLWEq，n，m，χ表示）。推论1.4表明，与LWEq，n，m，χ相比，MatLWEq，n，m，χ很难求解，只有多项式安全损失。

1.3.2处理阶段

在单服务器PIR方案中，有两种有状态的机器称为客户端和服务器端。本文方法包括两个阶段：（1）离线设置阶段只预先运行一次，它发生在客户端对服务器进行任何查询之前。（2）在线阶段，这个阶段可以重复多次。客户端向服务器端发送一条消息，服务器端响应一条消息。接下来将详细介绍这两个阶段：

（1）离线阶段

服务器设置（setup）：服务器是包含m个元素的数据库，采样种子μ∈{0，1}λ。

服务器预处理（sprec）：服务器导出矩阵A←PRG（μ，n，m，q），其中A∈n×mq。然后运行D←parse（DB，ρ），将DB编码为矩阵D∈m×ωρ，其中ω=「w/log（ρ）。

为了生成公共参数，服务器运行M←A·D，然后将（μ，M）∈{0，1}λ×n×ωq发布到公共存储库。

客户端预处理（cpreproc）：每个客户端从公共存储库下载（μ，M），并运行A←PRG（μ，n，m，q）。然后，客户端对向量sj←（χ）n，ej←（χ）m进行c个采样。最后，对于每个j∈［c］，计算bj←sTj·A+eTj∈mq，cj←sTj·M∈ωq，并将这些对内部存储为集合X=（bj，cj）j∈［c］。

（2）在线阶段

客户端查询生成（query）：对于客户端希望查询的索引i，客户端生成向量：fi=（0，…，0，q/ρ，0，…，0），即除fi［i］=p/ρ外的值全为0。然后客户端从它维护的内部状态表中弹出一对（b， c），计算出b～←b+fi∈mq，并将b～发送给服务器。

服务器响应（response）：服务器从客户端接收b～ ，响应c～←b～T·D∈ωq。

客户端后处理（process）：客户端接收c～ ，输出x←c～－cρ∈ωρ。

1.3.3正确性

客户端后处理阶段的输出为x←c～－cρ∈ωρ。将等式右边展开得到：

x=c～－cρ=（sT·A+eT+fTi）·D－（sT·A·D）ρ=（e+fi）T·Dρ。（3）

注意到在数组中第I 行D［i］∈ωρ被解释为列向量，则证明在数组中eT·D+fTi·Dρ=fTi·Dρ能够产生正确的输出。这就引出了下面的定义：

定义1.9如果q≥8ρ2m，则检索的结果有高概率是正确的。

1.3.4隐私性

首先，本文采用了标准的安全性定义，以确保客户端查询的不可区分性。在定义1.7中描述了安全方案的要求和生成参数的过程。这些步骤是确保系统在实际运行中能够有效抵御各种潜在攻击的关键措施。其次，可以扩展该定义以便更加具体地指定查询的不可区分性。这确保无论客户端查询的具体细节如何，服务器都无法区分两个大小为r的客户端查询集。通过定义1.7的扩展，系统可以保证在所有交互中，无论是在线阶段还是离线阶段，都能够维持高水平的安全性。这种安全性不仅仅是理论上的保证，还需要通过实际的实验来验证和证明。

1.4参数设置

待配置的方案主要包括以下几个关键参数。

（1）具体安全参数：安全参数直接影响到系统对于潜在攻击的抵抗力和数据泄露风险。

（2）LWE的维数n和模数q：这两个参数对于LWE问题的求解和加密的强度至关重要。

（3）采样分布：使用均匀三元分布来采样LWE秘密向量和误差向量，这是保证数据安全性和随机性的重要手段。

（4）数据库中每个条目的比特数w和元素个数 m：这些参数直接影响到服务器端数据库的大小和查询的复杂度。

（5）通信开销、计算运算次数和存储开销：通信开销涉及到客户端和服务器之间的数据传输量，计算运算次数涉及到加密和解密操作的复杂度，存储开销则关注服务器端存储数据的需求和成本。

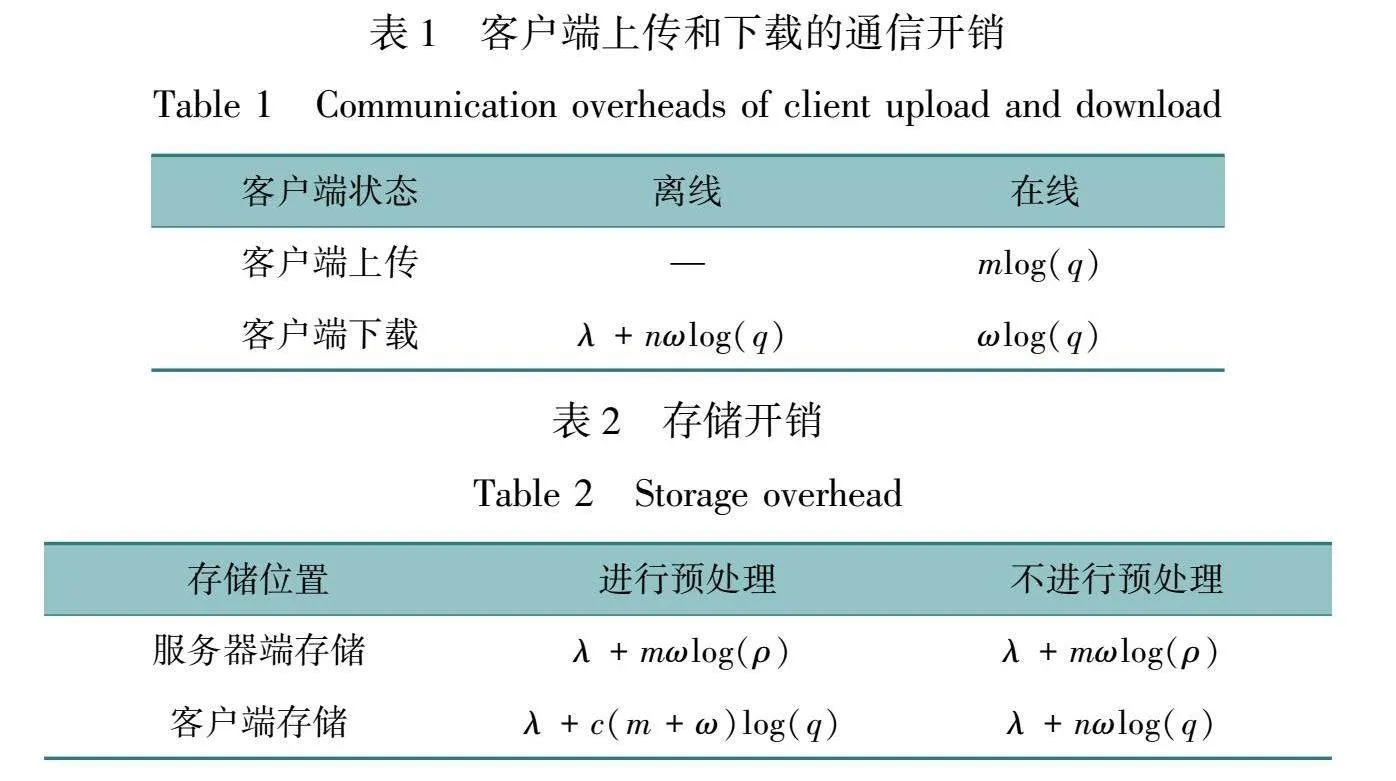
通过综合分析和优化上述参数，可以有效地设计出一个性能优越且安全可靠的私人信息检索系统，实现高效的在线和离线处理。通信开销如表1所示，存储开销如表2所示。显然，上述参数都对效率有影响。

1.4.1所需不变量

为了提高效率，本文方法满足定义1.8，设c为单个客户端查询的上界，此时可以得出：λ+nωlog（q）+c（m+ω）log（q）<mω，其次，为了正确性，方法满足q≥8ρ2m成立。最后，对于安全性，MatLWEq，n，m，χ，必须提供至少128位的具体经典安全性。本文用格安全估计器估计LWE实例的具体安全性。

1.4.2调整LWE参数

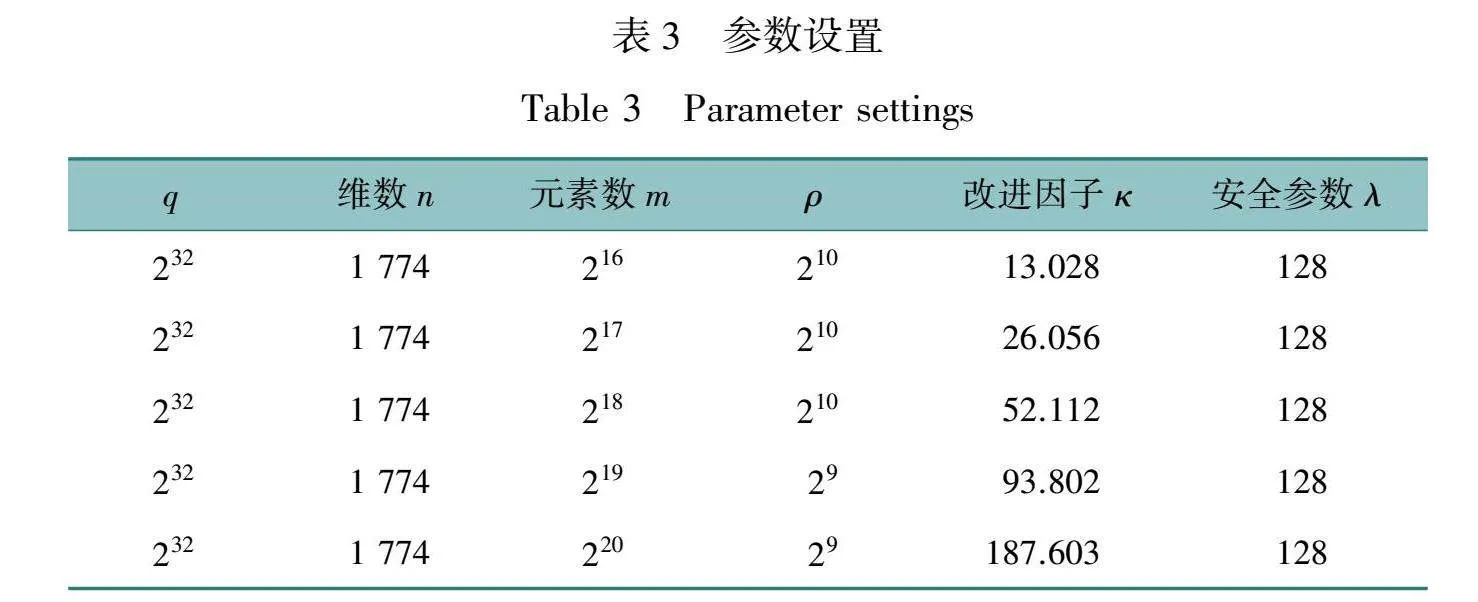
在配置本文方法用来提高效率之前，要确定一组参数，以提供必要的具体安全保证。首先，χ是均匀三元分布。其次，设置q=232，这允许本文使用标准的32位无符号整数操作来实现Zq操作。第三，设n=1 774为LWE维数。利用Albrecht等［20］的工作，可以得出v=LWEq，n，m，χ，然后利用原始USVP代价模型计算出具体的安全性参数为λ=v－log（推论1.4）。由于是服务器观察到的查询总数，我们设置=252作为一个合适的上界。达到上界后，A被重置，方案的安全性也被重置。因此，λ=v－52。

以上分析表明，对于大量的查询，实例的具体安全性将随着查询数量的增加而多项式地降低——直到重新采样一个新的LWE矩阵A。目前还不存在以这种方式对MatLWEq，n，m，χ，的安全性进行攻击。因此，在允许较小的维度n时，通过简单地估计较小的值的安全性，或仅估计v=LWEq，n，m，χ的安全性是有价值的。

1.4.3数据库推荐参数

设κ=（log（ρ）·m）/（n·log（q））表示与原始DB大小相比，相对于离线客户端下载的改进因子。表3给出了本文方法的推荐参数设置。对于252个客户端查询，具体的安全参数为128位。安全性通过增加维数n来提高，但这会降低κ。

2实验分析

在性能基准测试中，我们选择Amazon t2.2xlarge EC2实例作为测试平台，该实例配备8个CPU内核和32 GB RAM，以确保实验的稳定性和可靠性。所有的计算成本均按照CPU处理时间计算。带宽成本基于λ=128的详细开销表格计算，具体数据显示从服务器到客户端的数据传输成本为0.09 美元/GB，而客户端到服务器的数据传输成本则免费。此外，计算成本为0.371 2 美元/h，相当于每CPU每小时0.046 4 美元。单个服务器数据库的参数设置见表3，以提供非平摊的通信和计算基准。

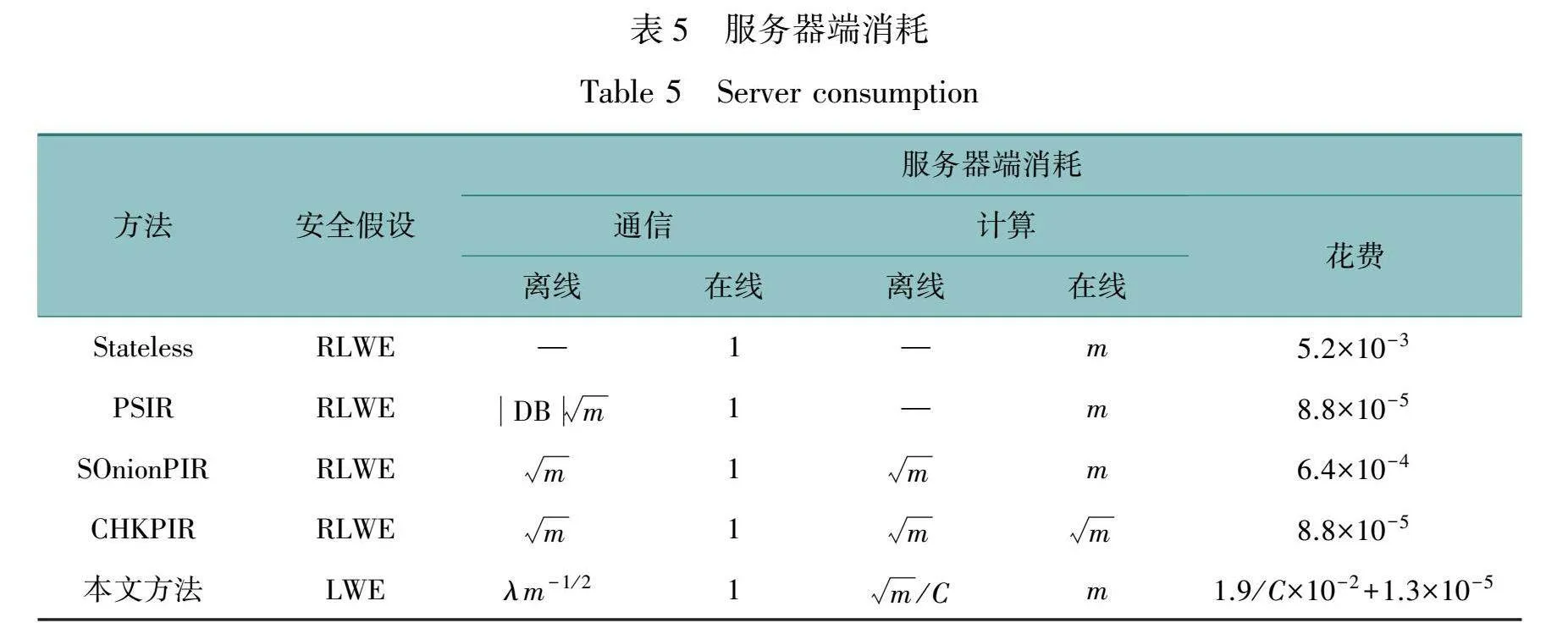
我们选定w=213位，对应1 kB的数据库元素大小；当数据库元素数m ≤ 218时，设置ρ=210，否则为29。我们的实验参数设计可以为大约252个客户端查询提供了128位安全性。这一安全性级别可以通过增加LWE维数n来进一步提高。总体来说，我们的实验框架和参数选择旨在提供一个全面的性能评估，确保方案在各种应用场景下均能表现出色。这些成本和性能数据不仅帮助我们验证了方案的可行性和效果，还将其与现有的PSIR［15］和SOnionPIR［6］方法进行了比较，展示了其在多个维度上的优势和竞争力。表4和表5给出了本文方法与以前的无状态/有状态检索方案之间的功能、效率和粗略的财务比较。

2.1性能结果

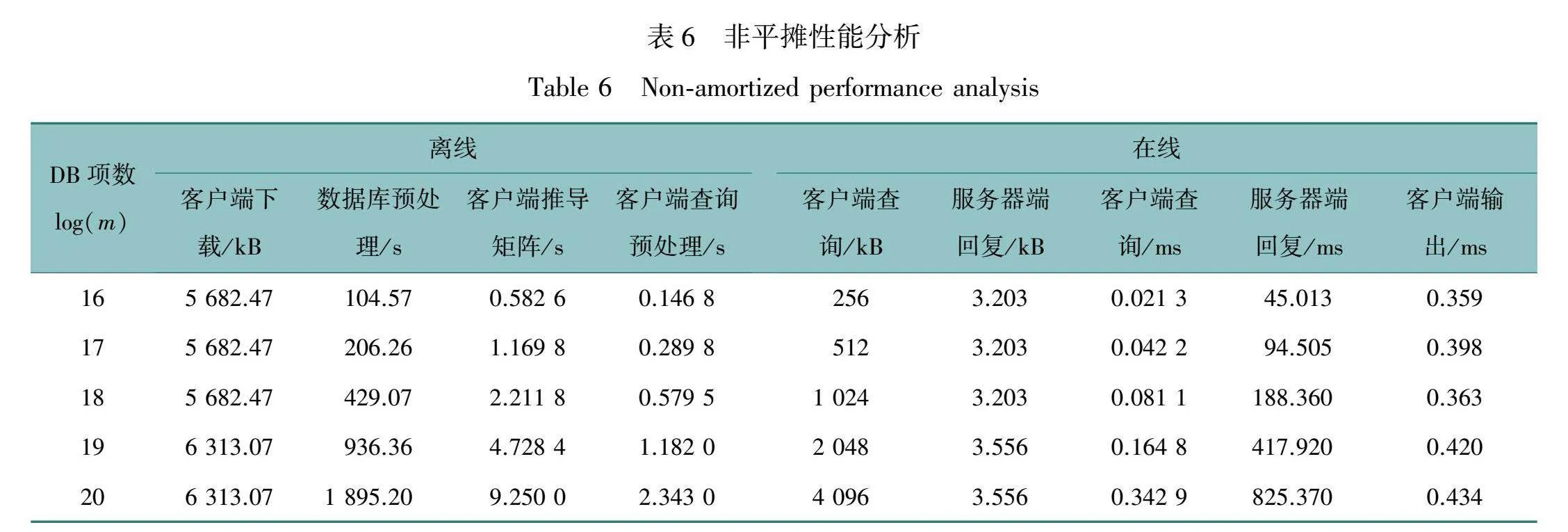
本文方法的非平摊性能如表6所示。这包括计算运行与单个客户端交互的单线程服务器实例的运行时间和带宽使用情况。随后，分析了离线成本如何在perquery的基础上摊销。摊销根据可变数量的客户端C和每个客户端查询的数量c来计算（我们将所有实验的C设置为500）。

在离线阶段，服务器首先生成数据库矩阵DB和公共参数。这个过程与客户端无关，其复杂度是线性的。具体而言，服务器会从一个单一的λ位种子计算得到假随机派生的LWE矩阵。一旦公共参数生成完毕并且客户端下载完成，客户端开始对每个查询进行与查询内容无关的预处理。这些预处理的结果会在在线阶段使用，这些成本大致呈线性增长，与m成正比。

在通信方面，服务器发布λ位种子μ和矩阵M∈n×ωq，其中ω=w/log（ρ）。对于log（ρ）的每个选择，客户机下载的大小是静态的。因此，总成本只在增加m导致ρ必须减小时才会增长。

在线阶段，客户端的计算任务主要包括两个方面：首先是执行单个加法操作，用于修改预处理数据的特定部分。其次，客户端需要对服务器返回的响应进行少量的后处理，这一步骤几乎在所有实验中都表现出静态性质，因为它与参数ω成线性关系，且与数据库大小无关。在服务器端，主要的计算成本集中在处理客户端的查询请求上。不论数据库的规模如何，服务器能够在每次查询中处理的时间都控制在0.83 s以内。此外，通信成本主要取决于客户端的查询内容，通常为mlog（q）位，这与数据库的大小成正比关系。关于服务器响应的大小，它通常远小于查询时传输的数据量。具体来说，服务器响应的大小大约为ωlog（q）位，这相对于原始的1 kB数据元素的大小增加不到3.6倍。这种低开销的响应确保了在处理和传输数据时的高效性和经济性。

离线阶段的摊销是实现系统经济性和性能优化的关键部分。在系统启动时，许多离线成本可以在服务的查询数量上分摊，这对于成本效益至关重要。在表6中列出的离线成本包括数据库预处理、参数生成和客户端下载。这些成本可以通过在一定查询量范围内分摊来显著减少每个查询的实际成本。例如，数据库预处理和参数生成步骤的摊销率可以根据服务的查询数量进行计算，使得在处理1 000到1×106个查询时，每个查询的离线成本相对较低而更加可控。类似地，客户端的离线预处理和下载成本也可以在客户群体中分摊，进一步降低每个客户端的成本。存储成本也是一个重要的考虑因素。随着数据库大小增长，客户端存储开销也会增加。当数据库大小达到220时，存储开销可能会显著增加，达到约2 GB。针对存储受限的客户端，可以通过实现log（m）的客户端存储开销来减少存储需求。这种方法虽然能够节省存储空间，但在在线查询处理时可能会引入额外的计算负担。通过合理的成本分摊和存储优化策略，可以有效控制运营成本和提高用户体验。

财务成本：对于一个220大小的数据库，服务器端数据库的初始预处理费用略高于1 美分。每个查询的在线成本非常低，即使对于最大的数据库大小，也只有大约0.001 美分。

2.2与其他方法对比

在安全性方面，本文方法提供了128位的安全性保证，它能够抵抗包括强大的计算资源在内的广泛攻击。这种高安全性级别适用于多达10亿个客户端查询的情况，确保了即使在极端情况下，例如量子计算机的威胁下，系统仍能保持稳固的保护。相比之下，SOnionPIR和PSIR提供的安全性最高为115位。虽然它们可以通过增加安全参数来提高安全级别，但这会导致服务器在处理大量并发查询时在线响应显著增加。因此，本文方法在提供更高安全性的同时，通过有效的算法设计和参数选择，尽量避免了在在线阶段引入过多的计算成本。这使得它在安全性和性能之间取得了良好的平衡。

在计算方面，PSIR中的客户端必须下载整个服务器数据库，以便在本地进行查询处理。这种设计使得客户端必须消耗大量的带宽和存储资源来处理大量数据。相比之下，本文方法在计算上的成本与数据库大小呈现线性增长。具体来说，随着数据库中数据量的增加，预处理阶段和在线查询响应的计算成本也会相应增加。这种线性关系使得本文方法能够根据需要灵活地调整成本和性能之间的平衡点。尽管在单个客户端的情况下，SOnionPIR可能在计算效率上优于本文方法，但随着查询负载的增加，SOnionPIR在服务器和网络资源方面的消耗也会显著上升。与此相反，本文方法中的所有预处理都与具体的客户端无关，这意味着无论查询负载c或客户端数量C如何变化，预处理和在线查询响应的成本都保持固定。这种特性使得本文方法在大规模多客户端环境中表现出色，尤其是在需要处理高并发查询和大量数据时，能够显著降低整体系统的运营成本和复杂度。

在在线阶段，PSIR方案以其高效的计算时间脱颖而出，这主要得益于其基于客户端的数据处理方式。PSIR要求客户端下载整个服务器数据库，使得在本地进行查询处理成为可能。与此同时，本文方法和SOnionPIR在在线计算时间上仍然保持着竞争力。特别是对于本文方法而言，在包含220个元素的数据库上，响应客户端查询的时间不超过0.825 s。这表明了本文方法在处理大规模数据集时的高效性和可靠性，能够满足对低延迟和高吞吐量的严格要求。SOnionPIR随着查询负载的增加，其计算时间和资源消耗也会显著增加。相比之下，本文方法在整体设计上考虑了计算成本的线性增长，并通过预处理阶段的优化来减少在线阶段的负担。

3总结

传统上，私人情报检索技术面临着实现成本高昂和效率低下的挑战，特别是在需要处理大规模数据和保护用户隐私的应用场景中。为了解决这些问题，本文通过成本互摊的方案设计了一种灵活高效的单服务器方法。采用Rust编程语言，显著提升了系统的安全性和执行效率。本文方法的另一个突出特点是其在实现成本方面的优势。通过简化和优化有状态方案的设计，降低了部署和维护的成本，使得这项技术更加可行和可接受，不仅仅局限于高端应用或研究领域，也适用于商业化和大规模应用的场景。综上，本文方法不仅为数据安全和隐私保护提供了可靠的解决方案，也为未来的数据密集型应用和服务开发提供了新的可能性和机会。

参考文献：

［1］ANGEL S， SETTY S. Unobservable communication over fully untrusted infrastructure［C］// Proceedings of the 12th USENIX Conference on Operating Systems Design and Implementation. Berkeley， CA： USENIX Association， 2016： 551-569.

［2］ZHOU M X， PARK A， SHI E， et al. Piano： extremely simple， single-server PIR with sublinear server computation［J］. IACRCryptol EPrint Arch， 2023， 2023： 452.

［3］MENON S J， WU D J. YPIR： high-throughput single-server PIR with silent preprocessing ［EB/OL］. ［2024-06-20］. https：//www.cs.utexas.edu/～dwu4/papers/YPIR.pdf.

［4］ULUKUS S， AVESTIMEHR S， GASTPAR M， et al.Private retrieval， computing， and learning： Recent progress and future challenges［J］. IEEE Journal on Selected Areas in Communications， 2022， 40（3）： 729-748. DOI： 10.1109/JSAC.2022.3142358.

［5］CORRIGAN-GIBBS H， HENZINGER A， KOGAN D. Single-server private information retrieval with Sublinear amortized time［M］//DUNKELMAN O， DZIEMBOWSKI S. Lecture Notes in Computer Science. Cham： Springer International Publishing， 2022： 3-33. DOI： 10.1007/978-3-031-07085-3_1.

［6］MUGHEES M H， CHEN H， REN L. OnionPIR： response efficient single-server PIR［C］// CCS ′21： Proceedings of the 2021 ACM SIGSAC Conference on Computer and Communications Security. New York， USA： Association for Computing Machinery， 2021： 2292-2306. DOI： 10.1145/3460120.3485381.

［7］PATEL S， PERSIANO G， YEO K. Private stateful information retrieval［C］// PROCEEDINGS OF THE 2018 ACM Sigsac Conference On Computer and Communications Security （CCS′18）. Toronto， CANADA： ACM， 2018.1002-1019. DOI：10.1145/3243734.3243821.

［8］SION R， CARBUNAR B. On the practicality of private information retrieval［EB/OL］.［2024-06-20］. https：//users.cs.fiu.edu/～carbunar/pir.pdf.

［9］KUSHILEVITZ E， OSTROVSKY R. Replication is not needed： Single database， computationally-private information retrieval［C］//Proceedings 38th Annual Symposium on Foundations of Computer Science. Miami Beach， FL， USA. IEEE， 1997： 364-373. DOI： 10.1109/SFCS.1997.646125.

［10］CACHIN C， MICALI S， STADLER M. Computationally private information retrieval with polylogarithmic communication［M］//Lecture Notes in Computer Science. Berlin， Heidelberg： Springer Berlin Heidelberg， 1999： 402-414. DOI： 10.1007/3-540-48910-x_28.

［11］GENTRY C， RAMZAN Z. Single-database private information retrieval with constant communication rate［M］//Lecture Notes in Computer Science. Berlin， Heidelberg： Springer Berlin Heidelberg， 2005： 803-815. DOI： 10.1007/11523468_65.

［12］AGUILAR-MELCHOR C， BARRIER J， FOUSSE L， et al. XPIR： Private information retrieval for everyone［J］. Proceedings on Privacy Enhancing Technologies， 2016， 2016（2）： 155-174. DOI： 10.1515/popets-2016-0010.

［13］MENON S J， WU D J. SPIRAL： Fast， high-rate single-server PIR via FHE composition［C］//2022 IEEE Symposium on Security and Privacy （SP）. San Francisco， CA， USA. IEEE， 2022： 930-947. DOI： 10.1109/SP46214.2022.9833700.

［14］ANGEL S， CHEN H， LAINE K， et al. PIR with compressed queries and amortized query processing［C］//2018 IEEE Symposium on Security and Privacy （SP）. San Francisco， CA， USA. IEEE， 2018： 962-979. DOI： 10.1109/SP.2018.00062.

［15］CORRIGAN-GIBBS H， KOGAN D. Private information retrieval with sublinear online time［C］// CANTEAUT A， ISHAI Y. 39th Annual International Conference on the Theory and Applications of Cryptographic Techniques （EUROCRYPT）. Zagreb， Croatia： Int Assoc Cryptol Res， 2020： 44-75.

［16］REGEV O. On lattices， learning with errors， random linear codes， and cryptography［J］.JOURNAL OF THE ACM， 2009，56（6）：34. DOI： 10.1145/1568318.1568324.

［17］BRAKERSKI Z， LANGLOIS A， PEIKERT C， et al. Classical hardness of learning with errors［C］// STEHLé D. 45th Annual ACM Symposium on the Theory of Computing （STOC）. Palo Alto， CA： Assoc Comp Machinery Special Interest Grp Algorithms & Computat Theory，2013： 575-584.

［18］MICCIANCIO D， PEIKERT C. Trapdoors for lattices： Simpler， tighter， faster， smaller［J］. IACRCryptol EPrint Arch， 2012， 2011： 501. DOI： 10.1007/978-3-642-29011-4_41.

［19］PATEL S， PERSIANO G， YEO K. Private stateful information retrieval［C］// Proceedings of the 2018 Acm Sigsac Conference on Computer and Communications Security （CCS′18）. New York， USA： Assoc Comp Machinery， 2018：1002-1019. DOI：10.1145/3243734.3243821.

［20］ALBRECHT M R， PLAYER R， SCOTT S. On the concrete hardness of learningwitherrors［J］. Mathematical Cryptology， 2015， 9（3）：169-203.