基于双层网络模型的城市公共交通系统抗毁性研究

摘要：为研究城市公共交通系统的抗毁性，采用复杂网络理论对地铁、公交系统进行映射和分析。首先，基于Space-L模型改进双层复杂网络构建方法，以实际换乘距离为指标构建连边，并以线路高峰小时载客能力为边权重构建地铁-公交双层网络；其次，通过度、强度、介数等指标分析双层网络与其子网络的特性；最后，分别采用随机攻击和蓄意攻击模型对双层网络及其子网络进行抗毁性分析。研究结果表明：地铁-公交双层网络呈现无标度特性，对蓄意攻击表现出脆弱性，且对不同蓄意攻击指标的敏感性不同。研究结论对于公共交通系统应对突发事件，提升系统韧性具有参考价值。

关键词：复杂网络；地铁-公交双层网络；网络特性分析；蓄意攻击；抗毁性

中图分类号：U491文献标志码：A文章编号：1002-4026（2024）05-0079-10

开放科学（资源服务）标志码（OSID）：

Research on the invulnerability of urban public transport systems

based on a double-layer network model

MA Xuexiang1，HAN Mengwei2，ZHOU Guangxin1*，LI Shubin3，SHEN Jiajia4，KONG Xiangke1

（1. Shandong Rail Transit Survey and Design Institute Co.， Ltd.， Jinan 250014 ， China; 2. Jinan Rail Transit Group Co.， Ltd.，

Jinan 250101， China; 3. Institute of Road Traffic Safety， Shandong Police College， Jinan 250014 ， China;

4. China Railway 18th Bureau Group the Fourth Engineering Co.， Ltd.， Tianjin 300350， China）

Abstract∶To study the invulnerability of urban public transport systems， the complex network theory is used to map and analyze the metro and bus systems. First， an improved double-layer complex network construction method is proposed based on the Space-L model. This method constructs connecting edges based on actual transfer distances and uses the peak-hour passenger capacity of lines as edge weights to develop a metro-bus double-layer network. Second， the characteristics of this network and its sub-network are analyzed using indicators such as degree， intensity， and betweenness. Finally， the random attack and intentional attack models are utilized to analyze the invulnerability of the metro-bus double-layer network and its sub-networks， respectively. The results show that the developed network exhibits a scale-free property and is vulnerabe to intentioanl attacks， exhibiting different sensitivities to various intentioanl attack indicators. Thus， the results of this study provide valuable guidelines to public transport systems for responding to emergencies and improving their robustness.

Key words∶complex network; metro-bus double layer network; network characteristic analysis; intentional attack; invulnerability

城市常规公交与轨道交通分别作为城市公共交通的主体和骨干，二者的高效衔接能够提高公共交通的可达性和出行效率，同时有效提升公共交通系统的韧性。近年来，随着城市轨道交通的快速发展，其与常规公交的换乘衔接问题日益凸显，加之在恶劣天气、突发大客流等状况时，城市公共交通的运输效率明显下降，因此从整体的角度研究多层次公共交通系统的抗毁性，对于应对突发事件、提升整体效能和系统韧性具有重要意义。

目前，国内外学者主要采用复杂网络理论对城市公共交通系统进行网络化研究。在网络构建方面：王波等［1］采用Space-L、Space-P和Space-R三种空间模型构建杭州市常规公交网络模型，论证了网络的小世界特性，网络的度符合指数型分布。陈烨［2］通过Space-L方法构建快速公交和轨道交通有向加权网络，以站点间距小于300 m的换乘站点建立连接，并提出了站点分级指标以提高城市公交系统的运营效率。沈犁等［3］以500 m为接驳半径，构建成都市公共交通复合网络，研究了恐怖袭击和拥堵失效对网络的影响。汪军等［4］利用Space-L方法构建地铁-公交网络，以200 m为阈值建立公交、地铁的复合连边，并提出了一种基于贪心介数的关键车站识别算法。汪淑良等［5］以耦合距离500 m为例，构建了武汉市公交-地铁相依公共交通网络，并通过深度学习对网络的拓扑属性进行识别，研究网络的韧性。在鲁棒性分析方面：Yang等［6］复合了公交和地铁网络，建立网络级联失效模型，研究在极端天气下公共交通网络的鲁棒性。程国柱等［7］构建了地铁-常规公交的双层网络模型，以哈尔滨市为例研究在严寒环境下，地铁-常规公交系统的网络承载能力，并对网络进行鲁棒性分析。宋英华等［8］构建了公交-地铁双层网络，研究内涝导致的站点失效对网络连通率、网络效率等方面的影响。郑乐等［9］以出行时间作为边权，构建地铁-公交加权复合网络，评估不同攻击模式和攻击策略下的网络性能。林兆丰等［10］提出一种基于换乘的加边策略，可以显著提高复合网络遭受攻击时的系统鲁棒性。张琳等［11］提出一种耦合站点失效判别的规则，并采用蓄意攻击、随机攻击分析复合网络的静态鲁棒性，证明了地铁与公交的耦合能够显著提高网络的鲁棒性。综上所述，目前相关研究存在以下不足：（1）在以换乘距离为指标构建网络时，往往以欧氏距离为阈值，而不是以实际换乘距离，这与乘客的出行选择存在差异；（2）对地铁-公交双层网络中边权重的选取以及不同类型公共交通方式的权重差异性研究不足；（3）对蓄意攻击依据的重要性指标研究不足，缺乏对综合性指标的研究。

本文提出了改进的地铁-公交双层网络模型并以济南市地铁、公交为研究对象进行双层网络的构建和抗毁性分析。主要创新点有：（1）以实际步行换乘距离为阈值判断是否建立公交节点和地铁节点之间的连边关系，相较于欧式距离，实际步行换乘距离更符合人的出行行为选择；（2）以高峰小时载客能力作为边的权重，一方面高峰小时载客能力可以反映出不同公交方式运量的差异性，并且一定程度上映射公共交通系统的高峰客流情况，另一方面依据该指标可以分析网络在运输能力上的抗毁性；（3）在度、介数等蓄意攻击的基础上，采用机器学习降维方法构建了一个新的综合指标，对比分析综合指标的攻击效果。研究结论有助于促进常规公交与轨道交通的融合发展，对城市公共交通系统的运输效能和韧性提升具有借鉴意义。

1地铁-公交双层网络模型

1.1地铁、公交单层网络构建

Space-L、Space-P和Space-R是三种常用的城市公交系统复杂网络构建方法。Space-L和Space-P方法构建的网络均是以站点作为网络节点，Space-L在每条线路中相邻站点之间添加连边；而Space-P着重于展现公交路线中的换乘关系，若两个站点之间存在直达的线路，则节点间添加连边。Space-R则是定义线路为网络节点，根据不同线路间是否存在公共站点，来确定节点间的连接。

为了更加真实的映射网络的连接状态，以Space-L模型为基础，引入线路高峰小时载客能力为边权重，分别构建公交和地铁加权网络。线路高峰小时载客能力与地铁、公交的车型及高峰小时发车频率有关。车型可以有效区分地铁、公交运量的差距，高峰小时发车频率的设定是运营公司根据乘客出行需求长期演化博弈的结果。因此，以站点间各线路高峰小时载客能力之和作为边的权重可以有效的描述站点间高峰时段的出行需求。网络构建说明如下：

（1）将站点定义为网络节点，当站点间存在有线路连接时，则在节点间建立连边，以站点间高峰小时载客能力作为边权重。

（2）公交高峰小时载客能力由车型和高峰小时发车频率计算确定。

（3）地铁高峰小时载客量由车型、列车编组和高峰小时发车频率计算，大、小交路通过不同的发车频率进行体现。

（4）由于公交线路和地铁线路的上下行线路差异较小，因此以上行线路为研究对象，构建无向网络。

1.2地铁-公交双层网络构建

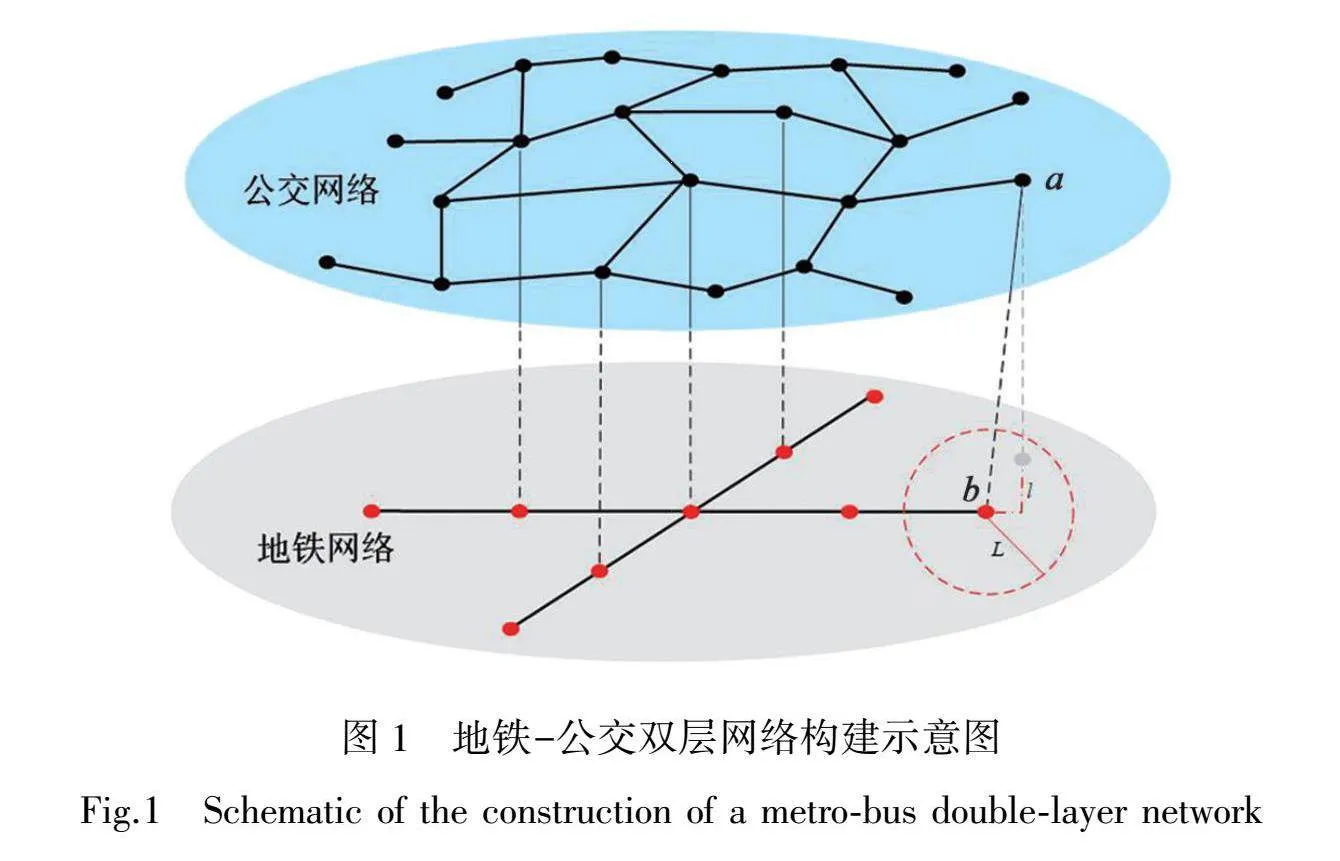
地铁-公交双层网络的构建在单层网络的基础上，考虑公交、地铁站点之间的步行换乘距离l和换乘阈值L。当l≤L时，认为二者之间存在接驳关系，则建立对应地铁、公交站点间的换乘边；反之，当l>L时，则二者之间无换乘边。相比于目前研究常用的欧式距离，采用换乘步行距离能够更加真实的反映实际情况，地铁-公交双层网络构建示意图如图1所示，构建说明如下：

（1）为每个节点嵌入站点的经纬度坐标信息。

（2）以地铁节点为中心，换乘阈值L为半径，建立换乘可接受范围。

（3）调用高德地图API计算地铁站点与换乘可接受范围内公交站点之间的最短步行距离，如图1中公交站点a与地铁站点b的步行换乘距离为l。

（4）如图1所示，若步行换乘距离l小于换乘阈值L，则在公交站点a与地铁站点b之间建立连边。

（5）考虑到本文以载客能力为网络边的权重，换乘连边的权重取无穷大。

2网络攻击模型

2.1网络攻击

抗毁性是指网络在某种因素的破坏或影响下，保持正常运营的能力。根据攻击策略的不同，网络攻击可以分为随机攻击和蓄意攻击。随机攻击是指在未知网络信息的情况下，以一定的概率随机攻击网络中的节点，直至网络瘫痪。因此，随机攻击时网络中各个站点受到的攻击概率是相等的，这种攻击方式主要模拟地震、洪水等自然灾害导致的网络故障。蓄意攻击策略是指在掌握网络部分或全部信息的情况下，有针对性地攻击网络中某些比较重要的节点，以使网络尽快瘫痪，这种攻击方式主要模拟突发大客流事件、恐怖袭击等引起的网络故障。目前，常见的蓄意攻击模型是依据网络中节点的度、强度、介数、聚类系数等重要性指标排序，依据重要程度依次攻击。

度、强度、介数、聚类系数是复杂网络中描述节点重要性的不同维度的定量指标［12］，度是指网络中节点的连边数，度量节点的中心性；强度是指节点连边的权重之和，度量节点与其他节点的转换频数；介数是指网络中通过该节点的最短路径数的占比，度量节点在网络中作为“桥梁”的重要程度；聚类系数是指节点与相邻节点之间连边的数占这些相邻节点之间最大可能连边数的比例，度量节点与其相邻节点的聚集程度。相关指标的计算公式见式（1）～（4）。

Di=∑vj∈Veij ，（1）

式中，Di为节点vi的度；V为网络节点的集合；eij为节点vi和vj的连边，若节点vi与vj相连，则eij=1，否则，eij=0。

Si=∑vj∈Vwij ，（2）

式中，Si为节点vi的强度；wij为节点vi和vj的连边的权重。

Bi=∑i≠jnij（i）nij ，（3）

式中，Bi为节点vi的介数；nij（i）为节点vi与vj的最短路径且经过节点vi的数目；nij为节点vi与vj的最短路径的总数。

CCi=2M′iDi（Di－1） ， （4）

式中，CCi为节点vi的聚类系数；M′i表示节点vi的邻域内节点间的连接边数，即由节点vi及其邻域内两个节点形成的三角形数量。

网络节点重要性的不同指标之间相互独立，又存在内在联系，为了多维度评价网络节点的重要性，本文引入机器学习中的主成分分析法（principal component analysis，PCA）对多维变量进行降维，以得到一维的综合性指标。PCA利用正交变换将一系列可能线性相关的变量进行降维，在减少分析指标的同时，尽量减少原指标包含信息的损失。PCA的主要计算步骤如下：

（1）设有p个样本，每个样本含q项指标，组成原始数据矩阵Xqp，对原始数据进行标准化处理，形成标准化后矩阵X。

（2）计算协方差矩阵R

R=1n－1XXT。（5）

（3）计算协方差矩阵R的特征值和特征向量。

（4）提取前k（1≤k<q）个最大的特征值对应的特征向量构成变换矩阵Ykq。

（5）通过变换矩阵Ykq计算低维主成分矩阵X′

X′=YkqXqp。（6）

2.2网络抗毁性指标

本文采用网络效率、网络最大联通率和运输能力损失率为指标，对网络的失效程度和抗毁性进行度量。网络效率E定义为所有最短路径长度的倒数之和与总最短路径数的比值，用于衡量网络节点之间的传输效率，计算公式如式（7）

E=1N（N－1）∑vi，vj∈V（i≠j）1dij ，（7）

式中，E为网络效率；N为网络中的总站点数；dij为节点vi与vj的最短距离。

网络最大连通率φ是衡量网络的整体连通性的指标。当网络遭受攻击后，网络分离为多个子图或孤立站点，其中，最大连通子图所含站点数与初始网络总站点数的比称为网络最大连通率，计算公式如式（8）

φ=N′N ，（8）

式中，N′为最大连通子图所含站点数。

运输能力损失率γ主要是网络功能抗毁性的指标，反映的是网络遭受攻击时，随着网络结构的改变，网络中客流运输能力的变化情况，即遭受攻击后，网络中因节点失效而损失的客流运输能力占初始客流运输能力的比例，计算公式如式（9）：

γ=1－∑1≤i≤N′Si∑1≤i≤NSi 。（9）

3案例分析

3.1网络特性分析

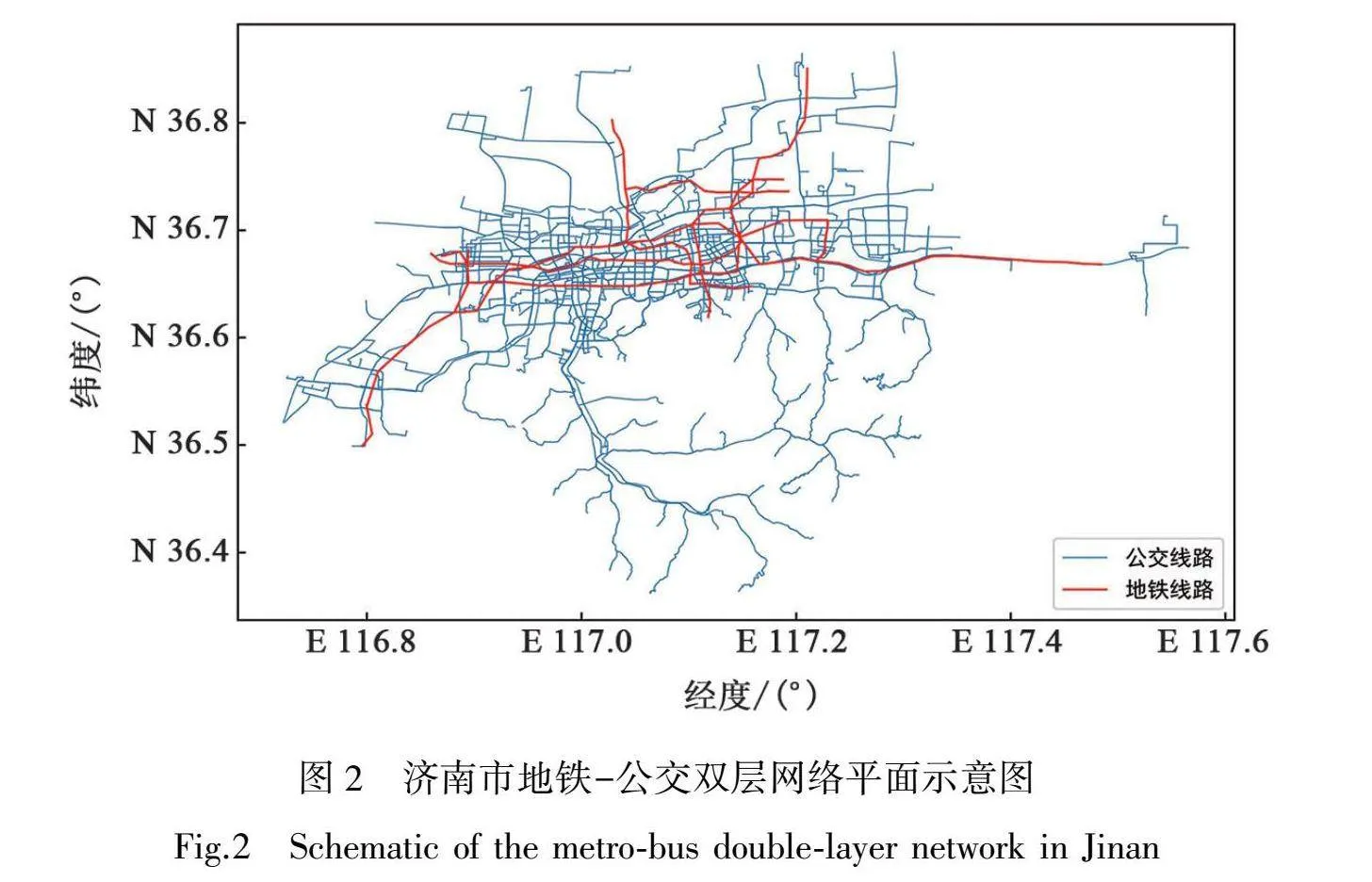
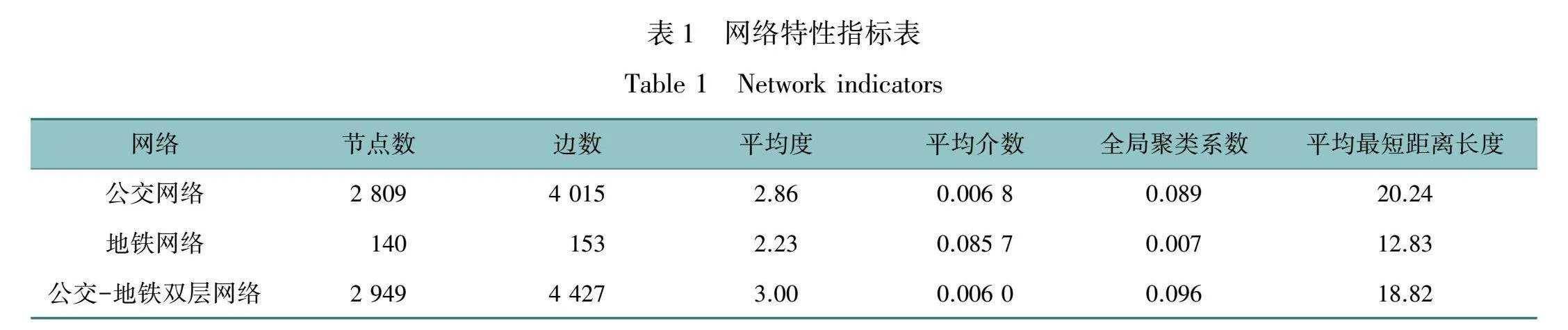
本文以济南市常规公交系统和城市轨道交通系统为研究对象，其中常规公交线路343条，公交站点2 809个；地铁线路8条，包括已运营线路3条，在建延长线1条，新建线5条，地铁站点140个（换乘站按照一个站点考虑）。利用Python中NetworkX库构建网络并计算特性指标，利用Gephi软件绘制网络结构图。网络结构如图2～3所示，网络特性指标如表1所示。

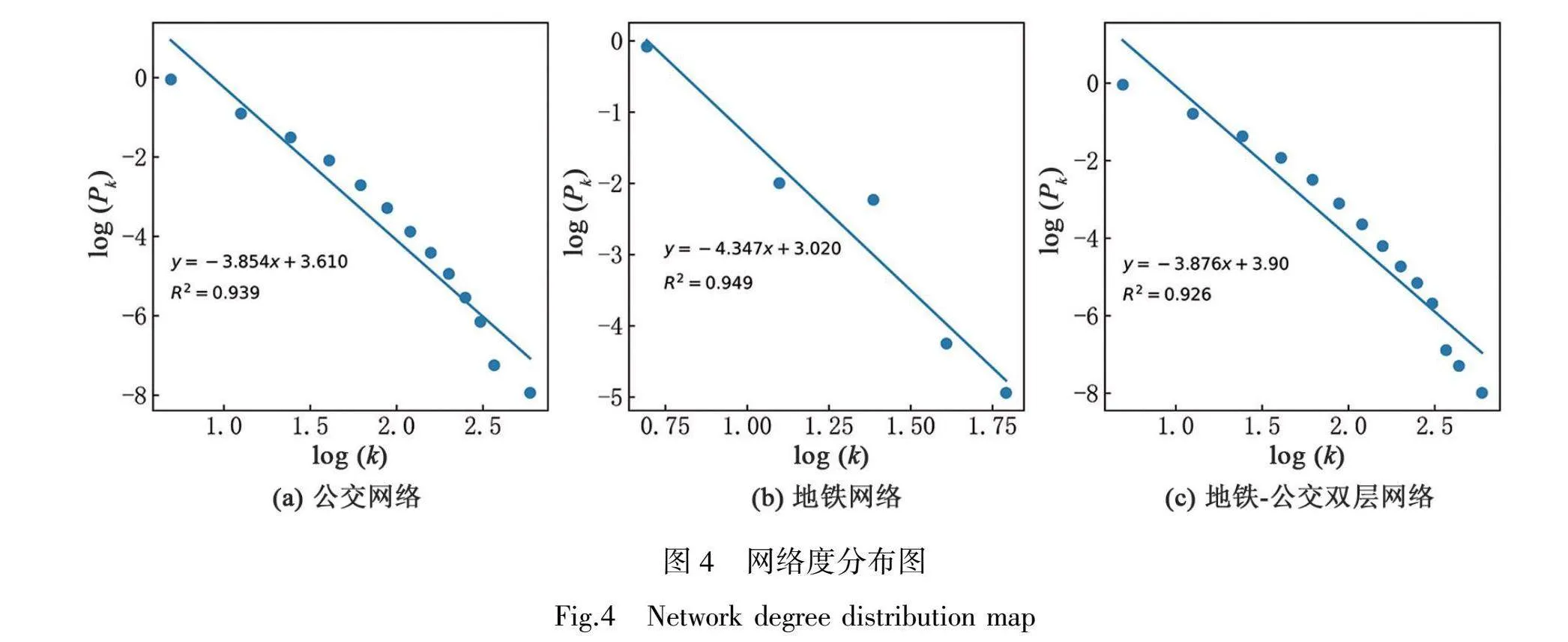
根据网络指标统计分析，双层网络的平均度为3，表明在双层网络中每个站点平均有3条连边，网络中度值为2的节点最多，占总站点数的50.3%；而度值为13、14、16的节点数之和仅占比0.001，即网络中大部分的节点具有较小的度，少量节点具有较大的度。在双对数坐标下，对三个网络的节点度分布进行拟合，如图4所示，节点的度分布在双对数坐标轴下可由线性回归方程进行较好的拟合，表明度分布符合幂律分布，网络具备一定的无标度特性。

从介数来看，公交网络和地铁-公交双层网络的介数相对较小，而地铁网络的介数较大，说明在地铁网络中，站点在联通方面的重要性较大，而公交网络和地铁-公交双层网络中，随着网络规模的扩大，网络之间的联通路径更多，站点在网络中起到的联通作用弱化。从聚类系数来看，公交网络和地铁-公交双层网络的聚类系数分别为0.089、0.096，表明公交网络和双层网络中站点具有一定的集聚性，而地铁网络由于规模较小，集聚性不明显，网络的平均聚类系数较小。从最短距离来看，双层网络的平均最短距离长度为18.82，这表明在双层网络中任意两个站点之间最短路径平均需要经历19个站点，同时，对比公交网络和双层网络可以看出，随着地铁网络的加入，缩短了公交网络的最短距离。

地铁-公交双层网络中各项指标重要性排名前十的站点指标如表2所示。由表2可以看出，在双层网络中度、介数和聚类系数较大的节点主要是公交站点，这与公交网络的规模较大，经过公交站点的线路较多有关，节点的联通作用和聚类性更加明显；强度较大的站点主要是地铁站点，这主要是节点的强度与边权重有关，由于地铁线路的高峰小时运输能力远大于公交线路，因此地铁站点的强度较高；而PCA综合指标较大的节点中，公交、地铁站点的占比相近，无明显趋向，这一定程度上表明PCA可以综合多维指标的主要信息，并计算形成具有参考价值的综合指标。

3.2网络抗毁性分析

本文对攻击策略做出如下设定：（1）每次按照网络节点总数的5%进行攻击；（2）站点被攻击后，不具备自我恢复能力；（3）网络中节点被攻击后，其连边全部断开，成为孤立节点。随机攻击利用Python中Random模块生成随机序列，以该序列作为站点索引依次进行攻击，至网络瘫痪后终止攻击。蓄意攻击分别以节点的度、强度、介数、聚类系数以及PCA综合指标为索引，按重要性由高到低依次进行攻击，至网络瘫痪后终止攻击。

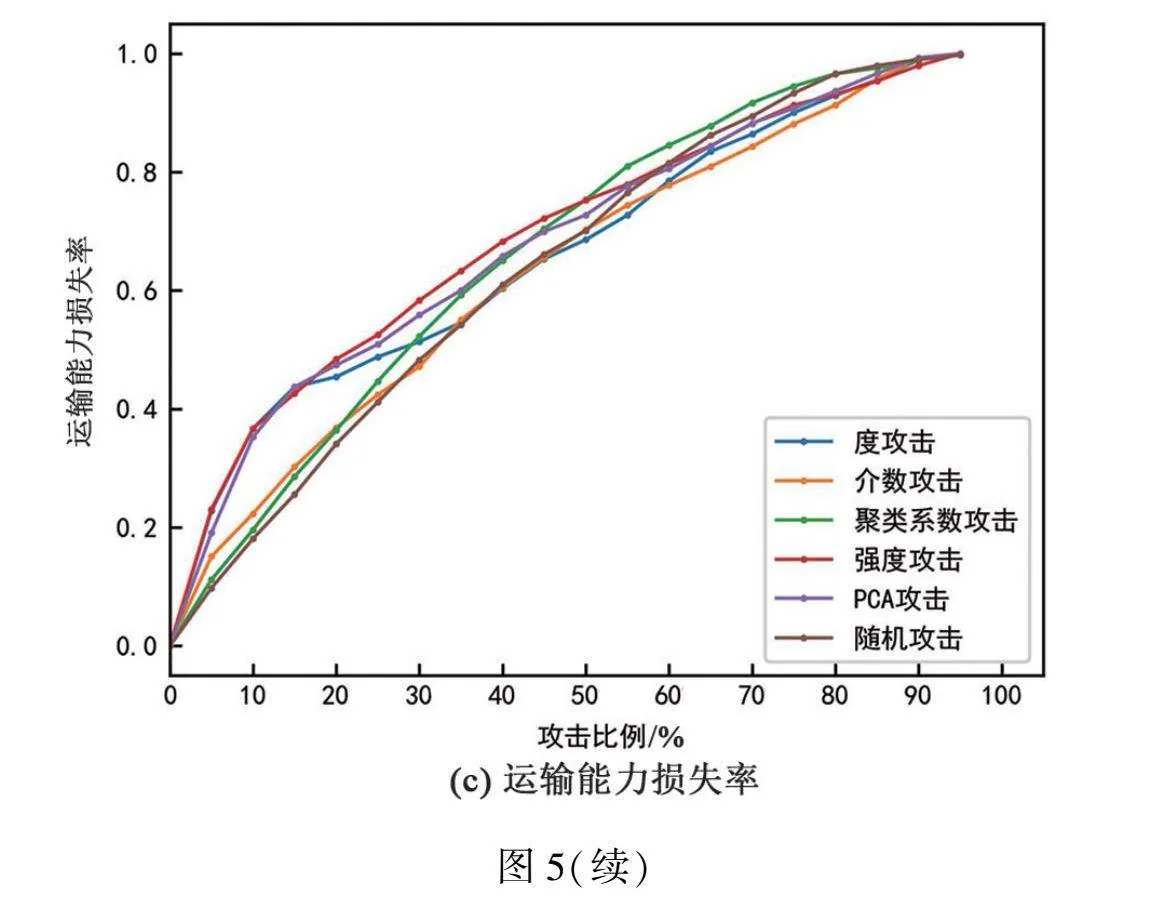
地铁网络、公交网络和地铁-公交双层网络在不同攻击指标下的仿真结果如图5～7所示。整体来看，在不同指标攻击下，网络效率和网络最大联通率均呈现出先快速下降后平缓趋近于0的趋势，运输能力损失率呈现出先快速增加后平缓趋近于1的趋势。

初始情况下地铁网络的网络效率为0.12，最大连通率为1。网络效率、最大连通率降低50%时，度攻击、介数攻击、强度攻击、PCA指标攻击的节点比例为5%，聚类系数攻击、随机攻击的节点比例为15%。网络运输能力损失率达到50%，度攻击、强度攻击、PCA指标攻击、聚类系数攻击的节点比例为30%，介数攻击、随机攻击的节点比例为35%。

初始情况下公交网络的网络效率为0.065，网络效率降低50%时，度攻击的节点比例为5%，介数攻击、强度攻击、PCA指标攻击的节点比例为10%，聚类系数攻击和随机攻击的节点比例为15%。初始情况下公交网络的最大连通率为1，最大连通率降低50%时，度攻击的节点比例为10%，介数攻击、PCA指标攻击的节点比例为15%，强度攻击的节点比例为20%，聚类系数攻击和随机攻击的节点比例为25%。网络运输能力损失率达到50%时，强度攻击、PCA指标攻击、度攻击的节点比例为10%，聚类系数攻击的节点比例为20%，介数攻击的节点比例为25%，随机攻击的节点比例为30%。

初始情况下地铁-公交双层网络的网络效率为0.069，网络效率降低50%时，度攻击、介数攻击、强度攻击、PCA指标攻击的节点比例为10%，随机攻击的节点比例为15%，聚类系数攻击的节点比例为20%。网络最大连通率降低50%时，度攻击、PCA指标攻击的节点比例为15%，介数攻击的节点比例为20%，强度攻击、随机攻击的节点比例为25%，聚类系数攻击的节点比例为30%。网络运输能力损失率达到50%，强度攻击、PCA指标攻击的节点比例为10%，度攻击的节点比例为15%，介数攻击的节点比例为20%，聚类系数攻击的节点比例为25%，随机攻击的节点比例为30%。

对比不同指标攻击效果可以看出，对于结构抗毁性指标网络效率和网络最大连通率，网络对各项指标攻击的敏感性由高到低依次为：度攻击、PCA指标攻击、介数攻击、强度攻击、随机攻击、聚类系数攻击。度攻击对网络结构破坏性最强，当攻击节点比例为15%时，网络已基本处于瘫痪状态。PCA指标攻击整体效果仅次于度攻击，当攻击节点比例为25%时，网络效率和最大连通率变化曲线与度攻击基本重合。对于功能抗毁性指标运输能力损失率，网络对各项指标攻击的敏感性由高到低依次为：强度攻击、PCA指标攻击、度攻击、介数攻击、随机攻击、聚类系数攻击。强度攻击和PCA攻击对网络功能破坏性最强且效果基本一致，当攻击节点比例为20%时，网络功能已基本失效。

对比PCA综合指标和单项指标可以看出，网络的结构抗毁性和功能抗毁性对于PCA综合指标均更为敏感，这表明PCA方法有效提取了不同指标的主要特征信息。PCA综合指标可作为分析网络抗毁性、识别网络重要节点的关键指标。对比随机攻击和蓄意攻击可以看出，蓄意攻击对网络的攻击效果整体上优于随机攻击，这体现出地铁网络、公交网络及其双层网络均具有一定的无标度特性，即对随机攻击具有鲁棒性，而对于蓄意攻击具有脆弱性。对比网络抗毁性指标可以看出，网络效率和网络最大连通率作为结构抗毁性指标，网络效率更容易呈现规律性，网络最大连通率曲线容易出现多次交叉和波动的情况，规律性相对较弱，但是在计算速率方面，网络最大连通率更具优势。网络运输能力损失率作为功能抗毁性指标，能较好的反映网络结构破坏对功能的影响。

4结论

复杂网络理论是描述和分析城市公共交通网络的有效方法。本文按照Space-L规则，以高峰小时运输能力为边权重，以实际换乘距离为阈值构建了济南市地铁-公交双层网络，通过计算网络度、聚类系数等指标分析了网络特性，并分别采用随机攻击和蓄意攻击模型对网络抗毁性进行分析。研究结论表明：地铁、公交以及双层网络均呈现出一定的无标度网络特性，在蓄意攻击下更具脆弱性，其中网络的结构抗毁性和功能抗毁性均对PCA综合指标更为敏感。因此，通过PCA综合指标识别影响网络韧性的关键节点，并针对性的采取一定的保护措施和应急方案，可以提高网络应对突发事件的能力。此外，公交网络复合地铁网络后，能够提升系统抗毁性，因此应进一步做好地铁、公交的换乘衔接，结合地铁站点的布设，优化一体化衔接布局。研究结论有助于城市公共交通管理、运营单位有针对性的制定应急处置方案，提升公共交通系统韧性。本研究在后续将考虑乘客换乘意愿、多维权重等因素进一步优化双层网络构建方法。

参考文献：

［1］王波， 柯红红， 蒋天发. 基于复杂网络理论的杭州公交网络建模与特性分析［J］. 武汉大学学报（工学版）， 2011， 44（3）： 404-408.

［2］陈烨， 高悦尔， 沈晶晶. 基于复杂网络的快速公交-轨道交通站点分级研究［J］. 热带地理， 2023， 43（7）： 1234-1246. DOI： 10.13284/j.cnki.rddl.003715.

［3］沈犁， 张殿业， 向阳， 等. 城市地铁-公交复合网络抗毁性与级联失效仿真［J］. 西南交通大学学报， 2018， 53（1）： 156-163. DOI： 10.3969/j.issn.0258-2724.2018.01.019.

［4］汪军， 夏永跃， 王运明， 等. 基于贪心介数的地铁-公交复合网络关键车站识别算法［J］. 铁道标准设计， 2022， 66（7）： 132-137. DOI： 10.13238/j.issn.1004-2954.202103170006.

［5］王淑良， 陈辰， 张建华， 等. 基于复杂网络的关联公共交通系统韧性分析［J］. 复杂系统与复杂性科学， 2022， 19（4）： 47-54. DOI： 10.13306/j.1672-3813.2022.04.007.

［6］YANG H H， AN S. Robustness evaluation for multi-subnet composited complex network of urban public transport［J］. Alexandria Engineering Journal， 2021， 60（2）： 2065-2074. DOI： 10.1016/j.aej.2020.12.016.

［7］程国柱， 张宇洁， 冯天军. 严寒城市地铁-公交复合网络承载力计算方法［J］. 哈尔滨工业大学学报， 2022， 54（9）： 101-110. DOI： 10.11918/202108087.

［8］宋英华， 李玉枝， 霍非舟， 等. 城区内涝条件下城市公交-地铁双层交通网络的脆弱性分析［J］. 安全与环境工程， 2021， 28（2）： 114-120. DOI： 10.13578/j.cnki.issn.1671-1556.2021.02.016.

［9］郑乐， 高良鹏， 陈学武， 等. 地铁-公交加权复合网络关键站点识别及鲁棒性研究［J］. 交通运输系统工程与信息， 2023， 23（5）： 120-129. DOI： 10.16097/j.cnki.1009-6744.2023.05.013.

［10］林兆丰， 李树彬， 孔祥科. 地铁建设对公交系统鲁棒性的影响［J］. 复杂系统与复杂性科学， 2023， 20（1）： 66-73. DOI： 10.13306/j.1672-3813.2023.01.009.

［11］张琳， 陆建， 雷达. 基于复杂网络和空间信息嵌入的常规公交-地铁复合网络脆弱性分析［J］. 东南大学学报（自然科学版）， 2019， 49（4）： 773-780. DOI： 10.3969/j.issn.1001-0505.2019.04.022.

［12］谌微微， 张富贵， 赵晓波. 轨道交通线网拓扑结构模型及节点重要度分析［J］. 重庆交通大学学报（自然科学版）， 2019， 38（7）： 107-113. DOI： 10.3969/j.issn.1674-0696.2019.07.18.