基于需求弹性的多模式铁路客运票价优化模型及算法

摘要：为增强铁路客运市场竞争力、提高其运营收入，对多模式铁路客运票价的多目标系统优化问题进行了研究。采用变分不等式模型对不同铁路客运产品客运需求之间的平衡关系进行描述，采用灵敏度分析的方法给出了多模式铁路客运产品需求弹性的计算方法，并构建了多模式铁路客运的市场需求函数；在此基础上，综合考虑了铁路客运企业的市场需求、客运收入、利润以及旅客出行费用等多个优化目标，提出了多目标双层规划模型来描述多模式铁路客运票价的系统优化问题。最后，采用北京至天津的真实铁路客运数据对提出的模型进行验证。结果表明本文提出的票价优化方法可以有效兼顾客运需求、客运收入以及利润等多个指标，为铁路客运部门在不同市场竞争阶段制定科学合理的铁路客运票价体系提供参考和支撑。

关键词：铁路客运；铁路客运票价；需求弹性；多目标；双层规划

中图分类号：U293.1文献标志码：A文章编号：1002-4026（2024）05-0069-10

开放科学（资源服务）标志码（OSID）：

Optimization model and algorithm for multimodal railway-passenger

transportation fares based on demand elasticity

WANG Hongyin1，YUAN Yuan1， CUI Hongmeng2，ZHENG Xuanchuan3 ， SI Bingfeng2

（1. Zhengzhou Metro Group Co.， Ltd.， Zhengzhou 450000， China；2. School of Systems Science， Beijing Jiaotong University， Beijing 100044， China;

3. Beijing Urban Construction Design &Development Group Co.， Ltd.， Beijing 100037， China）

Abstract∶To improve the competitiveness of the railway-passenger transportation market and increase its operational revenue， this study investigates the multiobjective system optimization issue of multimodal railway-passenger transportation fares. A mathematical model was used to describe the equilibrium relationship among the demands of different railway-passenger transportation products. Sensitivity analysis was performed to provide a calculation method for the demand elasticity of multimodal railway-passenger transportation products， and a market demand function for multimodal railway-passenger transportation was formulated. Considering multiple optimization objectives such as market demand， passenger transportation revenue， and profit of railway-passenger transportation enterprises along with passenger transportation costs， we proposed a multiobjective bi-level planning model for describing the system optimization issue of multimodal railway-passenger transportation fares. Finally， we used real passenger transportation data of the railway line between Beijing and Tianjin to validate the proposed model. The results show that the proposed method can effectively balance multiple objectives such as passenger transportation demand， passenger transportation revenue， and profit， providing reference and support for railway-passenger transportation departments to develop scientifically reasonable fare systems in different market competition stages.

Key words∶railway-passenger transportation; railway-passenger fare; demand elasticity; multi-objective; bi-level planning

随着我国高速铁路的快速发展，客运市场竞争愈加激烈。票价作为主要竞争手段，对国内客运市场的健康发展极为重要。中国铁路总公司对高铁的自主定价权。面对日益激烈的市场竞争，铁路运输企业应该考虑出行需求的差异性，对票价机制进行完善，并建立科学的综合票价体系。

国内外很多学者对铁路客运票价问题进行了研究。例如，Daniel［1］通过对悉尼到堪培拉的客运数据分析，指出铁路客运票价应按客流变化分时段制定，并分别以社会福利最大化和效益最大化为目标建立了票价优化策略；Kaan［2］考虑了旅客的时间价值并构建了基于时间价值的票价优化模型，通过美国新泽西州的铁路客运数据进行了验证；陈建华等［3］分析了铁路客运服务质量对需求的影响，采用交通网络平衡理论构建了基于双层规划的铁路客运票价优化模型；四兵锋等［4］分别考虑了铁路客运中的企业效益和乘客出行两个因素，通过双层规划构建了以市场占有率最大为目标的铁路客运票价优化模型。近些年来，随着我国高速铁路的快速发展，一些学者对高铁客运的票价问题展开研究。例如，陈方遒等［5］基于改进的LSTM（long short term memory networks，长短时记忆网络）模型，提出了考虑现行浮动定价策略的高铁定价模型，以京沪高铁为案例进行了分析；夏阳等［6］构建价格-时空的三维网络，建立了铁路客运票价优化问题的整数线性规划模型，以京沪高铁为例进行了分析；秦进等［7］构建了考虑停车方案的非线性混合整数规划模型来研究高铁动态票价优化问题，以京沪高铁为例对模型进行了验证；闫振英等［8］以高铁客运收益最大化为优化目标，基于偏好序选择行为建立了考虑高铁票价和售票时间窗的非线性规划模型，并给出了求解算法。

尽管这些研究从不同方面对铁路客运票价优化问题进行了研究，但只考虑了公路、民航、铁路等不同客运方式之间的市场竞争，并没有考虑铁路客运内部不同列车服务模式之间的竞争。而事实上，在客运市场竞争中，除了以高铁和民航为代表的不同运输方式之间的竞争，铁路内部也存在动车、高速、直达、普快、特快等多种客运产品。不同的客运产品在价格、行驶速度、服务质量等方面存在差异，这些差异在一定程度上会影响乘客的选择。因此，不同客运产品之间也存在着竞争关系。同时，随着国内客运市场的变化以及铁路客运市场化改革的推进，铁路客运企业参与竞争的目标也更加多元化，而不仅仅局限于某个单一目标。票价对客运市场中的需求起主要作用，票价变化会导致需求的变化，进而影响客运企业的市场份额、收入及利润，并且票价的变化对于这些不同指标的影响存在显著差异，铁路客票定价应在多个优化目标中寻优，或兼顾多目标进行系统优化。然而，目前关于铁路客运票价多目标优化的研究还很少。

在市场竞争中，需求弹性是指需求对其影响因素的敏感程度，反映了相关影响因素发生变化而引起的需求变化率，这一指标在产品价格制定中具有重要作用。在交通领域，关于需求弹性方面的研究主要集中在城市公交方面，例如，Johan［9］通过回归方法研究了公交需求弹性的偏差，计算了美国几个城市的公共交通价格需求弹性；David等［10］分析了城市人口、票价等因素对公交吸引程度的作用机制，同样采用统计方法分析了公交需求弹性；陈伯阳等［11］研究了城市公交价格对其需求的定量关系，并对不同情况下的公交客流需求以及价格需求弹性的变化规律进行了分析。近年来，一些学者对我国铁路客运的需求弹性进行了研究，例如，李文君等［12］采用需求弹性理论分析了我国高铁的需求变化规律，通过实际运营数据研究了企业收入、票价水平及车辆速度等关键因素的需求弹性；韦涛［13］分析了旅客出行需求的时间弹性及购票行为特征，提出了铁路客票销售的需求弹性控制及实施方法；车瑶等［14］引入交叉弹性表示客运产品之间的可替代程度，构建了指数需求函数以描述客运需求与票价之间的关系，并进一步研究了客运产品之间不同可替代程度下的最佳动态票价策略。然而，目前关于铁路需求弹性的研究大多是基于调查数据并采用统计方法来进行分析，这些研究只适用于特定的线路或者区域，而无法将其应用于铁路客运票价优化问题中。

本论文针对以上问题，对某两个城市之间的铁路客运票价优化展开研究。首先，分析了铁路乘客的选择行为，基于用户平衡准则构建了一个变分不等式模型，对不同客运产品客运需求之间的分配关系进行描述，并采用灵敏度分析的方法来表达铁路客运的需求与票价间的定量关系，再通过需求弹性分析给出了多模式铁路客运需求函数，在此基础上，综合考虑了铁路客运需求、票价收入、利润等市场竞争目标，构建了多目标双层规划模型来描述多模式铁路客运票价系统优化问题，并设计了求解算法。最后，采用北京到天津之间的实际铁路客运数据对模型及算法进行了验证。

1基于需求弹性的多模式铁路客运需求函数

由于本文针对同一起讫点建模，故假定在某两个城市之间的铁路客运共有N种模式，铁路客运总需求Q固定，不同模式的客运需求满足以下基本条件：

∑Nn=1qn=Q，（1）

式中，qn表示第n种客运方式的需求量。

旅客在确定铁路作为城际出行方式后，会根据各种条件选择铁路客运方式，比如高铁、动车、普通列车等。采用广义出行费用定量表达铁路客运产品之间的竞争差异性，广义出行费用是乘客对出行过程的整体评价，是旅客进行铁路客运产品选择的主要依据。本文根据铁路运输供给条件和乘客自身感受，将各种影响因素分为两类指标：第一类指标是可以量化的固定费用，包括列车运行时间和票价等；第二类指标是随情景变化且难以量化的因素，如舒适性、安全性、排队检票时间、排队上车时间等。

第二类指标难以直接量化，却与客运量有一定的关系［15］。如果客运量大，可能造成拥挤，存在一定的安全隐患，乘客的排队时间、找座时间也会增加，乘客在整个乘车过程中的舒适性随之降低，这些都会增加乘客的广义出行费用。第二类指标与客运量之间通常是反函数关系［16］：

Cn=Cn（qn），（2）

式中，Cn表示第n种客运方式的第二类综合指标。

本文将旅客的广义出行费用表示为：

GCn=αCn+βTn+Pn， n，（3）

式中，GCn表示客运方式n的广义费用；Tn和Pn分别表示第n种客运方式的列车运行时间和票价；α和β为参数。

按照消费者行为理论，旅客一般会选择广义费用最小的铁路客运方式，同时，旅客的选择行为又会受到其他旅客选择的影响。比如，假定某种铁路客运方式的广义出行费用低，此时，所有旅客都会选择该种方式，对应的客运需求就会上升，基于式（3），旅客广义费用也会随之上升，上升到一定程度时，就会有部分旅客转移到其他铁路客运方式，而其他客运方式的费用同样会随其需求的增长而上升。因此，在不同的铁路客运产品之间存在竞争和博弈关系。根据市场平衡原理，在长期旅客出行选择行为的作用下，客流需求会在不同的铁路客运产品间达到平衡状态，这就是交通系统中的用户平衡状态，可用下式进行描述：

GCn=Cmin ，

GCn≥Cmin ， qn>0qn=0，n，（4）

式中，Cmin表示平衡状态下的最小出行费用。

根据文献［16］，可通过求解变分不等式模型（5）得到满足用户平衡条件（4）的多模式铁路客运需求：

GC（q*）T（q－q*）≥0，（5）

式中，q*表示变分不等式模型（5）的解，q=q1，q2，…，qNT，q*=q*1，q*2，…，q*NT，GC（q*）=GC1（q*），GC2（q*），…，GCN（q*）T。

根据变分不等式的灵敏度分析方法，可将票价作为模型（5）的扰动参数，即当票价变动时，各客运方式的广义费用会随之变化，同时，各方式客运需求也会随之改变。

下面给出应用灵敏度分析方法计算多模式铁路客运需求弹性的过程。

首先，在给定的铁路票价P（0）n下，变分不等式模型（5）解的一阶必要条件可写为［17］：

GC（q*）－μ=0，（6）

Q=ΔTq*，（7）

式中，μ为基本守恒条件（1）的拉格朗日乘子向量；Δ=（1，…，1）T。

设y=q*，μT，用Jy表示公式（6）和（7）对于q，μ的雅克比矩阵，用JPn表示公式（6）和（7）对参数Pn的雅克比矩阵，可得出［17］：SymbolQC@yPn=J－1y·（－JPn）。（8）

根据式（8），就能计算出不同铁路客运方式下的客运需求对其票价的导数，即：qn/Pn。参考需求弹性的定义，铁路客运的需求弹性可以通过式（9）进行计算：

En=qnPn·P（0）nq*n，（9）

式中，q*n表示在给定的铁路票价P（0）n下第n种客运方式的满足用户平衡条件（4）的需求量。

根据铁路客运的需求弹性，就可以得出多模式铁路客运的需求量和票价之间的函数关系，基于式（9），应用泰勒展开式可得到如式（10）的多模式铁路客运需求函数：

qn（Pn）≈q*n1+En（P（0）nPn－1），n。（10）

2铁路客运票价多目标系统优化模型

随着我国铁路系统市场化改革的加快，票价改革已被提到越来越重要的位置。同时，由于我国铁路客运还承担着社会公益服务的职能，这在一定程度上也限制企业收入最大化。目前，对于铁路客运企业来说，在市场竞争中，客运量、客运收入以及企业利润是衡量铁路客运经济效益的三大指标，这三个指标可分别表示如下：

F1=∑Nn=1qn（Pn），（11）

F2=∑Nn=1qn（Pn）·Pn，（12）

F3=∑Nn=1qn（Pn）·（Pn-pminn×ln），（13）

式中，pminn和ln分别表示第n种铁路客运方式的最低票价率以及运营里程，pminn×ln代表了第n种铁路客运方式的最低客运成本。

客运成本是铁路票价制定的主要依据，而基于铁路客运社会公益性，政府会对铁路票价进行限定。假定宏观政策无较大变动，则铁路客运票价应在政府最高限价和铁路客运成本之间进行制定。即：

pminn×ln≤Pn≤Pmaxn（14）

式中，Pmaxn表示第n种铁路客运方式的政府限价。

在本文中，综合考虑了铁路客运企业的多种经济目标和旅客出行费用两方面的因素，采用基于多目标双层规划方法来描述多模式铁路客运的票价优化问题。其中，铁路客运企业在政府规定的票价范围内制定满足不同优化目标的最佳票价为上层优化问题，而下层优化问题则对铁路客运总需求在不同客运方式之间的平衡关系进行描述。

本文提出的多目标双层规划模型如下：

max（F1，F2，F3），（15）

s.t.pminn×ln≤Pn≤Pmaxn，n，（16）

qn（Pn）≈q*n1+En（P（0）nPn－1），n，（17）

其中，约束条件（17）是通过求解下层模型得到的，下层模型为公式（5）所示的变分不等式问题，即GC（q*（P））T（q－q*（P））≥0，其中P=P1，P2，…，PNT。

在双层规划模型中，上层优化问题的决策变量（即不同客运方式的票价）与下层优化问题的决策变量（即不同客运方式的客运需求量）是相互作用的。在其他条件不变的情况下，提高某种铁路客运的票价水平，那么，该铁路客运的需求必然转移到其他方式上；反之，如果降低某客运方式票价，则该方式就会吸引更多的客运需求。一方面，乘客总希望选择最佳的客运方式来降低自身的出行费用；另一方面，铁路客运企业则希望通过票价和市场需求来达到其经济目标。这两者存在相互作用机制，最终会达到一个均衡点，即双层规划模型的最优解。需要注意的是，本文提出的模型是针对某两个城市之间的铁路客运票价进行优化，不同的城市需要重新对应求解。

3求解算法

通常，双层规划问题是一个NP-hard问题，导致双层规划问题求解困难的主要原因是非凸性。目前，求解双层规划的算法都是启发式的，归纳起来，可分为五类，即K-T法、极点搜索法、下降法、非数值优化方法以及直接搜索法，其中下降法在解决实际问题中应用较为广泛［16］。本文采用下降法来求解多目标双层规划问题如公式（15）～（17），该方法的基本思想为：通过求解下层变分不等式模型，根据需求弹性得到需求函数（10），将其代入到上层多目标规划问题中，则双层问题转化为单层多目标优化问题，可用已有的方法求解得到最优解，最优解即为新的多方式客运票价，再对下层问题求解，可以得到新的需求函数，重复计算，最后可得到双层多目标规划的最优解。求解算法的具体步骤如下：

步骤1初始化，设置初始的铁路客运票价P（0）n，n，设置迭代次数k=0；

步骤2根据当前的铁路票价P（k）n，n，求解下层变分不等式模型得到均衡条件下的不同铁路客运方式的需求量q*（k），n；

步骤3通过需求弹性分析得到需求函数qn（Pn）表达式，将其代到上层多目标规划模型中，求解得出新的铁路客运票价ω（k）n，YfypTzVi3nSkcaS5qwijPJtKwNz+9u2P68ckVvXlK18=n；

步骤4根据式（18）对票价进行迭代

P（k+1）n=P（k）n+1k+1（ω（k）n－P（k）n），n;（18）

步骤5收敛性判断，如果max{|P（k+1）n－P（k）n|}≤ε或者k=M，则停止迭代；否则令k=k+1，转到步骤2，其中M表示最大迭代次数，ε表示迭代精度。

主要有两种思路来求解上层的多目标铁路票价优化问题：一种是在多个单目标的定价方案中进行选择，单目标定价方案指的是企业根据唯一优化目标制定的票价决策。如认为在铁路峰值期应该以票价收入为目标定价，非峰值期应以利润为目标定价，新线路开通宜根据客运需求目标定价等［18］；或者根据定价部门的要求将不同目标的定价方案进行对比，如以利润、收益、客运需求量作为定价目标［19］。这种思路不会涉及多目标之间的权衡与取舍，而是将单一目标定价结果制定的最佳方案进行对比。另一种思路则是多目标定价方案，即企业同时考虑多个优化目标来制定票价策略，线性加权和法较为常见，该方法是把每个目标赋权后的加和当做目标函数，现有的多目标定价研究大多采用线性加权和方法［20-21］。

本文采用线性加权和法来求解上层多目标优化问题。加权法需要事先给定每个目标权因子，权因子与约束参数的设定受到具体应用中交通政策、决策者偏好等多种因素的影响，是较为复杂的问题。线性加权模型是最为常见的妥协模型［22-23］，该模型对目标函数进行加权求和，对于本文所提出的上层多目标规划问题，其目标函数可转化为如式（19）的线性加权和模型：

max∑3i=1λiF-i，（19）

其中，λ1、λ2、λ3为非负实数，且λ1+λ2+λ3=1，表示不同优化目标的权重；F-i表示各优化目标经过归一化处理后的目标值，可采用min-max归一化方法。

求解变分不等式模型的常用算法为松弛算法，该算法的基本思想为：在第i次迭代中，用当前解对向量函数GC（q1，q2，…，qN）进行对角化处理，即假定向量q=q1，q2，…，qN中只有一个变量为决策变量，而其他变量为常数，则函数GC（q1，q2，…，qN）的Hession阵SymbolQC@

qGC（q）是对角阵，对应的优化子问题被称为对角化子问题，该子问题可以通过数学优化算法进行求解。

下面给出给出求解变分不等式问题（5）的一般过程［16］：

步骤1初始化，设定一个不同铁路客运需求的初始可行点q（0）∈{q（0）｜Q=δTq（0）}，令迭代次数i=1；

步骤2松弛化，求解如下的数学优化子问题

min Z（q（i））=∑Ni=1∫qn（i）0（αCn+βTn+Pn）dx，（20）

s.t∑Nn=1qn（i）=Q，（21）

可采用Frank-Wolfe算法或MSA算法进行求解，假设最优解为q*（i）；

步骤3收敛性检查，如果满足收敛性，则停止；否则，令i=i+1，转步骤2。

4算例分析

采用北京到天津之间的铁路客运数据来对模型和算法进行验证。目前，北京至天津的铁路客运方式共有5种：C列车、D列车、G列车、KTZ列车和普通列车，将其分别用1～5的数字表示。北京至天津京哈线的运距为137 km，京津城际高铁运距为120 km，根据2017年北京铁路局的统计资料，平均每日北京到天津的发送总客流Q=45 128人次。北京到天津不同的铁路客运方式的市场分担率、客运量、平均时耗和平均票价等数据由表1给出。

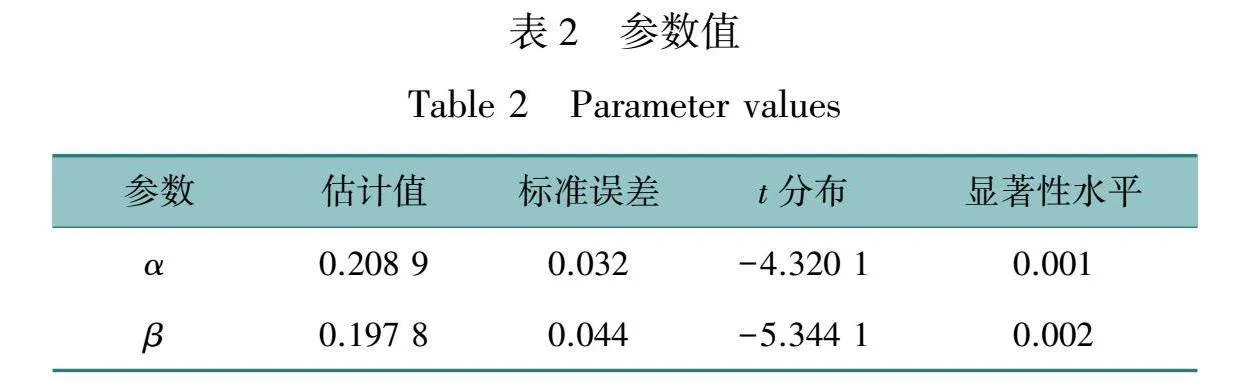
本例对约束（2）采用对数函数Cn=ln qn的形式。根据上面的数据采用回归方法对参数α和β进行估计，表2给出了计算结果。

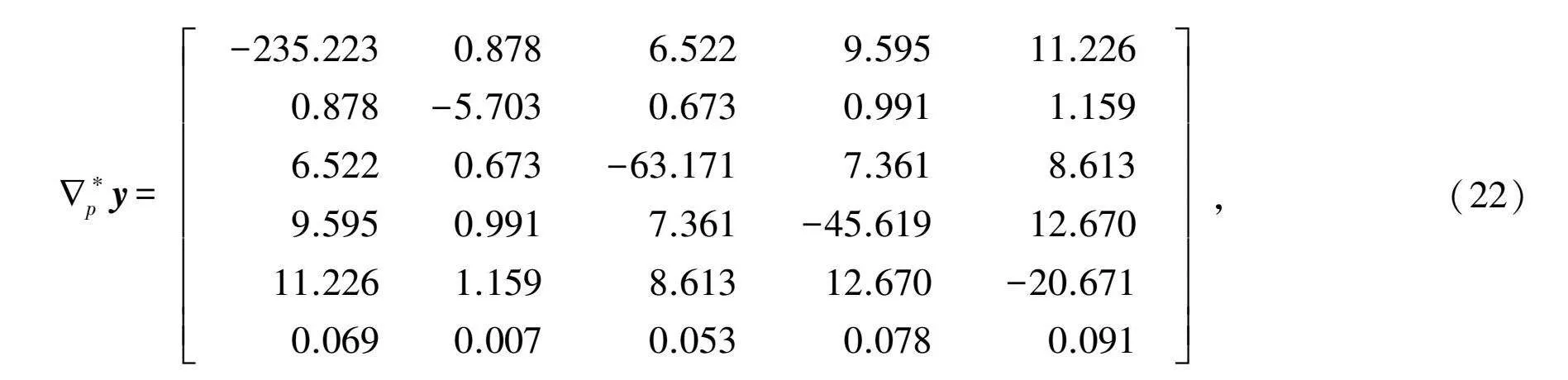
基于以上数据，采用松弛算法求解下层变分不等式模型得出在均衡条件下的不同铁路客运方式的需求量q*=（34 124.21， 378.59， 6 242.38， 4 023.44， 359.38）。根据灵敏度分析方法，计算得出如式（22）矩阵：SymbolQC@*py=-235.2230.8786.522 9.595 11.226 0.878-5.703 0.6730.9911.1596.5220.673 -63.1717.361 8.6139.5950.9917.361-45.619 12.67011.226 1.159 8.613 12.670 -20.6710.0690.0070.053 0.0780.091 ，（22）

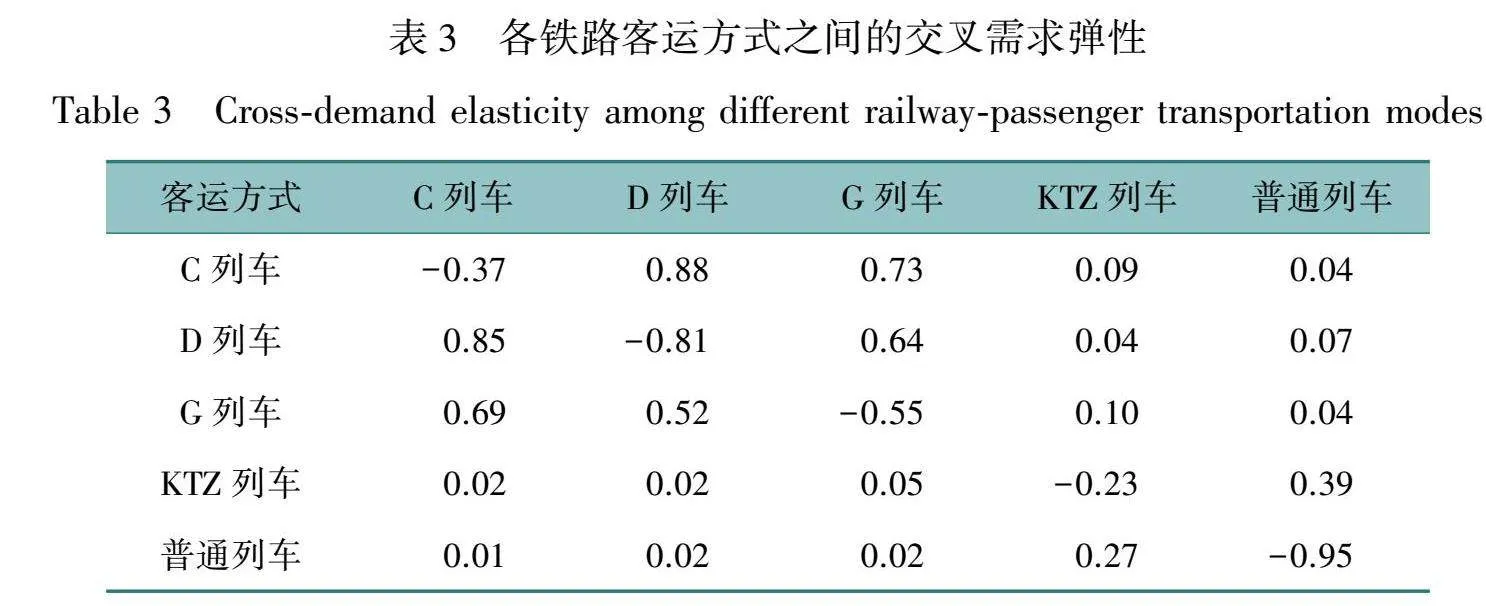
再根据需求弹性计算公式（9），计算得到不同铁路客运方式之间交叉需求弹性，如表3所示。

下面分析随着不同列车票价的变化，铁路客运需求、客运收入以及利润的变化趋势。图1给出了在其他条件保持不变的情况下，当北京到天津之间不同列车的票价从30元增加到70元时，铁路客运需求、收入以及利润的变化趋势。

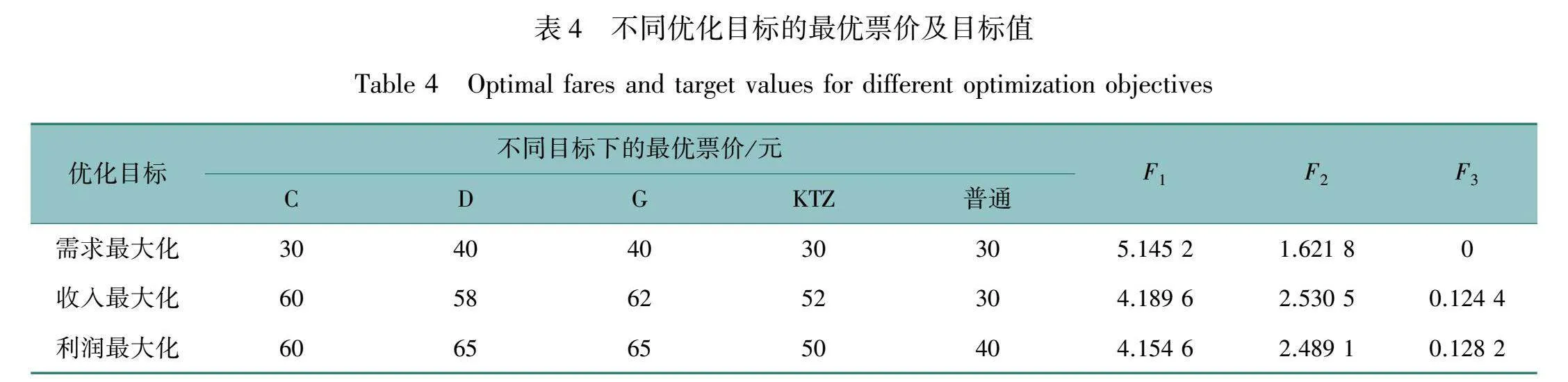
可以看出，对于铁路客运需求来说，随着各类旅客票价的提高，需求是持续下降的，这符合市场规律，无论哪一类旅客列车的票价提高，都会降低铁路客运需求，因此，当各类客运方式的票价在最低票价水平时，铁路客运需求会达到最大。对于铁路客运收入来说，在票价约束范围内，随着C列车票价的上升，铁路客运收入持续上升，随着普通列车票价的上升，铁路客运收入持续下降，而随着D列车、G列车和KTZ列车票价的上升，铁路客运收入先上升到一个峰值后再下降。对于铁路客运利润指标而言，随着C列车、D列车、G列车、KTZ列车票价的上升而持续上升，随着普通列车票价的上升，铁路客运利润先上升然后再下降。因此，在铁路客运市场中，并不是仅通过提高票价就可以增加铁路客运收入或利润，而是存在一个合适的客运票价体系，可以保障在其他因素不变的条件下，实现铁路客运的不同优化目标。表4给出了在约束条件下不同优化目标的最优票价以及对应的目标值。其中优化目标用F1、F2和F3表示，分别代表客运量、客运收入以及企业利润这三个指标。

从表中的计算结果可以看出，在不同的优化目标下，铁路客运票价具有不同的优化结果。如果只考虑市场需求，则票价在最低票价时，铁路客运需求达到最大，而此时对应的铁路客运收入并不是最好的，而利润则为0；如果只考虑客运收入最大化，此时铁路客运需求会下降，同时，利润也不是最佳的；而如果只考虑利润的话，则需求会更低，客运收入也会下降。因此，在制定科学合理的铁路客运票价体系中，需要在这些优化目标中寻找一个平衡值，这种平衡值取决于在不同市场竞争阶段铁路客运部门对于不同目标的侧重情况。

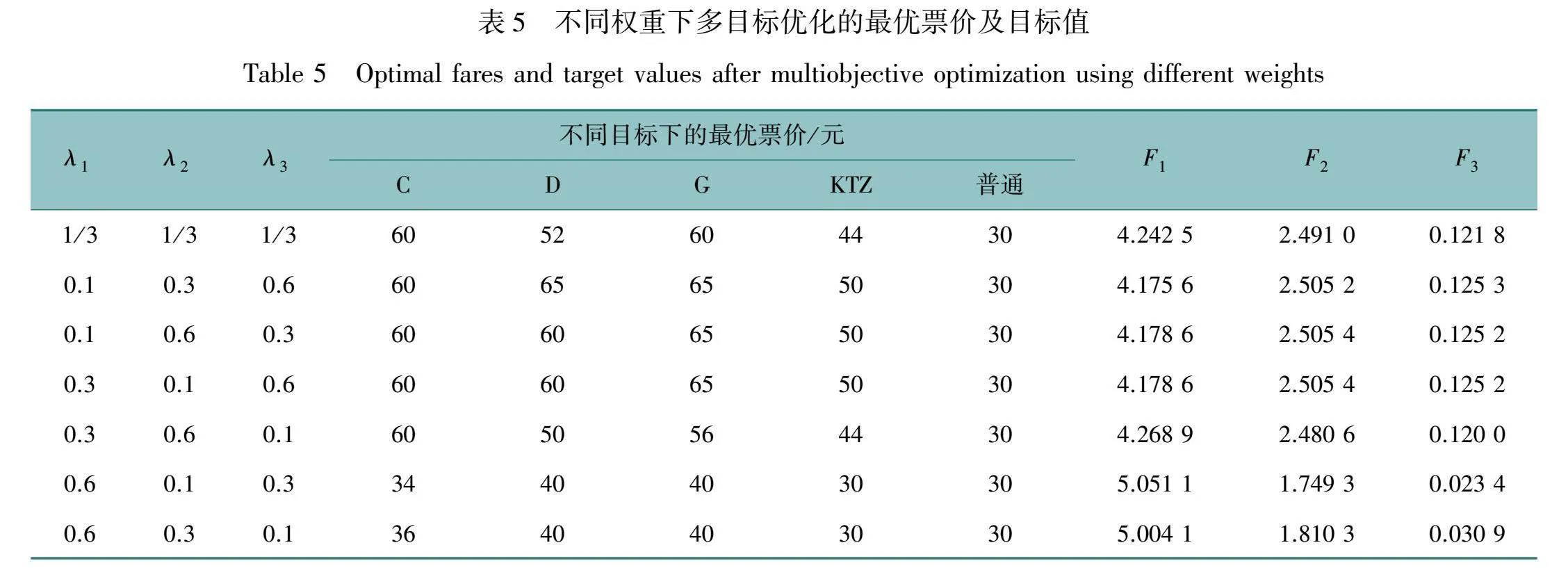
下面来分析多目标综合优化的计算过程，假定给定这三个优化目标所对应的权值λ1、λ2、λ3均取值为1/3，求解上层优化模型（19）可得到C列车、D列车、G列车、KTZ列车和普通列车的最优票价分别为60元、52元、60元、44元和30元。通过调整各个优化目标的权重，可以得到在不同市场阶段的铁路客运票价的优化结果，表5给出了在不同权重值条件下所得到的铁路客运票价优化结果。

如表5所示，如果优化目标侧重于市场需求（λ1=0.6），则票价趋于低价，此时若能更多地兼顾客运收入（λ2=0.3），就可以保障铁路客运需求趋向最大的同时，铁路客运收入和利润也不是最差的；通过对比可以发现，在这种情况下，更关注客运收入（λ2=0.3）比更关注利润（λ3=0.3）能获得更良好的经济效益，但无论何种权重分配，客运收入和利润都比只考虑市场需求的单目标优化结果要高（客运收入增加18.85万元，利润增加3.09万元）。同样的，如果客运收入的权重较大（λ2=0.6），市场需求和利润的侧重点不同，不同形式的客运方式的票价会有不同的组合，但都可以在保证收入接近最大的同时，兼顾铁路客运需求不会过少；与只考虑客运收入的单目标优化结果相比，市场需求增加1.89%，利润增加0.67%。而如果更重视利润的话（λ3=0.6），则票价应适当提高，此时更多地兼顾市场需求（λ1=0.3）可以更好地对客运收入和需求进行优化；与只考虑利润的单目标优化结果相比，需求增加0.58%，客运收入增加0.65%。

综上所述，在不同的权重下，多模式铁路客运票价具有不同的优化结果，这些优化结果介于单目标优化结果之间，使铁路客运票价优化在侧重某一个目标的同时兼顾其他优化目标。因此，通过本文提出的优化模型和算法，可以为铁路客运部门在不同市场竞争阶段制定科学合理的铁路客运票价体系提供参考和支撑。

5结论

本文考虑了不同铁路客运产品客运需求之间的分离关系，利用变分不等式对满足用户平衡的多模式铁路客运需求分配问题进行描述，基于经济学中的需求弹性的概念分析了客运需求与票价之间的定量关系，综合考虑了市场需求、企业收入及利润等因素，构建了多目标双层规划模型来描述市场竞争下的铁路客运票价优化问题，并设计了求解算法，应用京津城际的运营数据对模型和算法进行了验证。

尽管本文在多模式铁路客运票价优化方面进行了一定的探讨性工作，但所提出的模型方法仍存在可以完善的地方，比如：（1）本文的模型并没有考虑旅客类型的不同，而在现实中，不同类型的旅客在选择出行方式的时候有不同的标准，在后续的研究中可以考虑面对不同类型的旅客提出更加细化的铁路客运票价优化方法；（2）在本文的模型中，假定铁路客运的总需求是给定且不变的，而在现实中，铁路客运的主要竞争对象是公路客运以及航空客运，如何将铁路客运的需求视为弹性变量，构建更为普适的铁路客运需求模型和弹性计算方法，也是未来研究应该考虑的问题；（3）由于数据资源有限，在本文的算例分析中，采用的是2017年北京铁路局的统计数据，这可能会对研究结论的可靠性产生影响，在后续的研究中可以考虑收集更丰富、全面的数据进行进一步的实验分析；（4）本文仅以北京到天津的铁路数据为例进行优化，在后续的研究中，可以考虑扩大样本范围，探究不同城市之间的票价优化差异，并观察运营里程对优化结果的影响。

参考文献：

［1］HENSHER D A. A practical approach to identifying the market potential forhigh speed rail： a case study in the Sydney-Canberra corridor［J］. Transportation Research Part A： Policy and Practice， 1997， 31（6）： 431-446. DOI： 10.1016/s0965-8564（97）00001-3.

［2］OZBAY K， YANMAZ-TUZEL O. Valuation of travel time and departure time choice in the presence of time-of-day pricing［J］. Transportation Research Part A： Policy and Practice， 2008， 42（4）： 577-590. DOI： 10.1016/j.tra.2007.12.002.

［3］陈建华， 高自友. 多模式条件下需求变动时铁路客票价格制定的优化模型及算法［J］. 交通运输系统工程与信息， 2001， 1（4）： 299-305. DOI： 10.16097/j.cnki.1009-6744.2001.04.005.

［4］四兵锋， 高自友. 综合运输体系下铁路客运市场的优化策略模型及算法［J］. 铁道学报， 2005， 27（5）： 6-10. DOI： 10.3321/j.issn： 1001-8360.2005.05.002.

［5］陈方遒， 景云， 郭思冶. 基于旅客出行选择特征的高速铁路浮动定价策略研究［J］. 铁道学报， 2022， 44（6）： 11-17. DOI： 10.3969/j.issn.1001-8360.2022.06.002.

［6］夏阳， 王怀相， 周茵， 等. 基于价格—时空网络的高速铁路票价优化研究［J］. 铁道学报， 2022， 44（7）： 11-20. DOI： 10.3969/j.issn.1001-8360.2022.07.002.

［7］秦进， 张子璇， 黎熙琼， 等. 高铁动态票价与停站方案联合优化方法［J］. 铁道科学与工程学报， 2023， 20（3）： 812-823. DOI： 10.19713/j.cnki.43-1423/u.t20220599.

［8］闫振英， 王宇， 韩宝明， 等. 基于偏好序的高铁票价与售票时间窗联合优化［J］. 交通运输系统工程与信息， 2022， 22（5）： 164-173. DOI： 10.16097/j.cnki.1009-6744.2022.05.017.

［9］HOLMGREN J. Meta-analysis of public transport demand［J］. Transportation Research Part A： Policy and Practice， 2007， 41（10）： 1021-1035. DOI： 10.1016/j.tra.2007.06.003.

［10］HENSHER D A. Assessing systematic sources of variation in public transport elasticities： some comparative warnings［J］. Transportation Research Part A： Policy and Practice， 2008， 42（7）： 1031-1042. DOI： 10.1016/j.tra.2008.02.002.

［11］陈伯阳， 蒋明清， 四兵锋， 等. 多方式竞争下城市公交需求价格弹性实证分析［J］. 交通运输系统工程与信息， 2016， 16（4）： 241-247. DOI： 10.3969/j.issn.1009-6744.2016.04.035.

［12］李文君， 符卓. 高速铁路客运需求弹性分析［J］. 铁道科学与工程学报， 2016， 13（11）： 2115-2124. DOI： 10.19713/j.cnki.43-1423/u.2016.11.003.

［13］韦涛. 铁路客票销售策略的需求弹性控制方法研究［J］. 铁道运输与经济， 2018， 40（12）： 24-28. DOI： 10.16668/j.cnki.issn.1003-1421.2018.12.05.

［14］车瑶， 符卓， 袁雪莹. 考虑高铁客运产品间交叉弹性的动态票价策略［J］. 铁道科学与工程学报， 2020， 17（1）： 25-30. DOI： 10.19713/j.cnki.43-1423/u.T20190434.

［15］李树彬， 党文修， 傅白白. 制定铁路旅客票价的策略模型与求解算法研究［J］. 山东科学， 2014， 27（1）： 73-77. DOI： 10.3976/j.issn.1002-4026.2014.01.013.

［16］高自友， 四兵锋. 市场经济条件下铁路旅客票价系统分析： 优化模型与求解方法［M］. 北京： 中国铁道出版社， 2002.

［17］四兵锋， 高自友. 铁路旅客票价与客流量之间的灵敏度分析［J］. 铁道学报， 1999， 21（4）： 13-16. DOI： 10.3321/j.issn： 1001-8360.1999.04.003.

［18］van VUUREN D. Optimal pricing in railway passenger transport： theory and practice in The Netherlands［J］. Transport Policy， 2002， 9（2）： 95-106. DOI： 10.1016/s0967-070x（02）00005-7.

［19］BORNDRFER R， KARBSTEIN M， PFETSCH M E. Models for fare planning in public transport［J］. Discrete Applied Mathematics， 2012， 160（18）： 2591-2605. DOI： 10.1016/j.dam.2012.02.027.

［20］YANG H J， ZHANG A M. Effects of high-speed rail and air transport competition on prices，profits and welfare［J］. Transportation Research Part B： Methodological， 2012， 46（10）： 1322-1333. DOI： 10.1016/j.trb.2012.09.001.

［21］TALEBIAN A， ZOU B. A multi-stage approach to air-rail competition： focus on rail agency objective， train technology and station access［J］. Journal of Rail Transport Planning & Management， 2016， 6（1）： 48-66. DOI： 10.1016/j.jrtpm.2016.01.001.

［22］YIN Y F.Multiobjective bilevel optimization for transportation planning and management problems［J］. Journal of Advanced Transportation， 2002， 36（1）： 93-105. DOI： 10.1002/atr.5670360106.

［23］胡毓达. 多目标规划有效性理论［M］. 上海： 上海科学技术出版社， 1994.