数学之美 无处不在

袁亚湘，湖南资兴人，中国科学院院士，中国科学院数学与系统科学研究院研究员。现任全国政协常委、中国科协副主席。他给本报题词，并在《数学漫谈》一书中普及了数学在生产生活中的重要作用。以下摘录该书部分精彩内容。

几乎所有的数学家都认为数学是优美的。学过泛函分析的学生都知道著名的Hahn-Banach定理。这个定理的提出者巴拿赫曾说过，“数学是人类最美及最有力的创造”。

数学的美体现在很多方面，其中之一是对称美。古希腊著名哲学家亚里士多德曾说过：“数学科学特别表现次序、对称和限制，这些是美的最高形式。”

几何中很多图形具有对称性，比如平面上的长方形、圆形、等腰三角形，立体图形中的立方体、圆柱体、球等。平面上的对称图形有一条或多条对称轴，而对称立体图形则有一个或多个对称面。高维空间中人们所研究的不少集合也有对称性。更有意思的是，还有分数维空间。分形作为欧氏空间中的自相似子集，其维数通常都不是整数。大多数分形的图形都非常惊艳。

代数中也有大量的对称，从小学的a乘b等于b乘a，到中学的对称多项式，乃至大学的对称矩阵、对称群等等都是对称的例子。

数学的另一种美是比例美。人们喜欢把美好的东西形容为“如金子般闪闪发光”。因此“中末比”这一比例被德国数学家马丁·欧姆命名为“黄金分割”比例。20世纪 60年代，我国著名数学家华罗庚推广优选法，主要就是普及利用黄金分割的单因素优化方法。该方法俗称“0.618方法”。正因为如此，在我国，黄金分割比例通常是指“中末比”的倒数0.618。

简洁美也是数学的美之一。很多数学公式非常简洁。譬如欧拉公式：e iπ+1=0。一个短短的公式就把数学中的几个最重要的量：欧拉常数e、虚数i、圆周率π，以及1和0都联系在一起了。

数学的美还体现在数的奇妙。如勾股定理：直角三角形的三条边分别是3、4、5，三条边长满足3的平方加上4的平方等于5的平方。如果我们把勾股定理中的平方换成三次方，就找不到这样的整数组满足规律了。

另外一个神奇的数论例子是哥德巴赫猜想，简称为“1+1”。陈景润于1966年证明了“1+2”，这一结果至今仍是哥德巴赫猜想问题的最佳进展。

干净、整洁也是美的重要因素。英国哲学家、医生、自由主义之父约翰·洛克将数学证明的坚实、干净和无瑕比作钻石，可见他对数学证明的欣赏。

印度作家夏琨塔拉·戴维曾说过：“没有数学，你什么也不能做。你周围所有的东西都是数学，你周围所有的东西都是数字。”

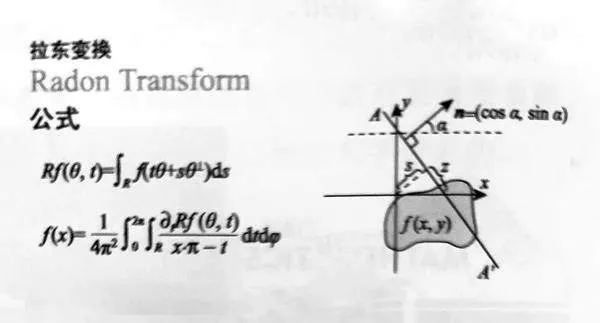
例如CT成像。2020年全世界各地暴发了新冠疫情。CT肺部影像是帮助医生确诊该病的重要依据。CT成像的原理其实是数学中的拉东变换。拉东是奥地利数学家，他在变分法、微分几何、测度论等方面有重要贡献，拉东变换就是以他的名字命名的。

数学还在土木工程中发挥了重要作用。无论是桥梁、水坝还是高层建筑，在设计中都需要用到有限元方法对其结构进行应力分析。

在地球勘探中，为什么我们能知道看不见、摸不着的地下结构，了解油、气、煤等资源的分布情况呢？除了钻井直接取样这样的高成本方法，更多的是依赖间接的方法，即地球物理勘探，而其核心则可以归结于数学中的求解微分方程反演问题。

数学在天气预报中同样发挥着核心作用。现代天气预报的准确性不仅是依赖先进的探测技术（如卫星、雷达），更需要依靠先进的数值天气预报模式以及快速的计算方法。而后者在本质上都是数学问题。我国著名气象学家、应用数学家曾庆存曾获得2019年度的国家最高科学技术奖。他曾任中国工业与应用数学学会理事长。他也是世界上第一个用原始方程进行天气预报的科学家。

在航空领域，飞机的外形设计、航空发动机的设计等等最终都是要解决数学问题。这些问题实质是复杂的流体力学问题。在飞机设计中，数学数值方法的引入可以大大减少风洞实验的次数，从而极大地缩小设计周期和降低成本。

在航天领域，数学同样也起着至关重要的作用。飞行轨道选择、推力规划方案制订、航天器有效载荷布局设计等等都有赖于数学方法。

在大数据、人工智能等领域的问题，其核心几乎都是数学问题。例如，通过机器自动识别手写阿拉伯数字可以自动识别信封上的邮政编码，提高分拣效率。而通过机器学习的手段“训练”计算机“识别”不同的手写数字本质上就是利用已有数据建立分类模型并对新数据进行分类。同样地，语音识别、指纹识别、虹膜识别等问题的核心都可以归结为数学上的优化问题。

自动导航和自动驾驶等能够得以实现，实质都是人类利用数学的方法和手段训练计算机、编写程序，使得计算机拥有这些能力。其中的道路规划，无论是路径最短还是时间最短，都可以归结为图与网络流的优化问题。

数学在图像分析和图像处理的发展中起着关键作用。比如，图像去噪实际上就是求解稀疏优化问题。我们可以使照片更清晰。压缩感知技术是用最少的存储单位记录尽可能清晰的图像。这个问题在科学、工程以及国防等诸多方面有重要应用，该问题的核心是求解一个大规模（变量个数几千万甚至上亿）的线性方程组问题，并且希望求得的解尽可能稀疏（即尽量多的分量为零）。

微分几何这样的纯数学在图像处理中也发挥着巨大作用。传统的肠镜检查往往给病人带来痛苦和不适，让人望而却步。而虚拟肠镜技术利用CT扫描获得断层图像，经过分割和三维重建，即可得到肠子的三维模型。在物理上类似于把肠子给切割抻开，从而在二维平面上进行病理检测。这种技术就是利用了数学的里奇流作为工具将弯曲的曲面保角地变换到平面上。

在通信中，数学也起着至关重要的作用。通信编码方式、天线设计、通信资源优化配置等本质上都是数学问题。我国在5G领域处于国际领先地位。而5G标准正是基于土耳其数学家阿勒坎提出的极化码理论。

在战争中，能否破译敌方密码对战争的走势影响巨大。事实上，无论密码设计还是密码破译都是数学问题。

谈到管理科学、金融经济等领域的发展，数学更是厥功至伟。金融衍生产品的定价、投资理财等本质上都是数学问题，涉及随机分析、统计、微分方程、运筹，等等。

生命科学中的许多重要问题，如蛋白质折叠、基因比对、药物设计等都需要利用数学方法。蛋白质折叠的过程和最终结构都可以通过数学方法进行模拟和预测。

总之，数学的应用随处可见。