基于高双折射侧边抛磨光子晶体光纤的表面等离激元共振双参量传感器

摘" 要： 利用表面等离激元共振（SPR）技术设计了一款高双折射光子晶体光纤（PCF）传感器，可以实现宽范围的双参量高灵敏度传感.采用侧边抛磨的结构，内部空气孔呈三角晶格排列.金纳米层涂覆在抛磨面直接与待测物接触作为测量折射率RI的通道，更加方便检测工作的进行，靠近纤芯的椭圆孔内充满氯仿用来探测温度.两个独立的通道以及由非对称引入的双折射可以确保独自测量折射率和温度的变化，解决了交叉灵敏度问题.借助全矢量有限元软件COMSOL Multiphysics，灵活使用散射边界条件可以很好的对光子晶体光纤传感器的光学特性进行数值分析研究.实验结果表明，文中提出的传感器可以测量折射率范围为1.32～1.39，温度范围是20～60℃，在500～1100 nm的波长范围内可以观察到明显的表面等离激元共振效应.为了进一步分析该结构的性能，对主要结构参数（抛光面金膜厚度m1、Ta2O5厚度m2、中心空气孔直径d1以及占空比）做了研究分析.仿真结果得到折射率传感下的平均波长灵敏度5 700 nm/RIU，最大波长灵敏度13 200 nm/RIU，最大振幅灵敏度818.44 RIU-1，传感器的折射率分辨率为1.75×10-5RIU.温度传感范围为20～60℃，得到最大波长灵敏度为2.6 nm/℃，最大振幅灵敏度为0.363 ℃-1，以及传感器的温度分辨率为3.84×10-2 ℃.该工作对于高灵敏度、实时、分布式、多参量测量SPR传感器的设计和实现具有指导意义.

关键词： 光子晶体光纤；表面等离激元共振；高双折射；折射率传感；温度传感

中图分类号：O441.6""" 文献标志码：A""""" 文章编号：1673-4807（2024）01-111-08

DOI：10.20061/j.issn.1673-4807.2024.01.017

收稿日期： 2022-03-07""" 修回日期： 2021-04-29

基金项目： 国家自然科学基金项目（11791240178）

作者简介： 裴俊凯（1997—），男，硕士研究生

Symbolj@@ 通信作者： 周青春（1964—），男，教授，研究方向为凝聚态物理. E-mail： zhouqc@just.edu.cn

引文格式： 裴俊凯，周青春，王颖.基于高双折射侧边抛磨光子晶体光纤的表面等离激元共振双参量传感器［J］.江苏科技大学学报（自然科学版），2024，38（1）：111-118.DOI：10.20061/j.issn.1673-4807.2024.01.017.

Surface plasmon resonance dual parameter sensor based onhigh birefringence side polishing photonic crystal fibers

PEI Junkai， ZHOU Qingchun*， WANG Ying

（School of Science， Jiangsu University of Science and Technology， Zhenjiang 212100， China）

Abstract：A high-birefringence photonic crystal fiber sensor is designed using surface plasmon resonance technology， which can realize a wide range of dual-parameter high-sensitivity sensing. The structure is polished on the side， and the internal air holes are arranged in a triangular lattice. The gold nano layer is coated on the polishing surface and directly contacts the object to be measured as a channel for measuring the refractive index， which is more convenient for the detection work. The oval hole near the fiber core is filled with chloroform to detect the temperature. Two independent channels and the birefringence introduced by asymmetry can ensure independent measurement of refractive index and temperature changes， which solves the problem of cross sensitivity. With the help of the full-vector finite element software COMSOL Multiphysics， the flexible use of scattering boundary conditions can perform numerical analysis and research on the optical characteristics of photonic crystal fiber sensor. The experimental results show that the sensor proposed in this paper can measure the refractive index range of 1.32～1.39， the temperature range of 20～60℃， and the obvious surface plasmon resonance effect can be observed in the wavelength range of 500～1 100 nm. In order to further analyze the performance of the structure， the main structural parameters （gold film thickness m1， Ta2O5 thickness m2， central air hole diameter d1， and duty cycle） are studied and analyzed. The simulation results show that the average wavelength sensitivity of refractive index sensing is 5700nm/RIU， the maximum wavelength sensitivity is 13200nm/RIU， the maximum amplitude sensitivity is 818.44RIU-1， and the refractive index resolution of the sensor is 1.75×10-5RIU. The temperature sensing range is 20～60℃， the maximum wavelength sensitivity is 2.6nm/℃， the maximum amplitude sensitivity is 0.363℃-1， and the temperature resolution of the sensor is 3.84×10-2℃. This work has guiding significance for the design and implementation of high-sensitivity， real-time， distributed， multi-parameter measurement SPR sensors.

Key words：photonic crystal fiber， surface plasmon resonance， high birefringence， refractive index sensing， temperature sensing

表面等离激元共振（SPR）是p偏振入射光与金属表面等离激元波（SPW）之间的耦合，由于其对周围介质的折射率变化非常敏感，因此广泛应用于物理、化学和生化传感［1］. 光子晶体光纤由于具有光学损耗小、光学非线性度高等许多独特的优点而广泛应用于生物传感、药品检测、气体检测等诸多领域.因此，产生了基于表面等离激元共振的光子晶体光纤（SPR-PCF）传感器，在一定程度上解决了传统光纤传感器交叉敏感、耦合损耗以及保偏特性等问题［2］.基于 SPR 的 PCF 传感器大致可分为四种结构：空气孔内金属涂层 PCF［3］、微流控开槽PCF［4］、D 型PCF［5］和包层外表面金属涂层PCF［6］.

最近，人们提出了多种基于微结构光纤（MOF）的传感器来测量折射率［7-9］、温度［9-11］等环境参数.文献［12］提出了一种双芯SPR-PCF传感器，光子晶体光纤由两种大小不同的空气孔围绕中心气孔构成，最外侧大空气孔直接与待测物质接触，实现了在中红外区域对气凝胶、七氟醚（麻醉剂重要成分）等折射率物质的检测.工作波长范围为2 505～3 181 nm，在1.12～1.37折射率范围内，最高灵敏度为12 000 nm/RIU，分辨率为8.33×10-6RIU.文献［13］提出了一种基于Ag-α-Fe2O3光栅的高灵敏度光纤SPR传感器，抛光面镀有一层特殊纳米材料构成的光栅作为传感层与待测物接触，在1.33～1.39的折射率范围内最高灵敏度为6 400 nm/RIU.文献［14］提出了一种T型光纤SPR传感器，T型传感头由带电浆平面的单模光纤（SMF）和带间隙的包层部分移除的单模光纤（CPR-SMF）组成.金膜不是沉积在CPR-SMF的侧面，而是沉积在SMF的末端.在1.33～1.36和1.37～1.4的折射率范围内，分辨率分别高达7.115×10-6RIU以及3.525×10-6RIU［14］.

值得注意的是，上面提出的传感器只能测量单一参数.在实际应用中，只测量一个参数的传感器往往会造成资源浪费，因此，同时测量多参量的传感器成为主流.而多参量的传感器最大的问题就是交叉敏感，因此文中提出一种新型高双折射、低损耗和高非线性的类椭圆纤芯光子晶体光纤（PCF）结构可以有效避免串扰问题，该SPR在环境污染监测、生物医学分析和食品安全控制方面有很好的应用前景.

1" 结构设计和理论分析

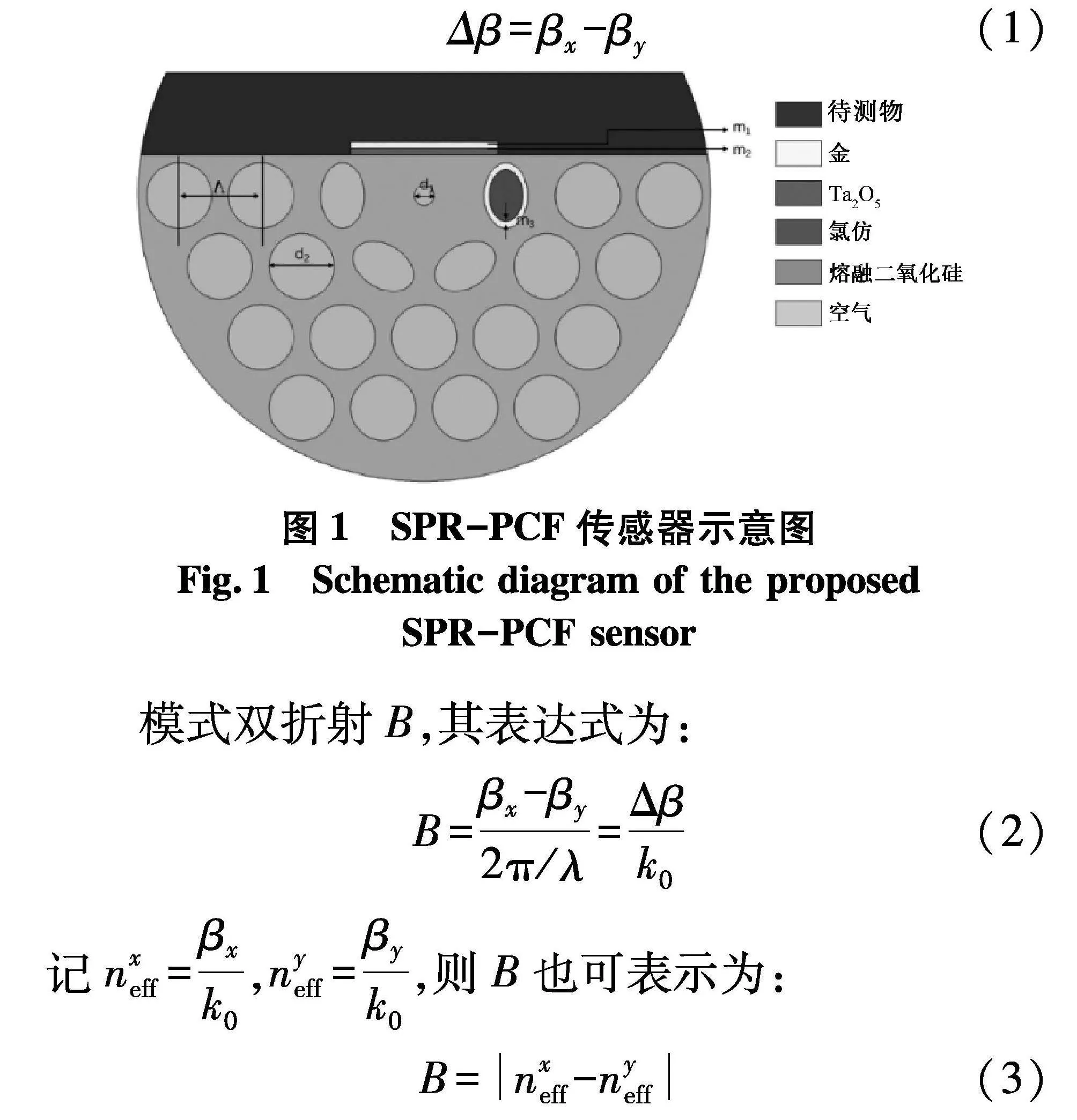
文中设计的D型SPR-PCF传感器截面如图1，光纤包层由3层空气孔组成，其中空气孔间距Λ=2 um，空气孔直径d2=0.8Λ.外围两层是圆形的空气孔按照三角晶格排布，靠近纤芯的内圈使用椭圆空气孔取代圆形空气孔.这样设计的目的是椭圆孔可以有效地打破纤芯附近模场的对称性以引入双折射，将模场限制在纤芯内部达到减少结构下方限制损耗的目的.两个基模传播常数的差定义为双折射：

Δβ=βx－βy（1）

模式双折射B，其表达式为：

B=βx－βy2π/λ=Δβk0（2）

记nxeff=βxk0，nyeff=βyk0，则B也可表示为：

B=nxeff－nyeff（3）

式中：nxeff和nyeff分别为X和Y偏振纤芯基模的有效折射率.若光纤中2个互相垂直的偏振模式的有效折射率差值的绝对值大于 1×10-4，则这 2 种偏振模式是彼此简并且可分离的，可以实现低串扰、可分辨的传输要求.基于此，高双折射的PCF在保偏特性和传输传感等领域被广泛应用［15］.选择金作为表面等离激元材料是因为金的谐振波长偏移较大，比银更稳定.抛光面金膜厚度m1=40 nm，直接与环境待测物接触.金纳米层下面有一层厚度为40 nm的Ta2O5，用来增强倏逝场［16］.根据Au-Ta2O5双涂层传感器具有良好的波长和振幅灵敏度的最新报道［17］，选择双层结构来激发SPR.Au-Ta2O5双涂层的宽度是1.8 Λ，较短的侧抛光长度提高了传感器的性能，这种结构的另一个优点是使贵金属涂层变得经济实惠.纤芯右侧椭圆孔内镀有一层厚度为m3=40 nm的金膜.采用飞秒激光辅助浸渗技术［18］结合湿化学沉积技术［19］，可在靶孔内表面选择性涂覆金层.椭圆长轴a=0.8 Λ，短轴b，a/b=1.5.纤芯中心设有空气孔，中心空气孔的半径d1/2=120 nm.中央空气孔负责降低纤芯模式的RI，以减轻调整纤芯模式和表面等离极化激元（SPP）模式之间的相位匹配.

该MOF的背景材料是由熔融二氧化硅制备，可以通过计算与温度有关的Sellmeier方程计算其折射率：

n2=A+B/1－C/λ2+D/1－E/λ2（4）

nT=n0+dn/dT·T－T0（5）

式中：n和λ分别代表硅的RI和当前光的工作波长；n0为室温下的折射率；nT为温度T时的折射率.系数A，B，C，D和E定义［20］：

A=1.315 52+0.690 754×10-5T

B=0.788 404+0.235 835×10-4T

C=0.011 019 9+0.584 758×10-6T

D=0.913 16+0.548 368×10-6

E=100（6）

金纳米层的折射率可由Drude-Lorentz公式来导出［21］：

ε（ω）=ε1+iε2=ε

SymboleB@ －ω2pωω+ωc（7）

式中：金属高频相对介电常数ε

SymboleB@ 取值为9.84，等离子体频率ωp取值为1.36×1016rad/s，阻尼频率ωc取值为1.45×1014rad/s.镀金气孔中填充了氯仿，其有较大的热光系数dn/dT=-6.328×10-4/K，可用来检测温度，可通过式（5）来计算氯仿的折射率.空气孔中空气折射率为1，Ta2O5的折射率可以表示为：

nTa2O5=1.88+178.4×102λ2+527×107λ4（8）

式中：λ是当前入射光的工作波长.在的计算中忽略了金属薄膜的表面粗糙度［19］和液体介质中的物质色散.

利用全矢量有限元软件COMSOL Multiphysics进行了计算仿真.使用波动光学模块进行模式分析研究，对波长进行参数化扫描.用自由三角形划分网格，保证网格质量，总共有9 602个域单元和1 024个边界单元.在xy二维平面进行模式分析，光沿着z轴传播，选择散射边界条件作为边界条件吸收光纤表面多余的输出波，避免对仿真结果产生影响.

如图2，X和Y偏振的纤芯基模和SPP模的色散关系以及纤芯基模损耗谱图，由于结构的非对称性，结构显示出强烈的双折射，X、Y偏振纤芯基模的有效折射率差值均大于10-4.从图3中可以很明显的看出纤芯模态可以分为两个正交模式，一个是平行于X轴，一个是平行于Y轴.

图3显示了表面电场模分布，箭头方向表示电场方向.

由于纤芯基模和SPP模的耦合，可以看到尖锐的共振峰.在共振波长处，有很大比例的能量从纤芯基模转移到SPP模中，并且在纤芯基模损耗谱中有一个明显的尖锐的损耗峰，通过记录共振峰的变化来检测外部环境的微小变化.此外，从损耗峰值可以看出Y方向的耦合强度远大于X方向.对于高阶SPP模与纤芯基模的耦合不予讨论，不影响共振峰的监测.

2" 结果与讨论

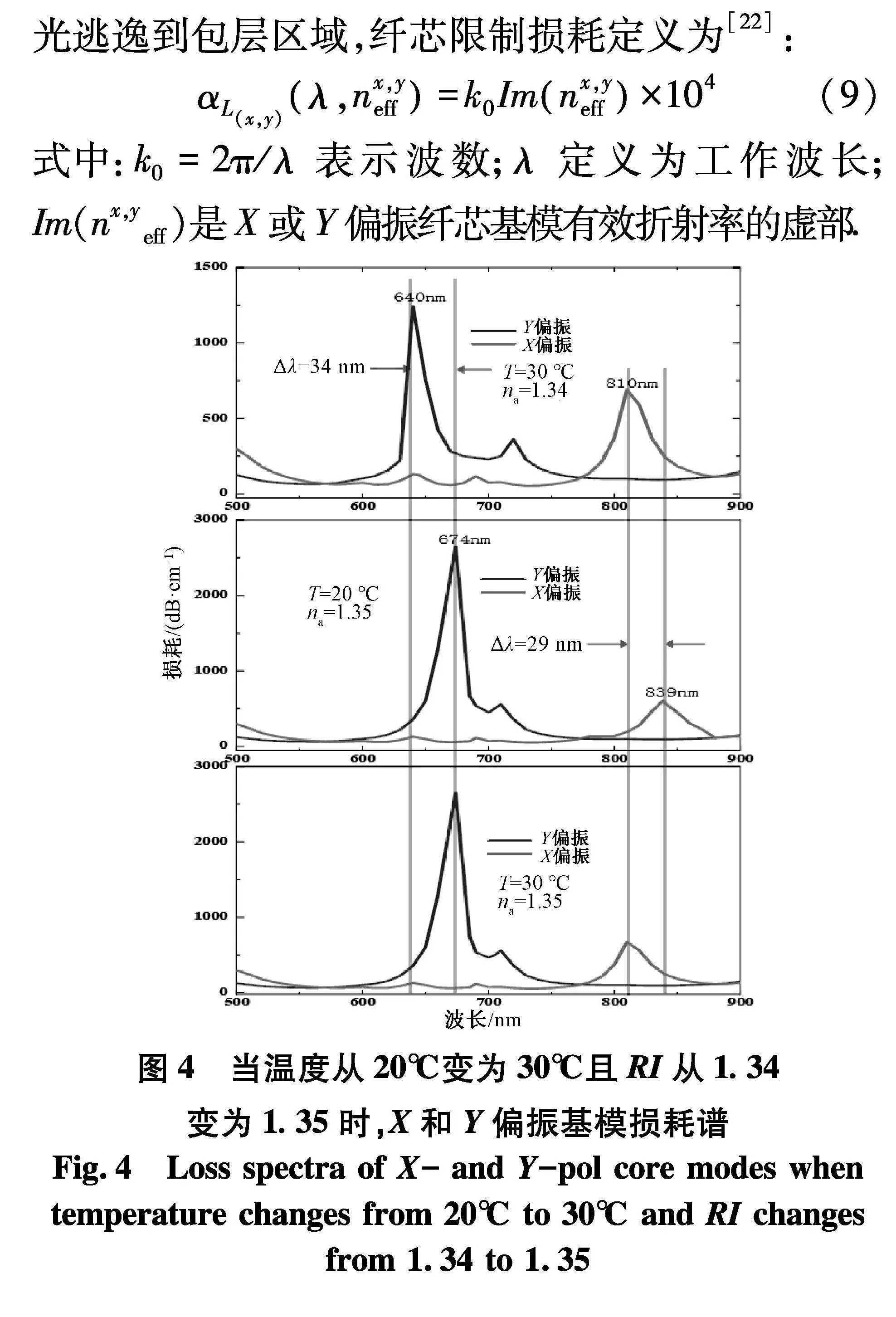
当RI或外部环境温度发生变化时，纤芯模式与SPP模式的相位匹配条件也随之发生变化，导致X和Y偏振的共振峰向不同波长移动.通过跟踪X和Y偏振共振峰的位移，可以检测到RI和温度的变化.如图4用控制变量法分别对温度从20℃变化到30℃， RI从1.33变化到1.34时X和Y偏振纤芯模的损耗谱进行了比较.众所周知，光通过纤芯的传播会产生一定的损耗，这主要是由于光逃逸到包层区域，纤芯限制损耗定义为［22］：

αL（x，y）λ，nx，yeff=k0Imnx，yeff×104（9）

式中：k0=2π/λ表示波数；λ 定义为工作波长；Im（nx，yeff）是X或Y偏振纤芯基模有效折射率的虚部.

如图4，在T=30℃恒定温度下，当待测物折射率从1.34变化到1.35，Y偏振损耗峰向长波长漂移，共振波长从640 nm增加到674 nm，与此同时X偏振共振波长固定在810 nm.同样，保持RI=1.35，当温度从20℃增加到30℃时，X偏振损耗峰向短波长漂移，共振波长从839 nm变化到810 nm，Y偏振共振波长保持在674 nm.

通常用振幅调制和波长调制的方法计算传感器的灵敏度.波长灵敏度定义为：

Sλ（na，λ）=ΔλpeakΔna（10）

式中：Δλpeak为共振峰的漂移量；Δna为待测物折射率的变化量.振幅灵敏度为［23］：

SA（α）=－1α（λ，na）×Δα（λ，na）Δna（11）

式中：α（λ，na）为限制损耗；Δα（λ，na）为同一波长处相邻待测物折射率下损耗值之间的差值.用ΔT，α（λ，T），Δα（λ，T）分别替换Δna，α（λ，na），Δα（λ，na）可以得到在温度传感下的振幅灵敏度.同样的，温度传感下的波长灵敏度为：

Sλ（T，λ）=Δλpeak（T）ΔT（12）

最后，对于微传感器来说一个很重要的参数就是分辨率，分辨率是衡量传感器可检测被测量最小变化的能力.可以由式（13、14）分别计算折射率和温度的分辨率.

RRI（na，λ）=Δna×ΔλminΔλpeak（RI）（13）

式中：RRI为折射率的分辨率；Δλmin为最小光谱仪分辨率，通常是0.1 nm；Δna为折射率的变化量；Δλpeak（RI）为折射率损耗谱上共振峰的漂移量.

RT（T，λ）=ΔT×ΔλminΔλpeak （T）（14）

式中：RT为温度的分辨率；ΔT是温度的变化量；Δλpeak （T）为是温度损耗谱上共振峰的漂移量.

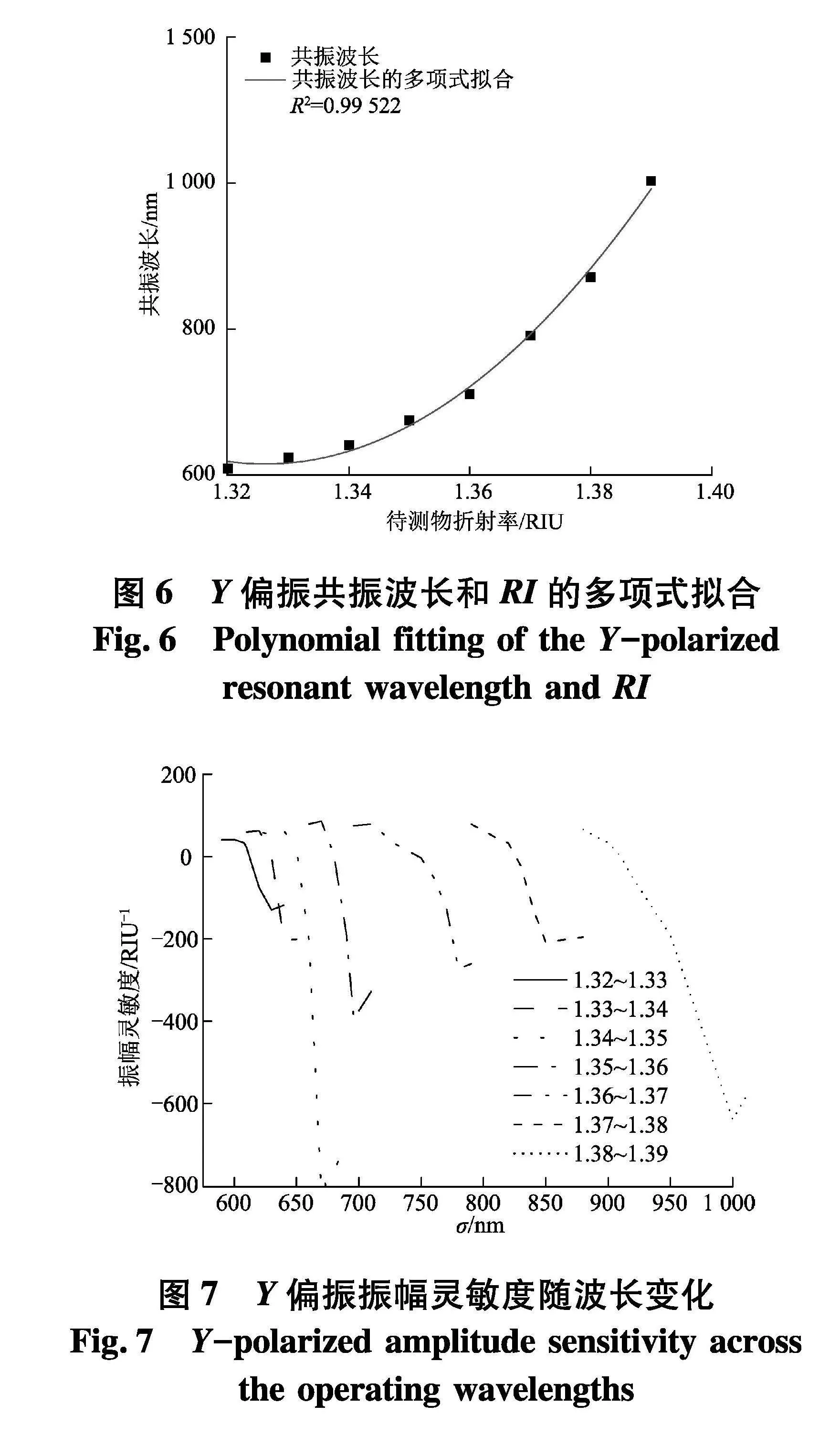
为了研究传感器的性能，需要考虑抛光面金膜周围不同折射率的待测物.从图5可以看出，当待测物折射率的范围从1.32增加到1.39，共振波长向长波长漂移.与此同时，随着待测物折射率的增加，Y偏振的纤芯损耗也增加.

一方面，不同折射率的分析物沉积在金膜上，间接影响了金膜激发的表面等离极化激元模式.随着被分析物折射率的增加，表面等离极化激元模的有效折射率也增加，而纤芯模的有效折射率变化不明显.因此，纤芯模和表面等离极化激元模的相位匹配点向长波长方向移动，即发生红移.另一方面，随着样品折射率的增加，引起纤芯的能量泄漏，从而促进了纤芯模与表面等离极化激元模的耦合.也就是说，这会导致更多的能量从纤芯转移到金膜表面，最终导致共振波长处的纤芯模式的损耗增加.图6为共振波长作为折射率的函数的多项式拟合结果，R2系数高达0.995 22.由式（10）计算得到平均波长灵敏度为5 700 nm/RIU，当待测物折射率从1.38变化到1.39时，共振波长从870 nm增加到1 006 nm，得到最大波长灵敏度为13 600 nm/RIU.由式（13）计算得到传感器的折射率分辨率为1.75×10-5RIU.同样，使用式（11）计算了微传感器对待测物折射率值从1.32到1.39的振幅灵敏度，结果绘制并呈现在图7中.当待测物折射率从1.34变化到1.35时，在波长670 nm处得到最大振幅灵敏度818.44 RIU-1.

通过改变D型光子晶体光纤的结构参数，分析传感器的传感特性和偏振特性.首先，对抛光面的金膜厚度以及增敏材料Ta2O5的厚度进行分析.其次，中心空气孔负责降低纤芯模式的折射率，减轻调整纤芯模式和SPP模式之间的相位匹配难度，需要对其半径大小进行分析研究.最后，研究光子晶体其它结构参数对传感器的性能影响，比如包层空气孔的大小，中心内圈椭圆孔的长短轴的比例，占空比等.

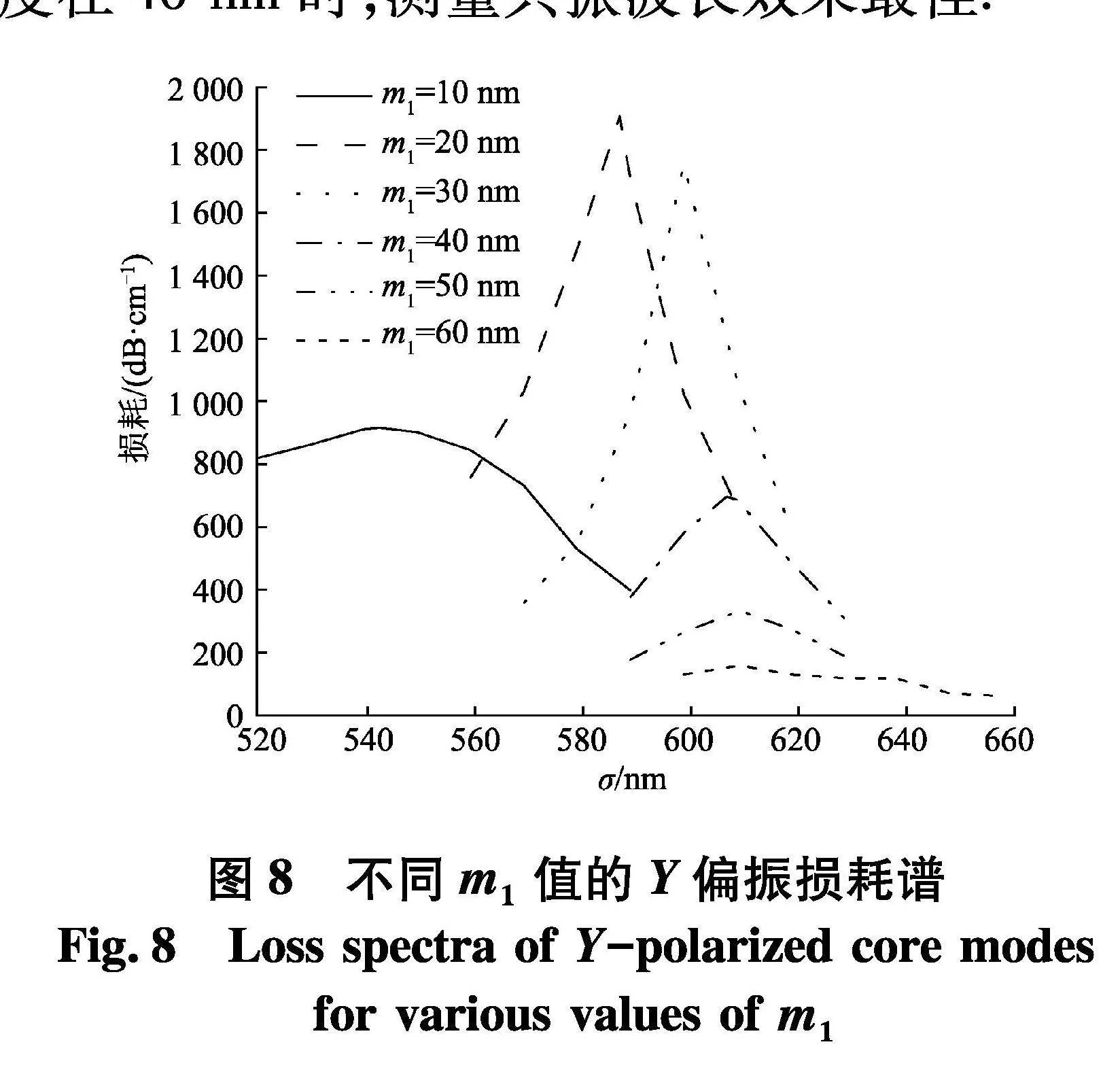
等离激元材料厚度的变化对SPR-PCF传感器传感特性的影响十分明显.当待测物折射率1.32，中心空气孔半径120 nm，让抛光面金膜厚度由10 nm增加到60 nm，结果如图8.可以看出，随着抛光面金膜厚度增加，共振波长会发生红移，刚开始纤芯模的损耗值增加随后一直减小，因为当金膜太厚时，倏逝波的电场很难穿透金膜，所以纤芯基模的能量很难转移到金属表面.为了进一步了解金膜厚度的具体影响，分析了待测物折射率从1.32～1.39时各个厚度下的损耗谱.当金膜厚度10 nm时，随着待测物质折射率升高，限制损耗变小，整体的限制损耗都很小，不适合表面等离极化激元模的激发.当抛光面金膜厚度为20 nm时，平均波长灵敏度5 600 nm/RIU，最大波长灵敏度12 800 nm/RIU.当抛光面金膜厚度为30 nm时，平均波长灵敏度5 100 nm/RIU，最大波长灵敏度10 900 nm/RIU.当抛光面金膜厚度为40 nm时，平均波长灵敏度5 700 nm/RIU，最大波长灵敏度13 200 nm/RIU.综上所述，如果金层太厚，则会引入较高的阻尼损失，削弱倏逝场的穿透，使得灵敏度和限制损耗降低；如果金膜太薄，则由于辐射阻尼，会导致等离激元被强烈抑制.选择抛光面金膜厚度在40 nm时，测量共振波长效果最佳.

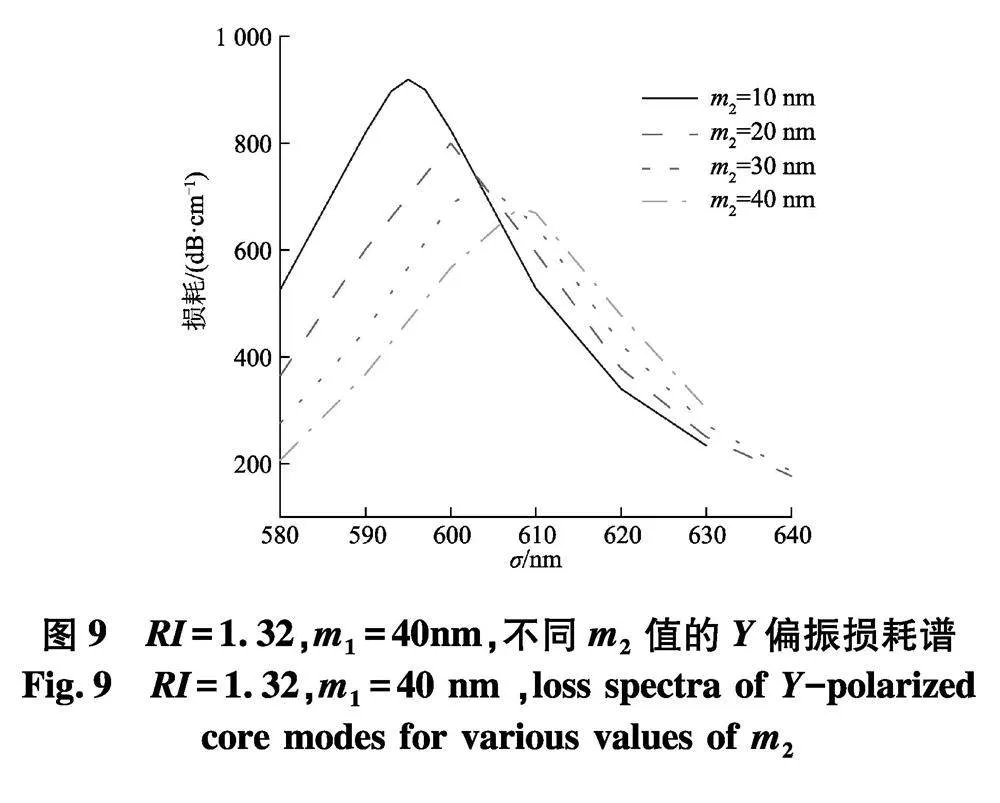
Ta2O5用于增强倏逝场，其厚度对于SPR-PCF传感器的传感特性也有很大的影响.图9为待测物折射率1.32，抛光面金膜厚度m1=40 nm时Ta2O5厚度由10 nm增加到40 nm的纤芯损耗谱.

从图中可以看出当Ta2O5厚度增加，限制损耗减小，同时共振波长发生红移.为了进一步研究Ta2O5厚度的影响，在不同Ta2O5厚度时，对折射率1.32～1.39整体做了仿真.结果表明：当Ta2O5厚度为40 nm时，平均波长灵敏度5 700 nm/RIU，最大波长灵敏度13 200 nm/RIU.当Ta2O5厚度为30 nm时，平均波长灵敏度5 100 nm/RIU，最大波长灵敏度16 000 nm/RIU.当Ta2O5厚度为20 nm时，平均波长灵敏度4 900 nm/RIU，最大波长灵敏度14 900 nm/RIU.当Ta2O5厚度为10 nm时，平均波长灵敏度为5 200 nm/RIU，最大波长灵敏度为14 400 nm/RIU.易见，当Ta2O5厚度为40 nm时，该结构得到最大的平均波长灵敏度，传感器的性能更加优越.

分别对中心空气孔半径为0，40，80，120，160 nm时，待测物折射率1.32～1.39的纤芯基模损耗谱进行分析研究.当空气孔半径为0时，平均波长灵敏度3 500 nm/RIU，最大波长灵敏度8 000 nm/RIU当空气孔半径为40 nm时，平均波长灵敏度为3 200 nm/RIU，最大波长灵敏度为5 700 nm/RIU.当空气孔半径为80 nm时，平均波长灵敏度为4 500 nm/RIU，最大波长灵敏度为13 600 nm/RIU.当空气孔半径为120 nm时，平均波长灵敏度为5 700 nm/RIU，最大波长灵敏度为13 200 nm/RIU.当空气孔半径为160 nm时，平均波长灵敏度4 000 nm/RIU，最大波长灵敏度8 000" nm/RIU.经比较发现，选用中心空气孔半径为120 nm时，传感器的性能更加优越.且此时并不会造成纤芯模式的分裂，不会对传感性能造成影响.

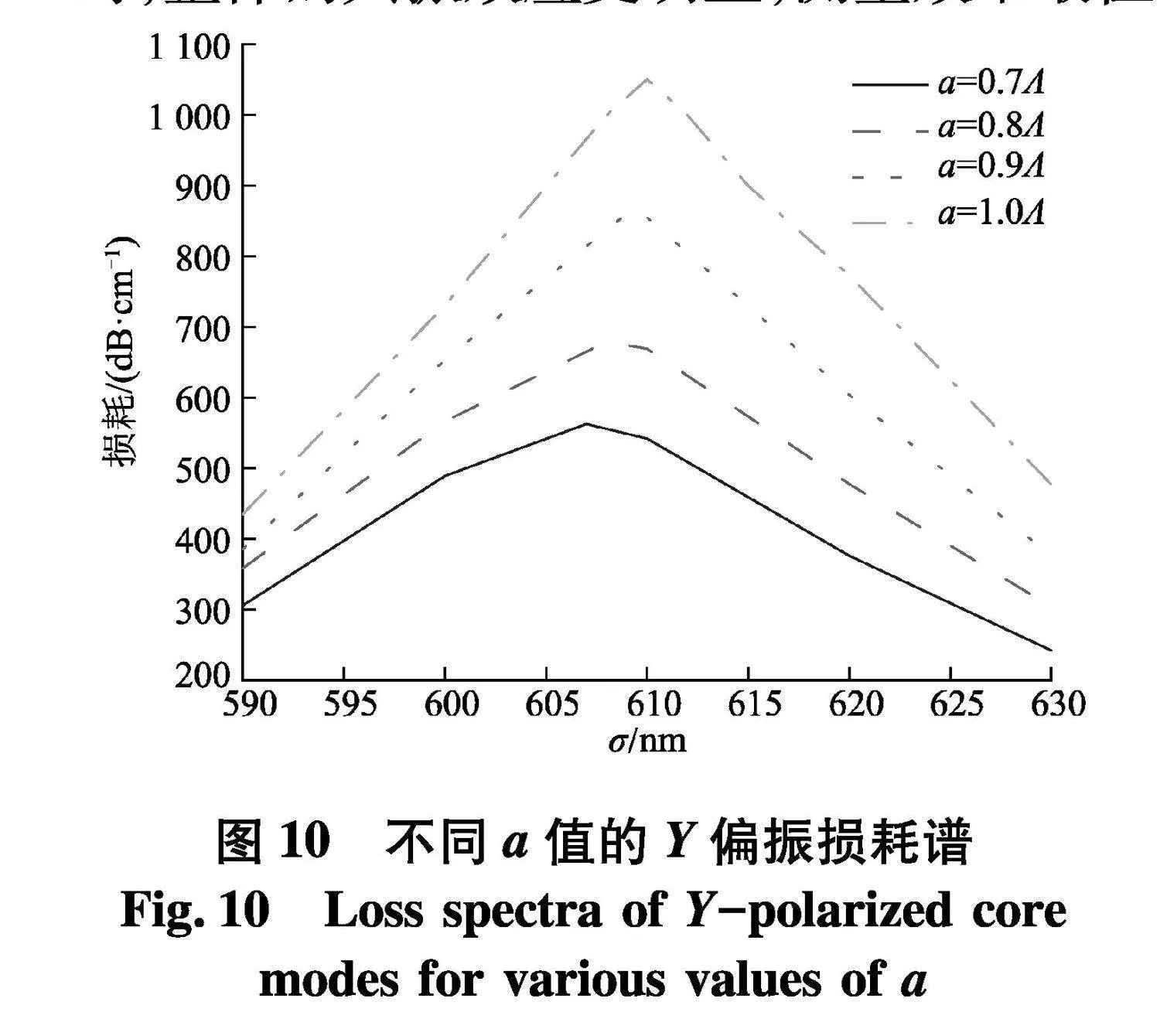
保持椭圆尺寸不变，改变占空比，外层空气孔从0.5Λ增加到0.8Λ，待测物折射率1.32，损耗谱基本没有变化，共振波长均固定在608 nm，损耗峰值678 dB/cm，传感器的性能不发生变化，这是因为包层外环的空气孔离纤芯很远，纤芯基模和表面等离极化激元模的有效折射率基本不变，导致相位匹配点不变，共振波长不会发生变化，因此包层外环的空气孔只会轻微影响损耗值的变化，同时说明椭圆结构很好的限制了纤芯模的能量.因此改变椭圆长轴，图10为椭圆长轴从0.7Λ增大到1.0Λ的损耗谱，共振波长有轻微的红移，损耗峰值不断增大，当长轴为0.8Λ时，整体的共振效应更明显，测量效果最佳.

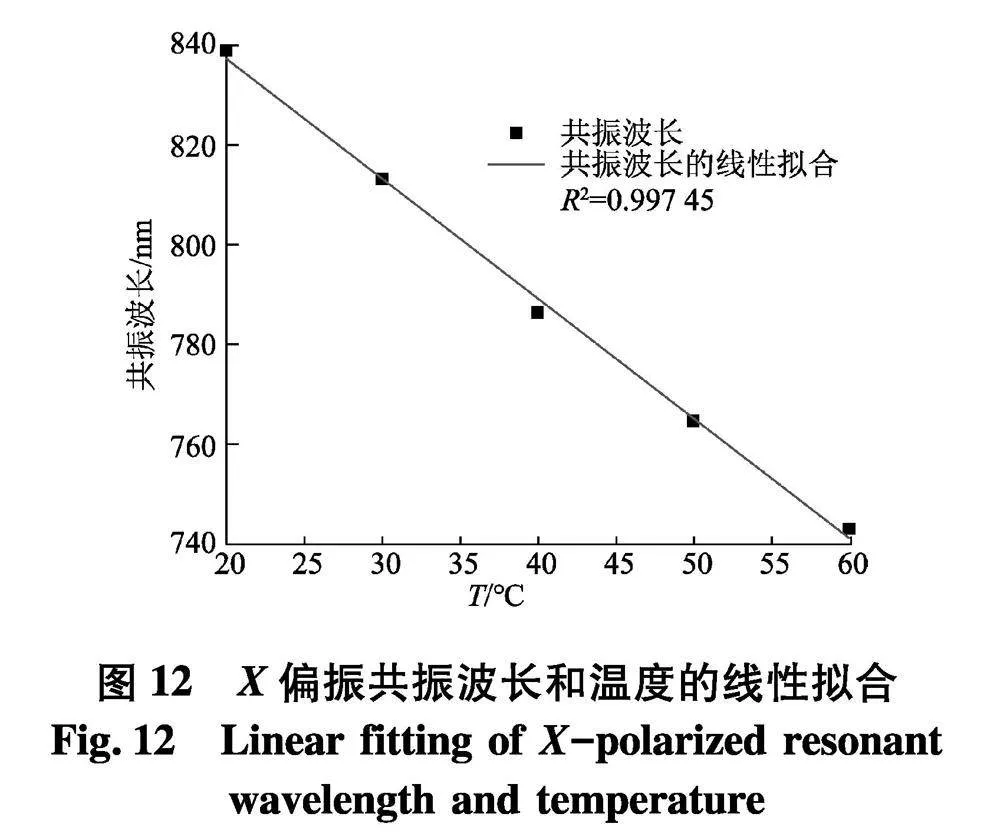
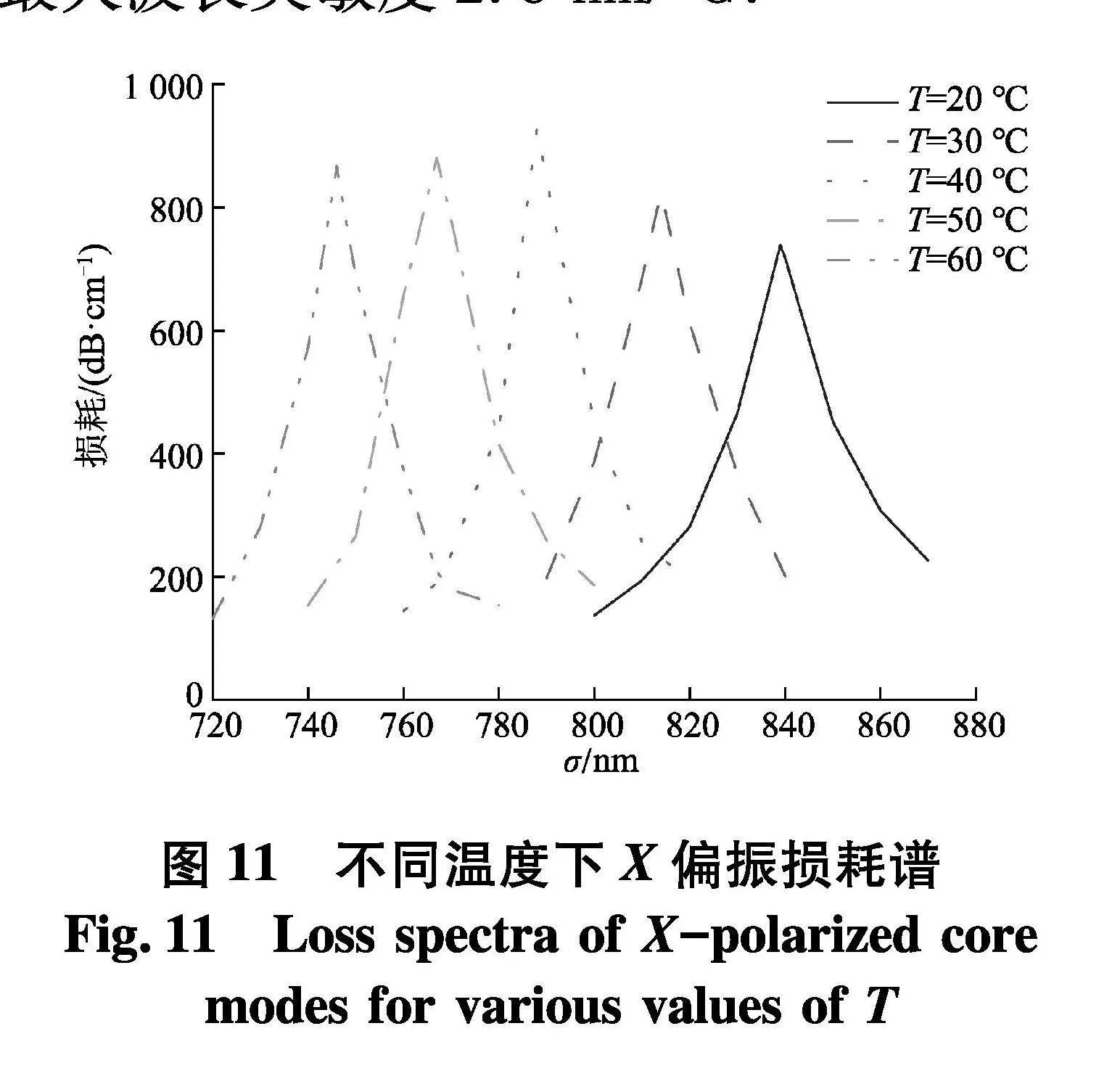
评估用于温度传感的微传感器的灵敏度指标，利用温敏液体氯仿将被分析物环境中的热效应转化为光学信号，以便有效地感知温度变化.图11为温度从20℃增加到60℃的X偏振损耗谱，从图中可以看出随着温度的增加共振波长发生蓝移，这是因为氯仿的负热光学系数会降低表面等离激元模有效折射率的实部.与折射率传感不同，温度检测的峰值波长在我们计算的整个温度范围内始终呈线性关系，图12为共振波长作为温度的函数的线性拟合，R2系数高达0.997 45.由式（12）计算得到平均波长灵敏度为2.325 nm/℃，当温度从30℃变化到40℃时，共振波长从814 nm减小到788 nm，得到最大波长灵敏度2.6 nm/℃.

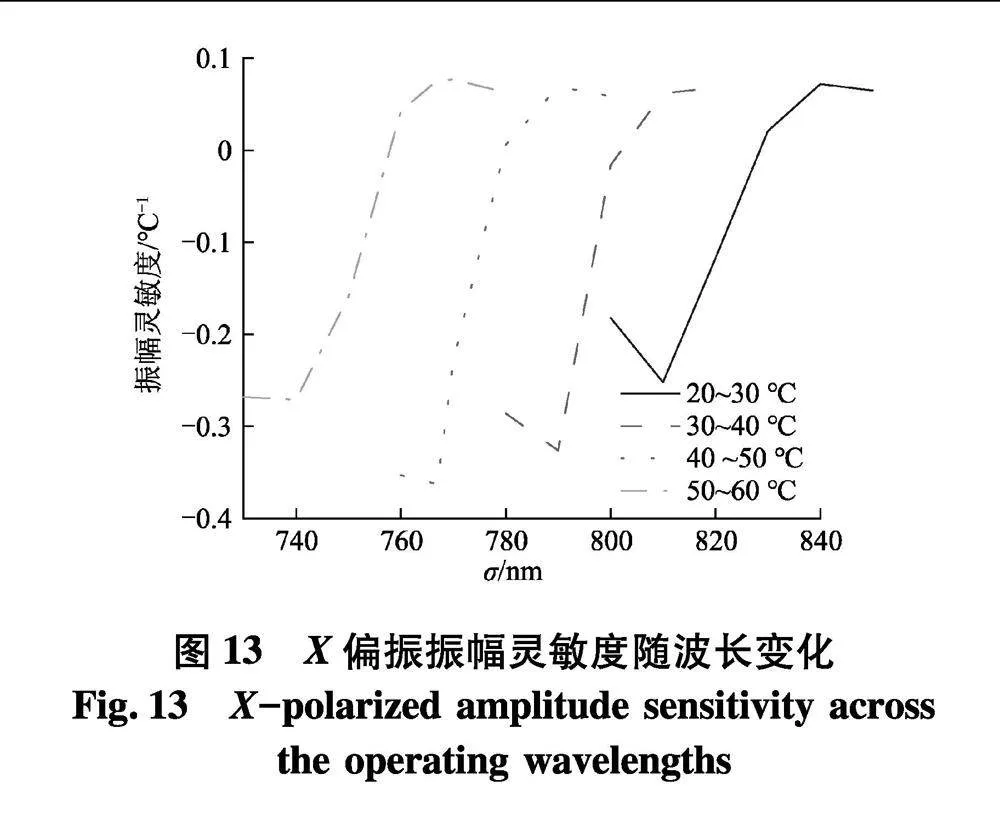
由式（14）计算得到传感器的温度分辨率为3.84×10-2℃.同样的，通过式（11）的变式计算了微传感器对温度值从20℃变化到60℃的振幅灵敏度，结果绘制并呈现在图13中.当温度从40℃变化到50℃时，在波长767 nm处得到最大振幅灵敏度为0.363℃-1.

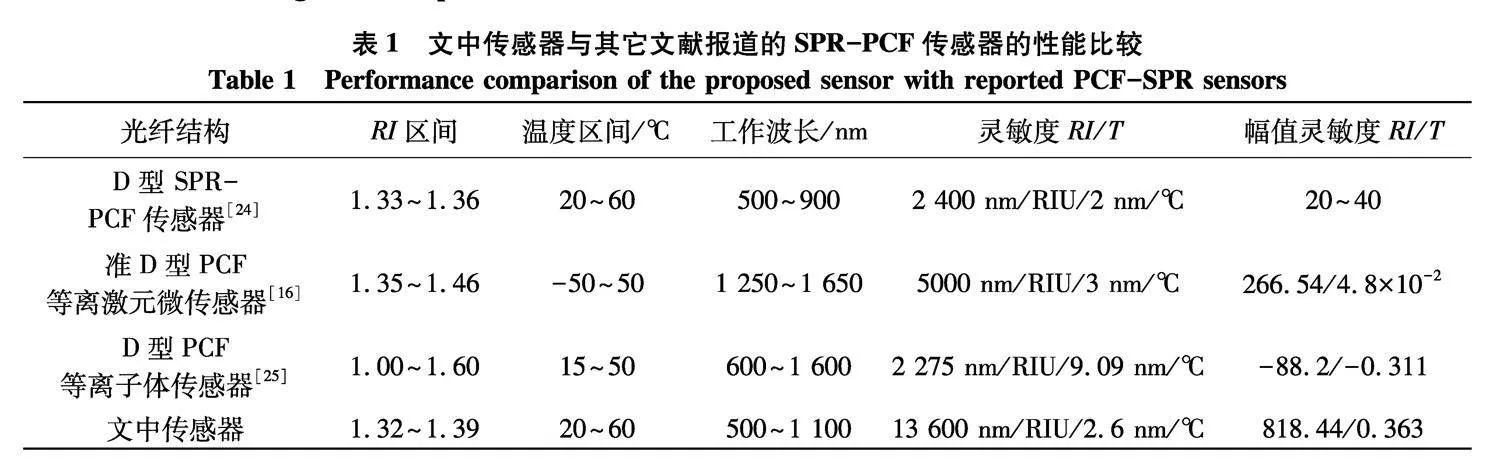
表1对文中提出的传感器和现有的用于折射率和温度检测的传感器进行了性能比较.可以很明显的看出，在波长灵敏度、振幅灵敏度指标上，所提出的传感器有明显的优势.

表1" 文中传感器与其它文献报道的SPR-PCF传感器的性能比较

Table 1" Performance comparison of the proposed sensor with reported PCF-SPR sensors

光纤结构RI区间温度区间/℃工作波长/nm灵敏度RI/T幅值灵敏度RI/T

D型 SPR-PCF传感器［24］1.33～1.3620～60500～9002 400 nm/RIU/2 nm/℃20～40

准D型PCF等离激元微传感器［16］1.35～1.46-50～501 250～1 6505000 nm/RIU/3 nm/℃266.54/4.8×10-2

D型PCF等离子体传感器［25］1.00～1.6015～50600～1 6002 275 nm/RIU/9.09 nm/℃-88.2/-0.311

文中传感器1.32～1.3920～60500～1 10013 600 nm/RIU/2.6 nm/℃818.44/0.363

3" 结论

（1） 提出并数值分析了一款新颖的高双折射D型SPR-PCF双参量传感器，创建了两个传感通道来产生两个独特的X和Y偏振模式，分别测量折射率和温度.

（2） 通过波长调制和振幅调制的方法研究了材料厚度以及其它结构参数对传感器性能的影响.当波长为500～1 100 nm，外部环境折射率为1.32～1.39时，最终得到折射率传感下最大波长灵敏度为13 600" nm/RIU，最大振幅灵敏度818.44 RIU-1，传感器的折射率分辨率为1.75×10-5 RIU.

（3） 温度传感为20～60℃，得到最大波长灵敏度2.6 nm/℃，最大振幅灵敏度0.363℃-1，以及传感器的温度分辨率3.84×10-2℃.所提出的微型传感器可应用领域包括分子科学、医学测量和分析、陆地环境工程和数据评估、水生生态系统调查、药物和消化过程控制和验证、低温研究等.

参考文献（References）

［1］" YANG X， LU Y， LIU B， et al. Simultaneous measurement of refractive index and temperature based on SPR in D-shaped MOF［J］. Applied Optics， 2017， 56（15）： 4369-4374.

［2］" 魏方皓， 张祥军， 唐守锋. 基于表面等离子体共振的光子晶体光纤折射率传感器的设计与分析［J］. 半导体光电， 2020， 41： 35-38，43.

［3］" GAO D， GUAN C， WEN Y， et al. Multi-hole fiber based surface plasmon resonance sensor operated at near-infrared wavelengths［J］. Optics Communications， 2014，313：1-8.

［4］" OTUPIRI R， AKOWUAH E K， HAXHA S. Multi-channel SPR biosensor based on PCF for multi-analyte sensing applications［J］. Optics Express， 2015， 23（12）： 15716-15727.

［5］" 肖功利， 张开富， 杨宏艳， 等. D型对称双芯光子晶体光纤双谐振峰折射率传感器［J］. 光学学报， 2020， 40（12）：1206001.

［6］" HAI L， BING B B， YAN Z Z. High-sensitivity temperature measurement based on SPR in gold-PDMS-coated photonic crystal fiber［J］. Chinese Journal of Lasers， 2020， 47（4）：04003.

［7］" ERDMANIS M， VIEGAS D， HAUTAKORPI M， et al. Comprehensive numerical analysis of a surface-plasmon-resonance sensor based on an H-shaped optical fiber［J］. Optics Express， 2011，19（15）：13980-13988.

［8］" LUAN N， WANG R， LV W， et al. Surface plasmon resonance sensor based on D-shaped microstructured optical fiber with hollow core［J］. Optics Express， 2015， 23（7）： 8576-8582.

［9］" XIAO F， MICHEL D， LI G， et al. Simultaneous measurement of refractive index and temperature based on surface plasmon resonance sensors［J］. Journal of Lightwave Technology， 2014， 32（21）： 3567-3571.

［10］" PENG Y， HOU J， ZHANG Y， et al. Temperature sensing using the bandgap-like effect in a selectively liquid-filled photonic crystal fiber［J］. Optics Letters， 2013， 38（3）： 263-265.

［11］" WANG R， YAO J， MIAO Y， et al. A reflective photonic crystal fiber temperature sensor probe based on infiltration with liquid mixtures［J］. Sensors， 2013， 13（6）： 7916-7925.

［12］" 郝丹， 王建帅， 解宇恒， 等. 基于双芯光子晶体光纤的中红外表面等离子体共振低折射率传感器［J］. 光子学报， 2020， 49： 146153.

［13］" KADHIM R A， YUAN L， XU H， et al. Highly sensitive D-shaped optical fiber surface plasmon resonance refractive index sensor based on Ag-α-Fe2O3 grating［J］. IEEE Sensors Journal， 2020， 20（17）： 9816-9824.

［14］" WANG X M， ZHAO C L， WANG Y R， et al. A proposal of T-structure fiber-optic refractive index sensor based on surface plasmon resonance［J］. Optics Communications， 2016， 369： 189-193.

［15］" 柳淘， 郜洋， 郭慧杰， 等. 高双折射类椭圆纤芯光子晶体光纤设计与分析［J］. 光通信技术， 2021， 45： 48-53.

［16］" DANLARD I， AKOWUAH E K. Design and theoretical analysis of a dual-polarized quasi d-shaped plasmonic pcf microsensor for back-to-back measurement of refractive index and temperature［J］. IEEE Sensors Journal， 2021， 21（8）： 9860-9868.

［17］" MAHFUZ A M， MOLLAH M A， MOMOTA M R， et al. Highly sensitive photonic crystal fiber plasmonic biosensor： Design and analysis［J］. Optical Materials， 2019， 90： 315-321.

［18］" WANG Y， LIAO C， WANG D. Femtosecond laser-assisted selective infiltration of microstructured optical fibers［J］. Optics Express， 2010， 18（17）： 18056-18060.

［19］" LIU B H， JIANG Y X， ZHU X S， et al. Hollow fiber surface plasmon resonance sensor for the detection of liquid with high refractive index［J］. Optics Express， 2013， 21（26）： 32349-32357.

［20］" HAN B， ZHANG Y N， SIYU E， et al. Simultaneous measurement of temperature and strain based on dual SPR effect in PCF［J］. Optics amp; Laser Technology， 2019， 113： 46-51.

［21］ "RAKIC＇A D， DJURISˇIC＇ A B， ELAZAR J M， et al. Optical properties of metallic films for vertical-cavity optoelectronic devices［J］. Applied Optics， 1998， 37（22）： 5271-5283..

［22］" GANDHI M A， NIVEDHA S， BABU P R， et al. Designing a refractive index based biosensor using a photonic quasi-crystal fiber［C］∥ 2015 Workshop on Recent Advances in Photonics （WRAP）. Bangalore India：［s.n.］，2015.

［23］" RIFAT A A， AHMED R， MAHDIRAJI G A， et al. Highly sensitive D-shaped photonic crystal fiber-based plasmonic biosensor in visible to near-IR［J］. IEEE Sensors Journal， 2017，17（9）：2776-2783.

［24］" HU J， LANG T， SHI G H. Simultaneous measurement of refractive index and temperature based on all-dielectric metasurface［J］. Optics Express， 2017，25（13）：15241-15251.

［25］" GUO Y， LI J， LI S， et al. Amphibious sensor of temperature and refractive index based on D-shaped photonic crystal fibre filled with liquid crystal［J］. Liquid Crystals， 2020，47（6）：882-894.

（责任编辑：贡洪殿）