贝叶斯优化的学生T过程用于微带天线谐振频率建模

摘" 要： 学生T过程的核心是核函数设计以及超参数优化，其中超参数直接影响模型的泛化能力.为提升学生T过程模型的预测精度，基于一种自适应的贝叶斯优化算法，实现对学生T过程超参数的全局优化.以多组Benchmark问题和矩形微带天线谐振频率建模为仿真实例，并与多种机器学习模型进行了对比实验.结果表明：采用贝叶斯优化超参数的学生T过程具有较高的拟合精度.

关键词： 超参数；学生T过程；贝叶斯优化；天线

中图分类号：TP301.6""" 文献标志码：A""""" 文章编号：1673-4807（2024）01-089-06

DOI：10.20061/j.issn.1673-4807.2024.01.014

收稿日期： 2021-11-11""" 修回日期： 2021-04-29

基金项目： 国家自然科学基金项目（61771225）；2021年度广东省重点建设学科科研能力提升项目（2021ZDJS057）；广东省基础与应用基础研究基金自然科学基金项目（面上项目）（2023A1515011272）

作者简介： 李清（1998—），男，硕士研究生

*通信作者： 田雨波（1971—），男，博士，教授，博士生导师，研究方向为机器学习及其电磁学应用.E-mail： tianyubo@just.edu.cn

引文格式： 李清，田雨波，韩束丹，等.贝叶斯优化的学生T过程用于微带天线谐振频率建模［J］.江苏科技大学学报（自然科学版），2024，38（1）：89-94.DOI：10.20061/j.issn.1673-4807.2024.01.014.

Resonant frequency modelling of microstrip antenna based onBayesian optimization students′ T process

LI Qing1， TIAN Yubo2*， HAN Shudan1， LI Rui1

（1.Ocean College， Jiangsu University of Science and Technology， Zhenjiang 212100， China）

（2.School of Information and Communication Engineering， Guangzhou Maritime University， Guangzhou 510725， China）

Abstract：The key issues of students′ T process （STP） are kernel function design and hyperparameter optimization， and the optimized hyperparameter affects directly the generalization ability of the model. In order to improve the prediction accuracy of STP， this study introduces an adaptive Bayesian optimization （BO） algorithm to optimize the hyperparameters of STP. Taking Benchmark questions and resonant frequency modeling of microstrip antenna as examples， the experimental comparisons are conducted with several machine learning models. This research results show that STP optimized by BO has higher fitting accuracy.

Key words：hyperparameter， students′ T process， Bayesian optimization， antenna

学生T过程（students′T process， STP）是高斯过程（gaussian process，GP）的推广，它服从学生T分布而不是高斯分布.文献［1］提出高斯过程的核函数进行逆Wishart过程，并以此推导学生T过程处理输入异常值.学生T过程不仅保持了高斯过程的主要优势，而且由于学生T分布的峰度高于高斯分布，因此其包容异常值的可能更大［2］，且学生T过程后验方差的增加和减少取决于观测数据样本值的方差.学生T过程的这两个不同于高斯过程的特性使得它更使适合解决含有异常值的样本数据.

作为一种核学习方法，学生T过程进行回归预测时具有计算量大且依赖于核函数的选择的缺点.研究发现，选择合适的超参数能够提高核学习方法模型的预测精度和核函数性能 ［3］.在实际应用中，优化超参数通常采用经验选择、网格搜索等方法，对于学生T过程的超参数优化则采用梯度法下降法［4］等.贝叶斯优化算法属于一类基于主动学习的机器学习方法，它能够对复杂的目标函数进行快速迭代从而实现全局的优化 ［5］.

文中基于一种自适应贝叶斯优化算法，并应用于学生T过程的超参数寻优，通过多组Benchmark问题和矩形天线谐振频率建模实例进行了算法验证，结果表明，经过贝叶斯优化的学生T过程建模精度得更高，泛化能力更强.

1" 背景知识

1.1" 学生T过程

学生T过程是一种服从联合学生T分布的随机变量集合的函数分布［6］.多元学生T分布除了位置参数μ和散射矩阵参数Σ外（散射参数Σ不是学生T分布的协方差矩阵，而是与其相关的散射参数矩阵），还带有一个额外的参数v，用于描述分布的自由度.学生T分布的概率密度为：

T（μ，Σ，v）=Γ（（v+d）/2）Γ（v/2）vd/2πd/2|Σ|1/2（1+1v（y－

μ）TΣ－1（y－μ））－（v+d）/2（1）

式中：d为T分布的尺寸；μ为T分布的位置参数；Σ是T分布的对称正定散射矩阵；T分布取正定散射参数Σ的行列式的值；v是自由度，且v大于2.与高斯分布一样.

E［（y-μ）T（y-μ）］=vv－2Σ（2）

STP由均值函数m（x）和协方差函数k（x，x′）参数化，但是，它还有一个附加参数，即自由度v.STP的性质可由m（x）、k（x，x′）和v共同决定，x，x′∈Rd为任意随机变量.于是，STP可表示为：

f（x）=STP（m（x），k（x，x′），v）（3）

随着自由度的增加，当v趋近于无穷大时，多元学生T分布收敛到具有相同均值和散射参数矩阵的多元高斯分布.

在STP中，均值函数m（x）定义了每个位置x的先验期望值，核函数表示了目标函数在任意两个位置x和x0的值之间的协方差，有限位置子集的联合分布概率为：

p（y|x）=T（μ，Σ，v）（y）=T（μ，v－2vK，v）y（4）

式中：μ为均值向量，μi=m（xi），v为自由度；K是核矩阵，Ki，j=k（xi，xj）.

多元学生T分布以及由此延伸的STP，在条件作用下是封闭的.具体地说，给定一组样本D={{x1，y1}，{x2，y2}，{x3，y3}，...}，在给定一个新的输入x～，STP的后验由式（5～8）给出，可以得到后验均值μ^、后验方差K^和自由度v^.

p（y|x，D）=T（μ，v－2vK，v）y（5）

μ^=Kx，xKx～，x～－1y～（6）

K^=v+y～TKx～，x～－1y～－2" v+|D|－2 "（Kx，x-Kx，x～Kx～，x～-1Kx～，x）（7）

v^=v+|D|（8）

式中：Kx，x为输入x之间的协方差函数；y～为观察到的目标的输出，y～TK－1x～，x～y～≈|D|.

一般的，其核函数选择平方指数核：

KSEard（x，x′）=σ2fexp（－（x－x′）T（x－x′）2ι2）（9）

式中：σ2f为信号方差，也可以为输出尺度幅值；参数ι为输入（长度或时间）尺度.

STP负对数似然函数的形式为：

L（θ）=－logp（y|x，θ）=N2log（（v－2）π）+

12log|Kθ|－logΓ（v+N2）+logΓ（v2）+

v+N2log（1+βv－2）（10）

式中：Kθ=Kff+σ2nI，β=y·Kθ－1y，Kffij=k（xi，xj）.

使用共轭梯度法求解最大似然参数可以获得最佳的超参数.

Kθσn2=（Kx，x+σ2I）σn2=I（11）

Κθσf2=K（x，x）σf2=Kx，xσf2（12）

（Kθ）ijιk2=12k（xi，xj）（xik－xjkιk2）2（13）

L（θ）v=N2（v－2）－ψ（v+N2）+ψ（v2）+12log（1+βv－2）－（v+N）β2（v+β－2）（v－2）（14）

式中σ2n为噪声方差；σf2和ιk2为核函数的超参数；v是自由度；ψ（x）=（（Γ′（x））/（Γ（x）））.

1.2" 贝叶斯优化算法

贝叶斯优化（Bayesian optimization， BO）是一种流行的监督学习方法，它能够在不变的设计空间内有效的寻求黑盒目标函数f的全局最优解，通过对目标函数f更新先验知识，获取对应的观测值，来更新更加接近于f的后验分布，从而快速的找到最优的解［7］.

x*=argminx∈χRdf（x）（15）

BO由两个模块构成，分别是负责目标函数拟合的代理模型模块以及负责获取新的观测值的采集函数模块，其框架如图1.

高斯过程（Gaussian process， GP）是一种非参数核学习方法，可表示为：

f（x）～GP（μ（x），k（x，x′））（16）

式中：μ（x）为均值函数，k（x，x′）为协方差函数.

D1：n={{x1，y1}，{x2，y2}，...，{xn，yn}}为已观测集合，此时协方差矩阵K为：

K=k（x1，x1）…k（x1，xn）……k（xn，x1）…k（xn，xn）（17）

每输入新的观测值xn+1，假定GP的均值为0，则输出y1：n和yn+1的联合高斯分布为：

y1：nyn+1～N0，kkkTk（xn+1，xn+1）（18）

k可表示为：

k=［k（xn+1，x1）·k（xn+1，x2）…·k（xn+1，xn）］（19）

得到yn+1的后验概率：

p（yn+1|D1：n，xn+1）=N（μ（xn+1），σ2（xn+1））（20）

式中：μ（xn+1）=kTK－1y1：n（21）

σ2（xn+1）=k（xn+1，xn+1）－kTK－1k（22）

经过上述计算，GP可以预测出xn+1处的输出值，得到预测均值和预测方差，从而使用采样函数就可以去开采下一个可信度最高的观测值.

BO框架通过最大化/最小化采集函数，以此寻求新的可信度最高的观测值.通过选择最佳的采集函数能使寻求得的观测值对应的输出损失最小，损失rn为［5］：

rn=|y*－yn|（23）

式中：y*为当前的最优观测值对应的输出预测值；yn为真实值.

2" 超参数优化算法

文中引入一种贝叶斯自适应直接搜索算法［8］，由网格搜索和贝叶斯优化混合而成，其中，采集函数为置信下界函数LCB：

aLCB（x;θ）=μ（x）－vβts2（x），βt=2ln（Dt2π2/（6δ））（24）

式中：vgt;0为一个可调参数；t为迄今为止函数计算的次数；δ gt;0为一个概率容限；β是在某些假设下为最小化累积遗憾而选择的学习率.具体伪代码如下：

算法：贝叶斯自适应直接搜索

输入：目标函数f；起始点x0=［x1，x2，x3，...，xN］；边界LB、UB

过程：

1：初始化：Δmesh0←2－10，Δpoll0←1，k←0，在起始点计算目标函数

2：for 1…nsearch do

3：xsearch←网格搜索新的点

4：在xsearch处计算目标函数f， 如果结果得到改善，则停止程序

5：如果网格搜索没有成功，则：

6：计算探测集pk

7：通过采集函数计算pk处的目标函数值

8：如果迭代k成功则：

9：更新现有的xk+1

10：如果探测步成功，则Δmeshk←2Δmeshk，Δpollk←2Δpollk

11：否则：

12：Δmeshk←12Δmeshk，Δpollk←12Δpollk

13：k←k+1

14：直到fevalsgt;Maxfunevals或者Δpollklt;10－6

15：返回：xend=argminkf（xk）

当输入存在依赖学生T分布的噪声，并且核不具备β属性时，STP具有更好的处理异常数据的能力.因此，STP使用不具备β属性的平方指数核函数：

KSEisoU=exp（－12ι2（x－z）T（x－z））（25）

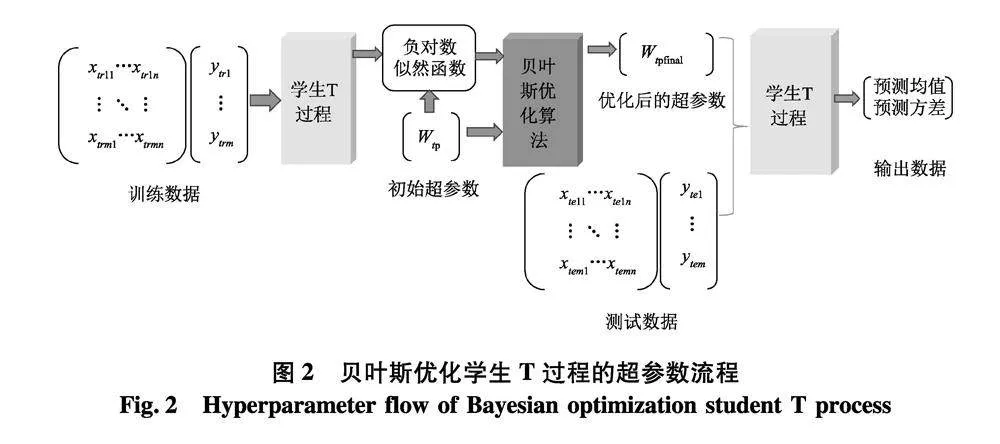
由STP的似然函数和上述核函数可知，贝叶斯自适应直接搜索算法需要对STP的自由度v、噪声方差σ2、核函数的超参数ι这3个超参数进行优化，其优化流程如图2.

3" Benchmark数据集实验

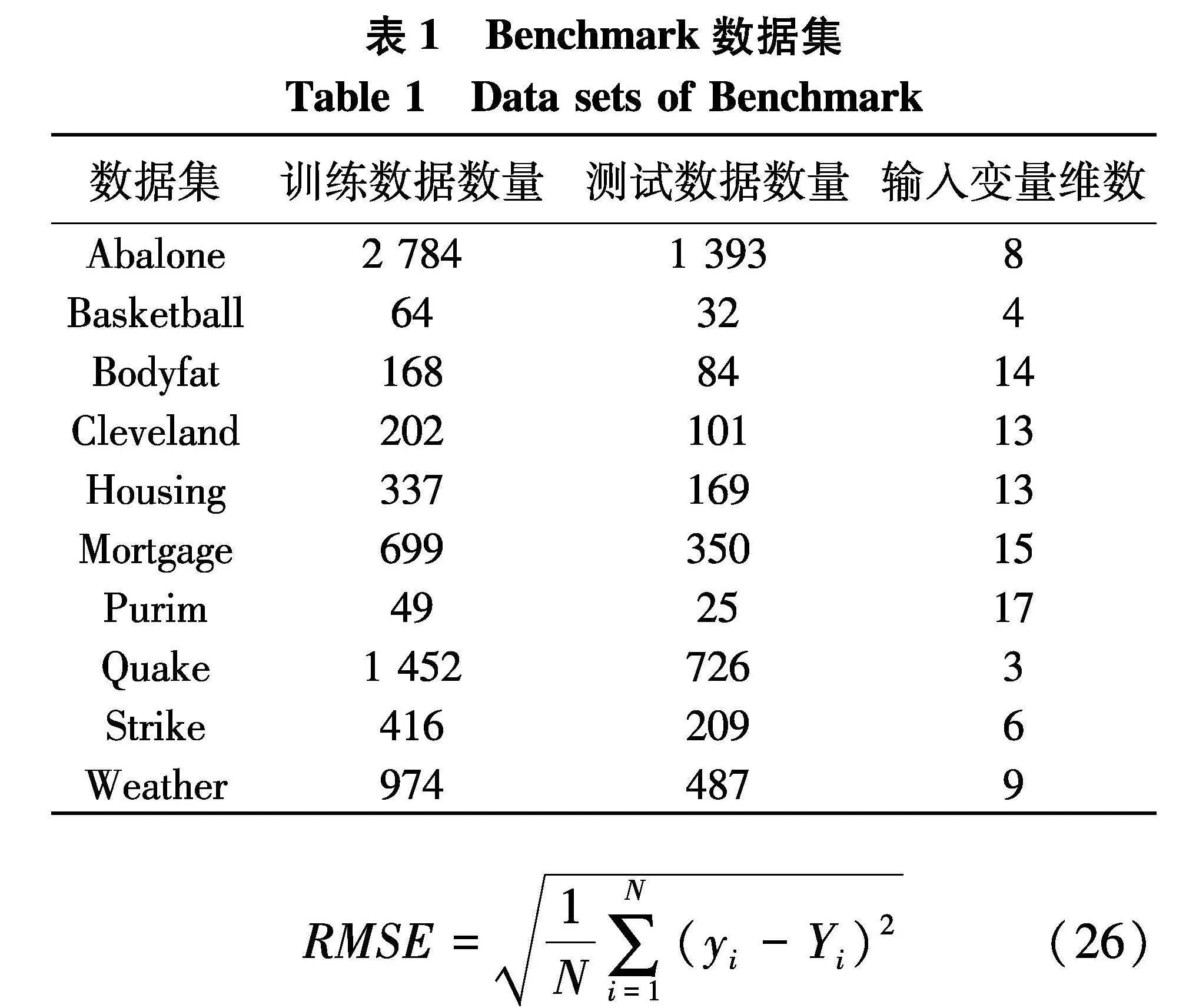
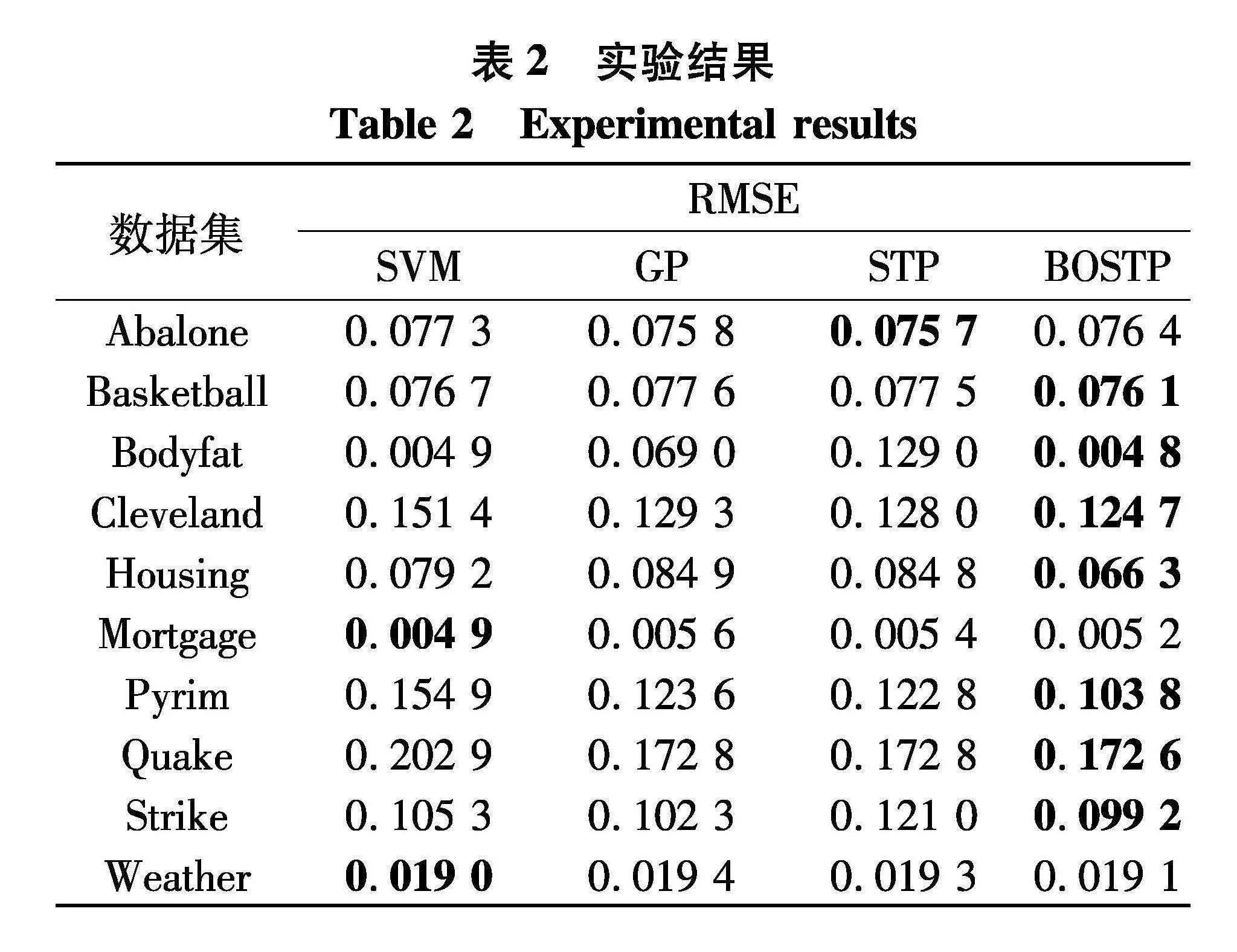
文中实验是在10个Benchmark回归数据集上进行的［9］，如表1.采用支持向量机（support vector machine， SVM）［10］、GP以及传统STP与文中BO优化的STP算法（BO-based STP， BOSTP）进行比较.评价指标使用均方根误差（root mean square error， RMSE），实验结果见表2，其中各数据集在不同模型下的最优RMSE以加粗形式展示.实验环境为Inter（R）Corte（TM）i5-7500 CPU @ 3.40GHz 16GB RAM， MATLAB2019b.

RMSE=1N∑Ni=1（yi－Yi）2（26）

式中：yi为数据集中用于测试的测试输出；Yi为测试输入对应的预测输出；N为数据的个数.

可以看出在这10个数据集上，使用BO优化超参数的STP在9个数据集上的表现均优于使用传统STP，在另一个Abalone数据集上BOSTP与STP的预测精度相差非常小.在Mortgage和Weather数据集上，BOSTPD与表现最优的SVM之间的差距也非常小.Benchmark数据集的实验结果表明，贝叶斯优化超参数的学生T过程有着很好的泛化能力.

4" 矩形微带天线谐振频率建模

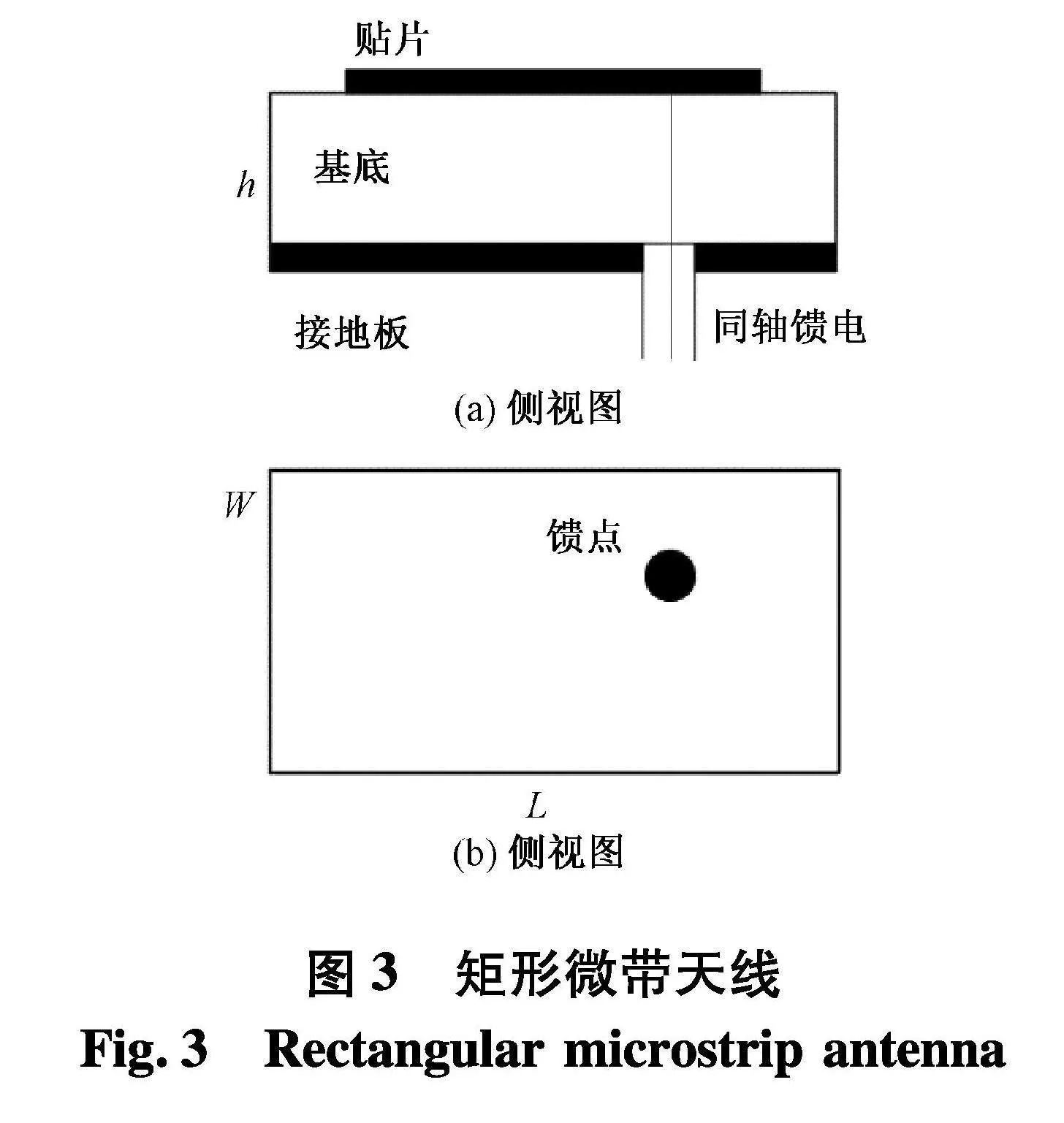
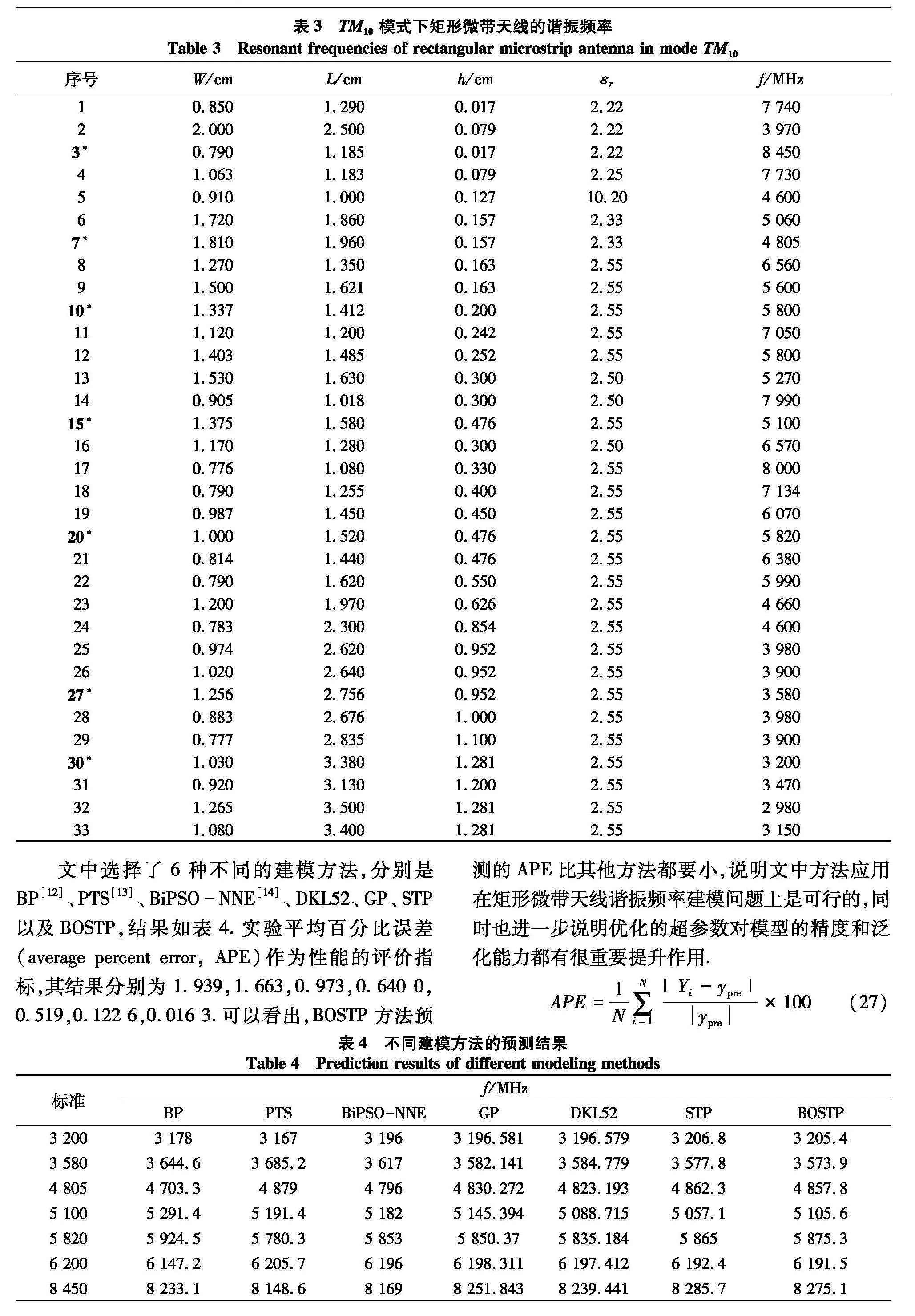
在天线设计领域，谐振频率是最重要的指标之一.以如图3矩形微带天线为例［11］，选择尺寸参数为输入，谐振频率为输出，实验数据如表3，其中X∈R33×4，Y∈R33×1.数据的输入为天线的长度L、宽度W、介质层厚度h和相对介电常数εr，输出为对应的谐振频率f.选取表4中的26组作为训练数据，用星号标记加粗的7组作为测试数据.

文中选择了6种不同的建模方法，分别是BP［12］、PTS［13］、BiPSO-NNE［14］、DKL52、GP、STP以及BOSTP，结果如表4.实验平均百分比误差（average percent error， APE）作为性能的评价指标，其结果分别为1.939，1.663，0.973，0.640 0，0.519，0.122 6，0.016 3.可以看出，BOSTP方法预测的APE比其他方法都要小，说明文中方法应用在矩形微带天线谐振频率建模问题上是可行的，同时也进一步说明优化的超参数对模型的精度和泛化能力都有很重要提升作用.

APE=1N∑Ni=1|Yi－ypre|ypre×100（27）

5" 结论

为提高STP模型的预测精度及泛化能力，提出了一种使用BO优化STP超参数的方法，并基于10个Benchmark数据集和微带天线谐振频率实例进行了算法性能测试.实验结果证明，经过超参数寻优的STP模型优于传统STP和大部分其他机器学习方法，模型预测精度和泛化能力均得到了提升，说明了所提方法的有效性.

参考文献（References）

［1］" SHAH A， WILSON A G， GHAHRAMANI Z. Bayesian optimization using student-t Processes［C］∥NIPS Workshop on Bayesian Optimization. USA：NIPS，2013：1-5.

［2］" O′HAGAN A. On outlier rejection phenomena in Bayes inference［J］. Journal of the Royal Statistical Society： Series B （Methodological）， 1979， 41（3）： 358-367.

［3］" SUNDARARAJAN S， KEERTHI S S. Predictive approaches for choosing hyperparameters in Gaussian processes［J］. Neural Computation， 2001， 13（5）： 1103-1118.

［4］" WANG W， YU Q， FASLI M. Altering Gaussian process to Student-t process for maximum distribution construction［J］. International Journal of Systems Science， 2021， 52（4）： 727-755.

［5］" 李海涛. 基于并行贝叶斯优化的蒙皮天线机电综合设计［D］. 西安：西安电子科技大学，2019：57-64.

［6］" TRACEY B D， WOLPERT D. Upgrading from Gaussian processes to Student′s-t processes［C］∥2018 AIAA Non-Deterministic Approaches Conference.USA：AIAA 2018： 1659.

［7］" 崔佳旭， 杨博. 贝叶斯优化方法和应用综述［J］. 软件学报， 2018， 29（10）：3068-3090.

［8］" ACERBI L， MA W J. Practical Bayesian optimization for model fitting with Bayesian adaptive direct search［C］∥Proceedings of the 31st International Conference on Neural Information Processing Systems.USA：Curran Associates Inc， 2017： 1834-1844.

［9］" BLAKE C， MERZ C J. UCI repository of machine learning databases ［DB/OL］.1995-11-30［2021-11-11］.http：∥www. ics. uci. edu/～mlearn/MLRepository. html.

［10］" DING W， TIAN Y， LI P， et al. Antenna optimization based on master-apprentice broad learning system［J］. International Journal of Machine Learning and Cybernetics， 2021： 1-10.

［11］" KARA M. The resonant frequency of rectangular microstrip antenna elements with various substrate thicknesses［J］. Microwave and Optical Technology Letters， 1996， 11（2）： 55-59.

［12］" GUNEY K， SAGIROGLU S， ERLER M. Generalized neural method to determine resonant frequencies of various microstrip antennas［J］. International Journal of RF and Microwave Computer+Aided Engineering： Co-sponsored by the Center for Advanced Manufacturing and Packaging of Microwave， Optical， and Digital Electronics （CAMPmode） at the University of Colorado at Boulder， 2002， 12（1）： 131-139.

［13］" SAGIROGLU S， KALINLI A. Determining resonant frequencies of various microstrip antennas within a single neural model trained using parallel tabu search algorithm［J］. Electromagnetics， 2005， 25（6）： 551-565.

［14］" TIAN Yubo， ZHANG Suling， LI Jingyi. Modeling resonant frequency of microstrip antenna based on neural network ensemble［J］. International Journal of Numerical Modelling： Electronic Networks， Devices and Fields， 2011， 24（1）： 78-88.

（责任编辑：曹莉）