基于模糊控制的柔性耦合梁压电主动抑振研究

摘" 要： 弯曲振动是影响柔性梁工作性能和稳定性的重要因素，而压电主动控制是实现柔性梁抑振的途径之一.为了提高压电主动控制系统的抑振效果，利用LabVIEW平台设计了基于模糊控制的柔性耦合梁压电主动抑振系统.根据耦合梁动力学理论，建立了压电柔性耦合梁的动力学模型，求解了柔性梁的耦合固有频率并分析其模态特性.根据模态振型，为了实现最佳抑振效果，将MFC压电片设置在振幅最大位置处，并以此设计压电振动控制系统.此外，利用LabVIEW平台和NI数据采集卡搭建了振动控制测试系统，对不同激励下柔性梁振动的抑振效果进行测试和比较.结果表明：当柔性梁的振动频率低于一阶固有频率时，梁末端处的振动位移最大.将MFC压电片设置在柔性梁末端，在连续激励振动下，通过模糊控制可以使柔性梁的振动幅值减小35%，且模糊控制的减振效果优于PID控制.

关键词： 耦合振动；柔性梁；模糊控制；压电抑振；LabVIEW

中图分类号：TH113.1""" 文献标志码：A""""" 文章编号：1673-4807（2024）01-049-06

DOI：10.20061/j.issn.1673-4807.2024.01.008

收稿日期： 2022-04-29""" 修回日期： 2021-04-29

基金项目： 国家自然科学基金项目（51905228），江苏省高校“青蓝工程”资助项目（苏教师函［2022］29号）

作者简介： 李冲（1988—），男，副教授，研究方向为压电驱动与控制、微机电系统、机械动力学等.E-mail：lichong@just.edu.cn

引文格式： 李冲， 沈亮，方记文，等.基于模糊控制的柔性耦合梁压电主动抑振研究［J］.江苏科技大学学报（自然科学版），2024，38（1）：49-54.DOI：10.20061/j.issn.1673-4807.2024.01.008.

Study on piezoelectric active vibration control of piezoelectricflexible coupled beams based on fuzzy control

LI Chong， SHEN Liang， FANG Jiwen， ZHONG Wei

（School of Mechanical Engineering， Jiangsu University of Science and Technology， Zhenjiang" 212100，China）

Abstract：Bending vibration is an important factor affecting the performance and stability of flexible beams， and piezoelectric active control is one of the ways to achieve vibration suppression of flexible beams. In order to improve the vibration suppression effect of piezoelectric active control systems， a piezoelectric active vibration control system of a flexible coupled beam based on fuzzy control was designed using LabVIEW platform. According to the dynamic theory of coupled beams， the dynamic model of a piezoelectric coupled flexible beam was established， the coupling natural frequency of the flexible beam was solved， and its modal characteristics were analyzed. According to the modal shape， in order to achieve the best vibration suppression effect， the MFC piezoelectric plate is set at the position of the maximum amplitude， and the piezoelectric vibration control system is designed accordingly. Besides， the vibration control test system was built by LabVIEW platform and NI data acquisition card， and the vibration suppression effects of flexible beams under different excitation were tested and compared. The results show that when the vibration frequency of the flexible beam is lower than the first-order natural frequency， the vibration displacement is the largest at the end of the beam. When an MFC piezoelectric plate is set at the end of flexible beam， the vibration amplitude of the flexible beam can be reduced by 35% by fuzzy control under continuous excitation， and the vibration reduction effect of fuzzy control is better than that of PID control.

Key words：coupled vibration， flexible beam， fuzzy control， piezoelectric vibration control， LabVIEW

由于压电智能元件具有良好的可埋入性、重量轻、频响范围宽，且同时具有正、逆压电效应等特点，目前已经广泛应用于结构的减振降噪领域.利用压电材料的逆压电效应，可以将压电元件作为作动器，进行主动振动控制.

压电主动控制技术是振动控制中的一个重要方向，现代控制理论的应用对压电主动抑振技术发展起到巨大推动作用.文献［1］利用压电致动器对船壳体结构进行了主动振动控制.文献［2］将压电主动控制应用于硬盘驱动器振动噪声的主动控制，采用遗传算法来确定压电致动器最优粘贴位置，结果显示压电致动器能够有效减弱振动噪声.文献［3］分析和测试了压电致动器对机翼后边缘摆动的主动控制.NASA格伦研究中心研究人员将压电主动控制技术应用于旋转叶片抑振［4］.近年来国内对于压电主动控制在薄壁结构抑振领域的研究与日俱增.文献［5］研究了大迎角下飞机尾翼抖振的压电主动控制，验证了压电主动控制在大迎角下尾翼抖振控制的可行性.文献［6］将压电材料制成的调谐质量阻尼器以及最优输出反馈控制策略应用于柔性航天器在轨振动主动控制，数值仿真显示该种方法能够有效控制扰动引起的振动.文献［7］将压电陶瓷应用于轿车顶棚主动抑振，实验结果显示，基于压电陶瓷的轿车顶棚振动主动控制系统能够有效的控制轿车顶棚的振动.文献［8］提出了将压电智能材料作为传感器和作动器，通过机电耦合抑制风机叶片的振动，研究表明该种方法能够使系统振幅减小20%.基于压电纤维复合材料.文献［9］对气动弹性抖振进行了振动控制，对MFC驱动器采用载荷比拟方法建模，利用速度负反馈算法设计控制律，研究结果为实际抖振主动控制提供了依据.文献［10］利用压电纤维复合材料对旋转叶片进行了主动控制，揭示了系统参数对系统稳态响应及稳定性的影响规律.此外，针对风机叶片的挥舞振动，文献［11］将风机叶片等效为悬臂梁，通过模糊PID控制对悬臂梁进行了振动抑制，且模糊PID比普通PID具有较好的抑振效果.

针对薄壁机构的振动，压电主动控制已经取得了众多研究成果，如何更好地提高振动控制效果以及实现控制系统简单可靠是压电主动控制需要不断探索的方向.因此，文中根据耦合梁动力学理论，建立了压电柔性耦合梁的动力学模型，分析了柔性梁的振动特性.利用LabVIEW平台设计了基于模糊控制的压电柔性耦合梁压电主动振动控制系统.搭建了实验测试系统，对不同激励下柔性梁振动的抑振效果进行测试和比较.

1" 压电柔性耦合梁动力学模型

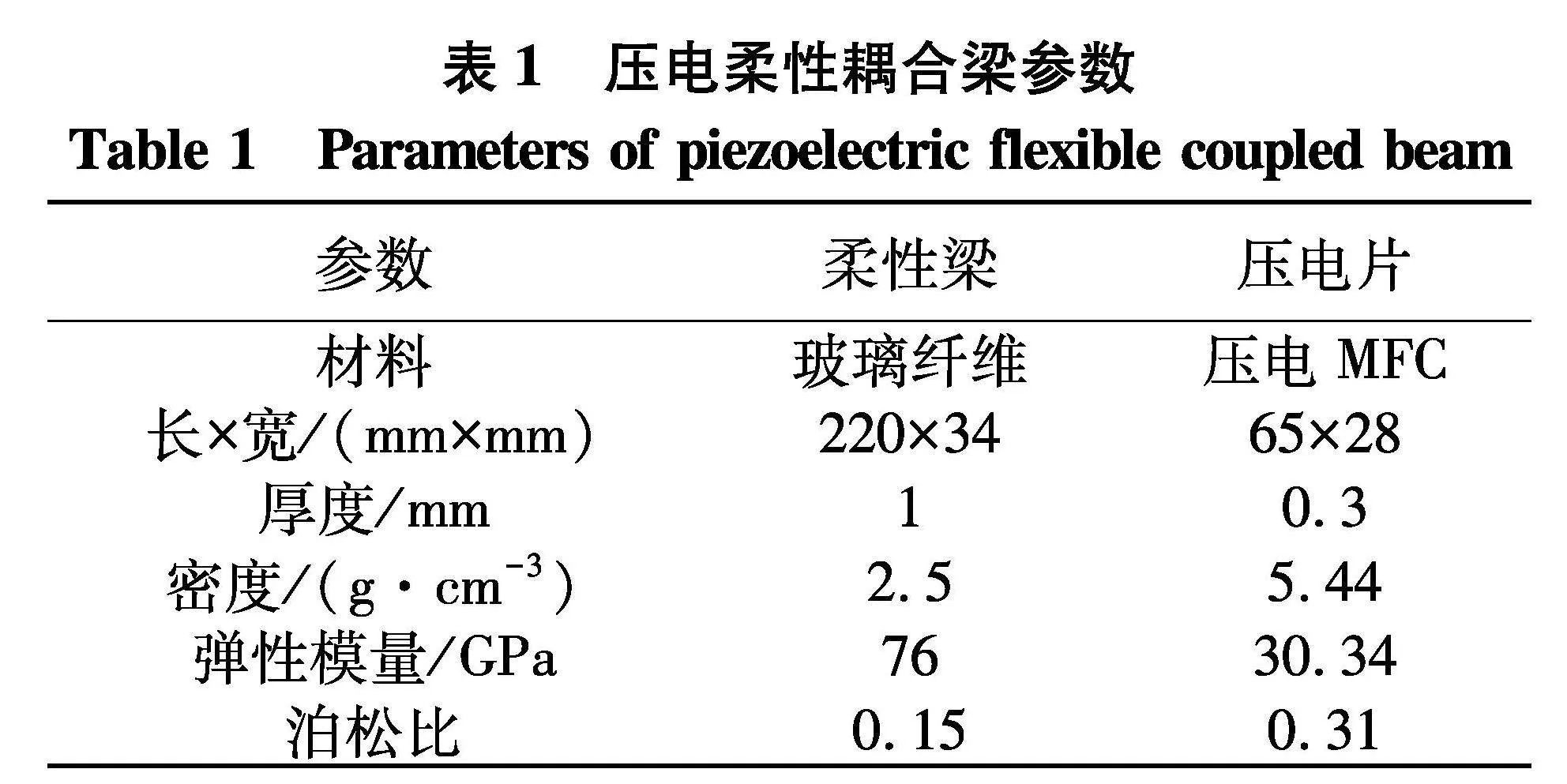
压电柔性耦合梁结构参数如表1，利用表1的耦合梁进行动力学特性分析.

压电柔性耦合梁动力学模型如图1，MFC压电片分布于柔性梁末端，由于l1段和l2段在其长度范围内均属于恒定刚度和截面梁，因此，可将两段分别建立梁模型，通过边界条件建立其耦合关系.

flexible coupled beam

图1中，x1、x2以及y1、y2为两段梁横纵坐标，f1、f2以及FS1、FS2分别为两段梁的剪力和分布载荷，M1和M2为两段的弯矩.根据欧拉-伯努利梁模型，可建立压电柔性耦合梁动力学方程为

E1I14y1（x1，t）x41+ρS12y1（x1，t）x21=f1（x1，t）（E1I1+c33Ip）4y2（x2，t）x42+""" （ρ1S1+ρpSp）2y2（x2，t）x22=f2（x2，t）（1）

式中：E1为柔性梁的弹性模量；c33为压电片的弹性模量；I1和Ip为l1和l2段的截面二次矩；ρ1和ρp为柔性梁和MFC压电片的密度；S1和Sp为柔性梁和MFC压电片的截面积.

当l1段梁和l2段梁的模态函数分别为1（x1）和2（x2）时，由式（1）可得

（4）1（x1）－4ρ1S1E1I1ω21（x1）=0（4）2（x1）－4ρ1S1+ρpSpE1I1+c33Ipω22（x2）=0（2）

模态函数的表达式为

1i（x1）=a1cos（β1x1）+a2sin（β1x1）+

a3cosh（β1x1）+a4sinh（β1x1）2i（x2）=b1cos（β2x2）+b2sin（β2x2）+

b3cosh（β2x2）+b4sinh（β2x2）（3）

式中：Ai和Bi（i=1，2，3，4）为积分常数；β1和β2为系数，β1=4ρ1S1E1I1ω2、β2=4ρ1S1+ρpSpE1I1+c33Ipω2.

通过边界条件可对式（2）进行求解，首先，l1段梁左侧为固定端，梁的挠度和转角都为0，同时，l1段梁右端为自由端，梁的弯矩和剪力均为0，此外，两段梁为连续梁，接触处挠度、转角、弯矩和剪力均相等，由此可得如下边界条件：

1i（0）=0′1i（0）=0″2i（l2）=02i（l2）=01i（l1）=2i（0）′1i（l1）=′2i（0）″1i（l1）=″2i（0）1i（l1）=2i（0）（4）

由式（4）可得，模态函数的系数表达式分别为

a3=－a1，a4=－a2

b1=12a1（1+χ2）cos（β1l1）－（1－χ2）cosh（β1l1）

+12a2（1+χ2）sin（β1l1）－（1－χ2）sinh（β1l1）

b2=－12a1χ（1+χ2）sin（β1l1）+（1－χ2）sinh（β1l1）

+12a2χ（1+χ2）cos（β1l1）－（1－χ2）cosh（β1l1）

b3=12a1（1－χ2）cos（β1l1）－（1+χ2）cosh（β1l1）

+12a2（1－χ2）sin（β1l1）－（1+χ2）sinh（β1l1）

b4=－12a1χ（1－χ2）sin（β1l1）+（1+χ2）sinh（β1l1）

+12a2χ（1－χ2）cos（β1l1）－（1+χ2）cosh（β1l1）（5）

式中：χ为系数，χ=β1/β2.

将模态函数系统的表达式代入式（2）中，可求得系统各阶固有频率.

2" 压电主动振动控制系统设计

2.1" 基于PID的主动振动控制

基于PID的主动振动控制的算法采用数字PID控制，如图2.

图2中，r（k）为平衡处位移，y（k）为悬臂梁振动测量点的实际位移，e（k）为实际与平衡处之间的误差值，u（k）为PID控制器的输出值，且有

e（k）=r（k）－y（k）（6）

u（k）=Kpe（k）+TTi∑kj=0e（j）+Tde（k）－e（k－1）T（7）

式中：Kp是比例系数，Ti是积分时间，Td是微分时间，T是采样时间.

在PID控制系统中，增大Kp可以加快系统的响应速度，有利于减小静差，但Kp过大会使系统产生超调，甚至发生振荡，增加响应时间；增大Ti，积分变弱，有利于减小超调，但同时会延长稳定时间；增大Td可以允许加大比例控制，但Td过大或过小时，系统的超调量、调节时间仍会很大.

由于采样时间T是常数，故式（7）也可以写为

u（k）=Kpe（k）+Ki∑ki=0e（i）+Kde（k）－e（k－1）（8）

2.2" 基于模糊控制的主动振动控制

针对柔性梁模型特点，设计了双输入单输出（DISO）的模糊控制器，其基本原理如图3.图3中r为系统设定值；e和ec分别为误差和误差的变化率；E和 EC分别是反映系统误差和误差变化率的模糊集合；U为模糊控制器的模糊输出；u为去模糊化后精确输出，y为系统反馈.

（1） 模糊化处理

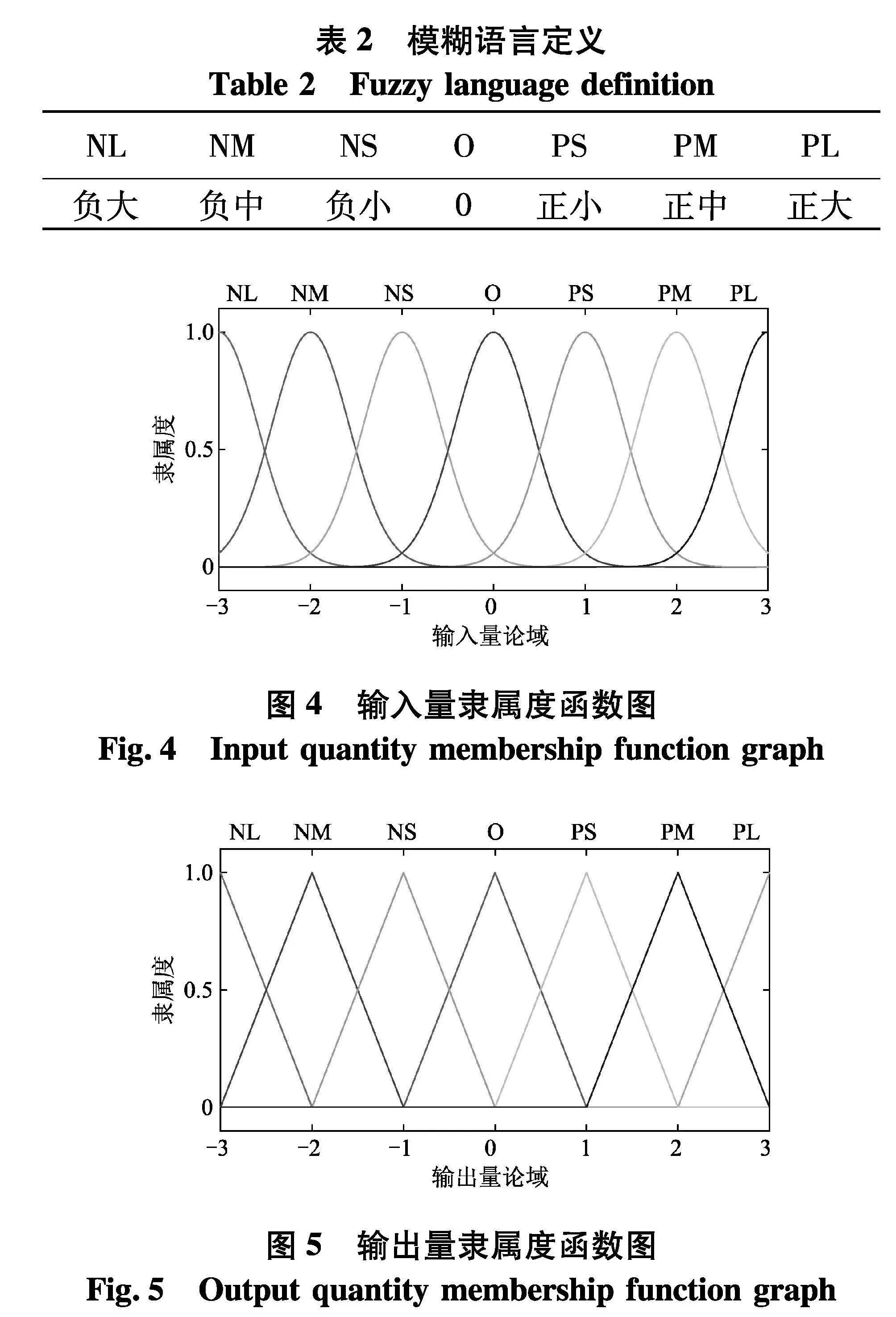
在文中设计的双输入单输出（DISO）的模糊控制器中，控制器的输入为激光位移传感器采集的振动电压与平衡位置的误差e和误差变化率ec，控制器输出u为MFC压电片输出电压.根据悬臂梁系统振动幅值的范围，选取输入量误差e、ec和输出量u所对应的模糊量E、EC和U的模糊子集论域均为［-3，3］，量化因子Ke、Kec和比例因子Ku按不同激振方式设置合理参数.选取采用七级模糊集合，表2为模糊集合中语言变量的具体定义.

文中输入量误差e和误差变化率ec采用高斯型隶属度函数，输出量u采用三角形隶属度函数.输入和输出隶属度函数如图4，5.

（2） 模糊控制规则

对于柔性梁系统，激光位移传感器与MFC压电片对面布置，MFC压电片采用收缩型，所以当梁有正向变形，激光位移传感器采集到正向电压，此时应该向MFC压电片施加正电压，MFC压电片收缩带动悬臂梁产生反向变形.同理，当悬臂梁负向变形时，应该向MFC压电片施加负电压.且梁的形变越大时，施加的控制电压越大.采用Mamdani模糊推理方法，模糊规则如下式：

If （e is NL） and （ec is NL）， then （u is NL）

……

If （e is PL） and （ec is PL） ， then （u is PL）

设计了以矩阵表的描述的7×7=49条规则，如表3.

（3） 去模糊化

去模糊化方法选择重心法，表达式如下：

u*=∑ni=1u*iμimax（u）∑ni=1μimax（u）（9）

式中：u*i为第i个模糊集合与坐标轴围成面积的平分线对应值，uimax（u）为该集合的隶属度.

3" 仿真与实验

3.1" 柔性梁振动特性分析

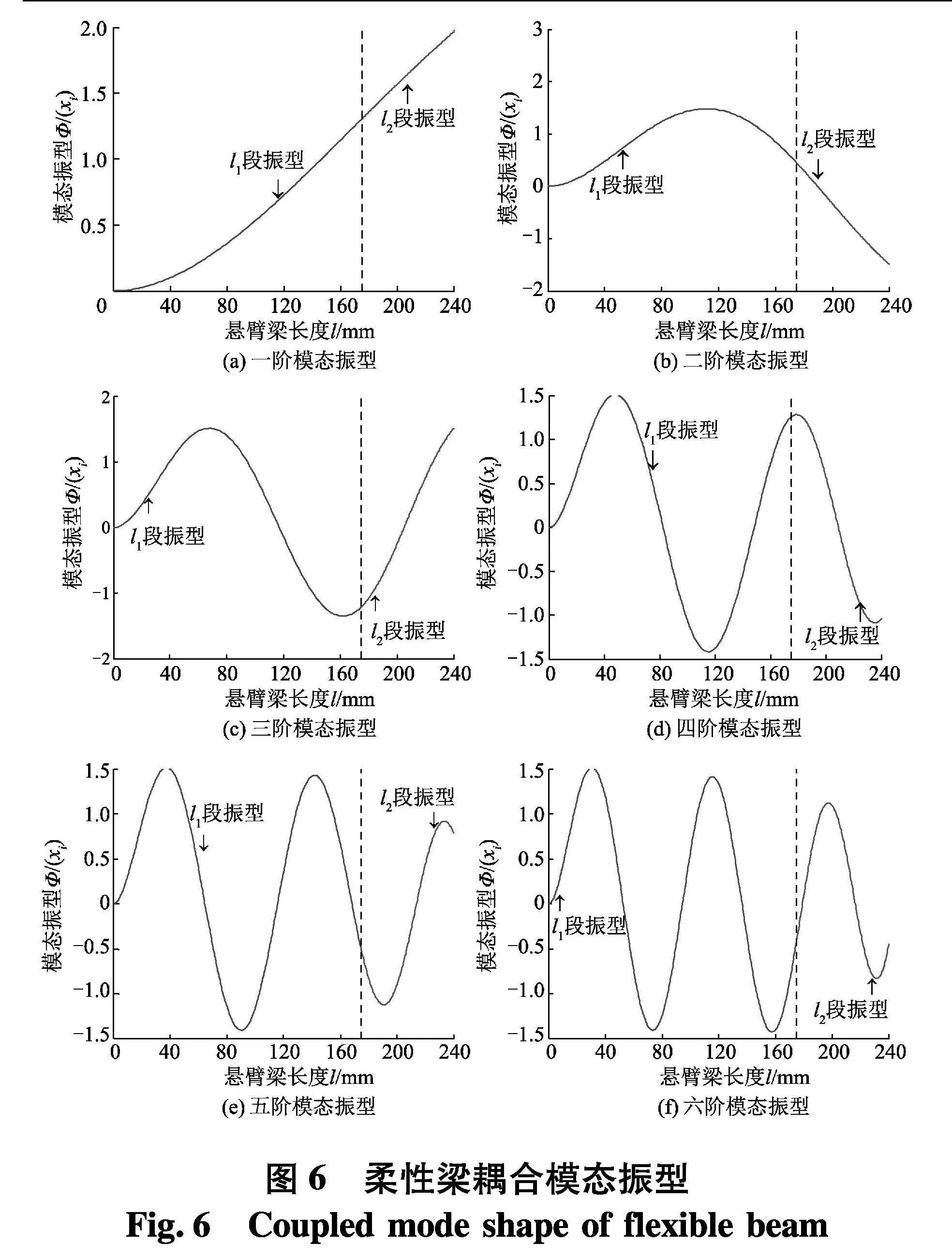
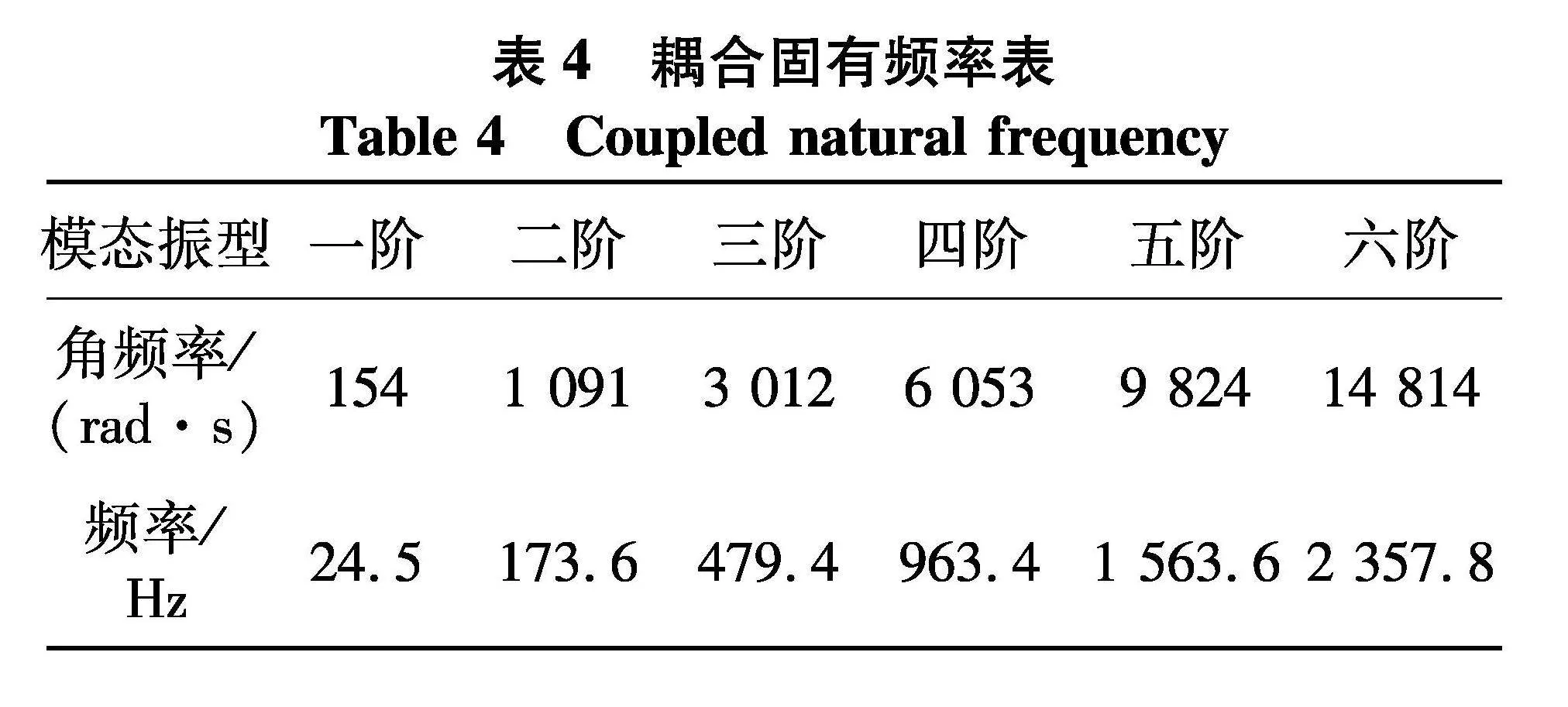
利用表1中的参数值，通过式（2）～（5）可计算出柔性梁系统的耦合固有频率和绘制模态振型，表4为系统耦合固有频率，图6为柔性梁的模态振型.由表4和图6可知：

（1） 柔性梁一阶固有频率值为24.5 Hz，其对应的振型为梁弯曲振动，没有出现峰值，梁末端位置处的位移最大.

（2） 在二阶模态振型中，振动峰值开始出现，且随着阶数的增加，振动峰值数量逐渐增加.前三阶模态振型中，梁末端振动位移与振动峰值相同，而在四～六阶模态振型中，梁末端振动位移小于振动峰值.

（3） 由振型曲线可推断，当柔性梁的振动频率低于一阶固有频率时，梁末端处的振动位移最大，因此，对柔性梁进行低频振动控制时，应当将MFC压电片布置在柔性梁末端位置处.

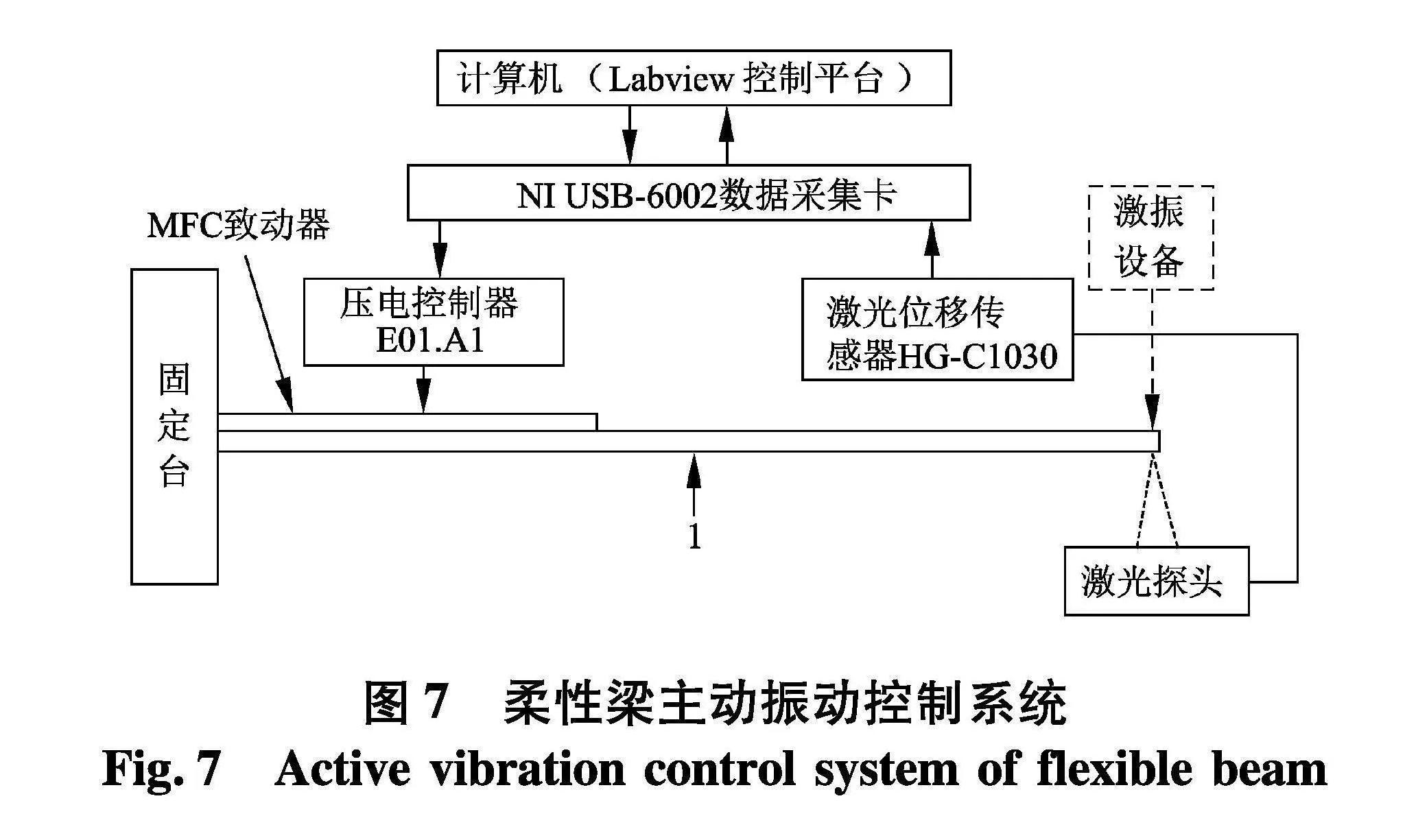
3.2" 柔性梁主动抑振实验

实验系统如图7，实验中，使用激光位移传感器检测悬臂梁末端距平衡位置的振动位移大小，然后转化为对应的电压经NI USB 6002数据采集卡传入计算机中，计算机应用数字PID控制算法对电压数据进行处理，计算出对应的控制电压，再控制数据采集卡输出此电压，经过压电驱动器放大后作用在MFC致动器上，使MFC致动器产生相应的形变来抑制悬臂梁的振动.本实验所有位移大小均使用对应的电压幅值大小来表示.

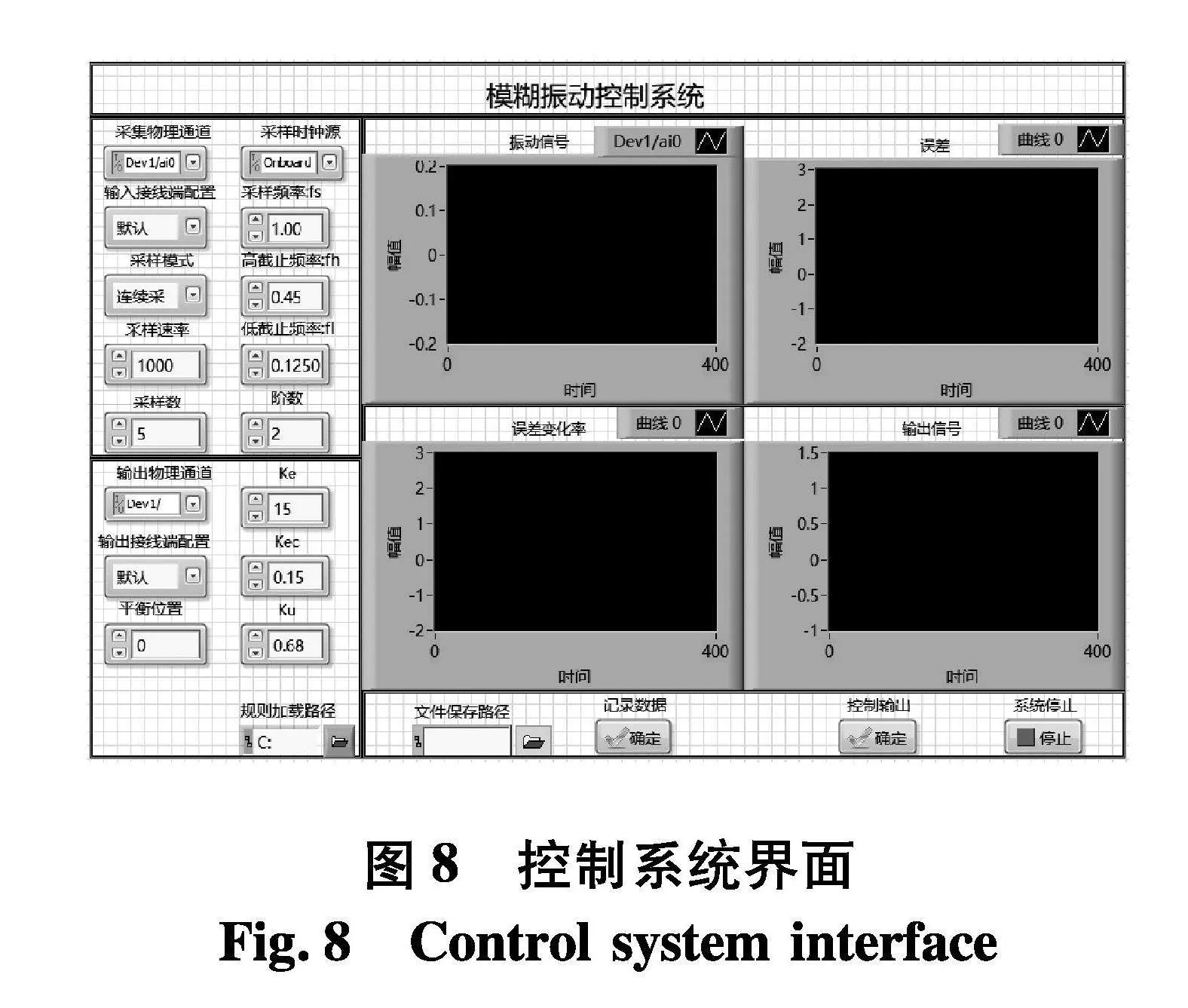
利用LabVIEW软件将图2和3的PID和模糊控制原理编写悬臂梁主动振动控制程序，程序集信号采集、数据存储、数据实时显示、数据处理、控制信号输出等功能于一体，操作界面如图8.

首先进行瞬态扰动下柔性悬臂梁振动控制实验，在本实验中，在悬臂梁端部系一根细线，通过拉

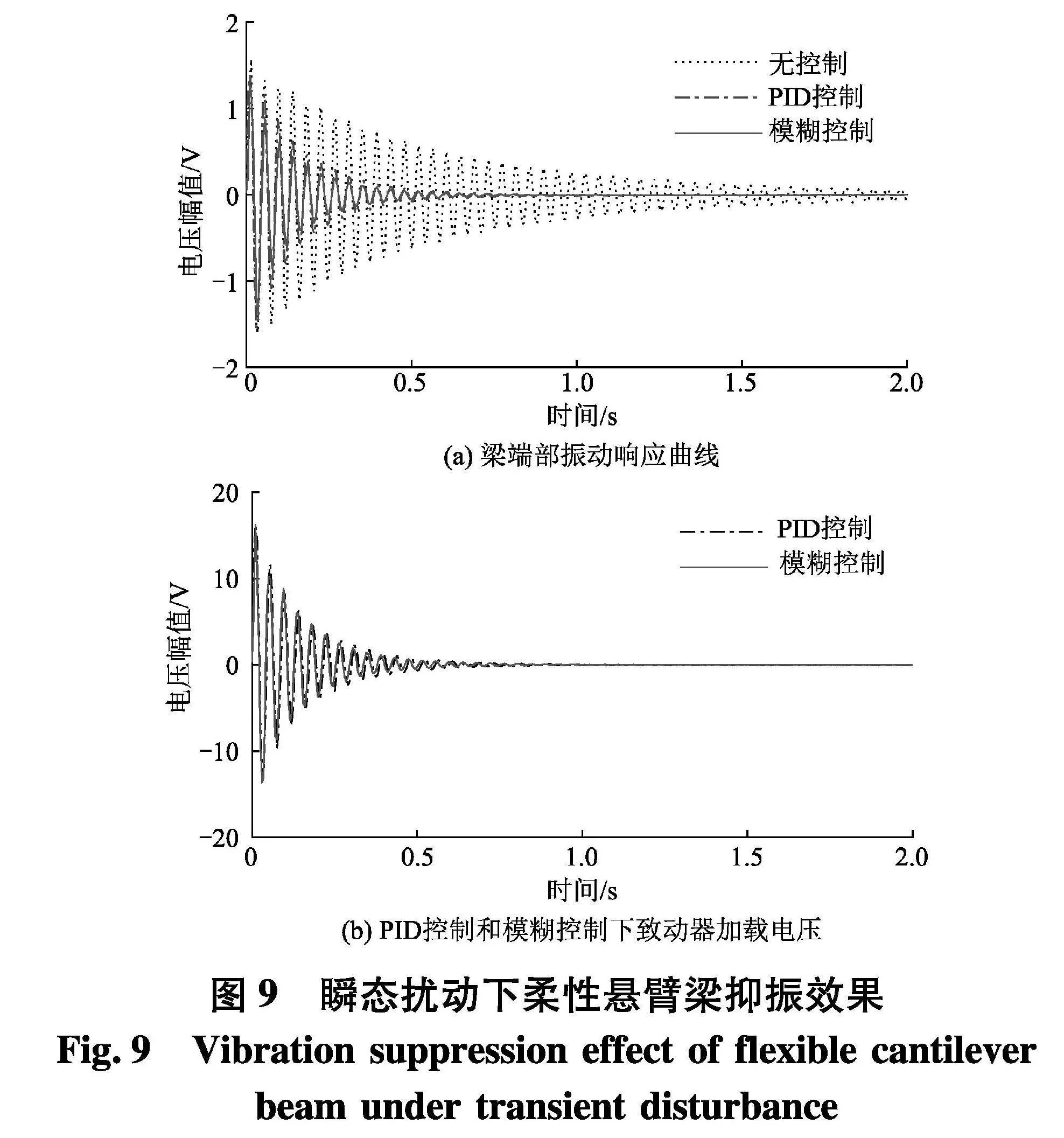
动细线并固定，给悬臂梁端部一个初始位移，使其偏移平衡位置6 mm，剪断细线后，使梁端部无控振动；在主动控制系统中，合理设置控制系统各运行参数，设置采样模式为连续采样，采样速率为1 000，每通道采样数为5，循环时间为5 ms，使其获得良好的运行效果.其中PID控制中，设定Kp=0.1，Ti=1 s，Td=0.005 s；在模糊控制中，设定量化因子Ke=2，Kec=0.2，输出通道比例因子Ku=0.6.压电控制器输出增益固定为100倍.再次重复上述步骤，使梁端部有控振动，得到无控制、PID控制和模糊控制状态下的梁端部振动响应曲线以及PID控制和模糊控制状态下的MFC压电片致动器加载电压，如图9.

由图9可知，给定初始位移后，无控时，梁端部的振幅在自身阻尼的作用下缓慢衰减，在5.2 s后彻底停止振动；施加PID控制和模糊控制后，梁端部的振动在1 s内均完全停止振动；施加模糊控制后在每个振动周期内的振幅均小于施加PID控制后的振幅，其抑振效果优于PID控制.

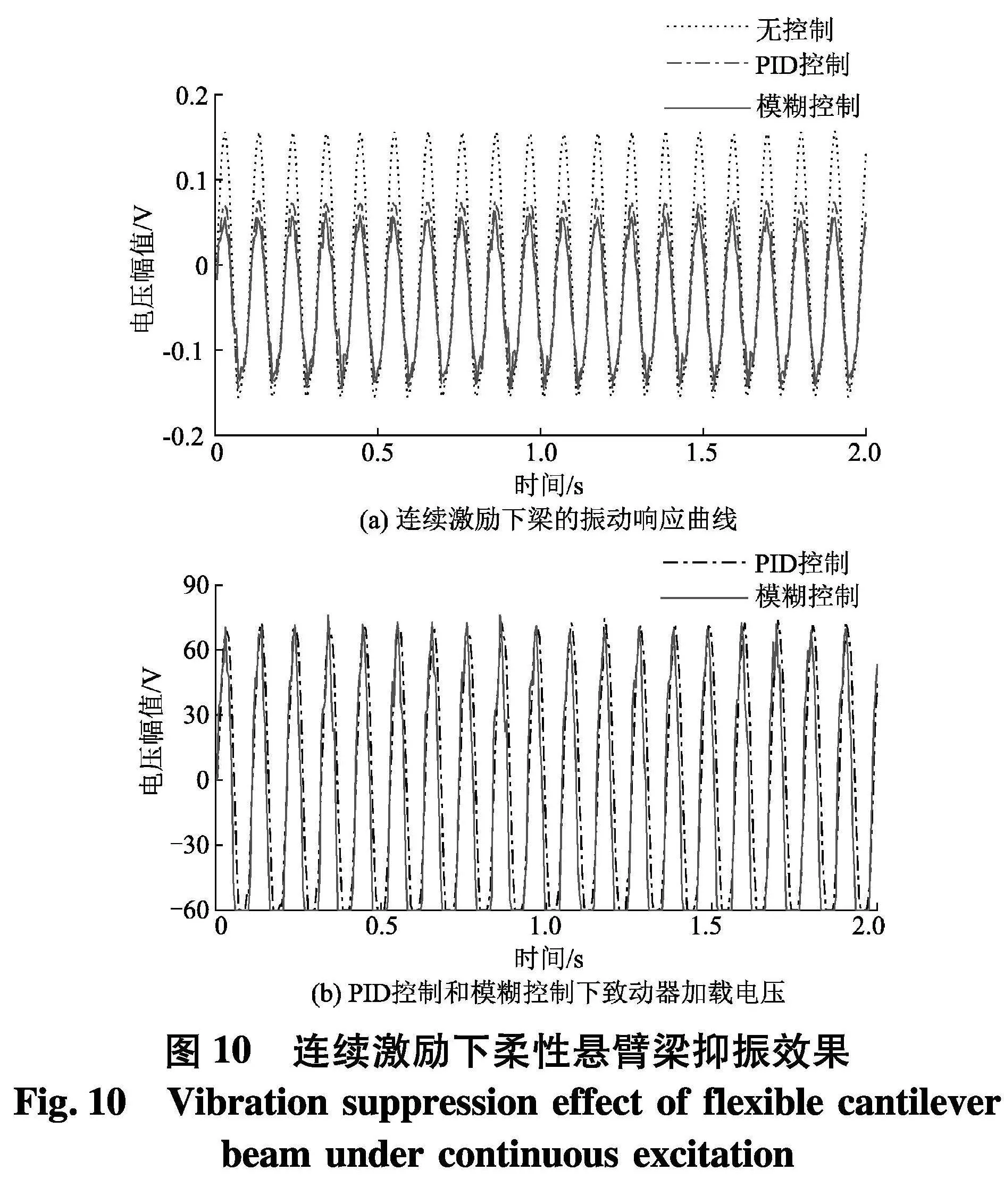
同时，对连续信号激励下柔性悬臂梁抑振效果进行了研究.采用激振仪对悬臂梁端部进行激励，同时激光传感器对图7中梁末端位置进行信号采集.手动设置激振设备的振动信号的频率和振幅，得到多组振动响应曲线，以激振设备产生频率10 Hz，幅值4 mm的振动信号为例，在PID控制中，设定比例Kp=9，Ti =2 s，Td =0.01 s；在模糊控制中，设定量化因子Ke=15，Kec=0.15，输出通道比例因子Ku=0.68.压电控制器输出增益固定为100倍.得到持续激励下，无控制、PID控制和模糊控制状态下的悬臂梁的振动响应曲线以及PID控制和模糊控制状态下的MFC致动器加载电压，如图10.

由图10可知，施加PID控制后，悬臂梁的振幅减小了30%左右.施加模糊控制后，悬臂梁的振幅被消减了35%左右.通过不同控制系统下压电致动器的振动响应比较可知，模糊控制稳定性弱于PID控制的稳定.

此外，施加控制后正负两方向的振幅衰减不一致，这是因为MFC压电致动器粘贴在悬臂梁的一面，压电致动器以收缩形变为主，带动悬臂梁单向产生形变为主，所以导致悬臂梁正负向振动抑制效果不一致.

4" 结论

文中建立了压电柔性耦合梁的动力学模型，分析了耦合梁的模态特性，利用LabVIEW平台设计了基于模糊控制的压电柔性耦合梁压电主动振动控制系统.搭建了实验测试系统，对不同激励下柔性梁的抑振效果进行了测试和比较.结果表明：

（1） 当柔性梁的振动频率低于一阶固有频率时，梁末端处的振动位移最大.

（2） 在柔性梁连续激励振动下，利用模糊控制可以使柔性梁的振动幅值减小35%.

（3） 模糊控制的减振效果优于PID控制，而PID控制的稳定性更好.

参考文献（References）

［1］" SOHN J W， CHOI S B， LEE C H. Active vibration control of smart hull structure using piezoelectric composite actuators［J］. Smart Materials and Structures， 2009， 18（7）： 074004.

［2］" GAO F， YAN Y， YAP F F. Active noise control using piezoelectric actuators in Hard Disk Drives［J］. Mechanics Based Design of Structures and Machines， 2003， 31（4）： 475-490.

［3］" WATANABE T， KAZAWA J， UZAWA S， et al. Numerical and experimental study of active flutter suppression with piezoelectric device for transonic cascade［C］∥ 2008 Proceedings of the ASME Turbo Expo： Power for Land， Sea， and Air. Berlin， Germany： June 9-13， 2008： 849-859.

［4］" DUFFY K P， CHOI B B， PROVENZA A J， et al. Active piezoelectric vibration control of subscale composite fan blades［J］. Journal of Engineering for Gas Turbines and Power， 2013， 135（1）： 011601.

［5］" WANG W， ZHANG X P， YANG Z C， et al. Piezoelectric active control for tail buffeting at high angle of attack［J］. Science China Technological Sciences， 2012， 55（10）： 2694-2699.

［6］" LI Y， QIU Y Y， PENG F J. Active vibration control for the flexible spacecraft structure based on an atmd/ppf strategy［J］. Applied Mechanics and Materials， 2011， 105-107： 668-674.

［7］" 邓国红. 基于压电陶瓷的轿车顶棚振动主动控制技术研究［D］. 重庆： 重庆大学， 2010： 67-87.

［8］" QIAO Y H， HAN J， ZHANG C Y， et al. Finite element analysis and vibration suppression control of smart wind turbine blade［J］. Applied Composite Materials， 2012， 19（3-4）： 747-754.

［9］" 孙杰， 黄庭轩， 孙禄君， 等. 基于压电纤维复合材料的抖振主动控制研究［J］. 机械强度， 2020， 42（4）： 770-776.

［10］" 张博， 丁虎， 陈立群. 基于压电纤维复合材料的旋转叶片主动控制［J］. 力学学报， 2021，53（4）： 1093-1102.

［11］" 张志强， 乔印虎. 风力机叶片等效悬臂梁模糊PID控制［J］. 佳木斯大学学报（自然科学版）， 2021，39（5）： 83-86.

（责任编辑：顾琳）