基于图网络的船舶柴油机健康监测

摘" 要： 为实现船舶柴油机的智能健康监测，本文提出了一种双图采样的图网络归纳式学习算法（Dual-GraphSAINT）.为充分挖掘柴油机振动信号中的潜在信息，分别基于局部与全局一致性假设，对振动信号和故障状态构造邻接图.通过邻接图内数据之间的连接关系对节点状态进行学习，以准确的挖掘出柴油机运行过程中的潜在故障信息.同时Dual-GraphSAINT是一种归纳式学习算法，突破了传统图网络不能对未见节点生成有效嵌入表征的弊端，实现了对柴油机健康状态实时检测的性能.文中所提出的健康监测方案与传统的数据驱动和深度学习方案进行比较，获得了最佳的性能，显著提高了船舶柴油机的健康监测效果.

关键词： 柴油机；健康监测；图网络

中图分类号：U664""" 文献标志码：A""""" 文章编号：1673-4807（2024）01-019-08

DOI：10.20061/j.issn.1673-4807.2024.01.004

收稿日期： 2021-08-28""" 修回日期： 2021-04-29

基金项目： 四川交通职业技术学院教改项目（2023-JG-46）

作者简介： 熊正华（1971—），男，副教授，研究方向为船舶轮机自动控制.E-mail： 1136652013@qq.com

引文格式： 熊正华，尚前明，杨安声，等.基于图网络的船舶柴油机健康监测［J］.江苏科技大学学报（自然科学版），2024，38（1）：19-26.DOI：10.20061/j.issn.1673-4807.2024.01.004.

Health monitoring of marine diesel engine based on graph network

XIONG Zhenghua1，SHANG Qianmin2，YANG Ansheng2，DU Hongcheng3

（1.Sichuan Transportation Vocational and Technical College， Chengdu 611130，China）

（2.School of Energy and Power Engineering， Wuhan University of Technology， Wuhan 430063， China）

（3.Urban Technician College of Sichuan， Chengdu 610000， China）

Abstract：In order to realize the intelligent condition monitoring of marine diesel engines， the graph network algorithm is introduced. In this paper， a dual graph sampling graph network inductive learning algorithm （Dual-GraphSAINT） is proposed for diesel engine health monitoring. Firstly， in order to fully mine the potential information in the diesel engine vibration signal， the adjacency graph is constructed for the vibration signal and fault state based on the local and global consistency assumptions respectively. Then， the node state is learned based on the connection relationship between the data based on the double adjacency graph， so as to accurately monitor the potential health state during the operation of the diesel engine. At the same time， Dual-GraphSAINT is an inductive learning algorithm， which breaks through the disadvantage that the traditional graph network cannot generate an effective embedded representation of unknown nodes， so it can analyze the health state of diesel engine in real time. The proposed health monitoring scheme obtained the best performance compared with the traditional data-driven and deep learning schemes. The health monitoring performance of the marine diesel engine is significantly improved.

Key words：diesel engine， health monitoring， graph convolution network

随着工业与科技的飞速发展，越来越多的大型智能柴油机在船舶中得到了广泛应用.同时，由于柴油机设备的复杂性和多样性，使其运行过程中的振动信号受多种不确定因素影响，从而导致潜在的故障特征会被淹没［1-2］.因此如何对柴油机潜在的故障特征进行有效的提取及分析仍是目前工业及学术界的主要难点.智能健康监测技术在柴油机健康监测领域取得了非常多的显著成果［3］.对于柴油机的大量监控信号，可以采用神经网络之类的人工智能技术代替专家诊断，以快速分析并提取这些监控信号中的潜在故障信息，并通过有效的学习对系统的健康状况做出识别与预测［4］.而现有的智能健康监测技术主要分为特征提取和故障识别两大步骤［5］，将现有的智能健康监测技术分为传统的数据驱动和深度学习两大类.文献［6］基于傅里叶变换的方法提取了电动机的故障特征，并通过马氏距离的方法来区分电动机的健康状况.文献［7］首先对数据进行统计处理，然后采用层次网络对健康状况进行分类识别.文献［8］通过特征增强来对数据信号进行处理以提高振动信号中潜在故障信息的状态特征，从而加强对此类特征信息的学习.文献［9］根据不同的小波分解提取振动信号的统计特征以获得潜在的有效信息，并应用k-近邻算法来识别健康状况.文献［10］专门设计了两个功能部件，并使用这些功能部件和相关矢量来识别系统的健康状况.由于传统的分类器无法从原始信号中提取有效特征，因此，需要人工设计特征［11］.这种特征设计过程需要利用信号处理和故障诊断等知识，这将花费大量的人工并且专业性要求较高，从而使得自动化程度降低.

文献［12］将卷积神经网络应用到健康状态检测过程中，通过深度学习对数据中潜在故障特征进行有效的提取，并根据提取的特征学习到高效的分类模型以解决健康诊断的问题.深度学习模型克服了传统的基于数据驱动的健康监测方案中需要专业的人员对数据特征进行处理的不足，并极大的提高了系统的自动化程度.在深度学习中，图网络（graph convolution network，GNN）通过邻接特征的相关性自动完成特征提取的任务［13］，并有效的学习数据之间特殊的拓扑关系，使其为健康监测问题带来了更好的解决方案.但是，目前GNN等相关算法还没有在健康监测上得到很好的应用，文中将GNN进一步改进使其更好的应用到柴油机的健康监测.

最近，在图上进行表征学习备受关注，因为它极大地促进了分类和聚类等任务，这将为GNN在健康监测领域上提供了良好的应用基础.与传统深度学习相比，GNN在学习过程中可以对节点的连接边，节点信息特征以及数据的全局语义结构进行学习.文献［14］将卷积运算推广到图域，克服了传统深度学习不能在拓扑空间中进行推理学习的缺陷.因此GNN将只能处理常规的欧几里德空间的传统卷积神经网络（convolutional neural networks，CNN）扩展到了非欧几里德空间，并在提取数据特征的同时考虑到了数据之间的相关性.同时，GNN可以通过数据的邻接图，对相邻节点的特征信息进行聚合以充分挖掘相邻节点中的潜在相关信息.此外，文献［15］使用Chebyshev展开的局部化滤波器加快了图卷积的计算速度.文献［16］提出进行小批量训练，在完整的训练图中对每一层的节点或边缘进行采样以形成小批量数据，通过学习对不同数据图结构的表征方式来解决对未知节点预测的问题.然而GNN在实际应用中仍存在以下缺陷：① 邻居爆炸：随着模型层数加深，GNN通过不断地学习相邻节点的潜在信息而使节点信息最终趋近相同，从而降低模型的性能；② GNN将所有数据点作为图输入训练，只能处理固定大小的图结构，因此对于新生成的样本点无法预测，必须加入原始数据重新学习，这在工业场景中是不利的.

为解决以上问题，一种双图采样的图网络归纳式学习算法（Dual-GraphSAINT）被提出并应用于柴油机的健康监测中，展示了船舶柴油机在运行过程中的不同健康监测流程.为充分挖掘柴油机振动信号中故障特征的潜在信息，分别基于局部与全局一致性假设，对振动信号和故障状态构造邻接图.同时在学习过程中，对邻接图进行采样以构造子图，通过学习节点的表示方式来训练模型，使模型可以预测新增加的样本点，这为Dual-GraphSAINT在柴油机的健康监测中得到实际应用提供了可行性.同时模型中采用跳跃知识网络（JK-net）［17］解决了“邻居爆炸”缺陷，最终该算法在柴油机振动信号上进行健康监测验证，取得了优越性的结果.

1" 图卷积神经网络方法

定义1：图通常表示为G=（V，E，A），其中：V表示图中节点的数目；E表示节点间相连的边；A表示邻接矩阵.其中在一个图中，vi∈V来定义一个节点，eij=（vi，vj）∈E来定义两个相邻节点的边，邻接矩阵A是一个N×N的矩阵，同时，如果eij∈E，则Aijgt;0，若eijE，则Aij=0.

1.1" 图卷积神经网络

从特征空间来划分，图卷积神经网络可以分为频域和空域两个类型.其中卷积通过使用图傅立叶变换将节点表示转换到光谱域中进行卷积；空间卷积通过考虑节点邻域进行卷积.图网络可以将原始图结构数据G=（V，E）映射一个新的特征空间，从而可以对邻接节点的特征充分表示.以图网络为例，第l层神经网络的特征用hl表示，这样针对图结构中的每个节点vi在计算时，每一层神经网络的输出hl+1都可以通过非线性函数表示为hl+1=f（hl，A），其中A为特征邻接矩阵.通过非线性激活函数ReLU=σ（·）实现一个图卷积神经网络结构，其分层传播规则为：

f（hl，A）=σ（D︿-1/2AD︿-1/2hlWl）（1）

式中：D︿=∑ijAij表示矩阵A的对角矩阵，Wl为第l层图网络的权值矩阵；通过分层传播规则，图网络将卷积神经网络局部参数共享的特性带入了图结构中，使得每一个节点的感受域的范围随着传播层数的增加而得更大的提升，从而获取到更多邻域节点的信息.

1.2" 基于频域的图卷积神经网络

卷积是CNN中最基本的操作.但是，对于CNN的标准卷积运算不能直接应用于图，因为图缺少网格结构.文献［13］首先将图拉普拉斯矩阵L引入了来自谱域的图数据卷积，它在信号处理中起着与傅立叶基础相似的作用.传统的卷积操作只能处理欧式空间的数据结构而不能应用于非欧几里德的图结构中.为克服这个缺陷，图网络通过引入图拉普拉斯矩阵L建立了不同数据之间的空间联系，具体的图卷积运算W*定义为：

viW*vj=U（（UTvi）⊙（UTvj））（2）

式中，U是L的特征向量.简单地说，乘以UT将图振动信号vi和vj变换到频谱域（即图傅里叶变换），而乘以U则执行逆变换.该定义的有效性基于卷积定理，即卷积运算的傅立叶变换是其傅立叶变换的逐元素乘积.然后，振动信号hl可以通过：

hl+1=UΘUThl（3）

式中，Θ=Θ（Λ）∈RN×N是可学习滤波器的对角矩阵，而Λ是L的特征值.

1.3" 基于空间的图卷积神经网络

基于传统CNN在训练样本上的卷积操作，图网络根据节点的空间关系定义图卷积.对于一般图，基于空间的图卷积采用中心节点通过其邻居的聚合来获得该节点的新表示.为了探索节点接收邻域信息的深度和广度，通常的做法是将多个图卷积层堆叠在一起.根据堆叠卷积层的不同方法，基于空间的GNN可以进一步分为两类，即基于循环的GNN和基于组合的GNN.文献［18］将几种现有图卷积网络概括为一个称为消息传递神经网络（MPNN）的统一框架. MPNN由两个阶段组成，即消息传递阶段和读取阶段.消息传递阶段实际上运行l层基于空间的图卷积.图卷积运算是根据消息函数Mt（·）和更新函数Ut（·）定义：

（hi）l+1=Ut（（hi）l，∑j∈N（i）Mt（（hi）l，（hj）l，eij））（4）

式中，（hi）l为节点vi在第l层神经网络对应的编码特征.

2" 基于Dual-GraphSAINT的柴油机健康监测流程

在Dual-GraphSAINT的柴油机健康监测算法中，通过学习节点特征信息的表示方法来对新增加的样本点进行预测.该算法流程如图1，在训练开始之前，首先对柴油机振动信号和故障状态构建邻接矩阵.其中基于局部一致性假设，认为相似的振动信号应该具有相同的标签，因此可根据k-近邻对柴油机的振动信号构建邻接矩阵A，其中如果eij∈E，Aij=e-‖vi-vj‖2σ2；若eijE，则Aij=0.同时基于全局一致性假设，对于故障状态构建邻接矩阵P，以避免被振动信号相似但故障信号不同的噪声数据影响，其中如果节点vi与节点vj标签相同，则Pij=1；若vi与节点vj标签不相同，则Pij=0.然后在每次迭代训练过程中，从节点V中随机采样|Vs|个节点，以通过无偏估计近似估计全图的训练模型，这样可以使得模型训练过程中学习不同图形结构的节点表示方式，而不是只能处理固定已知图的数据，使的模型无法对训练图以外的新增加的数据进行预测.同时采用SGD的方法来对模型参数进行更新以不断优化模型直到达到最优解.每次迭代训练过程中均独立的从大图中进行随机采样，其中采样子图定义为Gs（|Vs||V|）. 然后，建立全连接的双图GNN层以生成嵌入表示，可以通过以下方式计算：

ha，l+1=σ（A︿sha，lWa，l）（5）

hp，l+1=σ（P︿shp，lWp，l）（6）

式中：h为Vs对应的采样节点，代表柴油机振动信号；A︿s为采样后的振动信号的邻接子图；P︿s表示采样后故障状态的邻接子图；W为参数矩阵，其中下标a和p分别对应的是A︿s和P︿s所在的卷积层，l对应第l层神经网络.文中采用三层GNN，利用邻接矩阵在每个消息传递步骤中实现邻域信息的完全线性混合，可以有效地训练聚合参数，使模型学得针对不同图结构的节点的表示形式.同时引用了一种跳跃知识网络（JK-net）［17］以克服信息在传递与学习的过程中“信息爆炸”带来的危害，并可以灵活地利用每个节点的不同邻域范围节点信息来学习更好的结构感知表示.文献［17］具有一个额外的最终层，该层聚集了图卷积层1到3的所有输出隐藏特征，其中聚合层输出hJK：

hJK=σ（WTJK·（3l=1ha，l+3l=1hp，l））（7）

式中，是向量聚合运算，可以是最大池化，串联或基于LSTM的聚合［17］，文中采用串联运算符聚合所有隐藏特征.最后将模型挖掘的潜在特征hJK送入一个GNN层并通过softmax函数实现对柴油机不同健康状态的预测：

Hs=softmax（A︿shJKWJK）（8）

对于Dual-GraphSAINT的健康监测算法的优化，采用交叉熵损失：

Lbatch=∑Gs∈GYslogHS（9）

式中，Ys为从柴油机健康状态Y中采样子图对应的标签.传统的图网络只能针对固定已知图进行训练，而对图结构以外的未知的节点不能预测，这就使传统的图网络算法在实际柴油机健康监测的应用过程中无法对新生成的振动信号进行实时检测与识别.针对这个缺点，通过图采样的训练方法，采用无偏估计近似训练出原图模型，使模型学到对不同图结构节点的表示方法，从而可以对图结构以外的新增加的数据进行预测.因此Dual-GraphSAINT是归纳式学习算法，可以将训练好的模型应用到实际的柴油机健康状态检测的过程中.并且，为了最大化利用柴油机振动信号的潜在信息，分别对振动信号和故障状态构建邻接矩阵，通过从局部和全局的角度对柴油机振动信号的数据特征进行充分学习与挖掘，使其对测试集的正常工况数据与故障工况数据可以达到最佳的分类效果.Dual-GraphSAINT 的伪代码如算法1.

算法 1." Dual-GraphSAINT framework

输入： 训练图G=（V，E，A，P）；柴油机健康状态Y.

输出： 对未知故障状态的预测值

Process：

1： 初始化：

2： 构建实例特征邻接矩阵A和标签邻接矩阵P

2： for each minibatch do

3：" 子图采样Gs（其中|Vs||V|），分别对A︿，P︿s进行采样；

4：" 根据公式（5）（6）（7）（8）对采样子图进行GNN全连接训练；

5：" 最小化公式（9）并通过反向传播更新权值；

6： end for

3" 基于柴油机健康监测的实验研究

3.1" 数据描述

文中将四冲程船舶柴油机作为验证健康状态监测方案有效性的研究对象，通过对船舶柴油机运行过程中健康状态检测识别的准确率来评价不同算法的有效性［18］.振动信号和转速信号可以展示柴油机的状态信息数据.但是转速信号的波动是由气体压力的切向力以及活塞和连杆往复运动引起的垂直不平衡惯性力造成的，反映更多的是柴油机燃烧过程中的故障.而振动信号包含了往复运动、旋转运动、机械冲击和气体的高速流动等丰富的信息.能够反映出更多的柴油机状态信息.因此文中基于振动信号的分析是对内燃机健康状态监测的重要途径.图2为故障监测方案中使用的船舶柴油机测试平台.其中表1显示了测试台对船舶柴油机在4个不同工况以及模拟方案的介绍.文中以3 200个数据点为一个采样周期.为保证数据的均衡性，对于每种工况下，对转速稳定后的柴油机进行200组采样，总共800组.在实验中，对采集的船舶柴油机的振动信号进行随机打乱并提取其中的五分之一作为测试集，其余振动信号设为训练集.

故障设置现场操作如图3.

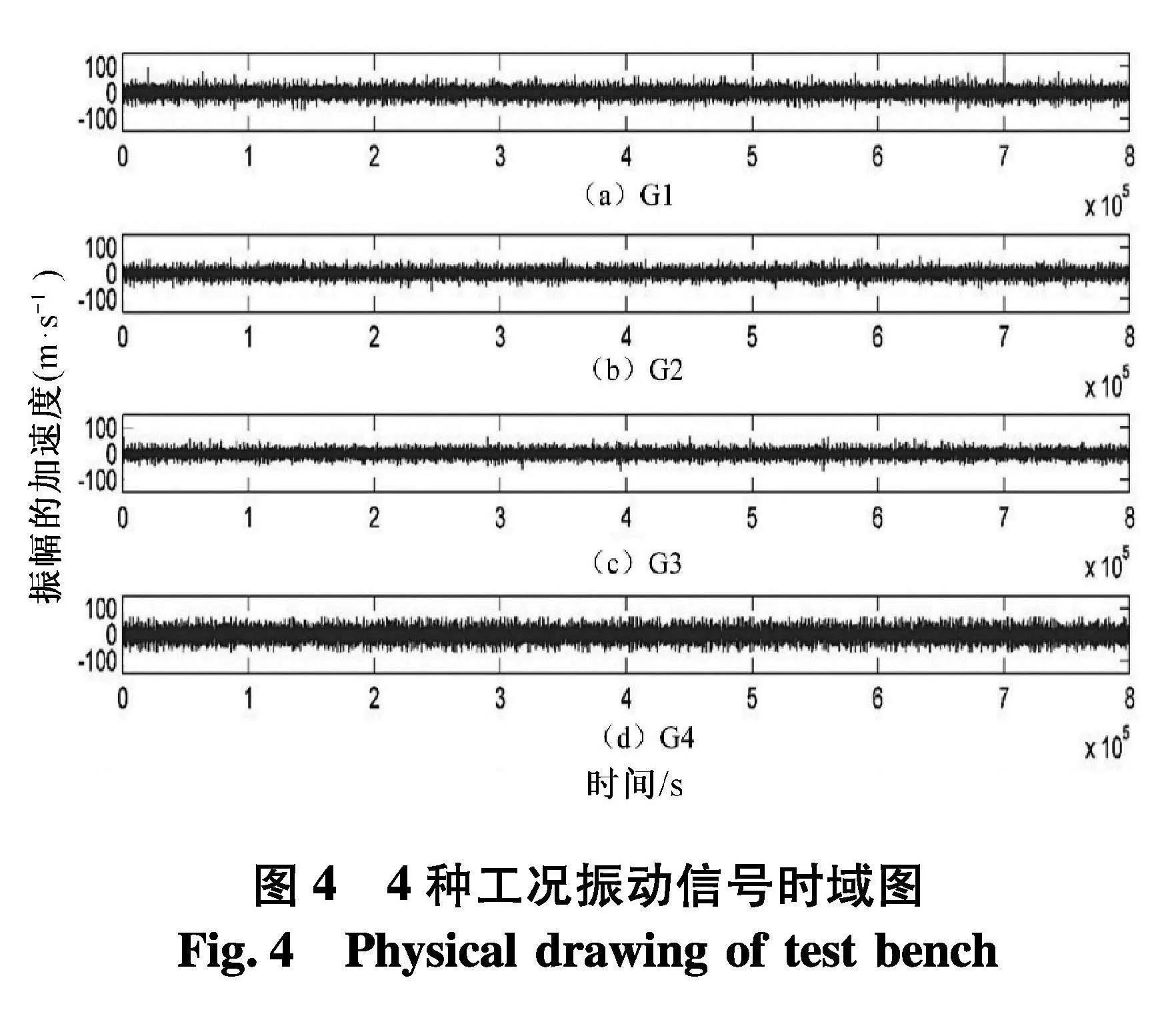
文中所采集船舶柴油机在4个不同工况下的振动信号时域，如图4.

3.2" 基于传统数据驱动的柴油机健康监测结果

文中所提出的Dual-GraphSAINT算法对柴油机健康监测方案的性能将与传统的数据驱动以及卷积神经网络监测方案进行对比.传统的数据驱动方案根据人工设计特征和简单分类器实现对未知数据健康状态的预测.而卷积神经网络监测方案通过从振动信号数据中进行潜在特征信息提取然后通过神经网络进行学习检测，达到端到端监测的目的，最终根据从原始数据学习的信息实现对未知数据健康状态的预测.

所有的算法都是基于python 3.6.8编写的，特别是深度学习模型是通过pytorch框架进行训练测试.同时模型在训练过程中会因为数据量的大小，迭代次数设置不同而使模型训练时间有所差别，但在训练好的模型中，运算速度非常快，可以达到实时检测.

3.2.1" 传统的数据驱动方法

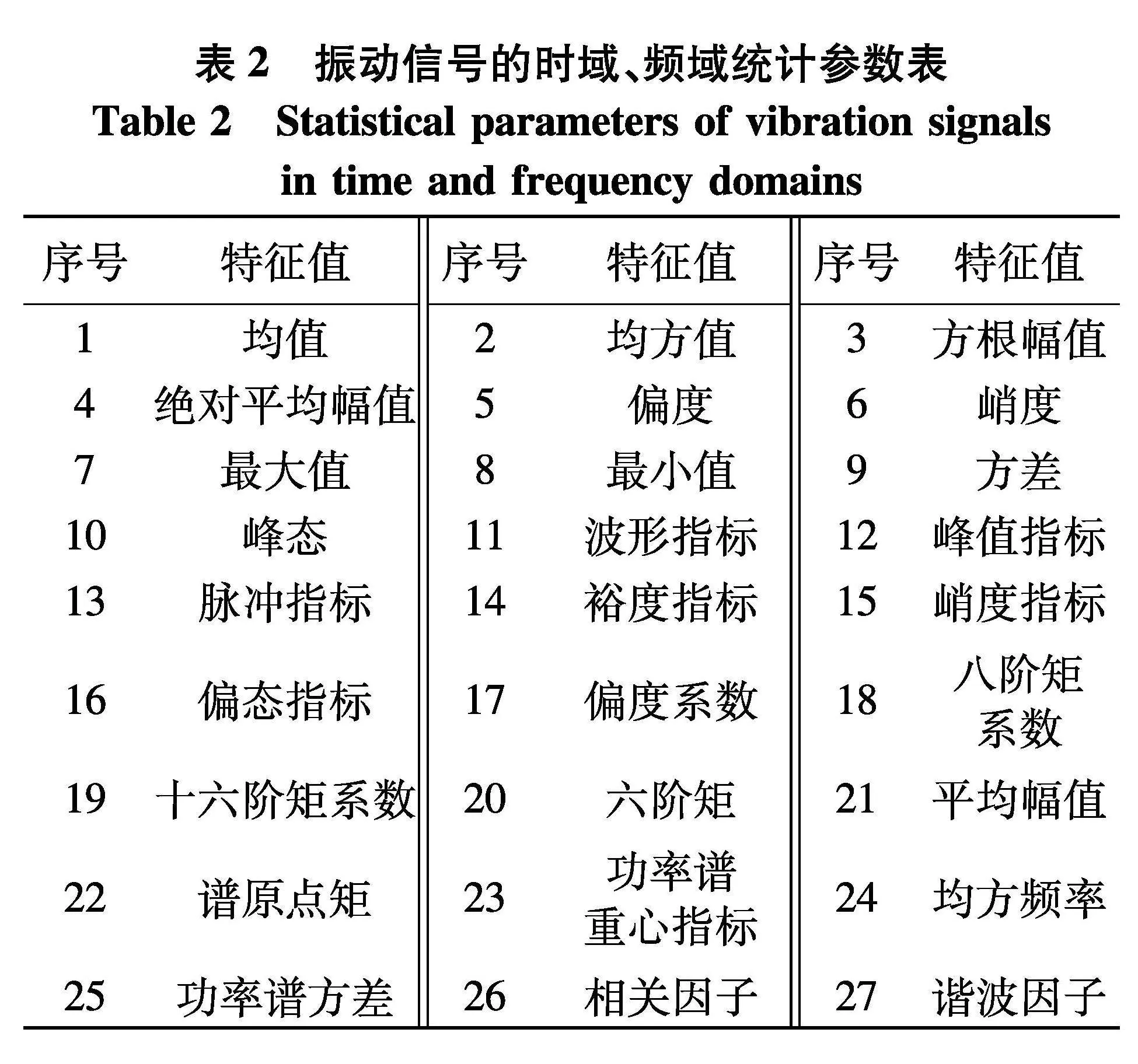
传统人工设计进行特征提取的方法是将柴油机运行过程中的振动的信号进行提取，通过在时域与频域上进行分析统计，使其幅值、能量分布等特征随着时间变化的规律用统计学方法进行描述.一般而言，柴油机设备的健康状态是根据时域波形的不同并分析其内在变化而判断的；而频域分析的目的是对柴油机振动信号中的组成部分进行分析判断.针对以上方法可以将柴油机振动信号通过统计参数（表2）进行分析表示.研究中，将时域、频域特征统计参数组合起来构成的融合特征向量作为信号的初始特征，可有效弥补单一时域或者频域特征的不足.

在传统的数据驱动方法中，当大量具有人工设计的27个高维特征作为振动信号同时输入到训练模型时，直接对信号进行学习分类，容易造成维数灾难，导致潜在的真实故障特征被大量的噪声数据所淹没，从而降低分类器的有效性，所以需要对原始的高维特征进行筛选.文中为验证Dual-GraphSAINT算法对柴油机健康状态监测的有效性，采用支持向量机（SVM），极限学习机（ELM）和随机森林（Random Forest）等传统的数据驱动算法作为对比进行故障状态监测的有效性验证.通过以上传统的数据驱动算法在故障诊断结果上的准确性对比，得到最优算法，其SVM，ELM和Random Forest算法的平均准确率分别为87.1%，89.7%和90.1%.由此可知，传统的数据驱动方法在进行柴油机健康监测中，平均准确率均超过87%，这主要是由于文中采用了大量的时、频域统计参数特征融合的方式来表示原振动信号.同时，在所比较算法中，Random Forest算法对船舶柴油机的健康诊断结果表现出最佳效果，达到了90.1%，这得利于其利用了集成学习思想，将多个决策树组合起来，最终通过“博采众长”达到较好的健康监测效果.

3.2.2" 传统的卷积神经网络

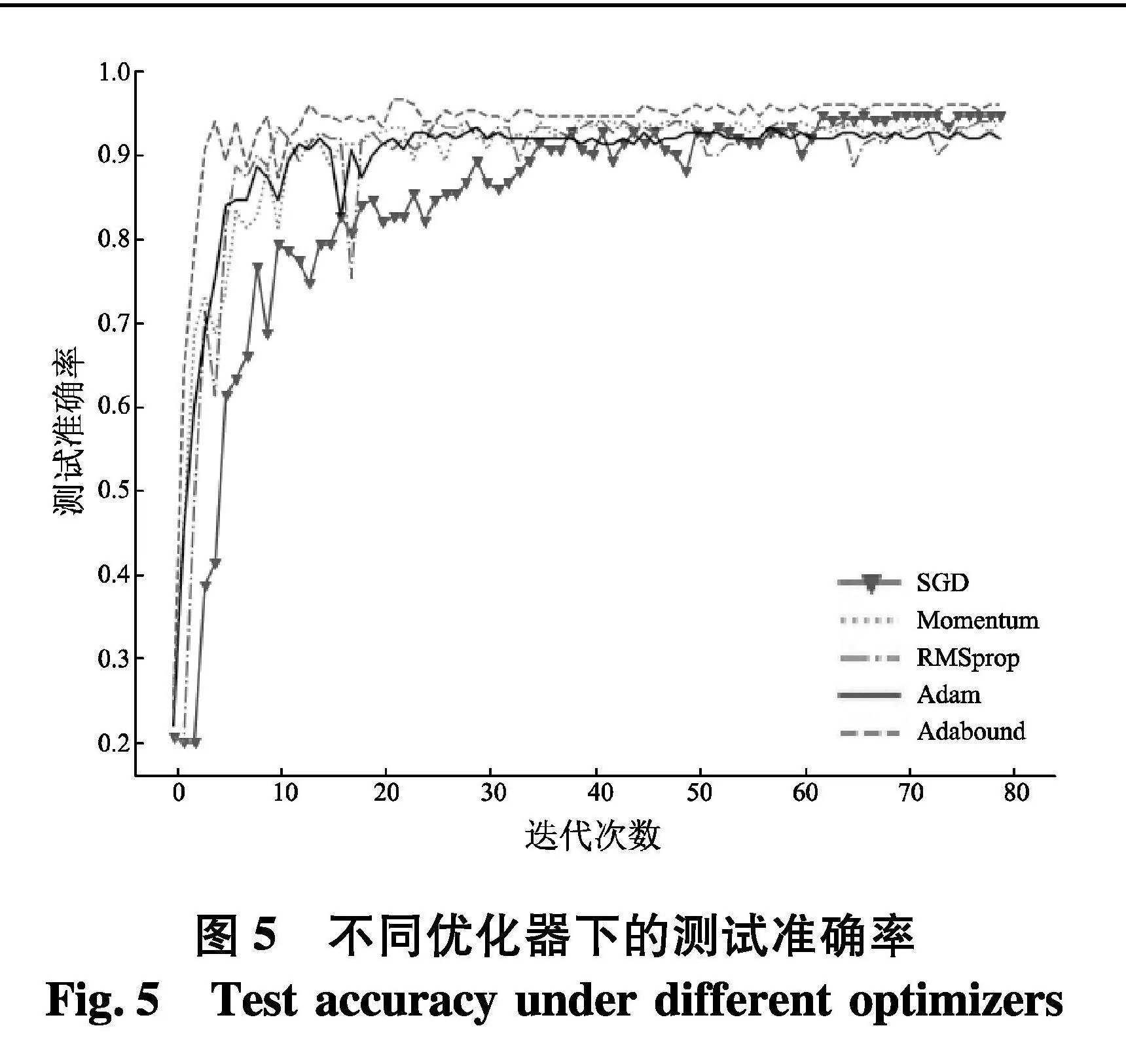
如图5，通过不同的优化器来训练模型使传统卷积神经网络在柴油机健康监测方案达到最佳的效果.同时为验证传统卷积神经网络对振动信号特征提取的有效性，将27个特征直接作为输入.在本文研究中，每个优化器的参数都是由默认值和实验确定［19］，其具体值为表3.

由表3分类结果可知，基于不同的优化器传统卷积神经网络在柴油机上的健康检测效果均达到了97%以上的准确率.在训练时间上，相对于SGD优化器，Adam、Adabound能够快速收敛于较好的结果，SGD优化器虽然收敛速率慢但随着训练迭代过程的不断增多最终模型的准确率达到了较好的效果.而在整体学习过程中，Adabound优化器在训练过程中达到了最佳的精度，最终的健康状态预测率达到了98.8%.因此将以Adabound优化器为基准的深度学习模型与文中提出的Dual-GraphSAINT算法进行健康监测比较.

3.3" 双图采样的图网络归纳式算法

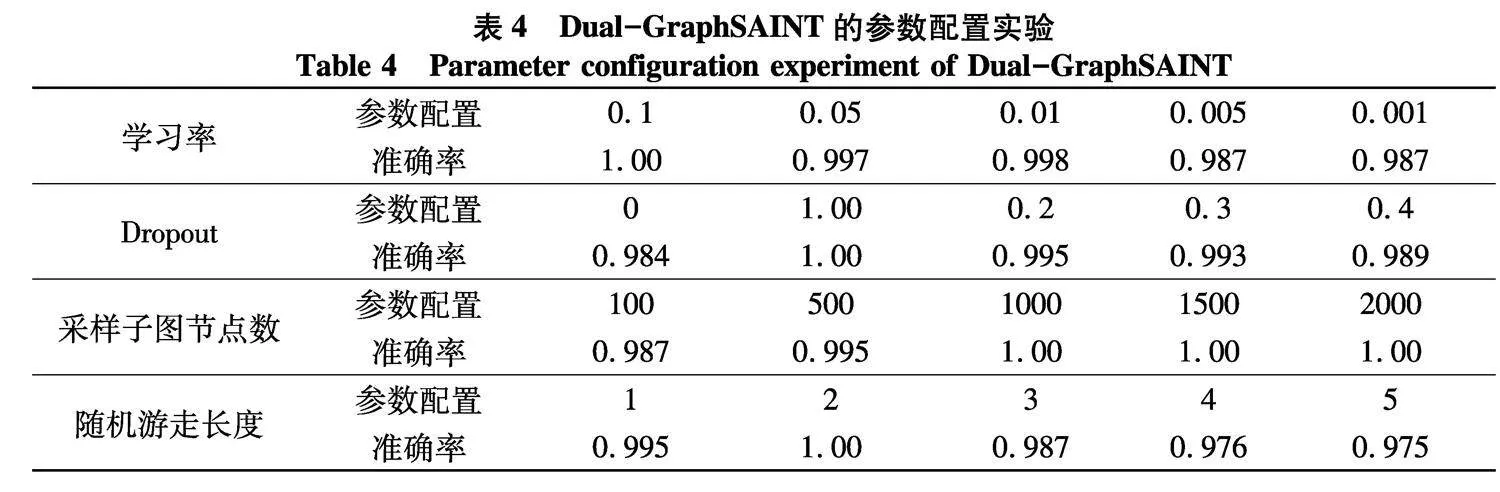
文中提出基于柴油机健康监测的双图采样图网络归纳式学习算法，对原图进行不断地随机采样，通过无偏估计近似的估计出原图模型，以学习归纳式的图表示算法，从而克服传统的图网络只能针对固定已知图进行训练，而对未知不可见的点不能应用的缺点.这就可以将训练好的模型应用到实际柴油机的健康状态监测过程.并且，文中为了在健康监测中最大化利用柴油机振动信号的潜在特征，分别建立实例特征邻接图和标签邻接图，通过从局部和全局的角度对柴油机振动信号的数据特征进行充分学习与挖掘，使其对测试集的正常工况数据与故障工况数据可以达到最佳的分类效果.其中表4列出了不同参数配置实验以确定最优参数.

根据实验结果，Dual-GraphSAINT算法在学习过程中的相关参数设置为：学习率为0.01， Dropout为0.1，采样子图节点数为1 000，根据随机游走进行采样并且随机游走长度为2.同时在学习过程中，图网络不同层的特征维度为{128，256，512}.

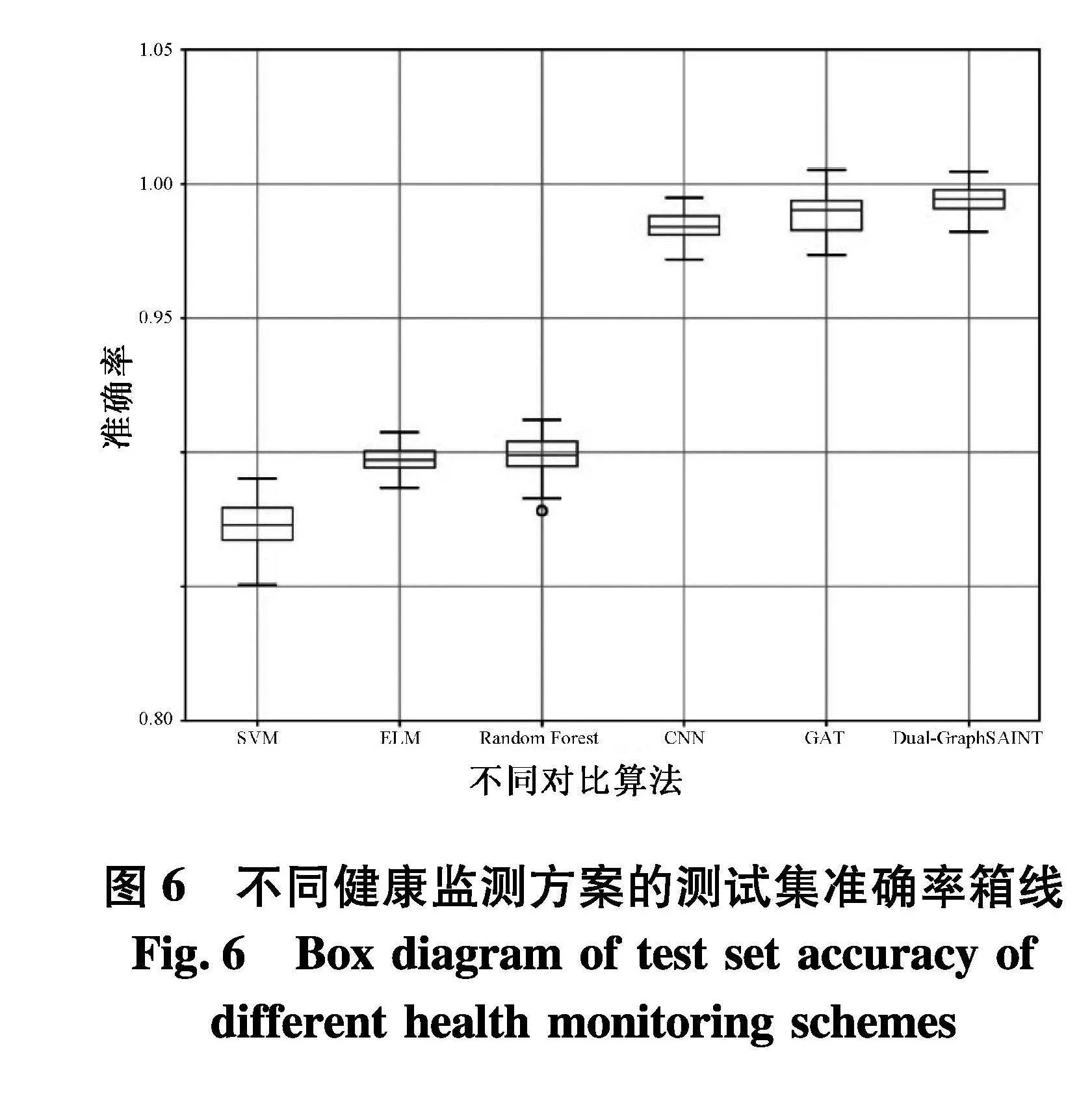
文中所用不同机器学习方法的健康监测性能对比结果如图6，通过采用箱线图来对不同健康监测方案的性能进行对比分析.在传统数据驱动的方法中，Random Forest在诊断稳定性方面比ELM和SVM更具有优势，但其性能低于深度学习模型.这主要是由于传统算法只能针对给定数据特征做运算，对数据之间的潜在信息以及内在相关性等无法学习，很多潜在故障特征被大量的其他因素导致的振动信号所淹没，从而使得学习性能下降.因此，在传统数据驱动的方法中，柴油机的特征设计对模型的诊断性能有主导的影响.而深度学习模型可以通过卷积操作对潜在的柴油机故障特征进行信息提取和挖掘以克服了传统数据驱动的方法中人工数据设计存在的缺陷与不足，使得这种端到端的学习模型更加方便有效并且使模型达到了98.8%测试准确率.同时为了更好的说明Dual-GraphSAINT算法的优越性，文中与图注意力网络（GAT）［21-22］进行对比，需要对柴油机的振动信号进行处理.首先，与Dual-GraphSAINT方法相同，对柴油机的振动信号构建邻接图，但在训练过程中我们需要将训练，测试数据同时输入模型，并对测试数据集的标签进行遮住.这样训练的模型最终达到99.2%的测试准确率.但这个算法的弊端是要对所有的数据构造邻接图进行学习，这在柴油机的实际应用中是不利的.为解决这个问题，文中所提出的Dual-GraphSAINT算法，振动信号的邻接图，有效的挖掘现在的相关特征以提高柴油机健康监测的准确率，最终实现的准确率接近100%.并通过图采样方法来学习不同图形结构的节点表示方式，从而可以对新增加的样本点进行实时检测.文中将图网络改进并应用到实际应用场景中，并在柴油机健康监测方案中取得了优越性结果.

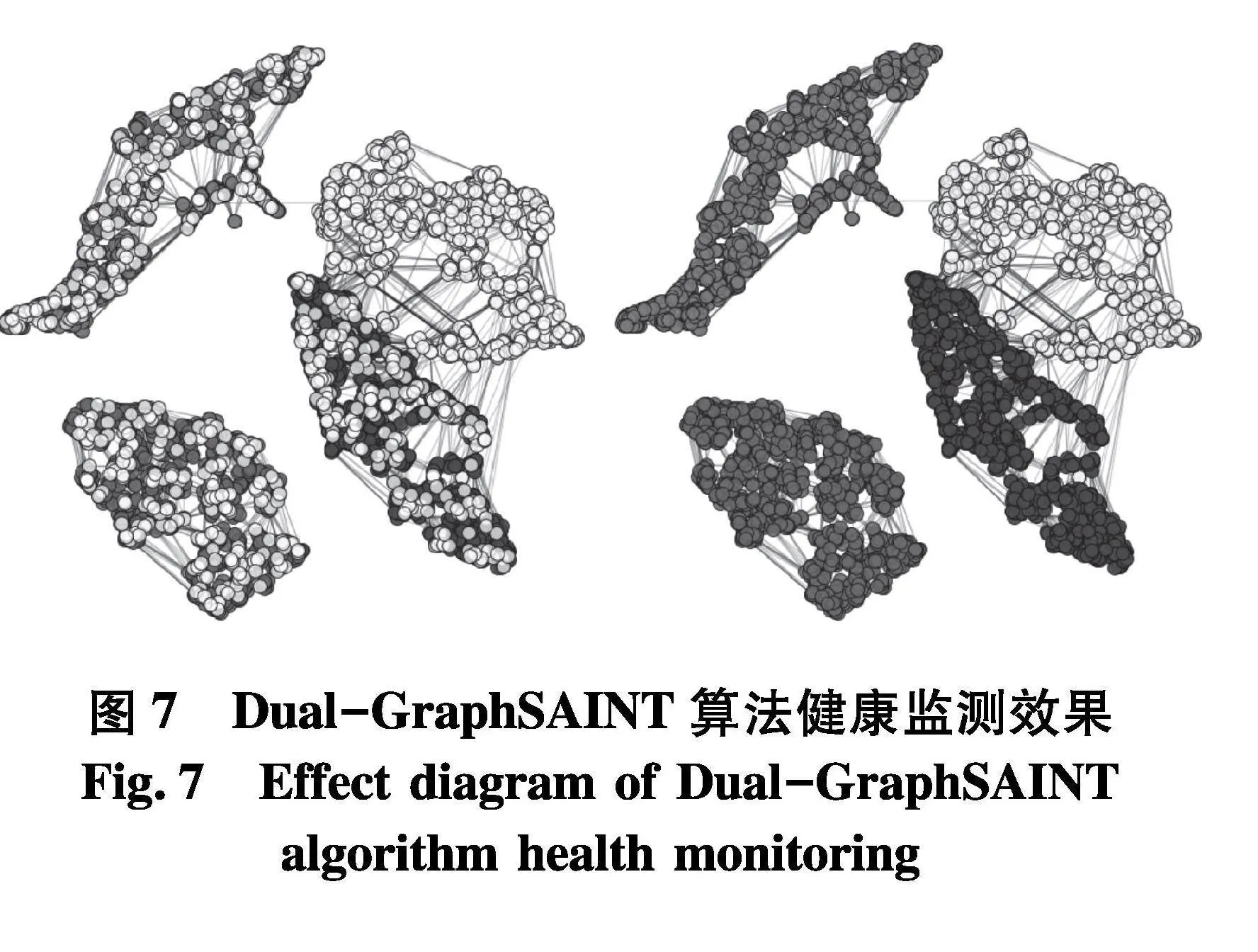
通过将Dual-GraphSAINT算法的健康监测结果可视化，可更直观的体现出图网络在柴油机健康监测方案中的优越性结果.在图7中，左图中4种不同模块的节点分别代表4种工况下的振动信号，而顶点表示测试节点，用于验证Dual-GraphSAINT算法的有效性.右图则表示Dual-GraphSAINT算法对验证振动信号的预测结果，从图中可以看出预测结果分别在所属于自己的分类簇中，达到了接近100%的准确性.并且在交叉的振动信号中，可见其中两种特征是非常相似的，但是文中算法Dual-GraphSAINT可以充分挖掘信号特征中的潜在信息，从而可以达到精准的分类预测效果.

4" 结论

（1） 传统的数据驱动方法Random Forest表现效果最佳，达到了90.1%的准确率，但较CNN跟Dual-GraphSAINT算法相比，性能较差，这很大程度上取决于特征设计与特征筛选的过程中不能很好的挖掘和利用潜在的有用信息.

（2） CNN算法在Adabound优化器下训练集和测试集上均能达到较高的准确率，较传统的数据驱动方法，CNN在柴油机健康监测领域具有更好的性能，这主要原因是CNN可以通过卷积操作多尺度的学习数据中的特征，因此能达到较好的预测结果.

（3） 所提出的Dual-GraphSAINT算法，在所有健康监测对比算法中以及不同的柴油机运行工况下均达到了最佳的性能.这主要归因于双图结构的图网络，分别对特征和标签关系构建邻接图，使得Dual-GraphSAINT模型在学习过程中可以充分的挖掘相邻特征的潜在关系.

（4） 通过引入JK-net，使模型可以灵活地利用每个节点的不同邻域范围的特征来实现更好的结构感知表示.

（5） 与GAT相比，Dual-GraphSAINT算法是一种归纳式图网络，可以将模型应用到不可见的节点上，从而克服了图网络在柴油机健康监测的过程可对实时数据进行检测与识别的缺陷.

（6） 所用的振动信号均在同一转速下采集到，考虑到实际情况下，柴油机的工作并不是在同一转速下.所以，将进一步研究双图采样的图网络归纳式学习算法在不同转速情况下的性能.

参考文献（References）

［1］" WANG R， CHEN H， GUAN C， et al. Research on the fault monitoring method of marine diesel engines based on the manifold learning and isolation forest［J］. Applied Ocean Research， 2021， 112（2）：102681.

［2］" 岳应娟，王旭，蔡艳平. 内燃机变分模态Rihaczek谱纹理特征识别诊断［J］. 仪器仪表学报， 2017， 38（10）： 2437-2445.

［3］" PACHECO F， OLIVEIRA J V， SNCHEZ， R V， et al. A statistical comparison of neuroclassifiers and feature selection methods for gearbox fault diagnosis under realistic conditions［J］. Neurocomputing， 2016，194：192-206.

［4］" LIU J， WANG W， GOLNARAGHI F. An enhanced diagnostic scheme for bearing condition monitoring［J］. IEEE Transactions on Instrumentation amp; Measurement， 2010， 59（2）：309-321.

［5］" SHEN Changqing， WANG Dong， KONG Fanrang，et al. Fault diagnosis of rotating machinery based on the statistical parameters of wavelet packet paving and a generic support vector regressive classifier［J］. Measurement， 2013， 46（4）：1551-1564.

［6］" GEORGOULAS G， CLIMENTE A V， ANTONINO J A， et al. The use of a multilabel classification framework for the detection of broken bars and mixed eccentricity faults based on the start-up transient［J］. IEEE Transactions on Industrial Informatics， 2017，2：625-634.

［7］" PRIETO M D， CIRRINCIONE G， ESPINOSA A G， et al. Bearing fault detection by a novel condition-monitoring scheme based on statistical-time features and neural networks［J］. IEEE Transactions on Industrial Electronics， 2013， 60（8）：3398-3407.

［8］" GONDAL I， AMAR M， WILSON C. Vibration spectrum imaging： A novel bearing fault classification approach［J］. IEEE Transactions on Industrial Electronics， 2014， 62（1）：494-502.

［9］" WANG D. K-nearest neighbors based methods for identification of different gear crack levels under different motor speeds and loads： Revisited［J］. Mechanical Systems amp; Signal Processing， 2016，（70/71）：201-208.

［10］" LEI Y， LIU Z， WU X， et al. Health condition identification ofmulti-stage planetary gearboxes using a mRVM-based method［J］. Mechanical Systems amp; Signal Processing， 2015，（60/61）：289-300.

［11］" ZENG N， WANG Z， ZHANG H， et al. Deep belief networks for quantitative analysis of a gold immunochromatographic strip［J］. Cognitive Computation， 2016， 8（4）：684-692.

［12］" JANSSENS O， SLAVKOVIKJ V， VERVISCH B， et al. Convolutional neural network based fault detection for rotating machinery［J］， Journal of Sound and Vibration， 2016， 377： 331-345.

［13］" WU Z， PAN S， CHEN F， et al. A comprehensive survey on graph neural networks［J］. IEEE Transactions on Neural Networks and Learning Systems， 2021，32（1）：4-24.

［14］" JOAN B， WOJCIECH Z， ARTHUR S， et al. Spectral networks and locally connected networks on graphs［J］. Computer Sciences， 2013，1312：6203.

［15］" KIPF T N， WELLING M. Semi-supervised classification with graph convolutional networks［J］. Mathernatics，2016，9：02907.

［16］" WILL H， ZHITAO Y， JURE L. Inductive representation learning on large graphs［J］. Advances in Neural Information Processing Systems， 2017，30：1024–1034.

［17］" KEYULU X， CHENGTAO L， YONGLONG T， et al. Representation learning on graphs with jumping knowledge networks［C］∥International Conference on Learning Representation. Ababa，Ethiopia：［s.n.］，2020.

［18］" GILMER J， SCHOENHOLZ S S， RILEY P F， et al. Neural message passing for quantum chemistry［J］. Proceedings of Machine Learning Research， 2017，70：1263-1272.

［19］" 周安众，罗可.一种卷积神经网络的稀疏性Dropout正则化方法［J］.小型微型计算机系统，2018，39（8）：1674-1679.

（责任编辑：贡洪殿）