极地冰撞载荷作用下船体典型箱型结构极限强度分析方法研究

摘" 要： 船舶在极地航行的过程中船体可能受到冰载荷的撞击，北极地区海域的温度最低可达-68℃，因此航行于极地的船舶将面临严重的冰载荷环境和低温环境.由于船体结构是典型的加筋板组合的变截面箱型梁结构，故将船体模型简化为箱型梁模型.基于LS-DYNA对箱型梁-冰碰撞的收敛性分析，在不同温度下对箱型梁-冰碰撞进行非线性有限元数值仿真，得到不同低温下箱型梁结构在冰载荷作用下的极限强度.引入冰厚、速度等敏感性参数，得到一般结论，箱型梁的极限强度随着温度的降低而升高，随着冰厚、温度的增大而增大.研究结果对低温下箱型梁-冰在碰撞的极限强度研究具有一定意义，为极地船舶船体结构的设计提供参考.

关键词： 箱型梁；LS-DYNA；有限元；极限强度

中图分类号：U661.43""" 文献标志码：A""""" 文章编号：1673-4807（2024）01-013-06

DOI：10.20061/j.issn.1673-4807.2024.01.003

收稿日期： 2022-07-13""" 修回日期： 2021-04-29

基金项目： 国家自然科学基金项目（51979130）

作者简介： 张健（1977—），男，博士，教授，研究方向为船舶与海洋结构物抗冰载荷性能.E-mail：justzj@126.com

引文格式： 张健，焦鑫晨，王蓓怡.极地冰撞载荷作用下船体典型箱型结构极限强度分析方法研究［J］.江苏科技大学学报（自然科学版），2024，38（1）：13-18.DOI：10.20061/j.issn.1673-4807.2024.01.003.

Research on ultimate strength analysis method of typical ship boxstructure under polar ice impact load

ZHANG Jian， JIAO Xinchen，WANG Beiyi

（School of Naval Architecture and Ocean Engineering，Jiangsu University of Science and Technology，Zhenjiang 212100， China）

Abstract：Ship hull may be impacted by ice load in the process of polar sailing， the temperature of the sea in the Arctic region is as low as -68℃， so ships sailing in the polar region will face severe ice load environment and low temperature environment. Since the hull structure is a typical box beam structure with variable cross-section combined with stiffened plates， the hull model is simplified to box beam model. Based on the convergence analysis of LS-DYNA for box beam-ice collision， the nonlinear finite element numerical simulation of box beam-ice collision was carried out at different temperatures， and the ultimate strength of box beam structure under ice load was obtained at different low temperatures. By introducing some sensitive parameters such as ice thickness and velocity， the general conclusion is drawn that the ultimate strength of box beam increases with the decrease of temperature， and increases with the increase of ice thickness and temperature. The above conclusions have certain significance for the study of ultimate strength of box beam-ice collision at low temperature， and the research results can provide certain reference for the design of polar ship hull structure.

Key words：box girder， LS-DYNA， finite element， ultimate strength

北极地区的海域常年被冰雪所覆盖，因此对船体结构的极限强度要求比较高.北极地区的温度最低可达-68℃，然而北冰洋海面还浮有大量的冰体，因此航行于北极地区的船舶将面临严重的冰载荷环境和低温环境 ［1］.研究成果发现，低温环境会使钢材的韧性降低，并且使钢材的屈服强度升高，从而影响钢材的极限强度；目前对船舶极限强度等方面的研究工作，主要是对常温环境中的船舶，对低温下船体极限强度的研究较少；如果将常温环境下船体结构极限强度的研究成果直接应用于极地船舶极限强度的评估中，可能会发生危险.

船体结构是典型的加筋板组合的变截面箱型梁结构，它的极限强度是呈现其承载性能的重要指标，一直以来都受到人们的广泛重视［2］.目前已有众多国内外学者都对箱形梁结构的极限强度做了大量的研究，文献 ［3-6］通过对箱形梁结构极限强度等方面的实验研究，把得出的实验结果对比分析，并得出一种新的箱形梁极限强度的理论算法.文献［7］通过研究箱形支条件下受纯弯矩作用的受力变形的实验过程，并对上述过程用 Ansys软件进行了模拟，得到的实验结果与有限元结果符合较好.文献［8］通过Marc软件对Nshihara论文提出的NST3箱形梁模型进行了极限强度度等方面的计算研究，得到较为符合的结果.文献［9］基于非线性有限元程序Sandy对弹性模量、初始缺陷、屈服应力、焊接残余应力、板厚等要素对船体结构中拱极限强度的影响进行了分析，他仅对一种工况进行了分析，缺乏应用的广泛性.而在实际中，一个结果往往受到多个变量的综合影响，对多个工况进行分析可以增加数据的可靠性.文中基于LS-DYNA在箱型梁-冰碰撞载荷作用下计算箱型梁变形损伤下的局部极限强度，且研究低温环境、速度以及冰厚等对箱型梁结构极限强度的影响，为极地船舶船体结构的设计提供参考.

1" 数值仿真模型

1.1" 箱型梁-冰材料参数

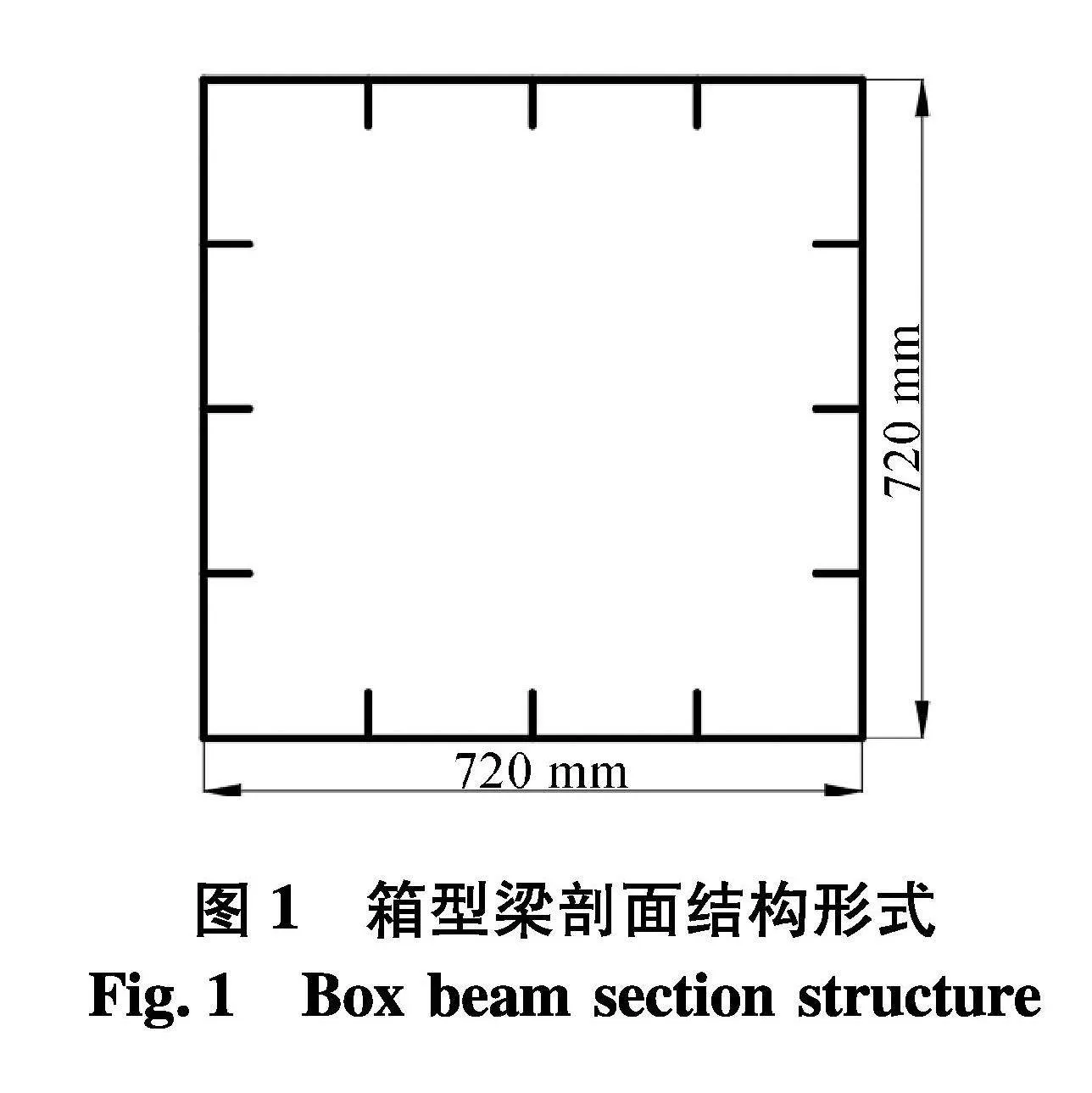
箱型梁是一种典型的加筋板组合起来的结构，拥有节省材料、强度优秀等优点，在船舶工程结构中箱型梁结构被普遍应用，箱型梁的极限强度素来被船舶行业工作者重视.箱型梁模型的剖面结构形式如图1.

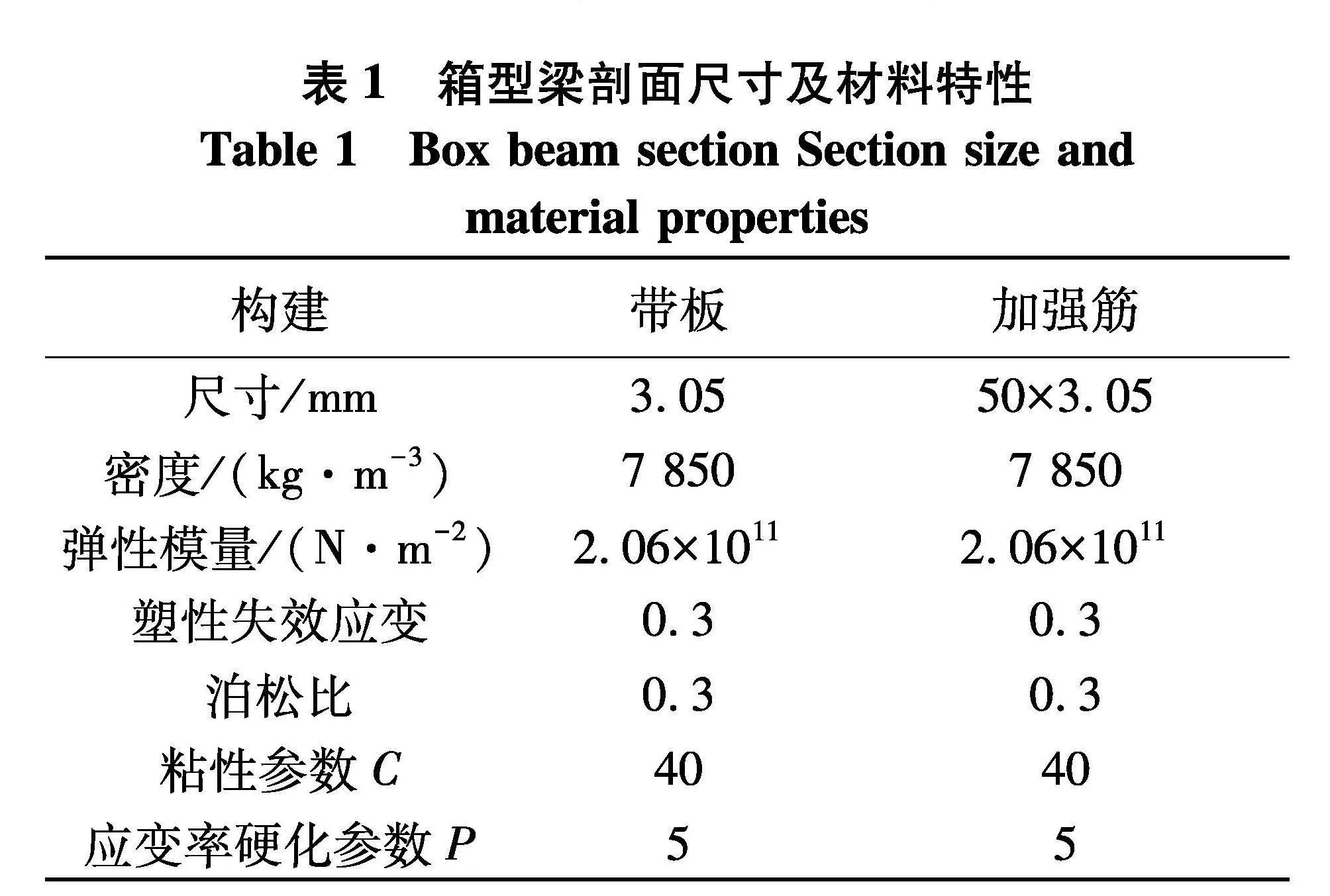
构件的有效跨长为540 mm.根据文献［1］文中选用AH32钢作为箱型梁主体材料，且在一个应变率点（2×10-4s-1）对箱型梁-冰碰撞进行模拟，常温下构件的详细尺寸和材料特性见表1.

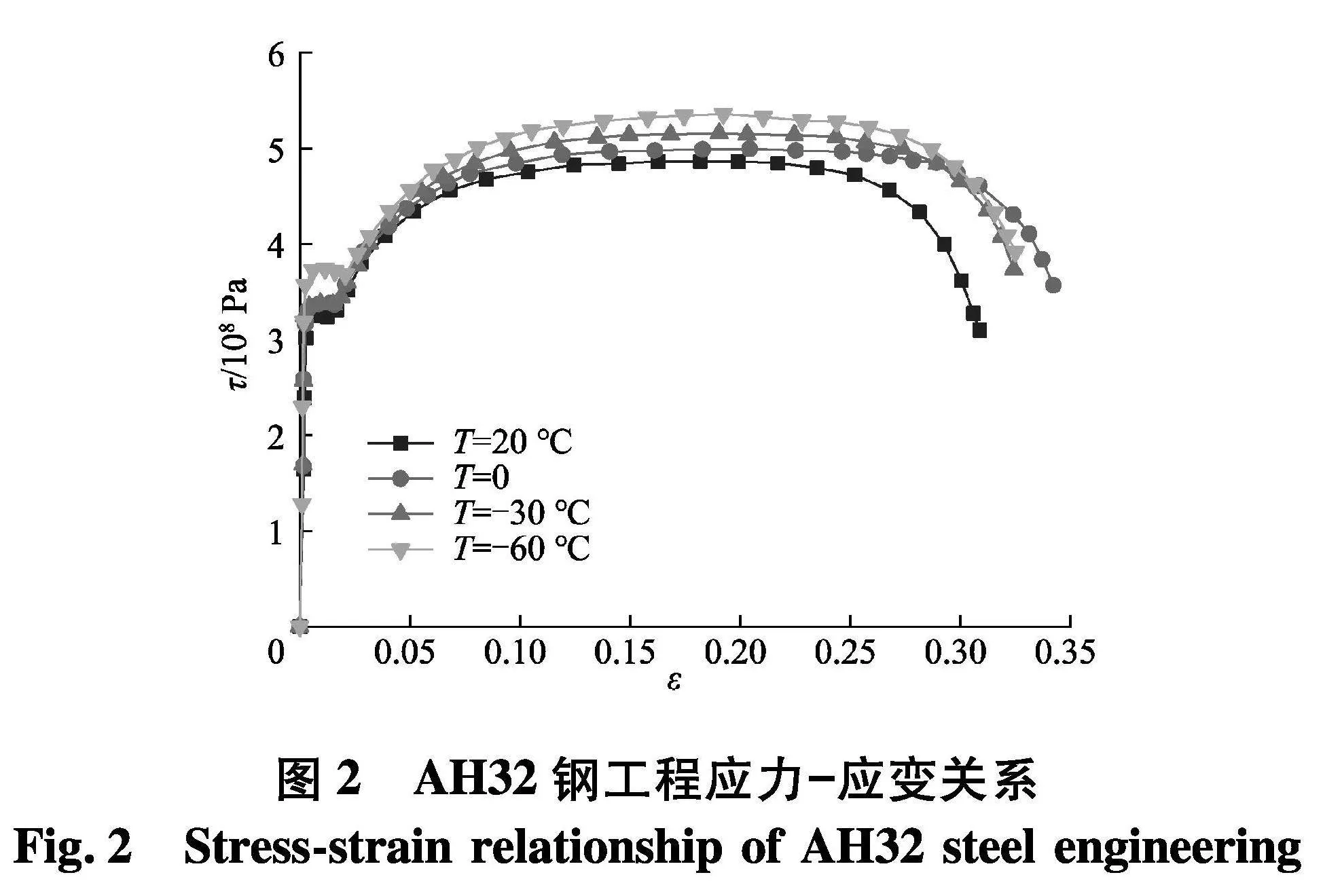
文献［1］通过实验得出AH32钢在低温条件下的工程应力τ-应变ε曲线，如图2.

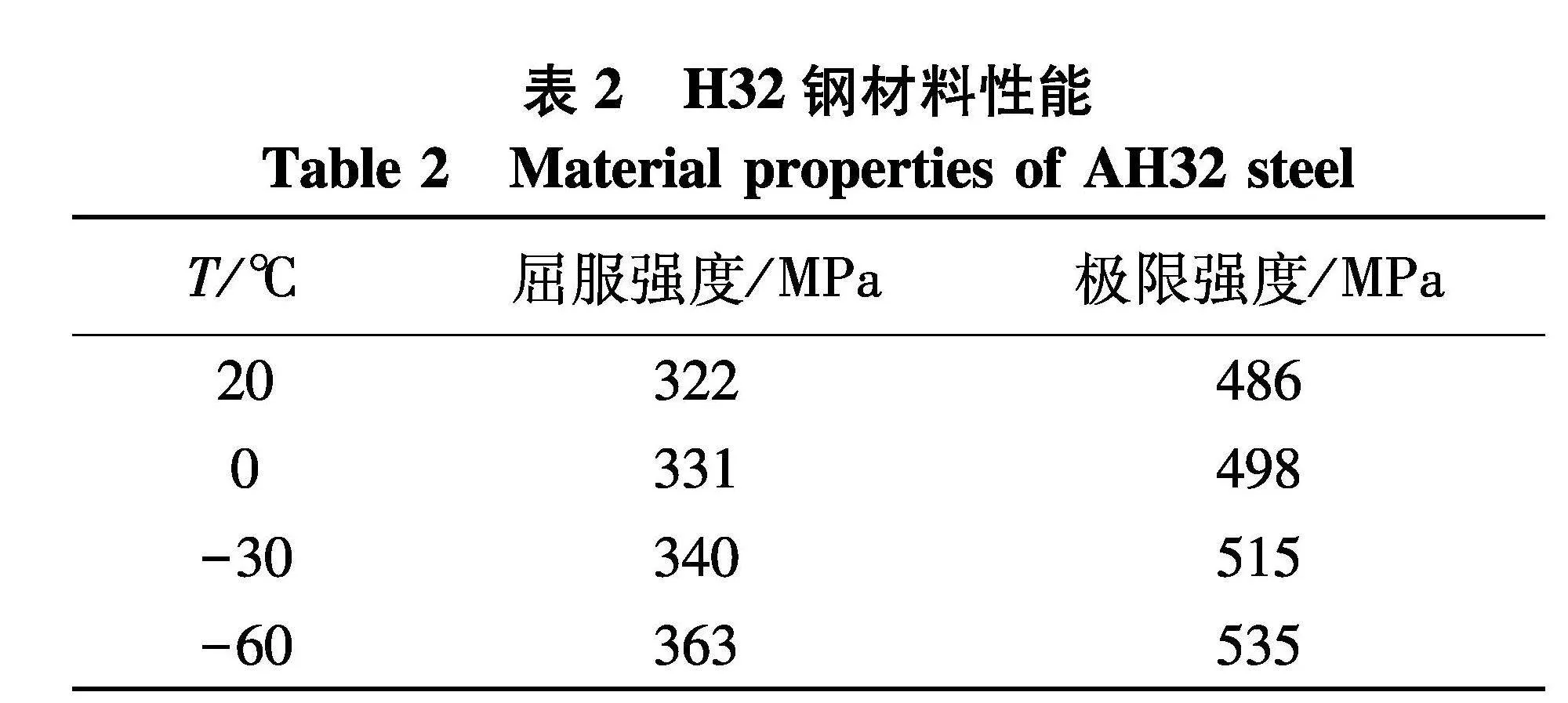
由图2可得出AH32钢在不同温度T下的屈服强度和极限强度，如表2.

为了工程需求，将AH32钢看作弹塑性材料，常温下屈服极限σy=322 Mpa，失效应变εy=0.3.多数有限元模拟中使用的钢材本构模型是Johnson-Cook模型和Cowper-Symonds模型，然而Johnson-Cook模型是否能有效地模拟材料应变硬化效应还存在争议.文献［10］对Q235钢材进行了多组准静态和高速拉伸试验，研究其动态力学性能，研究结果表明Cowper-Symonds模型符合Q235钢材的动态力学性能，故文中选择Cowper-Symonds本构模型.

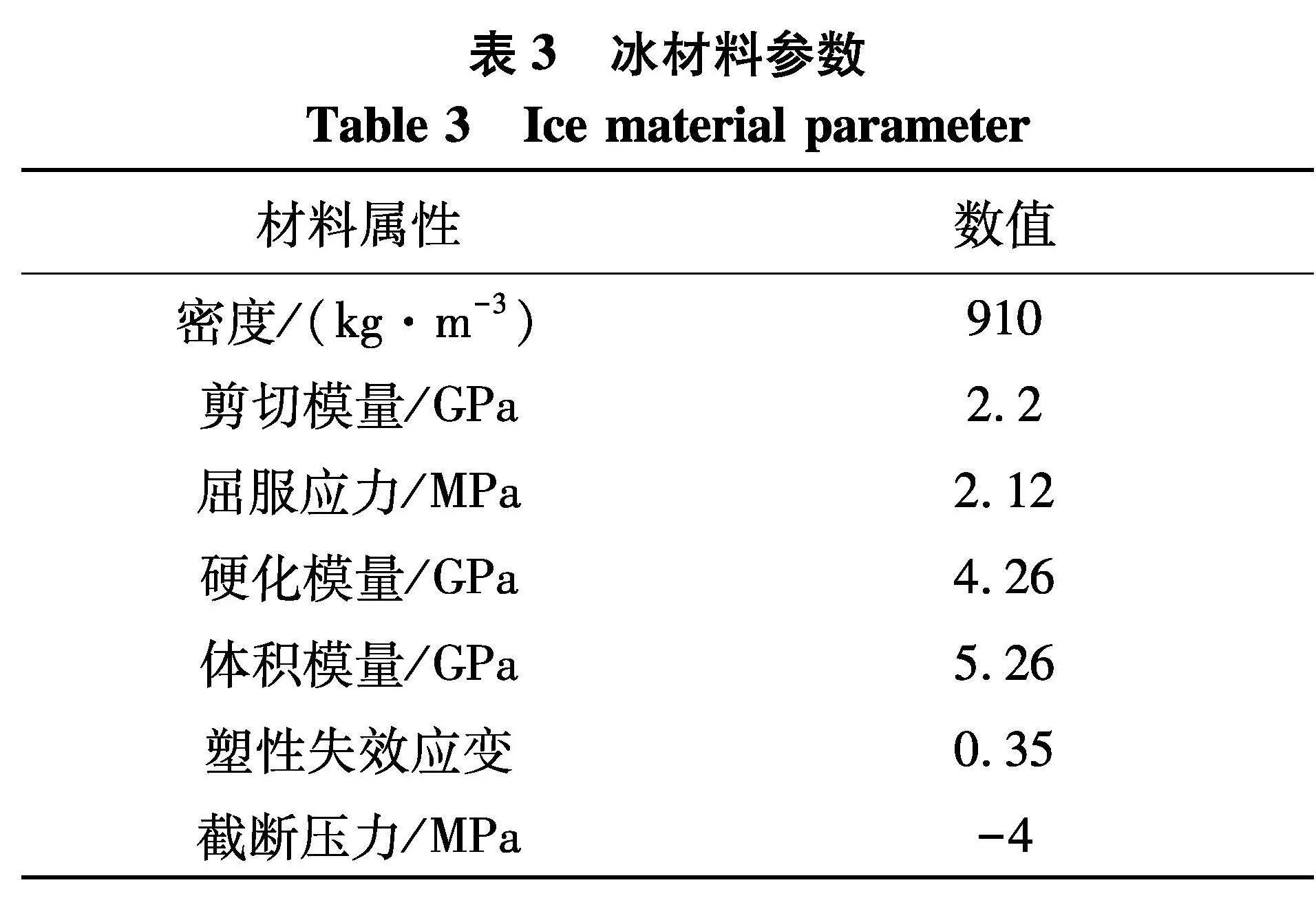
近几年，越来越多的学者对海冰的力学特性进行了研究［11］，但由于海冰材料非常复杂，到现在也没有形成一个统一的冰材料本构模型.根据文献［12-15］，对海冰采用弹塑性的海冰本构模型，具体为LS-DYNA材料库中的13号材料*MAT_ISOTROPIC_ELASTIC_FAILURE（打开VP=1命令），其中的冰材料参数如表3，主要考虑了泡沫材料模型仿真模拟中极易出现负体积的情况.

1.2" 箱型梁-冰有限元模型

对于箱型梁结构的极限强度分析，边界条件是一个非常重要的因素.对其直接计算可能会产生较大的误差，为了消除误差的影响，其中有效手段是延长研究对象的两端，并将边界条件设置在延长区域的两端，上述应用St·Venant 原理修正了边界条件的产生的误差.延长区域的纵向范围可以选取1跨长，为540 mm，故此箱型梁模型的总体长度为1 620 mm.

为了简化计算，碰撞过程采用规则层冰，且层冰的位置位于箱型梁侧面的中间稍微偏上处.碰撞过程对箱型梁左端3个方向的线位移进行约束，对绕x、z轴方向的角位移进行约束，右端延y、z两个方向的线位移进行约束，对绕x、z轴的角位移进行约束，约束冰体沿x、z两个方向的线位移以及绕x、z轴的角位移，并给冰体一个初始速度使其向箱型梁移动.

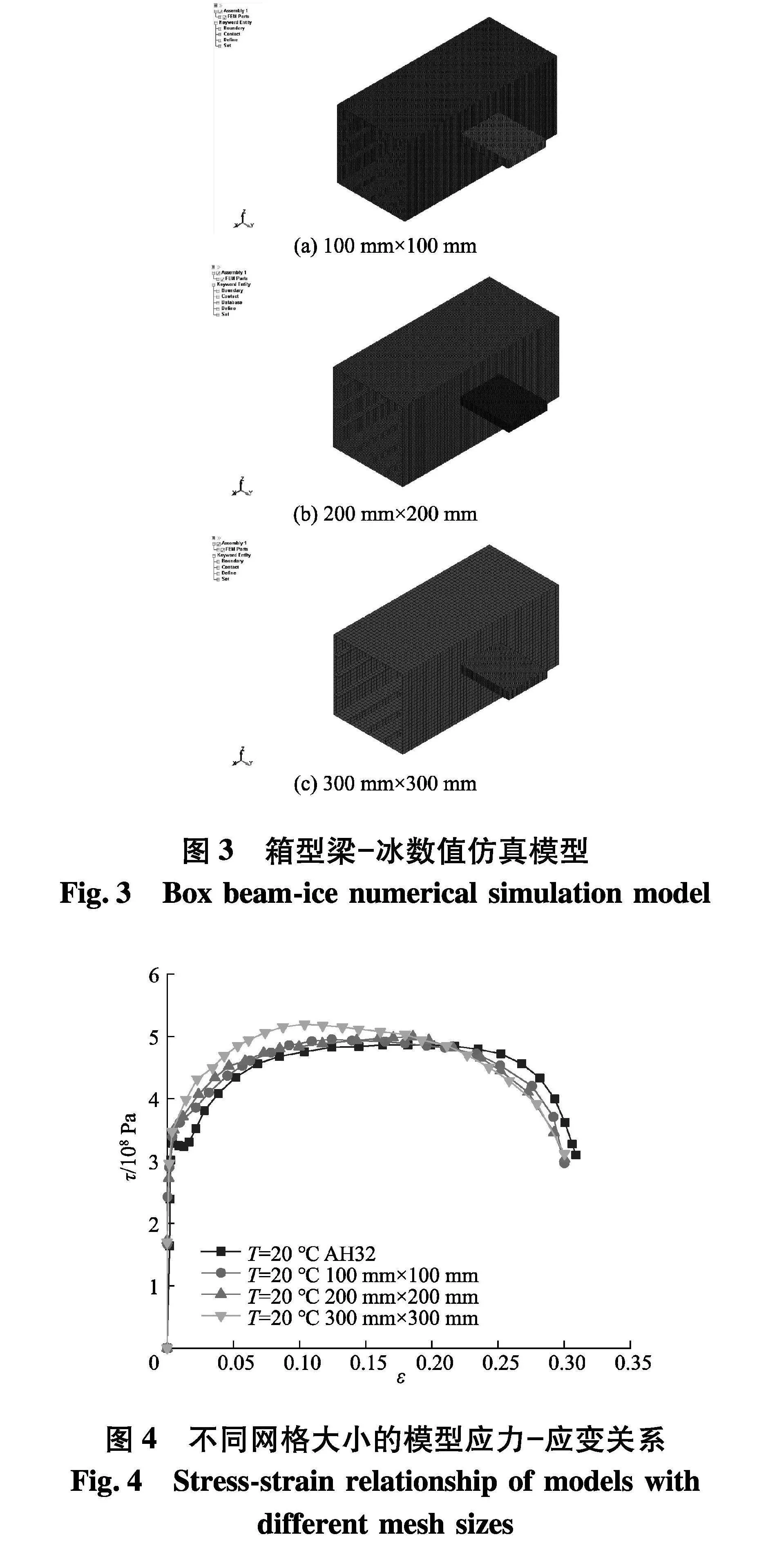
网格大小对箱型梁结构的极限强度可能会产生较大影响，故文中分别选取100 mm×100 mm、200 mm×200 mm、300 mm×300 mm的网格进行收敛性研究，从而验证网格大小对极限强度的影响，且建立箱型梁模型时选用具有4个节点的壳单元（shell 163）.箱型梁-冰有限元模型如图3.

分别对3种不同网格大小的模型在常温下进行数值模拟，得到所有局部失效单元的应力—应变关系，并对每个单元应力和应变的值取其平均值，最终得到箱型梁变形损伤下的局部极限强度（图4）.

从图中可以看出当网格大小为300 mm×300 mm时，应力-应变曲线与常温下AH32钢应力-应变曲线的偏差较大，不符合数值模拟的要求；网格大小为100 mm×100 mm和200 mm×200 mm时都与常温下AH32钢应力-应变曲线吻合较好，得到的误差较小；然而网格大小为100 mm×100 mm时在LS-DYNA中计算时间较长，故文中选择200 mm×200 mm的网格，有限元模型选择图3（b）.

2" 箱型梁-冰在碰撞载荷作用下极限强度

2.1" 计算工况设置

北极地区的冰厚度为1 m左右，尺度为2～7 m.当分析具体的某一参数时运用控制变量的方法对其进行改变，设置出不同的工况.且为了更加接近冰区的实际情况，通过材料属性的控制改变温度设置，研究不同温度下箱型梁结构极限强度的不同之处.由此，设置箱型梁-冰数值仿真模拟工况如表4.

2.2" 箱型梁-冰碰撞结果分析

2.2.1" 结构损伤

图5为不同工况下的箱型梁结构损伤变形云图.从图中可以看出箱型梁结构的损伤变形随着航行速度的增大呈现出更加严重的趋势，速度v为1.5 m/s，航行5 s时，可以清楚地观察到箱型梁由于碰撞产生的大缺口；箱型梁结构的损伤变形随着冰厚h的增大而更为严重，速度为0.5 m/s，航行5 s时，可以明显地观察到箱型梁由于碰撞产生的缺口越来越严重.综上所述，箱型梁结构的损伤变形在某一个时间点随著速度和冰厚的增加呈现出递增的趋势.

2.2.2" 结构极限强度

基于极地环境的需求展开，引入温度T作为敏感性参数，考虑不同航行速度及不同冰厚的箱型梁结构极限强度，并对最终结果真实应力应变曲线σ/σy、ε/εy［16］做无量纲的处理.

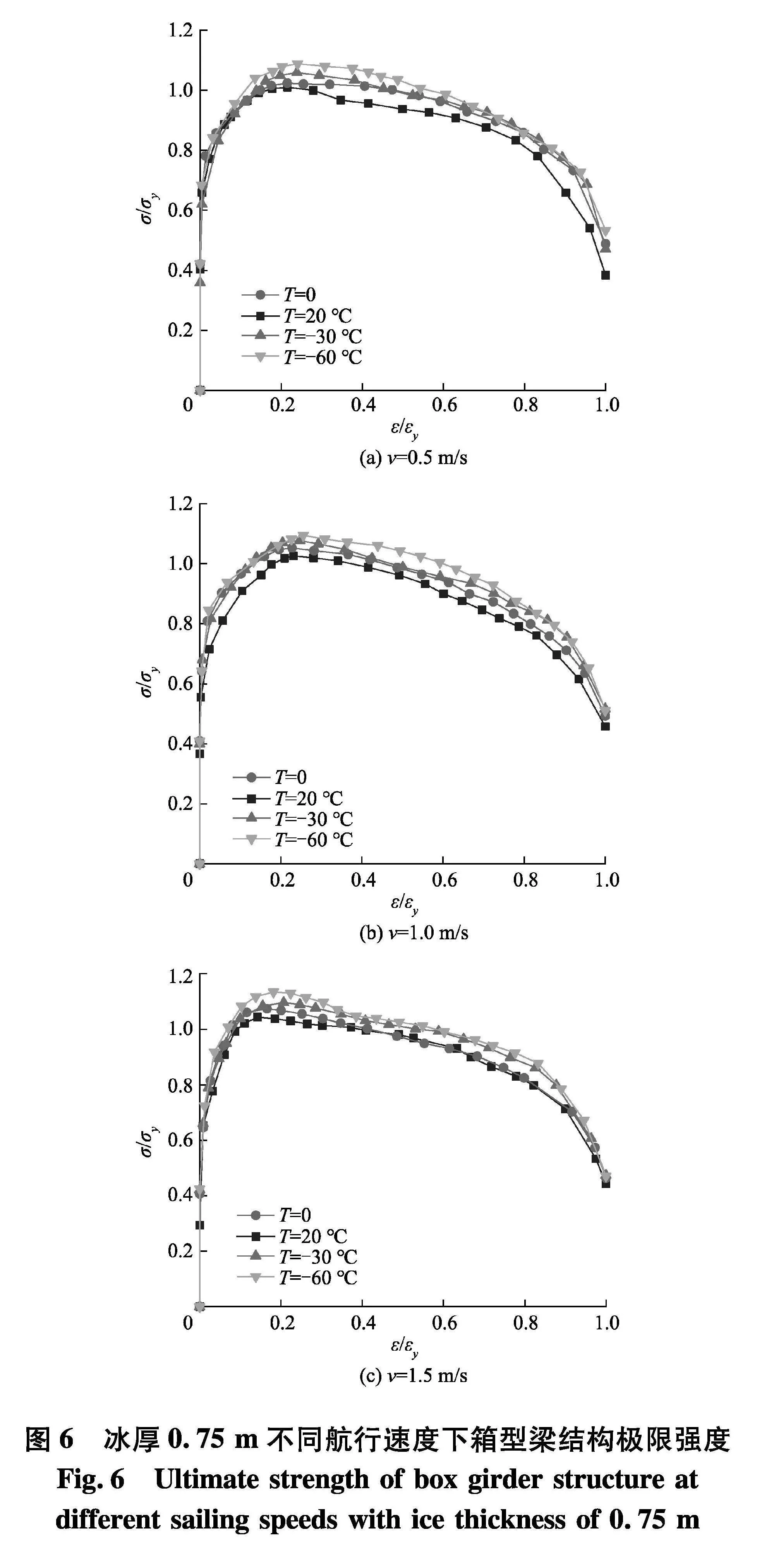
图6为冰厚0.75 m不同航行速度下箱型梁结构极限强度.从图中可以看出，当速度为0.5 m/s时，随着温度的降低，极限强度随之提高，其极限强度分别为常温静态时极限强度的1.016、1.023、1.059、1.088倍；当速度为1.0 m/s时，随着温度的降低，极限强度随之提高，其极限强度分别为常温静态时极限强度的1.025、1.052、1.077、1.094倍；当速度为1.5 m/s时，随着温度的降低，极限强度随之提高，其极限强度分别为常温静态时极限强度的1.043、1.074、1.096、1.134倍.

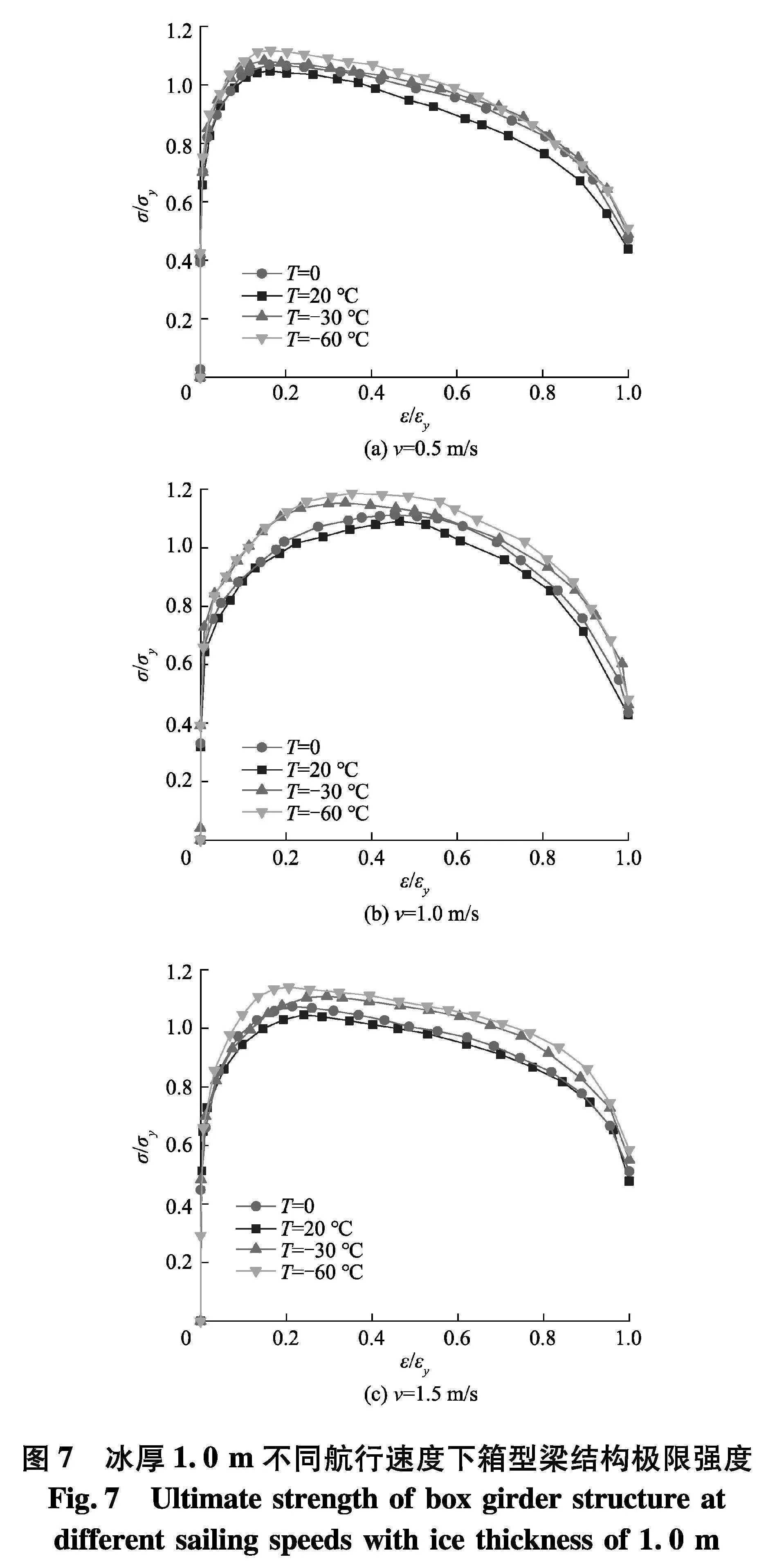
图7为冰厚1.0 m不同航行速度下箱型梁结构极限强度.从图中可以看出，当速度为0.5 m/s时，极限强度分别为常温静态时极限强度的1.047、1.068、1.082、1.117倍；当速度为1.0 m/s时，极限强度分别为常温静态时极限强度的1.059、1.089、1.106、1.144倍；当速度为1.5 m/s时，极限强度分别为常温静态时极限强度的1.064、1.108、1.163、1.177倍.

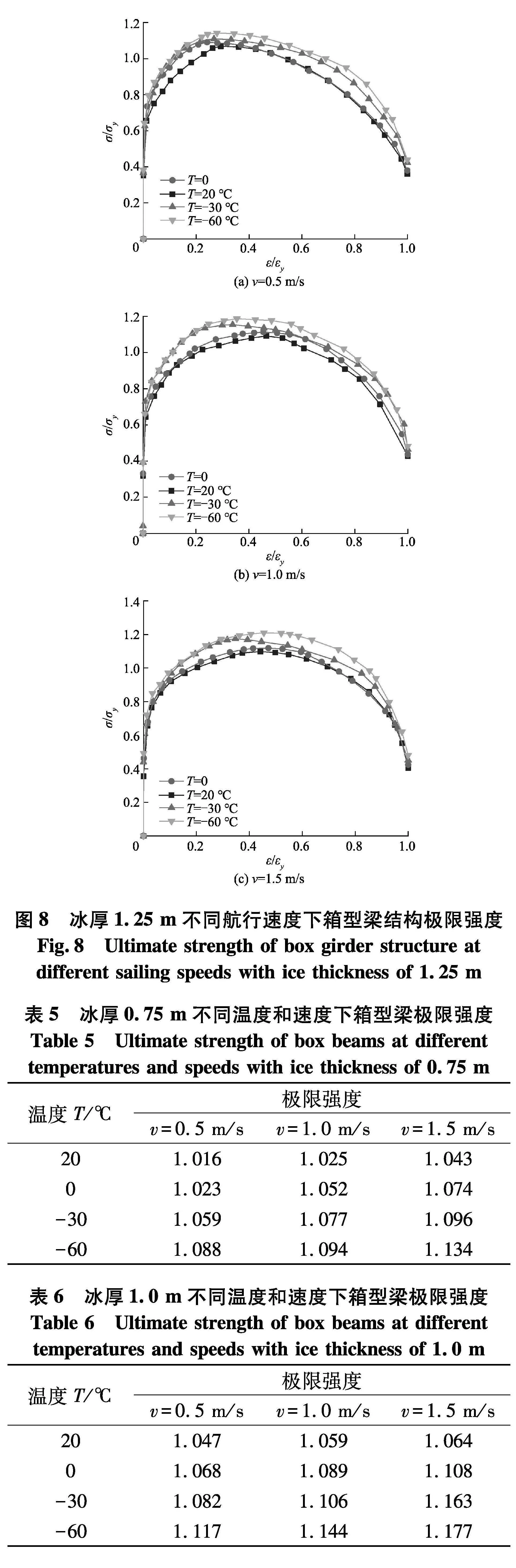
图8为冰厚1.25 m不同航行速度下箱型梁结构极限强度.从图中可以看出，当速度为0.5 m/s时，极限强度分别为常温静态时极限强度的1.068、1.090、1.109、1.142倍；当速度为1.0 m/s时，极限强度分别为常温静态时极限强度的1.090、1.112、1.153、1.186倍；当速度为1.5 m/s时，极限强度分别为常温静态时极限强度的1.098、1.118、1.173、1.209倍.

根据图6～8计算结果，以常温静态时箱型梁的极限强度作为衡量标准，不同温度T和速度v下箱型梁极限强度如表5～7.

根据上述数值模拟所得，在温度-60～20 ℃，速度0.5～1.5 m/s，冰厚0.75～1.25 m时，温度越低，箱型梁结构的极限强度越高；在此范围内，随着速度增大，箱型梁极限强度随之增大；随着冰厚的增大，箱型梁极限强度也随之增大.结合上述计算结果，能够为极地船舶设计中船体结构的安全性提供一定的参考，可以更加充分地利用船用钢材，提高经济效益.

3" 结论

（1） 温度不变的情况下，箱型梁的极限强度在一定速度范围内，随着速度的增大，其极限强度增大；箱型梁的极限强度在一定冰厚范围内，随着冰厚的增加，其极限强度也随之增大，且由表格可以看出，冰厚对其影响大于速度的影响.

（2） 在温度-60～20 ℃时，速度和冰厚各不相同的情况下，箱型梁的极限强度随温度的降低而增大，温度越低，其极限强度越大，故而此箱型梁的强度越好；且在此温度范围内，其极限强度都超过常温静态时的极限强度.在温度-60～20 ℃时，速度为敏感性参数时，速度越大其极限强度越大，且在1.5 m/s时极限强度变化幅度最大，0.5 m/s时极限强度变化幅度最小，说明在此范围内速度越大，箱型梁的极限强度随温度降低而增大这个特性呈现出递增的趋势；冰厚为敏感性参数时，冰厚越大其极限强度越大，但是其极限强度的变化幅度非常接近，这说明冰厚对箱型梁的极限强度随温度降低而增大这个特性影响相对较小.

参考文献（References）

［1］" 左永青.考虑温度效应的船体结构极限承载能力研究［D］.武汉：华中科技大学， 2019.

［2］" 王保森，冯亮，耿保阳.基于有限元法的箱型梁极限强度影响因素及敏感分析［J］.舰船科学技术， 2019， 41（15）： 28-33，54.

［3］" NISHIHARA S. Analysis of ultimate strength of stiffened rectangular plate （4th report） on the ultimate bending moment of ship hull girders［J］. Journal of the Society of Naval Architects of Japan， 1983， 154： 367-375.

［4］" NISHIHARA S. Ultimate longitudinal strength of midship cross section［J］. Naval Architecture and Ocean Engineering， 1984， 22： 200-214.

［5］" DOWLING P J， MOOLANI F M， FRIEZ PA. The effect of shear lag on the ultimate Strength of box girder［C］∥ Proceeding of International Conference， On Steel Plated Structures. London［s.n.］， 1976： 108-147.

［6］" REKLING K A.Behaviour of box girder under bending and shear［C］∥Proceeding of the International Shipamp;Offshore Structures Congress. Paris：［s.n.］，1997：46-49.

［7］" GORDO J M， SOARES C G， FAULKNER D. Approximate assessment of the ultimate longitudinal Strength of the hull girder［J］. Ship Research， 1996， 40（1）： 60-59.

［8］" 贺双元，吴卫国，陆浩华，运用MARC进行箱梁的极限强度分析［J］.武汉理工大学学报（交通科学与工程版），" 2006，30（5）： 889-891.

［9］" 白勇，徐向东，崔维成.船体结构极限强度的影响参数与敏感度探讨［J］.船舶力学， 1998， 4（5）： 35-43.

［10］" 陈俊岭，舒文雅，李金威.Q235钢材在不同应变率下力学性能的试验研究［J］.同济大学学报（自然科学版）， 2016， 44（7）： 1071-1075.

［11］" ZHANG Wenyuan， LI Junxing， LI Liang， et al.A systematic literature survey of the yield or failure criteria used for ice material［J］.Ocean Engineering， 2022，254：111360.

［12］" 涂勋程.极地物探船冰阻力预报及参数敏感性研究［D］.镇江：江苏科技大学， 2019.

［13］" YULMETOV R， LUBBAD R， LSET S. Planar multi-body model of iceberg free drift and towing in broken ice［J］. Cold Regions Science amp; Technology， 2015， 121（2）： 154-166.

［14］" 王凯民.考虑流固耦合作用的船舶破冰阻力预报及结构响应研究［D］.镇江：江苏科技大学， 2019.

［15］" 翟帅帅，高俊.基于Derradji-Aouat海冰本构模型的船冰碰撞数值模拟［J］.船舶设计通讯，2016，（S1）：51-59.

［16］" LIU Bin， VILLAVICENCIO R， TERNDRUP P. et al.Analysis of structural crashworthiness of double-hull ships in collision and grounding［J］. Marine Structures， 2021， 76：102898.

（责任编辑：贡洪殿）