基于RSM-NCGA算法的大型邮轮钢骨架复合材料夹芯板结构优化研究

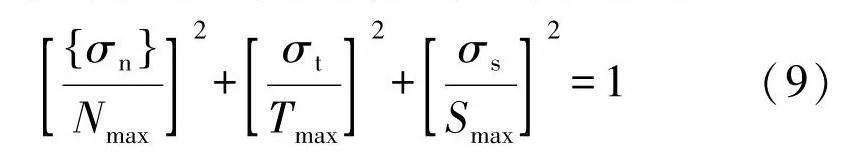
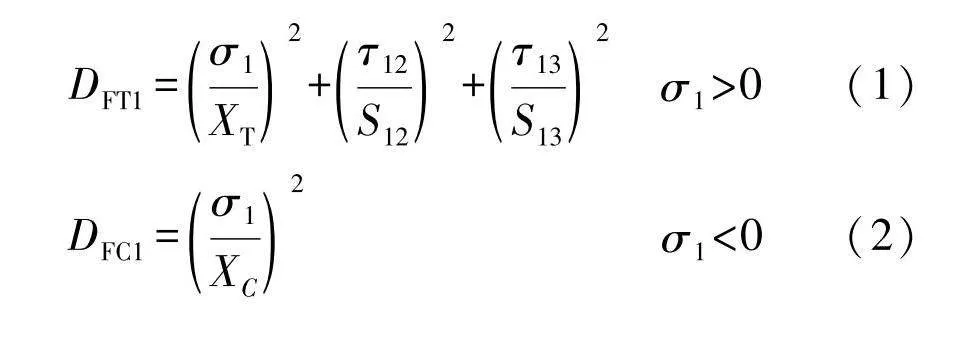
摘"要： 采用一种钢骨架复合材料夹芯板结构来降低大型邮轮上层建筑重量.运用3D-Hashin失效准则以及损伤材料刚度矩阵退化方法预测结构的渐进损伤，基于ABAQUS二次开发将该结构参数化建模.采用DOE试验设计中的优化拉丁超立方设计采样，依据采样点建立四次多项式响应面代理模型.以结构质量和极限载荷为优化目标函数，基于NCGA遗传算法在响应面代理模型上开展钢骨架复合材料夹芯板结构多目标优化.结果表明：优化结果的质量比初始方案降低12.1% ，极限承载能力提高17.4% ；通过DOE试验设计与遗传算法混合优化策略可以应用于钢骨架复合材料夹芯板结构设计中的不同问题.

关键词： 大型邮轮；复合材料；渐进损伤；多目标优化

中图分类号：U663.6"""文献标志码：A"""""文章编号：1673-4807（2024）04-009-07

Structural optimization of composite sandwich panels with steelstiffeners based on RSM-NCGA algorithm

JIANG Jingxiao1，2， LIU Bin1*， WU Weiguo1

（1.Green amp; Smart River-Sea-Going Ship，Cruise and Yacht Research Center， Wuhan University of Technology， Wuhan 430063， China）

（2.School of Naval Architecture，Ocean and Energy Power Engineering， Wuhan University of Technology， Wuhan 430063， China）

Abstract：A composite sandwich panel with steel stiffeners is used to reduce the weight of the superstructure of the large cruise ship. The 3D Hashin failure criterion and the stiffness matrix degradation method are used to conduct the finite element analysis of progressive damage to reveal the failure mode. The structure is modeled based on ABAQUS secondary development. Using the optimized Latin hypercube design sampling in DOE test design， a quartic polynomial response surface proxy model is established according to the sampling points. The structural mass and ultimate load are used as optimization objective functions in the response surface agent model， the multi-objective optimization of composite sandwich panel with steel stiffeners is carried out based on NCGA genetic algorithm. The results show that the mass of the optimized results is reduced by 12.05% and the ultimate bearing capacity is increased by 17.43%. The hybrid optimization strategy of DOE experiment design and genetic algorithm can be applied to different problems in the composite sandwich panel with steel stiffeners.

Key words：large cruise ship，composite material，progressive damage，multi-objective optimization

复合材料由于具有高的比刚度和比模量等多种优点，因此在船舶设计建造中被用来替代高强钢.钢骨架复合材料夹芯板结构在船舶上层建筑的应用被认为是一种实现轻量化设计的有效手段，然而钢与复合材料的应用又带来了系列的结构安全问题，钢—复合材料夹芯板结构分析与设计尚未完全掌握，制约了上层建筑轻量化设计的发展.分析掌握大型邮轮上层建筑钢骨架复合材料夹芯板结构的承载特性，可为我国大型邮轮上层建筑结构轻量化设计及安全性评估提供参考.

钢—复合材料夹芯板板架结构在弯曲、扭转和剪切等载荷的作用下，芯层失效、胶层脱粘以及钢结构失稳可能是整体结构失效的重要因素.文献［1］用径向基函数建立M形超弹性复合材料杆的代理模型，以弯曲刚度、扭转刚度和压缩刚度为优化目标，采用粒子群算法进行超弹性杆参数优化，得到最优刚度.文献［2］对碳纤维增强树脂复合材料层合板单搭胶接结构通过创建二次多项式响应面代理模型，基于遗传算法（GA）进行了多目标优化，提高了其结构性能.文献［3］用响应面法（RSM）建立了复合超薄吊杆的x轴和y轴弯曲刚度和z轴扭转刚度的代理模型；采用改进的非支配排序遗传算法进行多目标优化设计，结果实现了优化设计.文献［4］开发了一种数据驱动的计算框架，该框架结合了贝叶斯回归、不确定性量化和多目标优化.文献［5-6］基于多尺度方法提出的损伤刚度矩阵以及损伤控制因子能够很好模拟复合材料层合板中的渐进失效.文献［7］考虑了具有不同延性的不同接头配置和粘合剂，数值和实验结果表明，L形部分的几何形状和粘合剂类型影响接头的强度.文献［8］建立了拉伸载荷下由不同材料组成的L形接头的剥离应力分布的二维分析模型，分析结果表明，L形接头中的剥离应力分布由粘合剂的性质、机械性能和L形接头的几何形状决定.文献［9］采用遗传算法对船用复合材料接头进行优化，获得的最佳参数显著的提高了结构承载能力.文献［10］通过比较有效宽度的一些定义，研究了复合材料顶帽加筋结构的有效宽度的使用.文献［11］研究了CFRP复合材料修复损伤加筋板的拉伸极限强度，采用非线性有限元法研究碳纤维修复含裂纹加筋板的拉伸剩余极限强度.文献［12］分析了在不同冲量条件下，金属泡沫弹冲量、夹层板芯层面密度和芯层厚度对夹层板动态力学行为的影响规律.文献［13］建立了一种渐进损伤方法来模拟夹层L形接头的强度和破坏行为，并使用不同的破坏准则来处理GFRP层压板的各种破坏模式.文献［14］将原始T形接头和两组人工老化试样进行了准静态拉伸试验，为分析极限条件下蜂窝夹层T形接头的行为提供了数据.文中采用FORTRAN语言根据复合材料3D-Hashin失效准则与损伤刚度矩阵编制VUMAT子程序，通过ABAQUS二次开发对钢骨架复合材料夹芯板进行参数化建模形成脚本文件；采用DOE试验设计中的优化拉丁超立方设计对结构尺寸参数在设计空间均匀采样以此捕捉最有效的设计区域，根据样本点建立四次响应面代理模型；以结构质量最小、极限承载能力最大为优化目标，基于NCGA遗传算法对响应面代理模型开展多目标优化以获得最佳设计结果.

1"研究对象

1.1"钢—复合材料夹芯板板架结构

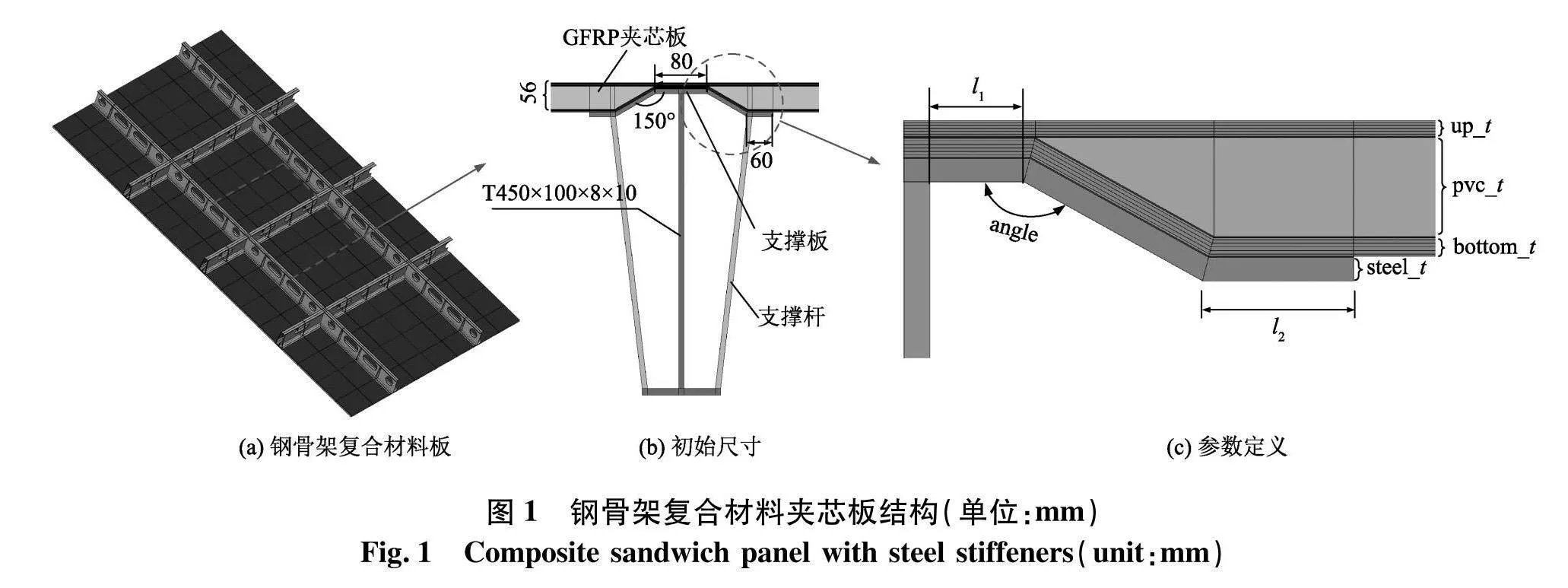
以某大型邮轮上层建筑大跨度甲板为研究对象，采用钢骨架复合材料夹芯板结构形式（图1），该结构在宽度方向上跨距大且纵桁与横梁采用高腹板开孔形式.该板架骨架结构纵桁和横梁由T型材、支撑板以及支撑杆组成，支撑板用于支撑复合材料夹芯板连接薄弱处，支撑板的斜角度为150°；复合材料夹芯面板的蒙皮之间填充有聚氯乙烯（PVC）泡沫，蒙皮由玻璃纤维增强聚合物制成，共同构成一种轻质、具有较大刚度的复合材料夹芯板；蒙皮与芯层、骨架与蒙皮之间采用环氧胶粘剂粘结.

1.2"复合材料夹芯板与材料参数

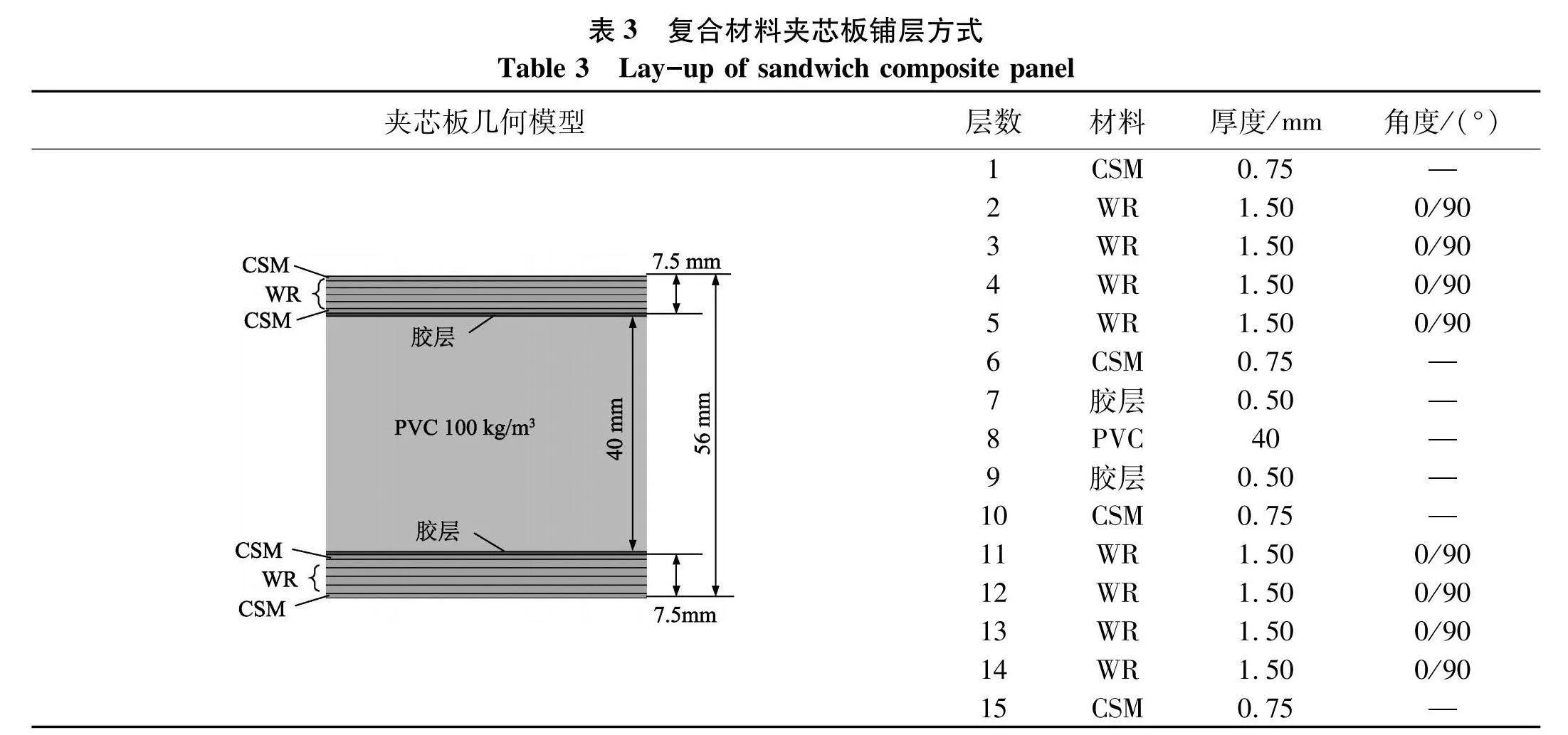
骨架均由AH36钢材料制成，弹性模量为2.06SymboltB@105 MPa，泊松比为0.3，屈服强度355 MPa，支撑板（图1）厚度为8.0 mm.芯层为40 mm厚的PVC（100 kg/m3）芯材，采用可压溃泡沫（Crushable Foam）本构模型，材料参数见表1.夹芯板要求蒙皮面板具有足够的抗弯刚度与弯曲强度，芯层具有足够的横向抗剪能力.复合材料蒙皮性能参数见表2.蒙皮材料CSM为面密度300 g/m2的短切毡，因含树脂量多而用于防渗层.WR为面密度600 g/m2的平纹编织玻璃纤维布增强复合材料，复合材料夹芯板铺层如表3，胶层参数取自Kotsidis ［15］.

2"模型材料参数与求解方法

2.1"失效准则

（1） 编织纤维层合板3D-Hashin失效准则

Hashin失效准则已被广泛用来预估复合材料层合板的初始损伤.复合材料铺层之间的界面层通过分层失效以材料的法向失效模式（基体方向）给予考虑.考虑编织纤维在两个方向有相同或相似的属性，文中基于采用考虑分层失效的3D-Hashin失效准则，表达式为：

DFT1=σ1XT2+τ12S122+τ13S132"σ1＞0（1）

DFC1=σ1XC2"""""""σ1＜0（2）

DR1=σ1XC2+τ12S122+τ13S132"σ1＜0（3）

DFT2=σ2YT2+τ12S122+τ13S132"σ2＞0（4）

DFC2=σ2YC2 σ2＜0（5）

DR2=σ2YC2+τ12S122+τ23S232"σ2＜0（6）

DMT3=σ3ZT2+τ13S132+τ23S232"σ3＞0（7）

DMC3=τ13S132+τ23S232""""σ3＞0（8）

式中：σi（i=1，2，3）为i方向的应力；τij（ i，j=1，2，3）为i-j方向的剪应力；Sij（i，j=1，2，3）为i-j方向的剪切强度；XT、YT、ZT以及XC、YC、ZC分别代表编织纤维1、2方向以及厚度3方向的拉伸和压缩强度；D为强度因子，下标F、M、R分别代表纤维、基体以及剪切失效，T、C分为代表拉伸和压缩，1、2、3为材料方向.当Di≥1时（i=FT1，FC1，FT2，FC2，R1，R2，MT3，MC3），纤维与基体开始失效，失效单元相应的应力值变为零，宏观上表现为材料刚度发生渐进式退化.

（2） 层间失效准则

钢与复合材料、芯材连接的胶层损伤起始采用ABAQUS中内置的二次应力失效准则判定，即：

σnNmax2+σtTmax2+σsSmax2=1（9）

式中：σn、σt、σs 为法向正应力和1，2方向的剪切应力；Nmax、Tmax、Smax为拉伸和剪切强度.当上式成立即满足损伤起始准则，胶层损伤扩展采用基于能量的BK准则进行损伤演化.

2.2"有限元模型

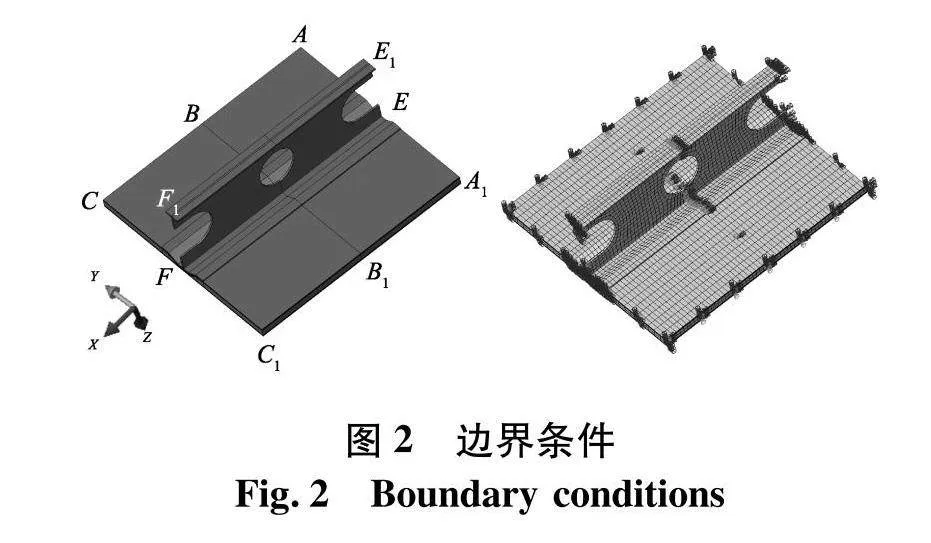
基于ABAQUS建立图1中框内局部结构有限元模型，蒙皮、芯材以及钢材的单元类型均采用C3D8R实体单元建模，实体单元相比壳单元不仅可以得到胶层剪切应力，还可以对复杂模型进行预测.复合材料上下蒙皮各划分实体单元层，每层代表一个铺层，每个铺层成90°交叉；模拟钢与复合材料、芯材连接的胶层采用实体结构COH3D8（三维八节点内聚力）单元模拟.文中在支撑杆B和B1处以限制节点z方向的位移做简化处理， 边界条件如图2.

其中AA1处施加x方向对称性边界条件，纵向位置施加y方向对称性边界条件，其中AC与A1C1：U2=R1=R3=0；AA1与EE1：U1=R2=R3=0；BB1包括纵桁截面：U3=R1=0；CC1截面： R2=R3=0；FF1截面：R1=R3=0；CC1、FF1截面相关U1；其中U为位移约束，R为转角约束，下标1、2、3表示在x、y、z轴方向施加；在模型x轴正向施加位移载荷以及0.32 t/m2的甲板面压设计载荷.通过ABAQUS/Explicit有限元分析软件，并根据失效准则和失效后的损伤退化编写VUMAT子程序开展钢复合材料结构的渐进失效分析.

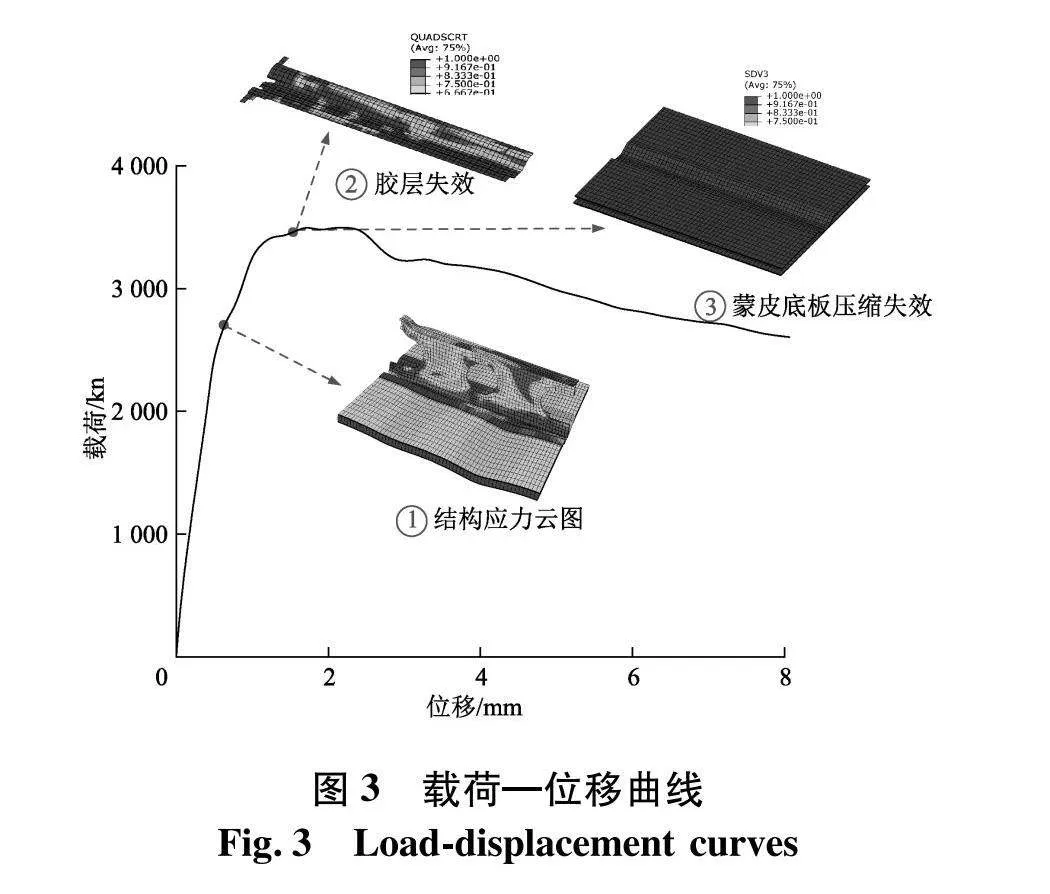
图3为钢骨架复合材料板载荷—位移曲线图，当轴向位移载荷较小时，载荷位移曲线初始阶段处于弹性阶段，由于钢结构相比复合材料有较大的弹性模量，此阶段钢骨架为主要承载结构，粘结层以及复合材料夹芯板为承载次要结构；随着载荷不断增加，达到钢的屈服强度，骨架纵桁局部结构形成较高的应力区域而发生局部屈曲，其中伴随着部分胶层脱粘最终导致曲线下降，复合材料夹芯板对于整体结构的纵向和垂向变形起着重要作用，同时此阶段复合材料夹芯板出现损伤并沿着上述方式进行退化（如图3中①的应力图），且与胶层单元都尚未发生完全失效；图3中②、③为底部复合材料面板与骨架粘结处，此时为复合材料面板损伤演化阶段，复合材料夹芯结构的上下面板部分单元均已发生压缩失效进而导致面板失稳，最后整个结构失去承载能力.初始方案结构总质量为0.138 t ，极限载荷3.507 8 MN.

3"优化方法

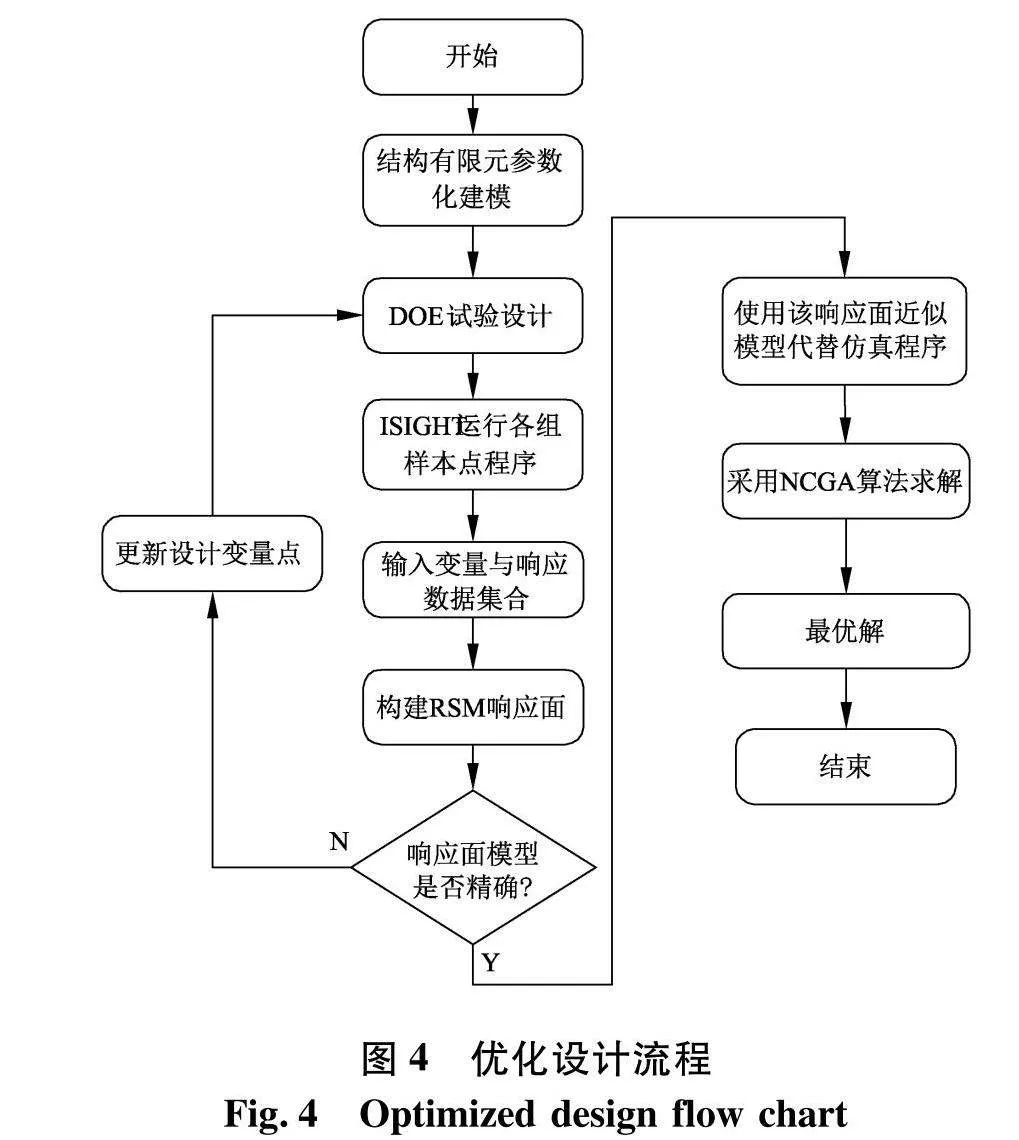
以模型（图1）的上蒙皮厚度（up_t）与下蒙皮厚度（bottom_t）、芯层厚度（pvc_t）、支撑板的厚度（steel_t）以及板长度（l1）与（l2）等7个设计变量作为输入参数因子，质量（mass）和极限载荷（max）作为输出响应.通过ABAQUS二次开发将上述变量进行参数化建模形成脚本文件，将脚本文件集成在ISIGHT开展试验设计（design of experiments，DOE）产生输入样本点，进行数值仿真得到输出响应值；代理模型是在输入样本点以及对应样本点响应值的基础上构造出近似的数学模型，文中则使用四次多项式响应面（response surface methodology，RSM）构造钢-复合材料夹芯板的代理模型；最后采用邻域培植多目标遗传算法（neighborhood cultivation genetic algorithm，NCGA）基于响应面模型进行局部空间寻优，最终获得最佳设计结果.基于NCGA优化的RSM响应面模型流程如图4.

3.1"DOE试验设计

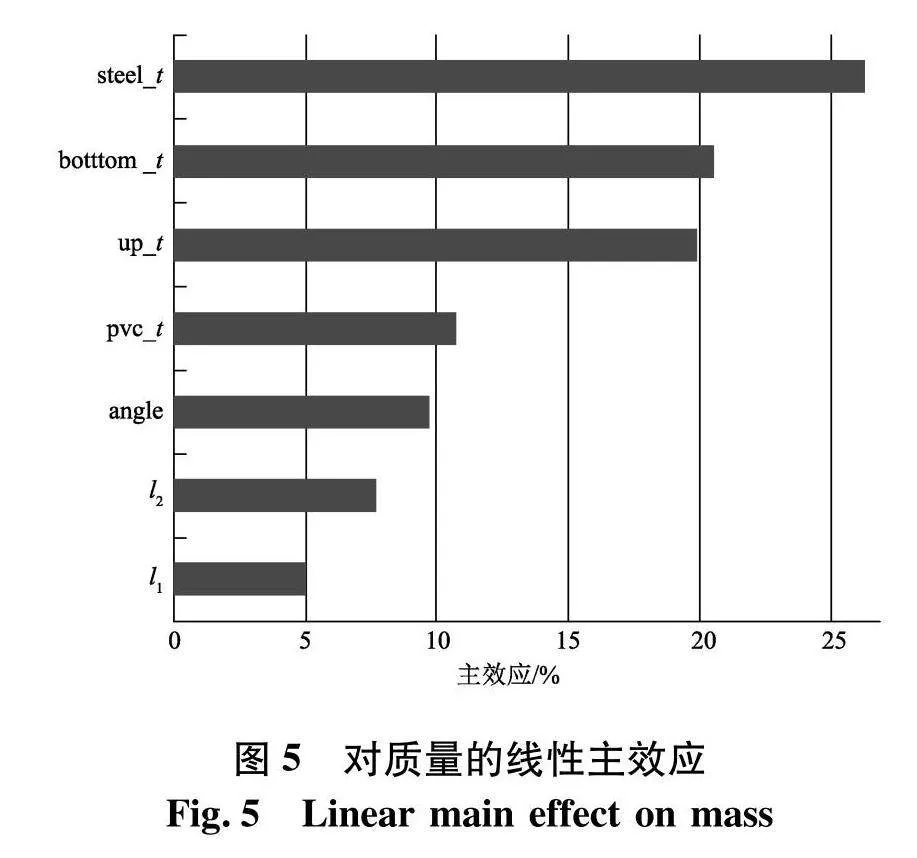
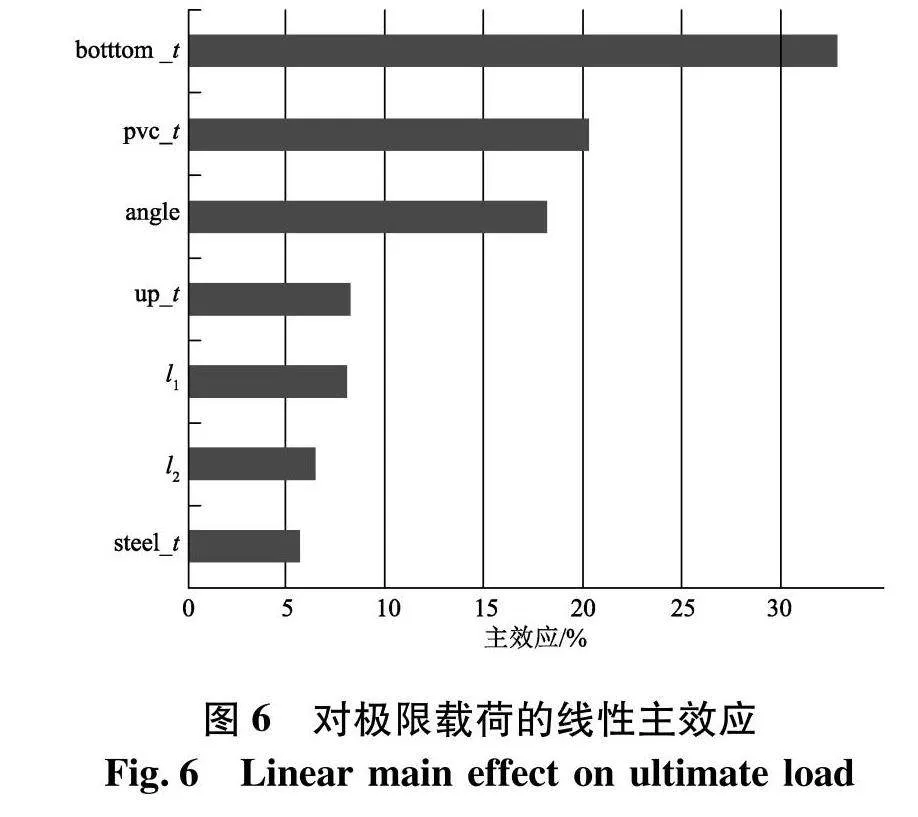
试验设计DOE中采用的优化拉丁超立方设计（optimal latin hypercube design，Opt LHD）在设计空间均匀采样，捕捉全局设计空间中最有效的设计区域，该方法具有非常好的空间填充性和均衡性；本文共生成207组设计样本点以及响应值，产生的线性主效应图如图5、6，图中反映了设计变量各项对质量、极限载荷响应值的贡献度百分比.图5中钢材的密度较大，其厚度参数对总质量占比影响较大，在图6中复合材料蒙皮在载荷作用下出现局部破坏是影响极限载荷的重要影响因素.

3.2"RSM响应面模型

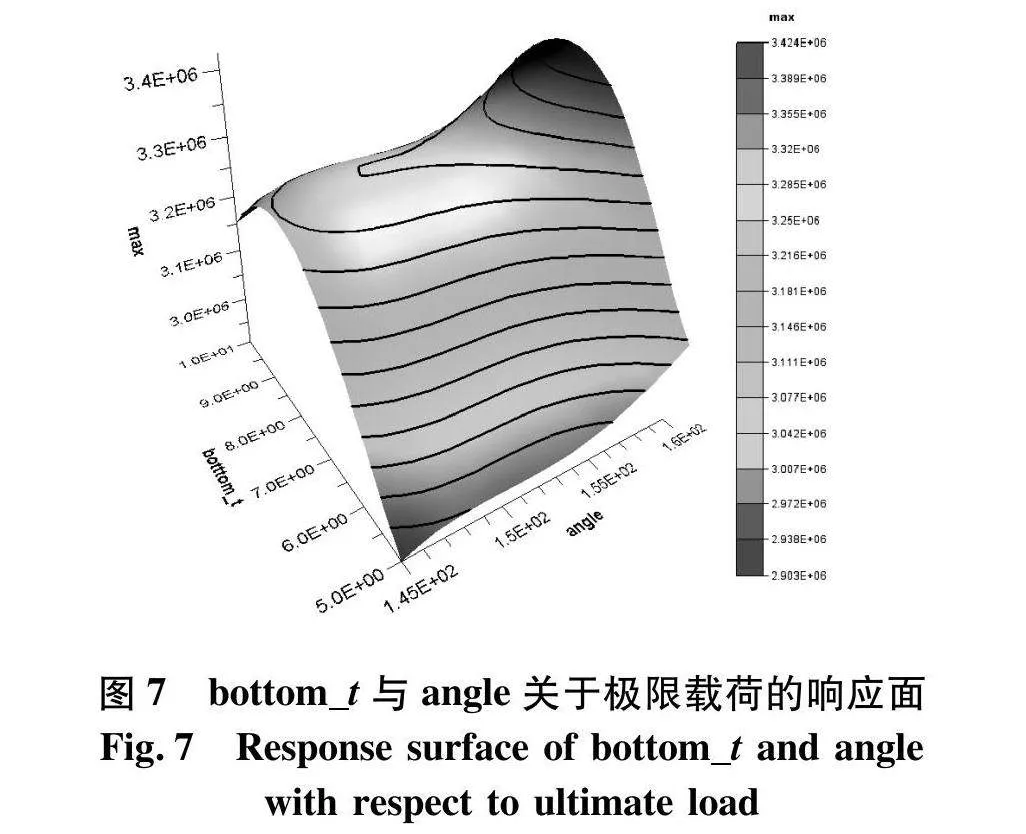
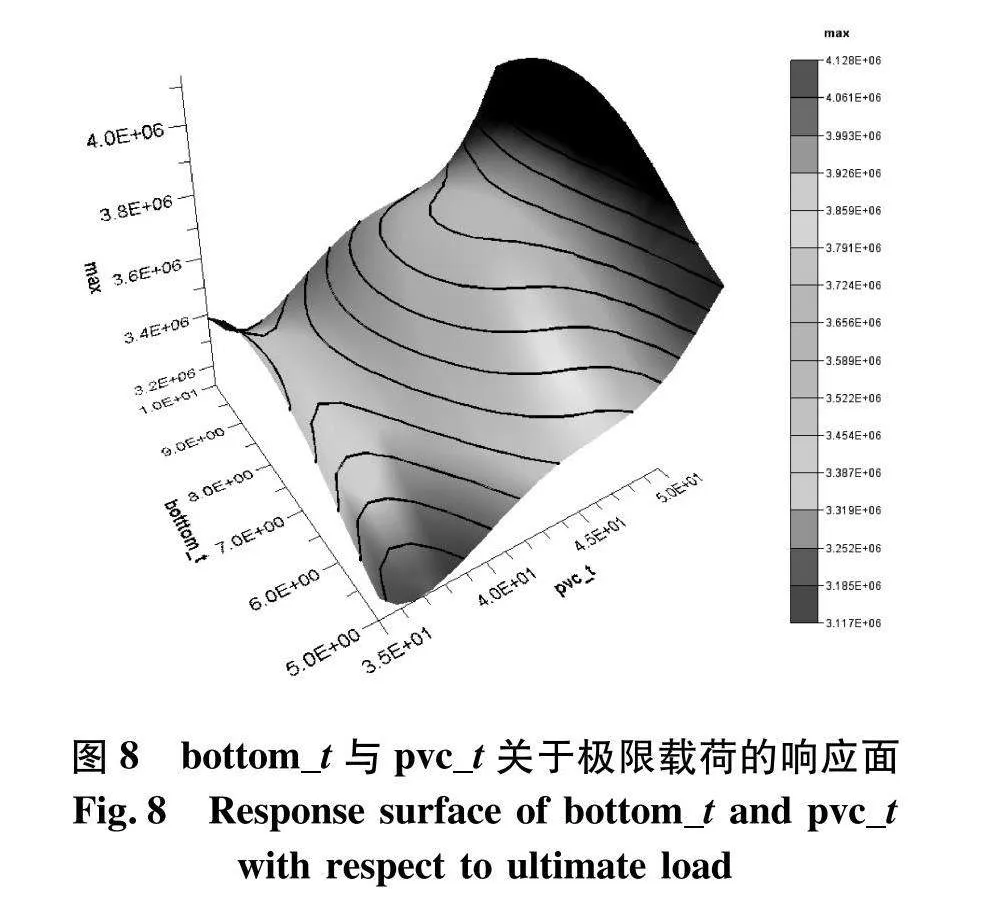
由于响应面模型可导性良好、优化时收敛速度快，可以拟合复杂的响应关系，文中RSM采用四阶响应面拟合，其中复合材料芯层厚度、下蒙皮厚度以及支撑板角度关于极限载荷的响应面如图7、8.

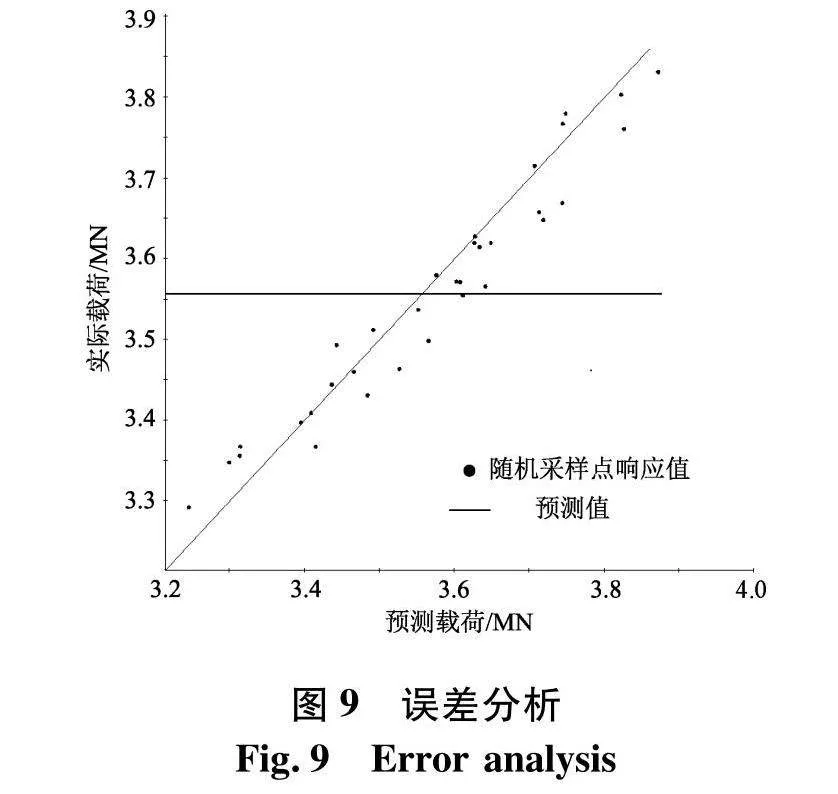
误差分析引入复相关系数R2衡量响应面与样本点符合程度，R2值越接近1则表示建立的RSM响应面模型具有高可信度.文中随机采样33组样本点并计算极限载荷与质量响应值，将样本点极限载荷真实值与预测值之间的均方差归一化处理.图9为样本点极限载荷实际值与预测值误差分析图，图中预测结果与样本的测试数据接近，样本点极限载荷的R2值为0.911 83，因此，该模型可以被认为是可靠的.

3.3"NCGA优化

3.3.1"多目标优化数学模型

对于船舶上层建筑主要要求是质量轻、安全可靠，因此选取钢—复合材料夹芯板的质量mass和极限载荷max作为多目标优化的函数，而多目标优化问题中的各个目标间可能是相互冲突的，它的优化的解是一个Pareto最优解集，对应的目标函数空间的像为Pareto前沿.遗传算法具有全局搜索的优良特性可以用于多目标求解的问题，故文中采用NCGA多目标遗传算法，该方法将问题可能的解随机形成多个基因的种群，通过排序分组进行交叉实现“相邻繁殖”的机制，从而使接近于Pareto前沿的解交叉繁殖的概率增大，从而加速收敛.优化数学模型为：

Find "X={X1，X2，X3......Xn}T（10）

Min "f（x）（11）

Max "g（x）（12）

s.t."5.0 mm≤bottom_t≤9.0 mm35.0 mm≤l1≤60.0 mm45.0 mm≤l2≤60.0 mm35 mm≤pvc_t≤50.0 mm5.0 mm≤steel_t≤9.0 mm5.0 mm≤up_t≤10.0 mm145°≤angle≤160°（13）

式中：Xi为设计变量；f（x）为质量目标；g（x）为最大极限载荷目标；各设计变量捕捉到DOE设计空间中有效的设计区域如式（13）.

3.3.2"优化结果分析

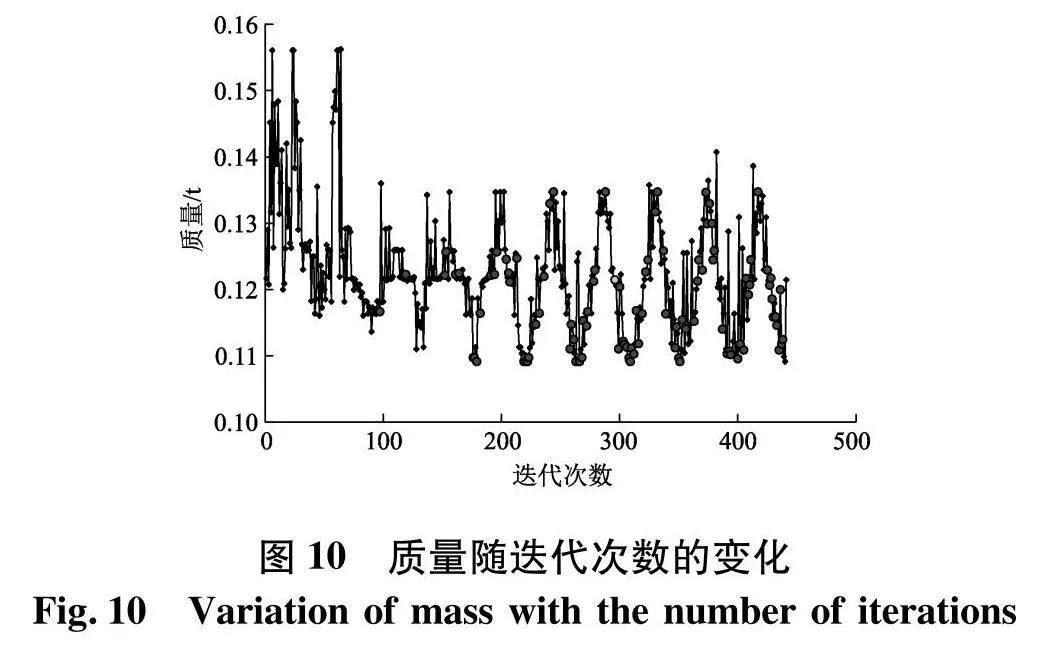
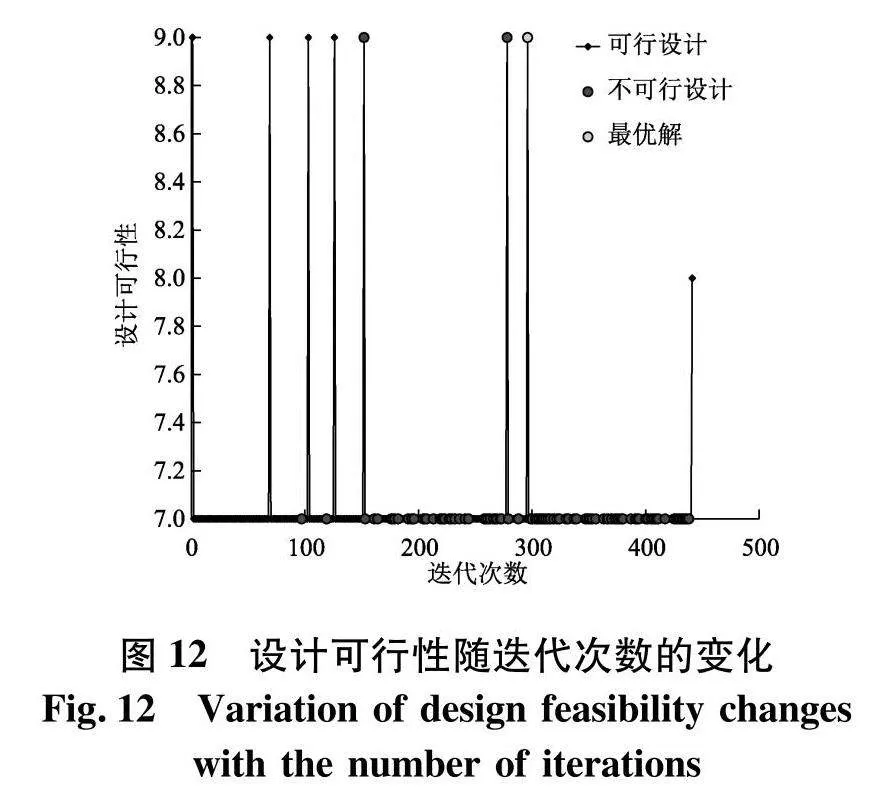
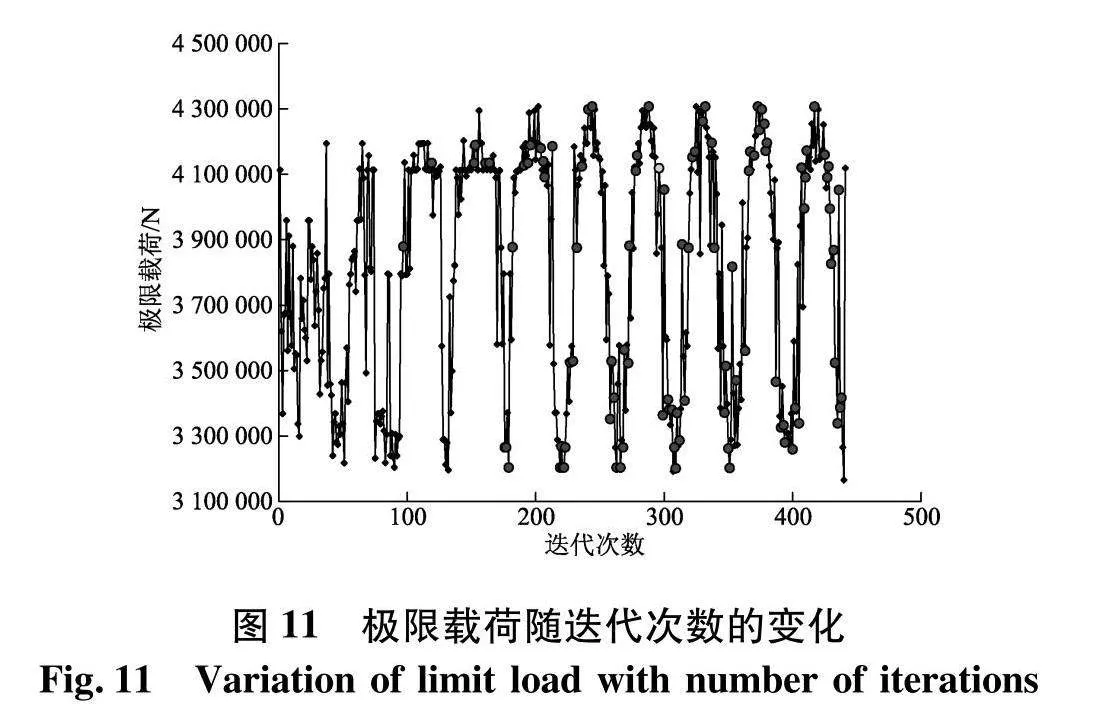
经过441次迭代优化，最优解点为第296次迭代结果.根据ISIGHT后台历史监控可知优化过程中响应目标质量、最大极限载荷函数以及设计可行性（Design feasibility）随迭代变化过程如图10～12，图中包括了不可行设计与可行设计点，其中最优设计为迭代次数为296的设计点.优化结果中angle_t=145.57°、bottom_t=7.35 mm、up_t=5.05 mm、l1=49.76 mm、l2=58.44 mm、pvc_t=49.93 mm、steel_t=5.01 mm为最优参数组合，对应模型质量为0.121 t，极限载荷为4.12 MN.优化结果质量比初始方案降低12.1%，极限承载能力提高17.4%.

3.3.3"优化结果参数取整的有限元结果

图13是将上述优化结果中的变量取整数开展有限元计算的载荷位移曲线，即angle_t=146°，bottom_t=7.0 mm，up_t=5.0 mm，l1=50.0 mm，l2=58.0 mm，pvc_t=50.0 mm，steel_t=5.0 mm，然后进行有限元计算得到结果：对应模型质量为0.120 3 t，极限载荷为3.69 MN.优化结果质量比初始方案降低12.8%，极限承载能力提高5.12%.

4"结论

（1） 采用分层失效的3D-Hashin失效准则对钢骨架复合材料面板展开展极限强度分析，随着轴向载荷增大，纵桁与面板下蒙皮最先开始脱粘；结构在极限载荷状态下主要破坏模式是蒙皮的压缩失效以及胶层脱粘失效，增加胶粘性能参数能更好的提高结构的承载性能.

（2） 应用DOE试验设计对输入参数在设计空间均匀采样，捕捉到了整个设计空间中最有效的设计区域，基于采样点构建四阶响应面代理模型，通过误差分析表明预测结果与样本的测试数据接近，该近似模型被认为是可靠的.

（3） 多目标遗传优化算法在构建的代理模型上开展优化可节省大量仿真分析时间，该组合优化方法用于预测和优化钢骨架复合材料夹芯板的几何结构，以最大限度地提高承载力以及减小结构重量，与初始参数相比，优化结果的质量比初始方案质量降低12.1% ，极限承载能力提高17.4%.

参考文献（References）

［1］"杨慧， 范硕硕， 王岩，等. 基于径向基函数代理模型的M形杆刚度优化［J］. 北京航空航天大学学报， 2022， 48（11）： 2121-2129.

［2］"胡春幸， 侯玉亮， 铁瑛，等. 基于遗传算法的碳纤维增强树脂复合材料层合板单搭胶接结构的多目标优化［J］. 复合材料学报， 2021，38（6）： 12.

［3］"YANG H， LU F， GUO H， et al. Design ofa new N-shape composite ultra-thin deployable boom in the post-buckling range using response surface method and optimization［J］. IEEE Access， 2019，7： 129659-129665．

［4］"BESSA M A， PELLEGRINO S. Design of ultra-thin shell structures in the stochastic post-buckling range using Bayesian machine learning and optimization［J］. International Journal of Solids and Structures， 2018，（139/140）：174-188.

［5］"LEE C S， KIM J H， KIM S K， et al. Initial and progressive failure analyses for composite laminates using Puck failure criterion and damage-coupled finite element method［J］. Composite Structures， 2015， 121： 406-419.

［6］"MAO J Z， SUN X S， RIDHA M， et al. A modeling approach across length scales for progressive failure analysis of woven composites［J］. Applied Composite Materials， 2013， 20（3）： 213-231.

［7］"DOMINGUES R N E， CAMPILHO R D，CARBAS R J C， et al. Experimental and numerical failure analysis of aluminium/composite single-L joints［J］. International Journal of Adhesion amp; Adhesives， 2016，64： 86-96.

［8］"DUAN Y， ZHANG K， LI L. Experimental and theoretical stress analysis for an interface stress model of single-L adhesive joints between CFRP and aluminum components［J］. International Journal of Adhesion amp; Adhesives， 2014， 50： 37-44.

［9］"LIU Y， LI Q S， LU X F. Parameter optimization of L-joint of composite sandwich structure based on BP-GA algorithm［J］"Composite Structures，2022： 115508.

［10］"LU J， ARNAUD E， SOBEY A J. Effective breadth for top-hat stiffened composite structures［J］. Ocean Engineering， 2020， 196： 106841.

［11］"张婧， 王锐， 徐烁硕， 等. 碳纤维复合材料加固损伤加筋板拉伸极限强度研究［J］. 江苏科技大学学报（自然科学版）， 2021， 35（5）： 8-14.

［12］"尹良良，任鹏，赵哲， 等.泡沫弹高速撞击下复合材料夹层板的动态力学响应仿真与实验研究［J］.江苏科技大学学报（自然科学版），2020，34（6）： 1-7.

［13］"GENG X A， KAI Q B， RY B， et al. Research on failure modes and ultimate strength behavior of typical sandwich composite joints for ship structures［J］. International Journal of Naval Architecture and Ocean Engineering， 2021， 14：100428.

［14］"KHOSRAVANI M R， WEINBERG K. Characterization of sandwich composite T-joints under different ageing conditions［J］. Composite Structures， 2018， 197（8）：80-88.

［15］"KOTSIDIS E A， KOULOUKOURAS I G， TSOUVALIS N G. Finite element parametric study of a composite-to-steel-joint［C］∥2nd International Conference on Maritime Technology and Engineering. Lisbon， Portugal：［s.n.］， 2014： 627-635.

（责任编辑：贡洪殿）