基于深度学习的机器人电气故障检测与诊断研究

［摘 要］机器人以其高效、高强度的作业方式，被广泛地应用于制造业及其相关领域。但当机器人出现故障时，通常会导致生产线停滞，浪费大量的人力、物力，甚至危及工作人员的生命安全。传统的故障诊断方法耗时长，诊断效率低，且故障辨识精度不高。文章基于深度学习相关理论，通过分析机器人机械臂各个关节及执行器的振动特性，建立了一种适用于工业机器人的故障诊断模型，并以ABBirb120机器人为例进行电气故障检测与诊断的准确率分析。结果表明，在迭代次数达到900 以上时，其故障识别准确率趋于99.4%。

［关键词］深度学习；机器人；电气故障；检测

［中图分类号］TP242 ［文献标志码］A ［文章编号］2095–6487（2024）03–0142–03

1 机器人电气故障分析

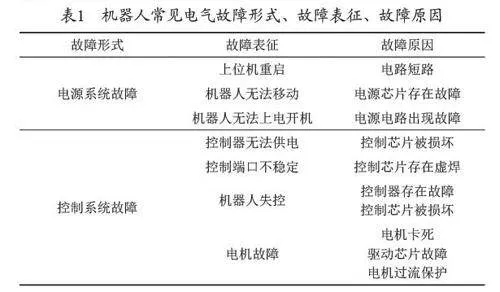
在工业机器人中，其电气故障的表现形式主要是控制系统故障和驱动系统故障。根据这一特点，可以将其划分为两种类型：逻辑故障和物理故障。逻辑故障是指机器人的控制系统失效，不能按命令完成工作。物理性故障指工业机器人的硬件故障，如电路老化或损坏等。工业机器人故障通常会引起振动信号的改变，所以可以利用其振动信号对其运行状况进行评价，并对其有无故障进行诊断。机器人常见电气故障形式、故障表征、故障原因见表1。

2 深度置信网络（DBN）

2.1 深度学习简介

深度学习是通过模仿人类大脑神经网络的构成及对外界刺激做出处理的方式，构建出一种深层的神经网络模型。深度学习由数据接收层、多层隐藏层及数据处理层组成，各层间相互独立、互不连通。这种方式与大脑的内在结构十分接近，能够更好地提取出数据中的特征，并对其本质进行刻画。目前应用最多的深度学习模型有深度置信网络（DBN）、卷积神经网络（CNN）和堆叠自动编码器（SAE），其中，DBN是目前应用最广、理论较为成熟的一种方法。

2.2 深度置信网络基本原理

DBN 是一种基于多层学习网络的无监督学习方法。其基本网络结构是基于约束玻尔兹曼向量机（RBM），通过分层学习，对隐藏层与可见性进行分层学习，并对各层间的权值及传输参数持续进行更新与优化。在此基础上，通过逐级的参数更新与优化，完成故障特征的辨识与提取，从而构建具有更高辨识精度的故障诊断模型。

3 基于深度学习的机器人电气故障检测与诊断

3.1 故障诊断模型创建流程

文章以DBN 为背景，研究面向工业机器人的小波包分解和重构问题。在此基础上，采用信息能量熵、归一化等手段，构造小波重建的能量熵、归一化特征矢量，并对其进行重建。最后，通过对特征矢量的分类与分层学习，完成反演修正与模型校验。

3.2 工业机器人振动信号预处理

从传感器获取的关节振动信号是一种不稳定的状态，其中包括关节本身的振动、噪声（外界噪声、设备噪声）和共振等。文章先对不稳定、多源干扰下的振动信号进行消噪，然后利用小波理论对其进行分析与处理。目前，对振动信号的研究主要有以下3个方面。

（1）时域方法是以时间为基础对信号进行分析，其中，时域参数的选择最为重要。利用这种方法，可快速方便地对原有结构进行振动分析，但其缺点是无法将与故障无关的扰动有效地抽取出来，无法准确反映故障的特性。

（2）从信号中提取振动频率的频域信息。分析手段包括频谱分析和包络分析法。频域分析法是通过对频率范围的分析，实现故障的识别与定位，但该分析方法因缺少时间信息而导致不能最大限度地储存和分析振动信号中的全部信息。

（3）同时提取振动信号时域与频域的时频分析方法。其通过将时域与频域相结合，实现对信号的分析。本项目将时域、频域有机地结合起来，具有很强的互补性，尤其适用于多源干扰下的振动信号分析。在时频分析中，常用的方法有傅立叶变换、经验模态分解、小波分析等，其中，小波分析是目前常用的一种检测设备振动信号的方法。在此基础上，提出了一种基于小波包分解与重构的小波分析方法，并对其进行时频分析。

3.3 DBN参数初始化

在设定 DBN 参数前， 要先对 RBM 网络中的θ={w，b，c} 进行初始化，w 为计算出的各个网络层的连接权重，b 为显层的偏置值，c 为隐含层的偏离值。采用以下公式将具有正态分布的N（0，0.1）初始化，明确显层偏置值b 的初始化为0，将隐藏层中c 的初始化也设为0。

如上所述，可以将偏置数值b 和c 初始化为0，或者可以利用常态随机分布进行初始化，如权重初始化方式相同。具体的设定要随着特定的运算情况而变化，不同的设定将使结果略有不同。如果程序必须进行一些优化，可以考虑对这个设定进行调整。

3.4 DBN网络结构的设置

将网络结构划分为两个层次，即网络结构的深度与节点个数。深度学习和传统神经网络不同之处在于其所具有的深度。在此基础上，文章提出了一种基于DBN 的神经网络模型，该模型能够有效地降低网络中各个层次的结点数量，并对其进行分类，但这也会造成网络结构的增加及训练时间的增加。若参数设定不合理，有可能造成多层的错误积累，从而造成过度的训练误差或过拟合。这里将神经网络的深度设定成1 个输入层、3 个隐藏层、1 个输出层的5 层网络结构。

3.5 学习率的初始化设定

在梯度下降法中，学习速率是一个非常重要的问题，其直接影响着每一步的梯度下降距离。当初始学习率较低时，会使模型向最小化函数的方向偏移得太慢，使得网络的训练时间变得更长；如果初始值取得过大，则可能导致重构误差，严重时还可能导致模型出错。BP 网络的前向无指导分层学习率通常设置为0.1，后向调整学习率通常设置在0.01。

3.6 动量因子的初始化设定

在学习DBN 的过程中，通过对前一次迭代得到的梯度进行估算，增强了学习过程的抗振荡性，使得该方法能够快速、稳定地收敛于容许的范围。公式如下：

3.7 故障诊断过程

基于DBN 的故障诊断方法对已有数据进行简单的预处理，较好地保持其原有的特性，将非监督学习和有监督调优相结合，实现对故障结果的快速准确辨识。基于DBN 的故障诊断流程为：①明确电气故障类型及诊断任务；②基于FFT、归一化等预处理方法，将训练集与测试集分隔开来；③初始化DBN、设置网络节点数量、学习率、迭代数等；④利用逐层特征抽取方法获得初始权值矩阵；⑤对整个网络进行逆向调整，使其参数最优。

DBN 实现故障样本的训练和分类后，与原始数据进行直观比较，直观地反映了DBN 的分类性能，但由于数据维度过大，不能直接将其表达出来，所以采用主成分分析法对各层次的特征矩阵进行处理，选择3 个最重要的特征来构造三维哈希图，以研究DBN的分类性能。

3.8 准确率分析

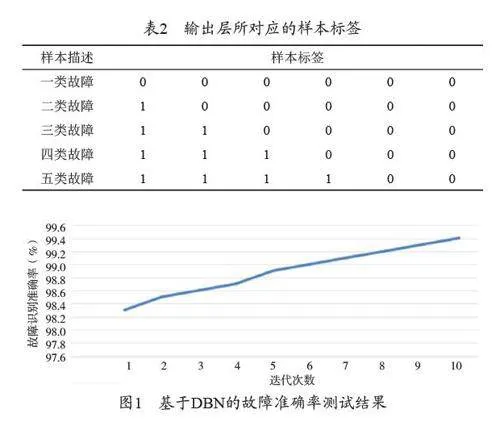
针对ABBirb120 机器人的电气故障， 采用MATLAB 2019 b，配置为Windows 10、英特尔i7 处理器、Nvidia 930 M、内存8 GB。将两组样本按照4 ∶ 1的比例分成两组。训练集合包含192 000 个试验（正常试验样品38 400，4 种缺陷试验样品38 400），其中试验集合48 000 个（正常试验样品9 600 个，4 种缺陷试验样品9 600 个）。基于7 级分解与小波基db1，将小波包分解与归一化，得到128 个单元的标准化能量熵向量。在训练集上，有192 000 个输入样本和48 000个测试集。DBN 网络模型以128 个输入单元、以采样错误标记作为输出层，并以6 个输出层为输出单元。输出层所对应的样本标签见表2。

将 DBN 模型的迭代次数设定为100，将反向调节的数目设定为100，并将其乘以1 000，并且将学习速率与动量系数设定为0.1 与0.9。基于DBN 的故障准确率测试结果如图1 所示。

从图1 可以看出，在迭代次数超过900 次的情况下，错误辨识的正确率已接近稳定的99.4%。结果表明，文章所采用的DBN 模型正向迭代次数为100 次，反向调优次数应不小于900 次。

4 结束语

以机器人电气故障为研究对象，采用深度学习技术对其进行了故障诊断，其中采用小波分析与信息能量熵相结合的方法，构建了基于多源信息的正则化特征矢量，并对其进行训练与检验，采用傅立叶变换与机械臂电气故障信息相结合的方法，对机器人电气故障进行特征提取，构建了DBN 模型的机器人电气故障诊断模型，实现了对机器人电气故障的诊断，其电气故障诊断正确率可达到99.4%。

参考文献

[1] 陈公兴. 基于深度学习的机器人电气故障检测与诊断研究[J]. 自动化与仪表，2020，35（12）：40-44.

[2] 黄威，袁廷翼，邓百川，等. 基于深度学习的机器人电路板自主故障检测系统[J]. 电工电能新技术，2022（2）：41.

[3] 周东华，席裕庚. 工业机器人故障的实时检测与诊断[J].机器人，1992，14（1）：1-6.

[4] 农权，陈伟，郝鹏祥. 一种破拆机器人电气故障检测方法及其装置：CN111590580A[P].2020-08-28.

[5] 董旭，刘微，李一顺，等. 一种特种机器人电气故障诊断系统：202111010206[P].2022-04-13.

[6] 彭建盛，覃勇，何奇文，等. 一种电气设备故障诊断机器人：CN106707054A[P].2017-05-24.