聚焦结构化思维 感悟运算一致性

［摘 要］在“数的运算”领域，结构化教学尤为重要，因为数的运算贯穿整个小学阶段的核心内容。五年级下册的“分数的加法和减法”单元是学生在掌握了整数和小数加减法的基础上开展教学的，文章将以本单元为例，论述如何利用结构化教学提高学生的推理意识和运算能力，使学生深刻体会数的运算的一致性。

［关键词］分数加减法；结构化教学；一致性

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）29-0058-04

【课前之思】

在对新旧课标的对比研读中发现“数的运算的一致性”是《义务教育数学课程标准（2022年版）》中的一项重要理念。史宁中教授在对《义务教育数学课程标准（2022年版）》的解读中提出：“当前的教材和教学中关于数的运算，加减乘除有各自的算理，整数、分数、小数运算有各自的算法，使得这些知识似乎是支离破碎、缺乏内在一致性。”那么，如何在分数加减运算中凸显运算的一致性，并通过单元整体教学使之更有利于学生的学习？笔者尝试将人教版教材五年级下册数学教材“分数的加法和减法”这一单元中的同分母分数与异分母分数内容进行整体设计，旨在体现结构化的教学方式，促进学生结构化的学习。

“分数的加法和减法”单元涵盖以下内容：同分母分数加减、异分母分数加减、分数加减混合运算、整数运算定律在分数中的推广及解决问题。该单元的重点在于掌握异分母分数加减的算法和算理，并能运用所学知识解决实际问题。由于异分母分数加减的学习是在同分母分数加减的基础上进行的，因此笔者对学生进行了一次同分母分数加减的前测，具体情况如图1所示。

前测结果显示，学生的计算正确率较高，大部分学生已经掌握了计算方法。那么，课堂上还需要教什么？教材为何还要安排一课时呢？显然，目的是让学生不仅要掌握计算方法，还要理解算理，为学习异分母分数加减打下基础。这就需要找到从同分母加减学习迁移到异分母加减学习的融合点，即让学生明白只要分数单位相同，就是对分数单位的个数进行相加减这一基本原理，将同分母加减和异分母加减融合在一课时内进行教学，以此增强学习的关联性和结构性。

【课堂实践】

一、回顾旧知，疏通“理”法

师：先回顾以前学过的分数加减法。[35+15]， [311+111]， [323+123]， [38+18]，你能直接算出得数吗？请大家一起快速口答。

师：它们有什么相同的地方？

生1：分母都相同，只要把分子加在一起就可以了。

师：你们想着怎样的一个算式？

生2：3+1=4。

师：为什么都可以想着3+1=4呢？下面以[38+18]和[38-18]为例，请用自己的喜欢的方式表示其中的原因，让别人一眼就能看明白。

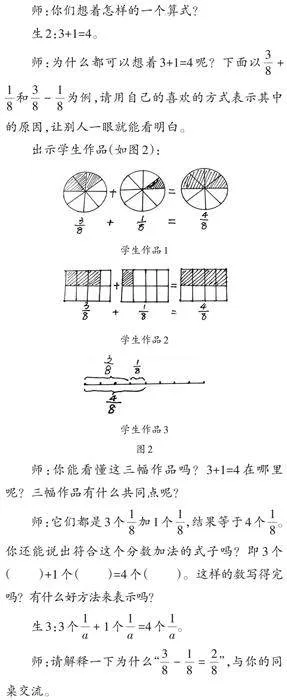
出示学生作品（如图2）：

师：你能看懂这三幅作品吗？3+1=4在哪里呢？三幅作品有什么共同点呢？

师：它们都是3个[18]加1个[18]，结果等于4个[18]。你还能说出符合这个分数加法的式子吗？即3个（ ）+1个（ ）=4个（ ）。这样的数写得完吗？有什么好方法来表示吗？

生3：3个[1a] + 1个[1a] =4个[1a]。

师：请解释一下为什么“[38-18=28]”，与你的同桌交流。

师：看来，当分数单位相同的时候，把分数单位的个数进行相加或相减就可以了。

【分析】分数加减法的核心在于实现分数单位的统一。尽管学生能够正确进行计算，但他们往往对计算背后的原理缺乏理解。在这一教学环节中学生认识到“只要分数单位相同，便可以将分数单位的个数进行相加减”，为后续学习异分母分数加减做好了铺垫。

二、深度探索，融通“理”法

（一）“串”驱动问题：击盲点，促内化

师：刚才借助“3+1=4”研究了同分母分数加减法。对于[14+112]，分母不相同了，还能用刚才的方法，即用“1+1=2”来计算吗？请在学习单（如图3）上试一试。

师（出示图4）：从这个图来看，计算[14+112]的结果好像真的是[216]。

生1：不对，分母不同，不能将分子相加。因为每一份的大小不一样，不能直接相加。

师：看来分母不同，也就是分数单位的大小不同，是不能直接相加减的，那该怎么办呢？

【分析】（1）捕捉“误区”，突破学习疑难点。学生能够按照“先通分再加减”的规则进行程序化的计算，然而，他们对于为什么异分母分数相加减需要先通分，以及通分的必要性往往缺乏理解。展示计算中的错例就能够一针见血地触及学生的学习疑难点。

（2）反思“错误”，填补知识薄弱点。通过探讨为什么“分子加分子，分母加分母”的计算方法是错误的，引导学生深入思考。借助直观的图形，学生豁然开朗：由于不同分数的单位大小不一，因此不能直接进行相加减，必须先统一计数单位，然后再进行计算。

（二）“链”直观表征：助支点，探本质

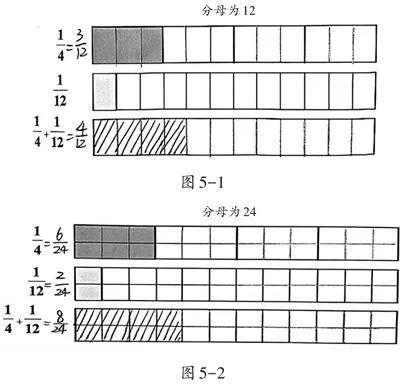
师：分母不相同，也就是分数单位不一样，异分母分数该怎样相加呢？谁能看懂这两种方法？（出示图5-1、图5-2）

师：比较这两种方法，你更喜欢哪一种？

生1：喜欢第一种方法，因为找分母的最小公倍数作为公分母时，计算简单，可能计算结果不需要约分。

师：异分母分数相加减，先转化成同分母，然后根据同分母分数加减法进行计算。

【分析】（1）遵循起点：算法多样化。教师给出了计算[14+112]的多种解题思路，充分体现了算法多样化。

（2）碰撞思维：策略更优化。虽然[14]和[112]的公分母可以是12，也可以是24，但学生通过交流后能够发现将最小公倍数作为公分母更方便，从而感悟算法多样化，学会灵活选择解题策略。

（三）“联”运算一致：找融点，建模型

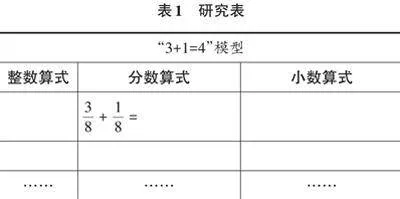
师：刚才大家运用“3+1=4”研究了同分母和异分母分数加减法，那么在整数和小数中能找到“3+1=4”的例子吗？请填表（见表1）。

师（出示图6）：今天大家学习了分数加减法，之前大家还学过整数加减法和小数加减法，它们之间在计算过程中是相差很多，还是差不多呢？

生1：我觉得差不多，无论是整数、小数还是分数，只要它们的计数单位相同，把计数单位上的数相加减就可以了。

师：是啊，整数的5+8就是5个一加上8个一，小数的就是6个0.01减去2个0.01，而当分数的分数单位相同时，3个[112]和1个[112]相加等于4个[112]。只要计数单位相同，把计数单位上的个数相加减就可以了。

师：可以用一个万能公式来表示——（ ）个a±（ ）个a=（ ）个 a。这里的a可以是什么？

师：对于万能公式“（ ）个a±（ ）个a=（ ）个a”，只要计数单位或计量单位相同都可以直接相加减。

【分析】（1）通“法”，在对比中沟通算理。通过问题“整数加减法、小数加减法是相差很多，还是差不多”可以引导学生发现：整数加减法是相同数位对齐，小数加减法是小数点对齐，而分数加减法是先通分再计算，其本质是一致的，就是将相同数位上的个数相加减。

（2）丰“型”，在思辨中建模算理。学生思辨后发现：分数加减法、整数加减法和小数加减法，它们的算理本质都是计数单位相同才能相加减。教师可就此引出“万能公式”，打通加减法的算理算法，引导学生“有关联地学”——构建整数、小数和分数加减法算理模型，从而感悟数的运算一致性。

三、进阶练习，内化“理法”

（一）基本练习，掌握算法

师：算一算[16+56]，[16-17]，[16+23]，[38-16]。为什么[16]在计算时一会儿变成[742]，一会儿又变成[424]呢？

生1：通分时要看另外的分母，要找两个分母的最小公倍数，所以就会发生变化。

师：是的，在计算异分母分数加减时，要进行通分，找几个分母的最小公倍数作为公分母。

（二）解决问题，提升能力

师：同学们，第19届亚运会在浙江杭州举办！为此，杭州亚运村项目从2018年6月就开始建设了。第一年完成了总量的[16]，第二年完成了总量的[14]，第三年完成了总量的[920]。

师：根据这些内容，你能编写出几个问题？三个分数相加减时，怎么通分呢？

（三）挑战升级，拓宽思维

师：通过今天的学习，我们得到了万能公式（ ）个a±（ ）个a=（ ）个a，如：3a+4a=7a，请你判断以下等式是否成立，说说你的理由。①7x-0.5x=6.5x；②5+y=5y；③4x+x2=5x；④3ab+2a+4ab=7ab+2a

师：利用万能公式的时候，只有计数单位相同时才能相加减。

四、课堂总结，拓展“理法”

师：我们今天发现了分数、小数和整数加减法之间的秘密，在运算的时候，只要计数单位相同，把它们的个数相加减就可以了。今后我们还会学习分数乘除法，它和整数、小数乘除法之间到底是“差不多”还是“差很多”？等着你们继续探究！

【课后有感】

整个学习过程紧紧围绕“统一计数单位”这一主线，让学生通过感悟运算的一致性掌握知识技能，有效提升数学素养。

一、研学：土壤衍生在“困知勉行”处

传统教学往往聚焦于单一课时，忽视了整体性的实践与思考。而整合教学要求教师从宏观角度分析，立足于学生的现实起点，全面审视学生的整体状况，让学生感悟知识点之间的内在联系，能够在任务驱动的模式下自主解决问题、自主获取知识，有效促进了学习行为的转变。本节课旨在探讨如何使计算课程既吸引学生的注意力，又能厘清算理、拓展思维，以引导学生理解分数加减法背后的算理为切入点，设计了疏通“理”法、融通“理”法、内化“理法”三个不同层次的环节，帮助学生破解疑惑，深刻感悟运算的一致性。

二、衍学：枝叶联结在“雾里看花”处

首先，基于算理与算法的一致性找到了教材核心知识点之间的结构，将其分为“内核结构”“因果结构”和“拓展结构”后进行整合。其次，引导学生通过迁移学习，构建知识间的联系，学会举一反三、触类旁通，让学习真正发生。最后，通过绘制直观图形，帮助学生理解通分的本质是“在不改变分数大小的前提下，统一分数的计数单位，将其转化为同分母分数的加减运算”，使学生感悟到异分母分数加减的关键在于转化。

三、延学：能量添加在“意犹未尽”处

数的运算重点在于理解算理、掌握算法，数与运算之间存在着紧密的关联。通过感悟数的运算及其之间的关系，学生能够体会到数的运算在本质上的一致性，从而深化对算理的理解，形成运算能力和推理意识。只有深入理解了算法，才能更好地掌握运算的本质，因此，教师最后通过问题鼓励学生进行深层次的思考，引导学生从“意犹未尽”达到“豁然开朗”的境界。

对于数的运算一致性，如何通过合适的结构化教学方式引导学生理解数学本质，构建知识体系，提升素养能力和数学素养，笔者作了粗浅的尝试。期待更多的教师能关注这一知识内容，探索出更成熟、更有效的教学之路。

［ 参 考 文 献 ］

[1] 余丽娟.小学生数学思维结构化的培养策略[J].教育观察，2019，8（17）：121-122，124.

[2] 袁仕理.“数的运算”教学需要厘清的几个问题[J].福建教育，2018（49）：45-46.

（责编 金 铃）