学生立场·真实体验·感悟本质

［摘 要］圆形是学生在小学阶段需要掌握的最后一个平面图形，也是他们接触的第一个曲线图形。文章分析了两节课中“三次画圆”的过程，从画圆任务、画圆顺序、画圆应用三个维度进行了深入分析，并探讨“变式画圆”与“感悟极限”的独特价值和意义。

［关键词］圆；三次画圆；变式画圆

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）29-0049-03

在2023年第十五届小学数学教学改革观摩交流展示培训活动中，浙江省诸暨市暨阳街道暨阳小学的魏琼老师执教的“认识圆”一课，所展现的“三次画圆”教学策略，不禁让笔者回想起十年前（2013年）自己也曾运用“三次画圆”的方法帮助学生理解圆的概念。那么，魏老师设计的“三次画圆”环节与笔者当年（2013年）设计的有何共通之处？又在哪些方面体现了更加深入的思考呢？笔者以为，通过对比分析前后十年两节课的教学设计及其背后的理念，可以构建一个积极的对话平台，开启教研之路上的探索。

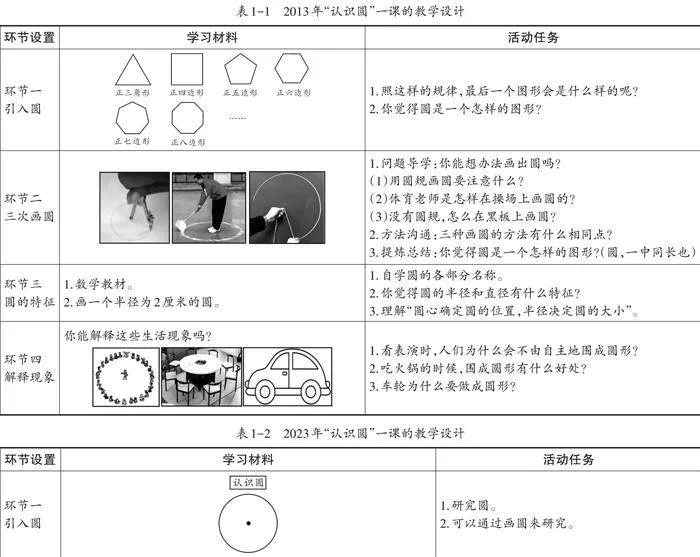
一、教学设计（见表1-1、表1-2）

二、比较分析

（一）两节课的相同点

“基于学生立场，引发真实学习”是两节课的显著共性。两节课均深入解读了圆的“一中同长”本质，并基于学生学习的思维逻辑精心设计了画圆活动，让学生在活动中体验，在体验中感悟。

1.画圆任务：动手操作助推概念形成

圆的静态定义是指“平面上到定点的距离等于定长的所有点的集合”，而其动态定义则为“平面上一动点以一定点为圆心、一定长为距离运动一周所形成的轨迹”。面对这样的抽象概念，如何引导学生认识并理解它？两节课均采用了概念形成的教学策略，即通过画圆活动，让学生在众多同类事物的不同例证中，探寻并发现相同的关键属性。

在笔者的教学设计中，通过圆规画圆、体育老师使用粉笔在地上画圆，以及利用绳子画圆这三种各具特色但本质一致的画圆方法，使学生深刻体会到，唯有遵循“中心点保持不动”和“中心点到圆上任意一点的距离相同”这两个原则，才能绘制出真正的圆。这三个例证让学生在“能够画出圆”与“无法画出圆”的对比中，逐步构建起圆的概念表象。

魏老师设计了“你能画出2个大小不同的圆吗？没有圆规的情况下能否画圆？用直尺可以画圆吗？”这三个核心任务，引领学生亲历画圆的过程。学生从依赖圆规画圆逐渐过渡到不依赖圆规，从使用工具画圆发展到“想象”中的画圆，从直观到抽象，逐步探索并理解圆的本质特征。同时，魏老师还通过直尺画圆的方法，让学有余力的学生进一步体会到圆的“一中同长”特性，并领悟到“圆出于方”的理念。

借助画圆时定点、定长的具体经验，学生对圆的认识已经提升至“一中同长”的层面。两节课都没有简单地采用画图、折叠、测量的操作方式，而是让学生在活动经验的基础上进行想象，理解“圆的每条半径相等”。这两节课都强调了通过具体内容的教学，帮助学生培养数学思维的能力。

2.画圆顺序：遵循认知确定材料立序

教学过程中需要深入研究学习内容与学习者。对于学习内容，应探讨其来源及其发展趋势；对于学习者，则需重视其生活背景和学习基础。

就学习内容而言，通过画圆任务激发学生的主动性和独立思考，从而让他们体验并理解圆的本质属性：“一中”揭示了圆心在平面上的独特地位，“同长”则是对圆内所有半径等长的简洁描述。例如，体育老师以自身为圆心画圆，这便是圆规画圆的现实原型。可以设想，必然存在其他画圆工具，但圆规因其完美契合“一中同长”的本质特性，成为目前最常用的画圆工具。

然而，对于学生来说，圆规往往是他们认知中的第一种画圆工具。魏老师在课堂上提到：“我刚才让大家画圆，并没有指定工具，但你们都自然而然地选择了圆规。”这一现象在笔者的教学中也出现过。学生认识事物的顺序与数学知识的形成过程往往并不一致。对数学家而言，从用绳子画圆到用圆规画圆是一种创新，而对学生来说，从用圆规画圆到用绳子画圆，则是在逐步理解圆的本质意义后的一种创新。

两节课都严格遵循了学生的认知规律，从用圆规画圆入手，引导学生将注意力从动手操作转向动脑思考，从关注“如何画好圆”转向探究“圆的性质”，从日常生活经验过渡到数学知识的理解。

3.画圆应用：现象解释深化圆的本质

在概念运用的环节中，两节课都提出了这样的问题：“你能用圆的知识解释生活现象吗？”除了“吃火锅时使用的圆桌，其设计仅仅是为了美观吗？人们在观看表演时，为何总是自然而然地围成圆形？”这两个问题，笔者还提出了“为什么车轮要做成圆形”的问题，而魏老师则提出了一个更具启发性的问题：国际圆桌会议，桌子实际上是方形的，那么为什么被称为圆桌会议呢？

这一环节有效地促使学生将抽象的概念用于现实情境中，进而加深对圆的本质属性的理解。这种设计超越了简单的知识点记忆和技能训练，强调了知识学习应从理解过渡到应用，在真实情境中解决问题的过程，实际上就是发展学科核心素养的过程。

（二）两节课的不同点

1.变式画圆：从“操作认识”到“结构认知”

笔者展示的用圆规画圆和体育老师用粉笔画圆，以及用绳子画圆的方法，本质上都是圆规或其原始形态的应用。这恰好体现了“变式理论”给予的重要启示：为了帮助学生顺利实现从具体实例过渡到抽象概念，在教学中不仅应提供“概念变式”和“标准变式”，还应提供“非概念变式”和“非标准变式”。

魏老师提出了问题，如“你能画出2个大小不同的圆吗？没有圆规还能画圆吗？用直尺可以画圆吗？”。学生在使用圆规画圆之后，魏老师会问：“有没有什么经验可以和大家分享？”而在不用圆规的情况下画圆时，魏老师又会提问：“为什么旋转一周就可以画出一个圆，是把圆的什么特点表现出来了呢？沿着这个思路继续思考，你还能想到其他画圆的方法吗？”接着，通过探讨“这些方法为什么都能画圆”的问题，引导学生意识到“万物皆可画圆”。当学生尝试用直尺画圆时，魏老师进一步提问：“为什么要画正方形来构图？哪些方法也能体现圆的半径相等？有没有方法可以画得更圆？”每一次画圆的过程，都不只是停留在实际操作的层面，还通过深入本质的操作来促进学生思考，从而实现从“操作性认识”到“结构性认识”的转变。

2.感悟极限：从“想象猜圆”到“实践画圆”

笔者在课程的引入部分巧妙地融入了这一概念：从正三角形到正四边形、正五边形……随着边的数量不断增加，当边数趋向于无穷时，便形成了圆。这种引入方法旨在让学生通过想象去感受圆与其他图形之间的联系，以及通过想象去领悟极限思想。

“圆拥有无数条半径”和“圆出于方”的理念，揭示了从有限到无限的过渡，这是一种质的飞跃。因此，学生很难仅通过简单的思考就能顺利地接受这一概念。魏老师在教学中巧妙地运用了“直尺画圆”的活动，将抽象的想象转化为具体的实践。学生在操作之后，魏老师展示了画圆的过程图（如图1），并引导学生思考：如果继续向下画，会出现什么情况？如果拥有足够的时间去画，这个圆是否就能成为一个完美的标准圆？

荷兰著名数学教育家弗赖登塔尔曾说：“对学生而言，与其说学数学，不如说学习数学化。” 基于学生立场的三次画圆练习，为个体生命成长的不确定性提供了发展空间；以学生为中心的教学设计激发了学生的想象力和创造力，使得学习过程充满了乐趣。

（责编 黄 露）