多维探究周长 感悟一致内涵

［摘 要］周长是小学图形与几何领域的一个重要概念，教师应在学生初步认识周长概念的基础上，通过有效的活动来加深学生对周长概念的理解，使其逐步形成整体性的认知结构。文章在一致性视角下探究有关周长的多维核心认知，以及周长概念的核心本质，并通过核心本质的串联与发散，引导学生积极参与实践探究，充分彰显了学生学习的主体地位，让学生经历实践操作、对比分析、内因探究、归纳总结等活动过程，发展了高阶思维能力。

［关键词］周长；多维探究；一致性视角

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）29-0045-04

在实际教学中我们常常发现这样的现象：学生已经学习了周长的概念，也能正确计算基本图形的周长，但一遇到“剪一剪”“拼一拼”“折一折”的图形问题时还是频频出错。造成这一现象的内在原因是什么呢？又该如何解决呢？不同学生有不同的错误，但在一致性的视角下不难发现，学生之所以对这类图形问题感到困惑，归根结底是没能深入理解周长的核心本质，只会死记硬背公式。教师在一致性的视角下引导学生从多维度深入感悟周长概念的本质，能让学生在解决这类问题时擦亮双眼、拨云见日。

一、多维理论探究周长

周长的本质是什么？周长的核心概念又该从哪些维度来理解呢？小学阶段对周长的定义是这样的：封闭图形一周边线的长度，就是它的周长。对于周长的概念，我们无须像初、高中一样刻意拔高，只需结合小学生的实际情况，引导学生从以下四个维度来解读。

【维度1】“一周边线”是从某一点出发，沿着周界回到起点的封闭路线。封闭图形内部的线段不属于周长的部分。

【维度2】“长度累加”说明周长是由周界边线累加得到的总和。例如，三角形的周长就是围成三角形三条线段的长度总和。又如，圆的周长是围成一周的许多圆弧的长度的总和，这是“化曲为直”思想的基础。通过平移的方法将不规则图形转化为规则图形也是利用了这一思想。因此，利用平移法求周长时一定要关注平移前后两个图形累加的线段是否一致或一一对应。

【维度3】周长与面积的相互依存性。在一个封闭的区域中，有面积就有周长，两者相互依存，而且两者的本质都是“度量单位的累加”。三年级的学生还没有学习面积的概念，但如果在教学周长时为降低面积概念的干扰，撇开面积只研周长，学生反而容易混淆面积与周长的概念。

【维度4】过程和结果的双重特性。周长是一个具体的值，是一个结果。可是要获得这个结果必然经历“找一周边线” “度量”“计算”等一系列整体的活动，这是周长具有的“过程性”。可见，周长概念从一个过程引进，然后转变为结果，最终两者在认知结构中共存，这就是它的“过程”和“结果”的双重特性。

以上是从四个不同的理论维度来理解周长的内涵，四个维度各有侧重，但又有着内在的联系。因此，教师只有在一致性视角下宏观指挥，通过不同的操作环节来引导学生从不同维度充分理解周长的本质，才能让学生触及周长概念的本质，实现思维的进阶。

二、实际活动探究周长

结合上述四个维度，笔者通过“周长是多少”一课的几个教学片段来分析。

（一）撕一撕：周长本质初感悟

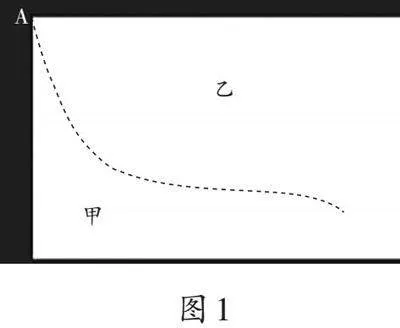
师（用PPT出示一张长方形白纸，如图1）：如果从A点沿着虚线撕开，甲、乙两部分谁的周长大？

生1：我觉得乙的周长大一些，因为乙这部分看着就比甲大。

生2：我觉得甲和乙的周长一样大。

生3：我觉得现在还无法确定，因为纸还没有撕完，甲和乙的边线还没有确定。

师：其他人更同意谁的说法？

生（齐）：生3说的更有道理。

师：看来，没撕完之前无法确定甲、乙两部分的边线，也就无法判定谁的周长大。那现在谁能用笔接着把这条线画完，并说出你的结果？

（教师展示学生的3种画法，如图2）

生4：按AB这条线撕，甲的周长小于乙的周长；按AC这条线撕，甲、乙的周长相等；按AD这条线撕，甲的周长大于乙的周长。

师：你们总结得真棒！图形的周长是一周边线的长度，与图形的大小无关。

[教学思考]以“撕一撕”这个活动导入，让学生尝试从两个维度来理解周长的概念：只有封闭图形才能确定周长，与图形的大小无关。学生虽然现在还没有正式学习面积的相关知识，但对图形的大小是有直观感悟的，这一导入能够很好地帮助学生区分周长与面积。

（二）拼一拼：寻找“消失的周长”

师：一个边长为1 cm的小正方形的周长是多少？

生1：4 cm。

师：那6个边长都是1 cm的小正方形的周长之和是多少？

生2：24 cm。

师：如果把这6个小正方形拼在一起，拼出的图形周长是24 cm吗？请自己拼一拼。

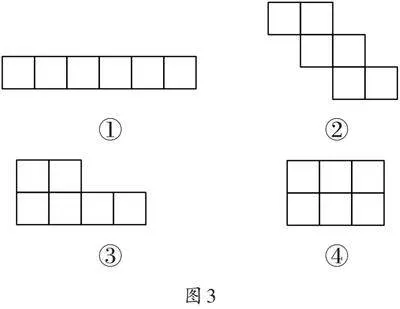
（展示部分学生拼成的作品，如图3）

生3：拼出的这4个图形的周长都不一样，且都比24 cm小。

师：你观察得很仔细。有谁知道“消失”的这部分周长都去哪了吗？

生4：拼组以后，图形内部的边不属于周长的一部分了。

生5：中间拼在一起的边不能算在周长里，拼在一起的边越多，图形的周长就越小。

生6：我还发现每2个小正方形拼在一起，就会减少2条边，周长也减少2 cm。

师：你们可真厉害，一下子发现了这么多的秘密。利用这些发现，你们能找到计算这4个图形周长的方法吗？

生7：可以用原来6个小正方形的周长之和减去中间拼接重合的部分，每拼接一处，周长就减少2 cm。如图形①，中间拼接了5处，减少了2×5=10（cm），图形的周长是24-10=14（cm）。

师（总结）：大家说得都很好。同样的6个小正方形拼出来的图形虽然大小是一样，但周长却可能是不一样的。

[教学思考]学生在“拼一拼”中寻找“消失的周长”，经历了“动手操作—分析原因—发现规律—归纳总结”的探究过程，再次从不同的维度获得了以下关于周长的核心认知。

周长是指图形一周边线的长，与图形内部的线段无关，拼接重叠在一起的内部线段不再是周长的一部分。因此，由几个小正方形拼接得到的图形的周长一定比这几个小正方形的周长之和要小。这也为计算组合图形的周长提供了新的思路。

计算图形周长时，可以通过一周边线分段累加得到，累加时可以逐段累加，也可以先平移部分线段，将不规则图形转化为规则图形进行计算。

拼在一起的6个小正方形虽然形状不同，但大小是相等的，周长则不一定相等，这再次说明图形的周长大小与面积大小没有本质关联，进一步渗透周长与面积的区别。在一致性的视角下再一次进行归纳，发现不同维度的解读又有着内在的联系：周长的本质是一周边线的长，因此可以分段累加边线求周长，也可以用6个小正方形的周长之和减去拼接后转变为图形内部线段的边长的长度；不同的拼法，重叠减少的线段也是不同的，这也解释了为什么拼出的图形大小相等但周长却不一致。

（三）比一比：探寻周长不变的原因

师（出示图4）：图中每个方格的边长为1 cm。仔细观察，这3个图形的周长相等吗？

生1：图①是长方形，周长是（6+5）×2=22（cm）。图②和图③是不规则图形，可以数边数计算，也可以用平移的方法计算（如图5），这3个图形的周长相等，都是22 cm。

师（出示图6）：右边图形的周长是否也是22 cm呢？

生2：它的周长不是22 cm。把中间凹进去的那条边平移到上方，图形也会变成一个长方形，但这个长方形的周长与原图形的周长相比，少了中间竖着的两条边，所以这个图形的周长是24 cm。

师：通过平移能把不规则图形转化成规则图形，但要注意平移前后图形的周长有没有发生改变。

[教学思考]图4的探究活动旨在让学生经历平移转化的过程，从中感受平移转化的优点，通过后续的追问环节，让学生意识到：虽然平移是个好方法，但一定要关注平移前后图形的周长是否会发生变化。图6的探究活动让学生再次感受多边形的周长就是将各部分边线的长累加起来，不论采用什么样的计算方法，这一点始终是不变的。

（四）估一估、量一量：在实践中感悟周长“过程与结果”的双重特性

师：规则图形的周长我们会想、会算、会画了，可生活中并不都是规则图形。如图7所示的2个图形的周长大约是多少呢？请先估一估，再量一量。

师（提示）：怎样估算才更准确呢？可以根据图形的特点，采取灵活的方法。

生1：对于图①，我们可以先估一条线段的长度，大约1 cm。图①有10条这样的线段，所以它的周长约是10 cm。

师：图②的边线是弯曲的，要一下子估算出它的周长比较难，误差也比较大。怎样估算才更准确呢？

生2：可以把它的一周平分成4份来看，其中一份的长大约是3 cm，那么它的周长是12 cm。

师：想要知道生1和生2估得准不准，我们还需要实际测量一下。经过测量，图①的一条线段确实是1 cm，它的实际周长是10 cm。我们该怎么测量圆②的周长呢？

生3：用化曲为直的办法，用线绕图②一周，再将线拉直量一量。

师：请同学们拿出准备好的棉线等工具，小组合作，测量图②的周长。

（测量结束后组织学生交流测量与计算过程中出现的问题与解决方案。）

生4：棉线应该紧贴图②的边缘。

生5：图②的周长与其内部线段无关。

生6：用彩笔在棉线上做记号的方式能使测量的结果更准确。

生7：如果围绕图案一周的线段太长，尺子一次无法测量的话，也可以对折后再测量，最后用结果乘2。

……

[教学思考]周长是一个具体的值，是一个结果。要获得这个结果必然经历“找一周”“度量”“计算” 等一系列活动，由此可见，周长具有清晰的过程性。在一致性的视角下，周长的测量过程与周长的计算结果同样重要，二者是相互依存、密不可分的。学生仅仅了解图形的计算方法还远远不够，还需要深入体会图形周长由实际度量到计算的完整过程，并在这一过程中感受化曲为直的思想和分段累加的思想。在真正的测量实践中，学生不仅顺利测出了图案的周长，还根据实际情形提出了存在的问题和相应的解决方案。如此，学生便不需要死记什么是周长，周长的意义已经随着活动的探究深入了学生的内心。周长“过程与结果”的双重特性在此得以展现，学生思维能力、合作探究能力也在活动中得以提升。

综上所述，对刚开始学习周长的小学生来说，深入理解周长的本质无疑是有些困难的。因为不同维度下的解读有着不同的内涵，学生理解得不透彻，解决实际问题时便会犹如雾里看花，难辨真假。而在一致性视角下，周长不同维度的解读有着本质的内在联系，教师通过合适的实践活动就能够很好地激发学生自主探究的热情，使学生在有效的探究过程中加深对周长概念的理解，从而拨云见日，透过现象看清问题的本质。与此同时，学生的思维能力、合作探究能力等高阶能力也能在活动中得以发展提升。

（责编 覃小慧）