单元整体教学的一致性与阶段性

［摘 要］结构化教学内容具有整体性、一致性、阶段性，教师应用整体性眼光处理好一致性与阶段性的关系，帮助学生系统地学习知识与技能，积累基本的数学思想和活动经验。文章以人教版教材“数与代数”领域单元整体教学为例，分别从“抓住‘数与运算’‘数量关系’一致性的学科本质”“了解‘数与运算’‘数量关系’的学科本质在不同阶段的表现”“运用整体性思维处理好‘数与运算’‘数量关系’一致性与阶段性的关系”三个方面，阐述单元整体教学的一致性与阶段性。

［关键词］单元结构；整体性；一致性；阶段性

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）29-0015-04

《义务教育数学课程标准（2022年版）》（以下简称《课程标准》）对“数与代数”内容领域进行了结构化整合，形成“数与运算”和“数量关系”两大主题。两大主题内容既关注学科本质，相互关联，具有一致性，又明确了各阶段内容教学间的阶段性目标。这就需要教师处理好一致性与阶段性的关系，引导学生逐步建立相关主题的知识结构，以核心概念为统领，建立内容间的关联，在学习过程中形成知识和方法间的迁移，从而更好地理解和掌握核心概念和方法，发展学生的核心素养。

一、抓住“数与运算”“数量关系”一致性的学科本质

根据有着共同学科本质的主题内容，《课程标准》提出了“一致性”的核心思想，目的是有助于教师从整体上理解和把握主题知识的核心内容。

（一）“数与运算”主题学习内容的一致性

关于“数与运算”主题学习内容的一致性，《课程标准》明确提出：“初步体会数是对数量的抽象，感悟数的概念本质上的一致性，形成数感和符号意识；感悟数的运算以及运算之间的关系，体会数的运算本质上的一致性，形成运算能力和推理意识。”

教师在进行数概念教学时，首先都是提供熟悉的情境，使学生在具体情境中感受数量，再抽象出具体的数，然后总结其本质都具有一致性，即都是用抽象的符号表达具体的数量，最终目的是引导学生在认、读、写的基础上理解并掌握数的含义。

例如，人教版教材在“整数”的主题内容中，无论是一年级“5以内数的认识和加、减法”“6～10的认识和加、减法”“11～20的认识”“100以内数的认识”，二年级“万以内数的认识”，还是四年级“1亿有多大”，都是引导学生在熟悉的具体情境中完成对数量的抽象，以及数的认读写、基数、序数、数的顺序、数的组成、比大小、数位、计数单位等含义的理解，其主题内容学习的本质是一致的，主题内容学习的思想方法也具有一致性，即都是在几个一、几个十、几个百、几个千……数位上的累加。又如，在“分数”“小数”的主题内容中，教师也是先引导学生在具体的情境中进一步完成对分数、小数的抽象，帮助学生在认识几个几分之一、几个十分之一……的基础上完成对分数、小数意义的理解。从计数单位个、十、百、千到几分之一、十分之一（0.1）、百分之一（0.01）来看，整数、分数、小数具有一致性。

可见，计数单位的一致性不仅体现在数的概念内容的表达上，还体现在数的运算中。整数、分数、小数的运算，从本质上可以理解为整数、分数、小数中相同数位或相同计数单位的累加，具有一致性。同样，这种一致性可以拓展到四则运算。

（二）“数量关系”主题学习内容的一致性

“数量关系”主题学习内容主要是在解决问题的情境中收集信息、发现问题、提出问题并解决问题，其一致性体现在收集信息、分析问题的过程中建立数量关系的模型，并应用这种模型解决问题。

例如，人教版教材在第一学段利用动画、实物操作、画图等方法，引导学生在具体情境中理解把两部分合起来、求一共有多少、原来有多少的运算都用加法，这是加法模型的雏形；在此基础上解决求其中一份是多少、还剩多少的运算都用减法，感悟减法是加法的逆运算；在具体情境中引导学生经历乘法是加法的简便运算的过程，以及除法是乘法的逆运算。第二学段是在具体情境中，利用加法和乘法表示数量间的关系，建立加法和乘法模型。第三学段中的“用字母表示数”和“比”的教学，则是加法和乘法数量关系模型的拓展，虽然两个数相除可以用“比”表示，但其实质表示的是两个量之间的倍数关系，是一种特殊的乘法模型。

二、了解“数与运算”“数量关系”的学科本质在不同阶段的表现

“数与运算”“数量关系”主题学习本质上具有一致性，但不同主题内容分布在不同学段，而不同学段的主题内容要求、学业要求都不一样，具有阶段性。教师首先要了解不同学段的主题内容，然后才能从阶段性视角理解和处理不同学段主题内容的呈现方式，进而对学生的学习提出阶段性要求。

（一）“数与运算”主题学习内容的阶段性

《课程标准》对不同学段“数与运算”主题学习的内容要求和学业要求不同。在第一学段的“教学提示”中要求“数的认识教学应提供学生熟悉的情境，使学生感受具体情境中的数量”“10以内数的教学重点是使学生体验1～9从数量到数的抽象的过程”“利用对应的方法理解加法的意义”“理解乘法是加法的简便运算”等；在第二学段的“教学提示”中相应提出“在认识整数的基础上，认识小数和分数”“知道大数的意义和四位一级的表示方法”“感悟分数单位”“利用整数的乘法运算，理解算理与算法之间的关系”等；在第三学段的“教学提示”中又相应提出“进一步感悟计数单位在运算中的作用”“注重对整数、小数和分数四则运算的统筹”等。其中具有一致性的核心概念——计数单位，贯穿整个“数与运算”主题教学，但不同学段有着不同层次的要求。

例如，人教版教材在数的认识内容中，第一学段一年级安排的是0～100的认识；二年级安排的是“万以内数的认识”，教材提供学生熟悉的情境，学生在具体情境中抽象出数量，并经历数的认读写、比大小、数的组成等过程，理解不同数位上的数表示不同的值。第二学段三年级安排了分数、小数的初步认识内容，引导学生在具体情境中理解分数和小数表达的现实意义，初步感悟分数单位；四年级安排更大数的认识，教材提供现实情境使学生感知更大数的应用，认识更大的计数单位和数位顺序表，会根据数级认、读、写数等，在内容安排一致性基础上体现数概念教学的阶段性。在第三学段分数、小数的意义理解中安排了感悟分数、小数计数单位的一致性。“数与运算”就是引导学生在数的认识基础上，通过逐步对数位理解的表达和拓展来厘清运算算理。

（二）“数量关系”主题学习内容的阶段性

不同阶段对“数量关系”主题内容学习均有不同的要求。第一学段的重点是“利用画图、实物操作等方法，引导学生用学过的知识表述情境中的数量关系”，解决简单的问题；第二学段的重点是“能在真实情境中，发现常见数量关系，感悟利用常见数量关系解决问题”，形成初步的模型意识；第三学段的重点是数量关系模型的建立、运用和拓展，“引导学生会用字母或含有字母的式子表达实际情境中的数量关系”，形成初步的代数思维，发展学生的符号意识、推理意识和初步的应用意识。

人教版教材在安排“数量关系”主题内容时，通常与“数与运算”主题内容融合，在现实情境中利用运算的意义来理解数量关系，逐步形成“数量关系”模型。例如，第一学段教材安排的是看图写算式，解决一共有多少、还剩多少、比多少、原来有多少、几个相同加数的和、还可以装几袋等问题，以及等分除、包含除等内容，通过直观具体情境分析数量关系，利用运算的意义理解数量关系，并解决问题，从而积累数量关系模型。第二学段教材安排的是在理解运算意义的基础上完成数量关系的抽象，建立和运用数量关系模型：四年级上册中常见的两个乘法模型“单价×数量=总价”“速度×时间=路程”，就是对相应数量关系的抽象表达；四年级下册中加减乘除法的意义、各部分之间的关系及运算律，则是在对量的合并、去除、比多少等理解和运用基础上加以抽象，形成“总量=分量+分量”模型，并用图形或字母表达出来，形成一般模型，从而解决数学现实情境中更多的关于“数量关系”主题的问题。第三学段中分数、小数的计算则是加法模型的具体应用，“用字母表示数”“方程”是用字母表示数量关系，形成初步的代数思维，“比”表示两个量相除的数量关系等，都是运用数量关系模型来解决相关问题。

三、运用整体性思维处理好“数与运算”“数量关系”一致性与阶段性的关系

教学中，教师不仅要抓住“数与运算”“数量关系”两个学习主题一致性的学科本质，还要了解“数与运算”“数量关系”阶段性学习主题的学科本质在不同阶段的表现，同时要运用整体性思维处理好“数与运算”“数量关系”两个学习主题的一致性与阶段性的关系，才能在核心概念的统领下引领学生在不同阶段发展相应的数学核心素养。

（一）“数与运算”的一致性与阶段性的关系

“数与运算”主题学习内容从整体上看，有整数、分数和小数等数概念的认识及相关的运算。在学习这部分内容时，学生必须经历由数量抽象到数的形成过程，经历数的运算时算理和算法的探究过程，体会它们之间的关系，在此基础上感悟数的概念和数的运算本质上的一致性。但对于学生不同阶段的不同表现，“数与运算”主题内容的安排在整体性、一致性基础上体现了阶段性。

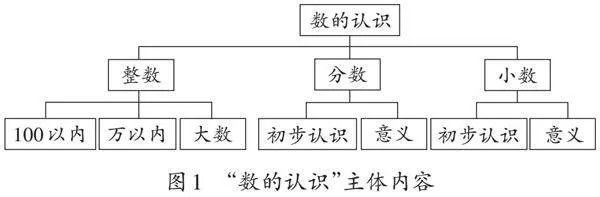
从整体性思维角度看，人教版教材中“数的认识”主体内容如图1所示。

不同学段、不同年级对“数的认识”内容安排也不同（见表1）。

用整体性思维的眼光来看“数的认识”，不难发现，教材在不同阶段的教学是建立在前一个知识的基础上，且不同学段教学的侧重点不同：第一学段侧重于对整数意义的理解和抽象，第二、三学段则是在此基础上进一步认识更大的整数及各数位的含义，并发展学生对分数、小数的认识和抽象。

“数与运算”主题内容则是在认识整数、分数、小数的基础上，在解决现实问题情境中，使学生经历算理、算法的探索过程，知道减法是加法的逆运算、乘法是加法的简便运算、除法是乘法的逆运算。在此过程中，学生感悟将未知转化为已知，理解数的运算及运算之间的关系，从而厘清算理、掌握算法，体会数的运算本质上的一致性，形成运算能力和推理意识。

（二）“数量关系”的一致性与阶段性的关系

“数量关系”主题的教学，从整体性上说主要是引导学生在具体情境中经历运用数量关系解决问题的过程，从中感悟其数量关系，并抽象出加法和乘法模型，提高发现和提出问题、分析和解决问题的能力，形成初步的模型意识和应用意识。“数量关系”的教学同样存在一致性和阶段性，用整体性思维的眼光来看，不同学段有不同表现。

第一学段，学生是在具体情境中通过操作、观察、画图等方法来理解数量关系，主要运用对数的意义的理解和运算的意义表示数量关系来解决具体问题。如人教版教材一年级“池塘里有6只鸭子，又来了3只，一共有多少只鸭子？”这道题，基本的数量关系就是“池塘里鸭子只数+又来的鸭子只数=总只数”。第二学段是在第一学段积累的一些运用数的意义和运算解决问题的基础上，运用加法或乘法表示数量之间的关系，建立加法和乘法模型，并运用这些模型及变式来理解数量关系，进而解决问题。如人教版教材四年级下册“四则运算”中“加、减法的意义和各部分间的关系”，在“和=加数+加数”基础上抽象出“总量=分量+分量”的加法模型，并借助具体情境，通过对比分析帮助学生理解减法是与加法相反的运算，构建“逆运算”的概念，从而抽象出“分量=总量-分量”的变式模型。第三学段是在第二学段构建模型基础上的应用，并拓展到“用字母表示数量关系”，从而解决问题。如人教版教材五年级上册“简易方程”中的“用字母表示数”中，创设了“爸爸的年龄比小红大30岁”的情境，得出基本的数量关系“爸爸的年龄=小红的年龄+ 30”，如果小红的年龄用ɑ表示，则爸爸的年龄就是“ɑ+30”。由于《课程标准》要求在小学阶段不出现方程，而是将字母表示数拓展为表示数量关系，因此对于人教版教材中的“解简易方程”，教师可以尝试用“用字母表示关系”及加法、乘法模型组合来分析、解决问题。

小学阶段数学知识及核心素养的学习是一个阶段性的过程，教学中教师要抓住主题学习核心内容的一致性来设计教学活动，并用整体性眼光和思维处理好每个主题内容或单元主题学习一致性与阶段性的关系，帮助学生系统地学习数学知识与技能，积累基本的数学思想和活动经验，从而形成良好的数学核心素养。

［ 参 考 文 献 ］

[1] 中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

（责编 李琪琦）