残差修正的加权多项式回归色彩特征化算法

摘 要：在数字印刷领域，精确再现计算机图像的颜色是高质量印刷的前提，其中色彩特征化是关键环节。传统多项式回归模型由于高阶项会放大特征化样本集中的奇异值，导致模型振荡从而影响色彩特征化的准确性。基于神经网络的色彩特征化算法精度较高，但算法复杂度也呈数量级的提高，难以满足工业生产中的效率要求。为解决上述问题，提出残差修正的加权多项式回归算法，采用具有较强抗差能力的Huber损失函数来替代均方误差。通过自适应机制确定各个样本权重，并利用残差值迭代优化得到最佳权重矩阵，从而降低奇异值样本对系统的影响；此外，修正模块捕获第一个模型可能遗漏的非线性情况辅助调整转换结果，进而提高颜色再现准确性。结果表明，该算法与普通多项式回归相比，平均色差降低1.2，与基于深度置信网络的推理算法精度接近，但运行时间比其减少99.37%。

关键词：色彩特征化； 多项式回归； 自适应加权； 色彩复制； 色彩管理

中图分类号：TP301 文献标志码：A

文章编号：1001-3695（2024）10-044-3188-06

doi：10.19734/j.issn.1001-3695.2023.11.0597

Weighted polynomial regression color characterizationalgorithm with residual correction

Yang Chen1， Lian Kaicheng1， Xu Hao1， Wu Qin1，2， Chai Zhilei1，2

（1.School of Artificial Intelligence & Computer Science， Jiangnan University， Wuxi Jiangsu 214122， China; 2.Jiangsu Provincial Engineering Laboratory of Pattern Recognition & Computational Intelligence， Wuxi Jiangsu 214122， China）

Abstract：In the field of digital printing， accurately reproducing the color of computer images is a prerequisite for high-quality printing， where color characterization is a key step. Traditional polynomial regression models tend to amplify outliers in the characterization sample set due to high-order terms， causing model oscillation and affecting the accuracy of color characterization. Color characterization algorithms based on neural network have higher precision but significantly increase in algorithmic complexity， making them unsuitable for the efficiency requirements in industrial production. To address these issues， this paper proposed a color characterization method based on weighted polynomial regression algorithm with residual correction. This algorithm employed the Huber loss function， known for its strong robustness against outliers， as a substitute for mean squared error. It determined the weight of each sample through an adaptive mechanism and iteratively optimizes the residual values to obtain the optimal weight matrix， effectively reducing the impact of outlier samples on the system. Additionally， the correction module captured nonlinear scenarios that the initial model might miss， significantly improving the adjustment of the transformation results and thereby enhanced characterization precision. The results show that compared to conventional polynomial regression， this algorithm reduces the average color difference by 1.2. It achieves a precision close to that of deep belief network algorithms but with more than 99.37% reduction in inference time.

Key words：color characterization; polynomial regression; adaptive weighted; color reproduction; color management

0 引言

打印机作为最常用的彩色图像输出设备，在其输出流程中，图像需经过多次颜色转换以生成打印设备所能识别和处理的数据格式。打印机和显示器的呈色特性不同。CMYK打印机通过颜料介质来表达颜色，采用减色呈色法；RGB显示器使用色光介质来表达颜色，采用加色呈色法。由于不同设备的呈色方式不一致且色彩再现能力不同，若想将计算机制版或扫描拍摄的图像打印出来，需要将显示器下的RGB颜色空间转换为印刷设备的CMYK颜色空间。

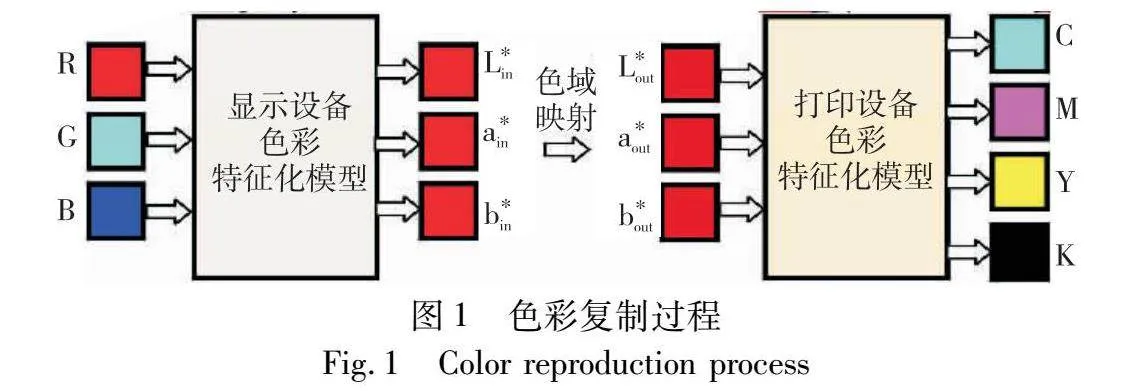
为了精确控制颜色信号在不同颜色器件之间的传输，国际色彩联盟将与设备无关的颜色空间CIE Lab或CIE XYZ作为连接色彩空间（profile connection space，PCS），该颜色空间是与设备无关的色度颜色空间，任何设备到设备的转换都需要经过该媒介。在印刷流程中，需要先将RGB颜色空间转换为PCS，由于设备的色域不一样，还需要在PCS空间下进行色域映射，最后将PCS转换成CMYK颜色空间［1］，如图1色彩复制过程。在整个色彩复制过程中，通常将建立PCS和设备颜色空间关系的过程称为色彩特征化。在实际印刷流程中，主要依赖于特征化模型中PCS空间色度值到印刷设备空间CMYK值的转换，该过程是印刷色彩管理的一个重要过程和关键技术，对提升印刷质量和视觉效果有着不可或缺的作用［2］。

在已有的特征化算法中，主流是上述基于色度匹配的方式。近年来，也有少量使用光谱模型进行特征化，如文献［3，4］寻找最佳光谱再现所需的墨水数量。然而，光谱的研究主要集中在理论上，在实际应用时，由于受到光谱图像数据获取以及硬件设备等因素的影响，其精度也没有预期高，导致光谱打印产品屈指可数。常见的基于色度的匹配方式主要有多维度查找表法、模型法、多项式回归法以及神经网络法。刘菊华［5］在四色印刷中使用多维查找表进行色彩特征化，但是随着颜色数量的增多，样本集也急剧增加，不适用于多色打印情况。文献［6］通过纽介堡方程模拟打印输出的呈色机理，然而打印输出受到半色调、输出设备以及多方面因素的影响，其色彩特征化精度较低。随着技术的进步和AI的崛起，许多人工智能技术被应用于颜色管理领域，文献［7，8］使用DNN，文献［9］通过深度置信网络进行颜色预测，虽然再现效果显著，但训练和推理阶段的耗时较长。此外，每当更换墨水或打印材料时，都需要对特征化样本集进行重采集，这不可避免地导致工作量大幅增加，影响了打印流水线的正常运作。由于模型的复杂性，在客户端机器上的部署变得尤为困难，进一步增加了AI方法在打印领域应用的挑战。在3D打印领域，Chen等人［10～12］提出深度学习特征化框架，可以达到较高的预测效果，但是由于神经网络模型的训练时间长、训练数据需求大、超参数的不确定性，模型训练起来通常需要较大的计算资源。该类方法大多还是用在高分辨率的全彩色3D打印中。在色彩学领域，多项式回归以其计算量小、模型简单的优势占据着主导地位，尤其在特定高实时性要求的领域有着较好的应用前景。武汉大学Yang等人［13］使用传统多项式建立特征化模型，文献［14，15］阐述多项式回归精度优于其他传统算法，但是此类回归算法由于模型受到奇异值影响而振荡，因此无法满足更高精度的色差需求。在后续的工作中，研究人员通过对样本集中的奇异值样本进行限制以提高精度，例如文献［16～18］通过添加约束项以及修正多项式阶数，减少样本集中奇异值对多项式模型的影响，但是阶数达到三阶以上时约束项的推导会变得相当复杂。Zhao等人［19］使用KPLS进行色彩特征化，精度较为理想，但是需要选择合适的核函数和相关参数，这增加了模型调整的复杂性，并且有时会造成过拟合风险，且神经网络方法大同小异。

本研究聚焦于提高工业印刷的生产效率与色彩复现的精确性。对传统的多项式回归算法进行改进，以减轻其在高精度应用中因高阶项引入而导致的模型振荡问题。在考虑样本集奇异值对多项式回归模型影响的工作基础上，本文创新性地引入了样本迭代加权策略，同时融合了残差修正机制，构建了一个轻量化的高精度特征化模型。算法采用以Huber算子为影响函数的迭代加权最小二乘方法来求解转换关系。迭代过程根据当前残差动态调整权重，即对于残差较小的点，赋予较大的权重，而对于残差较大的点，赋予较小的权重，有效减少了奇异值点对系统的影响，从而提升了常规数据点的预测准确度；再引入更高阶多项式计算修正值，并对转换后的预测设备值进行修正，不仅显著提高了对奇异值的预测精度，同时也优化了常规数据点的预测效果。实验结果表明，本方案相较于传统的纽介堡方程、查找表等算法，在各项指标上表现均较优。与普通多项式回归算法相比，平均减少1.2个色差，最大色差减少了10.6%。与在配备16核的i7-5960X CPU和GeForce RTX 2080 Ti GPU上运行的深度置信网络相比，本文算法色差降低了约8.3%，推理时间减少了99.37%，模型训练节省了7.9 h。

1 问题背景

1.1 样本集中奇异值说明

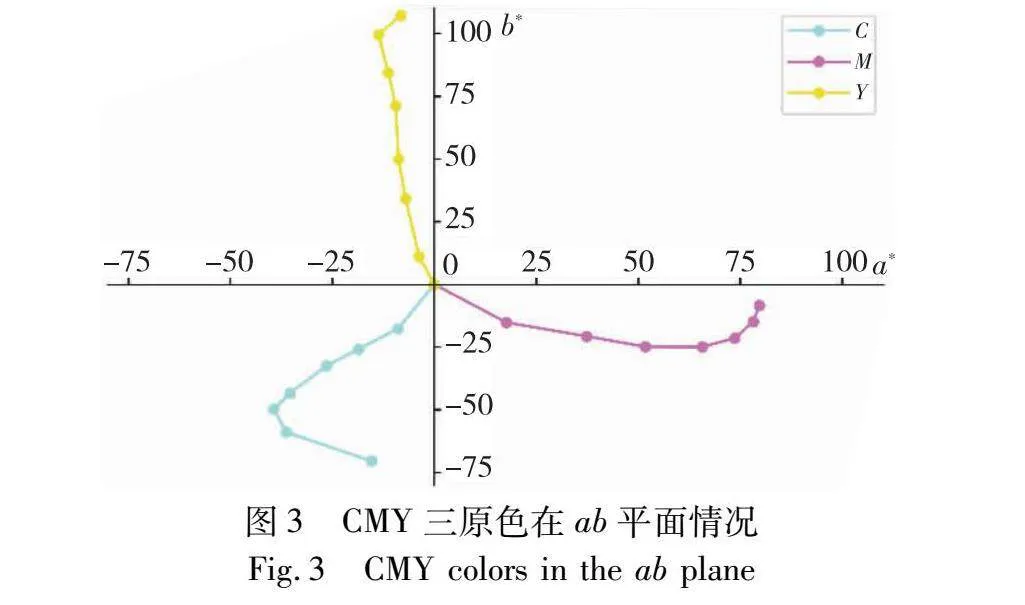
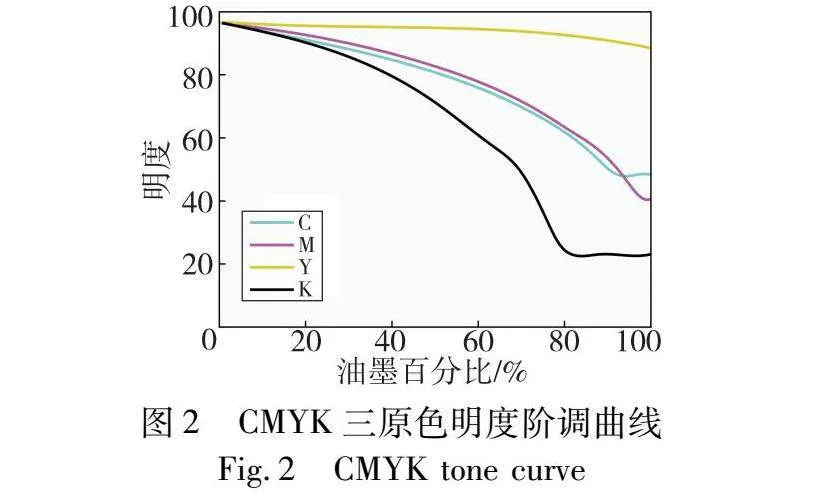
原色墨水的原料缺陷和纸张等多种因素导致打印效果和理想状态偏差较大。在理想打印状态下，不同百分比单色墨水的色相应该恒定不变，并且明度随着墨量的均匀变化也会产生相同变化。如图2的CMYK三原色明度阶调曲线所示，当墨量百分比达到一定程度之后，由于纸张墨量限制、油墨密度等原因，造成墨量较高时，明度曲线呈非线性趋势。同样的情况也体现在色度分量上，如图3所示，由若干个点连接而成的线段表示随着墨量增大时a、b变量的变化情况。每级墨量的色相角为图中的点和原点连线后的线段和x轴的夹角，可以发现高墨量原色的色相角偏离正常轨迹。由此可知，彩色打印机的原色墨量和L、a、b之间的关系存在非线性，尤其是在高墨量和暗部区域，导致叠印之后，非线性更强。在特征化印刷样本集中，由于较强的非线性导致部分样本偏离常规轨迹。该部分样本和其他样本特征明显不同，将这类样本点称为奇异值点，也称为离群点。在多项式算法中，由于回归后所拟合的是样本的常规规律，所以往往将预测结果和实际标签有较大差距的点认定为奇异值点。

在陶瓷、包装、纺织品、金属和玻璃等特殊印刷领域，印刷工艺和材料特性会导致最终效果与预期色彩有所差异。例如，在陶瓷印刷中的高温窑炉处理，包装印刷中的覆膜和上光等后期处理，以及金属、玻璃等特殊承印物上的打印，都可能影响油墨的颜色表现。这些过程中产生的奇异值是正常现象，而且往往是不可避免的。

1.2 特征化算法应用瓶颈

神经网络在色彩复现领域精度较高，但用于工业生产会遇到一些实际问题。它们训练耗时，并需要昂贵的计算资源，这让它们难以在成本和硬件资源有限的情况下使用。相对而言，多项式回归模型更加高效、易于部署。随着打印环境的变化，例如墨水和承印物的更换、温度的变化、印刷速度的改变以及打印设备的磨损和老化，轻量级的多项式回归模型可以快速迭代。在考虑成本效益和效率的同时，多项式回归模型在许多实际应用场景中比神经网络模型更具优势。

尽管在色彩学领域中，轻量级的多项式模型显示出其独特的优势，但其适用性受到样本集中奇异值的限制，特别是在算法需要采用高阶项以获得更高精度的场景。因此，采取相应的措施以应对这种局限性变得至关重要。

2 改进的多项式回归特征化算法

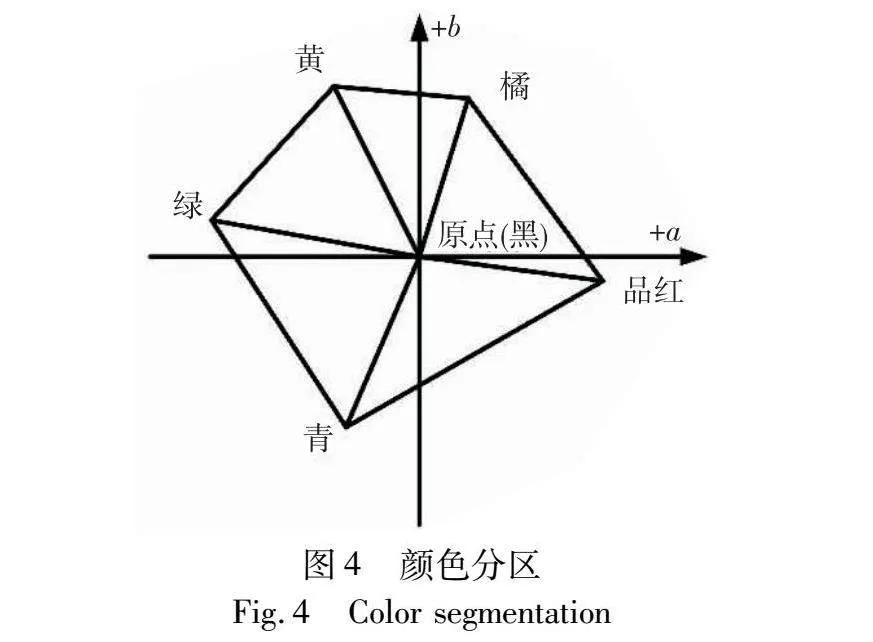
彩色打印机的特征化模型的主要目标是建立设备颜色空间和PCS之间的转换关系。在高保真多色印刷中，考虑到多色样本集的建立以及色度值和颜色通道之间一对多的映射关系，将多个基色在色相平面下划分为多个区域。图4为颜色分区图。本文通过计算原稿中某个颜色的色相角来确定其所属区域，然后根据该颜色所在区域的三个基色合成该颜色，并使用回归模型建立它们之间的关系［20］。因此，在建立特征化模型的时候，首先要对整个颜色空间进行分区，即将CMYKOG颜色在LAB颜色空间下按照色相角分为GCK、CMK、MOK、YOK、YGK五个区域。然后，对每个分区采取多项式回归方法建立特征化模型。

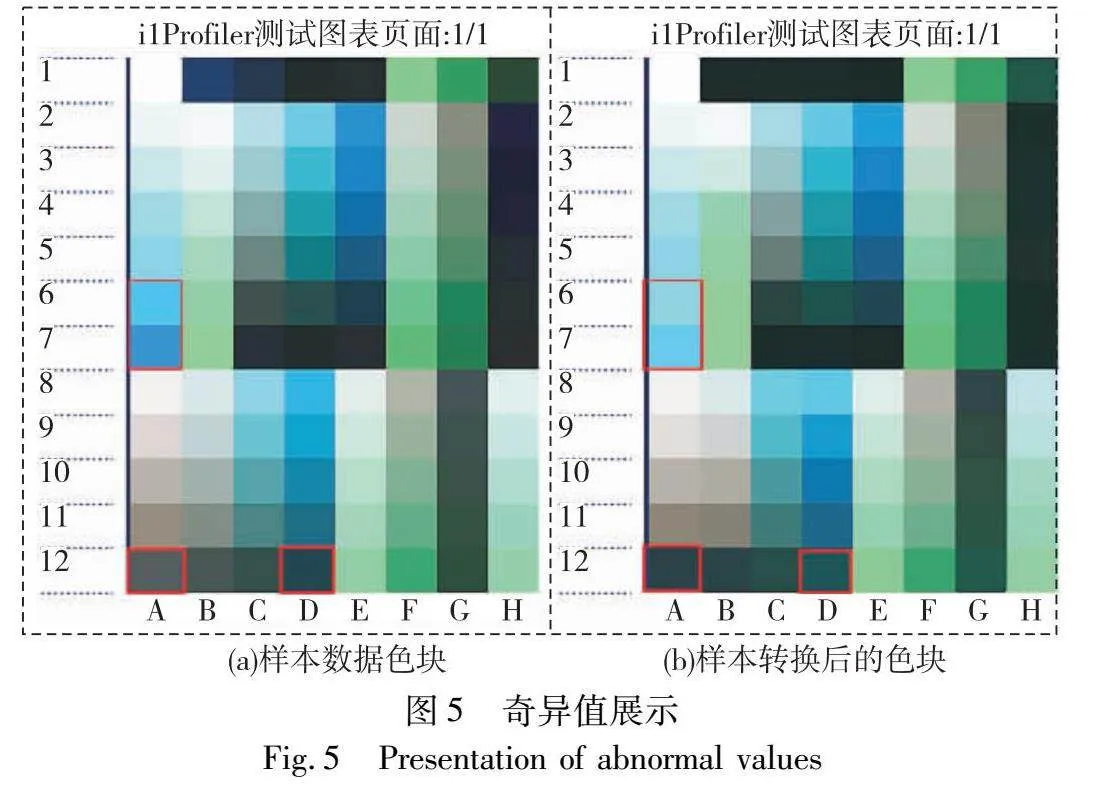
在需要高精度颜色复现的应用场景下，添加高阶项可以显著提高多项式模型的精度，但高阶项可能会放大数据中的奇异值。如果直接将多项式回归应用于实际复杂的打印场景中，由于各种材料和承印物的不稳定性，导致样本集存在奇异值，模型可能会变得不稳定。例如在图5奇异值展示中，图（a）是特征化模型的训练数据，图（b）是使用多项式回归算法转换得到的结果。下面以此图来说明传统多项式模型在引入高阶项后的局限性。在图（a）的第一列高墨量的青油墨样本中，随着墨量的增加，其色相发生变化，导致其色度值和设备值之间存在较强的非线性，普通的多项式拟合的关系和其真实情况有较大偏差。如图（b）所示，转换后的颜色和原色块颜色差别较大，其他红色框标注的色块也是同样情况，这些和原始样本差别较大的数据就是奇异值样本。由于多项式回归模型旨在捕捉样本点中普遍存在的规律，所以此类奇异值样本不仅会干扰模型的拟合过程，还会削弱模型的预测效果。

当多项式回归引入高阶项时，这些高阶项可能会放大数据中的离群值。此外，与数据相关性较高的数据集不同，本实验数据集中包含了奇异值样本。对于这些奇异点，常规多项式回归模型可能不具备足够的鲁棒性。因此，本文采用了稳健估计算法并集成误差修正技术。采用更稳健、更具预测性的Huber影响函数，再使用Huber算子求得标准残差，并以迭代的方式不断调整样本权重，进而求得每个训练样本的最佳权重。该策略极大地提高了模型的鲁棒性［21］，但鉴于离群点有时也代表有效的样本数据，对其进行准确估计也很重要。为进一步提高模型对少量离群点的预测能力，还需将奇异值和常规数据点一同进行修正。该修正模型不仅仅提高了此类奇异点的预测能力，还能提高模型整体的非线性表现能力，以达到更高的特征化精度。

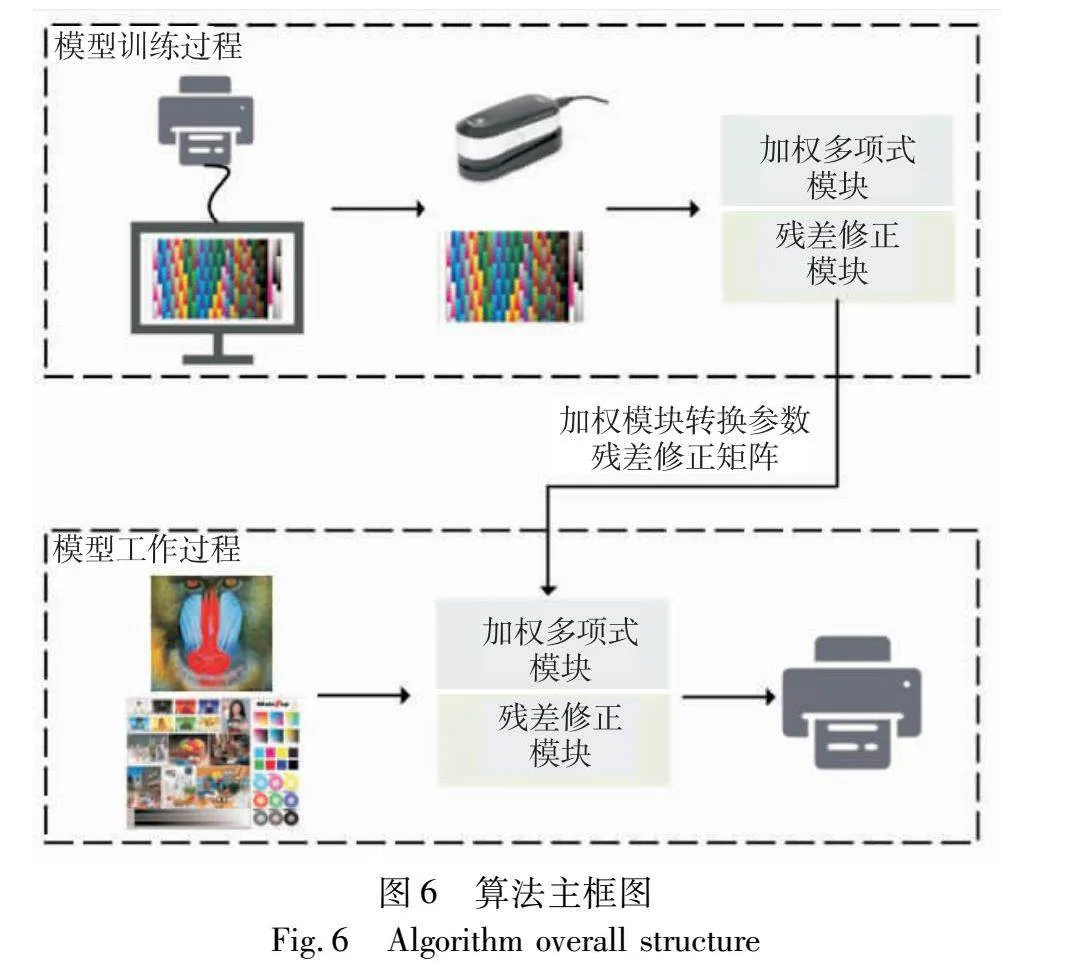
如图6所示，本文算法在实际应用过程中，首先通过打印输出预设计的色彩特征化样本集，并使用色度计对打印色块进行测量。由于考虑到上述奇异值对模型的影响，所以接下来会使用残差修正的加权多项式回归算法拟合样本集变量中存在的非线性关系。当图片或其他数据输入本文算法模型后，通过训练得到的转换关系生成特征化结果。最后，这些结果将被用于指导打印设备，完成打印工作。加权多项式回归算法和残差修正算法的具体细节见2.1、2.2节。

2.1 自适应样本加权策略

回归方法主要是研究一个因变量和一个或多个自变量之间关系的方法。通过对已知的自变量和因变量之间建立多项式方程获取两者之间的转换关系，实现对其他未知自变量的预测。该转换矩阵可由影响函数为Huber函数的迭代加权最小二乘法来求得，通过求得的系数矩阵，把源色空间转换到目标色空间。

以最常见的二阶十项式为例：有H*βfinal=T，H是N×L的输入矩阵，βfinal是L×3转换矩阵，T是N×3输出矩阵，N是样本数，L是多项式项数。取项数L=10，Hi的表达式如式（1），式中Li、ai、bi分别对应样本集中色块i的PCS颜色空间的色度值L、a、b，则所有色块的输入色度矩阵H如式（2）所示。以GCK分区为例，所有色块的输出矩阵为T，GCK各分量表示设备值，下标对应相应的样本编号，表达式如式（3）所示。

Hi=［1，Li， ai，bi，Li*ai，Li*bi，ai*bi，L2i，a2i，b2i］（1）

H=h11h12…h1Lh21h22…h2LhN1hN2…hNL（2）

T=G1C1K1G2C2K2GNCNKN（3）

下面以预测G分量然后扩展到三维分量GCK为例。一般情况下H*β=G是无解的（G是G分量的矩阵形式），因此是求解一个最优的，使得设备的预测值尽量和真实值接近。是G分量的回归系数，是L×1的转换矩阵。通过最小二乘法，可以最小化每个方程结果的残差平方和［22］，经过分析有

=arg minβ Q（β）（4）

那么关于残差的目标函数为Q（β），如式（5）所示，必须保证预测值和真实值之间的残差平方和最小。

Q（β）=∑Ni=1（ei）2=∑Ni=1（Gi-Hiβ）2=

（G1-H1β，G2-H2β，…，GN-HNβ）G1-H1βG2-H2β GN-HNβ=

（G-Hβ）T（G-Hβ）（5）

此时对Q（β）求偏导并令表达式为0，得到

=（HTH）-1HTG（6）

由于普通最小二乘法尚未考虑每个样本的权重，可能导致较大的误差，所以对每个样本赋予权重，权重函数为ρ，从而可以得到更为精准的结果。那么样本加权后的目标函数为

Q（β）=∑Ni=1ρ（ei）=∑Ni=1ρ（Gi-Hiβ）（7）

则目标函数对参数β求偏导，原理和上面一样，并令偏导数等于零，得到式（8），Ψ（x）为ρ（x）的导函数。

∑Ni=1Ψ（Gi-Hiβ）Hi=0（8）

此时令Wi=ψ（Gi-Hiβ）Gi-Hiβ，有HTW（G-Hβ）=0，最终求得

=（HTWH）-1HTWG（9）

将G分量推广到GCK的三维分量形式T，可求解最终转换矩阵final，其表达式如式（10）所示，此时W只是初始权重矩阵。

final=（HTWH）-1HTWT（10）

ρ往往采用均方误差，但是为了使模型不易受异常值影响，使用Huber算子作为影响函数。当误差较大时，Huber损失趋向于平均绝对值误差（mean absolute error，MAE），当误差较小时，趋向于均方误差（mean squared error，MSE）。这个分段线性的设计使得当误差在k范围内时，损失函数类似于均方误差（平方损失），它对异常值的惩罚相对较小；而当误差超出k时，损失函数的增长是线性的，对异常值的惩罚变得更大。因此，异常值对整体损失的影响被有效地限制在一定范围内，其表达式ρ（x）如式（11）所示，k为调和函数，默认取1.345。

ρ（x）=x2/2 |x|≤kk|x|-k2/2|x|>k（11）

本文采用GCK各分量之间的欧氏距离作为ei，为了使估计更具稳健性，引入绝对离差中位数s使得残差标准化。标准化残差ui通过绝对离差中位数，除以一个常数0.674 5后得到，如式（12）所示。

ui=eis=0.6745×eimed（|ei|）（12）

其中：med代表中位数计算。那么使用标准化残差过后的Q（β）求偏导并令表达式为0后的结果如式（13）所示。

∑Ni=1Ψ（ui）Hi=∑Ni=1Ψ（ui）ui·uiHi=∑Ni=1Wi·ui·Hi=0（13）

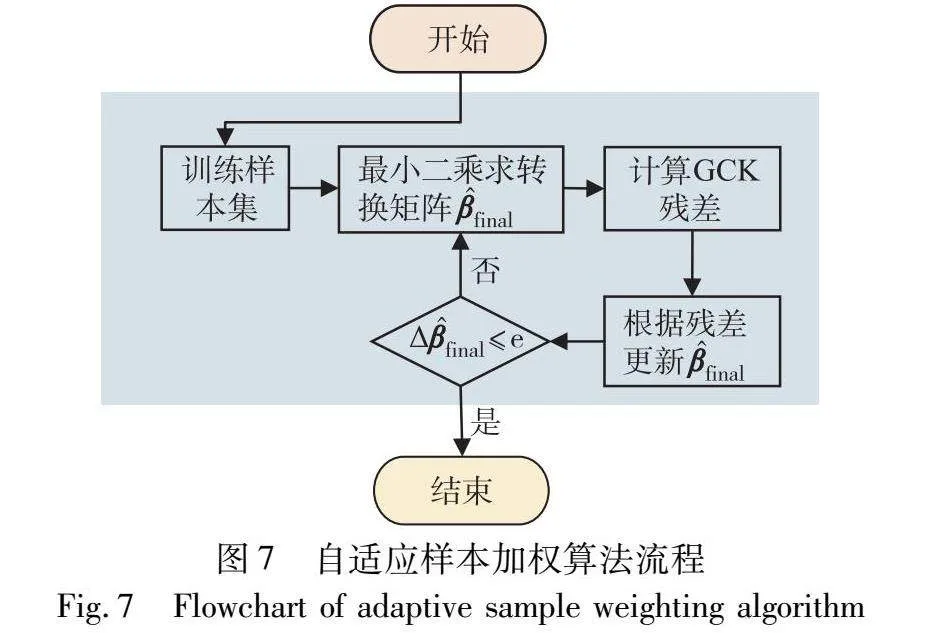
其中：Wi是序号为i的样本权重，通过该式可以得到标准化残差操作后的转换矩阵也是式（10）。为进一步提高预测精度，β的稳健估计可用迭代加权最小二乘求解。通过不断计算目前转换矩阵的残差，对样本集进行重新分配权重，当转换矩阵变化很小时结束迭代，得到最佳权重矩阵，流程如图7所示。

最终迭代加权后的转换矩阵结果如式（14）所示，Wfinal为最佳权重矩阵。对于任意输入的N个三维LAB数据，首先按照式（1）的形式将该N×3矩阵拓展成N×10矩阵X，再与得到的转换矩阵相乘，得到自适应迭代加权的结果为Y，其维度为N×3，如式（15）所示。后续残差修正模块将在此Y的基础之上进行修正。

final=（HTWfinalH）-1HTWfinalT（14）

Y=X*final（15）

2.2 残差修正策略

在迭代加权求解后，部分预测还存在较大误差，往往需要对特征化结果进行进一步优化。在不同的色度值下，特征化结果和标准设备值都有一个偏差。通过建立色度值和设备值偏差之间的关系，再计算相应色度值对应的损失，将损失累加到原始设备值，则对结果可以起到辅助修正作用。通过该策略可以对异常值点进行误差修正，同时通过更高阶多项式捕获第一个模型可能遗漏的非线性情况，从而提高特征化精度。

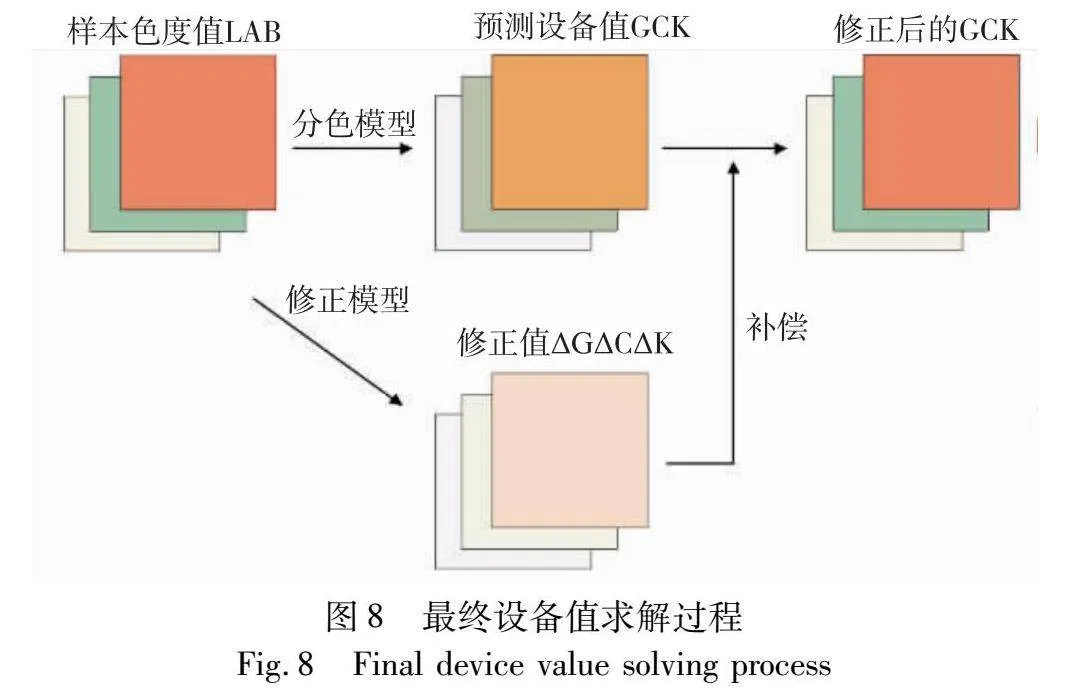
下面进行算法介绍，同样以GCK分区为例进行说明。颜色值GCK通过色度计测量得到的真实色度值为LAB，使用模型对LAB进行预测得到预测设备值G^C^K^，对预测值进行测量得到该设备值对应的预测色度L^A^B^。若想得到预测模型的修正值，需要经过两次多项式回归从而建立LAB和ΔGΔCΔK的关系。首先对样本集真实值和预测值进行采集并计算，得到LAB和L^A^B^的差值ΔLΔAΔB；接着，将LAB和ΔLΔAΔB的若干组数据作为训练数据，建立LAB和ΔLΔAΔB的多项式回归模型，以求得当前色度值下对应的色度损失；进而建立色度损失ΔLΔAΔB和颜色损失ΔGΔCΔK之间的关系。这样对于任意一个输入的LAB色度值就可以得到一个校正值，那么利用该修正值对预测值进行补偿即可达到提高精度的效果，修正过程如图8最终设备值求解（以GCK分区设备值为例）。由于特征化模型的最终评价是在LAB颜色空间下进行的，所以引入预测设备值G^C^K^对应的色度值L^A^B^，通过色差计算补偿值，该方法可以更精准地计算出ΔGΔCΔK的值，从而对预测结果进行修正。从理论上来说，该校正模块首先使用低阶多项式进行迭代加权求解，从而确保对于未见过的数据具有较好的泛化能力。在初步转换结束后，引入更高阶多项式用于校正，从而减少了过拟合的风险。通过修正模块可以调整原始结果，提高了模型的预测能力，使得最终特征化结果融入了预测值和修正值，从而对加权回归后的数据有更好的提升效果，尤其是奇异值部分。

3 实验结果与分析

3.1 实验环境

为了验证所提出模型在存在奇异值的情况下有较好的特征化精度，本研究在600dpi的喷墨打印机上对特征化模型进行部署并与其他算法进行比较。对于数据集，本文采用i1 Profiler软件创建了一系列自定义设备色值的色块文件，并通过RIP软件控制打印机打印这些色块。使用分光光度计i1 Pro3对打印出的色块进行了LAB色度值的测量。

本实验过程主要分为样本集的生成、模型的训练和模型精度的测试三个阶段，具体步骤如下：

a）设计供打印机打印的GCK分区色块，并用分光光度计测量其打印色块的LAB色度值，将得到的GCK数据与对应的LAB测量值配对，形成数据集，并随机划分为训练集和测试集。

b）应用本文算法、查找表方法、纽介堡方程以及神经网络方法，分别建立GCK设备值与LAB色度值间的映射关系，从而得到各自的特征化模型。

c）在测试集上应用这些特征化模型，将LAB色度数据转换为GCK设备值。接着，根据预测的GCK值创建可打印的色块文件，并指导打印机进行打印。打印后，测量不同算法转换后色块的LAB值，并计算与测试集原始LAB值之间的色差。

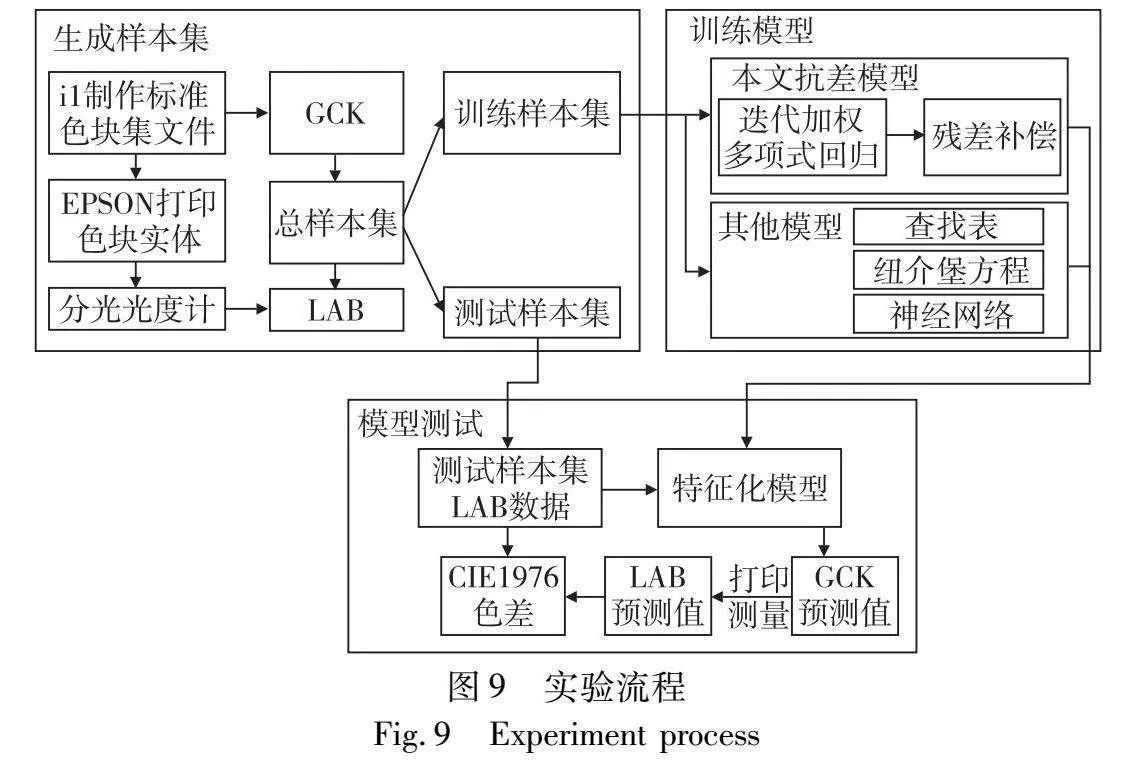
为了更加清晰明了地理清各个步骤的具体操作以及内部关系，本文对实验流程进行图片展示，如图9所示。

3.2 结果与分析

本实验使用传统算法、单独加权和修正模块、粒子群算法优化（particle swarm optimization，PSO）的深度信念网络（deep belief network，DBN）以及本文算法进行色差量化分析。特征化精度评价一般以色差为主，ΔEab色差公式如式（16），其更符合人眼的形式。ΔE00见文献［23］推导，本文以ΔE00作颜色评价。

ΔEab=（L^-L）2+（A^-A）2+（B^-B）2（16）

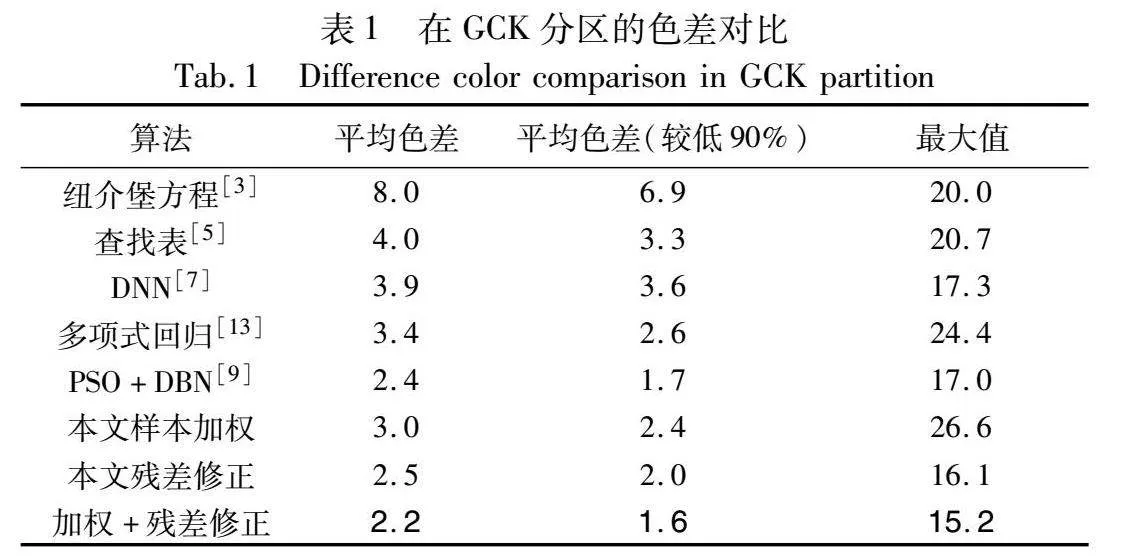
下面展示不同算法在GCK分区的平均色差、平均色差（较低90%）、色差最大值，在GCK分区的色差对比结果如表1所示。

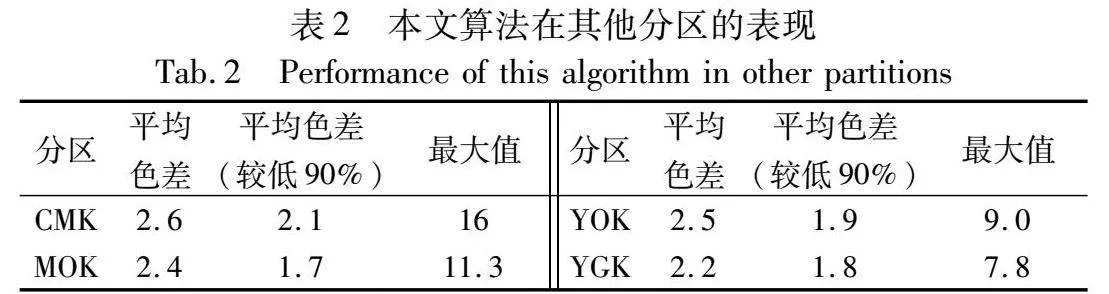
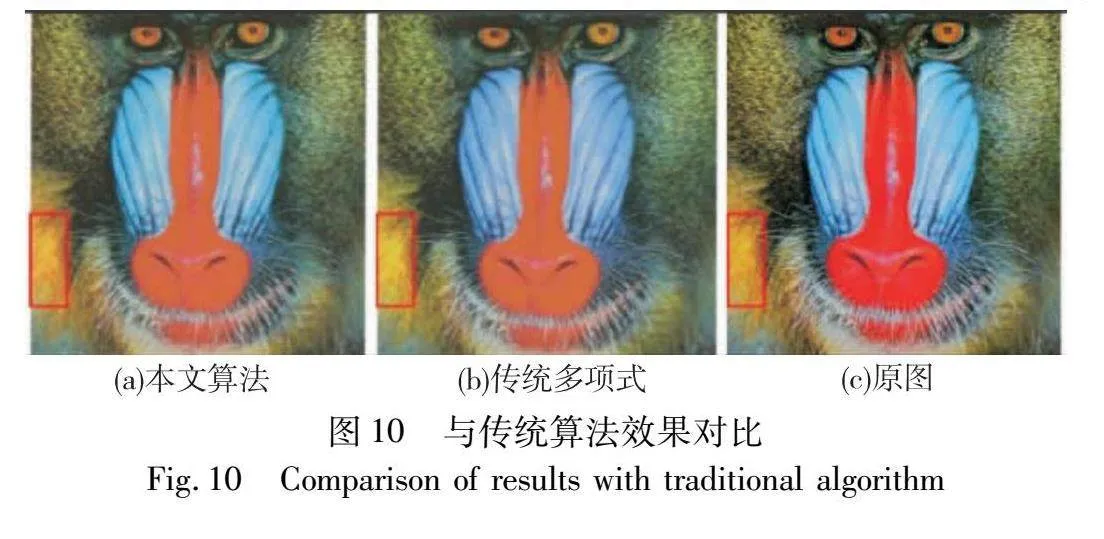
结果表明，样本加权模块使用自适应策略调整样本集权重，提高了模型的稳定性，因此对整体的预测效果有较大的改善。单独的加权模块将平均色差从3.4降低到3.0，但是对于奇异值点的预测不佳。残差修正可以在回归模型比较稳定的基础上对奇异值等进行更好的补偿，单独使用时可以将色差最大值从24.4降低到16.1，同时平均色差减少26.47%。残差修正的自适应加权多项式回归在样本集中存在奇异值的情况下较传统的特征化算法具有更好的复现效果，有较高的鲁棒性，对于更复杂的打印场景有较好的预测水平，相比于传统多项式回归，平均色差从3.4降低到2.2，色差升序排序后，前90%样本的平均色差也从2.6降低至1.6，而且更重要的是，色差最大值得到了较好的改善，降低了9.2个色差，效果比较明显。本文算法在其他颜色分区也有着较好的表现效果，如表2所示，最终特征化结果的色差约为2.3左右，能够满足国际标准ISO 12647-7规定的ΔE00≤2.5。在本项研究中，为了评估所提算法相较于传统多项式回归方法和机器学习算法的准确性，本文进行了一系列实验。实验过程中，利用这些算法生成的特征化结果被输送至打印机以执行打印任务，随后采用具有600 DPI分辨率的扫描仪进行图像捕获，以获取最终打印效果的视觉呈现。如图10所示，实验输出包括三部分：左侧图像展示了本文算法的效果，中间图像代表传统多项式回归模型的输出，而右侧为原始图像。通过与原图的比较分析可以观察到，由于打印机色域限制，特定的饱和颜色区域，尤其是红色区域，并未得到精确复现。特别值得注意的是，在图中标注红框的黄色区域以及面部的蓝色部分（参见电子版），本文算法在颜色还原方面表现出了比传统多项式回归方法更高的准确度。从表1中的数据可知，本文算法与PSO+DBN模型在精度上表现接近。图11展示了本文算法与PSO+DBN模型的对比结果。从图（a）（b）中可以看出，在使用这两种不同的特征化算法时，肉眼几乎无法区分它们之间的差异。

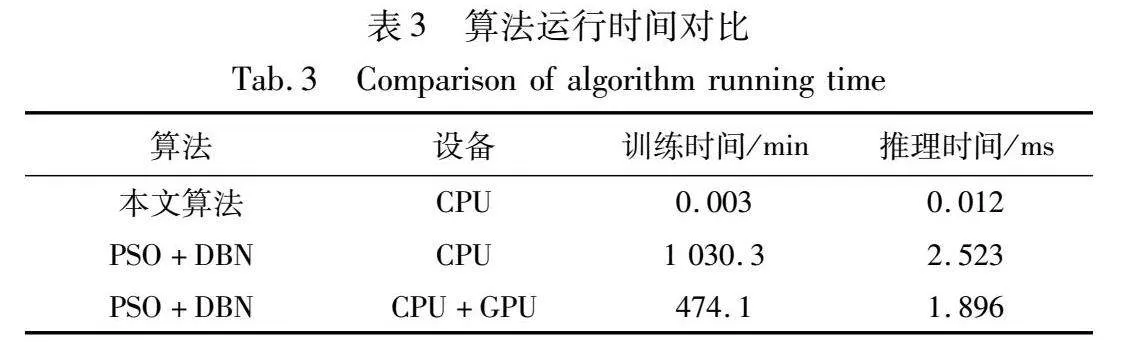
另外，对于PSO+DBN的神经网络模型而言，该算法用PSO寻找DBN模型的最优隐含层神经元数量等超参数后进行训练，模型预测精度较高。本文模型精度在和其精度接近的情况下，训练时间和计算时间都大幅度降低。实验在配备16核的i7-5960X CPU和GeForce RTX 2080 Ti GPU上完成，以训练2 033个样本以及预测343个样本进行测试，结果如表3所示。结果表明，由于PSO+DBN模型的复杂性，即使在GPU上进行训练，训练时间和本文算法相比相差甚远，在CPU上运行网络模型就更耗时。另外，该神经网络模型在CPU上的推理时间是本文算法的210倍左右，CPU+GPU的异构处理平台上处理时间是本文算法的25倍左右。在GPU上进行数据处理虽然提升了处理效率，但是也带来额外的主机端和设备端的传输开销。本文算法在模型训练方面更是占据绝对优势，比在CPU上训练缩短17.1 h，比训练较快的CPU+GPU模式还要少7.9 h。多项式回归模型简单，所以计算和训练时间都非常短，而且在精度要求比较高的领域，多项式回归可以通过添加项数或者增加样本集达到更好的效果。如果将该特征化模型直接应用到宽幅打印、实时打印、高分辨率打印等领域，按照该方法处理可以更好地满足实时性的要求。而且这种处理方式具有显著的优势，因为它不依赖于高配置的硬件设备，为广泛应用提供了灵活性。

在色彩特征化领域，基于所进行的深入分析，验证了本文算法在实际应用场景中的可行性与有效性。

4 结束语

本文致力于开发一种具有高生产效率和低计算复杂度的模型，旨在满足工业印刷领域的需求。本文提出的特征化模型通过加权样本的策略提高了鲁棒性，并集成修正模块调整原始结果，极大地提高了特征化精度。实验结果表明，本文算法优于传统的多项式回归方法，有更好的色彩复现效果。同时其计算复杂度远远小于神经网络模型，能解决印刷效率和模型部署问题。该算法对于陶瓷、包装、玻璃打印以及近年来兴起的3D打印、在线打印等具有较高的实用价值。

参考文献：

［1］Sharma A. Understanding color management［M］. Hoboken， NJ： Wiley， 2018.

［2］Morovic J， Arnabat J， Richard Y， et al. Sampling optimization for printer characterization by greedy search［J］. IEEE Trans on Image Processing， 2010， 19（10）： 2705-2711.

［3］Babaei V， Hersch R D. N-Ink printer characterization with barycentric subdivision［J］. IEEE Trans on Image Processing， 2016， 25（7）： 3023-3031.

［4］Ansari N， Alizadeh-Mousavi O， Seidel H P， et al. Mixed integer ink selection for spectral reproduction［J］. ACM Trans on Graphics， 2020， 39（6）： 1-16.

［5］刘菊华. 彩色打印机色彩特性化关键技术研究［D］. 武汉： 武汉大学， 2014. （Liu Juhua. Research on key technologies for color characterization of color printers［D］. Wuhan： Wuhan University， 2014.）

［6］Deshpande K. N-colour separation methods for accurate reproduction of spot colours［D］. London： University of the Arts London， 2015.

［7］Velastegui R， Pedersen M. CMYK-CIELAB color space transformation using machine learning techniques［EB/OL］. （2021-09-20）. https：//doi.org/10.2352/issn.2694-118x.2021.lim-73.

［8］MacDonald L. Color space transformation using neural networks［C］//Proc of Color and Imaging Conference. Springfield， VA： Society for Imaging Science and Technology， 2019： 153-158.

［9］Su Zebin， Yang Jinkai， Li Pengfei， et al. A precise method of color space conversion in the digital printing process based on PSO-DBN［J］. Textile Research Journal， 2022， 92（9-10）： 1673-1681.

［10］Chen Danwu， Urban P. Deep learning models for optically characterizing 3D printers［J］. Optics Express， 2021， 29（2）： 615-631.

［11］Chen Danwu， Urban P. Inducing robustness and plausibility in deep learning optical 3D printer models［J］. Optics Express， 2022， 30（11）： 18119-18133.

［12］Chen D， Urban P. Multi-printer learning framework for efficient optical printer characterization［J］. Optics Express， 2023， 31（8）： 13486-13502.

［13］Yang Huifang， Yi Yaohua， Liu Juhua， et al. Research on multi-color separation model based on polynomial regression［J］. Applied Mechanics and Materials， 2015， 731： 27-31.

［14］Lyu Guangwu， Cao Peng. Color space conversion technology and comparative research［C］//Proc of the 8th International Conference on Information Technology： IoT and Smart City. London： Springer， 2020： 115-118.

［15］Bi Zhicheng， Cao Peng. Color space conversion algorithm and comparison study［C］//Proc of International Conference on Computer.［S.l.］： IOP Publishing， 2021： 012008.

［16］Finlayson G D， Mackiewicz M， Hurlbert A. Color correction using root-polynomial regression［J］. IEEE Trans on Image Processing， 2015， 24（5）： 1460-1470.

［17］Yamakabe R， Monno Y， Tanaka M， et al. Tunable color correction between linear and polynomial models for noisy images［C］//Proc of IEEE International Conference on Image Processing. Piscataway， NJ： IEEE Press， 2017： 3125-3129.

［18］Ji Jing， Fang Suping， Shi Zhengyuan， et al. An efficient nonlinear polynomial color characterization method based on interrelations of color spaces［J］. Color Research & Application， 2020， 45（6）： 1023-1039.

［19］Zhao Siyu， Liu Lu， Feng Zibing， et al. Colorimetric characterization of color imaging system based on kernel partial least squares［J］. Sensors， 2023， 23（12）： 5706.

［20］曹朝辉. 多色印刷分色模型研究［D］. 郑州： 解放军信息工程大学， 2007. （Cao Zhaohui. Research on color separation model for multicolor printing［D］. Zhengzhou： Information Engineering University，2007.）

［21］Sun Qiang， Zhou Wenxin， Fan Jianqing. Adaptive Huber regression［J］. Journal of the American Statistical Association， 2020， 115（529）： 254-265.

［22］胡义函， 张小刚， 陈华，等. 一种基于鲁棒估计的极限学习机方法［J］. 计算机应用研究， 2012， 29（8）： 2926-2930. （Hu Yihan， Zhang Xiaogang， Chen Hua， et al. Extreme learning machine on robust estimation［J］. Application Research of Computers， 2012， 29（8）： 2926-2930.）

［23］Gómez-Polo C， Muoz M P， Luengo M C L， et al. Comparison of the CIELab and CIEDE2000 color difference formulas［J］. The Journal of Prosthetic Dentistry， 2016， 115（1）： 65-70.