基于同模型匹配点聚集的图像多匹配模型估计算法

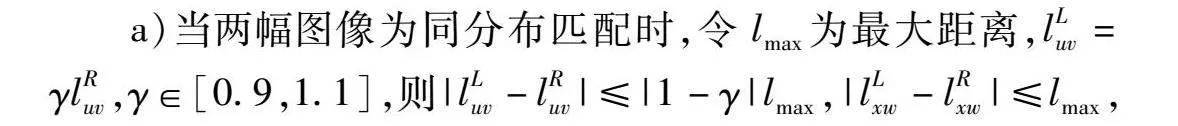
摘 要：宽基线或大视角图像间多匹配模型的估计是图像处理中一项非常有挑战性的任务。现有算法虽然能较好估计图像间的多匹配模型及其内点集，但是其结果容易出现匹配对错误分配的问题。为了精确估计图像间的多匹配模型从而分配匹配对，提出一种基于同模型匹配点聚集的图像多匹配模型估计算法（AMPSM）。首先，为提升正确匹配对占比，根据近邻区域内正确匹配对的分布特点对错误匹配对进行过滤；然后，根据匹配点所属不同匹配模型程度查找疑似的多模型的交集点，即干扰点，同时，为了降低干扰点对匹配对分类精度的影响，将其去除；之后，为了提高同模型匹配点的聚集程度，根据抽样过程中同模型内点与其点集重心的距离动态移动位置；最后，通过基于高斯核的Mean Shift算法对聚集后的匹配点分类，进而得到多匹配模型。将所提算法分别与基于经典框架的算法RANSAC、PROSAC、MAGSAC++、GMS、AdaLAM、PEARL、MTC、Sequential RANSAC和基于深度学习的算法SuperGlue、OANet、CLNet、CONSAC等进行比较，结果表明该方法内点率可提高30%以上，多模型估计的错分率可降低8.39%以上，即所提方法在错误匹配对过滤和多模型估计等方面具有显著优势。

关键词：图像匹配； 多模型估计； 抽样一致性； 聚集

中图分类号：TP249 文献标志码：A

文章编号：1001-3695（2024）10-042-3173-10

doi：10.19734/j.issn.1001-3695.2023.12.0638

Image multi-matching model estimation algorithm based onaggregation of matching points of same model

Wang Weijie1， Wei Ruoyan1， Zhu Xiaoqing2

（1.School of Management Science & Information Engineering， Hebei University of Economics & Business， Shijiazhuang 050061， China; 2.Faculty of Information Technology， Beijing University of Technology， Beijing 100124， China）

Abstract：The estimation of multiple matching models between wide baseline or large angle images is a quite challenging task in image processing. The existing algorithms can be used to estimate multiple matching models and their inliers between images well， but their results are prone to matching pairs mis-classification issues. In order to accurately estimate the multiple matching models and allocate matching pairs， this paper proposed an image multi-matching model estimation algorithm based on the aggregation of matching points of the same model（AMPSM）. Firstly， for improve the proportion of correct matching pairs， it filtered out incorrect matching pairs based on the distribution characteristics of correct matching points in the neighboring region. Furthermore， based on the different matching model degrees to which the matching pairs belong， searched for the suspected intersection matching pairs of multiple models， that was interference matching pairs. Meantime， for reducing the impact of interference matching pairs on the accuracy of matching classification， they were removed. Afterwards， for improve the clustering degree of matching points with the co-model， the position was dynamically moved based on the distance between the points within the same model and the center of gravity of the point set during the sampling process. Finally， classifying clustered matching points by Mean Shift to obtain a multi matching model. And the proposed method was compared with classical framework based algorithms RANSAC， PROSAC， MAGSAC++， GMS， AdaLAM， PEARL， MTC， Sequential RANSAC， and deep learning based algorithms SuperGlue， OANet， CLCNet， CONSAC， etc. Results indicate over 30% increase in the inlier rate， 8.39% reduction in the mis-classification rate of multi model estimation. It is concluded that the new algorithm has significant advantages in incorrect matches filtering and multi-model estimation.

Key words：image matching; multi-model estimation; sample consistency; aggregation

0 引言

图像匹配是机器视觉领域的关键技术，广泛应用于三维重建、定位与地图构建以及飞行器导航等领域［1］。图像匹配算法根据是否估计图像匹配模型，分为非匹配模型估计算法和匹配模型估计算法。匹配模型估计算法根据图像间存在的几何变换模型数目，分为单模型估计算法和多模型估计算法。

非匹配模型估计算法包括GMS［2］、ACNe［3］、OANet［4］、SuperGlue［5］、CLNet［6］等。GMS算法将图像划分为固定数目的网格，根据网格中的匹配对数量过滤错误匹配对。ACNe和OANet算法将全局注意力机制和局部注意力机制结合，在高维空间找到正确匹配对。SuperGlue算法将自注意力机制和交叉注意力机制嵌入图神经网络，兼顾全局和局部信息过滤错误匹配对。CLNet算法为各匹配对动态构建局部图，根据全局和局部一致性分数过滤错误匹配对。窄基线或小视角差异的图像间仅存在平移、旋转以及缩放变化，只需求解最优模型，即单模型估计。RANSAC［7］及其衍生算法适用于解决此类问题，包括PROSAC［8］、P-NAPSAC［9］、MAGSAC++［10］、NG-RANSAC［11］、Deep MAGSAC++［12］等。RANSAC算法随机选取少量匹配对并估计匹配模型，然后回代模型得到内点（符合匹配模型的匹配对），内点数目最多的模型为最优匹配模型。PROSAC算法使用相似性度量数值最高的样本子集进行半随机抽样，估计匹配模型，该算法依赖匹配点的描述信息，最坏情况与RANSAC相同。P-NAPSAC算法将NAPSAC和PROSAC相结合，融入局部和全局采样的优点。MAGSAC++算法不需要计算距离误差阈值，减少了其对内点准确率及精确度的影响。NG-RANSAC算法利用神经网络预测各匹配对权重，从而过滤错误匹配对。Deep MAGSAC++是MAGSAC++算法和NG-RANSAC算法的结合。宽基线或大视角差异的图像间存在多个匹配模型，更具有挑战性。Sequential RANSAC［13］、PEARL［14］、Multi-X［15］、MCT［16］及CONSAC［17］等算法适用于解决此类问题。Sequential RANSAC算法通过重复RANSAC操作得到多匹配模型，时效性较差。PEARL算法通过RANSAC进行初始化，优化能量函数以估计多匹配模型。Multi-X算法将多模型拟合问题转换为全局能量最小化问题，并根据匹配对分布密度聚集，估计多匹配模型，该算法是PEARL算法的扩展。MCT算法利用几何约束指导采样。CONSAC算法根据已找到的单匹配模型更新采样权重来估计多匹配模型。Barath等人［18］专门为多匹配模型估计设计一个新采样器，逐步找到多个匹配模型，而不形成清晰的匹配对到匹配模型的分配。

随着深度学习技术的发展，基于深度学习的图像匹配算法顺势而生，但现有的大多数基于深度学习的图像匹配算法仅匹配特征点，无法估计匹配模型。现有算法主要有以下问题：a）P-NAPSAC、OANet等算法认为局部区域内的正确匹配对具有相似分布，但当图像间视角差异过大或缩放明显时无法确定局部区域的范围；b）PROSAC、P-NAPSAC、Sequential RANSAC、AdaLAM［19］等算法利用distance ratio提升正确匹配对占比，进而估计匹配模型，但distance ratio的值需要随视角差异的增大而趋近于1；c）基于深度学习的匹配算法大多数仅匹配特征点，无法估计匹配模型，算法效率依赖数据集质量，数据集无法包含所有变化的图像，并且神经网络模型的训练时间过长；d）在图像多匹配模型估计过程中，多匹配模型的交集匹配对会对多模型估计的结果产生影响。

为解决以上问题，本文提出了一种基于同模型匹配点聚集的图像多匹配模型估计算法（AMPSM）。针对问题a）b），提出了基于近邻区域匹配点同分布的内点率提升方法（IREM），该方法根据正确匹配点在近邻区域具有的分布特点对错误匹配对进行过滤；针对问题d），提出了基于匹配点动态抽样分布特征的干扰点去除方法（DIPR），本文提出“干扰点”概念，并根据多次迭代中各匹配对所属内点集的点集重心的变化对高疑似的干扰点进行去除；针对问题c），提出了基于同模型匹配点聚集的多模型估计方法（AGSM），抽样过程中同模型匹配点根据其与内点集重心的距离动态移动以显著提高不同模型的匹配点在图像平面空间中的分离度，然后用基于高斯核的Mean Shift［20］算法对聚集后的数据进行区分，从而得到多模型及所对应的内点集。

1 本文方法

1.1 算法流程

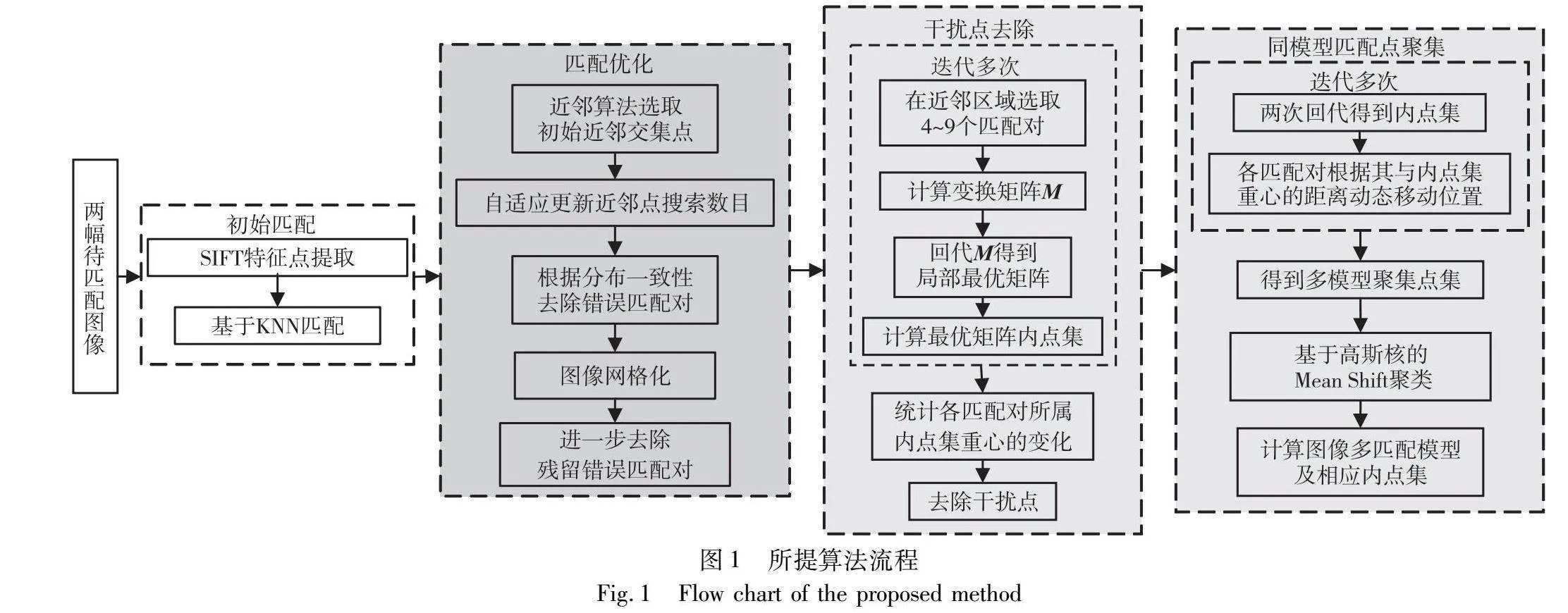
本文算法分为三步，分别对应三个创新点：a）提出一种基于近邻区域匹配点同分布的内点率提升方法（IREM），以达到过滤错误匹配对的目的；b）首次提出“干扰点”的概念，并提出一种基于匹配点动态抽样分布特征的干扰点去除方法（DIPR），以达到提高多匹配模型估计精度的目的；c）提出一种基于同模型匹配点聚集的多模型估计方法（AGSM），以达到提高同模型匹配点的聚集程度，并降低多匹配模型错分率的目的。算法流程如图1所示，其中灰色模块对应上述三个创新点。

1.2 基于近邻区域匹配点同分布的内点率提升

文献［21］中所提方法的原理是保留待匹配的两幅图像中正确匹配点的局部邻域结构，即对于旋转、平移变化的图像，正确匹配点间的距离保持不变，正确匹配点间的局部邻域结构保持不变。对于大视角差异的图像，正确匹配点间的距离可能存在显著变化，但由于匹配点周围区域的物理约束，正确匹配点间的局部邻域结构通常不会自由变化。

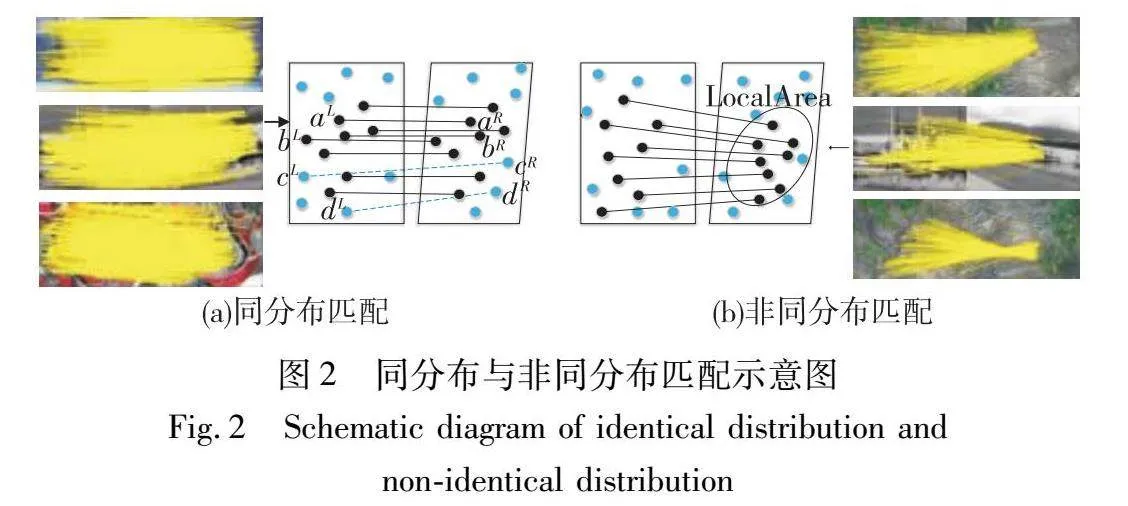
文献［22］中将图像匹配分为同分布匹配与非同分布匹配。对于同分布匹配，图像之间的匹配点分布相似，如图2（a）所示；对于非同分布匹配，匹配图像之间的比例明显放大，图像之间的匹配点分布不同，如图2（b）所示。

当匹配类型为同分布匹配时，图像间正确匹配对分布差异较小，如图2（a）所示，其中黑点为正确匹配点，蓝点为错误匹配点。正确匹配对为（aL，aR）和（bL，bR），错误匹配对为（cL，cR）和（dL，dR），因此，|aLbL-aRbR|≤|cLdL－cRdR|。当匹配类型为非同分布匹配时，如图2（b）所示，其中LocalArea为一个局部区域，图像间LocalArea的面积明显不同，所以两幅图像的LocalArea内正确匹配对间的距离分布差异较大。令pi（i=1，2，…，n）为一幅图像的n个匹配点，lKuv=|pKu-pKv|，1≤u，v≤n，u≠v，K=L，R为图像中任意两个正确匹配点间的距离，其中，L和R表示左图和右图。若lLuv=γlRuv，且γ∈［0.9，1.1］，则两幅图像为同分布匹配，否则为非同分布匹配，如图2所示。

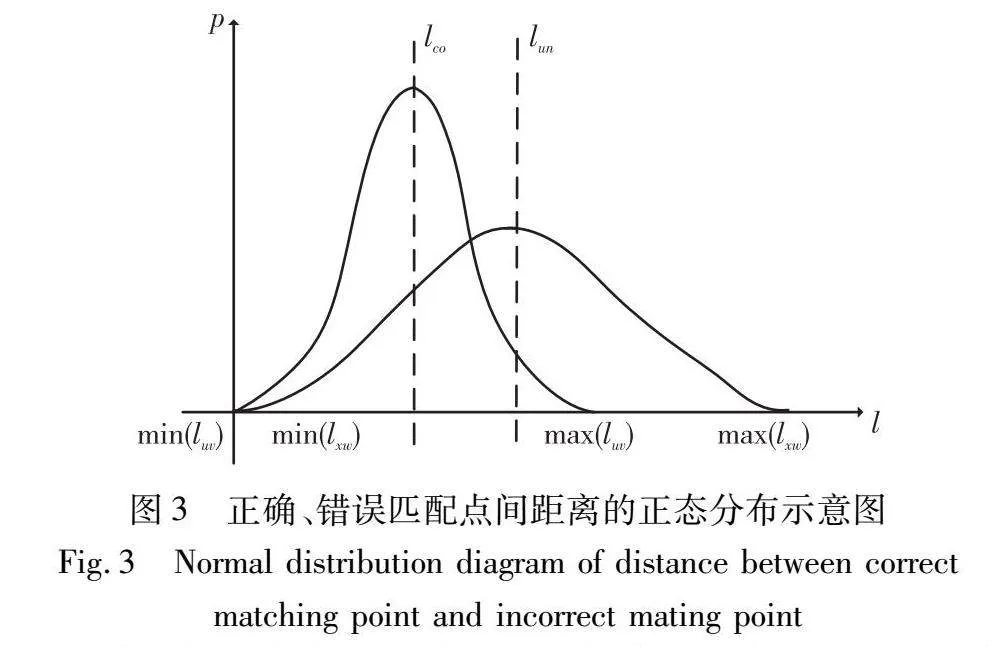
令pi（i=1，2，…，n）为一幅图像的n个匹配点，l=|pu-pv|，1≤u，v≤n，u≠v为任意两个匹配点间的距离，p（l）=numl/C2n为数值为l的距离的概率，其中numl为数值是l的距离数目，C2n为图像中的距离数目。当匹配点数目足够多，即匹配点间的距离数值足够多，且匹配点之间的距离分布未知时，可以认为匹配点之间的距离l的分布为正态分布l～N（μ，σ2），其中μ为匹配点间距离的平均值，σ2为匹配点间距离的方差。令lKco=∑lKuv/numKco，K=L，R为正确匹配点间的平均距离，其中，lKuv为任意两个正确匹配点间的距离，numKco为正确匹配点间距离的数目；lKun=∑lKxw/numKun，K=L，R为错误匹配点间的平均距离，其中，lKxw为任意两个错误匹配点间的距离或任意一个正确匹配点与一个错误匹配点间的距离，numKun为错误匹配点间距离的数目。根据上述内容可知，匹配点间距离的分布服从正态分布，则min（lKuv）≈min（lKxw），max（lKxw）≥max（lKuv）。由于正态分布具有对称性，所以lKco≤lKun，其分布如图3所示。

a）当两幅图像为同分布匹配时，令lmax为最大距离，lLuv=γlRuv，γ∈［0.9，1.1］，则|lLuv－lRuv|≤|1-γ|lmax，|lLxw-lRxw|≤lmax，因此，E（|lLuv-lRuv|）≤E（|lLxw-lRxw|），则p（|lLuv-lRuv|<|lLxw-lRxw|）=

p（|lLuv-lRuv|-|lLxw-lRxw|<0）=ΦE（|lLxw-lRxw|）-E（|lLuv-lRuv|）σuv+σxw≥0.5。因此，当两幅图像为同分布匹配时：

P（|lLuv-lRuv|<|lLxw-lRxw|）=

Φ（E（|lLxw-lRxw|）-E（|lLuv-lRuv|）σuv+σxw）≥0.5（1）

其中：lLuv和lLxw为左图中正确匹配点间的距离和错误匹配点间的距离；lRuv和lRxw为右图中正确匹配点间的距离和错误匹配点间的距离；σuv和σxw为两幅图像中正确匹配点间距离和错误匹配点间距离的方差。

b）当两幅图像为非同分布匹配，且lLuv=γlRuv，γ∈［1.1，+∞）时，lRuv～N（lRco，sRco），lRxw～N（lRun，sRun），其中，lRco和lRun为右图正确匹配点的平均距离和错误匹配点平均距离，sRco和sRun为右图正确匹配点的距离方差和错误匹配点的距离方差，则

p（lRuv<lRxw）=plRuv-lRxw-（lRco-lRun）sRco+sRun<0-（lRco-lRun）sRco+sRun=ΦlRun-lRcosRco+sRun，由于lRco≤lRun，所以，P（lRco-lRun）≥0.5。当lLuv=γlRuv，γ∈（0，0.9］时，同理可得P（lLco-lLun）≥0.5。因此，当两幅图像为非同分布匹配时：

P（lKco-lKun）=ΦlKun-lKcoσKun+σKco≥0.5（2）

其中：lKco为左图或右图中正确匹配点间距离的平均值；lKun为左图或右图中错误匹配点间距离的平均值；σKco为左图或右图中正确匹配点间距离的方差；σKun为左图或右图中错误匹配点间距离的方差。

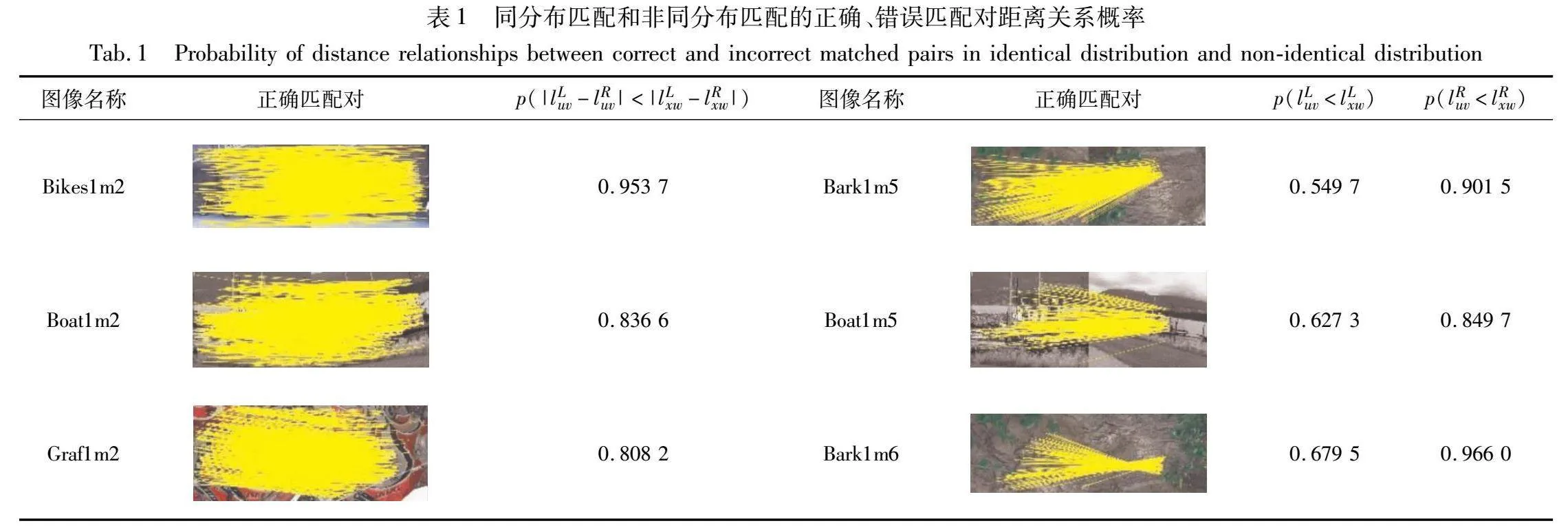
表1展示三组同分布匹配图像（Bikes1m2、Boat1m2、Graf1m2）中p（|lLuv-lRuv|<|lLxw-lRxw|）的数值和三组非同分布匹配图像（Bark1m5、Boat1m5、Bark1m6）中p（lLuv<lLxw）、p（lRuv<lRxw）的数值。通过表1可以看出，当图像间的匹配是同分布匹配时，|lLuv-lRuv|的分布范围明显小于|lLxw-lRxw|的分布范围，且p（|lLuv-lRuv|<|lLxw-lRxw|）的数值均大于0.5，并且若左图中任意两个正确匹配点间距离与右图中对应的两个正确匹配点间距离的差值越小，即E（|lLuv-lRuv|）越小，则p（|lLuv-lRuv|<|lLxw-lRxw|）≥0.5的可能性越大。当图像间的匹配为非同分布匹配时，p（lKuv<lKxw）的数值均大于0.5，并且若单幅图像中正确匹配点间的距离越小，即lKco（K=L，R）越小，则p（lKuv<lKxw）≥0.5的可能性越大。

综上所述，若两幅图像间任意两个正确匹配点间距离的差值越小，即E（|lLuv-lRuv|）越小，则图像间错误匹配点的距离差值大于正确匹配点的距离差值的可能性越大；若单幅图像中正确匹配点间距离越小，即lKco越小，则图像内错误匹配点的距离大于正确匹配点的距离的可能性越大。

根据上述内容可知，近邻区域内的正确匹配对在空间分布上具有一致性［23～25］，即在大视角差异的情况下，同一场景或对象的图像间，同一区域的正确匹配对的局部空间关系被很好地保留。GMS、P-NAPSAC等算法均利用了该性质。图4是正确匹配对位置变化矢量图，可看出在局部区域内，正确匹配对的变化矢量具有较高的方向一致性。

基于上述现象，本文提出了一种基于近邻区域匹配点同分布的内点率提升方法（IREM），该方法根据近邻区域内匹配对的平均距离比值及余弦相似度过滤错误匹配对。具体步骤如下：

a）利用近邻算法搜索匹配对集合U中各匹配点的αL和αR个近邻点，其中L和R分别表示待匹配的两幅图像，一般取αL=αR=10。

b）若各匹配点与两幅图中的近邻点交集非空，则计算近邻交集点到各匹配点的平均距离，并根据式（3）（4）更新αL和αR并得到新的近邻点交集。

γ=dLi/dRi i=1，2，…，n（3）

αL=γαR γ≥1αRγγ<1（4）

其中：dLi为左图中第i个交集点到各匹配点的平均距离；dRi为右图中第i个交集点到各匹配点的平均距离；n为搜索的近邻点的数目。

c）各匹配点的近邻点交集取并集得到集合S。

d）图像网格化。以图片对角线长度乘以0.05为每个网格的边长对图像进行网格化［24］，如图5所示。若网格内匹配点的平均距离fku<F，则将其平分为3×3网格。F的计算公式为

F=∑Nv=1fKv/N K=L，R（5）

其中：N为网格数目。

e）根据集合S中匹配对的坐标得到位置变化矢量集合PM。根据式（6）计算各网格中匹配点位置变化矢量的余弦相似度cossimi，若网格中匹配点位置变化矢量数目小于估计模型所需的最小样本数目mmin（基础矩阵时，mmin=7；单应性矩阵时，mmin=4），则将其周围9个网格包含进来，若其仍小于mmin，则网格中匹配对被当作错误匹配对过滤；否则重新计算余弦相似度cossimi，将均值满足cossimi≥thre，thre∈［0.8，1.0］的匹配对当作正确匹配对保留，得到过滤后的匹配对集合Q。

cos θ=xi·xj‖xi‖‖xj‖ i=1，…，m； j=1，…，m（6）

其中：xi和xj为匹配点位置变化矢量的坐标；m表示匹配点位置变化矢量的数目。cos θ∈［-1，1］，cos θ的值越接近1，表示两个匹配点位置变化矢量越相似。

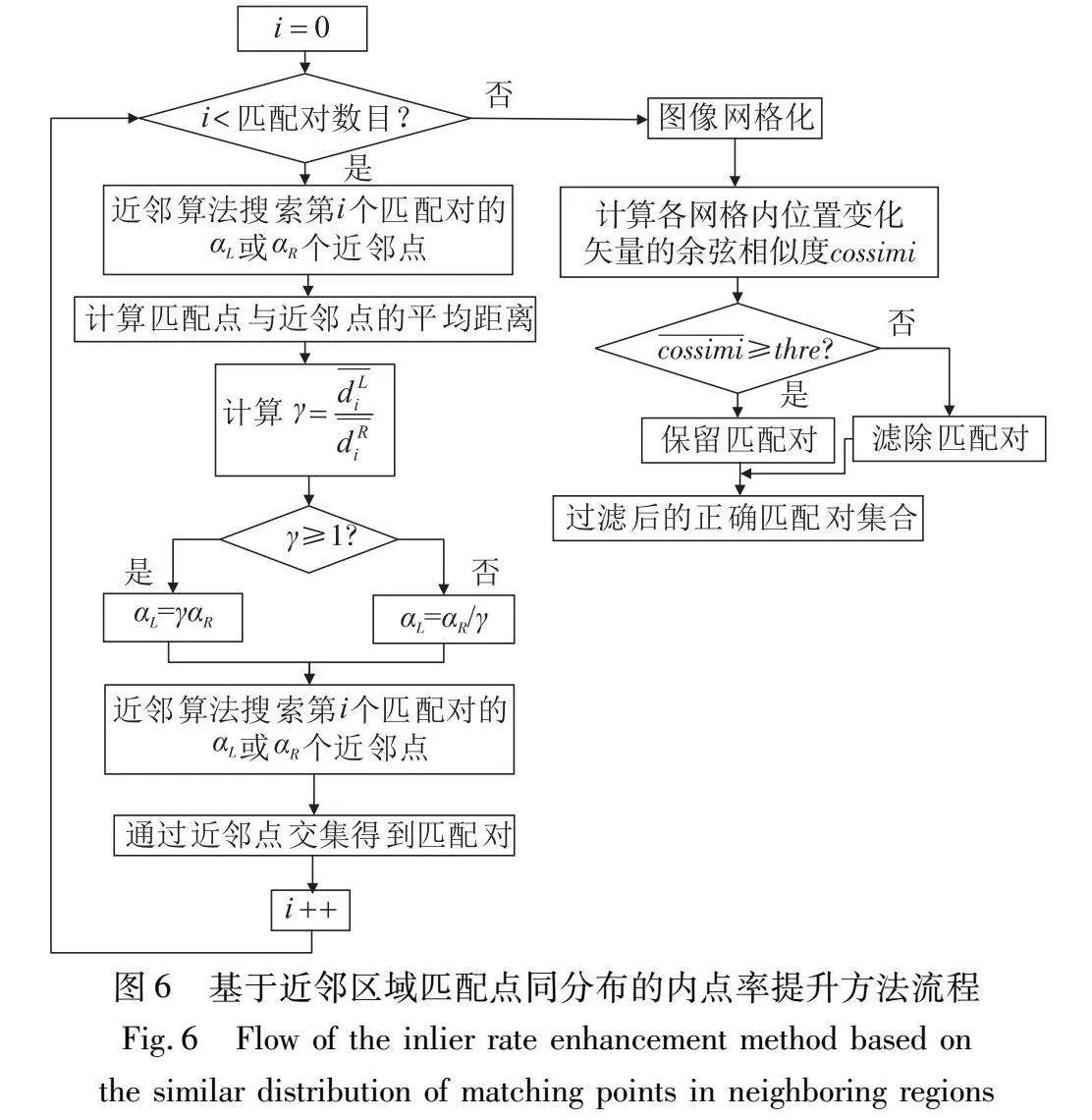
基于近邻区域同分布的内点率提升方法流程如图6所示。

1.3 基于匹配点动态抽样分布特征的干扰点去除

所有图像多匹配模型估计算法都将多模型拟合问题转换为寻找不相交的匹配对集合的问题，每个匹配对集合代表一个匹配模型。在某种情况下，一个匹配对符合多个匹配模型，这种现象使问题无法解决［14，17，18］。如图7（a）所示，当将点分配给单条直线模型（按颜色）时，无法找到所有9个模型，即黑色虚线表示的模型无法找到。当将平面模型拟合为7个点中的4个点时，只能找到一个平面模型［18］。即使人工处理，匹配对到匹配模型的分配也常常不清晰，特别是匹配对集合的交集。如图7（b）所示，不同颜色匹配对属于不同匹配模型所在的平面，黑色匹配对属于多个匹配模型，即黑色匹配对为内点集的交集。图7中，黑点为干扰点，其他不同颜色点为多模型内点集，通过观察可以发现：交集往往位于模型所在平面的交界处。这一现象是客观存在的，主要原因在于多匹配模型交集区域的匹配对在不同匹配模型中的距离误差均小于阈值，即其被认作不同匹配模型的内点。

内点集的交集在本文中之所以被称为干扰数据，主要有以下两个原因：a）不同的匹配模型数据属于不同类别，干扰数据将在多模型估计过程中扰乱匹配数据的分类精度，导致模型估计不准确；b）文献［14，15，26］中利用多匹配模型估计方法对图像内容进行几何空间估计，该过程中需要计算各模型数据点的聚类中心，但干扰数据点将使聚类中心发生偏移，从而影响几何空间估计效果。文献［14，17，27］虽然对干扰数据的存在和影响有所提及，但没有提出具体的干扰数据去除方案。

若两幅待匹配图像间存在多个匹配模型，M={M1，M2，…，Mn}为匹配模型集合，n为匹配模型数目，I={I1，I2，…，In}为符合各匹配模型的内点集。一般认为经匹配模型变换后距离误差小于e的匹配对为该匹配模型内点。本文将匹配对集合中符合多个匹配模型的匹配对视为干扰点。例如：Iu和Iv为两个内点集，Iu={（aL，aR），（bL，bR），（cL，cR），（dL，dR），…}和Iv={（cL，cR），（dL，dR），（eL，eR），（fL，fR），…}分别符合匹配模型Mu和Mv，即f（Iu，Mu）≤e，f（Iv，Mv）≤e。相应计算公式为

f（p，M）=

|［pRi，1］T-M［pLi，1］T| M=H

［pRi，1］M［pLi，1］T（MpLi）21+（MpLi）22+（MTpRi）21+（MTpRi）22M=F（7）

其中：f（p，M）为距离误差公式；p为匹配对集合；M为匹配模型。因为， f（c，Mu）≤e，f（c，Mv）≤e， f（d，Mu）≤e， f（d，Mv）≤e，所以（cL，cR）和（dL，dR）同时属于多个匹配模型，即为干扰点。

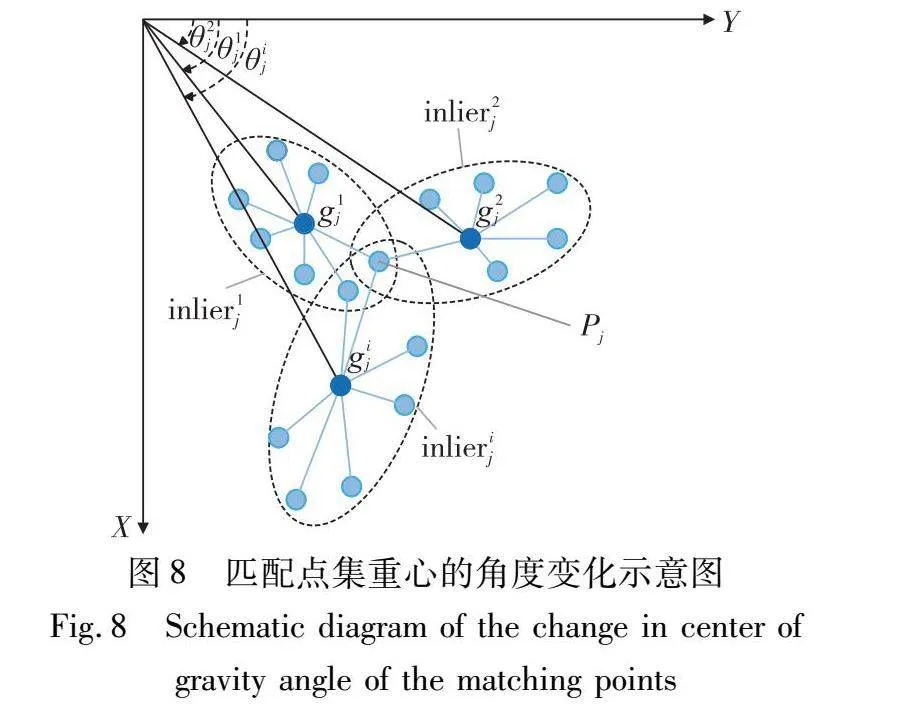
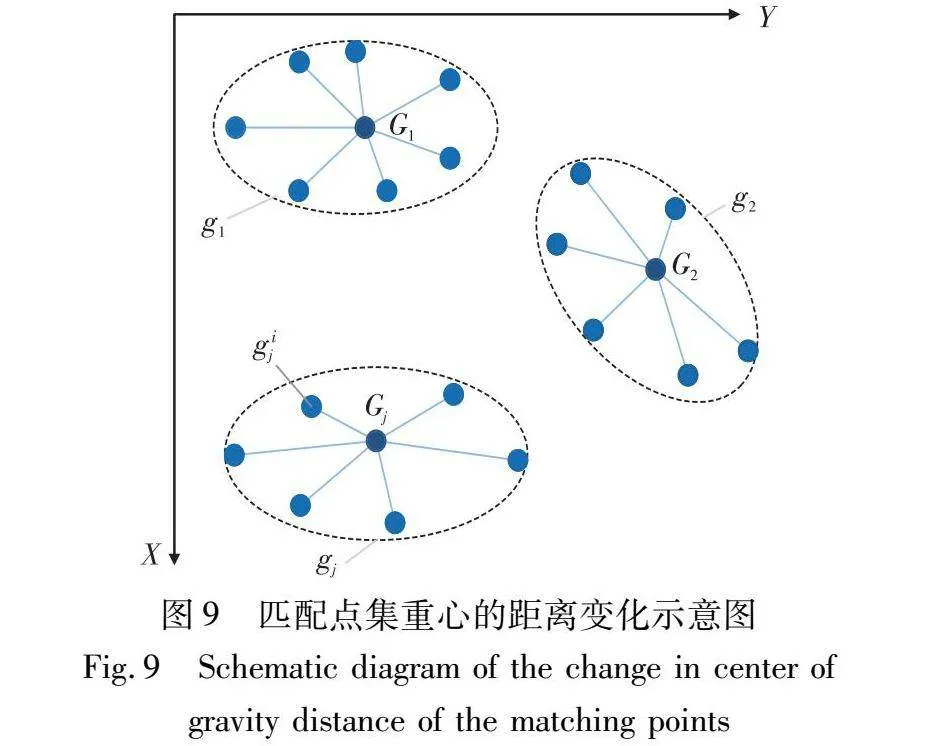
通过实验发现，干扰点对应的匹配模型的内点集重心变化大于非干扰点，并且近邻区域内的匹配对基本符合同一匹配模型。图8为某一匹配点所属的匹配点集重心的角度变化示意图，图9为不同匹配点所属的匹配点集重心的距离变化示意图。其中Pj为第j个匹配点，inlierij为Pj所属的第i个匹配模型内点集，gij为inlierij的点集重心，Gj为Pj所属的全部内点集重心的重心，gij与Gj的连线表示两者的距离。可以看出，若匹配对所属的内点集重心变化越大，则内点集重心相对于图像左上角的角度变化越大，内点集重心之间的距离变化越大。

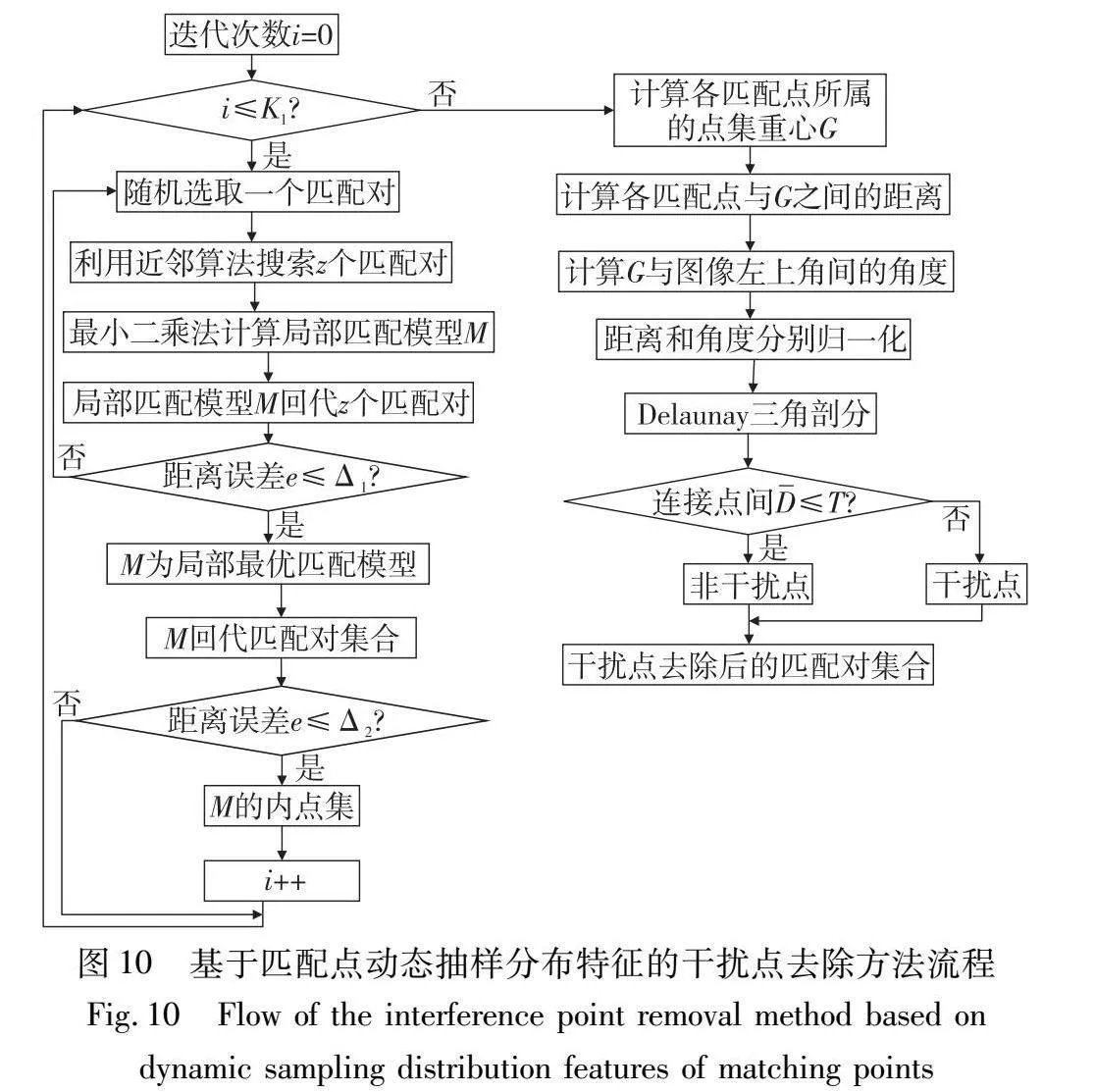
基于上述现象，本文提出了一种基于匹配点动态抽样分布特征的干扰点去除方法（DIPR），该方法根据模型估计过程中匹配对与从属模型内点集重心间的角度和距离特征筛选并去除干扰点。方法中设置两次模型回代，第一次回代为得到局部最优模型，第二次回代为在匹配对集合中得到符合该模型的内点集。由于回代过程的作用不同，距离误差阈值的设置范围也不同。具体步骤如下，流程如图10所示。

a）利用近邻算法在集合Q中随机选取z个匹配对，如果z过大，则抽取的匹配对分布范围较大，可能不在局部区域内，所以本文z的取值为4～9。利用最小二乘法计算图像匹配模型矩阵M，将M回代到z个匹配对，若匹配对的距离误差e≤Δ1，根据文献Δ1一般取值为1.0～1.5［28］，距离误差公式如式（7）所示，则M为局部区域最优模型矩阵。

b）将M回代到集合Q，计算满足e≤Δ2的匹配对集合，Δ2一般取值为2.0～3.0。

c）将步骤a）b）迭代K1次，经过多次实验确定K1为3 000，将每次得到的匹配对集合于左图的匹配点存储于集合Ci（i=1，…，K1），并将各匹配点所属的点集重心存储于集合G，G的尺寸为v×K1，其中v是集合Q中左图匹配点的数目。

d）计算Ci中各匹配点的点集重心与图像左上角的角度，存储于P，P的尺寸为v×K1，其中v是集合Q中左图匹配点的数目。计算P中各匹配点所属的点集重心的角度标准差及G中的距离标准差，并分别进行归一化处理。

e）各匹配点以横坐标为距离标准差，纵坐标为角度标准差的点表示，并利用Delaunay［29，30］算法进行三角剖分。

f）计算连接点之间的距离：

D1：d11…d1n1D2：d21…d2n2Dm：dm1…dmnm（8）

其中：Di为三角剖分中的第i个点，i=1，…，m，m为点的数量；dij为第i个点中第j个连线的长度，其中j=1，…，ni，ni为与第i个点相连的点的数量。然后计算每个点与相邻点的均值距离，公式为

Di=∑nij=1dijni（9）

所有点与相邻点的均值距离的概率分布密度，如下所示。

∑mi=1pi=1（10）

pi=kim（11）

ki=sum（max（D）×（i-1）m<D<max（D）×（i+1）m）（12）

匹配对若保留，需满足条件：

∑mLi=1pi≤T（13）

其中：T为阈值。若数据量可观，根据中心极限定理，所有点与相邻点的均值距离的概率分布近似于正态分布，将均值距离的最大概率值当作期望值，T设置为使期望值右端概率和与其左端概率和相等的概率值。最后得到干扰点去除后的匹配对集合W。

1.4 基于同模型匹配点聚集的多模型估计

待匹配图像中各匹配模型内点集的分布范围较大，为提高各匹配模型内点集的聚集程度，并根据聚集后的数据团估计多匹配模型，提出了一种基于同模型匹配点聚集的多模型估计方法（AGSM）。该方法根据各匹配模型内点集中匹配点与点集重心的距离动态移动匹配点位置，重复此操作直到各匹配点位置不再变化，得到多模型聚集点集。然后利用基于高斯核的Mean Shift［20］算法对聚集点集进行聚类，最后得到对应数据团间的变换匹配矩阵，即图像多匹配模型。

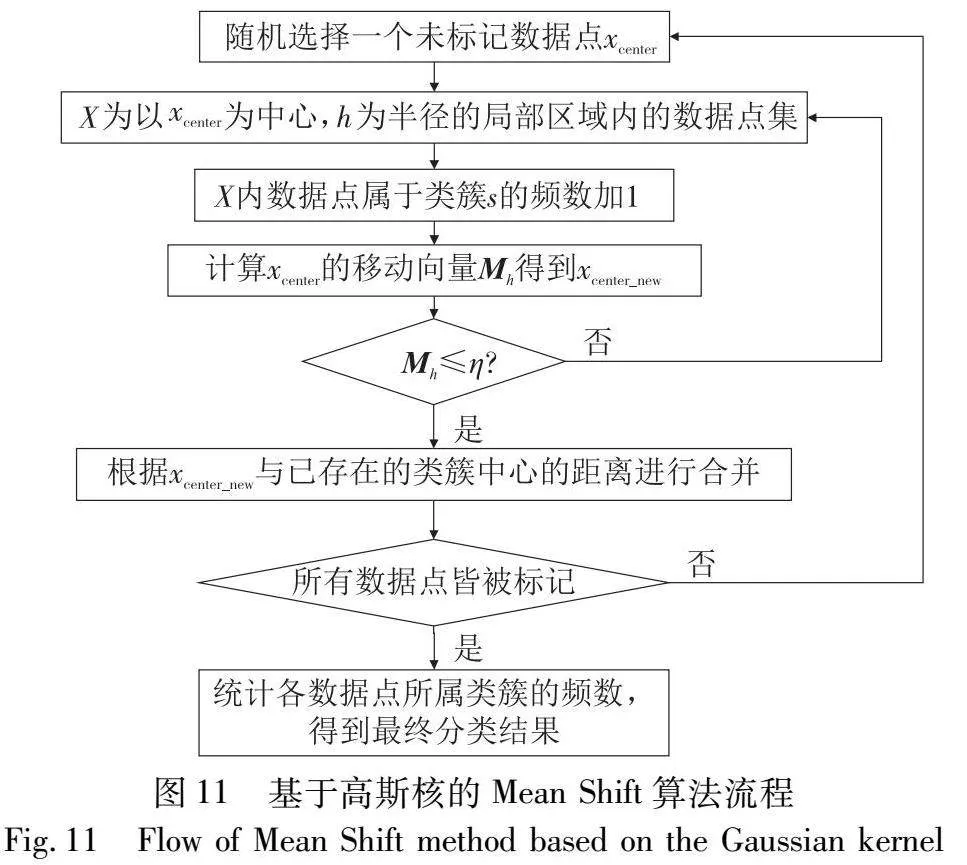
经典Mean Shift算法认为每个数据点对聚类结果的贡献相同。基于高斯核的Mean Shift算法是经典Mean Shift算法的改进，该算法引入高斯核函数，使每个数据点对最终结果的贡献不同。基于高斯核的Mean Shift算法的流程如图11所示。

Mh（xcenter）=∑xi∈X［H（xi-xcenterh）（xi-xcenter）］∑xi∈XH（xi-xcenterh）（14）

H（xi-xcenterh）=12πe-（xi-xcenter）22h2（15）

其中：H（·）为高斯核函数。

基于同模型匹配点聚集的多模型估计方法（AGSM）的具体步骤如下：

a）利用近邻算法在集合W中随机选取z个匹配对，本文z的取值为4～9。利用最小二乘法计算图像匹配模型矩阵M，将M回代到当前所选的z个匹配对，若匹配对的距离误差e≤Δ1，根据文献Δ1一般取值为1.0～1.5，则M为局部区域最优模型矩阵。

b）将M回代到集合W计算距离误差e，计算满足e≤Δ2的匹配对集合I，Δ2一般取值为2.0～3.0。

c）根据式（16）计算匹配对集合I中各匹配点相对于点集重心的距离dkj。

dkj=|pkjXki| j=1，2，…，m；i=1，2，…，n；k=L，R（16）

其中：pkj为匹配点坐标；Xki为点集重心坐标。

d）根据式（17）（18）对各个匹配点向点集重心聚集。

|Δd|=dkj dkj≤α×dkjdkj> j=1，2，…，m（17）

α=1dkj- j=1，2，…，m（18）

其中：|Δd|为各匹配点向重心方向移动的距离；是距离阈值，根据匹配点到重心距离分布进行设置。

e）重复步骤a）～d）直到各匹配点的位置变化小于1像素，获得多模型聚集点集E。

f）利用基于高斯核的Mean Shift算法［20］将E分别聚类为左图的数据团CL={CL1，CL2，…，CLn}和右图的数据团CR={CR1，CR2，…，CRn}，其中n为数据团数目。

g）分别计算CL和CR对应子团的变化模型矩阵Mi及内点集Ii，若Ii中内点数目大于估计模型所需的最小样本数目mmin（基础矩阵时，mmin=7；单应性矩阵时，mmin=4），则保留，否则舍弃。最后得到待匹配图像间的多匹配模型M及内点集I。

2 实验

为验证本文算法的有效性，对本文提出的内点率提升方法、干扰点去除方法、多匹配模型估计方法均进行了实验，初始匹配对利用SIFT［28］获得。实验测试环境为：Windows 10 操作系统（64位），Core i5处理器，16 GB运行内存，运行环境为Python 3.7。

2.1 内点率提升方法的对比实验

2.1.1 近邻关系的对比实验

选择三组图像展示使用IREM方法前后匹配点间的近邻关系，如图12所示。

其中前两组图像间存在单个匹配模型，后一组图像间存在多个匹配模型。图12中第一列为错误匹配对过滤前匹配点间的近邻关系，可以看出左右两幅图像中各匹配点与其近邻点之间的关系连线的形状有明显差异，图12中第二列为错误匹配对过滤后匹配点间的近邻关系，可以看出左右两幅图像中各匹配点与其近邻点之间的关系连线的形状基本相同。根据两列效果图的对比，可以看出IREM方法可以在有效保留匹配点间的近邻关系的基础上过滤错误匹配对。

2.1.2 单模型估计算法内点率的对比实验

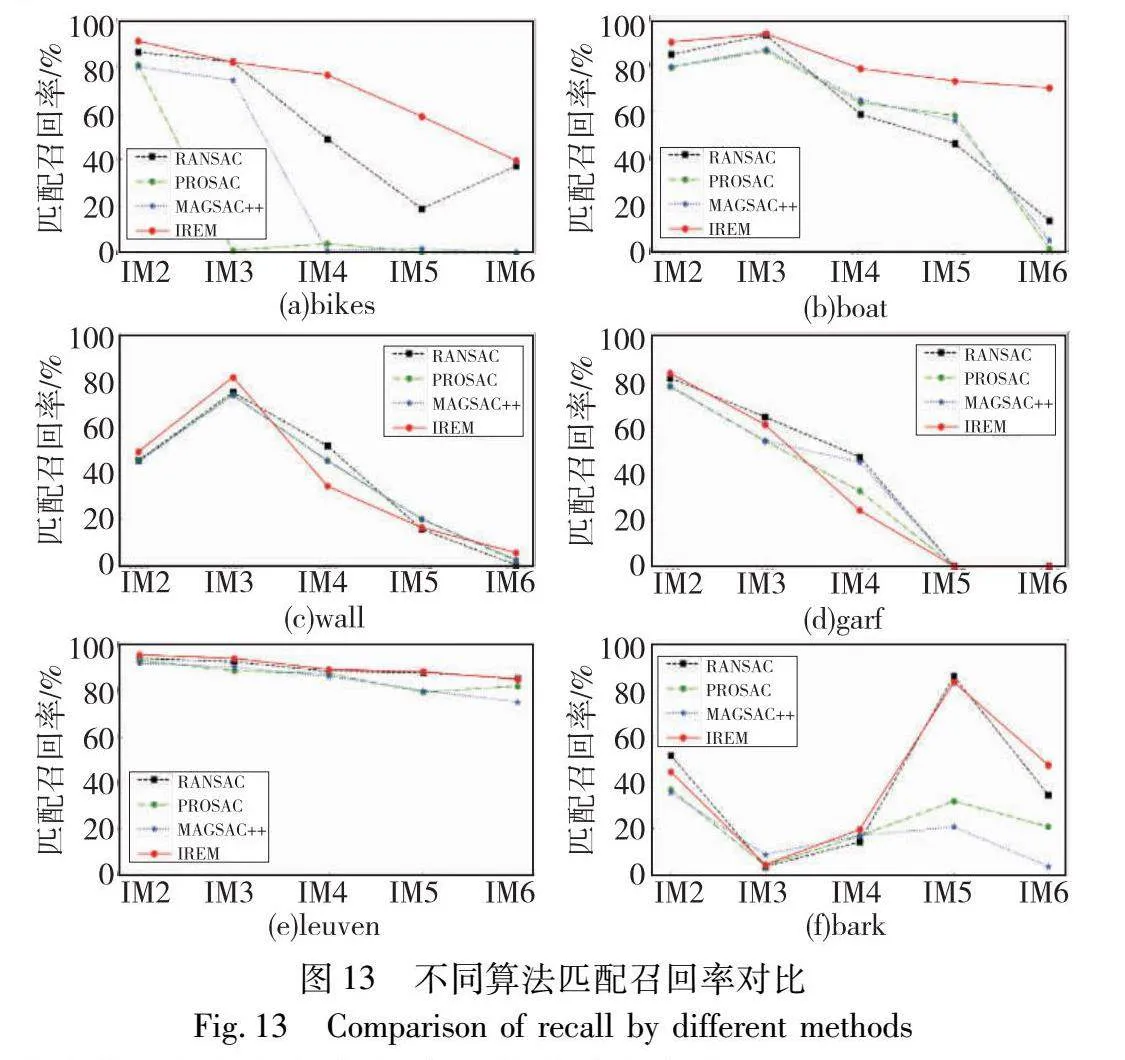
Oxford标准数据集［31］包含六个子数据集，子数据集内图像变化分别为图像模糊（bikes）、旋转缩放变化（boat）、视点变化（wall、garf）、光照变化（leuven）及尺度变化（bark）。每个子数据集包括6幅相同场景不同变化程度的图像，图像间仅存在一个匹配模型。每个子数据集提供第2～6幅图像与第1幅图像间的图像单匹配模型。对比算法为单模型估计算法：RANSAC、PROSAC、MAGSAC++，可以计算图像单匹配模型及其内点集，使用OpenCV内的函数实现。实验过程中各算法对各子数据集的第一幅图像与其他五幅图像依次进行匹配，并以1MN表示（M表示匹配，N为2～6）。实验分析中使用匹配召回率（recall）对各算法进行分析评价。recall定义为

recall=matchescorrectmatchescorrect+matchesincorrect（19）

其中：matchescorrect为利用算法去除错误匹配对后正确匹配对数目；matchesincorrect为未去除的错误匹配对数目。显然，recall值越大，代表该算法匹配效果越好。

图13为不同算法在Oxford子数据集上经过匹配实验后得到的匹配召回率的对比实验结果。可以看出对于图像模糊（bikes）、旋转缩放变化（boat）、光照变化（leuven），IREM方法的匹配召回率明显优于其他三种算法；对于视点变化（wall、graf），可以看出，四种算法的匹配召回率随着视点变换逐渐增大而急剧降低；对于尺度变化（bark），可以看出，IREM方法与RANSAC的匹配召回率相差不大，且优于其他两种算法。RANSAC、PROSAC、MAGSAC++算法均通过估计最优匹配模型内点集过滤错误匹配对，而IREM方法仅根据近邻区域正确匹配对的分布特点过滤错误匹配对，因此IREM方法更具优势。

2.1.3 内点率和残留外点率的对比实验

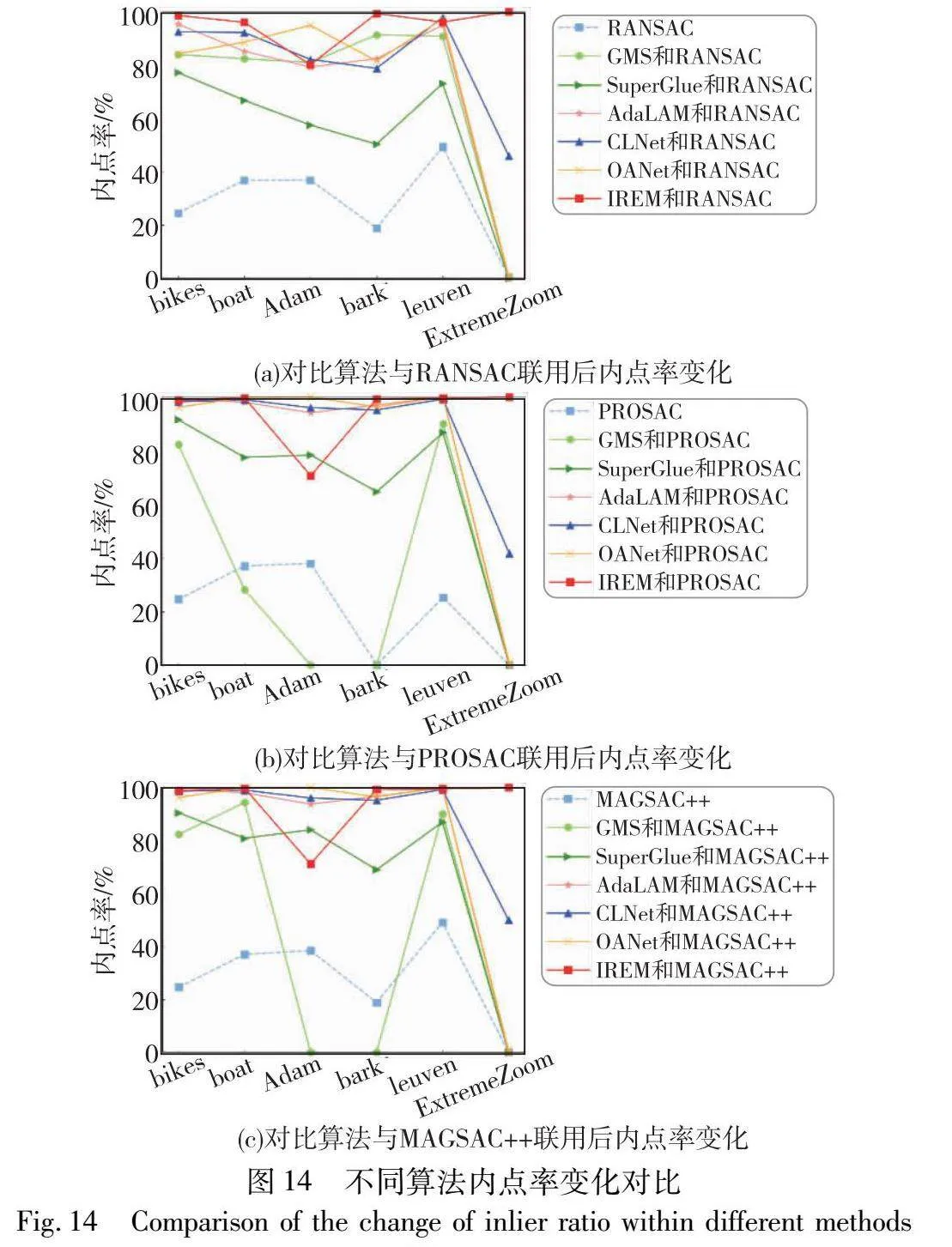
在bikes、boat、EVD、bark、leuven、homogr数据集［31，32］中选择六组图像进行实验，图像间变化包含图像模糊、缩放旋转、尺度变化以及光照变化，且图像间只存在一个匹配模型。对比算法为基于传统框架的GMS、AdaLAM和基于深度学习的SuperGlue、CLNet、OANet，均只能过滤错误匹配对，无法估计匹配模型。实验目的为验证IREM方法或对比算法使用前后，RANSAC、PROSAC、MAGSAC++算法所求变换模型内点率的变化，即IREM算法与对比算法对RANSAC等单模型估计算法的效果改善程度。RANSAC、PROSAC、MAGSAC++算法均使用OpenCV内的函数实现，图14为实验结果。可以看出，单独使用RANSAC、PROSAC、MAGSAC++算法时，所计算的变换模型内点率均低于50%，且ExtremeZoom的内点率均低于1%；使用IREM方法过滤错误匹配对后，再使用RANSAC、PROSAC、MAGSAC++算法，所计算的变换模型内点率均有明显提升，且除Adam图像外均能达到98%以上。相对于GMS算法，IREM方法内点率提升效果更明显；相对于SuperGlue、AdaLAM、CLNet、OANet算法，除Adam图像外，IREM方法内点率提升效果更好。对于Adam图像，近邻区域内正确匹配对数量少，因此内点率提升效果低于SuperGlue等四种算法。但经IREM方法剔除错误匹配对之后计算的模型内点率达到70%以上，提升了30%以上。对于ExtremeZoom图像，IREM方法的内点率提升效果明显优于五种对比算法。

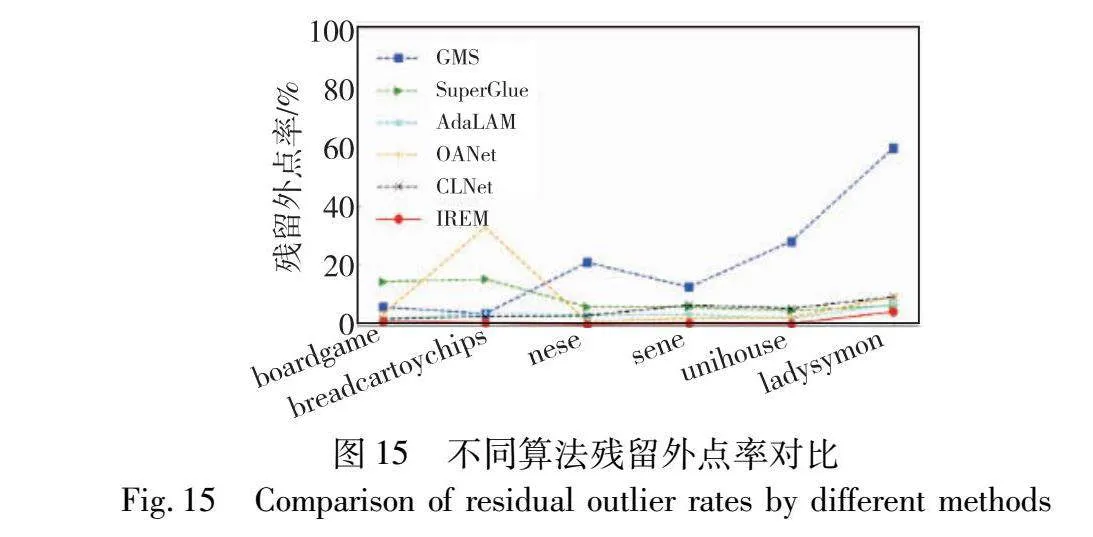
在Adelaidermf数据集［33］中选择六组图像进行实验，所用图像间均包含多个匹配模型。对比算法为基于传统框架的GMS、AdaLAM和基于深度学习的SuperGlue、OANet、CLNet，均无法估计匹配模型。实验目的为验证包含多匹配模型的图像应用IREM方法或对比算法后匹配对集合的错误匹配对占比。IREM和GMS、AdaLAM、OANet、CLNet算法皆利用SIFT算法提取特征点，SuperGlue算法利用SuperPoint算法提取特征点。GMS算法将图片划分为20×20个不重叠的网格，单个网格代表局部区域，以每个网格进行错误匹配对过滤，但当图像间视角差异较大、缩放明显时，单个网格无法代表局部区域。SuperGlue算法将自注意力和交叉注意力嵌入到图神经网络中，可以兼顾全局和局部过滤。AdaLAM算法依赖distance ratio选择正确匹配对。OANet算法以学习的方式捕获无序稀疏匹配对的局部上下文信息并对其进行聚类，然后将聚类结果在空间上进行关联以形成全局上下文信息，根据全局和局部上下文信息过滤错误匹配对。CLNet算法构建局部到全局的动态图，根据局部和全局一致性分数过滤错误匹配对。IREM方法自适应确定局部区域，根据匹配点的分布一致性和匹配点位置变化矢量的方向一致性对错误匹配对进行过滤。图15为实验结果，可以看出IREM方法的残留外点率最低，AdaLAM和CLNet算法效果明显优于GMS、SuperGlue和OANet算法。IREM算法的残留外点率与AdaLAM算法相比降低了61.13%，与SuperGlue算法相比降低了83.56%，与CLNet算法相比降低了71.09%。

综上所述，从匹配点间近邻关系上分析，IREM方法可以有效保留匹配点间的近邻关系，滤除近邻关系不一致的匹配点。从匹配召回率、内点率和外点残留率指标进行分析，本文IREM方法的错误匹配对剔除率较高，匹配性能更稳定。

2.2 干扰点去除实验

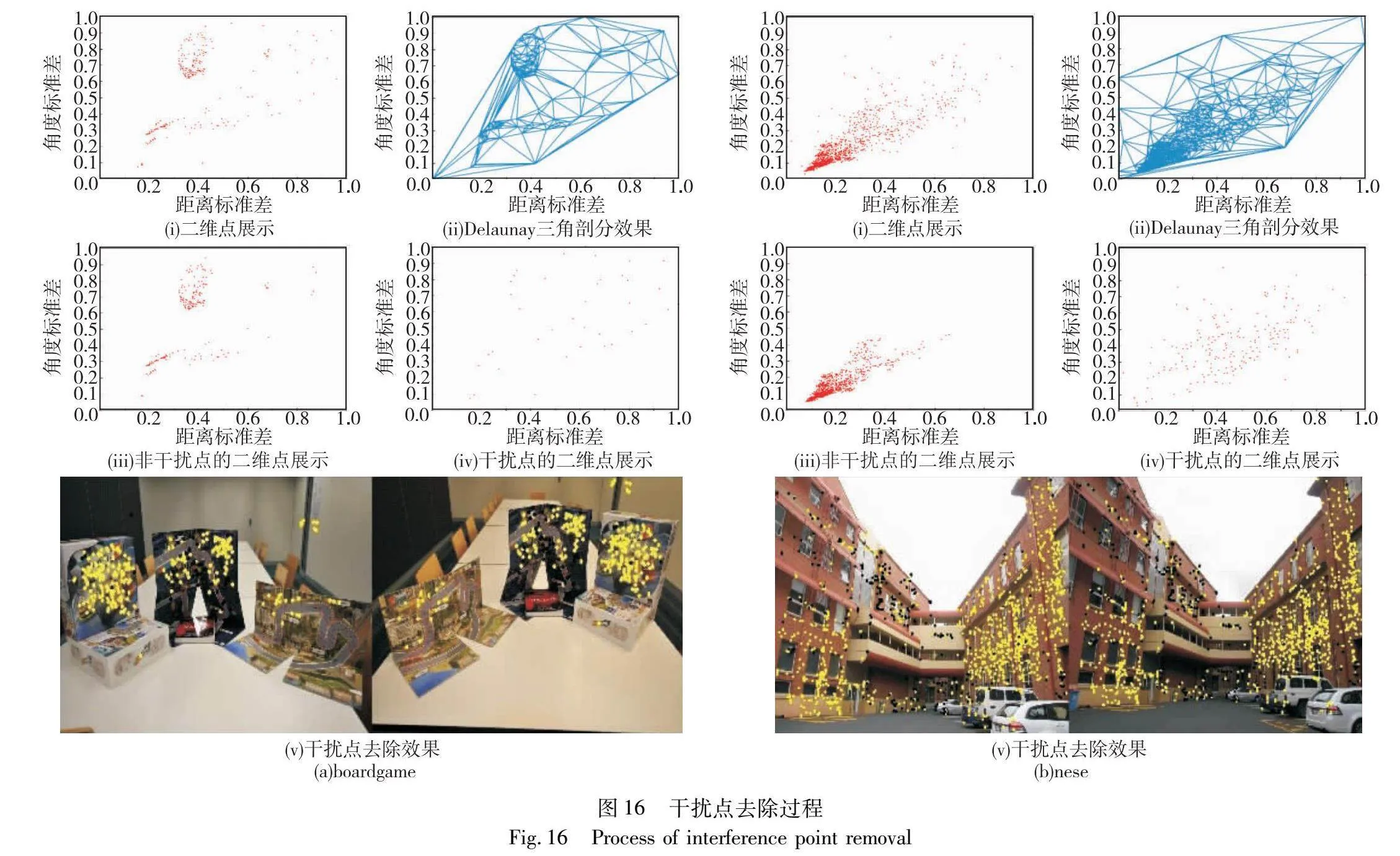
在Adelaidermf数据集中选取两组图像进行展示，boardgame是相同视角下多个物体的不同摆放，unihouse图像有视角差异。本文DIPR方法多次迭代估计局部近邻区域的匹配模型及其相应的内点集，统计各匹配点所属的内点集重心，进而得到匹配点所属的所有内点集重心之间的距离标准差和内点集重心相对于图像左上角的角度标准差。标准差反映数据的离散程度，根据两者所形成的二维点，反映各匹配点在迭代过程中所属内点集的变化。聚集的二维点在距离标准差和角度标准差方面更相似，因此所对应的匹配点是非干扰点的可能性更大。图16中横坐标为各匹配点所属的所有内点集重心的距离标准差，纵坐标为各匹配点所属的所有内点集重心相对于图像左上角的角度标准差。每组图像中图（i）为二维点展示图，图（ii）为Delaunay三角剖分的效果展示图，图（iii）为经本文所提方法处理后保留的二维点展示图，图（iv）为去除的干扰点的二维点展示图，图（v）为干扰点去除结果，黑色点是干扰点，黄色点是去除干扰点后的匹配点（参见电子版）。

图17展示其中两组图像有无干扰点去除步骤的聚集效果。sene图像中左右两个模型平面交界处的匹配对若存在，则其在后续聚集中可能属于左边的模型平面，也可能属于右边的模型平面；unihouse图像中存在梯状模型平面，各梯状模型平面交界处的匹配对在后续聚集中可能属于其他模型平面。本文DIPR方法将不同模型平面的匹配点动态移动，使不同模型平面内匹配点更加聚集，进而估计图像间存在的多个匹配模型，但干扰点的存在影响后续的多模型估计过程。通过图16、17可以看出，本文DIPR方法可以有效去除图像中可能属于多个匹配模型的匹配对，进而缓解同平面点聚集中干扰点的干扰。

2.3 多匹配模型估计的对比实验

AdaLAM、GMS和SuperGlue等算法可以找到图像间多个匹配模型的大部分内点，但无法对模型进行估计。PEARL、MCT、CONSAC和Sequential RANSAC等算法可以进行图像多匹配估计。Adelaidermf数据集中19对图像是多个或单个物体在不同视角下的室内图像，另外19对图像是不同建筑物的宽基线室外图像。现有图像多匹配模型估计算法的多模型匹配对错分问题出现在宽基线图像，因此本文选取Adelaidermf数据集内的19对宽基线室外图像进行对比实验。

图18为同模型点聚集效果图，可以看出AGSM方法可以提高同一模型平面匹配点的聚集程度。图19为Adelaidermf数据集中6组图像的不同匹配模型内点的效果，不同颜色匹配点为不同模型内点，可以看出AMPSM算法可以有效估计图像多匹配模型及其内点集。

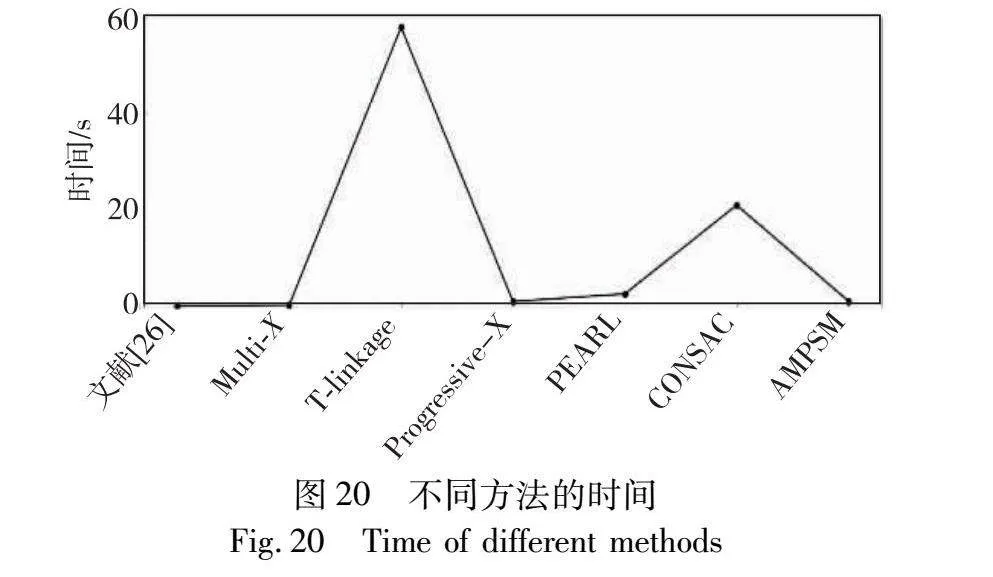
图20为Adelaidermf数据集中19组图像的不同多模型估计算法的平均运行时间。文献［18］通过PROSAC进行采样，利用MAGSAC++计算多个匹配模型，然后采用T-linkage算法将模型到模型的残差作为偏好向量的tanimoto距离，并在偏好向量的域中使用DBSCAN算法找到聚类以寻找相似的匹配模型，然后利用MAGSAC++计算相似匹配模型的内点集所符合的一个匹配模型。运行过程中寻找相似匹配模型及模型估计交叉迭代进行。Multi-X和PEARL算法通过最小能量函数聚集相同平面的匹配对，然后利用Mean Shift算法和α-expansion计算图像多匹配模型。T-linkage算法使用基于匹配对残差的偏好分析进行图像多匹配模型估计。Progressive-X算法通过迭代估计候选模型和候选模型优化以估计图像多匹配模型。

本文AMPSM算法在干扰点去除过程中通过多次迭代随机抽取近邻区域匹配对估计匹配模型，并回代以验证该模型是否为局部最优匹配模型，然后计算符合局部最优模型的内点集，根据多次迭代后每个匹配对的动态分布特征（匹配对所属内点集的平均距离及其与图像左上角的角度）去除干扰点，最后聚集同模型内点集，并使用基于高斯核的Mean Shift算法和RANSAC算法计算多匹配模型。上述步骤需要多次迭代得到每个匹配对的动态分布特征以去除干扰点，因此AMPSM方法的运行时间较长，处于中等水平。

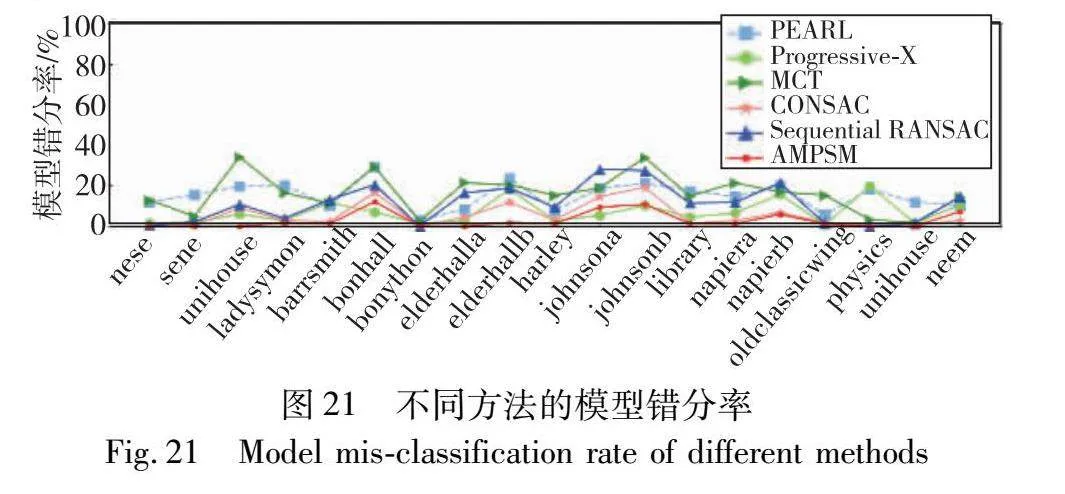
图21为Adelaidermf数据集中19对室外图像的多模型估计错分率，表2为不同方法匹配点模型错分率的对比结果，即模型估计中错分的匹配点所占的比例，包括平均错分率和平均错分标准差。部分数据来源于Florian Kluger关于CONSAC的论文。可以看出，由于建筑景物的各模型平面的变化相近，bonhall、elderhalla等图像间的多匹配模型估计相对较难，反之建筑景物的各模型平面的变化不相近，导致其余图像间的多匹配模型估计相对简单。通过图21可以看出，AMPSM算法与CONSAC效果较为接近，且这两个算法的多模型估计错分率低于其他四个算法。通过表2可以看出，AMPSM算法与CONSAC相比平均错分率有效降低45.50%以上，与文献［18］相比平均错分率有效降低8.39%。在模型平均错分标准差上可以看出，本文AMPSM算法位于第二，说明AMPSM算法有稳定的效果。

3 结束语

为降低多匹配模型错分率，提出了一种基于同模型匹配点聚集的图像多匹配模型估计算法（AMPSM）。该方法分为三步，分别对应本文提出的三个创新点。首先，为了提升匹配对集合的内点率，提出了一种基于近邻区域匹配点同分布的内点率提升方法；然后，为了提高多匹配模型估计的精度，定义了干扰点并提出了一种基于匹配点动态抽样分布特征的干扰点去除方法；最后，为了提高同模型匹配对的聚集程度并估计多匹配模型，提出了一种基于同模型匹配点聚集的多模型估计方法。将所提算法与RANSAC、PROSAC、MAGSAC++、GMS、SuperGlue、AdaLAM、OANet、CLNet、PREAL、MCT、Sequential RANSAC以及CONSAC等算法进行实验对比，结果表明所提算法的内点率提升30%以上，残留外点率降低61%以上，多模型估计的错分率降低8.39%以上。本文所提的基于匹配点动态抽样分布特征的干扰点去除方法通过多次迭代统计各匹配对的分布特征，运行时间较长，且本文算法为基于传统框架的图像多匹配模型估计算法。今后将围绕该问题且在本文方法的基础上引入图神经网络开展后续的研究。

参考文献：

［1］陈素雅， 何宏. 基于特征点动态选择的三维人脸点云模型重建［J］. 计算机应用研究， 2024， 41（2）： 629-634. （Chen Suya， He Hong. 3D face point cloud model reconstruction based on dynamic selection of feature points［J］. Application Research of Computers， 2024， 41（2）： 629-634.）

［2］Bian Jiawang， Lin Wenyan， Liu Yun， et al. GMS： grid-based motion statistics for fast， ultra-robust feature correspondence［J］. International Journal of Computer Vision， 2020， 128（6）： 1580-1593.

［3］Sun Weiwei， Jiang Wei， Trulls E， et al. ACNe： attentive context normalization for robust permutation-equivariant Learning［C］//Proc of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE Press， 2020： 11283-11292.

［4］Zhang Jiahui， Sun Dawei， Luo Zixin， et al. OANet： learning two-view correspondences and geometry using order-aware network［J］. IEEE Trans on Pattern Analysis and Machine Intelligence， 2022， 44（6）： 3110-3122.

［5］Sarlin P E， DeTone D， Malisiewicz T， et al. SuperGlue： learning feature matching with graph neural networks［C］//Proc of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE Press， 2020： 4937-4946.

［6］Zhao Chen， Ge Yixiao， Zhu Feng， et al. Progressive correspondence pruning by consensus learning［C］//Proc of IEEE/CVF International Conference on Computer Vision. Piscataway， NJ： IEEE Press， 2021： 6444-6453.

［7］Fischler M A， Bolles R C. Random sample consensus： a paradigm for model fitting with applications to image analysis and automated carto-graphy［J］. Communications of the ACM， 1981， 24（6）： 381-395.

［8］Chum O， Matas J. Matching with PROSAC-progressive sample consensus［C］//Proc of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE Press， 2005： 220-226.

［9］Barath D， Ivashechkin M， Matas J. Progressive NAPSAC： sampling from gradually growing neighborhoods［EB/OL］. （2019-06-05）［2023-12-04］. https：//arxiv.org/abs/1906.02295.

［10］Barath D， Noskova J， Ivashechkin M， et al. MAGSAC++， a fast， reliable and accurate robust estimator［C］//Proc of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE Press， 2020： 1301-1309.［11］Brachmann E， Rother C. Neural-Guided RANSAC： learning where to sample model hypotheses［C］//Proc of IEEE/CVF International Conference on Computer Vision. Piscataway， NJ： IEEE Press， 2019： 4321-4330.

［12］Tong Wei， Matas J， Barath D. Deep MAGSAC++［EB/OL］. （2022-03-11）［2023-12-04］. https：//arxiv.org/abs/2111.14093.

［13］Park Y H， Kwon O S. Multiple homographies estimation using a guided sequential RANSAC［J］. The Journal of the Korea Contents Association， 2010， 10（7）： 10-22.

［14］Isack H， Boykov Y. Energy-based geometric multimodel fitting［J］. International Journal of Computer Vision， 2012， 97（2）： 123-147.

［15］Barath D， Matas J. Multi-class model fitting by energy minimization and mode-seeking［C］//Proc of European Conference on Computer Vision. Cham： Springer， 2018： 229-245.

［16］Magri L， Fusiello A. Fitting multiple heterogeneous models by multi-class cascaded T-linkage［C］//Proc of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE Press， 2019： 7452-7460.

［17］Kluger F， Brachmann E， Ackermann H， et al. CONSAC： robust multi-model fitting by conditional sample consensus［C］//Proc of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE Press， 2020： 4633-4642.

［18］Barath D， Rozumnyi D， Eichhardt I， et al. Finding geometric models by clustering in the consensus space［C］//Proc of IEEE/CVF Confe-rence on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE Press， 2023： 5414-5424.

［19］Cavalli L， Larsson V， Oswald M R， et al. AdaLAM： revisiting handcrafted outlier detection［EB/OL］. （2020-06-07）［2023-12-04］. https：//arxiv.org/abs/2006.04250.

［20］Comaniciu D， Meer P. Mean shift： a robust approach toward feature space analysis［J］. IEEE Trans on Pattern Analysis and Machine Intelligence， 2002， 24（5）： 603-619.

［21］张晓闻， 任勇峰. 结合稀疏表示与拓扑相似性的图像匹配算法［J］. 计算机工程与应用， 2021， 57（8）： 198-203. （Zhang Xiaowen， Ren Yongfeng. Image matching algorithm combining spare representation and topological similarity［J］. Computer Engineering and Applications， 2021， 57（8）： 198-203.）

［22］魏若岩， 王俊峰， 朱晓庆. 基于图像匹配点全局拓扑分布的内点率提升算法［J］. 激光与光电子学进展， 2022， 59（10）： 169-182. （Wei Ruoyan， Wang Junfeng， Zhu Xiaoqing. Inliers ratio promotion algorithm based on global topological distribution of image matching points［J］. Laser & Optoelectronics Progress， 2022， 59（10）： 169-182.）

［23］甄国涌， 刘慧芳， 储成群. 基于局部保持匹配的改进图像匹配算法［J］. 激光杂志， 2022， 43（2）： 82-88. （Zhen Guoyong， Liu Huifang， Chu Chengqun. Improved image matching algorithm based on locality preserving matching［J］. Laser Journal， 2022， 43（2）： 82-88.）

［24］魏若岩， 霍思园， 朱晓庆. 图像非刚体匹配的多模型估计算法设计与实现［J］. 激光与光电子学进展， 2022， 59（12）： 407-419. （Wei Ruoyan， Huo Siyuan， Zhu Xiaoqing. Design and implementation of multimodel estimation algorithm for nonrigid matching images［J］. Laser & Optoelectronics Progress， 2022， 59（12）： 407-419.）

［25］Rocco I， Cimpoi M， Arandjelovic＇ R， et al. NCNet： neighbourhood consensus networks for estimating image correspondences［J］. IEEE Trans on Pattern Analysis and Machine Intelligence， 2022， 44（2）： 1020-1034.

［26］Barath D， Matas J. Progressive-X： efficient， anytime， multi-model fitting algorithm［C］//Proc of IEEE/CVF International Conference on Computer Vision. Piscataway， NJ： IEEE Press， 2019： 3780-3788.

［27］Barath D， Rozumny D， Eichhardt I， et al. Progressive-X+： clustering in the consensus space［EB/OL］. （2023-04-17）［2023-12-04］. https：//arxiv.org/abs/2103.13875v1.

［28］Lowe D G. Distinctive image features from scale-invariant keypoints［J］. International Journal of Computer Vision， 2004， 60（2）： 91-110.

［29］Zhao Muhan， Alimo S R， Beyhaghi P， et al. Delaunay-based derivative-free optimization via global surrogates with safe and exact function evaluations［C］//Proc of the 58th IEEE Conference on Decision and Control. Piscataway， NJ： IEEE Press， 2019： 4636-4641.

［30］Favreau J D， Lafarge F， Bousseau A， et al. Extracting geometric structures in images with Delaunay point processes［J］. IEEE Trans on Pattern Analysis and Machine Intelligence， 2020， 42（4）： 837-850.

［31］Affine covariant features［EB/OL］. （2007-07-15）［2023-12-04］. https：//www.robots.ox.ac.uk/～vgg/research/affine.

［32］Acute3D Aiguille du Midi MVS［EB/OL］.［2023-12-04］. http：//certis.enpc.fr/demos/stereo/Data/Aiguille/index.html.

［33］Executive Dean， Faculty of Sciences， Engineering and Technology. AdelaideRMF［EB/OL］. （2023-09-07）［2023-12-04］. https：//set.adelaide.edu.au/computer-and-mathematical-sci ences/.