基于SM9聚合签名局部可验证算法

摘 要：针对目前SM9签名方案生成的n条消息的签名占用较大存储空间的问题，提出了一种基于SM9算法的聚合签名方案。该方案使得验证多条签名的时间开销相较于原SM9方案有所降低，空间开销约为原SM9方案的66.7%。在此基础上，针对目前聚合签名算法在验证签名时，验证者仅需验证特定消息的正确性，但仍需知道完整消息列表的问题，提出了基于SM9聚合签名局部可验证方案。对于单个用户生成的n条消息的聚合签名S，签名者生成特定消息m的验证提示信息aux，验证者可以在不知道完整的消息列表的情况下，对消息m的签名正确性进行验证。理论与实验分析表明，该方案在给定聚合签名S的情况下，验证特定消息的时间复杂度为O（1）。

关键词：SM9； 聚合签名； 局部可验证

中图分类号：TP309.2 文献标志码：A

文章编号：1001-3695（2024）10-040-3160-06

doi：10.19734/j.issn.1001-3695.2023.11.0640

Aggregate signature local verifiability algorithm based on SM9

Du Jian Ma Limina，b，c

（a.School of Computer Science， b.Beijing Advanced Innovation Center for Future Blockchain & Privacy Computing， c.Beijing Laboratory of National Economic Security Early-warning Engineering， Beijing Information Technology University， Beijing 100101， China）

Abstract：This paper proposed an aggregate signature scheme based on the SM9 algorithm to address the issue of excessive storage space occupied by the signatures of n messages generated by the conventional SM9 signature scheme. This scheme reduced the time cost of verifying multiple signatures compared to the original SM9 scheme， with a space cost of about 66.7% of the original SM9 scheme. Furthermore， the scheme introduced a locally verifiable approach based on the SM9 aggregate signature to tackle the problem where validators need only verify the correctness of specific messages when verifying signatures in current aggregate signature algorithms but still require knowledge of the complete message list. For the aggregated signatures S of n messages generated by a single user， the signer generated verification tags for a specific message m， enabling the verifier to verify the correctness of the message’s signature without knowledge of the complete message list. Theoretical and experimental analysis confirm that the proposed scheme achieves a time complexity of O（1） for verifying specific messages given an aggregated signature.

Key words：SM9; aggregate signature; locally verifiable

0 引言

SM9算法[1]属于标识密码算法（identity-based cryptography，IBC）[2]的一种，在兼有IBC算法优点的同时，解决了公钥基础设施（public key infrastructure，PKI）[3]体系中证书管理和密钥托管的问题。SM9算法随着待签名消息数量的增加，验证签名的计算开销也会线性增长，导致在有大量数据待验证时，验签效率较为低下。理论上，使用SM9算法生成的单个签名大小为96 Byte，计算开销主要为椭圆曲线上的2次标量乘法运算和2次双线性配对运算。若签名个数为n，则n个签名的总大小为n×96 Byte，验签时需要执行n×2次椭圆曲线标量乘法运算和n×2次双线性配对运算，存储占用与计算开销均与签名个数呈正线性关系。为了解决上述问题，本文在SM9算法的基础上进行了改进，将单个用户生成的多条签名进行线性聚合，实现了一种基于SM9算法的聚合签名（aggregate signature，AS）方案。

在某些情况下，验证者仅需要对聚合签名中的特定消息进行验证，而无须验证所有消息，也不必获取完整的消息列表。但以往的聚合签名算法中，验签者通常需要验证所有签名才能确认特定签名的有效性，并且需要获取完整的消息列表，导致验签的时间复杂度为O（n），其中n是签名的数量。例如，在区块链交易中，聚合签名技术被用于减轻区块链交易数据传输负担，但交易中收款方的验证者往往只关心与自身相关的交易，当前的聚合签名算法在验签时要求验证者下载区块上的所有消息，并验证所有签名才能确认交易成功，这导致验签效率不高，降低了区块链网络交易的吞吐率。在进行区块链数据校验时，任何验证方均能获取所有交易信息，同样会存在隐私泄露的潜在风险。另一方面，用户访问互联网网站时，需要先与服务器建立连接，验证服务器身份，证书透明日志（certificate transparency logs，CT）技术用于在互联网上辅助验证身份。CT创建公共日志以记录证书颁发机构签发的所有证书，用户的浏览器在接收到来自网站的证书后，在继续建立连接之前会检查该证书是否存在于CT日志中。目前为了减轻CT日志的存储压力，使用聚合签名的技术将一组证书的签名合并成一个短小的聚合签名，并搭配一个紧凑的数据结构来存储消息列表。尽管用户的浏览器可能存储或下载了聚合签名，但在验证特定条目是否存在于日志中时仍需要下载所有条目，这导致在访问互联网时产生了不必要的网络开销。

针对上述问题，本文在实现SM9聚合签名算法的基础上，进一步提出了基于SM9聚合签名局部可验证算法。该算法使得验证方在验证签名时的时间成本大大降低，提升了签名的验证效率。同时采用了局部可验证技术，使得验证方在对聚合签名中特定明文消息进行验证时，无须获取所有消息明文，只需获取特定明文消息和一个简短提示即可验签，减轻了验证方的计算负担，并能降低数据传输的网络开销。

1 相关工作

聚合签名是一种数字签名的变体，它将多个签名合并成一个签名，从而减少签名数据的存储和传输成本，降低验证签名的计算开销。针对聚合签名技术，国内外学者做了大量研究。聚合签名的技术起源于2001年Boneh等人[4]提出的基于双线性映射的聚合签名方案，该方案将n个签名聚合成一个签名，但是要求所有的签名者使用相同的消息。2003年Boneh等人[5]提出了BGLS聚合签名方案，它允许不同的签名者使用不同的消息和公钥验证签名。在BGLS聚合签名之后，许多学者对聚合签名进行了进一步的研究和改进，主要集中在以下几个方面：

a）研究如何提高聚合签名的安全性，防止签名被伪造或窜改，如在标准模型下抵抗伪造攻击、在不可信环境下保证聚合签名的不可否认性等。周彦伟等人[6]针对基于证书的密码体制的泄露攻击问题，提出了基于证书的抗泄露签名机制，并使用离散对数困难性进行形式化证明，以确保其不可伪造性，同时维持较高的计算效率；杨忆欧等人[7]提出了一种支持并行密钥隔离的无证书聚合签名方案，采用并行密钥隔离机制和无证书椭圆曲线密码技术，通过定时更新参与签名用户的密钥，确保密钥前向和后向安全，同时降低了密码运算复杂度；游民国[8]通过设计三种基于量子隐形传态和叠加态原理的量子聚合签名方案，克服了传统聚合签名方案所依赖的经典密码学问题在量子计算崛起下面临的挑战，确保了签名的不可否认性、不可伪造性，并且能抵御纠缠测量攻击；周利峰[9]针对智慧医疗环境中的通信安全和隐私保护问题，设计了一种高效安全的无证书聚合签名方案，解决了智慧医疗中可能存在的公钥替换攻击、身份隐私泄露和数据完整性等问题。

b）研究如何提高聚合签名的签名验签效率，降低计算、存储和通信开销。郭瑞等人[10]提出了一种基于区块链的无双线性对的无证书聚合签名方案，解决了无线医疗传感网络中存储资源限制的问题，方案实现了医疗数据的高效聚合，扩展了区块链的存储性能，降低了计算和数据传输的开销；翟嘉祺等人[11]改进了序列聚合签名方案，通过消除先前方案中的一个随机预言机，实现了更高效的序列聚合签名，从而提高了聚合签名方案的效率；王竹等人[12]构建了一种基于双线性对的无证书有序聚合签名方案，以解决之前方案中因逐一验证签名导致整体计算时间过长的效率问题，该方案中多个用户按照一定的顺序对文件进行签名和认证生成聚合签名，验证者只需验证最终一个签名，即可确认签名顺序的正确性以及多个用户签名的合法性；唐飞等人[13]通过将聚合签名方法用于区块链共识机制中的消息验证，降低了共识过程中的验证复杂性，同时结合分布式密钥生成技术实现多中心的密钥授权机制，解决了密钥中心权限过大的问题；陈佳伟等人[14]提出了一种聚合签名的拜占庭容错算法，用于解决在联盟链中应用实用拜占庭容错共识算法时遇到的通信复杂度限制问题，通过改进实用拜占庭容错的信息交互方式和引入BLS签名，成功地将通信复杂度降低为O（n）；张博鑫等人[15]提出了一种可撤销的SM9标识签名算法，解决标识签名算法中存在的密钥撤销难题和SM9特殊结构导致技术无法完全适用的问题。该算法引入完全子树，使密钥中心能够快速实现对用户签名权限的撤销和更新操作。

c）研究如何扩展聚合签名的功能，将聚合签名技术与实际场景结合，如医疗、物联网、云计算、社交网络、电子投票等领域。安涛等人[16]针对车辆自组织网络中的车辆隐私泄露和繁琐的信息认证问题，提出了一种基于国产密码SM9算法的聚合签名方案，方案基于IBC密码体制，使用假名代替真实身份，有效地保护了车辆隐私信息，同时利用聚合签名技术提高了认证效率；刘琪等人[17]提出了一种基于BLS聚合签名技术的平行链共识算法优化方案，通过在平行链上对共识交易进行签名和聚合，有效解决了重复发送共识交易到主链的问题，减少了主链的存储空间占用，节省了交易手续费；周利峰等人[18]提出了一种基于区块链的无证书聚合签名方案，采用分布式哈希表存储机制，保障医疗数据的安全，实现了数据的去中心化存储，并通过智能合约技术实现身份认证，满足不可伪造性、可追踪性和匿名性等安全需求；张晓均等人[19]针对可穿戴设备上传的医疗数据的安全传输问题，提出了基于移动边缘服务计算的容错机制的医疗密态数据聚合方案，结合同态加密和聚合签名技术，确保医疗数据在传输过程中的机密性、完整性。

在2022年，Goyal等人[20]针对验证者在验证指定明文消息和聚合签名时仍需获取完整消息集合的问题，引入了局部可验证聚合签名的概念，以实现对聚合签名的高效验证。方案中新增了Local-Open、Local-Agg-Verify操作步骤，签名聚合方使用Local-Open生成短提示，而验证方则利用Local-Agg-Verify对聚合签名、短提示以及指定消息进行局部验证。通过这一方法，验证方在对聚合签名进行验证时不再需要获取整个消息集合，只需获取指定消息及其对应的短提示即可完成聚合签名的验证。此外，研究团队还提出了基于RSA和双线性对的两种局部可验证聚合签名的构造方案。

2 相关技术和算法

2.1 双线性映射

三个阶为素数N的加法循环群G1、G2和一个乘法循环群GT，群G1、G2的生成元分别为g1（另记为P1）、g2（另记为P2）。设有一个双线性映射e：G1×G2→GT满足如下关系：

a）双线性：a，b∈Z+，aP1∈G1，bP2∈G2，e（aP1，bP2）=ab*e（P1，P2）。

b）非退化性：Q1∈G1，Q2∈G2，e（Q1，Q2）≠1。

c）可计算性：P∈G1，Q∈G2，存在多项式时间内有效计算出e（P，Q）的算法。

2.2 Diffie-Hellman问题

Diffie-Hellman问题[21]是一个离散对数问题。任取一个λ-bits的大素数p，设G∈Zp是一个阶为素数q的加法循环群，其生成元为g。

2.2.1 CDH（computational Diffie-Hellman）问题

x，y∈Zp，输入g、gx、gy，在多项式时间内计算gxy是困难的。

2.2.2 SCDH（square computational Diffie-Hellman）问题

x∈Zp，输入g、gx，在多项式时间内计算gx2是困难的。

2.2.3 ICDH（inverse computational Diffie-Hellman）问题

x∈Zp，输入g、gx，在多项式时间内计算gx-1是困难的。

2.2.4 BIDH（bilinear inverse computational Diffie-Hellman）问题

三个阶为素数p的循环群G1、G2（生成元分别为g1、g2）、GT，存在一个非退化的双线性映射：e：G1×G2→GT，x∈Zp，给定g1、g2、gx1、gx2、e（g1，g2），在多项式时间内计算e（g1，g2）x-1是困难的。

2.3 签名方案概述

2.3.1 系统参数生成

定义大素数p，Fp为有限域，设g是椭圆曲线群的生成元，N是椭圆曲线的阶，H（）为哈希算法，e（.）为双线性对配对算法。

2.3.2 密钥生成

签名者生成随机数α∈Fp，α即为签名者私钥。

2.3.3 消息签名

给定消息m，签名者构造S=g1α+H（m）作为消息m的签名，且（α+H（m）） mod N≠0，则消息签名结果为（S，gα）。

2.3.4 消息签名验证

验证者获取签名（S，gα），计算H（m），并构造

e（S，gagH（m））=（g1α+H（m））（a+H（m））=g（1）

进行验签。

2.3.5 消息聚合签名

假设有n条消息m1，…，mn，则单个消息的签名为Si=g1α+H（mi）。将α视为变量，则存在一组γ1，γ2，…，γn，使得

∏ni1α+H（mi）=∑niγiα+H（mi）（2）

成立。因此可得聚合签名：S^=∏niSγii。消息聚合签名结果为（S^，{gai}），i∈（1，n）。

2.3.6 消息聚合签名验证

验证者收到聚合签名（S^，{gai}），i∈（1，n），已知：

∏ni=1（α+H（mi））=∑ni=0（βi×αi）（3）

则验证者构造：e（S^，g∑ni（βi×αi））=（g∏ni1α+H（mi））∏ni（α+H（mi））=g进行验签。当常数集合{hi}已知时，可计算出系数集合{βi}。进行签名验证时，需要将{gαi}包含在验证公钥中进行验签。

2.3.7 消息签名局部验证提示消息生成

签名者生成聚合签名（S^，{gai}），i∈（1，n），假设验证者只需要验证消息mj，则签名者需要生成mj的局部验证提示信息。由式（3）可得

∏ni=1（α+H（mi））=（α+H（mj））∏ni≠j（α+H（mi））=

α∏ni≠j（α+H（mi））+H（mj）∏ni≠j（α+H（mi））=∑n-1i=0（β0i×αi+1）+H（mj）∑n-1i=0（β1i×αi）（4）

则签名者生成auxj，1=∑n-1i=0（β0i×αi），auxj，2=∑n-1i=0（β0i×αi+1）两份提示信息。最终的聚合签名局部可验证签名结果为（S^，{gai}，auxj，1，auxj，2），i∈（1，n）。

2.3.8 消息聚合签名局部验证

验证者收到签名（S^，{gai}，auxj，1，auxj，2），i∈（1，n），验证：

e（S^，（gauxj，1）H（mj）gauxj，2）=e（g，g）是否成立，成立则验证通过。

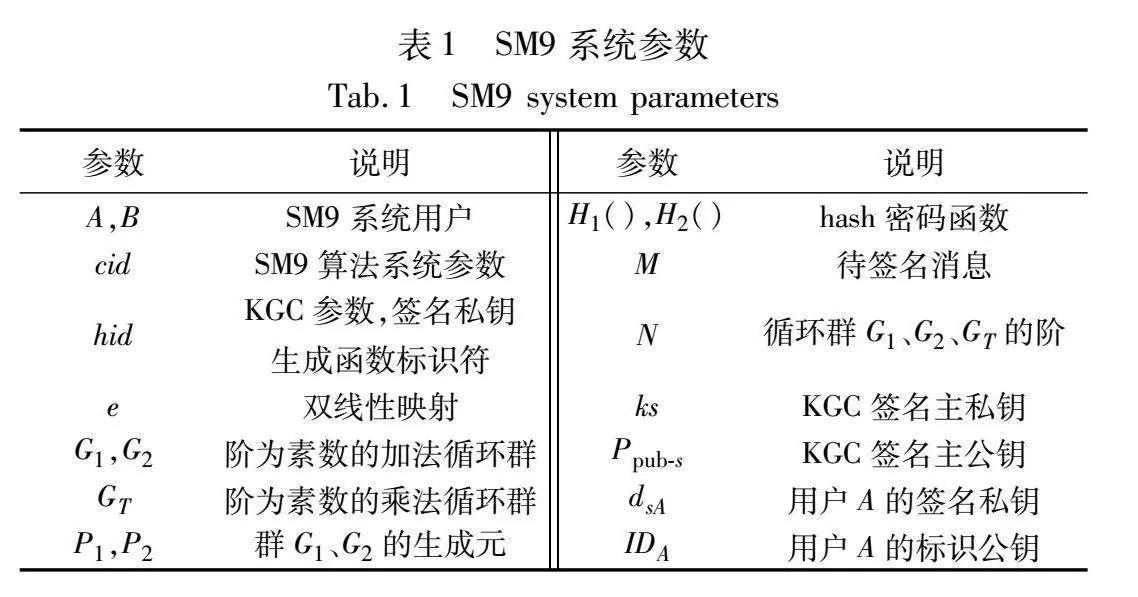
2.4 SM9系统参数

SM9系统使用的参数配置如表1所示。

3 基于SM9聚合签名局部可验证算法

本章将详细介绍基于SM9聚合签名局部可验证算法。算法包括密钥生成（Key-Gen）、消息签名（Sign）、消息签名验证（Verify）、消息聚合签名（Aggregate-Signature）、消息聚合签名验证（Aggregate-Verify）、消息聚合签名局部验证提示信息生成（Local-Open）、消息聚合签名局部验证（Local-Aggregate-Verify）七个部分。

3.1 密钥生成

设置SM9系统参数，KGC产生随机数ks∈［1，N-1］作为签名主私钥，计算G2中的元素Ppub-s=ks×P2作为签名主公钥，签名密钥对为（ks，Ppub-s）。KGC秘密保存ks，公开Ppub-s。

KGC选择并公开1 Byte表示的签名私钥生成函数识别符hid。用户A的标识为IDA，KGC计算t1=（H1（IDA‖hid，N）+ks） mod N。若t1=0，则需要重新产生主私钥ks，并计算和公开新的签名主公钥，更新已有用户的签名私钥；否则计算t2=（ks-1×t1） mod N，最后计算dsA=t2×P1。

以上所有计算由KGC完成，计算结果dsA发送给用户A。

3.2 消息签名

假设待签名消息为M，用户A计算以下数据：

a）产生随机数r∈［1，N-1］；

b）计算G2中的元素w=r×Ppub-s；

c）计算整数h=H2（M，N）；

d）计算整数l=（r+h） mod N，若l为0，则返回步骤a）；

e）计算群G1中的元素S=l-1×dsA；

f）消息M的签名为（w，S）。

3.3 消息签名验证

为检验收到的消息M及其数字签名（w，S）的正确性，验证者B计算以下数据：

a）计算整数h=H2（M，N）；

b）计算G2中的元素T=h×Ppub-s+w；

c）计算整数h1=H1（IDA‖hid，N）；

d）计算G2中的元素P3=h1×P2+Ppub-s；

e）根据式（1）验证e（S，T）=e（P1，P3）是否成立。若成立则验证通过；否则验证不通过。

3.4 消息聚合签名

假设有n条待签名的消息（M1，M2，…，Mn），用户A计算以下数据：

a）产生随机数r∈［1，N-1］；

b）计算G2中的元素：w=r×Ppub-s，w2=r2×Ppub-s，…，wn=rn×Ppub-s；

c）计算整数hmi=H2（Mi，N），i∈［1，n］；

d）计算整数li=（r+hmi）mod N，若li为0，则返回步骤a）；

e）计算群G1中的元素：S^=∏n（l-1i）×dsA；

f）消息（M1，M2，…，Mn）的聚合签名为（{wi}，S^）。

3.5 消息聚合签名验证

为检验收到的消息（M1，M2，…，Mn）及其聚合签名（{wi}，S^）的正确性，验证者B计算以下数据：

a）计算整数hmi=H2（Mi，N），i∈［1，n］；

b）已知{hmi}，根据式（3）计算出系数{βi}；

c）计算整数h1=H1（IDA‖hid，N）；

d）计算G2中的元素P3=h1×P2+Ppub-s；

e）验证e（S^，∑ni=0（βi×wi））=e（P1，P3）是否成立，若成立则验证通过；否则验证不通过。

3.6 消息聚合签名局部验证提示信息生成

假设用户A为消息（M1，…，Mj-1，Mj，Mj+1，…，Mn）生成了聚合签名（{wi}，S^），验证者B仅需要验证消息Mj的正确性，则用户A计算：

a）产生随机数r∈［1，N－1］；

b）计算G1中的元素K=r×P1；

c）计算G2中的元素：w=r×Ppub-s，w2=r2×Ppub-s，…，wn=rn×Ppub-s；

d）计算整数hmi=H2（Mi，N），i∈［1，n］，i≠j；

e）已知{hmi|i≠j}，根据式（3）计算出系数{βi}；

f）计算群G2中的元素：auxj，1=∑n-1i=0（βi×wi），auxj，2=∑n-1i=0（βi×wi+1）；

g）签名消息为（K，S^，auxj，1，auxj，2）。

3.7 消息聚合签名局部验证

假设用户A为消息（M1，…，Mj－1，Mj，Mj+1，…，Mn）生成了聚合签名（K，S^，auxj，1，auxj，2），验证者B仅需要验证消息Mj，验证者B计算如下数据：

a）计算整数hmj=H2（Mj，N）；

b）计算整数h1=H1（IDA‖hid，N）；

c）计算G2中的元素P3=h1×P2+Ppub-s；

d）验证e（K，auxj，1）=e（P1，auxj，2）是否成立，若不成立则验证不通过；

e）验证e（S^，auxhmjj，1×auxj，2）=e（P1，P3）是否成立。若成立则验证通过；否则验证不通过。

4 正确性与安全性分析

4.1 正确性分析

4.1.1 消息签名验证方案正确性分析

e（S，T）=e（l-1×dsA，h×Ppub-s+w）=

e（1r+h×ks－1×（h1+ks）×P1，（r+h）×ks×P2）=

1r+h×ks－1×（h1+ks）×（r+h）×ks×e（P1，P2）=

（h1+ks）×e（P1，P2）=e（P1，P3）（5）

根据签名的验证结果可知，消息签名与消息签名验证方案满足正确性要求。

4.1.2 消息聚合签名验证方案正确性分析

e（S^，∑ni=0（βi×wi））=

e（S^，∑ni=0（βi×ri×Ppub-s））=

e（S^，ks×（β0×r0+β1×r1+…+βn×rn）×P2）=

e（S^，ks×∏ni（r+hmi）×P2）=

e（ks-1×（h1+ks）×∏ni（1r+hmi）×P1，ks×∏ni（r+hmi）×P2）=

ks-1×（h1+ks）×∏ni（1r+hmi）×ks×∏ni（r+hmi）×e（P1，P2）=

（h1+ks）×e（P1，P2）=e（P1，P3）（6）

根据签名的验证结果可知，消息聚合签名与消息聚合签名验证方案满足正确性要求。

4.1.3 聚合消息局部验证方案正确性分析

e（S^，auxhmjj，1×auxj，2）=

e（S^，hmj×auxj，1+r×auxj，1）=

e（S^，（r+hmj）×auxj，1）=

e（S^，（r+hmj）×∑n-1i=0（βi×wi））=

e（S^，∑ni=0（βi×wi））=e（P1，P3）（7）

根据签名的验证结果可知，消息聚合签名局部验证提示信息生成与消息聚合签名局部验证方案满足正确性要求。

4.2 安全性分析

定理1 如果求解ICDH问题是困难的，则本方案是随机预言模型安全的。

证明 由ICDH问题可知，x∈Zp，输入g、gx，在多项式时间内计算gx-1的难度与解决DLP问题难度相当，故而在给定Ppub-s=ks×P2的前提下，在多项式时间内计算出ks-1×P2是困难的，进而无法求出ks-1。

1）系统建立阶段

挑战者B根据Key-Gen密钥生成算法生成系统参数。

2）询问阶段

H2询问：挑战者B生成消息m，发送给攻击算法A，A返回给挑战者B消息m的哈希值H2（m）。

签名询问：挑战者B生成m，发送给攻击算法A，A返回m的有效签名（w，S）给挑战者B。

3）伪造阶段

假设敌手能成功找出哈希函数的碰撞，挑战者B可获取诚实的算法A在不改变随机数r的情况下所产生的签名S1、S2，其中：

S1=l-11×dsA=1（r+h1）×ks-1×（ks+hid）×P1（8）

S2=l-12×dsA=1（r+h2）×ks-1×（ks+hid）×P1（9）

敌手γ计算：

S1-S2=（1（r+h1）-1（r+h2））×ks-1×（ks+hid）×P1（10）

敌手γ想找出一组r、h1、h2，使得：

1（r+h1）-1（r+h2）=1 mod N（11）

假设δ=r+h1，h2=h1+θ，r+h2=δ+θ，那么：

1（r+h1）-1（r+h2）=1δ-1δ+θ=1

θδ×（δ+θ）=1

δ=－θ±θ2+4×θ2∈［1，N－1］

r+h1=δ=－θ±θ2+4×θ2

r=－θ±θ2+4×θ2-h1（12）

等式右边仅和h1、h2的值相关，挑战者B可找到hash函数碰撞，因此可以在选择密文攻击的情况下，构造上述等式，使得式（12）成立，进而获取签名私钥r。

综上所述，若攻击算法A可以在多项式时间内求出ks-1，则挑战者B可以在多项式时间内攻破ICDH问题，所以若ICDH问题无法在多项式时间内被攻破，则攻击算法A无法在多项式时间内求出ks-1。

5 算法效率分析

假设n条签名进行了聚合。国密SM9算法签名验证时间的复杂度如表2所示。

假设n条签名进行了聚合。基于SM9的局部可验证签名验签算法的时间复杂度如表3所示。

从表2和3可以看出，原SM9算法在验证多条签名消息时，ECC点乘操作、ECC点加法操作和双线性配对操作时间复杂度为O（n）。改进后的算法在验证聚合签名消息时，时间复杂度为O（n）；验证某一条特定消息的签名时，验证签名的时间复杂度为O（1），验证效率非常高。

下面将对基于SM9的签名方案与几种性能较好的方案进行对比。表4列举了几种现存的聚合签名方案，主要对消息签名验证和消息聚合签名验证的效率进行对比，其中B表示双线性对运算，M表示椭圆曲线标量乘法运算，“—”表示没有此功能，n表示签名数量。

假设n条签名进行了聚合，SM9算法和基于SM9聚合签名局部可验证算法生成的签名，其空间复杂度结果如表5所示。

从表5可以看出，本方案相较于原SM9算法，签名数据占用空间有一定的减少，在签名消息条数为n，ECC点不进行压缩的情况下，本方案生成的签名所占空间与原SM9算法生成的签名所占空间，比值约为512×n512×n+256×n≈66.7%。在仅需验证某一条特定消息时，签名数据仅占用常数大小的空间。

6 实验分析

本方案使用国家密码标准SM9推荐的椭圆曲线构建，基于GmSSL密码库编写代码。CPU为AMD Ryzen 5 PRO 4650G；操作系统为Unraid 6.11.5，在虚拟机中安装Ubuntu20.04；编程语言版本为Python3.11.2，GCC版本为12.2.0。

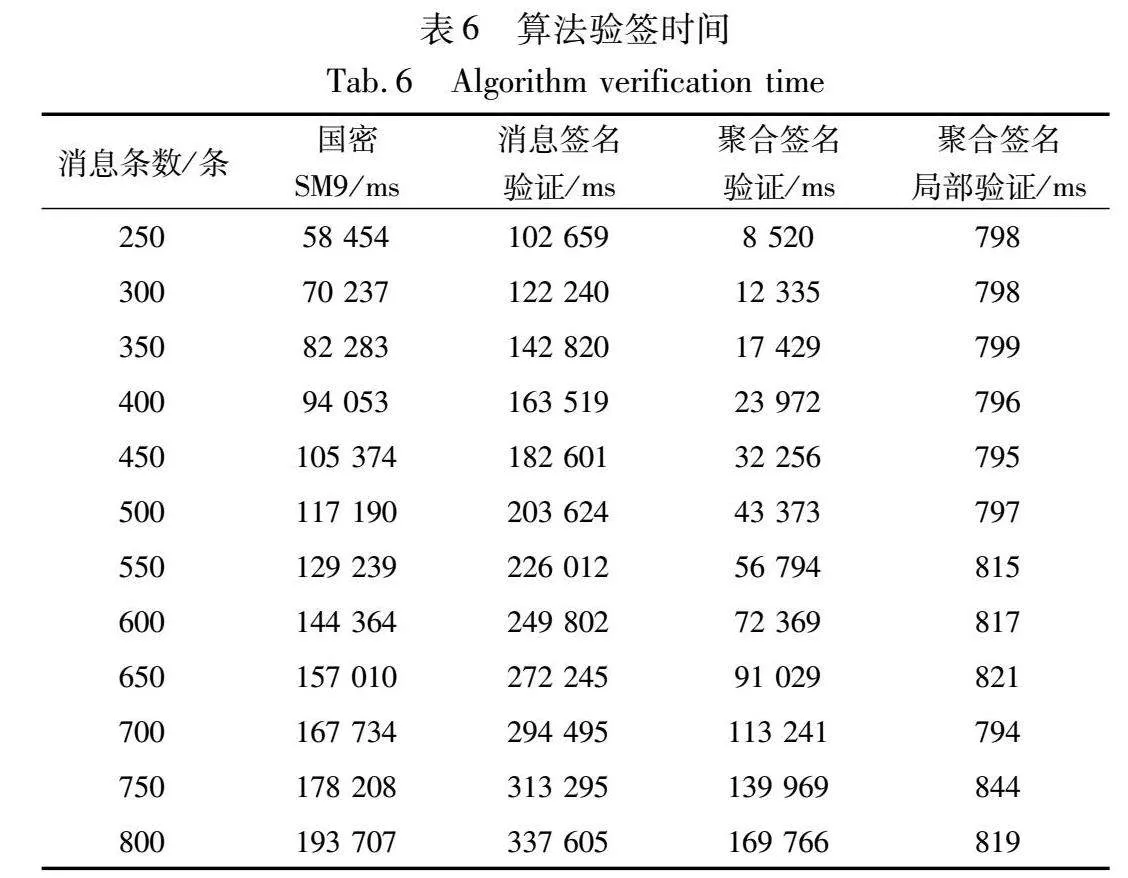
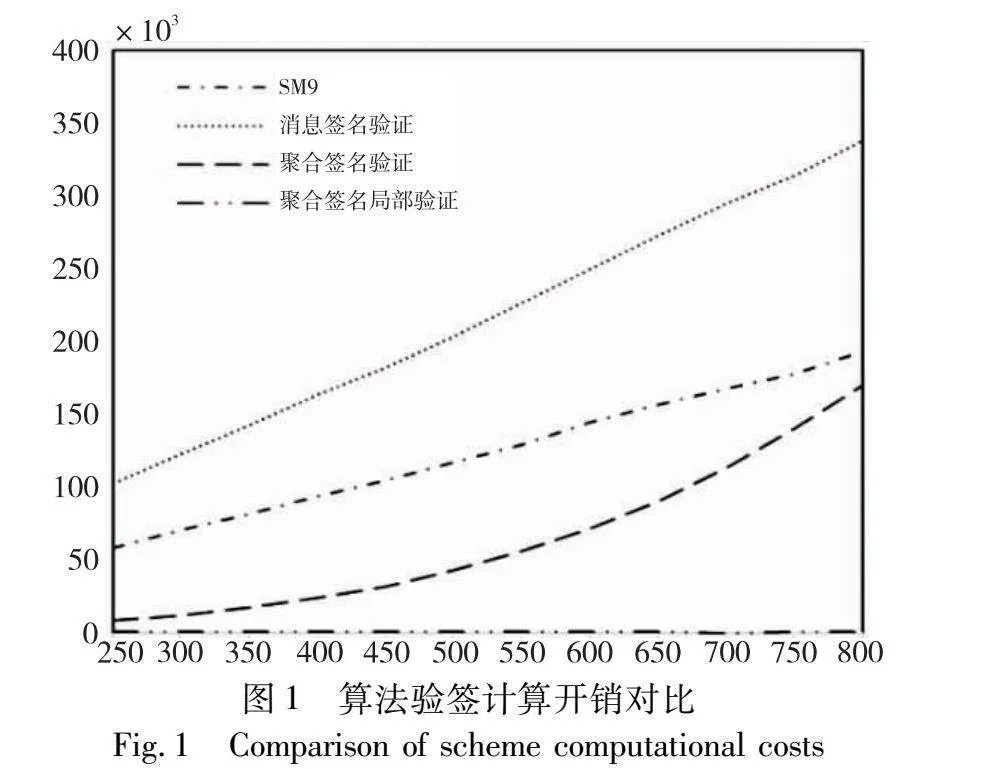
实验方法：使用SM9算法生成一条签名，对其进行n次签名验证操作；使用本方案的消息签名算法生成一条签名，并对其进行n次签名验证操作；使用本方案的消息聚合签名算法生成n条消息的签名，对已经生成的聚合签名进行验证操作；使用本方案的消息聚合签名算法生成n条消息的签名，选择其中一条特定消息，使用消息聚合签名局部验证提示信息生成算法生成特定消息的验签提示信息，并对其进行验证操作。方案未进行多线程优化，实验消息条数分别为250，300，350，400，450，500，600，700，800。实验记录各个算法计算耗时，单位为毫秒（ms）。实验结果如表6和图1所示。

由表6与图1可以看出，SM9算法验证多条消息计算开销时间复杂度为O（n）；消息签名验证算法验证多条消息计算开销时间复杂度为O（n）；聚合签名验证算法验证多条消息的聚合签名时，其计算开销小于SM9算法计算开销；聚合签名局部验证算法验证聚合签名中某一条消息的计算开销，其时间复杂度恒定为O（1），约为800 ms。实验结果符合预期。

7 结束语

本文介绍了聚合签名技术研究方向，指出其在节省签名存储成本、提高验证效率和保护隐私方面的潜力，并分析了目前聚合签名算法存在的问题，即验证签名时需要知道所有消息。针对这一问题，本文提出了基于SM9算法的聚合签名方案，并引入了局部可验证签名的机制，允许验证者可以仅对聚合签名中特定消息的签名进行验证，而无须验证所有消息的签名。但当前的算法仅能够满足单一用户对一组消息进行签名的需求，无法适应多用户协作或多方计算场景。因此，未来的研究方向需要对算法进行进一步改进，以支持多用户之间的协同签名操作，提升算法的适用性和实用性。

参考文献：

[1]GM/T 0044—2016， SM9标识密码算法[S]. 2016. （GM/T 0044， 2016， SM9 identity-based cryptographic algorithm[S]. 2016.）

[2]TellenbachB.Identity-based cryptography[M]. [S.l.]： IOS Press， 2009.

[3]林璟锵， 荆继武， 张琼露， 等. PKI技术的近年研究综述[J]. 密码学报， 2015， 2（6）： 487-496. （Lin Jingqiang， Jing Jiwu， Zhang Qionglu， et al. Recent advances in PKI technologies[J]. Journal of Cryptologic Research， 2015， 2（6）： 487-496.）

[4]Boneh D， Lynn B， Shacham H. Short signatures from the Weil pairing[C]//Proc of International Conference on the Theory and Application of Cryptology and Information Security. Berlin： Springer， 2001： 514-532.

[5]Boneh D， Gentry C， Lynn B，et al. Aggregate and verifiably encrypted signatures from bilinear maps[C]//Proc of International Conference on Theory and Applications of Cryptographic Techniques. Berlin： Springer， 2003： 416-432.

[6]周彦伟， 马岿， 乔子芮，等. 基于证书的抗连续泄露签名机制[J]. 计算机学报， 2022， 45（11）： 2363-2376. （Zhou Yanwei， Ma Kui， Qiao Zirui， et al. Certificate-based signature scheme with continuous leakage resilience[J]. Chinese Journal of Computers， 2022， 45（11）： 2363-2376.）

[7]杨忆欧， 彭长根， 丁红发，等. 一种支持并行密钥隔离的无证书聚合签名方案[J]. 计算机技术与发展， 2022， 32（11）： 106-114. （Yang Yiou， Peng Changgen， Ding Hongfa， et al. A certificateless aggregation signature scheme supporting parallel key-isolated[J]. Computer Technology and Development， 2022， 32（11）： 106-114.）

[8]游民国. 基于量子隐形传态的量子聚合签名方案研究[D]. 西宁：青海师范大学， 2023. （You Minguo. Research on quantum aggregated signature scheme based on quantum teleportation[D]. Xining：Qinghai Normal University， 2023.）

[9]周利峰. 面向智慧医疗的无证书聚合签名方案研究[D]. 扬州：扬州大学， 2023. （Zhou Lifeng. Research on certificateless aggregate signature schemes for smart healthcare[D]. Yangzhou：Yangzhou University， 2023.）

[10]郭瑞， 陈宇霜， 郑东. 无线医疗传感网络中基于区块链的高效无证书聚合签名方案[J]. 信息网络安全， 2020， 20（10）： 6-18. （Guo Rui， Chen Yushuang， Zheng Dong. A blockchain-based efficient certificateless aggregate signature scheme for wireless medical sensor networks[J]. Netinfo Security， 2020， 20（10）： 6-18.）

[11]翟嘉祺， 刘建， 陈鲁生. 高效的基于陷门置换的可延迟验证聚合签名（英文）[J]. 南开大学学报： 自然科学版， 2021， 54（1）： 54-63. （Zhai Jiaqi， Liu Jian， Chen Lusheng. Efficient SAS scheme with lazy verification from TDPs[J]. Acta Scientiarum Naturalium Universitatis Nankaiensis： Natural Science Edition， 2021， 54（1）： 54-63.）

[12]王竹， 杨思琦， 李凤华，等. 高效可证明安全的无证书有序聚合签名方案[J]. 通信学报， 2022， 43（5）： 58-67. （Wang Zhu， Yang Siqi， Li Fenghua， et al. Efficient and provably-secure certificateless sequential aggregate signature scheme[J]. Journal on Communications， 2022， 43（5）： 58-67.）

[13]唐飞， 刘文婧， 冯卓，等. 支持多中心聚合签名的实用性拜占庭容错改进方案[J]. 重庆邮电大学学报： 自然科学版， 2022， 34（4）： 705-711. （Tang Fei， Liu Wenjing， Feng Zhuo， et al. Improved scheme of practical Byzantine fault tolerance based on multi-authority aggregated signature[J]. Journal of Chongqing University of Posts and Telecommunications： Natural Science Edition， 2022， 34（4）： 705-711.）

[14]陈佳伟， 冼祥斌， 杨振国， 等. 结合BLS聚合签名改进实用拜占庭容错共识算法[J]. 计算机应用研究， 2021， 38（7）： 1952-1955，1962. （Chen Jiawei， Xian Xiangbin， Yang Zhenguo， et al. Improved practical Byzantine fault tolerant consensus algorithm combined with BLS aggregating signature[J]. Application Research of Computers， 2021， 38（7）： 1952-1955，1962.）

[15]张博鑫， 耿生玲， 秦宝东. 高效的可撤销SM9标识签名算法[J]. 计算机应用研究， 2022， 39（9）： 2837-2842，2849. （Zhang Boxin， Geng Shengling， Qin Baodong. Efficient revocable SM9 identity-based signature algorithm[J]. Application Research of Compu-ters， 2022， 39（9）： 2837-2842，2849.）

[16]安涛， 马文平， 刘小雪. VANET中基于SM9密码算法的聚合签名方案[J]. 计算机应用与软件， 2020， 37（12）： 280-284，321. （An Tao， Ma Wenping， Liu Xiaoxue. Aggregated signature scheme based on SM9 cryptographic algorithm in VANET[J]. Computer Applications and Software， 2020， 37（12）： 280-284，321.）

[17]刘琪， 郭荣新， 蒋文贤， 等. 基于BLS聚合签名技术的平行链共识算法优化方案[J]. 计算机应用， 2022， 42（12）： 3785-3791. （Liu Qi， Guo Rongxin， Jiang Wenxian， et al. Parallel chain consensus algorithm optimization scheme based on Boneh-Lynn-Shacham aggregate signature technology[J]. Journal of Computer Applications， 2022， 42（12）： 3785-3791.）

[18]周利峰， 殷新春， 宁建廷. 一种适用于无线医疗传感器网络的基于区块链的无证书聚合签名方案[J]. 小型微型计算机系统， 2022， 43（6）： 1128-1135. （Zhou Lifeng， Yin Xinchun， Ning Jian-ting. Blockchain-based certificateless aggregated signature scheme for wireless medical sensor networks[J]. Journal of Chinese Compu-ter Systems， 2022， 43（6）： 1128-1135.）

[19]张晓均， 张经伟， 黄超，等. 可验证医疗密态数据聚合与统计分析方案[J]. 软件学报， 2022， 33（11）： 4285-4304. （Zhang Xiaojun， Zhang Jingwei， Huang Chao， et al. Verifiable encrypted medical data aggregation and statistical analysis scheme[J]. Journal of Software， 2022， 33（11）： 4285-4304.）

[20]Goyal R， Vaikuntanathan V. Locally verifiable signature and key aggregation[C]//Proc of Annual International Cryptology Conference. Cham： Springer， 2022： 761-791.

[21]Bao Feng， Deng R H， Zhu Huafei. Variations of Diffie-Hellman problem[C]//Proc of International Conference on Information and Communications Security. Berlin： Springer， 2003： 301-312.

[22]赵楠， 章国安， 谷晓会. VANET中隐私保护的无证书聚合签名方案[J]. 计算机工程， 2020， 46（1）： 114-120，128. （Zhao Nan， Zhang Guoan， Gu Xiaohui. Certificateless aggregate signature scheme for privacy protection in VANET[J]. Computer Engineering， 2020， 46（1）： 114-120，128.）

[23]王大星， 滕济凯. 车载传感网中基于聚合签名的认证方案[J]. 吉林大学学报： 理学版， 2018， 56（3）： 657-662. （Wang Daxing， Teng Jikai. Authentication scheme based on aggregate signature in VSNs[J]. Journal of Jilin University： Science Edition， 2018， 56（3）： 657-662.）

[24]刘二根， 王露， 易传佳，等. 基于聚合签名的变电终端数据安全传输[J]. 计算机工程与设计， 2019， 40（7）： 1809-1815. （Liu Ergen， Wang Lu， Yi Chuanjia，et al. Data security transmission of substation based on aggregate signature[J]. Computer Engineering and Design， 2019， 40（7）： 1809-1815.）