理想格上强指定验证者的可截取签名方案

摘 要：现存的大多数可截取签名方案具有公开验证性，但在某些情况下可能会导致签名者的隐私泄露。为提高安全性，并使签名方案具有抗量子性，基于理想格上的ring-SIS问题，结合强指定验证者签名方案，提出一种新型的可截取签名方案。该方案采用均匀采样的异常中止技术，能够抵抗侧信道攻击。同时，证明了该方案的安全性和正确性。相较于其他方案，该方案在安全性、重复次数和签名尺寸等方面都表现出明显的优势。

关键词：可截取签名； 强指定验证者签名； 理想格； ring-SIS

中图分类号：TP391 文献标志码：A

文章编号：1001-3695（2024）10-038-3149-06

doi：10.19734/j.issn.1001-3695.2024.01.0011

Strongly specifying verifier’s interceptable signature scheme on ideal lattice

Wang Yu1， Chen Huiyan1， Wang Ke1， Xin Hongcai1， Wang Qingnan1， Yao Yunfei2

（1.Dept. of Electronic & Communication Engineering， Beijing Electronic Science & Technology Institute， Beijing 100070， China; 2.School of Cyberspace Security， Beijing University of Posts & Telecommunications， Beijing 100876， China）

Abstract：Most of the existing content extraction signature schemes publicly verify signatures， but in some cases， they may compromise the signer’s privacy. To enhance security and render the signature scheme resistant to quantum attacks， this paper proposed a new interceptable signature scheme based on the ring-SIS problem on the ideal lattice and integrated it with the strong specified verifier signature scheme. The scheme employed the anomaly abort technique of uniform sampling， capable of thwarting side-channel attacks. Additionally， this paper validated the security and correctness of the scheme. Compared to other schemes， this scheme exhibits clear advantages in security， number of repetitions， and signature size.

Key words：content extraction signature; strong designated verifier signature; ideal lattice; ring-SIS

0 引言

可截取签名是指无须与签名者互动的情况下，删除已签署数据中的敏感信息，并为截取后的数据生成有效签名。2001年，Steinfeld等人［1］最先阐述了可截取签名（content extraction signatures，CES）方案。2019年，文献［2］结合可截取签名提出了一种可被修改签名方案，该方案提出修改容忍度的概念，扩展了数字签名方案的同时，还保证了可修改签名的隐私。文献［3］提出了一种前向安全的可截取签名方案，通过固定公钥，不断变化私钥的方式确保安全，但是依赖复杂的双线性对运算。2017年，Ma等人［4］提出具有细粒度单调修订控制的可截取签名方案。2019年，Liu 等人［5］提出门限型的可截取签名方案，限制了可删除数据块数量的阈值。

指定验证者签名（designated verifier signature，DVS）［6］是指只有被指定的验证者才有权验证签名的正确性。然而，若签名在传递至验证者之前被敌手截获，敌手将获悉签名源自签名者而非验证者。为了抵抗此类攻击，1996年Jakobsson等人［7］第一次阐述强指定验证者签名（strong designated verifier signatur，SDVS）。2003年，Saeednia等人［8］利用Schnorr签名等方案设计了一个SDVS方案，该方案在签名验证过程中结合了验证者的私钥，从而满足强指定验证者签名方案的安全性要求。Wang等人［9］在2012年提出了第一个基于格的强指定验证者签名方案。文献［10］在2019年提出了一种高效的SDVS方案，该方案基于环上的小整数解（R-SIS）问题，并对其安全性进行了证明。

格密码具有抵抗量子计算攻击、实现简单高效等优点，是目前应用比较广泛的后量子密码之一。Goldreich等人［11］在1997年提出了基于格的数字签名方案。此后，格签名一直是数字签名领域研究的热点。特别是，在美国国家标准与技术研究院（National Institute of Standards and Technology，NIST）经过三轮严格评选后，公布了首批三种后量子签名标准算法［12］，基于格的方案占据两个席位。

目前存在的可截取签名方案，大多数都具备公开验证性，即所有拿到签名的个体都有权利验证签名的有效性，这在某些情况下会泄露签名者的隐私［13］。而且由于现存的可截取签名方案大多建立在传统数论难题之上，所以不具备抵抗量子攻击的能力。本文结合可截取签名方案和强指定验证者签名方案，在理想格上设计出一个强指定验证者的可截取签名方案（ideal lattice-based strongly designated verifier extractable signature scheme，VES），不仅可以实现对数据的替换、删除、整合等合理操作［14］，而且可以更好地保护签名者的隐私，同时还具有抵抗量子攻击的能力。VES在Fiat-Shamir签名框架的基础之上，结合均匀采样的异常中止技术，相比于现有方案，在签名尺寸、重复次数以及安全性等方面均具有较高的优势。此外，VES能够抵抗侧信道攻击。

在基于区块链的共享电子病历系统中，由于区块链中数据是公开的，如果直接上链存储，会导致隐私泄露［15］。而且，患者去不同的医院就医时，希望透露的信息各不相同［16］。同时，为了更好地保护患者的隐私权，医生查看电子病历时需要向患者提出申请［17］。VES就可以很好地解决此类问题。比如患者A去医院C就诊，患者A可以提供历史就诊医院B签发的电子病历。然而电子病历中涵盖了家庭住址、身份证号码、联系电话以及患者过往治疗记录等隐私信息，患者A不愿向医院C透露家庭住址等信息。那么医院B在签发电子病历时就可以使用VES进行签名。然后，患者A可以对电子病历进行适当的删改操作，然后将删改后的文件及签名提供给医院C。在提出申请的医生列表中，只有被患者A指定的医生才有权解密此电子病历。

1 预备知识

1.1 符号

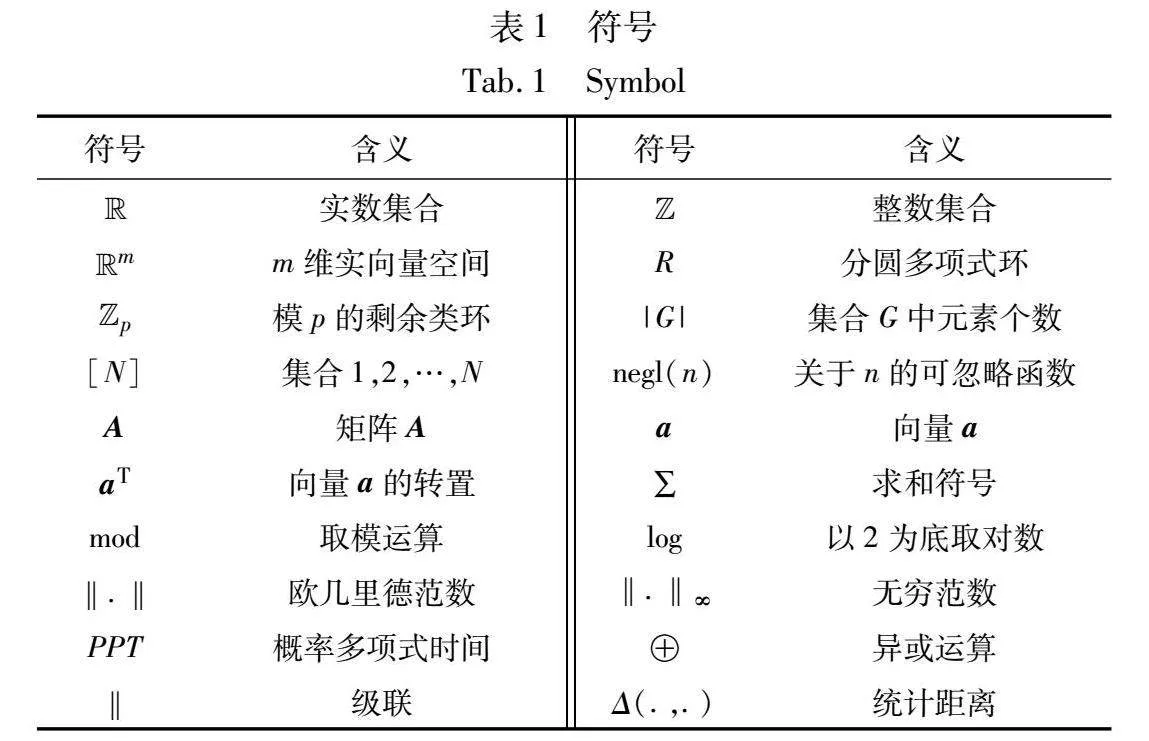
表1给出本文中所使用的符号及其含义。

1.2 格与理想格

定义1 设B=b1，b2，…，bn是向量空间Euclid ExtraaBpm上n个线性无关的向量，则由B生成的格Λ定义为

Λ=Euclid Math OneLAp（B）={∑ni=1xibi：xi∈Euclid ExtrabBp}

其中：称B为Λ的一组基。m表示格的维数，而n表示格的秩。当m=n时，该格被称为满秩格。

定义2 设Euclid ExtrabBp［x］是全体整系数多项式构成的多项式环，给定次数为n的分圆多项式f（x）∈Euclid ExtrabBp［x］，R=Euclid ExtrabBp［x］/（f（x））为分圆多项式环。给定素数q=1 mod 2n，Rq=R/qR=Euclid ExtrabBpq［x］/（f（x））为模f（x）和q的整数多项式环。

本文所采用的多项式环均为R=Euclid ExtrabBp［x］/（xn+1），其中n取2的幂次。

定义3 标准格是由一组格基构成的，而理想格充分使用了理想格基的循环性，一个主格基就可构成。理想格与多项式环Euclid ExtrabBp［x］/f（x）相对应。

定义4 设q是一个素数，可以定义多项式环上模格如下：

Λq（a）={e∈Euclid ExtraaBpm，s.t. s∈Rq，s.t.aTs=e（mod q）}

Λ⊥q（a）={e∈Euclid ExtraaBpm，s.t. ae=0（mod q）}

Λuq（a）={e∈Euclid ExtraaBpm，s.t. ae=u（mod q）}

1.3 离散高斯分布

定义5 对任意正实数s，向量c∈Euclid ExtraaBpn，n维高斯函数定义为：ρ（x）=exp（-π（‖x-c‖/s）2），x∈Euclid ExtraaBpn。

定义6 对任意正实数s，向量c∈Euclid ExtraaBpn，n维格Λ上的离散高斯分布被定义为DΛ，s，c（x）=ρ（s，c）（x）ρ（s，c）（Λ），x∈Λ

1.4 ring-SIS

定义7 环上小整数解问题（ring shortest interger solution，ring-SISn，m，q，β）［18，19］。给定正整数m、q，实数β和向量a=（a1，a2，…，am）T∈Euclid ExtraaBpmq，找到一个小系数的非零多项式向量x=（x1，x2，…，xm）T∈Euclid ExtraaBpm，满足

aT x=∑mi=1aixi=0 mod q

‖x‖∞≤β

若将环R变为整数Euclid ExtrabBp，则可以得到经典SIS问题。与SIS 问题相比，ring-SIS问题因其独特的多项式环结构使得结构更加紧凑，计算更加高效。

1.5 统计距离

定义8 假设X和Y是离散集合D上的两个随机变量，定义Δ（X，Y）=12∑x∈D|Pr［X=x］-Pr［Y=x］|为X和Y之间的统计距离。

对于任意的函数f，统计距离满足Δ（f（X），f（Y））≤Δ（X，Y）［20］。

1.6 Filtering引理

引理1［21］ 令q=Ω（n），任意a∈{v∈Euclid ExtrabBpq：‖v‖∞≤A}，随机选取b←{v∈Euclid ExtrabBpq：‖v‖∞≤B}，参数θ∈Euclid ExtraeBp+。如果B≥θqA，那么Pr［‖a-b‖∞≤B-A］>1e1/θ-o（1）。

Filtering引理的基本思想是为了确保签名的安全性，生成签名的长度必须在一个“安全区间”范围内，只有在这个范围内，签名才能有效输出，从而防止私钥泄露的风险。在该“安全区间”内生成的签名要么与均匀分布不可区分，要么服从均匀分布。目前的签名框架中，a-b一般是签名，要使签名落在“安全区间”内需要重复1/（e1/θ）次。

1.7 拒绝采样引理

引理2［22］ 设V是Euclid ExtrabBpm的一个子集，且任意v∈V都满足‖v‖≤T。h是一个概率分布，可以将V映射到Euclid ExtraaBp。令ψ=ω（Tlog m）∈Euclid ExtraaBp，那么可以找到一个常数C，确保过程1、2输出分布的统计距离最多为2-ω（log m）/C。

过程1：v←h，y←Euclid Math OneDApmψ，以1/C的概率输出（z，y）。

过程2：v←h，y←Euclid Math OneDApmv，ψ，以min（Euclid Math OneDApmψ（z）CEuclid Math OneDApmv，ψ（z））的概率输出（z，y）。

拒绝采样引理提供了一种采用高斯采样但是不泄露私钥的方法。在此方案中，签名需要以一定概率输出，这个概率说明签名与均匀分布不可区分，需要重复C次输出的签名才是安全的。

1.8 Fiat-Shamir签名框架

Fiat-Shamir签名框架分为运用高斯采样的拒绝抽样引理和运用均匀采样的filtering引理两种。下文简单地介绍一下这两类框架。

a）Fiat-Shamir签名框架使用拒绝抽样引理［22～25］，采用高斯采样获得临时密钥。基本思想在于，给定概率分布函数F，若能找到一个常数C以及另外一个分布函数G，确保定义域中所有x都满足F（x）≤CG（x）。而要做到不泄露私钥的话，则要求所有的x←G要以F（x）/CG（x）的概率输出。由于高斯采样不能抵抗侧信道攻击，所以本文主要采用均匀采样构造签名方案。

b）Fiat-Shamir签名框架使用filtering引理，采用均匀采样获得私钥和临时密钥，从而达到保护私钥的目的。这类框架［21，26～29］的主签名为y=Ax+e，如果‖Ax‖∞≤β，‖e‖∞≤γ（其中x为哈希签名值，e为临时性密钥，A为私钥），只有输出‖y‖∞≤γ-β范围内的签名，才能保障私钥不被泄露。也就是说，只有过滤性的输出签名，签名才是安全的。

2 方案定义及安全模型

根据文献［2］定义，可截取签名中CEAS表示内容截取访问结构，签名人可以通过CEAS控制消息M的截取规则，从而防止恶意截取。假设规定截取者至少截取CEAS对应的所有子消息，比如M={M［1］，M［2］，M［3］，M［4］，M［5］}，若令CI（M′）={1，2，3}，M′={M［1］，M［2］，M［3］，*，*}，满足CEAS∈CI（M′），则截取方式合法；令CI（M′）={1，2，4，5}，M′={M［1］，M［2］，*，M［4］，M［5］}，使得CEASCI（M′），则截取方式不合法。CI（M）表示对M中非空数据块的索引集合。

2.1 强指定验证者的可截取签名方案

定义9 VES包含五个概率多项式时间算法：

a）密钥生成算法KenGen（1n）。给定安全参数n，生成主公钥A以及签名者Alice和指定验证者Bob的公私钥对（Ya，Sa）和（Yb，Sb）。

b）签名算法Sign（Yb，Sa，M）。输入消息M，指定验证者Bob的公钥Yb和签名者Alice的私钥Sa，输出消息M的签名σ。

c）截取算法ESExt（M，σ，CEAS）。输入消息M、签名σ和截取规则CEAS，输出截取消息M′和截取签名σE。

d）验证算法Verify（A，Ya，Sb，σE）。输入主公钥A、签名者Alice的公钥Ya，指定验证者Bob的私钥Sb和截取签名σE，输出“0”或“1”。其中“0”表示截取签名σE无效，“1”表示截取签名σE有效。

e）模拟算法Simulation（A，Ya，Sb，σ，M）。输入主公钥A、签名者Alice的公钥Ya，指定验证者Bob的私钥Sb、签名σ以及消息M，返回与签名σ计算不可区分的签名σ′。

VES的正确性。对所有有效的公私钥对（Ya，Sa），（Yb，Sb）和消息M，有

a）全局签名σ的正确性：Verify（A，Ya，Sb，M，Sign（Yb，Sa，M））=1。

b）截取签名σE的正确性：Verify（A，Ya，Sb，M′，ESExt（M，Sign（Yb，Sa，M），CEAS））=1。

2.2 安全模型

一个安全的强指定验证者的可截取签名方案，必须同时满足正确性、不可伪造性、不可转移性、匿名性以及隐私性的要求。除了正确性以外，其他性质都是通过挑战者Euclid Math OneCAp和PPT敌手Euclid Math OneAAp之间的游戏进行刻画的。下面给出具体的定义：

定义10 不可伪造性是指除签名者Alice和指定验证者Bob外，其他任何人都不能伪造一个有效的数据签名对。假设在PPT时间内，如果可以忽略敌手Euclid Math OneAAp赢得下面游戏的概率，那么在适应性选择消息攻击下，强指定验证者的可截取签名方案具备不可伪造性（EUF-CMA）。下面给出游戏的详细描述：

a）挑战者Euclid Math OneCAp执行密钥生成算法，获得公私钥对（Ya，Sa）和（Yb，Sb），并将公钥（Ya，Yb）发送给敌手Euclid Math OneAAp。

b）敌手Euclid Math OneAAp适应性地选取q个消息{M1，M2，…，Mq}询问签名预言机，挑战者Euclid Math OneCAp运行签名算法返还给敌手q个签名。

c）敌手Euclid Math OneAAp在PPT时间内根据自己获取的知识，输出伪造的数据签名对（M，σ）。

d）如果数据签名对（M，σ）在进行签名验证时满足Verify（A，Ya，Sb，M，Sign（Yb，Sa，M））=1，并且Euclid Math OneAAp从未对消息M进行过提取询问，则本文认为Euclid Math OneAAp赢得了上述游戏。

定义11 不可转移性是指持有验证者公钥的人都能够模拟出一个和真正签名难以区分的签名。假设在PPT时间内，如果可以忽略敌手Euclid Math OneAAp赢得下面游戏的概率，那么在适应性选择消息攻击下，强指定验证者的可截取签名方案具备不可转移性。游戏的具体描述如下：

a）挑战者Euclid Math OneCAp执行密钥生成算法，获得公私钥对（Ya，Sa）和（Yb，Sb），并将公钥（Ya，Yb）发送给敌手Euclid Math OneAAp。

b）敌手Euclid Math OneAAp适应性地选取q个消息{M1，M2，…，Mq}，询问签名预言机，挑战者Euclid Math OneCAp运行签名算法返还给敌手q个签名。

c）敌手Euclid Math OneAAp询问一个新的消息M，挑战者Euclid Math OneCAp通过掷币随机选取参数b∈{0，1}。如果b=0，则执行签名算法，返回签名σ=Sign（Yb，Sa，M）；如果b=1，则执行模拟算法，返回签名σ=Simulation（A，Ya，Sb，σ，M）。

d）敌手Euclid Math OneAAp收到签名σ后，可以继续询问除M之外的任何新的消息。

e）敌手Euclid Math OneAAp输出b′，如果b′=b，敌手赢得游戏，转移攻击成功。

不可转移性确保了指定验证者签名的两个重要特性：首先，只有持有验证者私钥的个体才能够验证签名的正确性；其次，指定验证者无法向任何第三方证明签名是由Alice生成的。

定义12 匿名性是指没有私钥的个体无法向任何第三方说明签名的出处，即敌手不能区分签名来自Alice和Bob还是Cindy和Bob。假设在PPT时间内，如果可以忽略敌手Euclid Math OneAAp赢得下面游戏的概率，那么在适应性选择消息攻击下，强指定验证者的可截取签名方案具备匿名性。游戏的具体描述如下：

a）挑战者Euclid Math OneCAp执行密钥生成算法，获得公私钥对（Ya0，Sa0）（Ya1，Sa1）和（Yb，Sb），并将公钥（Ya0，Ya1，Yb）发送给敌手Euclid Math OneAAp。

b）敌手Euclid Math OneAAp询问任意消息Mi的签名。挑战者Euclid Math OneCAp执行σi=Sign（Yb，Sa0，Mi）或σi=Sign（Yb，Sa1，Mi）返回给敌手Euclid Math OneAAp。

c）敌手Euclid Math OneAAp询问一个新的消息M，挑战者Euclid Math OneCAp通过掷币随机选取参数b∈{0，1}。签名σ=Sign（Yb，Sab，M）。

d）敌手Euclid Math OneAAp收到签名σ后，可以继续询问除M之外的任何新的消息。

e）敌手Euclid Math OneAAp输出b′，如果b′=b，敌手赢得游戏。

定义13 隐私性是指被截取的消息不会泄露完整信息。假设在PPT时间内，如果可以忽略敌手Euclid Math OneAAp获取已被删除的信息的优势，那么在适应性选择消息攻击下，强指定验证者可截取签名方案具备可截取签名隐私性。游戏的具体描述如下：

a）挑战者Euclid Math OneCAp执行密钥生成算法，获得公私钥对（Ya，Sa）和（Yb，Sb），并将公钥（Ya，Yb）发送给敌手Euclid Math OneAAp。

b）敌手Euclid Math OneAAp自适应地询问签名，然后输出（i，X，M0，M1）。其中，数据M0和M1除了索引i对应的数据块不同之外，其余均相同，并且iX。

c）挑战者Euclid Math OneCAp随机选取b∈{0，1}，令M=Mb，然后输出关于消息Mb的截取签名σE。最后，C将σE发送给敌手Euclid Math OneAAp。

d）敌手Euclid Math OneAAp继续询问签名，然后输出b′。若b′=b，则Euclid Math OneAAp成功，返回“1”；否则，Euclid Math OneAAp失败，返回“0”。

3 方案描述

3.1 方案设计

本文方案由以下五个算法构成：

算法1 密钥生成算法

输入：安全参数n。

输出：公钥A、Ya、Yb；私钥Sa、Sb。

a）私钥Sa，Sb←Euclid Math OneDApm×md;

b）公钥A，Ya，Yb∈Rm×mq，且满足ASb=Yb mod q，ATSa=Ya mod q；

c）哈希函数h：{0，1}→{r：r∈{-1，0，1}m，‖r‖1≤η}。

算法2 签名算法

输入：公钥A、Ya、Yb；私钥Sa；消息M；标签f。

输出：消息M的签名σ=（r，z，t，f）。

a）选取可逆t←Euclid Math OneDApmγ（γ≤q）；

b）选取k←Euclid Math OneDApmγ，f［i］←{0，1}m；

c）c=YTbk mod q，g［i］=M［i］⊕f［i］，i=1，2，…，N，r=h（c，g［i］i∈N），z=Sar+kt-1；

d）输出消息M的签名σ=（r，z，t，f）。

算法3 截取算法

输入：消息M；签名σ=（r，z，t，f）；截取规则CEAS。

输出：截取消息M′和截取签名σE=（r，z，t，g［i］i∈［N］＼X， f［i］i∈X）。

a）对于不在截取规则内的消息块M［i］，i∈［N］/X，计算g［i］=M［i］⊕f［i］；

b）截取者根据截取规则CEAS和消息M，输出截取消息M′和截取签名σE=（r，z，t，g［i］i∈［N］＼X， f［i］i∈X）。

算法4 验证算法

输入：公钥A、Ya、Yb；私钥Sb；签名σE=（r，z，t，g［i］i∈［N］＼X，f［i］i∈X）；截取消息M′。

输出：0或1。

a）对于i∈X，计算g［i］=M［i］⊕f［i］；

b）如果h（c，g）≠h（STb（ATz-Yar）t mod q，g），返回0；

c）如果‖z‖∞>γ-β，返回0；

d）其他情况返回1。

算法5 模拟算法

输入：公钥A、Ya、Yb；私钥Sb；签名σ=（r，z，t，f）；消息M。

输出：与签名σ计算不可区分的签名σ′。

a）随机选取z′和r′，其中‖z′‖∞≤γ-β，‖r′‖1≤η；

b）选取f［i］′←{0，1}m，计算z=z′t-1，r=r′t-1；

c）计算STb（ATz-Yar）t=c=c′=STb（ATz′-Yar′）mod q；

d）输出σ′=（r′，z′，t′，f′）。

3.2 正确性证明

a）全局签名σ的正确性验证。首先验证‖z′‖∞≤γ-β是否成立。其次，验证

ATz=AT（Sar+kt-1）=ATSar+ATkt-1=Yar+ATkt-1

STb（ATz-Yar）=STbATkt-1=YTbkt-1

h（STb（ATz-Yar）t mod q，g）=h（YTbk，g）=h（c，g）。

b）截取签名σE的正确性验证。首先验证CEASCI（M′）。其次验证‖z′‖∞≤γ-β。对于i∈X，计算g［i］=M［i］⊕f［i］。最后，验证h（c，g）=h（STb（ATz-Yar）t mod q，g）。后续论证过程与a）相同。

3.3 安全性分析

定理1 若ring-SIS2n，m，q，β设论成立，则在适应性选择消息攻击下，本文方案具备不可伪造性。

证明 假设敌手Euclid Math OneAAp能在PPT时间内产生一个能通过验证的数据签名对（M，σ），那么敌手Euclid Math OneAAp可以计算：

a）STb（ATz-Yar）t=（YTbz-STbYar）t mod q。

b）（YTbz-STbYar）t（t）-1-YTbz=

-STbYarmod q=-YTbSar mod q。

如果‖Sar‖≤β（0<β<mdη），那么就可以说敌手Euclid Math OneAAp得出了ring-SIS2n，m，q，β问题的解。这与ring-SIS2n，m，q，β问题的难解性矛盾。

定理2 在自适应选择消息攻击下，本文设计的方案具备不可转移性。

证明 下面介绍挑战者Euclid Math OneCAp和敌手Euclid Math OneAAp间进行的游戏Game。

a）系统建立。挑战者Euclid Math OneCAp执行密钥生成算法，获得公私钥对（Ya，Sa）和（Yb，Sb），并将公钥（Ya，Yb）发送给敌手Euclid Math OneAAp。

b）询问阶段。敌手Euclid Math OneAAp在PPT时间内可以适应性进行以下几种询问。

（a）敌手Euclid Math OneAAp适应性选择消息Mi，进行签名询问。挑战者Euclid Math OneCAp运行算法σi=Sign（Yb，Sa，Mi），发送给敌手Euclid Math OneAAp。

（b）敌手Euclid Math OneAAp询问一个新的消息M，挑战者Euclid Math OneCAp通过掷币选取参数b∈{0，1}，如果b=0，则返回签名σ=Sign（Yb，Sa，M）；如果b=1，则返回签名σ=Simulation（A，Ya，Sb，σ，M）。

（c）敌手Euclid Math OneAAp继续询问挑战者Euclid Math OneCAp除M之外的消息。

c）区分输出。敌手Euclid Math OneAAp输出猜想比特b′。

下面计算两种算法输出签名的概率分布。假设σ1=（r1，z1，t1，f）是随机选取的一个有效签名。

签名算法输出的签名概率分布为

Pr［（r，z，t，f）=（r1，z1，t1，f）］=

Prk，t≠0r=h（YTbk mod q，g［i］i∈N）=r1t=t1z=Sar+kt-1=z1=1γm（γm-1）

模拟算法输出的签名概率分布为

Pr［（r，z，t，f）=（r1，z1，t1，f）］=

Prk′，t′≠0r=h（STb（ATz′-Yar′），g［i］i∈N）=r1t=r′r-1=t1z=z′rr′-1=z1=

1γm（γm-1）

所以，两种算法输出的签名概率分布一样，即敌手Euclid Math OneAAp不能区分这两种情况。

定理3 在自适应选择消息攻击下，本文方案具备匿名性。

证明 设计一种挑战者Euclid Math OneCAp和敌手Euclid Math OneAAp之间的交互游戏Game如下。

a）系统建立。挑战者Euclid Math OneCAp执行密钥生成算法，获得公私钥对（Ya0，Sa0）、（Ya1，Sa1）和（Yb，Sb），并将公钥（Ya0，Ya1，Yb）发送给敌手Euclid Math OneAAp。

b）询问阶段。敌手Euclid Math OneAAp在PPT时间内可以适应性进行以下几种询问。

（a）敌手Euclid Math OneAAp对任意消息Mi进行签名询问。挑战者Euclid Math OneCAp通过计算σi=Sign（Yb，Sa0，Mi）或σi=Sign（Yb，Sa1，Mi）回答敌手签名。

（b）敌手Euclid Math OneAAp询问一个新的消息M，挑战者Euclid Math OneCAp通过掷币随机选取参数b∈{0，1}。签名σ=Sign（Yb，Sab，M）。

（c）敌手Euclid Math OneAAp继续询问挑战者Euclid Math OneCAp除M之外的消息。

c）区分输出。敌手Euclid Math OneAAp输出猜想比特b′。

下面分析b′=b即敌手Euclid Math OneAAp成功的概率。

Pr［b=b′］=

|Pr［Euclid Math OneDAp（STb（ATz-Ya0r）t）］-Pr［Euclid Math OneDAp（STb（ATz-Ya1r）t）］|=

|Pr［Euclid Math OneDAp（STbYa0rt）］-Pr［Euclid Math OneDAp（STbYa1rt）］|=

|Pr［Euclid Math OneDAp（STbATSa0rt）］-Pr［Euclid Math OneDAp（STbATSa1rt）］|=

|Pr［Euclid Math OneDAp（YTbSa0rt）］-Pr［Euclid Math OneDAp（YTbSa1rt）］|

因为Sa0rt和Sa1rt是关于公钥YTb的两个不同的解。如果敌手Euclid Math OneAAp能区分ring-SISq，2n，m，β分布与均匀分布，那么敌手Euclid Math OneAAp就能区分ring-SISq，2n，m，β不同的解。

定理4 在自适应选择消息攻击下，本文方案具备隐私性。

证明 下面介绍挑战者Euclid Math OneCAp与敌手Euclid Math OneAAp间进行的游戏Game0和Game1。

Game0的具体过程如下：

a）系统建立。挑战者Euclid Math OneCAp执行密钥生成算法，获得公私钥对（Ya，Sa）和（Yb，Sb），并将公钥（Ya，Yb）发送给敌手Euclid Math OneAAp。

b）询问阶段。敌手Euclid Math OneAAp进行签名询问，并输出（i，X，M0，M1）。其中，iX且M0［i］≠M1［i］；对任意的i∈X，有M0［i］=M1［i］。挑战者Euclid Math OneCAp随机选取b∈{0，1}，令M=Mb。当i∈［N］，计算g［i］=M［i］⊕f［i］和数据M的签名σ=（r，z，t， f）。其次，挑战者Euclid Math OneCAp执行截取算法，生成数据对（M，X）截取后的签名σE=（r，z，t，g［i］i∈［N］＼X， f［i］i∈X ）。最后，挑战者Euclid Math OneCAp将（〈M〉i∈X，σE）发送给敌手Euclid Math OneAAp。

c）区分输出。敌手Euclid Math OneAAp输出猜想比特b′。若b′=b，输出1；否则，返回0。

Game1在Game0的基础上改变挑战阶段，具体过程如下：

挑战者Euclid Math OneCAp首先设置M。当i∈X，令M［i］=M0［i］=M1［i］，即〈M〉i∈X=〈M0〉i∈X=〈M1〉i∈X；当i∈［N］＼X，令M［i］=；其次，当i∈X，计算g［i］=M［i］⊕f［i］；当i∈［N］＼X，计算签名σ=（r，z，t，f）。最后，挑战者Euclid Math OneCAp输出截取签名（〈M〉i∈X，σE）。

下面分析敌手Euclid Math OneAAp成功的概率：

根据游戏的设置可知，在Game0和Game1中，有〈M〉i∈X=〈M0〉i∈X=〈M1〉i∈X。因此，M被截取的部分未泄露未被截取部分的数据。

总体来看，在自适应选择消息攻击下，本文签名方案具备隐私性。

4 比较分析

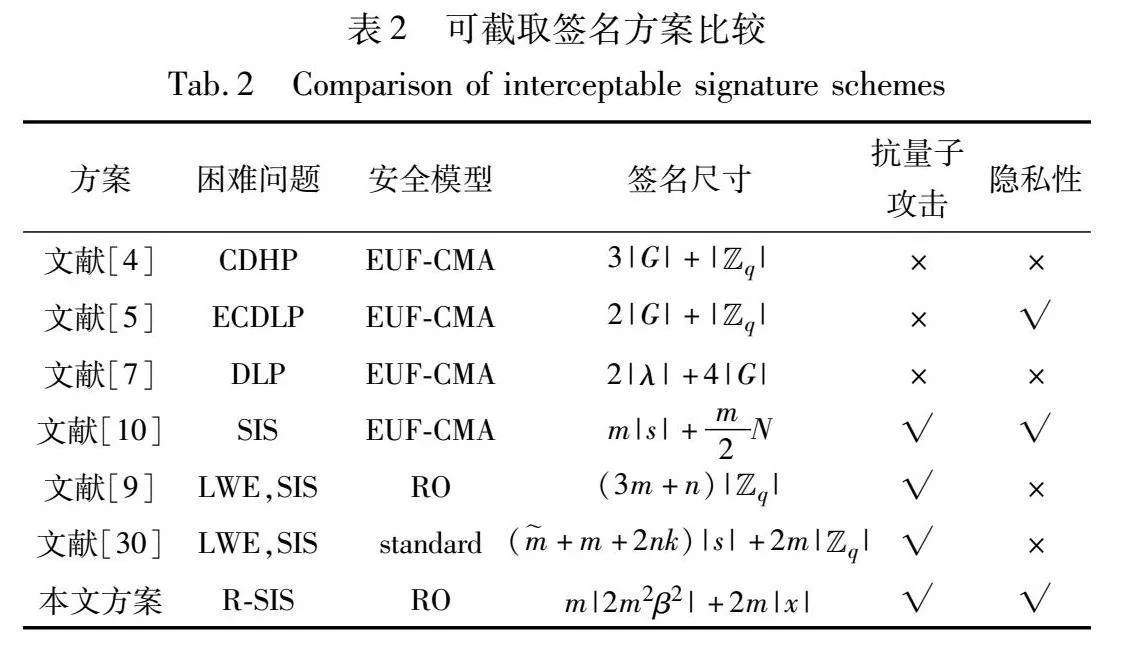
本文选取四种可截取签名方案以及两种强指定验证者签名方案进行比较分析，如表2所示。

首先是VES与四种可截取签名方案之间的对比分析。在安全模型方面，文献［4，5，7，10］均为EUF-CMA，在自适应选择消息攻击下不能满足不可伪造性，也无法有效抵抗量子攻击。并且，对于可截取签名而言，需要具备隐私性和不可伪造性这两个基本的要求，而文献［4，7］没有给出签名的隐私性证明。相比之下，VES不仅满足可截取签名的隐私性和不可伪造性，还具备抗量子攻击能力，安全性更高。

然后是VES与两种强指定验证者签名方案之间的对比分析。由于文献［9，30］两个方案不具备可截取签名的性质，所以不支持对数据的替换、删除、整合等合理操作，具有一定的局限性。而且文献［15，16］两个强指定验证者签名方案必须选择较大的参数来使用原像采样函数和高斯采样，这在一定程度上导致了签名尺寸的增加，重复次数也会随着高斯采样的次数增加而增加。由于本文方案是基于均匀采样的R-SIS假设，所以VES的签名尺寸和重复次数都优于其他方案。

另外，VES建立在R-SIS问题之上，环上的n次多项式可以生成随机矩阵，且可以用NTT技术加速实现特定环上的多项式乘法，实现效率更高。而且，VES在一定程度上可以抵抗侧信道攻击。综上，VES在签名尺寸、公钥长度以及实现效率上均具有明显优势。

5 结束语

本文提出理想格上强指定验证者的可截取签名方案，充分利用了多项式环结构更加紧凑和格密码的抗量子攻击、便捷高效等特点，并给出安全性证明。 由于可截取签名支持对完整签名进行截取操作，并且验证者不需要同签名人进行交互即可验证签名的真伪，拓宽了传统数字签名的应用场景。 强指定验证者的可截取签名解决了数字签名的公开验证问题，相比于普通可截取签名安全等级进一步提高。 今后，将进一步考虑将可截取签名方案推广到格上其他困难问题以及基于属性的认证方式等，亦或是结合其他截取控制规则构造出更加高效的签名方案。

参考文献：

［1］Steinfeld R， Bull L， Zheng Yuliang. Content extraction signatures［C］//Proc of the 4th International Conference on Information Security and Cryptology. Berlin： Springer， 2002： 285-304.

［2］李旭， 杜小妮， 王彩芬， 等. 基于RSA的可截取签名改进方案［J］. 计算机工程与应用， 2014， 50（24）： 96-99. （Li Xu， Du Xiao-ni， Wang Caifen， et al. Improved scheme of content extraction signatures based on RSA［J］. Computer Engineering and Applications， 2014， 50（24）： 96-99.）

［3］Wang Caifen， Li Yahong， Huang S Y， et al. A new forward secure content extraction signature scheme［C］//Proc of 12th International Conference on Fuzzy Systems and Knowledge Discovery. Piscataway， NJ： IEEE Press， 2015： 1698-1702.

［4］Ma Jinhua， Liu Jianghua， Huang Xinyi， et al. Authenticated data reduction with fine-grained control［J］. IEEE Trans on Emerging Topics in Computing， 2020， 8（2）： 291-302.

［5］Liu Jianghua， Ma Jinhua， Xiang Yang， et al. Authenticated medical documents releasing with privacy protection and release control［J］. IEEE Trans on Dependable and Secure Computing， 2021，18（1）： 448-459.

［6］李明祥， 郑艳娟， 许明. 格基强指定验证者签名方案［J］. 小型微型计算机系统， 2013， 34（10）： 4. （Li Mingxiang， Zheng Yanjuan， Xu Ming. Gejiqiang specifies the verifier signature scheme［J］. Small and Micro Computer Systems， 2013， 34（10）： 4.）

［7］Jakobsson M， Sako K， Impagliazzo R. Designated verifier proofs and their applications［C］//Proc of the 15th Annual International Confe-rence on Theory and Application of Cryptographic Techniques. Heidelberg： Springer-Verlag， 1996： 143-154.

［8］Saeednia S， Kpemer S， Markowitch O. An efficient strong designated verifier signature scheme［C］//Procs of the 6th International Confe-rence on Information Security and Cryptology. Berlin： Springer， 2003： 40-54.

［9］Wang Fenghe， Hu Yupu， Wang Baocang. Lattice-based strong designate verifier signature and its applications［J］. Malaysian Journal of Computer Science， 2012， 25（1）： 11-22.

［10］Jie Cai， Han Jiang， Zhang Pingyuan， et al. An efficient strong designated verifier signature based on R-SIS assumption［J］. IEEE Access， 2019， 7： 3938-3947.

［11］Goldreich O， Goldwasser S， Halevl S. Public-key crypto-systems from lattice reduction problems［C］//Proc of the 17th Annual International Cryptology Conference on Advances in Cryptology. Berlin： Springer， 1997： 112-131.

［12］NIST. NIST announces first four quantum-resistant crypto-graphic-algorithms［EB/OL］. （2022-07-05）. https：//www.nist.gov/news-events/news/2022/07/nist-announces-first-four-quantum-resistant-cryptographic-algorithms.

［13］李元晓， 周彦伟， 杨波. 一个改进的强指定验证者签密方案［J］. 计算机应用研究， 2020， 37（2）： 518-520，534. （Li Yuanxiao， Zhou Yanwei， Yang Bo. Improved strong designated verifier signcryption scheme［J］. Applied Research of Computers， 2020， 37（2）： 518-520，534.）

［14］赵勇， 杨少军， 张福泰， 等. 基于格的可截取签名方案［J］. 密码学报， 2022， 9（4）： 767-778. （Zhao Yong， Yang Shaojun， Zhang Futai， et al. A lattice-based extraction signature scheme［J］. Journal of Cryptologic Research， 2022， 9（4）： 767-778.）

［15］冯梦迪. 基于区块链的电子病历系统的研究与实现［D］. 沈阳： 辽宁大学， 2023. （Feng Mengdi. Research and implementation of blockchain-based electronic medical record system［D］. Shenyang： Liaoning University， 2023.）

［16］李晓璐. 基于区块链的电子病历共享及隐私保护研究［D］. 西安： 西安电子科技大学， 2019. （Li Xiaolu. Research on electronic medical record sharing and privacy protection based on blockchain［D］. Xi’an： Xidian University， 2019.）

［17］李亚辉. 基于区块链的电子病历共享系统的设计与实现［D］. 杭州： 浙江大学， 2021. （Li Yahui. Design and implementation of electronic medical record sharing system based on blockchain［D］. Hangzhou： Zhejiang University， 2021.）

［18］Lyubashevsky V， Micciancio D. Generalized compact knap-sacks are collision resistant［M］//Bugliesi M， Preneel B， Sassone V， et al. Automata， languages and programming. Berlin： Springer-Verlag， 2006： 144-155.

［19］Peikert C， Rosen A. Efficient collision-resistant hashing from worst-case assumptions on cyclic lattices［M］//Halevi S， Rabin T. Theory of Cryptography. Berlin： Springer， 2006： 145-166.

［20］王凤和. 后量子安全的格公钥密码设计［D］. 西安： 西安电子科技大学， 2014. （Wang Fenghe. Design of lattice public-key crypto-graphy for post-quantum security［D］. Xi’an： Xidian University， 2014.）

［21］Markus R. Lattice-based blind signatures［C］//Proc of the 16th International Conference on the Theory and Application of Cryptology and Information Security. Berlin： Springer， 2010： 413-430.

［22］Vadim L. Lattice signatures without trapdoors［C］//Proc of the 31st Annual International Conference on the Theory and Applications of Cryptographic Techniques. Berlin： Springer， 2012： 738-755.

［23］Leo D， Tancrede L， Vadim L， et al. Crystals-dilithium： digital signatures from module lattices［EB/OL］. （2018-09-10）. https：//eprint.iacr.org/2017/633.

［24］Leo D. Accelerating bliss： the geometry of ternary poly-nomials［EB/OL］. （2014-10-22）. https：//ia.cr/2014/874.

［25］Leo D， Alain D， Tancrede L， et al. Lattice signatures and bimodal Gaussians［C］//Proc of the 33rd Annual International Cryptology Conference. Berlin： Springer， 2013： 40-56.

［26］Thomas P， Leo D， Tim G. Enhanced lattice-based signatures on reconfigurable hardware［C］//Proc of the 16th International Workshop on Cryptographic Hardware and Embedded Systems. Berlin： Springer， 2014： 353-370.

［27］Erdem A， Nina B， Johannes B， et al. Revisiting TESLA in the quantum random oracle model［C］//Proc of the 8th International Workshop on Post-Quantum Cryptography. Cham： Springer， 2017： 143-162.

［28］Shi Bai， Galbraith S D. An improved compression technique for signatures based on learning with errors［M］//Benaloh J. Topics in Cryptology. Cham： Springer， 2014： 28-47.

［29］Vadim L. Fiat-shamir with aborts： applications to lattice and factoring-based signatures［C］//Proc of the 15th International Conference on the Theory and Application of Cryptology and Information Security. Berlin： Springer， 2009： 598-616.

［30］Geontae N， Ik R. Strong designated verifier signature scheme from lattices in the standard model［J］. Security and Communication Networks， 2017， 9（18）： 6202-6214.

［31］蔡杰. 基于格的指定验证者数字签名方案及身份鉴别协议研究［D］. 济南： 山东大学， 2020. （Cai Jie. Research on lattice based designated validator digital signature scheme and identity authentication protocol［D］. Jinan： Shandong University， 2020.）

［32］张平， 迟欢欢， 李金波， 等. 基于格的强指定验证者签名方案［J］. 北京航空航天大学学报， 2023， 49（6）： 1294-1300. （Zhang Ping， Chi Huanhuan， Li Jinbo， et al. Lattice-based strongly designated verifier signature scheme［J］. Journal of Beijing University of Aeronautics and Astronautics， 2023， 49（6）： 1294-1300.）