基于均匀线性阵列的超大规模MIMO混合场信道估计算法

摘 要：超大规模MIMO（extremely large-scale massive MIMO，XL-MIMO）是未来6G通信的关键技术之一。现有的XL-MIMO混合场信道模型大多对均匀线性阵列和单天线用户之间信道建模，且采用散射体最后一跳模型。若收发双端均配备线性阵列，现有的混合场信道估计方案将不再适用。为此，针对收发端均部署超大规模线性阵列的XL-MIMO场景，采用Saleh-Valenzuela模型进行信道建模，并提出了一种基于正交匹配追踪（OMP）的混合场信道估计算法。该算法首先利用角域变换矩阵对远场分量进行估计，然后通过极域变换矩阵估计近场分量。此外，引入克拉美罗-下界（CRLB）对所提算法进行评估。仿真结果表明，提出的混合场估计算法相较于仅考虑远场和近场的估计算法在信道估计性能上有约0.6 dB的提升。

关键词：超大规模MIMO； 信道估计； 混合场； 线性阵列； 克拉美罗-下界

中图分类号：TP929.5 文献标志码：A

文章编号：1001-3695（2024）10-034-3124-05

doi：10.19734/j.issn.1001-3695.2024.01.0042

Hybrid field channel estimation algorithm for extremely large-scale MIMObased on uniform linear array

Wang Dan， Fang Jiening， Xie Changjiang

（School of Communications and Information Engineering， Chongqing University of Posts and Telecommunications， Chongqing 400065， China）

Abstract：Extremely large-scale massive MIMO （XL-MIMO） emerges as a crucial technology for future 6G communication. Existing XL-MIMO hybrid-field channel models primarily model channels between uniform linear arrays and single-antenna users， employing the last-hop model of scatterers. However， if both transmitter and receiver are equipped with linear arrays， existing hybrid-field channel estimation schemes become inadequate. To address this， this paper proposed a channel modeling approach for XL-MIMO scenarios with both transmitter and receiver equipped with large-scale linear arrays， utilizing the Saleh-Valenzuela model. Additionally，it introduced a hybrid-field channel estimation algorithm based on orthogonal matching pursuit（OMP）. This algorithm initially estimated far-field components using the angle-domain transformation matrix， followed by estimating near-field components using the polar-domain transformation matrix. Furthermore，it introduced the Cramér-Rao lower bound（CRLB） to evaluate the proposed algorithm. Simulation results demonstrate approximately 0.6 dB improvement in channel estimation performance compared to algorithms considering only far-field and near-field components.

Key words：XL-MIMO; channel estimation; hybrid field; linear arrays; CRLB

0 引言

超大规模MIMO （XL-MIMO）已被视为增强未来6G无线通信系统传播环境的创新技术[1]。通过为基站（BS）配备极大量的天线，XL-MIMO可以有效地提高波束形成增益和频谱效率。大规模MIMO的各种应用已经在文献[2]得到了广泛的研究。

主流的大规模MIMO低导频开销信道估计方法通常假设信道为远场信道模型或近场信道模型。由于远场的特性，其阵列导向矢量仅取决于信道路径的角度，所以远场在角度域中具有稀疏性。因此，可以使用离散傅里叶变换（DFT）矩阵将信道转换为稀疏角度域的表示，并且文献[3～5]已经提出了基于压缩感知的信道估计方法。而对于近场信道模型，其阵列导向矢量除与路径角度有关外，还与距离参数有关。由于DFT矩阵不再适用于这种情况，所以文献[6]提出了极域变换矩阵，利用极域中的信道稀疏性使用较少数量的导频进行准确的信道估计。针对均匀平面阵列（UPA），文献[7]提出了一种低复杂度的顺序角度-距离信道估计算法（SADCE）。通过对角度和距离的解耦，设计了一种用于角度参数估计的二维傅里叶变化（2D-DFT）方法。同时提出了一种具有闭式解的低复杂度的距离估计方法。

在现有的远场或近场信道模型中，假设所有的散射体要么在远场，要么在近场。实际上，XL-MIMO系统的信道模型更可能为混合场，其中一些散射体位于远场区域，而另一些散射体位于近场区域[8]。因此，文献[8]首次提出了混合场信道模型，并且结合混合场信道模型提出了一种基于混合场的OMP信道估计算法（HF-OMP）。

针对混合场信道，现有方法实现有效估计的最大困难是远场路径和近场路径的比例未知。文献[9]提出了一种混合场信道估计方案，该方案的目标是先确定远场和近场分量比例值，然后再完成混合场信道的估计。文献[10]提出了一种混合场降秩MUSIC（H-RM）信道估计方法，利用MUSIC算法对接收信号的协方差矩阵进行分解，进而可以估计出混合场接收信号中近场分量和远场分量。为了解决混合场信道估计性能严重依赖采样角度和距离的分辨率问题，文献[11]提出了一种基于交替方向乘法器（ADMM）的混合场上行信道估计方法，将XL-MIMO信道估计问题公式化为具有两个范数约束的优化问题。文献[12]通过将近似消息传递（AMP）算法确定的信道参数馈送到特别设计的卷积神经网络（CNN）中来实现两步估计策略。在这个两阶段预测系统中，CNN增强了压缩感知算法的输出。文献[13]提出了一种基于卷积自动编码器（CAE）的混合场信道估计方法，提高了正交匹配追踪（OMP）算法的错误性能和鲁棒性，特别是在低信噪比条件下。文献[14]提出了一种去伪峰混合场信道估计方案，通过伪峰角度与真实角度之间的函数关系，判断出信道的真实角，大大降低了信道估计的均方误差。

上述XL-MIMO混合场信道估计算法中，都是对配置均匀线性阵列的基站以及单天线用户之间信道进行建模。但是在实际通信场景中，发送端和接收端都可能配备了超大规模天线阵列。例如，车辆顶部安装了超大规模天线阵列[15，16]，同时发射端也部署了超大规模天线阵列。因此，上述混合场信道估计算法无法运用到收发端均为线性阵列场景中。此外，现有的混合场信道模型都是基于散射体最后一跳模型，但是在实际的通信场景中，应该考虑所有散射体路径之间的影响。基于收发端都部署超大规模均匀线性天线阵列并且采用Saleh-Valenzuela模型对混合场信道进行建模，在该模型基础上基于OMP算法提出了一种混合场信道估计算法。仿真结果表明，提出的混合长信道估计算法在较低导频开销的情况下，比文献[3，6，9]取得更好的信道估计性能，在XL-MIMO系统收发阵列均为线性阵列情况下提高了混合场信道估计的性能。

1 系统模型

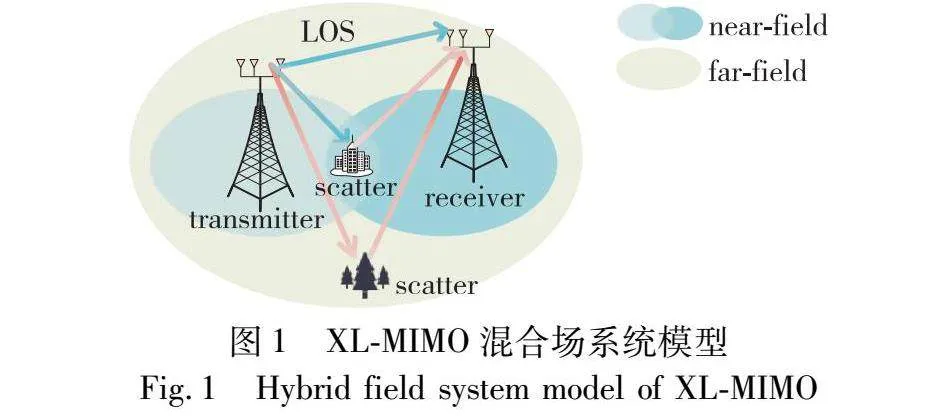
如图1所示，在XL-MIMO混合场系统模型中，发射端和接收端都部署了超大规模均匀线性阵列天线，其中发射端天线数为N1，接收端天线数为N2。

1.1 信号模型

由于天线阵列通常采用数字-模拟混合方式实现，并配备有一定数量的射频（RF）链，所以假设发射阵列和接收阵列的RF链数为NRFt和NRFr。假设H∈Euclid ExtracBpN2×N1表示从发送端到接收端的信道，则接收端对应信号可以表示为

ym=WHQsm+nm（1）

其中：ym∈Euclid ExtracBpNRFr×1，W∈Euclid ExtracBpNRFr×N2，Q∈Euclid ExtracBpN1×NRFt，sm∈Euclid ExtracBpNRF×1t分别表示第m个时隙的接收信号，混合合并矩阵，混合预编码矩阵以及发送导频信号，nm～Euclid Math OneCApEuclid Math OneNAp（0，σ2INRFr）表示第m个时隙均值为0，方差为σ2的高斯复噪声。其中合并矩阵和预编码矩阵中每个元素W［i］，Q［i］应分别满足1/N2，1/N1的恒模约束。令pm=Qsm∈Euclid ExtracBpN1×1，则接收端在M个时隙内接收到的导频信号可表示为

Y=WHP+N（2）

其中：P=［p1，p2，…，pM］∈Euclid ExtracBpN1×M，Y=［y1，y2，…，yM］∈Euclid ExtracBpNRFr×M表示发送导频和接收导频信号；N=［n1，n2，…，nM］∈Euclid ExtracBpNRFr×1表示接收噪声，且N～Euclid Math OneCApEuclid Math OneNAp（0，σ2INRFrIM）。在XL-MIMO系统中，发送天线阵列N1的数量通常很大。因此，为了减少实际通信系统中的导频开销，应当利用具有低开销的信道估计方案，即导频数量应小于发送天线数（M<N1）。

1.2 信道模型

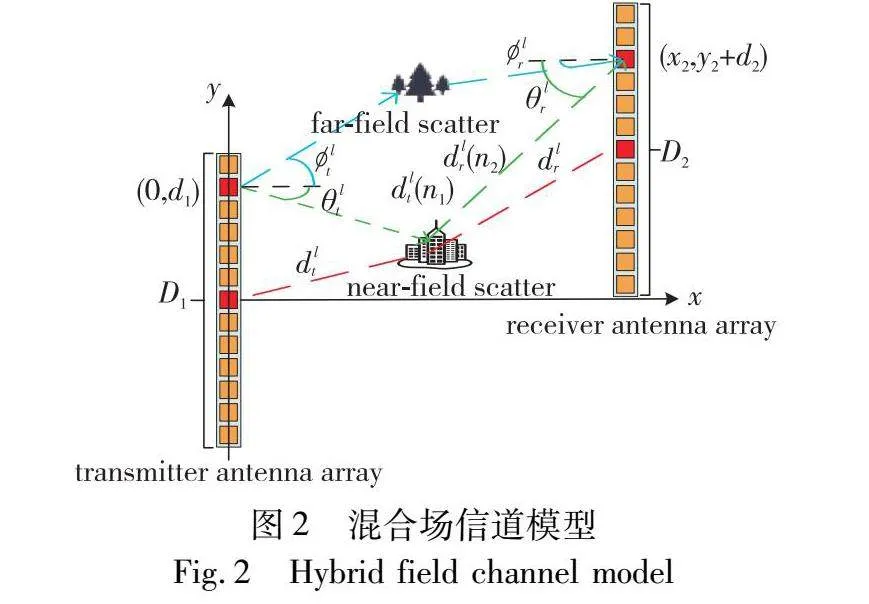
天线孔径为D1的发送阵列和天线孔径为D2的接收阵列之间的混合场信道模型如图2所示。现有的XL-MIMO混合场信道估计算法大多都是只考虑散射体最后一跳模型，即只对散射体到接收阵列一方路径进行建模，忽略发送阵列到散射体一方路径，这在实际场景中是不可行的。为了更好地描述信道特性，对发送阵列到散射体和散射体到接收阵列两方路径进行建模。

1.2.1 近场信道模型

当散射体与天线阵列之间距离小于瑞丽距离Z=2D2/λ时，其中D为天线阵列孔径，λ表示波长。此时模型应建模为近场信道，利用近场阵列导向矢量代替远场阵列导向矢量来对近场XL-MIMO信道进行建模[17]，其表示为

Hnear-field=∑lnl=1glb（θlr，dlr）bH（θlt，dlt）（3）

其中：ln表示近场路径数；gl表示近场路径复增益；b（θlr，dlr）、bH（θlt，dlt）分别表示基于球面波假设建模的发射端和接收端的近场阵列导向矢量，其表示为

b（θlt，dlt）=1N1［e-j2πλ（dlt（1）-dlt），…，e-j2πλ（dlt（N1）-dlt）］H（4）

b（θlr，dlr）=1N2［e-j2πλ（dlr（1）-dlr），…，e-j2πλ（dlr（N2）-dlr）］H（5）

其中：θlt、θlr分别表示发送阵列天线和接收阵列天线处第l条路径的角度；dlt、dlr表示第l个散射体到发射阵列天线和接收阵列天线的中心距离；dlt（n1）、dlr（n2）为第l个散射体到发送阵列天线n1的距离和接收阵列天线n2的距离，可以表示为

dlt（n1）=dlt2+δ2n1d2-2dltδn1d sinθlt（6）

dlr（n2）=dlr2+δ2n2d2-2dlrδn2d sin θlr（7）

其中：d=λ/2表示天线间距;δn1、δn2分别表示发送天线n1和接受天线n2与中心阵列天线距离，其表达式如下：

δn1=2n1-N1-12 n1=1，2，…，N1（8）

δn2=2n2-N2-12 n2=1，2，…，N2（9）

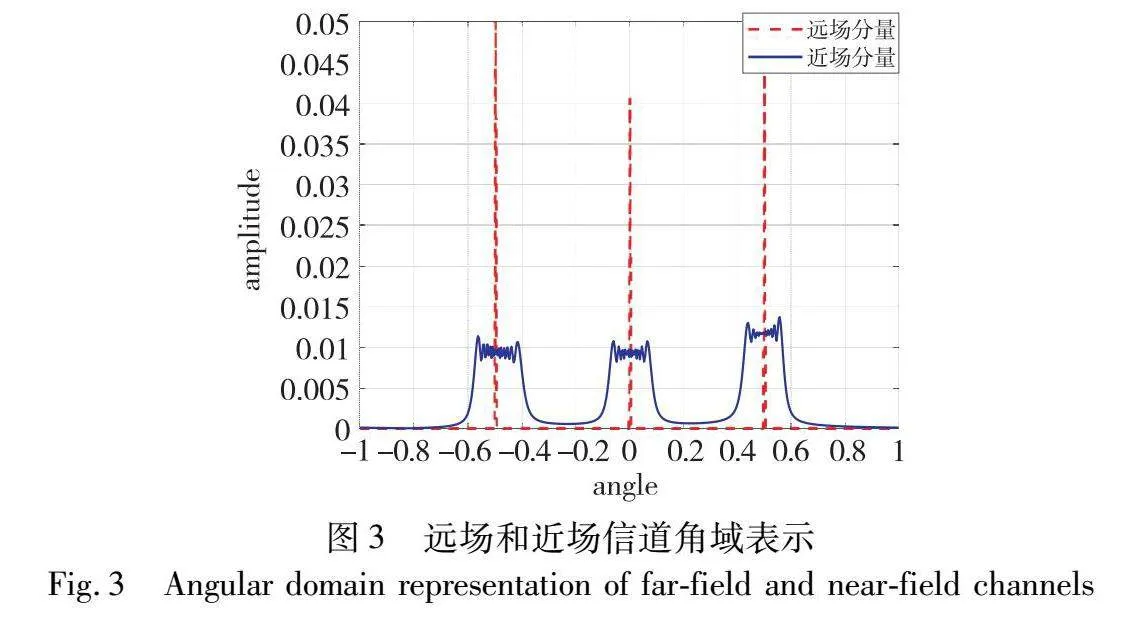
由于近场导向矢量引进了距离参数，导致其在角度域存在严重的能量扩散问题，传统的傅里叶变换矩阵（DFT）不适用于近场信道，如图3所示。为了探究近场信道的稀疏性，文献[6]提出了近场的极域表示，近场路径在该域中具有稀疏性，其中极域变换矩阵表示为

Dt=［b（θ1，d11），…，b（θ1，dS11），…，b（θN1，d1N1），…，b（θN1，dSN1N1）］（10）

Dr=［b（θ1，d11），…，b（θ1，dS11），…，b（θN2，d1N2），…，b（θN2，dSN2N2）］（11）

其中：矩阵Dt、Dr中每列元素表示在角度θn1（θn2）和距离dsn1n1（dsn2n2）上采样的近场阵列导向矢量，其中sn=1，2，…，Sn1（Sn2），Sn1（Sn2）表示在角度θn1（θn2）上的采样距离点数。通过计算每个角度上的采样距离点数，可以得出矩阵Dt、Dr的列数满足S1=∑N1n1=1Sn1，S2=∑N2n2=1Sn2。

在构造近场极域变换矩阵时，应对角度θn进行均匀采样，对距离rs进行非均匀采样[6]，如式（12）～（14）所示。

rs=1sZΔ（1-θ2） s=0，1，2，3，…（12）

ZΔ=N2d22λcβ2Δ（13）

θn=2n-N+1N n=0，1，…，N-1（14）

其中：βΔ为门限阈值；基于上述极域变换矩阵Dtn、Drn，可将近场信道表示为

Hnear-field=DrHPnDtH（15）

其中：HPn∈Euclid ExtracBpS2×S1表示极域XL-MIMO信道，其在极域中具有稀疏性。

1.2.2 远场信道模型

当散射体与天线阵列之间距离大于瑞丽距离时，信道位于远场区域，信道模型应基于平面波进行建模，此时远场阵列导向矢量只与角度参数有关。远场信道模型表示为

Hfar-field=∑lfl=1αla（θlr）a（θlt）（16）

其中：lf为远场路径数;αl表示远场路径复增益;a（θlr）、a（θlt）分别表示接收阵列天线和发送天线处的远场阵列导向矢量。

a（θlt）=1N1［e-jη1n1πθlt，…，e-jηN1n1πθlt］（17）

a（θlr）=1N2［e-jη1n2πθlr529198ea8eb27618fc2d0835536a9dd6，…，e-jηN2n2πθlr］（18）

其中：θlt=2dλsin（φlt），θlr=2dλsin（φlr），其中φlt，φlr分别表示第l条远场路径在发送天线阵列和接收天线阵列处的实际物理角度，取值为（-π2，π2），ηnn1=2n1-N1-12，ηnn2=2n2-N2-12。

在XL-MIMO通信环境中，由于散射体的数量是有限的，如图3所示。此远场信道在角域具有稀疏性。为了减少信道导频的开销，上述远场非稀疏信道可通过稀疏角域信道表示：

Hfar-field=FrHPfHHt（19）

其中：HPf为远场稀疏角域信道；Ft、Fr分别表示发送端和接收端处阵列导向矢量的傅里叶（DFT）变换矩阵，其表示为

Ft=［a（β1t），…，a（βN1t）］（20）

Fr=［a（β1r），…，a（βN2r）］（21）

其中：βn1t=2n1-N1-12、βn2r=2n2-N2-12分别表示远场导向矢量在发送阵列和接收阵列处的采样角度。对于远场路径分量的变换矩阵，其角度采样满足均匀采样。

1.2.3 混合场信道模型

实际XL-MIMO通信环境中的散射体可能会同时出现在近场区域和远场区域，如图1所示。此时的信道包含了远场路径分量和近场路径分量，因此考虑两种路径分量将信道建模为混合场信道是更合适且可行的。本文基于发送端和接收端都部署了超大规模的均匀线性阵列天线通信场景，并且考虑了所有散射体路径的影响而非最后一跳模型，提出的混合场信道模型表示为

Hhybrid-field=Hfar-field+Hnear-field=

Fr（∑Llf=1αlfa（θlfr）aH（θlft））FHt+

Dr（∑Sln=1αlnb（θlnr，dlnr）b（θlnt，dlnt））DHt（22）

其中：第一项和第二项表示远场和近场路径分量；L、S分别表示远场和近场路径数；αlf～Euclid Math OneCApEuclid Math OneNAp（0，pf），αln～Euclid Math OneCApEuclid Math OneNAp（0，pn）分别表示远场和近场信道分量的路径增益，其中pf和pn是两个信道的大尺度衰落因子；θlft，θlfr为远场路径的角度参数；θlnt，θlnr为近场路径的角度参数；dlnt，dlnn为近场路径的距离参数。

2 混合场信道估计算法

现有的混合场信道估计算法都是基于BS端部署了超大规模MIMO和单天线用户通信模型，对于收发端都部署了超大规模MIMO的通信场景，这些算法将不再适用。在现有的OMP算法基础上，结合提出的混合场信道模型，提出了一种混合场信道估计算法。其基本思想是基于不同的信道变换矩阵，首先估计出远场路径分量，其次消除远场路径分量的影响，再对近场路径分量进行估计。根据式（2）（6）（9）接收信号可以进一步表示为

Y=WHfar-fieldP+WHnear-fieldP+N=

WFrHPfFHtP+WDrHPnDHtP+N（23）

其中：Hfar-field和Hnear-field分别表示XL-MIMO混合场信道的远场和近场路径分量。HPf表示角度域中的远场路径分量，而HPn表示极坐标域中的近场路径分量，它们都是稀疏的。因此可以利用较少的导频开销单独估计HPf和HPn，进而直接获得整个混合场信道的估计结果。

相较于现有的混合场信道估计算法，本文算法更关注于矩阵而不是向量之间的运算。本文混合场信道估计算法具体流程可以总结为算法1所示。算法中出现的数学符号argmax‖·‖22、vec（·）、floor（·）、mod（·）、分别表示求向量模值的最大值位置、矩阵向量化、向下求整、取余数以及克罗内克积。

算法1 本文混合场信道估计算法

输入：接收信号Y；本地导频P；混合预编码矩阵W；远场发送端变换矩阵Ft;远场接收端变换矩阵Fr;近场发送端变换矩阵Dt;近场接收端变换矩阵Dr；远场路径分量数L;近场路径分量数S。

输出：信道估计结果H^。

初始化：初始远场原子支撑集Ωf=，Ωtf=，Ωrf=，初始近场原子支撑集Ωn=，Ωtn=，Ωrn=，初始残差矩阵R=Y，初始远场和近场稀疏矩阵A=0N1N2×1，B=0S1S2×1。

阶段一：远场路径分量估计

a）计算远场传感矩阵At=FtHP，Ar=WFr；

b）根据表达式：nf=argmax‖vec（AHrRAHt）‖22，找到与当前远场路径lf相关性最强的支撑索引nf；根据计算的支撑索引nf，通过式子： ntf=floor（（nf-1）/N2）+1，nrf=mod（nf-1，N2）+1分别计算出传感矩阵At，At的索引ntf，nrf；将索引更新到集合Ωf=Ωf∪nf，Ωtf=Ωtf∪ntf，Ωrf=Ωrf∪nrf；

c）更新远场稀疏矩阵A=［A At（Ωtf，：）HAr（：，Ωrf）］；基于更新的远场支撑集合Ωf，通过最小二乘算法h^f（Ωf）=（AHA）-1AHvec（Y）计算当前远场稀向量h^f；将远场稀疏向量h^f转成N2×N1维矩阵Hf^；

d）更新远场残差矩阵：R=Y-ArH^fAt；

e）令t=t+1，如果t≤L返回步骤b）继续迭代，否则结束迭代，保留最后一次迭代的远场稀疏矩阵H^f；

阶段二：近场路径分量估计

f）计算近场传感矩阵Bt=DtHP，Br=WDr；

g）根据表达式：nn=argmax‖vec（BHrRBHt）‖22，找到与当前近场路径ln相关性最强的支撑索引nn；根据计算的支撑索引nn，通过式子： ntn=floor（（nn-1）/S2）+1，nrn=mod（nn-1，S2）+1分别计算出传感矩阵Bt，Bt的索引ntn，nrn；将索引更新到集合Ωn=Ωn∪nn，Ωtn=Ωtn∪ntn，Ωrn=Ωrn∪nrn；

h）更新近场稀疏矩阵B=［B Bt（Ωtn，：）HBr（：，Ωrn）］；基于更新的近场支撑集合Ωn，通过最小二乘算法h^n（Ωn）=（BHB）-1BH vec（Y）计算当前近场稀向量h^n；将近场稀疏向量h^n转成S2×S1维矩阵H^n；

i）更新近场残差矩阵：若Ωf≠，则R=Y-ArH^fAt-BrH^nBt，否则R=Y-BrH^nBt；

j）令t=t+1，如果t≤S返回步骤g）继续迭代，否则结束迭代，保留最后一次迭代的远场稀疏矩阵H^n；

阶段三：输出信道估计结果

k）对估计信道矩阵初始化：H^=0N2×N1；

l）若远场支撑集合Ωf≠，则H^=H^+FrH^fFHt；若近场支撑集合

Ωn≠ ，则H^=H^+DrH^nDHt；

算法复杂度分析如下：阶段一和二的计算复杂度主要来自步骤b）g）和步骤c）h）相关性的计算和最小二乘法的计算，可以分别表示为O（N1N2（N1+N2）L）和O（N1N2（S1+S2）S）。第三阶段的计算复杂度来自步骤l）中混合场信道估计结果的计算，表示为O（（N1+N2）（S1+S2））。因此，算法总计算复杂度为O（N1N2（N1+N2）L）+O（N1N2（S1+S2）S）+O（（N1+N2）（S1+S2））。

3 克拉美-罗下界

为了评估算法的性能，引入了克拉美-罗下界（CRLB）对算法性能进行评估。CRLB界是评估信道估计算法的MSE的理论界。利用克罗内克积和矩阵乘积的结合性质，即引理vec（ABC）=（CTA）vec（B），可将式（2）表示为

y=（PTW）h+n=Qh+n（24）

其中：y，Q，h，n可以表示为

y=vec（y）∈Euclid ExtracBpNRFrM×1，h=vec（H）∈Euclid ExtracBpN1N2×1（25）

n=vec（N）∈Euclid ExtracBpNRFrM×1，Q=（PTW）∈Euclid ExtraaBpNRFrM×N1N2（26）

由于Q为实数矩阵，y，h，n为复数向量，所以可以将式（24）分解成实数和虚数两部分，如式（27）（28）所示。

yu=Qhu+nu（27）

yv=Qhv+nv（28）

其中：yu=Re（y），yv=Im（y），hu=Re（h），hv=Im（h），nu=Re（n），nv=Im（n）。若将信道估计结果表示为h^=h^u+h^v，则无偏估计量CRLB可以分为两部分，如式（29）所示。

CRLB=CRLBu+CRLBv=E{‖h^-h‖2}=

E{‖h^u-hu‖2}+{‖h^v-hv‖2}（29）

在式（27）中，由于nu服从均值为0，方差为σ2的高斯分布。对于给定的hu，yu的条件概率密度函数可以表示为

pyu|hu（yu;hu）=1（2πσ2）NRFrM/2exp{-12σ2‖yu-Qhu‖2}（30）

通过计算条件概率密度函数pyu|hu（yu;hu）在参数hu处的负二阶导数的期望，yu的费舍尔信息矩阵可以由式（31）表示。

［J］m，n-Epyu|hu（yu;hu） hu，m hu，n=1σ2［QHQ］m，n（31）

其中：hu，m、hu，n分别表示矩阵hu的第m和n个元素。通过式（29）（31），yu的克拉美-罗下界CRLBu可以表示为

CRLBu=E{‖hu^-hu‖2}≥Tr{J-1u}=σ2Tr{（QHQ）-1}（32）

其中：Tr{·}表示矩阵的迹。由于Q=（PTW），式（32）中的（QHQ）-1可以进一步表示为

（QHQ）-1=（（PTW）H（PTW））-1=

（（PPH）T（WHW））-1=

（（PPH）-1）T（WHW）-1（33）

通过式（33），Tr{（QHQ）-1}可以进一步表示为

Tr（（QHQ）-1）=Tr（（（PPH）-1）T）Tr（（WHW）-1）=

Tr（（PPH）-1）Tr（（WHW）-1）=

（∑N1i=1λ-1i）（∑N2j=1η-1j）≥

N1（N1/∑N1i=1λi）N2（N2/∑N2j=1ηj）=

N21Tr{PPH}N22Tr{WWH}（34）

其中：λi，ηj分别表示矩阵PPH和WWH的特征值。若满足λ1=λ2=…=λN1，η1=η2=…=ηN2，则式（34）等号成立，即导频矩阵PH和混合预编码矩阵W的列是正交的。由Hermite矩阵的性质可得，此时Tr{PPH}=N1M，Tr{WWH}=N2NRFr。在这种情况下，可将式（35）表示为

CRLBu=E{‖h^u-hu‖2}=σ2N1N2MNRFr（35）

由于CRLBu和CRLBv有着相同的形式，所以CRLBu=CRLBv=σ2N1N2MNRFr，式（29）可以表示为

CRLB=CRLBu+CRLBv=2σ2N1N2MNRFr（36）

4 仿真结果分析

为了验证所提混合场信道估计算法的性能，与文献[3]只考虑远场分量算法、文献[6]的近场分量的信道估计算法、文献[9]提出的混合场信道估计算法以及CRLB下界进行归一化均方误差（NMSE）性能对比。其中信道估计算法和CRLB的NMSE定义如式（37）（38）所示。

NMSEh=E‖h-h^‖22‖h‖2（37）

NMSECRLB=ECRLB‖h‖22（38）

其中：E［·］表示数学期望；‖·‖22表示求向量模的平方；h为真实信道；为各种信道估计算法输出的估计结果；CRLB是利用式（36）计算出来的克拉美-劳下界。

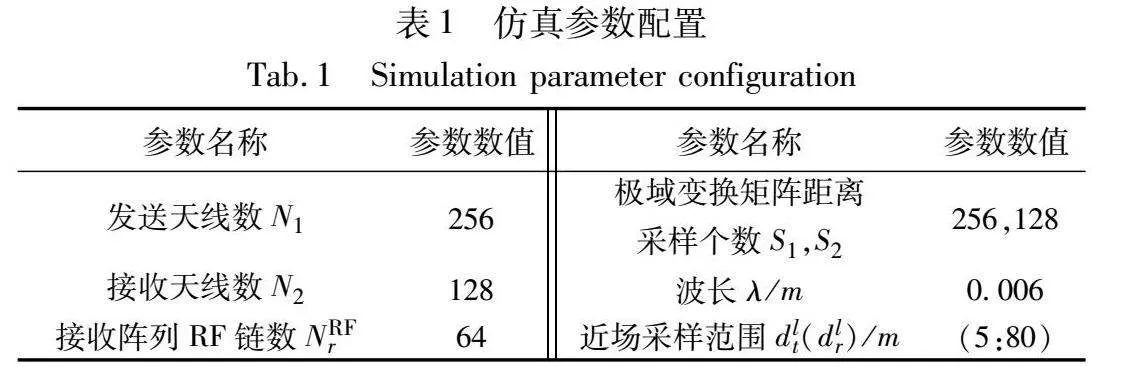
利用MATLAB仿真工具搭建XL-MIMO混合场信道模型进行相关仿真，首先根据式（3）和（16）分别搭建近场和远场信道，再通过式（22）构建混合场信道模型，其中远场和近场的大尺度衰落因子分别为ρf=ρ0（dbr/d0）-αf，ρn=ρ0（dbr/d0）-αn，其中ρ0=-30 dB表示在参考距离d0=1 m处的大尺度衰落因子，dbr=100 m为收发天线距离，αf～Euclid Math OneUAp（2，4），αn～Euclid Math OneUAp（2，4）分别是远场和近场的路径损耗指数，最后通过式（2）构造接收信号Y。通过文献[7]中的算法1构造近场极域变换矩阵Dt、Dr，远场变换矩阵Ft、Fr通过式（20）（21）构造，其中N1，N2设置为256和128。本文算法中的导频矩阵P和混合预编码矩阵W通过MATLAB的rand函数生成分别满足1M，1N2衡模约束的N1×M和NRFr×N2维均匀分布随机矩阵。仿真过程中信噪比SNR定义为1/σ2，本文算法仿真涉及到参数如表1所示。

本文仿真对比结果中的远场，近场和混合场的NMSE性能分别由文献[3]的算法1，文献[6]的算法2和文献[9]的算法1计算得出，本文算法NMSE性能由算法1计算得出。

如图4所示，对比了本文算法与文献[3]远场算法、文献[6]近场算法、文献[9]混合场算法以及CRLB界在信噪比为0～10 dB下的NMSE性能，其中导频长度设置为72，远场路径数L和近场路径数S都设置为3。由仿真结果可知，随着信噪比的增大，所有信道估计算法的NMSE都随之减小。基于远场和近场的信道估计算法性能相近，本文算法均方误差最小。由于导频矩阵PH和混合预编码矩阵W的列元素并不是正交的，导致实际的信道估计算法NMSE性能达不到CRLB下界。因此，在混合场信道条件下，本文算法能够实现更好的信道估计结果，比文献[3，6]道估计算法有0.6 dB左右的提升，比文献[9]算法提升约0.3 dB。

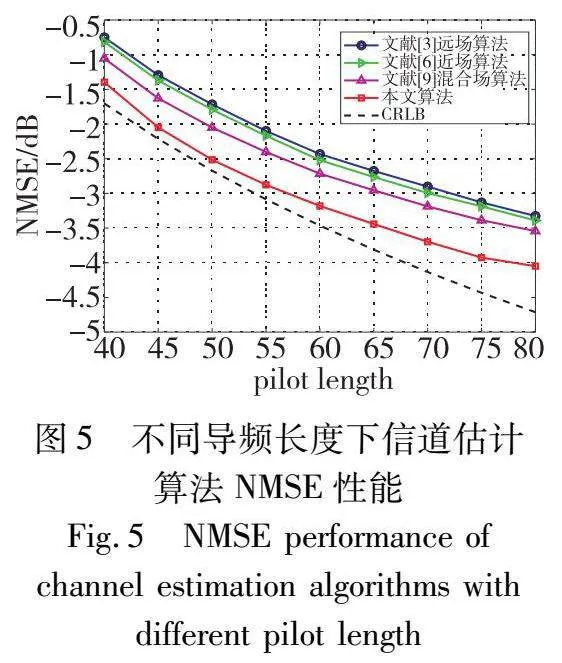
图5在信噪比为5 dB情况下，对比了不同算法在导频长度为40～80下的NMSE性能，远场路径数L和近场路径数S都设置为3。随着导频长度的增加，NMSE都随之下降。混合场算法的NMSE性能更接近CRLB下界，比文献[3，6]信道估计算法有0.6 dB左右的提升，比文献[9]提升了0.4 dB左右。结果表明，所提算法在使用较少导频开销的情况下，能够获得更好的信道估计结果。

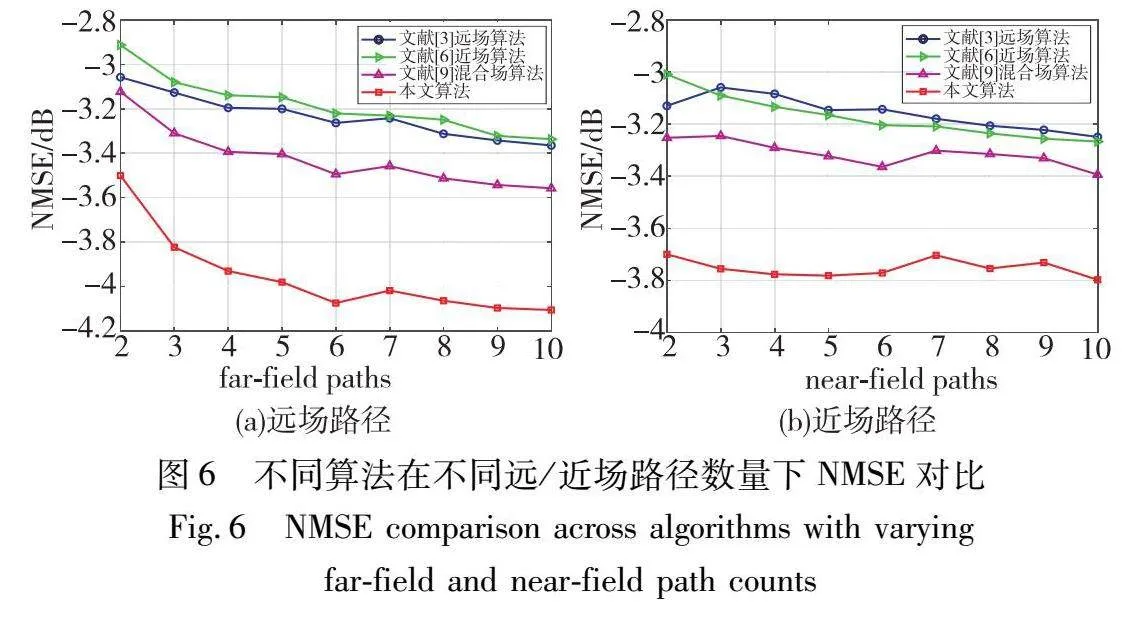
图6为在信噪比为5 dB条件下，不同算法在不同远场和近场路径下的NMSE性能，其中导频长度设置为72。由式（36）可知，CRLB下界与路径数量无关，因此在对比不同路径数下算法的NMSE性能时不考虑CRLB下界。其中图6（a）近场路径数为3，远场路径数量取值为[2，10]。图6（b）远场路径数为3，近场路径数量取值为[2，10]。从仿真结果可以发现，不管是远场路径增加还是近场路径增加，本文算法NMSE性能均好于远场和近场信道估计算法，且NMSE稳定在-4 dB左右。由此可知，本文算法在不同远场和近场路径数量下都能够达到良好的信道估计效果。

5 结束语

基于收发端均部署了均匀线性阵列的超大规模MIMO混合场信道进行建模。同时，为了更好地描述混合场信道，与基于散射体最后一跳模型相比，本文信道模型考虑了发送端到散射体，散射体到接收端两方路径分量。针对上述信道模型，基于OMP算法，提出了一种混合场信道估计算法。同时推导了CLRB对本文算法进行评估。最后通过仿真，验证了本文算法在使用较小的导频开销情况下，信道估计性能相比于只考虑远场和近场的信道估计算法在信道估计性能上提升了约0.6 dB，比文献[9]中的混合场算法提升了0.4 dB。在未来的XL-MIMO信道估计研究中，相比于均匀线性阵列，基于均匀平面阵列（UPA）的信道模型将会成为热门研究方向之一。

参考文献：

[1]Rappaport T S， Xing Yunchou， Kanhere O，et al. Wireless communications and applications above 100 GHz： opportunities and challenges for 6G and beyond[J]. IEEE Access， 2019，7： 78729-78757.

[2]Faisal A， Sarieddeen H， DahroujHghSU6dE/m0YPtX563+RhpqTVR6vxX9V3NUfbPEIrqY= H，et al. Ultramassive MIMO systems at terahertz bands： prospects and challenges[J]. IEEE Vehicular Technology Magazine， 2020，15（4）： 33-42.

[3]Lee J， Gil G T， Lee Y H. Channel estimation via orthogonal matching pursuit for hybrid MIMO systems in millimeter wave communications[J]. IEEE Trans on Communications， 2016， 64（6）： 2370-2386.

[4]Hu Chen， Dai Linglong， Mir T，et al. Super-resolution channel estimation for mmWave massive MIMO with hybrid precoding[J]. IEEE Trans on Vehicular Technology， 2018， 67（9）： 8954-8958.

[5]Liu Kaihui， Li Xingjian， Fang Jun，et al. Bayesian mmWave channel estimation via exploiting joint sparse and low-rank structures[J]. IEEE Access， 2019， 7： 48961-48970.

[6]Cui Mingyao， Dai Linglong. Channel estimation for extremely large-scale MIMO：far-field or near-field？[J]. IEEE Trans on Communications， 2022， 70（4）： 2663-2677.

[7]Huang Chun， Xu Jindan， Xu Wei，et al. Low-complexity channel estimation for extremely large-scale MIMO in near field[J]. IEEE Wireless Communications Letters， 2024，13（3）： 671-675.

[8]Wei Xiuhong， Dai Linglong. Channel estimation for extremely large-scale massive MIMO：far-field， near-field， or hybrid-field？[J]. IEEE Communications Letters， 2021， 26（1）： 177-181.

[9]Yang Wanning， Li Ming， Liu Qian. A practical channel estimation strategy for XL-MIMO communication systems[J]. IEEE Communications Letters， 2023， 27（6）： 1580-1583.

[10]Peng Xingxing， Zhao Lei， Jiang Yuan，et al. Channel estimation for extremely large-scale massive MIMO systems in hybrid-field channel[C]//Proc of IEEE International Conference on Communications. Piscataway， NJ IEEE Press， 2023： 1-6.

[11]Li Yiqing， Jiang Miao. ADMM-based hybrid-field uplink channel estimation for extremely large-scale MIMO systems[C]//Proc of IEEE International Conference on Communications. Piscataway， NJ： IEEE Press， 2023： 1-5.

[12]Nayir H， Karakoca E， Grin A，et al. Hybrid-field channel estimation for massive MIMO systems based on OMP cascaded convolutional autoencoder[C]//Proc of the 96th IEEE Vehicular Technology Conference. Piscataway， NJ： IEEE Press， 2022： 1-6.

[13]Hu Zhengdong， Chen Yuhang， Han Chong. PRINCE：a pruned AMP integrated deep CNN method for efficient channel estimation of millimeter-wave and terahertz ultra-massive MIMO systems[J]. IEEE Trans on Wireless Communications， 2023， 22（11）： 8066-8079.

[14]李汀， 张春洁， 夏雨婷. 超大规模混合场MIMO去伪峰信道估计技术[J]. 信号处理， 2023， 39（6）： 1131-1140. （Li Ting， Zhang Chunjie， Xia Yuting. Channel estimation technique for eliminating spurious peaks in ultra-massive hybrid-field MIMO[J]. Journal of Signal Processing， 2023， 39（6）： 1131-1140.

[15]Gong Zijun， Li Cheng， Jiang Fan，et al. Data-aided doppler compensation for high-speed railway communications over mmWave bands[J]. IEEE Trans on Wireless Communications， 2020， 20（1）： 520-534.

[16]Chen Binghao， Zhong Zhangdui， Ai Bo，et al. A geometry-based stochastic channel model for high-speed railway cutting scenarios[J]. IEEE Antennas and Wireless Propagation Letters， 2014， 14： 851-854.

[17]Zhou Erning， Jiang Hong， Qi Han. 4-D parameter estimation in bistatic MIMO radar for near-field target localization[C]//Proc of IEEE International Wireless Symposium. Piscataway， NJ： IEEE Press， 2015： 1-4.