复杂事件处理中多聚合查询共享方法

摘 要：复杂事件处理技术是在持续不断的流数据中检测满足特定事件序列或对匹配的事件进行统计的一种流数据处理技术。在处理带有Kleene操作符的事件趋势聚合查询时，需缓存中间结果来实现不定数量事件序列的匹配，故对查询系统的资源需求较大。利用多个查询之间存在的共享机会，生成用于指导查询处理的共享计划，可以有效提高事件趋势聚合查询的处理效率。但现有的聚合查询处理方法生成的共享计划无法做到随执行环境的变化而进行实时调整，来支持查询系统的持续高效处理。针对上述问题，提出了一种可以动态更新的多聚合查询共享方法，以支持实时变化的复杂事件检测的持续高效处理。通过提出共享图数据结构和代价模型，实现对所生成共享计划的实时调整，并引入在线增量聚合执行共享方法，进一步提升带有Kleene操作符的事件趋势聚合查询的处理效率。在真实数据集和模拟数据集上分别进行实验，并与其他处理聚合查询的方法进行了实验对比。实验结果表明，提出方法能够有效降低查询延迟，提高整体查询的处理性能。

关键词：复杂事件处理； 增量聚合； 多查询共享； 事件趋势

中图分类号：TP315 文献标志码：A

文章编号：1001-3695（2024）10-031-3100-10

doi：10.19734/j.issn.1001-3695.2024.02.0037

Multi-aggregate query sharing method in complex event processing

Dong Panpan， Su Hang， Gao Hongyu

（Faculty of Information， Beijing University of Technology， Beijing 100124， China）

Abstract：Complex event processing technology is a streaming data processing technique that detects specific event sequences or performs statistics on matching events in continuously flowing data. When processing trend aggregation queries with Kleene operators， caching intermediate results is necessary to match an indefinite number of event sequences， thus requiring significant resources from the query system. Exploiting opportunities for sharing among multiple queries， generating shared plans to guide query processing can effectively enhance the processing efficiency of trend aggregation queries. However， existing me-thods for handling aggregate queries do not dynamically adjust the generated shared plans in real-time to support continuous and efficient processing of complex event detection in response to changes in the execution environment. Addressing these issues， this paper proposed a dynamically updatable method for multiple aggregate query sharing to support the continuous and efficient processing of real-time changing complex event detection. By introducing the shared graph data structure and cost model， this method achieved real-time adjustment of the generated shared plans. And by using the online incremental aggregation execution sharing method， it further enhanced the processing efficiency of event trend aggregation queries with Kleene operators. This paper conducted experiments on both real and simulated datasets， compared the method with other approaches for handling aggregate queries. The results of the experiments indicate that the method effectively reduces query latency and improves the overall processing performance of queries.

Key words：complex event processing（CEP）; incremental aggregate; multi-query sharing; event trend

0 引言

复杂事件处理（CEP）是一种在事件存储前对连续的事件流进行处理的技术［1］，其目的是根据一组预定义的模式实时地识别有意义的事件或者事件组合［2，3］。CEP广泛应用于股票、交通运输和公共卫生等领域［4］。这些应用通常依赖于使用包含Kleene操作符的复杂查询模式。用Kleene操作符表示的子模式能够匹配一个或者多个与该模式匹配的事件序列（称为事件趋势）［5］。由于事件趋势是任意长度的，所以带来的计算成本非常高，对于这类查询的大量工作负载，实时响应难以保证［6，7］。

在实际应用中，CEP往往需要同时处理多个查询，并且查询之间存在大量共享数据［8］。事件趋势的多查询优化技术涵盖了对聚合函数的处理和多查询的共享优化。作为复杂事件处理的核心研究方向之一，其主要目标是通过共享工作负载中的查询计算，以有效降低并发查询的处理成本［9］。在处理事件趋势聚合查询时，优化技术首先需识别Kleene模式的共享机会，其次需要确定如何充分利用这些共享机会以加快指定工作负载的执行过程。

在聚合查询处理领域，已经有了丰富的研究成果。最初的两步法首先构造所有的事件趋势，再从这些事件趋势中统计聚合值［6］。Poppe等人［2］为应对CET（complex event trend）中共享公共事件子序列导致的性能问题，提出了CET图的概念，对所有查询匹配的CET进行编码。接收到新事件时，系统从每个结束事件节点向前遍历以查找与新事件匹配的事件。因此这种设计方法在新事件发生时会增加CET图遍历的成本，存在因部分结果呈指数增长而导致内存爆炸的问题。Zhang等人［10］对CEP中的模式查询进行了深入分析，详细阐述了导致趋势聚合代价高昂的查询特征。并将现有的CEP系统映射到相同的层次结构中，为比较不同系统提供了一致的理论框架。这种两步法处理聚合查询时需要先进行模式匹配，生成所有的事件序列之后进行统计。尤其是在处理Kleene操作符时，相同的事件可能会被存储上百至千次，不仅需要大量的内存存储中间结果，还需要额外的时间开销用于统计聚合值，导致处理效率较低。

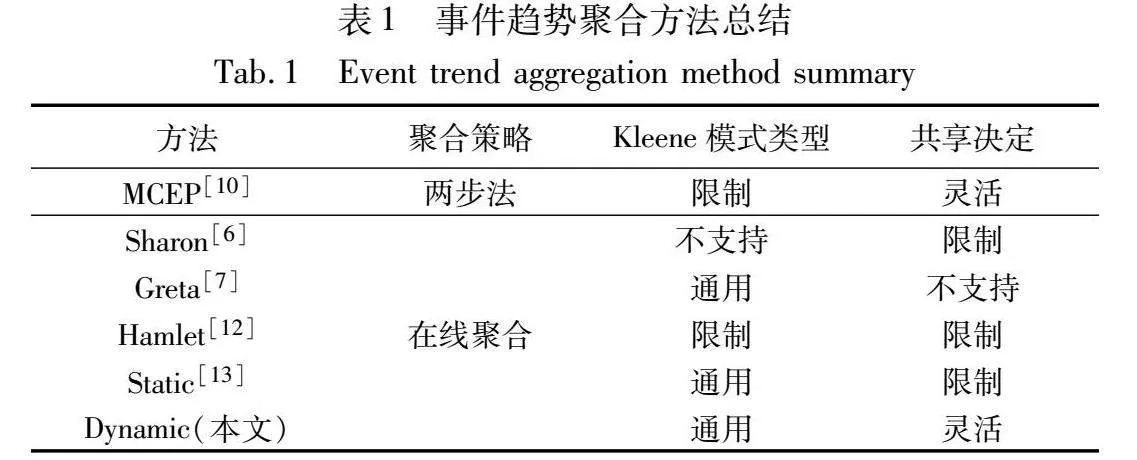
在线聚合方法［11］将聚合操作整合到模式匹配阶段，避免了先构建事件趋势的复杂性，将计算复杂度从指数级降低到线性。然而在线聚合方法在处理特定场景下存在两个关键限制。表1按照三个维度对现有的在线聚合方法进行了优劣对比。

首先，模式中可以包含SEQ和Kleene操作符，在对包含Kleene模式的查询处理上，现有方法大多限制或完全禁止事件趋势聚合中的Kleene模式［13］。MCEP［10］仅支持共享非嵌套Kleene模式，而Sharon［6］仅支持共享固定长度的SEQ模式，不支持共享Kleene模式。对Kleene模式的这种限制降低了共享方法的适用性。其次，现有方法对共享决策施加严格的限制。Sharon引入了共享冲突的概念，限制一个子模式参与多个共享查询组。Hamlet［12］和Static［13］方法是事件趋势聚合查询处理方法，均对Kleene操作符和查询之间的共享执行进行了优化，是目前处理效果较好的两个方法，但是分别具有不同的局限性。Hamlet仅关注非嵌套Kleene子模式的单一事件类型的共享机会。Static方法通过预先生成共享计划，然后按照生成的共享计划严格执行聚合计算。这种不关注动态变化信息的方法通常会导致次优的共享计划，错过潜在的共享机会。

在查询优化方面，主要涉及对多个查询的共享和对嵌套查询的处理［14］。多查询共享技术通常利用查询操作符的交换性和结合性来支持查询中的语义等价［15］，即原始查询可能会更改为不同的形式，但输出应保持不变。SASE［16］和ZStream［17］分别利用自动机和树结构处理单一查询模式，在处理包含Kleene操作符的查询和嵌套查询时性能较差且不支持查询共享。MOTTO［15］利用合并、分解和操作符转换共享三种技术减少模式查询的冗余计算，设计多查询优化器提高并发模式查询的性能，但不支持包含Kleene操作符的查询。处理嵌套查询时，存在两个主要问题：首先，某些可共享的内部查询的完整结果可能在共享结果前被直接丢弃［18］；其次，嵌套否定子表达式中只需检测到其中一个事件即可否定整个结果，但是执行时仍需要生成完整的结果［19］，导致资源浪费。大多数CEP系统通常通过转变操作符来处理包含嵌套模式的查询［20］。NEEL［20］使用查询重写技术处理嵌套模式查询，使用基于堆栈的查询评估策略和迭代嵌套执行策略处理嵌套查询。但在处理带有Kleene操作符的查询时仍存在指数级时间复杂度。

针对以上问题，给定包含SEQ和Kleene操作符以及嵌套模式的事件趋势聚合查询工作负载。本文设计共享图数据结构，将共享优化问题映射为图路径搜索问题，获取所有可能的共享计划。设计生成和修剪图的代价模型，考虑事件流和工作负载的特征，确定查询在子模式上的共享方案，并实时调整共享计划。引入在线增量聚合执行共享方法，提升事件趋势聚合查询的处理效率。

综上所述，本文的主要贡献如下：

a）提出了一种共享优化方法，用于处理包含Kleene模式的事件趋势聚合查询。将涉及Kleene子模式工作负载的共享问题抽象为加权有向无环图的最短路径搜索问题，为工作负载提供了灵活的共享策略。在生成图的过程中进行修剪，以降低后续路径搜索的时间复杂度，从而提高执行效率。

b）设计了一种综合考虑事件流和工作负载特征的代价模型，将其引入到共享图的生成和路径搜索过程中，在这些特征发生变化时高效更新共享计划，并应用于执行过程。

c）引入在线趋势聚合方法，使用动态更新的共享计划指导多聚合查询结果的增量计算。

d）在真实和模拟数据集上对本文方法进行对比实验和分析，验证了动态更新共享计划方法的适用性和高效性。

1 相关概念

1.1 基本概念

定义1 事件流。事件流I由事件源［21］（如车辆和移动设备）生成的一组连续的事件组成。事件e是描述应用程序所关注事件的数据元组，每个事件含有一个由事件源分配的时间戳e.time［22］。原始事件e属于一个特定的事件类型E，表示为e.type=E，由指定该事件属性集及值域的模式来描述该事件。E的特定属性attr表示为E.attr。本文假定事件按时间戳顺序到达，文中的符号和解释如表2所示。

定义2 事件序列模式P。事件序列模式P定义事件流中的特定事件序列或结构，由操作符和事件类型组成。模式P的形式可以包含E，P1+，（NOT P1），SEQ（P1，P2），（P1∨P2），（P1∧P2），其中E是一个事件类型、P1和P2是模式、+表示Kleene操作符，NOT表示否定，SEQ是事件序列，∨是析取，∧是合取，P1和P2称为P的子模式。

定义3 Kleene模式。在定义2中的事件序列模式P中，如果P中包含Kleene操作符，那么P就是一个Kleene模式，如果P中的一个Kleene模式的结果应用于另一个Kleene模式，那么P就是一个嵌套Kleene模式［23］。否则，P是一个平坦Kleene模式。

定义4 聚合。在数据库和数据处理领域，聚合是指通过汇总、组合或计算数据集的值，生成单一的结果。这个结果可以是一个总和、平均值、计数，或者其他统计性质的值。

定义5 事件趋势聚合查询。事件趋势聚合查询由5个子句组成。

RETURN子句：返回的聚合结果值；

PATTERN子句：定义2中介绍的事件序列模式；

WHERE子句：谓词（可选）；

GROUPBY子句：分组（可选）；

WITHIN/SLIDE子句：窗口。

定义6 可共享的模式。一个工作负载Q由一组查询组成。如图1所示，工作负载Q1={qa，qb，qc}。给定一个事件趋势聚合查询的模式P和一个工作负载Q，如果P出现在至少两个查询的模式子句中，则这个模式P是可共享的。在图1中，三个查询都包含子模式（P，T）+，（P，T）+即可共享的子模式。

Uber（主要业务是提供网约车服务和食品配送服务）和Door Dash（在线食品配送平台）使用复杂的事件趋势聚合查询来进行价格计算、预测和路线选择［12］。由于每个地区有数百名用户、数千次交易和全国数百万个地区，实时事件分析成为一项具有挑战性的任务。

如图1所示，查询工作负载计算各种行程统计信息，例如每个地区的订单总数、总持续时间和平均速度。工作负载Q1包含qa，qb，qc三个事件趋势聚合查询，每个查询匹配不同的订单事件趋势。每个事件类型对应客户或送餐员的操作，例如AppOrder和WebOrder分别表示来自APP和网页上的订单。事件流中的每个事件都是由客户和送餐员标识符、操作、地区和时间戳组成的元组。实际应用中，送餐员通常会在附近接多个订单，以缩短行驶路程，因此事件趋势中可出现任意次数的（P，T）+。查询qa的返回值为在任意平台下单并在30 min内完成配送的订单数量。谓词［driver_id］要求订单中的所有事件必须具有相同的送餐员标识符。查询qb返回在APP下单且送餐地点为泳池的订单数量。查询qc的返回值为在APP下单但是送餐员行驶速度小于10，因此客户取消的订单数量。三个查询都包含可共享的子模式SEQ（R，（P，T）+），然而共享SEQ（R，（P，T）+）并不是唯一的共享方案。qa和qb可以共享更长的子模式SEQ（R，（P，T）+，D），而qb和qc包含另一个更长的子模式SEQ（A，R，（P，T）+）。因此在实际应用中，共享包含SEQ和Kleene子模式的查询，并解决多个相互冲突的共享机会，以最大化共享收益，是一项复杂的任务［24］。

聚合函数。本文关注可以递增计算的聚合函数，对一组值执行计算并返回单一的统计结果值［25］。令e为E事件类型的事件，attr为e的属性。COUNT（*）返回事件趋势的数量，MIN/MAX（E.attr）返回所有事件趋势中事件e的attr最小（最大）值，SUM（E.attr）/AVG（E.attr）计算事件趋势事件e的attr值的总和或平均值。本文使用COUNT（*）作为默认聚合函数。

1.2 事件趋势聚合共享问题

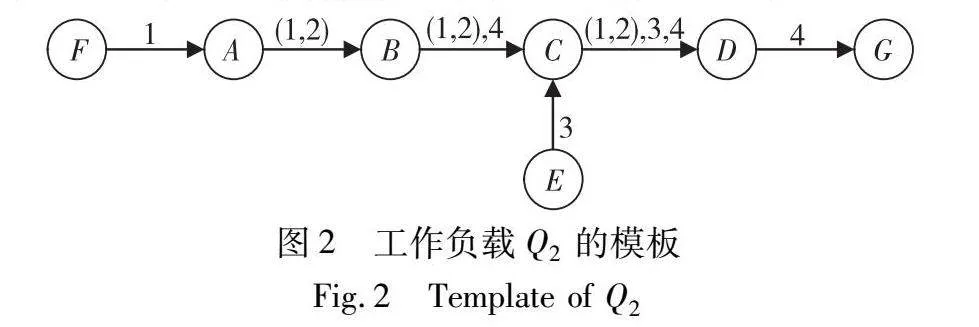
为了便于分析多个查询之间的共享机会，采用SASE中的方法将查询工作负载表示为有限状态自动机，称为模板。模板中的每个节点表示查询中的事件类型E，结束事件类型的节点加粗表示。模板中的“→”（转换）对应事件序列模式P中的操作符，连接P中的两个相邻的事件类型Ei和Ej，表示为convert（Ei，Ej）。在查询q中，Ej之前的事件类型Ei表示为pe（Ej，q）。查询工作负载Q2由四个查询组成，Q2={q1，q2，q3，q4}，分别为：q1=SEQ（F， D），q2=SEQ（ D），q3=SEQ（E，C，D），q4=SEQ（B，C，D，G）。

按照SASE中的模板生成方法，Q2生成的模板如图2所示。模版中存在多个共享机会，查询q1，q2可以共享SEQ（A，B，C）的转换，查询q1，q2，q4可共享SEQ（B，C，D）的转换。

每个convert上的共享方案将一个工作负载中具有该convert的所有查询划分为一个查询集QS，以确保每个QS中的查询可以分别共享由该convert建模的执行过程。图2中convert（B，C）上的（1，2），4分别表示查询q1，q2，q4，若查询q1，q2在执行时进行共享，那么convert（B，C）的一个Qs为{q1，q2}。

定义7 工作负载共享计划。给定工作负载Q的模板，模板中所有convert的共享方案组成一个工作负载共享计划。

2 动态共享方法

给定事件趋势聚合查询工作负载Q和高速事件流I，多事件趋势聚合查询问题就是在事件流I上评估工作负载Q，使得Q中所有查询的平均查询延迟时间最小［12］。

2.1 动态共享方法框架

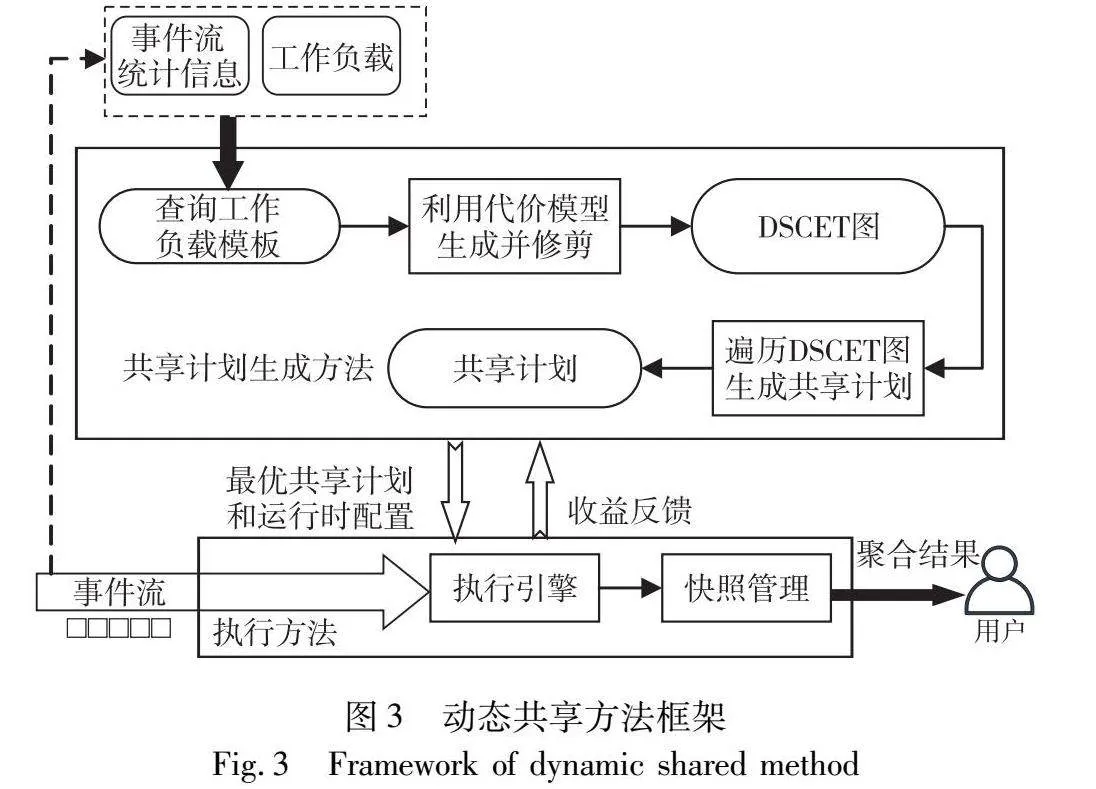
聚合查询的动态共享方法分为共享计划生成方法和聚合查询执行方法两部分。共享计划生成方法首先将查询工作负载转换成模板，并分析潜在的共享机会。分析事件流和工作负载的特征以及共享收益，构建出代价模型。根据模板和代价模型生成加权有向无环图，编码所有可能的共享机会。在生成图的过程中对图进行修剪，最优的共享计划对应图中权重最小的路径。图3展示了动态共享方法的框架。

执行方法使用共享计划生成方法生成的共享计划，在事件流I上评估工作负载Q。引入在线聚合方法［12］，将中间聚合从已经匹配过的事件传播到新的事件，利用快照维护每个查询的中间聚合值，以增量方式计算趋势聚合值，避免中间结果的构造。当事件流统计信息或者工作负载发生变化时，将信息反馈回共享计划生成方法中，根据当前事件流状态更新共享计划并重新作用于执行过程中。

2.2 执行方法

执行过程采用在线增量聚合的方法支持非共享和共享执行。通过以下例子说明执行代价，工作负载Q3={q2，q4}，其中q2=SEQ（ D），q4=SEQ（B，C，D，G），两个查询的返回值均为COUNT（*）。Q3在事件流S（a1，a2，b1，c1，c2，d1，d2，g1）上进行查询，并且Q3中有一个共享查询集QS={q2，q4}。

a）非共享执行聚合。在执行过程中，对于匹配事件e的每个查询，维护一个中间聚合值，表示q匹配的以e结尾的聚合数。在执行过程中e的值递增，递增的值为由q匹配的e的前驱事件的中间聚合的总和。如果e是q的结束事件类型，则将此聚合值作为查询q的最终结果输出。

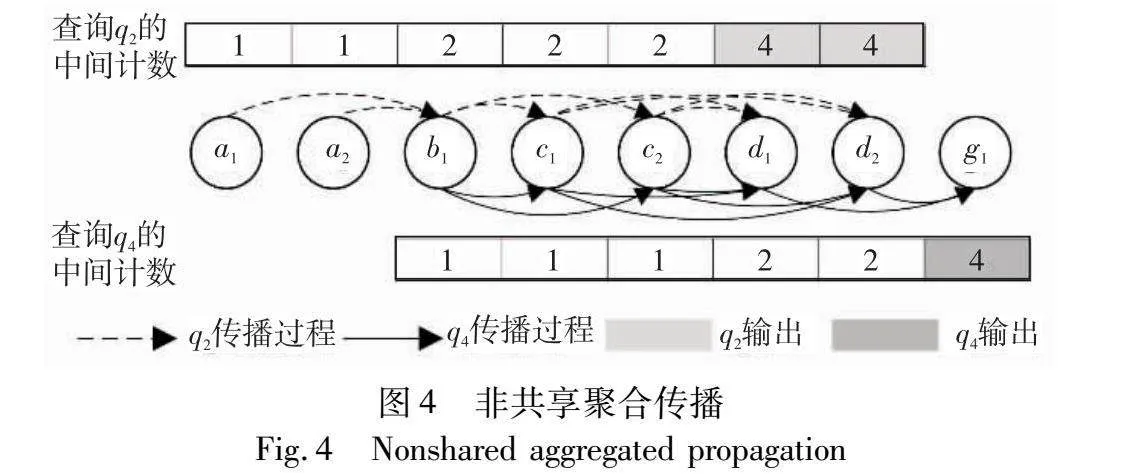
图4为工作负载Q3在事件流I上的非共享执行情况。当b1到达时，分别为q2和q4创建新的计数，其中间聚合值对于查询q2和q4来说分别为2和1。当事件c1到达时，其对于q2和q4的中间聚合从它的前置事件b1传播得到。对于后续每个事件，在为每个查询传播聚合值时将前置事件的聚合值求和得到其中间聚合值。最后当d1到达时，其中间聚合结果4作为查询q2的最终聚合值输出。查询q2和q4的执行成本在于将中间聚合值从前置事件传播到新到达事件的聚合值中。例如：cost（c1，q2）=cost（c1，q4）=1，cost（c2，q2）=cost（c2，q4）=1。对于工作负载Q3，所有C类事件的非共享执行代价为cost（C，Q3）=1×2+1×2=4（由b1指向c1和c2均有两个箭头）。

因此得出对于给定的工作负载Q，事件类型E非共享执行时的代价为

costnonshare（E，Q）=∑q∈Q ∑Ep∈pe（E，q）|E|×|Ep|（1）

其中：q为工作负载Q中的查询；|E|和|Ep|分别表示E的事件统计信息和E的前置事件Ep的事件统计信息。

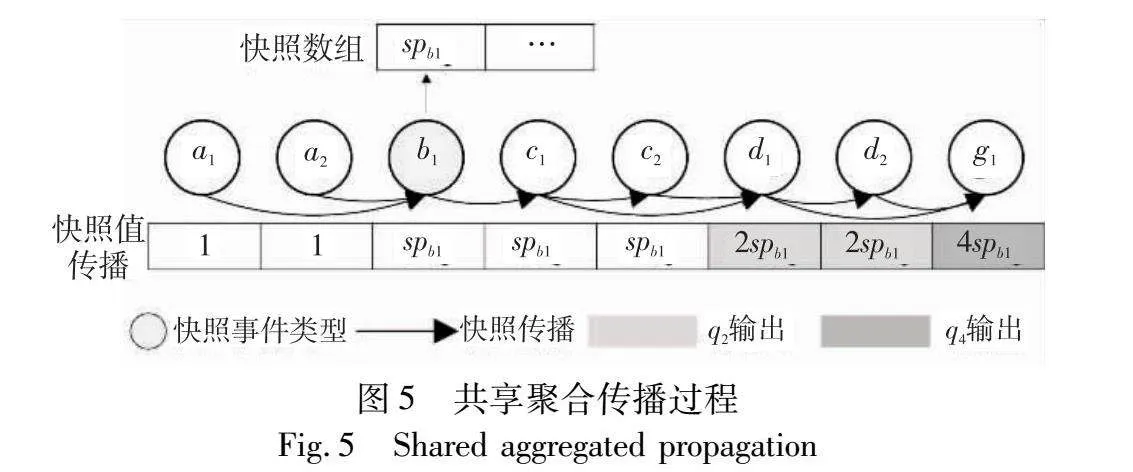
b）共享执行聚合。非共享在线聚合会导致对多个查询的公共子模式进行重复计算，如图4所示，对于q2和q4来说，b1到c1的中间聚合均需要被传播一次。为了避免这种重复计算，利用快照来支持高效共享。快照可以是与查询的中间聚合相对应的一个变量，也可以是一个由多个快照值组成的表达式。执行方法在传播过程中通过对其前置快照进行求和不断更新快照值。共享快照的所有查询对应的中间聚合值以map的形式存储在快照中，执行时只需要从前置事件到当前事件进行一次快照传播。如果e的事件类型为查询q的结束事件类型，则会进行快照值的计算，并输出聚合结果。

图5为Q3的共享执行情况。查询q2和q4在共享公共子模式SEQ（B，C，D）时使用事件类型B的快照进行共享，表示为（2，4）B。b1到达时，q2和q4的中间聚合值分别为2和1，将每个查询对应的值存储到新的快照spb1，之后将spb1插入到快照数组中。对于共享查询集QS即整个工作负载Q3，到事件类型C的传播由4次减为2次：cost（C，QS）=cost（C，Q3）=2。

得出一个查询集QS将快照传播到事件类型E的代价为

costshare（E，QS）=|Ep|×|snap（Ep，Qs）|=

（Ep==Esn）？|Ep|：|Ep|×|Esn|（2）

其中：Ep表示事件类型E的前置事件；snap（Ep，QS）为Ep对于QS的快照事件表达式，表示为Esn；|Esn|为其事件发生频率。满足括号中的等式时选取“：”前的表达式进行计算，不满足时选取冒号后的表达式进行计算。若一个工作负载Q中有多个QS，则Q对于事件类型E的共享执行代价为

costshare（E，Q）=∑QSQcostshare（E，QS）（3）

其中：Q表示工作负载;QS为Q中的共享查询集;costshared（E，QS）为式（2）中QS对事件类型E的执行代价。

如果E是查询q的结束事件类型或者需要创建新的快照，就会触发对快照表达式的求值。对于事件类型D，当d1到达时，需要为q2输出聚合结果：costeval（D，Q4）=cost（D，q2）=|B|×|D|=2。

对于一个工作负载Q，快照表达式的计算代价为

costeval（E，Q）=∑q∈Q|Ep|×|snap（E，q）|（4）

3 动态更新图方法

本文设计共享计划图模型，将工作负载共享计划问题转换为最佳路径搜索问题。给定工作负载模板，分析模板中每个转换的共享机会。根据模板生成共享计划图，涵盖工作负载中所有可能的共享计划，为生成最优的共享计划提供搜索空间，使共享收益最大化。

3.1 共享计划图模型

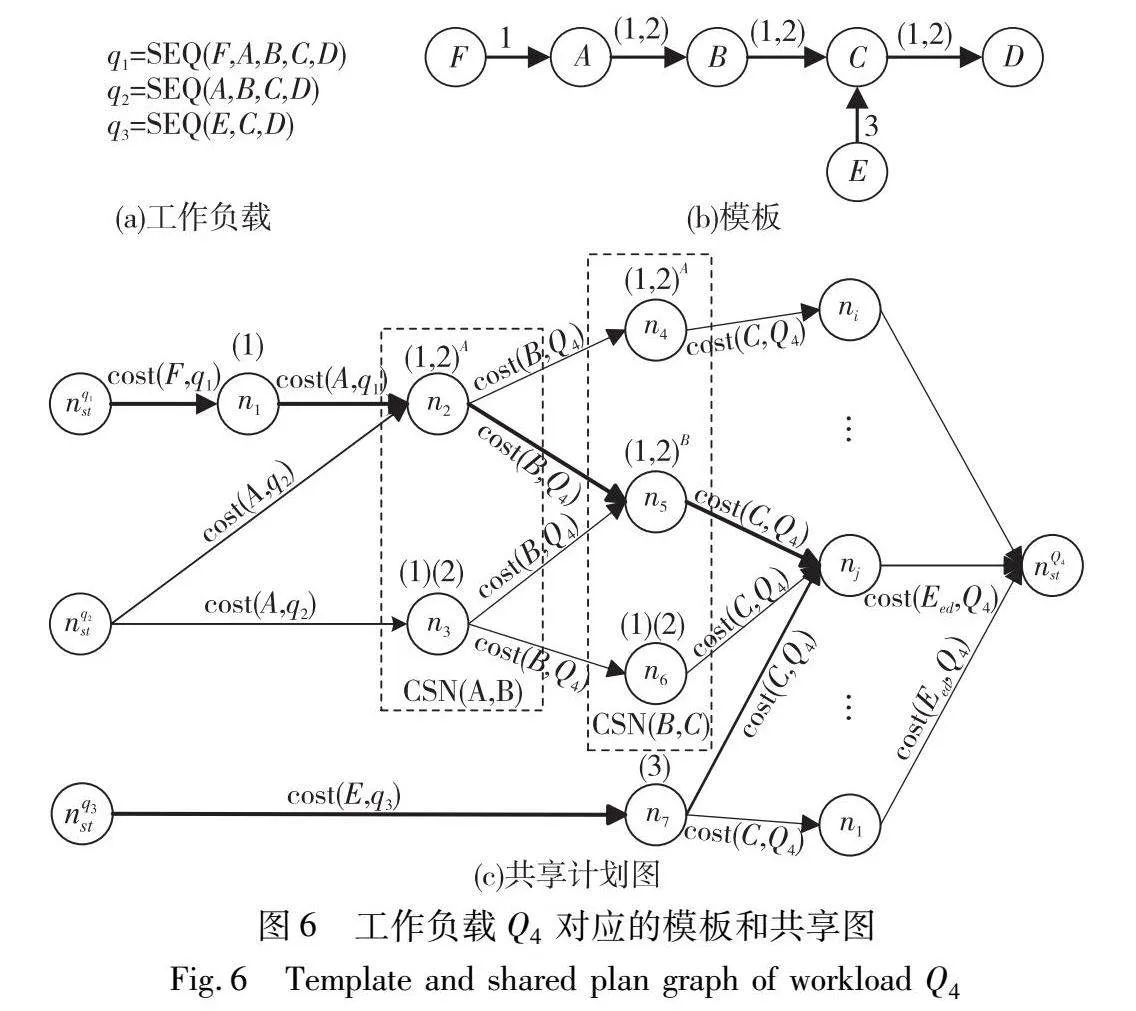
定义7 共享计划图。共享计划图（简称为共享图）是一个具有节点集和有向边集的加权有向无环图。图6（c）为一个共享图模型，图中的节点nk表示convert（Ei，Ej）的一个共享方案，Ei和Ej为两个相邻的事件类型，Eh为Ej的后置事件。开始节点nqst指示一个查询q的开始，结束节点nqed指示一个查询q的结束，如果部分查询Qe具有相同的结束事件类型，则可以为Qe生成同一个结束节点nQeed。convert（Ei，Ej）的所有候选共享方案节点（candidate sharing node，CSN）组成CSN（Ei，Ej）。如果存在nk和nm属于相邻的两个CSN，则有向加权边edge（nk，nm）连接nk到nm。设QS为nk（convert（Ei，Ej））和nm（convert（Ej，Eh））的一个共享查询集，那么edge（nk，nm）的代价w代表在执行nk到nm的共享方案时整个工作负载Q中所有的QS对Ej的执行代价（cost（Ej，Q））。

工作负载Q4包含3个查询，Q4={q1，q2，q3}，其中q1=SEQ（F， D），q2=SEQ（ D），q3=SEQ（E，C，D）。图6（c）中CSN（A，B）对应的convert（A，B）的共享方案有n2和n3，CSN（B，C）对应的convert（B，C）的共享方案有n4，n5，n6。n2上的（1，2）A表示查询q1和q2通过共享事件类型A的快照执行快照的传播，n3上的（1）（2）表示查询q1和q2各自执行聚合结果的计算。nq1st，nq2st，nq3st分别表示查询q1，q2，q3的开始。

CSN（A，B）和CSN（B，C）这样的连续CSN中的节点相连，每个nk∈CSN（A，B）都有一条出边指向nm∈CSN（B，C）。图6（b）中convert（A，B）上有两个查询q1和q2，在图6（c）中n2到n5的共享方案中两个查询共享执行，因此edge（n2，n5）.w=costshare（B，Q4）=cost（B，q1）（或cost（B，q2））。n3到n6查询q1和q2非共享执行，因此edge（n3，n6）.w=costnonshare（B，Q4）=cost（B，q1）+cost（B，q2）。由于工作负载Q4中的三个查询具有相同的结束事件，所以nQ4ed表示整个工作负载的结束。

共享图中的所有开始节点到结束节点的路径表示整个工作负载中的所有共享计划，代价最小的路径对应当前情况下的最优共享计划。图6（c）中当前最优共享计划为加粗表示的路径。

3.2 共享图生成

3.2.1 节点生成原则

如果两个连续的节点共享不同的查询或者快照，执行时需要按照式（4）不断进行快照的计算和更新，以适应具有不同QS和快照的共享计划，从而损害共享收益。为了使共享收益最大化，为尽可能多的convert保留一个QS。因此在生成节点时，不是在每个CSN中独立枚举节点［18］，而是从一个节点nk∈CSN（Ei，Ej）生成下一个节点nm∈CSN（Ej，Eh）。CSN（Ei，Ej）中的节点nk可以在CSN（Ej，Eh）中生成多个节点，但是并非所有节点都值得生成。如果已知生成的节点nm∈CSN（Ej，Eh）的入边和出边的权重大于同一个CSN中的其他节点，与其他节点相比，这样的局部高代价节点nm不会生成。

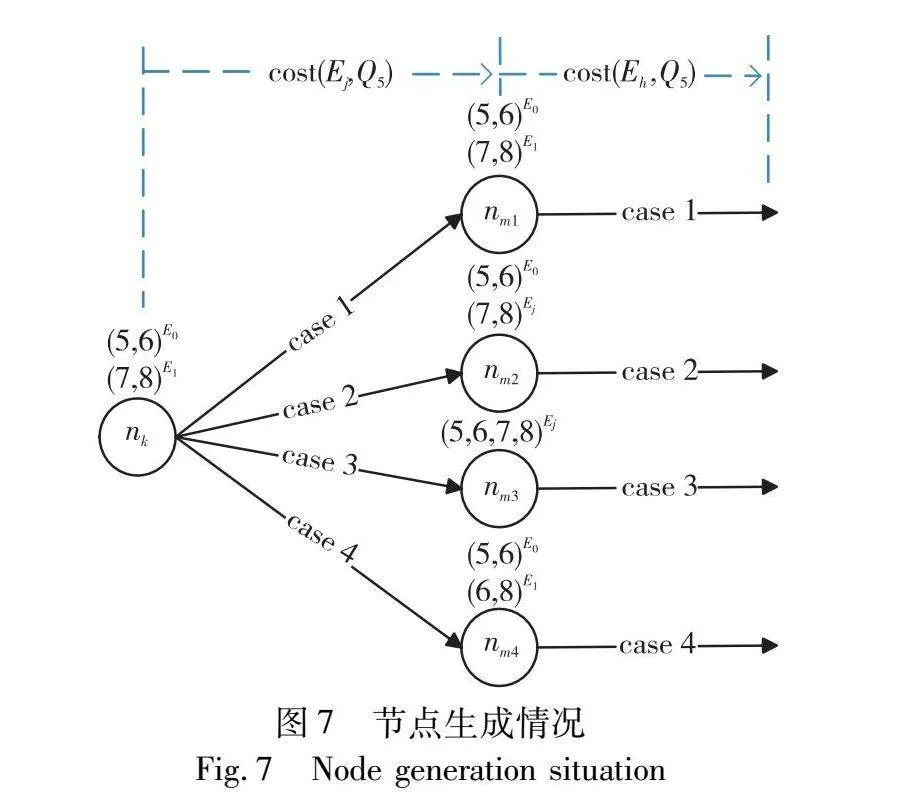
假设在节点nk中，工作负载Q5={q5，q6，q7，q8}中有两个共享查询集：Q1S={q5，q6}，Q2S={q7，q8}。nk的共享方案为查询q5和q6共享事件类型E0的快照，查询q7和q8共享事件类型E1的快照，在图7中表示为节点nk上的（5，6）E0，（7，8）E1。由节点nk∈CSN（Ei，Ej）生成CSN（Ej，Eh）中的节点有四种可能，如图7所示。case 1继承所有来自nk的查询集和快照；case 2保持nk的查询集不变，为查询集Q2S生成新的快照；case 3合并所有的查询集并为新的查询集生成新的快照；case 4更新了nk的所有查询集。根据式（4）得出，case 4生成的节点对应的入边和出边权重都很大，这样的局部高代价节点没有潜在的共享收益，因此不会生成这样的节点。下面根据case 1到case 3的三种情况，提出了三个节点生成原则。

a）节点生成原则1（继承原则）。给定一个节点nk∈CSN（Ei，Ej），生成节点nm∈CSN（Ej，Eh），nm继承所有来自nk的QS和快照。

对于这种情况生成的节点，如图7中的case 1所示，nm1维持nk的共享方案，继承来自nk的共享查询集和快照事件类型。在按照该计划执行时，只需要将快照传播到后续事件，不必按照代价模型计算式（4）进行快照表达式的计算。因此生成的节点只需要考虑共享成本，根据式（2）得出，nm1的入边权重为Q1s和Q2s的共享代价。继承原则生成的节点具有最小的入边权重：

edge（nk，nm1）.w=cost（Ej，Q5）=

costshare（Ej，Q1s）+costshare（Ej，Q2s）

b）节点生成原则2（更新快照原则）。给定一个节点nk∈CSN（Ei，Ej），当Ej的发生频率小于之前的快照事件类型的发生频率时，生成节点nm∈CSN（Ej，Eh），nm重用来自nk的QS并创建Ej的快照。

使用继承原则生成的节点没有考虑出边权重，经过nm1节点的路径可能在nm1之前具有较轻的权重但是在nm1之后具有较重的权重，导致后续利用该共享方案执行时具有较大的代价。因此需要考虑入边权重较大但是出边权重变小的情况，降低后续的执行代价。使用更新快照原则生成的节点需要额外的代价为共享查询集创建当前事件类型的快照，但是具有较小的出边权重。如case 2生成的节点nm2所示，nm2继承nk的共享查询集，当|Ej|<|E1|时，为Q2s创建事件类型Ej的快照。因此根据式（4），nm2的入边权重还需加上为Q2s生成Ej的新快照的代价。但是使用nm2这种共享方案在后续将快照传播到Eh时，Q2s的共享执行代价由式（2）中“：”前的计算表达式确定，具有较小的后续执行代价。nm2入边权重为

edge（nk，nm2）·w=cost（Ej，Q5）=costshare（Ej，Q1s）+

costshare（Ej，Q2s）+costeval（Ej，Q2s）

c）节点生成原则3（合并原则）。给定一个节点nk∈CSN（Ei，Ej），生成节点nm∈CSN（Ej，Eh），nm合并nk的QS并创建Ej的快照。

另一种降低执行代价的情况是工作负载中的所有查询都可以共享Ej的快照，可以合并所有的QS并为其创建Ej的快照。使用这种原则生成的节点虽然入边权重较大，但是后续只需要为一个共享查询集传播快照，降低后续事件Eh的执行成本。如case 3生成的节点所示，nm3合并所有的QS，因此不仅需要对Q1s和Q2s分别输出前一个共享查询集的聚合值，还要为新的共享查询集创建新的快照。得出nm3的权重代价为

edge（nk，nm3）·w=cost（Ej，Q5）=costshare（Ej，Q1s）+

costshare（Ej，Q2s）+costeval（Ej，Q1s）+costeval（Ej，Q2s）

使用合并原则生成的节点入边权重均大于继承和更新快照原则，但是后续执行时只需要为一个共享查询集传播快照，其执行代价由式（2）中“：”前的表达式确定。

综上所述，在构造共享图时，从开始节点按照生成原则1～3构造每个CSN中的节点。为每个节点nk∈CSN（Ei，Ej），生成多个nm∈CSN（Ej，Eh）并为其生成边和相应的代价，直至生成结束节点。

3.2.2 修剪原则

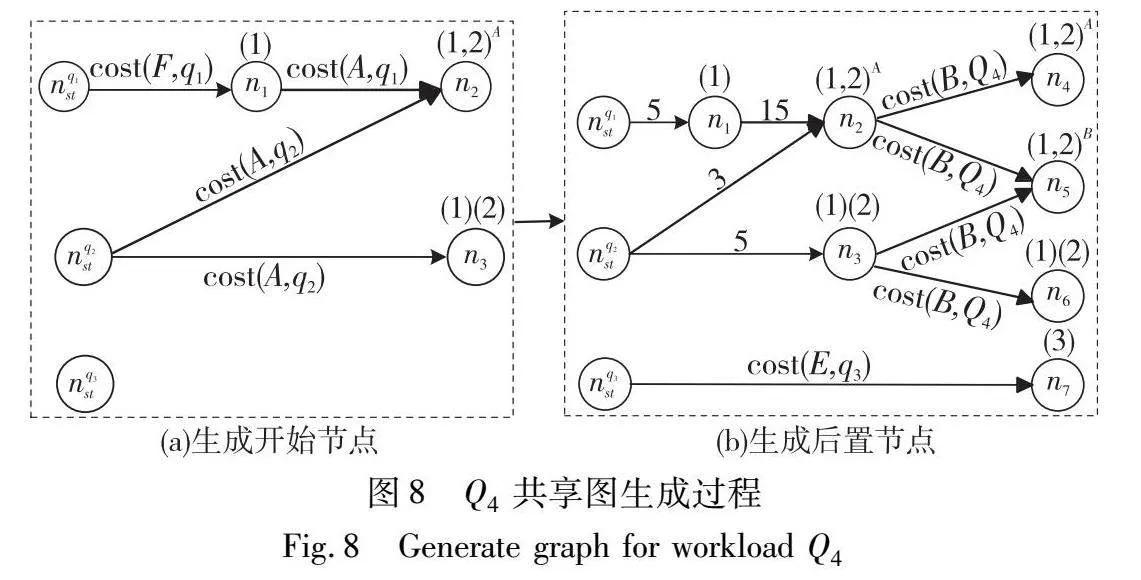
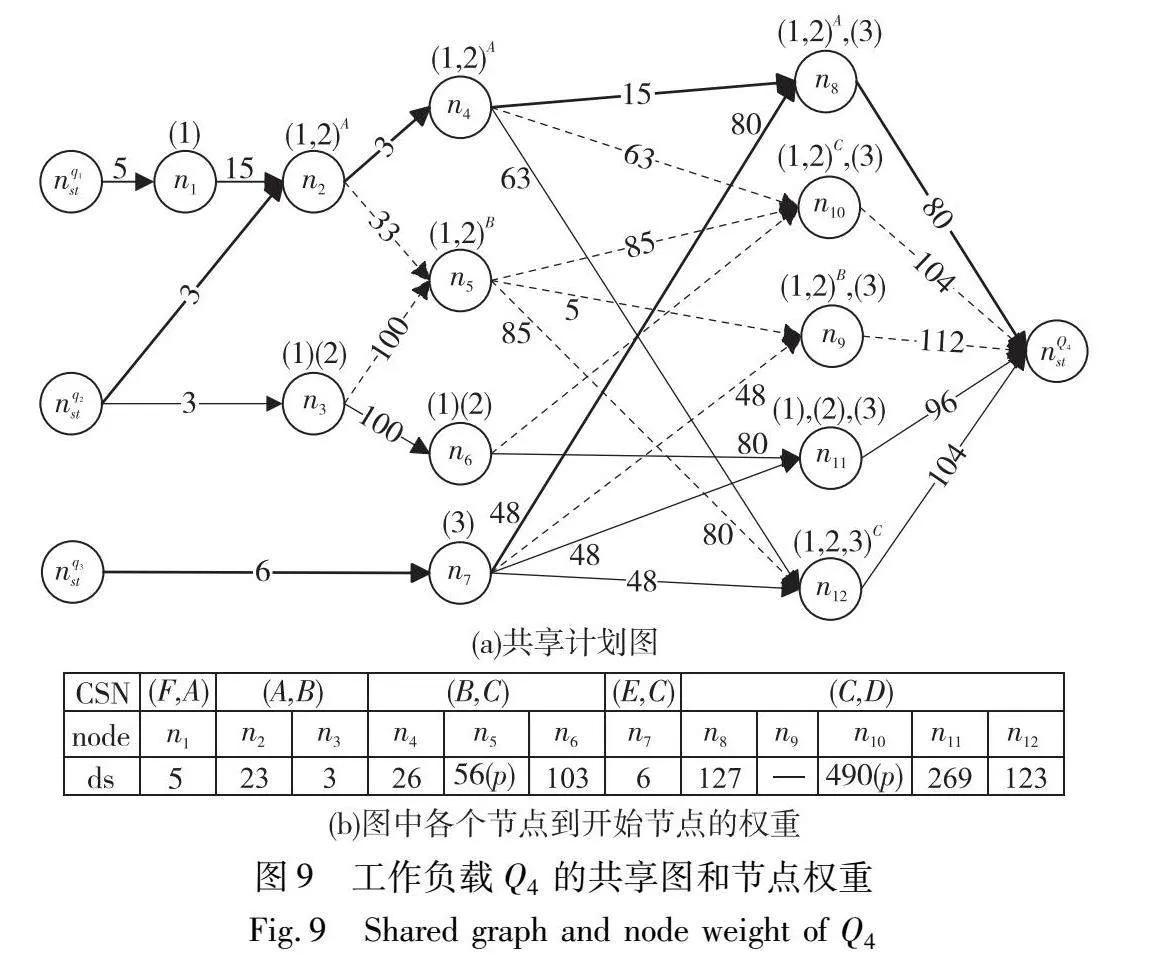
在构造图的过程中通过修剪边和每个CSN中的节点以减少图中的节点数量，这种策略虽然可能修剪掉更新时需要用到的节点，但是可以避免共享图在早期出现节点爆炸的现象，有利于初始共享计划的路径搜索［12，18］。以图6（a）所示的工作负载Q4为例，说明在生成共享图时的修剪过程。初始流统计信息为：|A|=3， |B|=5，|C|=8，|D|=4，|E|=3，|F|=5，工作负载Q4={q1，q2，q3}，对应的开始事件分别为A、B、F，因此为三个查询各生成一个开始节点，并为查询q1和q2生成共享计划。如图8（a）所示。

节点nq1st→n1需要考虑查询q1的开始事件F，由图6（b）可知F并未与任何查询共享，因此cost（F，q1）=|F|=5。由convert（F，A）可知下一步需要将聚合值传播到事件类型A并生成下一个共享方案节点n1。节点n1→n2需要为查询q1将聚合值传播到事件类型A并创建事件类型A的快照。因此cost（A，q1）=costshare（A，q1）=|F|×|A|。

生成的后置节点如图8（b）所示，在由节点n2生成后继节点的时候按照3.2.1节所述有两种选择。原则1：继续维持事件类型A的快照（节点n4）；原则2：创建事件类型B的快照（节点n5）。对于n2→n4，由于事件类型B的前置事件就是A，所以只需要对A的快照进行统计即可，且q1和q2共享A的快照，有cost（B，Q4）=costshare（B，Q4）=|A|=5；对于n2→n5，不仅需要将A的快照传播到B，还需要分别为q1和q2生成B的快照，因此cost（B，Q4）=costshare（B， Q4）+costeval（B，Q4）=|A|+2×|A|×|B|=33。后续节点根据节点生成原则生成整个共享图，结果如图9（a）所示。

如图9中的n5所示，nq2st到n5有两条路径，对于n2→n5，nq2st到n5的代价为36；对于n3→n5，nq2st到n5的代价为103。因此n3→n5的边可以修剪，修剪的边不影响共享计划的最优性。

边修剪原则：给定一个节点nm，当从起始节点到nm有多条路径时，只需保留权重最小的最优路径，其他路径通过的边可以安全地修剪。

命题1 按照边修剪原则修剪边之后，不会影响共享计划的最优性。

证明 通过反证法证明命题一，给定一个节点nm∈CSN（Ej，Eh），n0和n1分别是来自CSN（Ei，Ej）的两个节点，对应的边分别为edge（n0，nm）和edge（n1，nm），假设n0.ds+edge（n0，nm）.w<n1.ds+edge（n1，nm）.w。如果最优路径P沿edge（n1，nm）经过n1和nm，将P分为两部分，第一部分P1为所有的开始节点到节点nm，第二部分P2为nm到所有的结束节点。路径P的代价为：P.w=P1.w+P2.w=n1.ds+edge（n1，nm）.w+P2.w。当经过n0访问nm时对应的路径为代价为：.w=n0.ds+edge（n0，nm）.w+P2.w，得出.w<P.w，因此P不是最优路径，edge（n1，nm）可以安全地修剪。

节点n4和n5属于相同的QS={q1，q2}，但是分别具有不同事件类型的快照A和B，由于|A|<|B|，由式（2）和（4）得出n4.ds<n5.ds，并且n4.de<n5.de，节点n5可以安全地修剪，并且节点n9完全由n5生成，所以n9也会被安全地修剪。修剪后每个节点代价如图9（b）所示，根据两个修剪原则，图9（a）中的虚线部分的边和n5，n9，n10节点可以安全地被修剪。

给定同一个CSN中的两个节点，如果这两个节点属于同一个共享查询集，那么这两个节点是可比节点。

节点修剪原则：给定两个可比节点nm和nk，如果nm到所有开始节点和结束节点的权重都比nk大，那么节点nm可以安全地修剪，并且该节点的出边和完全由该节点生成的后置节点也可以安全地修剪。

命题2 按照节点修剪原则修剪节点之后，不会影响共享计划的最优性。

证明 通过代价模型证明命题2，给定CSN（Ej，Eh）中分别共享事件类型A和B的两个节点nk和nm，其中|A|<|B|。根据式（2）得出，由于nk的快照事件发生频率较小，应用nm的共享成本小于应用nk的成本。后续如果需要进行快照计算，根据式（4）得出A快照的计算成本小于B的计算成本，因此从nk到所有结束节点的路径权重比nm都小，并且nk.ds<nm.ds。因此节点nm可以安全地修剪。

3.2.3 对Kleene模式的优化

在执行过程中，Kleene模式可以匹配任意多个满足模式的事件趋势，其匹配的事件数量呈指数增长。因此本节重点关注对Kleene模式的共享优化，将Kleene模式的优化同其他部分隔离，为其构建Kleene子图。若需要同其他部分连接，则将Kleene子图的最优共享计划插入到共享图的相应位置，并在整个图中进一步修剪，得到全局最优共享计划。

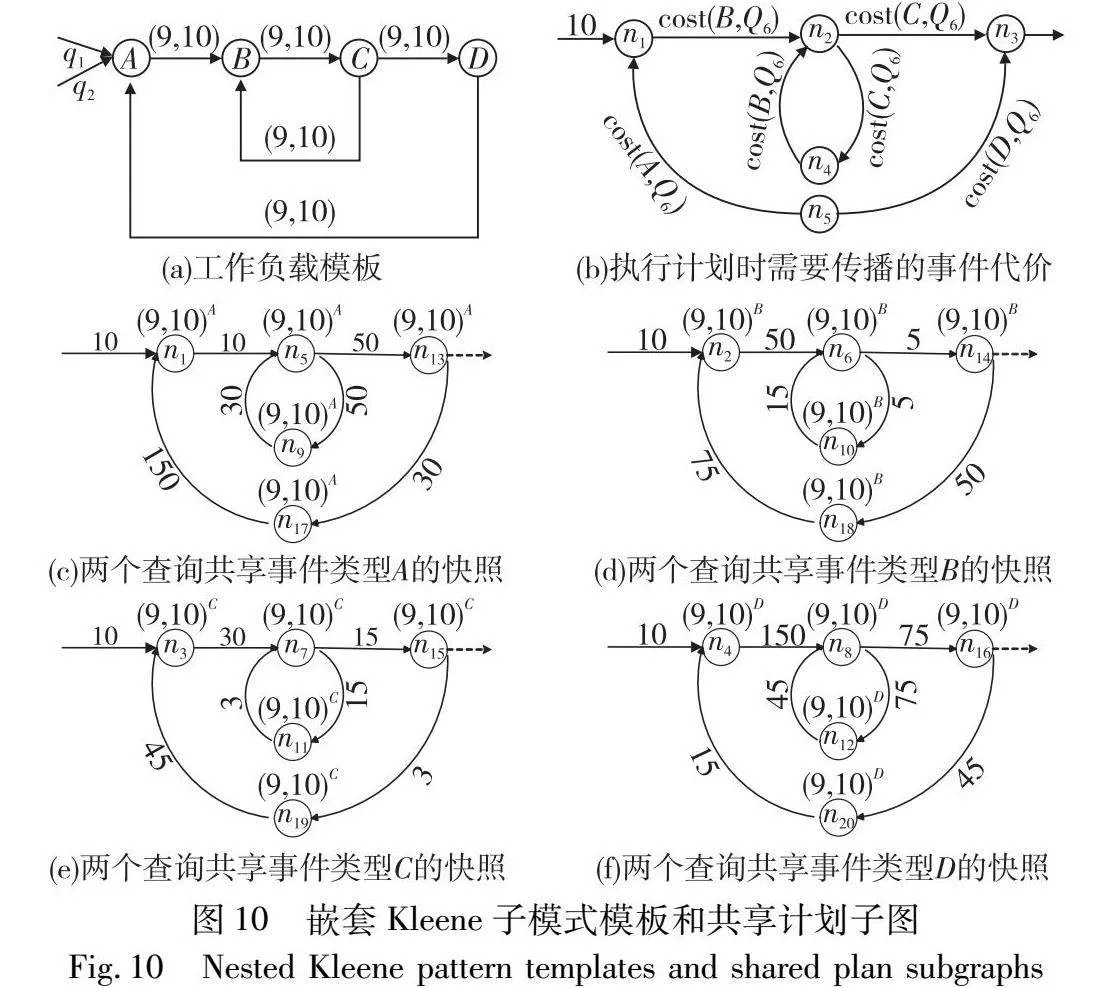
为了更有效地展示对Kleene模式的优化方法，本节以工作负载Q6={q9，q10}的共享计划生成过程为例进行介绍。假设工作负载Q6中的两个查询需要共享子模式SEQ（A，（B，C）+，D）+。图10（a）为Q6的工作负载模板，在该模板中存在两条可以构成循环的convert，分别为convert（C，B）和convert（D，A），将这种convert称为Kleene convert。

在共享图模型中，连续的两个CSN中的节点相连。图10（a）中的两个Kleene convert为convert（C，B）和convert（D，A），这两个convert的候选共享方案分别为CSN（C，B）和CSN（D，A）。两个CSN中的节点同样在Kleene子图也会构成循环。为方便区分，将Kleene子图的路径称为循环路径。在Kleene子图的所有循环路径中，具有不同的共享方案的路径会导致较高的执行代价，这样的路径没有必要生成。

59f06becbab66c0a32a773e36b26faade565e53186f898c3d58ec2fec5a6ec57

命题3 具有不同共享方案节点的循环路径可以安全地修剪。

证明 设nk和nm是循环路径P中的两个节点，共享查询集为QS，证明共享方案：nk=nm。若nk和nm通过不同事件类型的快照对QS进行共享（分别为E0和E1）。假设|E0|>|E1|，则根据节点生成原则（更新快照），由于nk的快照多于nm的快照，nk到nm之间一定存在一条具有潜在收益的路径。然而，由于P是一个循环，从nm到nk也存在一条路径。根据节点生成原则（更新快照原则），将快照数量从E0和增加到E1伴随着额外的计算成本，并不会带来共享好处。因此P.w一定会大于P′.w（P′经过的所有节点均通过事件类型E1的快照对QS进行共享）。P不是最优路径，循环路径P可以被安全地修剪。

排除上述不会生成的循环路径之后。提出循环路径生成原则：假设模板中存在平坦的Kleene子模式SEQ（E0，E1，…，Ek）+，该子模式的Kleene子图有k+1个CSN，其中k个是SEQ的CSN（Ei，Ei+1）（0≤i<k），一个是Kleene循环CSN（Ek，E0）。Kleene子图中的路径P是一个循环，包含每个CSN中的一个节点。当且仅当路径P经过的所有节点使用的是相同事件类型的快照共享相同的QS时，才会生成循环路径P，否则，所有节点上的共享方案均是非共享执行。

循环路径生成原则同样适用于嵌套Kleene子模式的Kleene子图，对应的路径是嵌套循环路径。由于每个单循环路径中的节点具有相同的共享方案，那么嵌套循环路径中的所有节点同样具有相同的共享方案。

以工作负载Q6为例，事件流统计信息分别为：|A|=10，|B|=5，|C|=3，|D|=15。图10（b）表示从节点nk∈CSN（Ei，Ej）生成节点nm∈CSN（Ej，Eh）时需要传播的事件类型的执行代价，图10（e）（f）分别为选取不同事件类型的快照进行共享的嵌套循环路径。路径中的每条边都用代价模型计算的权重进行标记。

同样对Kleene子图采用修剪原则，对高代价的节点进行修剪。对于每条路径，都有一条来自Kleene子图前一部分共享图的边，以及作为后续延伸的源节点nk，令nk.ds为各路径的权重。工作负载Q6都从事件类型A开始，n1到n4来自同一个节点，入边权重均为10。各节点到开始节点的代价如表3所示。

选取事件类型C为快照事件类型时，整个共享执行过程代价最小，因此选择C为此工作负载的快照事件类型。

3.3 共享计划更新方法

在处理事件趋势聚合查询时，可能发生变化的信息有事件流统计信息和工作负载信息。当工作负载减少时，直接从当前共享计划中删除对应的查询，并且不再为该查询传播聚合值以及生成最后结果。当工作负载增加时，由于在已经生成的共享图中搜索可共享的节点需要消耗大量的内存，所以只为新的工作负载单独生成共享计划，不再参与之前的共享。

本文设计了检测更新计划的代价模型，用于实时更新共享计划方法，提高事件趋势聚合查询的处理性能。当事件流统计信息发生变化时，对于带有Kleene操作符的工作负载，在3.2.3节已经详细阐述过Kleene模式和SEQ模式单独分析共享机会，因此只需单独进行更新。

在事件流信息发生变化时，需要考虑以下两个问题：a）是否需要更新共享计划；b）需要更新计划时，如何更新节点的信息。分析发现，未参与共享的事件类型频率发生变化，或者快照事件类型的发生频率变小时，根据式（2）得出不会更改共享的快照事件类型，因此不需要更新共享计划，按照原计划执行；参与共享的快照事件类型频率变大或者快照事件类型的后置事件频率变小，则需要考虑更新共享计划，并将新的共享计划应用到后续的执行过程中。判断条件如下。

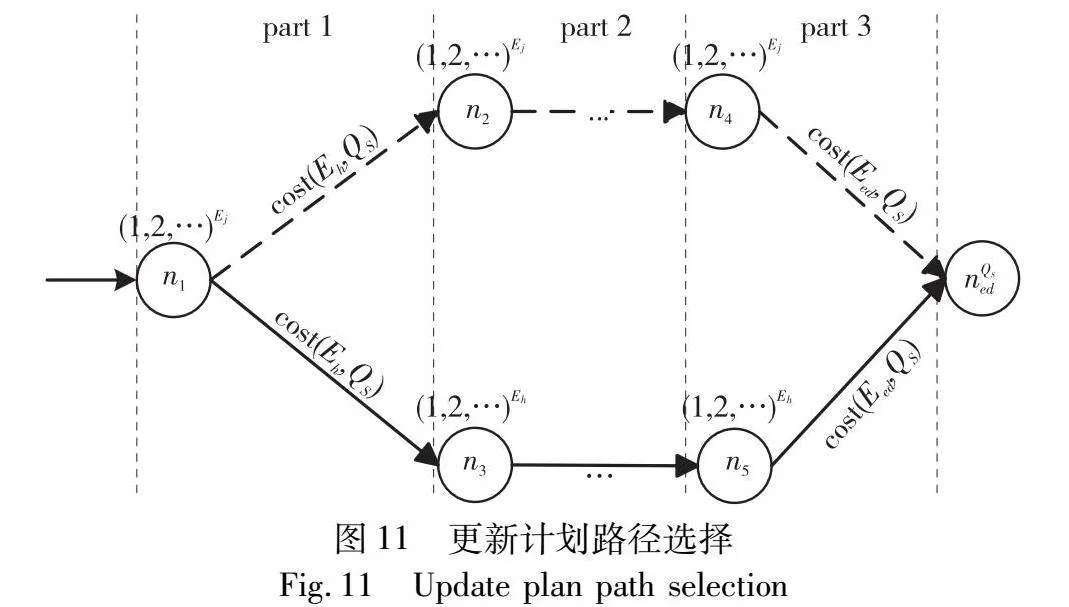
以SEQ模式为例，在一个共享的查询集QS中，查询的数量为|QS|。图11为QS的共享图中的一部分，节点n1处的共享方案是以Ej为QS的快照事件类型进行共享，之后需要将快照传播到事件类型Eh。P1和P2分别为虚线表示的初始路径和实线表示的更新后的路径。

图11中三部分的代价计算如表4所示。

在初始条件为|Ej|<|Eh|时，每个部分的代价均有P1.w<P2.w，得出总路径代价P1.w<P2.w，因此选取P1为共享计划。但是当Ej和Eh的事件频率发生变化之后，三部分的代价均发生变化。当P1.w>P2.w时，该查询集的共享计划需要进行调整。

表4中|QS|为共享查询 集中查询的数量，|Ej|、|Eh|和|Es|分别为QS 共享的快照事件类型Ej、Eh和Eh的所有后缀事件Es的事件发生频率，Eed为当前QS共享的最后一个事件类型。

本文设计了动态更新共享计划的算法以适应实时变化的事件流信息，如算法1所示。

算法1具有四个输入参数。P为原始路径，SE为事件流统计信息，工作负载模板T中存储了工作负载中查询的信息，E1为检测到事件发生频率产生变化的事件类型。

算法1首先将原始路径P以及对应的路径代价赋值给更新后的路径P′（第1行）。之后在模板T中通过广度优先搜索算法得到事件发生频率变化的事件类型E1对应的convert，得到其前置和后置事件类型，并分别将前置和后置事件类型存储在对应的集合中（第2～4行）。

第5行中snapSet为当前QS的快照事件类型集合，检测E1是否在snapSet中。若E1是快照事件类型，则检测E1是否比后置事件类型Es的事件发生频率大（第6，7行），当E1的事件发生频率大于Es的时候，需要检测E1和Es是否满足式（5）以更新共享计划（第8行）。如果满足不等式，则在原始路径P中找到convert（E1，Es）对应的节点n1（第9行）。在n1之后按照节点生成原则（更新快照）生成以Es为快照事件类型的共享方案节点（第10行）。updatePath（）方法将生成的节点插入到新的共享计划P′中，并更新相应的代价，之后按照节点生成原则（继承）生成后续节点直至得到新的共享计划P′（第11行）。

若E1不是快照事件类型，需要在路径P中搜索到convert（E0，Es）对应的共享方案节点n2，在n2中得到共享查询集QS以及共享的快照事件类型Esn（第12～15行）。当|E1|<|Esn|时，需要检测Esn和E1是否满足式（5）以更新共享计划（第16行）。如果满足不等式，则在n2之后按照节点生成原则（更新快照）生成以E1为快照事件类型的共享方案节点，直至得到新的共享计划P′（第17，18行）。最后返回新的共享计划P′（第19行）。

算法1 共享计划更新算法updateSharingPlan

输入：原始路径P；事件流统计信息SE；工作负载模板T；事件发生频率产生变化的事件类型E1。

输出：更新后的路径P′。

1 P′←P，P′.w←P.w；

2 在模板T中搜索到convert（Ep，E1）以及convert（E1，Es）；

3 prefixSet←Ep；

4 suffixSet←Es；

5 if E1 in snapSet

6 for each Es in suffixSet

7 if |E1|>|Es| then

8 if E1和Es满足式（5） then

9 在P中找到convert（E1，Es）对应的节点n1；

10 n1.rightNode←generateNode（n′，Es）；

11 updatePath（P′，P′.w，n′）；

12 else for each Ep in prefixSet

13 在P中找到convert（Ep，E1）对应的节点n2；

14 QS←node.getSet（）；

15 Esn←snap（Ep，QS）；

16 if |E1|<|Esn| then

17 n2.rightnode←generateNode（n′，E1）；

18 updatePath（P′，P′.w，n′）；

19 return P′；

4 实验

通过实验对本文提出的动态更新共享计划方法的有效性进行了分析和验证。硬件环境为12th Gen Intel CoreTM i7-1260P，64 GB内存，2.5 GHz频率。软件平台为Ubuntu 22.04，编程语言是Java，使用OpenJDK 16.0.1实现了方法的编写并运行实验。从多个维度对实验结果进行分析说明，每个实验平均运行15次。通过性能对比证明本文方法的有效性。

4.1 实验设置

4.1.1 事件流数据集

在三个数据集上进行了实验，两个数据集是真实的股票和公交车数据集，一个数据集是通过事件流生成方法生成的模拟数据流，事件的变化频率为3～5倍。

股票数据集包含NASDAQ 20年的股票价格历史记录。每条记录代表一个事件，包含公司标识符、时间戳（分钟）、开盘价和收盘价、最高价和最低价以及交易量。事件类型与3 258个唯一的公司标识符相对应。

公交车GPS数据集为2018年收集的都柏林公交车GPS记录组成。每条记录都是带有时间戳的元组（微秒），包含线路ID、车辆行程ID、拥堵指示、坐标和延迟时间。有4 368个唯一行程ID。

模拟数据流是ABC类型的事件流，每个事件都带有时间戳以及各自的属性值。根据自定义的事件类型数量、属性个数和属性值的范围生成相应的事件流，事件流中的每个事件都根据指定的频率随机生成和变化，包含5 000个原始事件。

4.1.2 工作负载数据集

为了评估共享计划更新方法在不同查询负载下的有效性，在每个数据集上设置了三种类型的工作负载。SEQ工作负载具有不同的可共享SEQ模式、分组、谓词和聚合函数（count（*）、max等）。Kleene模式的工作负载分为可共享的平坦Kleene模式和嵌套Kleene模式，Kleene子模式的长度为2～10；嵌套Kleene子模式的嵌套层数为1～5层，谓词、时间窗口和聚合设置与SEQ工作负载相同。混合工作负载包括SEQ子模式和Kleene子模式，Kleene模式占比由20%调整到100%。

4.1.3 衡量指标

对于执行工作负载的优化，以秒为单位度量执行时间，即接收工作负载与生成聚合结果的平均时间差。包括模板构建、图构建、路径搜索、图更新和生成聚合结果值的时间。峰值内存是执行过程中消耗的最大内存。执行时，使用以秒为单位的延迟时间作为产生聚合结果的时间与最后一个相关事件到达时间的平均时间差。吞吐量是所有查询每秒处理的平均事件数。

4.2 实验分析

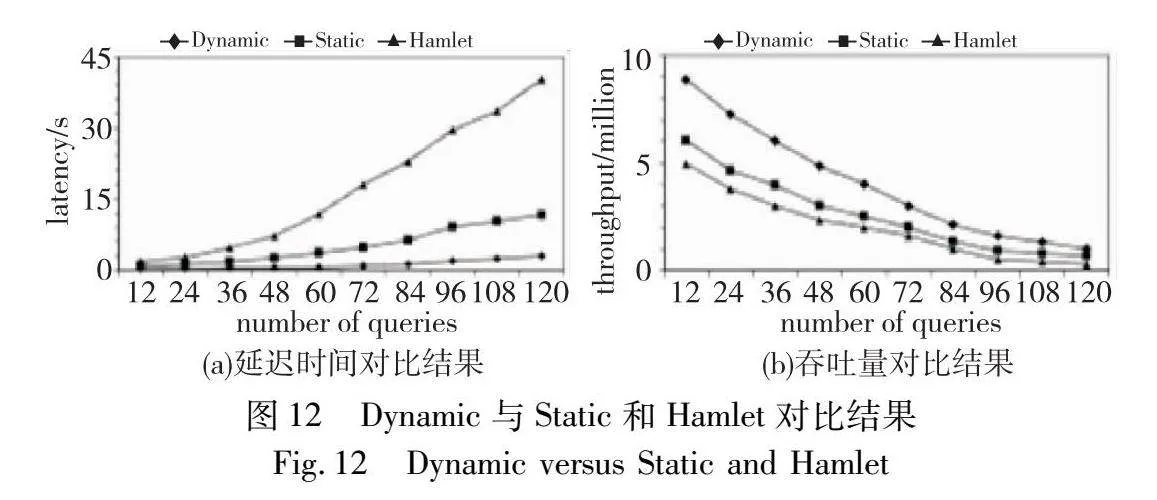
实验1 首先比较了本文方法Dynamic和当前处理聚合查询效果较好的两个方法（Static［12］和Hamlet［11］）执行的延迟时间和吞吐量。这两种方法均支持处理Kleene操作符以及共享查询之间的执行。但是Static方法所生成的共享计划并不适用于实时变化的动态数据流。在事件流或工作负载出现波动时，Static方法的性能显著下降。Hamlet方法只针对E+这种平坦的Kleene模式进行了优化，将短时间内发生的同一事件类型的事件视为突发事件。每次发生突发事件时，都需要进行共享决策，导致执行效率不高。

Kleene模式占比为固定的60%，将工作负载查询数量从12增加至120在股票数据集上进行了实验。图12（a）（b）分别为延迟时间和吞吐量的对比。在延迟时间上本文方法分别比Hamlet和Static方法性能提升大约9倍和3倍，吞吐量上分别比Hamlet和Static提高了80%和50%。Dynamic方法在动态数据流环境下，不断分析当前的执行信息和共享计划，评估共享收益以选择不同事件类型的快照，进行动态调整。因此能够更高效地评估工作负载。

实验2 比较了本文的Dynamic方法和由严格的共享计划指导方法的整体运行时间，包括生成图和共享计划，处理聚合查询工作负载并生成最后的结果值。并对修剪和未修剪的方法分别进行了对比实验。

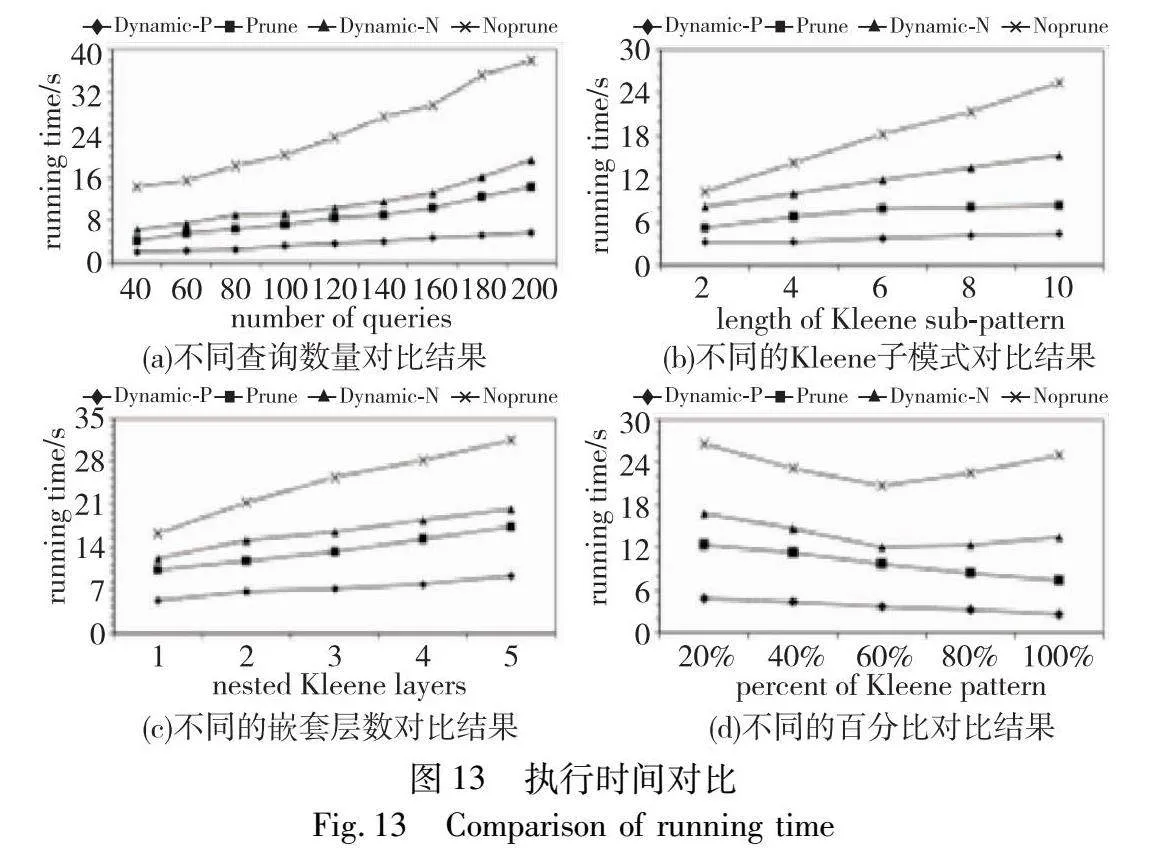
对于SEQ工作负载，分别评估了对修剪和不修剪的共享图上更新共享计划的延迟时间。工作负载中的查询数量由40增加到200，事件频率变化为3～5倍，评估了对公交车数据集的处理时间。执行过程中，判断是否需要更新共享计划需要占用一定的时间和内存空间，未修剪共享图的路径搜索时间大于修剪之后的搜索时间，但是如果需要更新共享计划，修剪的共享图在生成图时可能会删除更新之后的候选共享计划中的节点，因此需要重新生成新的节点并重新对图进行修剪。如图13（a）所示，本文方法始终优于静态共享计划执行的3～5倍。综上所述，动态更新共享计划有效地加快了聚合查询的执行速度。

对于Kleene子模式，比较了在包含9lyT4iOY4zEq1w5wDJ5fT7Zh61UhSOP1c5/tEvMOal0=平坦Kleene子模式的100个查询的工作负载，将Kleene子模式的长度由2变化到10。本文方法对于给定的Kleene工作负载，如图13（b）所示，为Kleene子模式生成的子图总是很小，因此在更新共享计划时会消耗更少的时间和更低的内存。对于嵌套的Kleene子模式，将Kleene子模式的嵌套层数从1层调整到5层进行了对比实验，如图13（c）所示，随着嵌套层数的增加，静态方法的执行时间增加得越多，而本文方法可以对共享计划进行动态调整，因此对比静态方法，执行时间显著减少。

对于混合工作负载，图13（d）展示了在包含100个查询的混合工作负载下动态更新和静态共享计划的执行时间。将包含Kleene模式的查询（以下简称为Kleene查询）所占百分比从20%调整到100%。随着Kleene查询数量的增加，本文方法的优化性能达到静态执行方法的3倍。当Kleene查询的比例增加到40%时，SEQ查询的数量减少，降低了SEQ查询处理的复杂度。当Kleene查询的比例大于50%时，优化时间主要用于优化Kleene查询共享的时间。由于对Kleene子图采用了修剪原则，所以优化性能随着Kleene查询的增多而减少。

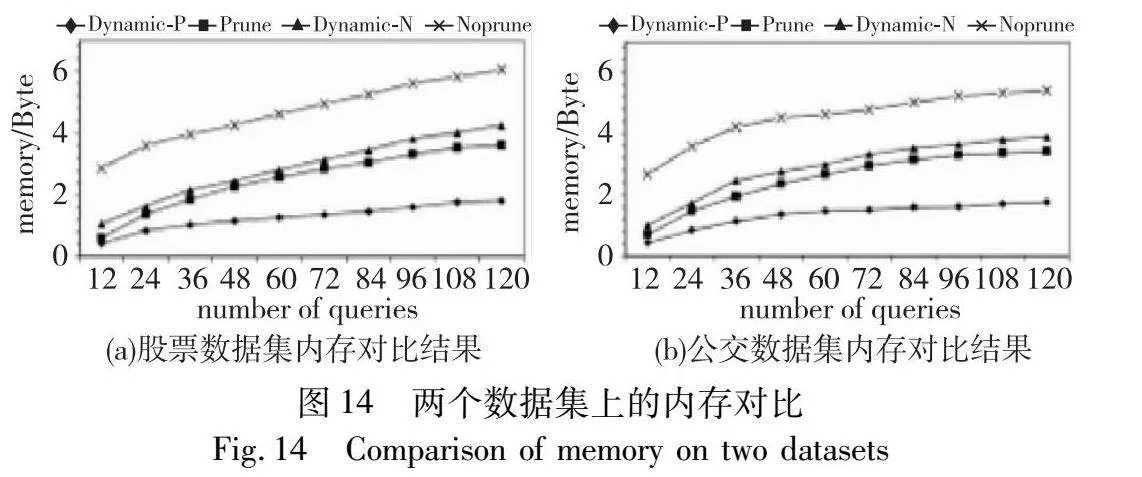
实验3 图14（a）（b）分别为在股票和公交车数据集上将工作查询负载中的查询从12增加到120的峰值内存的对比结果。由于动态调整了共享计划，减少了不必要的快照传播的代价，本文方法在两个数据集上的峰值内存消耗占静态方法内存消耗的50%～70%。

上述实验表明，本文提出的动态更新共享计划的方法能够有效适应实时变化的事件流和工作负载，无论是在SEQ模式还是在Kleene模式下，都表现出较好的性能。

5 结束语

本文研究了应对动态变化的数据信息时处理聚合查询的问题。针对包含Kleene操作符的多个聚合查询，设计了共享图模型，将查询之间的共享问题抽象为加权有向无环图的最佳路径搜索问题。综合考虑了实时变化的事件流和工作负载信息，设计出代价模型，以最大化共享收益。将代价模型应用到图生成过程，并在生成图时对其进行修剪，加快了生成共享计划的时间。降低了处理聚合查询的延迟时间，提高了系统的吞吐量，实现了高效的更新共享计划。实验结果验证了动态更新共享计划方法对执行性能的有效提升，在处理动态数据的聚合查询时提供了有力的解决方案。

参考文献：

［1］邱涛， 谢沛良， 邓国鹏， 等. 面向实时事件流的复杂事件处理方法［J］. 计算机应用研究， 2022， 39（9）： 2677-2682， 2688. （Qiu Tao， Xie Peiliang， Deng Guopeng， et al. Complex event processing method over real-time event streams［J］. Application Research of Computers， 2022， 39（9）： 2677-2682，2688.）

［2］Poppe O， Lei Chuan， Ahmed S， et al. Complete event trend detection in high-rate event streams［C］//Proc of the ACM SIGMOD International Conference on Management of Data. New York： ACM Press， 2017： 109-124.

［3］夏秀峰， 武孟达， 张杨， 等. 基于动态匹配策略的复杂事件处理方法［J］. 计算机应用研究， 2023， 40（11）： 3341-3347. （Xia Xiu-feng， Wu Mengda， Zhang Yang， et al. Efficient complex event processing based on dynamic matching strategy［J］. Application Research of Computers， 2023， 40（11）： 3341-3347.）

［4］乔雅正， 程良伦， 王涛，等. 地铁列车环境中多依赖复杂事件处理研究［J］. 计算机应用研究， 2019， 36（8）： 2355-2358， 2367. （Qiao Yazheng， Cheng Lianglun， Wang Tao， et al. Study on multi-dependency complex event processing in subway train environment［J］. Application Research of Computers， 2019， 36（8）： 2355-2358，2367.）

［5］Kolchinsky I， Schuster A. Real-time multi-pattern detection over event streams［C］//Proc of ACM SIGMOD International Conference on Management of Data. New York： ACM Press， 2019： 589-606.

［6］Poppe O， Rozet A， Lei Chuan， et al. Sharon： shared online event sequence aggregation［C］//Proc of the 34th ICDE International Conference on Data Engineering. Piscataway， NJ： IEEE Press， 2018： 737-748.

［7］Poppe O， Lei Chuan， Rundensteiner E A， et al. GRETA： graph-based real-time event trend aggregation［J］. The VLDB Endowment， 2017， 11（1）： 80-92.

［8］Perera K P D， Ahangama S. A review of query optimization techniques for complex event processing［C］//Proc of the 4th ICITR International Conference on Information Technology Research. Piscata-way， NJ： IEEE Press， 2019： 1-7.

［9］Hong M， Riedewald M， Koch C， et al. Rule-based multi-query optimization［C］//Proc of the 12th ACM EDBT International Conference on Extending Database Technology： Advances in Database Techno-logy. New York： ACM Press， 2009： 120-131.

［10］Zhang Haopeng， Diao Yanlei， Immerman N. On complexity and optimization of expensive queries in complex event processing［C］//Proc of ACM SIGMOD International Conference on Management of Data. New York： ACM Press， 2014： 217-228.

［11］Qi Yingmei， Cao Lei， Ray M， et al. Complex event analytics： online aggregation of stream sequence patterns［C］//Proc of ACM SIGMOD International Conference on Management of Data. New York： ACM Press， 2014： 229-240.

［12］Poppe O， Lei Chuan， Ma Lei， et al. To share， or not to share online event trend aggregation over bursty event streams［C］//Proc of ACM SIGMOD International Conference on Management of Data. New York： ACM Press， 2021： 1452-1464.

［13］Mei Huiyao， Chen Hanhua， Jin Hai， et al. Efficient complete event trend detection over high-velocity streams［C］//Proc of the 50th ACM ICPP International Conference on Parallel Processing. New York： ACM Press， 2021： 1-12.

［14］赵会群， 李会峰， 刘金銮. RFID物联网复杂事件模式聚类算法研究［J］. 计算机应用研究， 2018， 35（2）： 339-341. （Zhao Huiqun， Li Huifeng， Liu Jinluan. Study on RFID complex event pattern clustering algorithm of Internet of Things［J］. Application Research of Computers， 2018， 35（2）： 339-341.）

［15］Zhang Shuhao， Vo H T， Dahlmeier D， et al. Multi-query optimization for complex event processing in SAP ESP［C］//Proc of the 33rd ICDE International Conference on Data Engineering. Piscataway， NJ： IEEE Press， 2017： 1213-1224.

［16］Wu E， Diao Yanlei， Rizvi S. High-performance complex event processing over streams［C］//Proc of ACM SIGMOD International Conference on Management of Data. New York： ACM Press， 2006： 407-418.

［17］Mei Yuan， Madden S. Zstream： a cost-based query processor for adaptively detecting composite events［C］//Proc of ACM SIGMOD International Conference on Management of Data. New York： ACM Press， 2009： 193-206.

［18］Ma Lei， Lei Chuan， Poppe O， et al. Gloria： graph-based sharing optimizer for event trend aggregation［C］//Proc of ACM SIGMOD International Conference on Management of Data. New York： ACM Press， 2022： 1122-1135.

［19］Liu Mo， Rundensteiner E， Dougherty D， et al. High-performance nested CEP query processing over event streams［C］//Proc of the 27th International Conference on Data Engineering. Piscataway， NJ： IEEE Press， 2011： 123-134.

［20］Liu Mo， Ray M， Rundensteiner E A， et al. Processing nested complex sequence pattern queries over event streams［C］//Proc of the 7th ACM DMSN International Workshop on Data Management for Sensor Networks. New York： ACM Press， 2010： 14-19.

［21］邱涛， 丁建丽， 夏秀峰，等. 基于有序事件列表的高效复杂事件匹配算法［J］. 计算机应用， 2023， 43（2）： 423-429. （Qiu Tao， Ding Jianli， Xia Xiufeng， et al. Efficient complex event matching algorithm based on ordered event lists［J］. Journal of Computer App-lication， 2023， 43（2）： 423-429.）

［22］施建明， 王伟， 王功. 基于Flink复杂事件处理的空间站实验柜排废气安全监测［J］. 载人航天， 2023， 29（1）： 102-109. （Shi Jianming， Wang Wei， Wang Gong. Safety monitoring of exhaust gas discharge of experimental rack onboard space station based on Flink CEP［J］. Manned Spaceflight， 2023， 29（1）： 102-109.）

［23］Schultz-Mller N P， Migliavacca M， Pietzuch P. Distributed complex event processing with query rewriting［C］//Proc of the 3rd ACM DEBS International Conference on Distributed Event-Based Systems. New York： ACM Press， 2009： 1-12.

［24］Ray M， Lei Chuan， Rundensteiner E A. Scalable pattern sharing on event streams［C］//Proc of ACM SIGMOD International Conference on Management of Data. New York： ACM Press， 2016： 495-510.

［25］Liu Mo， Rundensteiner E， Greenfield K， et al. E-cube： multi-dimensional event sequence analysis using hierarchical pattern query sharing［C］//Proc of ACM SIGMOD International Conference on Management of Data. New York： ACM Press， 2011： 889-900.

［26］Poppe O， Lei Chuan， Rundensteiner E A， et al. Event trend aggregation under rich event matching semantics［C］//Proc of ACM SIGMOD International Conference on Management of Data. New York： ACM Press， 2019： 555-572.