基于分区再训练的RRAM阵列多缺陷容忍算法

摘 要：针对RRAM单元制造工艺不完善造成神经网络矩阵向量乘法计算错误问题，根据RRAM阵列多缺陷特性进行建模，提出了多缺陷容忍算法。首先根据RRAM阵列常见的转变缺陷和粘连缺陷对神经网络计算准确度的影响，对两种缺陷统一建模；然后对神经网络进行划分，基于改进的知识蒸馏方式进行分区训练；最后选择适配的损失函数加入归一化层，进一步优化算法。在MNIST和Cifar-10数据集上进行实验，结果表明该方法在多个神经网络上能够得到98%以上的恢复率，说明该方法可有效降低RRAM阵列多缺陷对神经网络计算准确度的影响。

关键词：RRAM阵列； 缺陷容忍； 神经网络； 知识蒸馏

中图分类号：TP391.7 文献标志码：A

文章编号：1001-3695（2024）10-026-3068-05

doi：10.19734/j.issn.1001-3695.2024.01.0046

Partition retraining based multi-fault tolerance algorithm for RRAM crossbar

Wang Mengke， Yang Zhaohui， Zha Xiaojing， Xia Yinshui

（Faculty of Electrical Engineering & Computer Science， Ningbo University， Ningbo Zhejiang 315211， China）

Abstract：To address the issue of calculation errors in neural network matrix-vector multiplication caused by manufacturing processes of RRAM cells， this paper modeled the characteristics of multiple faults in RRAM crossbar arrays and proposed a multi-fault tolerant algorithm. Firstly， it modeled the impacts of common transition fault and stuck at fault in RRAM crossbar arrays on the accuracy of neural network computations. Secondly， it partitioned the neural network and conducted partitioned training based on an improved knowledge distillation method. Lastly， it further optimized the algorithm by selecting an appropriate loss function and incorporating normalization layers. Experimental results on the MNIST and Cifar-10 datasets demonstrate that the proposed method can achieve a recovery rate of over 98% across multiple neural networks， indicating its effectiveness in mitigating the impact of multiple faults in RRAM crossbar arrays on the accuracy of neural network computations.

Key words：RRAM crossbar; fault tolerance; neural network; knowledge distillation

0 引言

深度神经网络（deep neural network，DNN）在解决复杂的机器学习问题方面具有良好的性能，目前已经研究了许多DNN加速器架构［1，2］。阻变式存储器（resistive random access memory，RRAM）凭借擦写速度快、耐久性强和非易失性［3］等优势，通过结合纳米交叉阵列结构可以快速进行列电流求和，从而并行实现神经网络矩阵向量乘法（matrix vector multiplication，MVM）计算，因而在DNN加速器设计方面具有重要地位。

在加速器设计中，神经网络的权值对应为RRAM的电导值，通过网络权重与RRAM阵列的一对一映射，实现神经网络的硬件部署。然而，由于不成熟的纳米级制造技术和RRAM固有非线性特性，RRAM阵列通常会遭受严重的粘连缺陷（stuck at fault，SAF）和转变缺陷（transition fault，TF），这将永久或暂时改变RRAM内存储的权值状态，从而导致错误的硬件计算结果［4］。RRAM中SAF和TF的出现会降低神经网络硬件部署的可靠性，成为神经网络加速设计中的重要瓶颈问题［5］。所以，如何解决此问题已经成为基于RRAM的DNN加速器设计的主要关注点之一。

现有研究主要从三个方面针对SAF的容忍进行设计：再训练［6～9］、修正［10，11］、重映射［11，12］。再训练是指基于SAF缺陷分布图使用梯度下降算法再次训练DNN，使得再训练后的DNN部分权值固定为常数，以满足硬件缺陷特性。再训练方法需要两个基础数据：缺陷分布图［13，14］和训练数据集，分为在线训练和离线训练两种形式［15～17］。其中在线训练是指在设备上进行实时训练，根据缺陷变化可灵活进行训练，但训练过程需要频繁进行读写操作，对设备损耗很大；离线训练根据缺陷分布图在计算机上进行再训练之后映射到设备上使用，训练时不消耗硬件资源，灵活可控，易于操作，但训练结果不能根据阻值变化实时改变，泛化性较低。Charan等人［6］提出了基于知识蒸馏（knowledge distillation，KD）的再训练算法。该方法采用在线训练形式，使用师生模型，通过学生模型向教师模型逐次逼近实现性能恢复。但只针对输出结果进行再训练，对缺陷容忍不能达到很好的效果。Li等人［9］提出一种对抗性实例缺陷检测方法，在KD的基础上在线训练进行缺陷容忍，但是适用的电路规模较小。

修正是一类通过增加冗余硬件资源来恢复计算准确度的方法。He等人［10］提出了一种增加冗余列来替换出现SAF缺陷较多的列来进行修正的方法，可以得到较好的精度恢复，但是此类方法只针对SAF缺陷进行容忍，而且冗余列的MVM操作提高了计算成本，增加的数字硬件模块导致了额外的硬件开销［5，11］。

重映射方法主要通过对DNN权值矩阵进行行列置换再重新映射于RRAM阵列中，从而避免把对计算准确度影响较大的权值映射于缺陷RRAM上，以此来降低缺陷对计算准确度的影响。矩阵置换［11］是使用重塑矩阵来降低缺陷对计算准确度影响的方法，使缺陷位置的值尽可能与缺陷值相匹配。此类方法需要不断检测缺陷RRAM的阻值与权值是否匹配，随着网络规模的增加，为了寻找最合适的匹配方式，需要消耗大量时间，严重影响计算效率。

综上所述，虽然已经有许多针对不同缺陷的容忍方法，但这些方法要么只针对SAF缺陷，要么求解规模有限，缺乏同时针对多种缺陷、综合考量资源消耗和恢复效果的容忍方法。其中，再训练算法凭借硬件友好特性和离线高效训练能力，成为容忍缺陷的有效途径。RRAM阵列的多缺陷容忍问题，核心在于缩小神经网络理想权值与RRAM阵列实际阻值的差异，该思想与知识蒸馏的“参考教师模型训练学生模型”模式本质相同，因此本文结合知识蒸馏方法，提出基于再训练的多缺陷统一容错方法。通过对SAF和TF缺陷统一建模，扩展再训练算法的适用范围；结合知识蒸馏方法，提出神经网络模型分块训练思想，通过模型中间特征的有效提取，提升网络模型对硬件阵列缺陷特性的泛化容忍能力；最后通过加速再训练反向传播过程，提升网络模型收敛速度。本文的主要贡献为：

a）通过一一对应的映射关系，将RRAM阵列的缺陷信息反映为待映射网络模型特征，基于再训练架构用学生模型拟合教师模型来进行多缺陷容错；

b）通过修改网络结构和分区训练加快网络收敛速度，获得更好的容错效果。

1 研究背景

1.1 RRAM单元基础

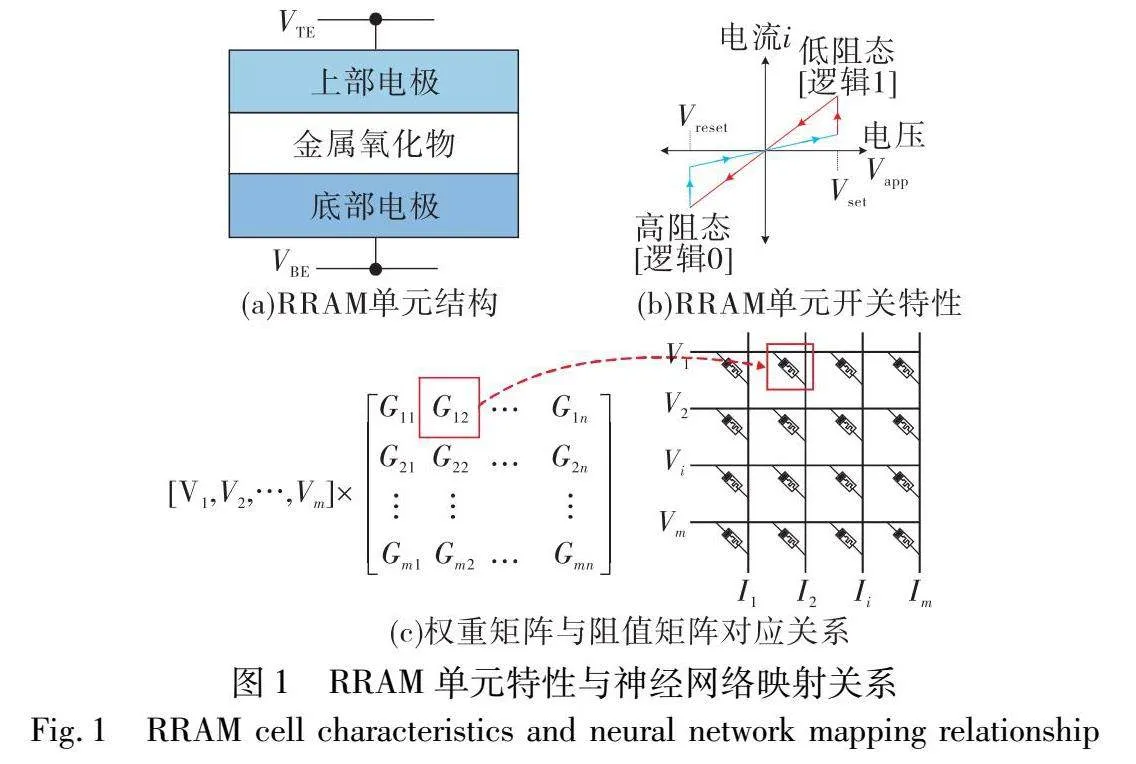
RRAM是一种新兴的非易失性存储器，又称为忆阻器［3，18］。如图1（a）所示，RRAM单元为无源双极性器件，通常采用金属-绝缘体-金属结构。从图1（b）可以看出，RRAM的阻值在一定电压范围内不会改变，此特性可使其用于模拟近似计算［19，20］。RRAM的另一个特性是，即使在移除电源后也能够保持其电阻状态。利用RRAM的电阻开关特性，研究人员探索了其在存内计算方面的潜力。利用欧姆定律和基尔霍夫电流定律，基于RRAM的交叉阵列可有效执行复杂的MVM计算，从而消除传统计算架构中需要多次访问计算和存储元件所带来的能耗瓶颈问题。图1（c）表示在神经网络计算过程中权重矩阵与RRAM单元的一一对应关系。交叉阵列的输入是字线电压，卷积层和全连接层乘法运算的输出结果是位线读取的总电流［6］，可表示为

I（j）=∑N-1i=1G（j，k）·V（j）（1）

其中：V∈（j=1，…，N-1）是输入到字线的电压矢量;G表示RRAM参数的电导矩阵;I为每列的总电流，对应神经元的输出结果。

1.2 知识蒸馏算法

深度神经网络模型计算复杂性高、存储需求大，部署在资源有限的设备上是一个挑战。作为模型压缩和加速的代表类型，知识蒸馏是一种基于“教师-学生模式”的网络模型再训练方法，主要思想是在高计算复杂度的教师模型指导下用结构较简单的学生模型主动拟合，即以有限的计算准确度为代价完成大型神经网络模型向小型网络模型的压缩和加速，从而改善硬件部署难度问题［21，22］。知识蒸馏的关键在于“知识”的设计、提取和迁移方式的选择［23］。原始知识蒸馏中信息的传递只依赖于模型的输出，当模型结构变深，需要传递教师模型中更多的“知识”。而中间特征是在网络中间层输出的特征图中表达的信息，可弥补输出层知识信息单一的不足。

基于中间特征的知识蒸馏以最小化蒸馏损失为目标来训练学生模型。蒸馏损失函数用数学公式表示为

LKD=‖ft（x;Wt）-fs（x;Ws）‖F（2）

其中：ft和fs分别为教师和学生模型;x是中间层输入的特征;Wt和Ws为教师和学生模型的中间层参数，即权重信息;F为范数值，表示损失函数的具体实现形式。

1.3 RRAM交叉阵列的非理想效果

电路缺陷是发生在器件的制造或操作过程中，引发实际硬件产生与预期理想性能不符的异常现象［14］。根据交叉阵列中缺陷的性质，对可能发生的最常见缺陷类型进行分类，总结如下［24］：

a）粘连缺陷（SAF）：由可变的氧化层厚度产生，忆阻器的阻值固定且不能改变［24］。SAF有SAL（stuck at low）和SAH（stuck at high）两种情况，表示阻值呈低阻态或高阻态。

b）转变缺陷（TF）：由不规则的掺杂变化和器件内部结构间磨损引起，可能会阻止忆阻器变化到理想状态［24］。TF有慢写缺陷（slow write fault）和快写缺陷（fast write fault）有两种情况，表示阻值低于或高于理想阻值。

c）地址解码器缺陷（address decoder fault，ADF）：由开放缺陷引起，导致交叉阵列的行/列合并在一起，访问到不需要的单元［24］。

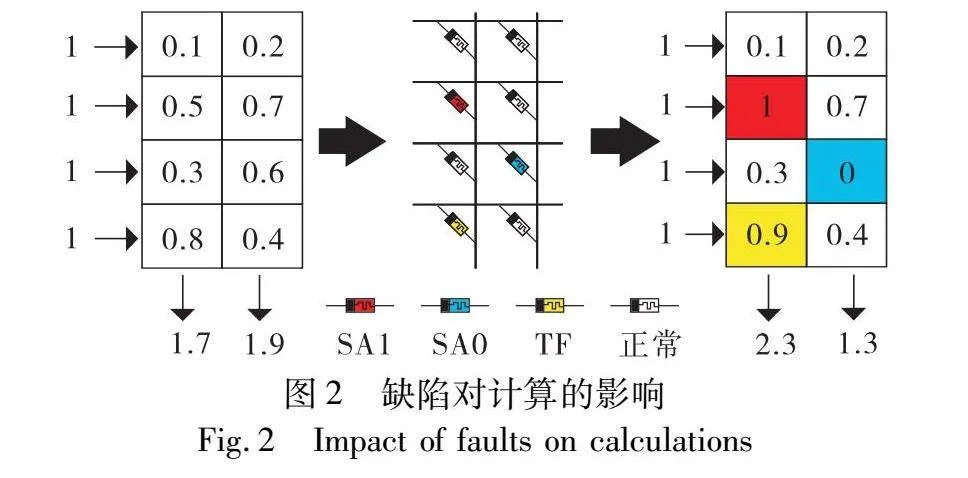
实验结果表明［14，24］，基于忆阻器的RRAM阵列有约30%的缺陷，其中TF约为14%，SAF约10%，ADF约3%，其他缺陷约3%。由此可见，RRAM阵列中TF和SAF是影响计算的两类主要缺陷，其中两类缺陷对矩阵向量乘法计算的影响如图2所示。理想情况下，输入为1时，矩阵的输出结果分别为1.7和1.9。映射到RRAM阵列上，红色位置表示缺陷SAF为1时阻值由0.5固定为1；蓝色位置表示缺陷SAF为0时阻值由0.6固定为0；黄色位置表示发生TF时阻值由0.8波动到0.9，矩阵的输出结果变为2.3和1.3（参见电子版）。由此可见，在进行矩阵向量乘法计算时，SAF和TF缺陷会使计算结果产生较大偏差。

2 基于分区再训练的缺陷容忍

由于RRAM单元本身的制造缺陷，RRAM交叉阵列在进行神经网络的矩阵向量乘法计算时，会产生计算错误导致神经网络的计算准确度严重受损。为此，将缺陷映射在RRAM阵列对应位置上，通过离线再训练的方式增加RRAM的容错能力，从而提高神经网络的计算准确度。

2.1 缺陷数字化建模

综合考虑两种缺陷对RRAM阵列计算的影响，在缺陷已知的情况下对两种缺陷进行建模。分析SAF和TF在RRAM阵列计算时的表现，两种缺陷对RRAM阵列阻值的影响本质上是一致的，即在计算时，实际权值会固定在某一数值上。因此，只要确定了数值转变的规则，就能实现统一建模，也能实现物理特性在网络模型上的反应。基于此，为方便表述，对RRAM单元的阻值归一化，然后针对TF和SAF的缺陷特性进行建模。其中TF缺陷表示为在理想权值的基础上增添一个随机噪声进行模拟，噪声服从对数正态分布，eθ表示发生缺陷RRAM单元的阻值波动范围，其中N（0，σ2）表示θ服从均值为0，方差为σ2的正态分布，σ一般为0.1～0.5［25］。发生SAF缺陷的RRAM单元处于开路或者短路状态，其阻值固定在0/1上。基于上述分析，可建立如下公式表示缺陷环境下阻值与理想环境下阻值间的关系：

Ractual=Rideal F=0

Rideal×eθ，θ～N（0，σ2）F=11F=20F=3（3）

其中：Ractual表示RRAM阵列的实际阻值;Rideal表示理想阻值;F用于判断缺陷类型，当F=0时，表示RRAM器件处于无缺陷状态；当F=1时，表示RRAM器件存在TF缺陷；当F=2时，表示RRAM器件存在SAF为1的缺陷；当F=3时，表示RRAM器件存在SAF为0缺陷。本文通过对缺陷特性的统一建模，以便后期进行多缺陷的统一容错设计。

2.2 算法框架

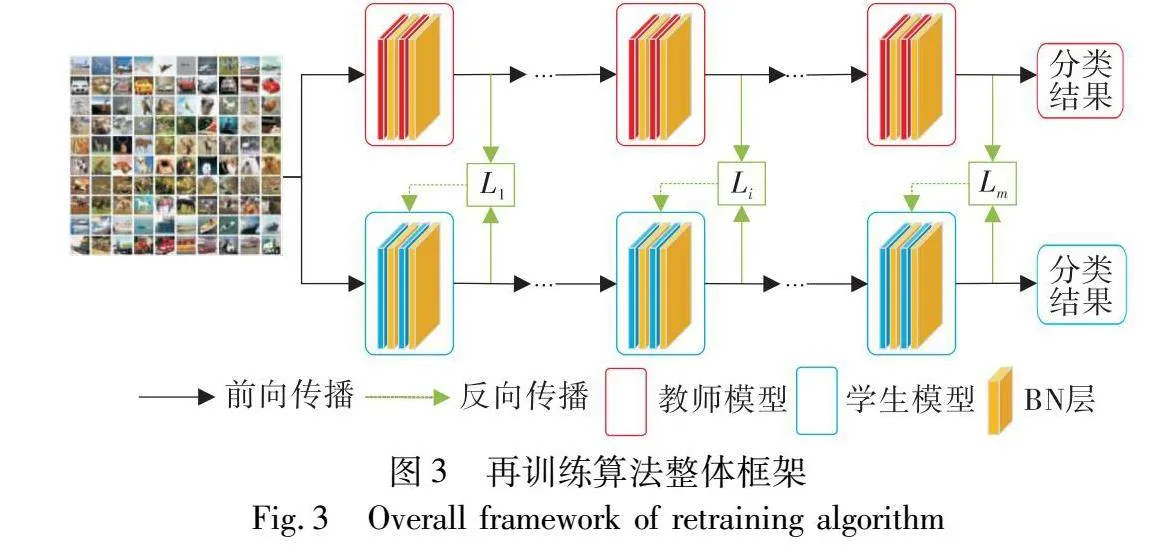
鉴于传统的知识蒸馏训练方法，只能根据最后的输出结果进行反向传播，随着网络结构变得更加复杂，中间特征的缺失使得训练模型无法获得良好的拟合效果，实现缺陷容忍在网络模型上的有效反应。因此，本文在传统知识蒸馏方法的基础上，主张利用中间特征信息实现再训练过程。根据结构对模型进行划分，逐层提取理想模型的中间特征信息，从而提高缺陷模型的容错能力。本文算法的总框架如图3所示，其中红色框和蓝色框表示教师模型和学生模型分区后的区块；红色层和蓝色层表示教师模型和学生模型中的卷积层，黄色层表示进行归一化处理的批归一化（batch normalization，BN）层（参见电子版）；Li表示第i区块教师模型与学生模型损失函数。再训练算法以改进的知识蒸馏为基础，建立无缺陷教师模型和有缺陷学生模型。首先将模型按照网络结构进行划分，便于提取模型的中间特征；然后在块间以掩码方式进行反向传播训练，区块间的训练使用Huber损失函数作为蒸馏损失，可以在缺陷率较大的情况下保证模型收敛；最后通过训练得到可以容忍多种缺陷的模型。与传统以大模型训练小模型的基于中间特征的知识蒸馏不同，本文学生模型的结构与教师模型相同。

再训练的目标是最小化教师模型与学生模型对应区块的输出差异，其目标函数可以表示为

minWsΔ（Bs，Bt）（4）

其中：Bs和Bt分别表示学生模型和教师模型对应区块的输出层参数;Ws表示学生模型的权重。

2.2.1 网络划分

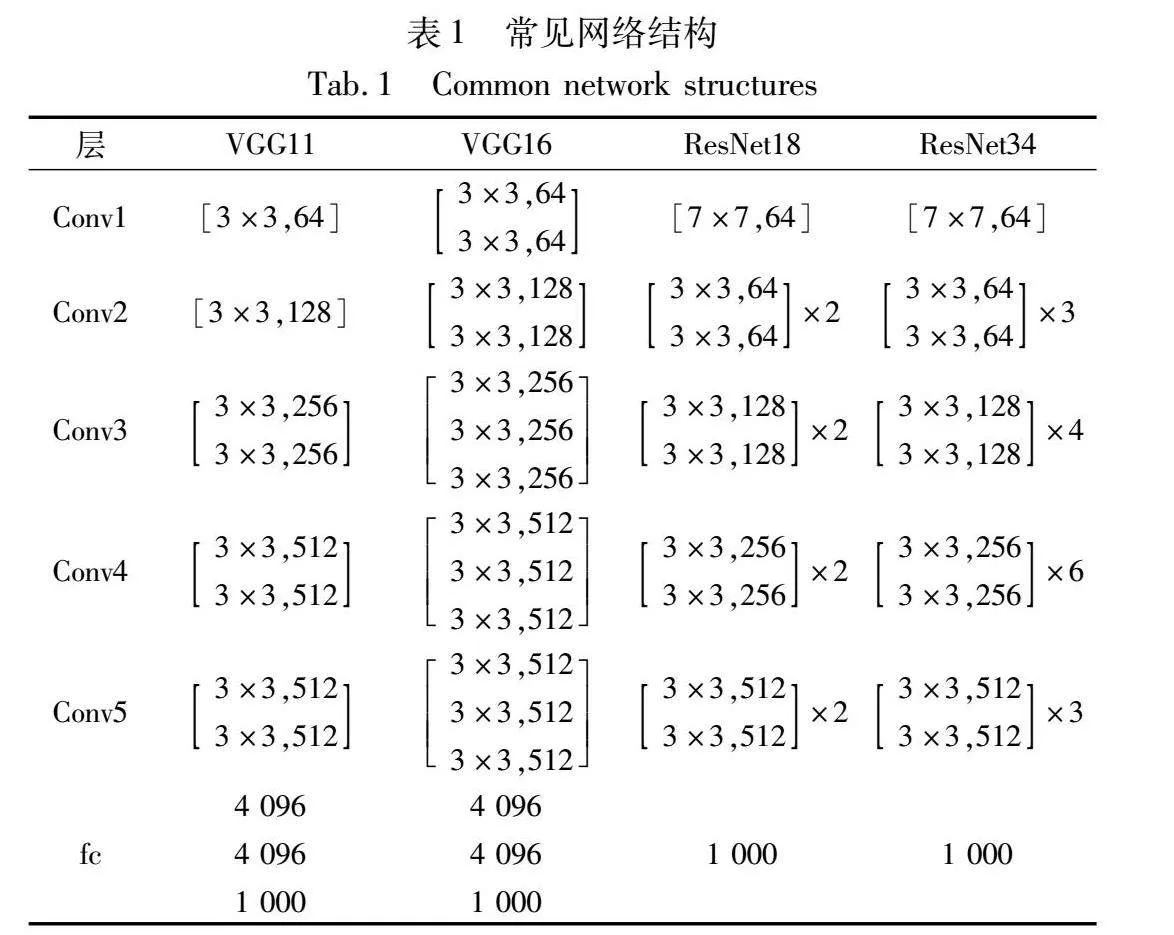
随着神经网络的发展，网络结构越来越复杂，需要训练的数据也成倍增加。传统的再训练算法是在提取硬件缺陷图的前提下进行整个网络的前向传播，训练过程中网络数据在缺陷的影响下发生偏差，偏差量逐级累积，从而造成损失函数不稳定，恶化反向传播的数据更新能力，影响再训练效果。从提高损失函数稳定性的角度，需要将数据偏差控制在一定范围内。为此，本文基于“分治”思想，将神经网络根据其网络结构特性进行划分，在保证获取中间特征的前提下，通过局部训练的方式来控制网络在硬件缺陷作用下的累积数据偏差量。部分网络结构如表1所示，表中［3×3，64］表示当前层级使用［3×3］的卷积核，输出通道数为64。鉴于神经网络的通道数会影响网络复杂度和数据量［26］，其中，通道数相同的层级捕获特征的能力近似，因此本文主张将通道数相同的层级划分为同一个区块。根据上述分析，可按照式（5）明确当前卷积层所属的区块编号：

k=logC/f2（5）

其中：k表示当前卷积层所属的区块编号；C表示当前输出通道数；f表示第一层的输出通道数，全连接层与最后一块合并进行计算。以ResNet18为例，第一层的输出通道数为64，在Conv4层级中输出通道数为256，根据式（5）的计算，此层级的4个卷积层都属于第2个区块。

2.2.2 掩码训练

本文中采用离线方式进行学生模型训练，DNN本身具有自我恢复能力，可以从损坏的权重中重新训练，应用反向传播算法，可以通过迭代训练自适应缺陷［27］。权值的更新过程用←表示：

Wi←Wi－η L Wi（6）

其中：L为损失函数;η为学习率;Wi为神经网络的权值。为了减少SAF和TF缺陷造成的性能下降，在模型训练阶段对缺陷位置的值进行屏蔽，具体来说，权值更新过程可以描述为

Wi←Mask（Wi-η E Wi）（7）

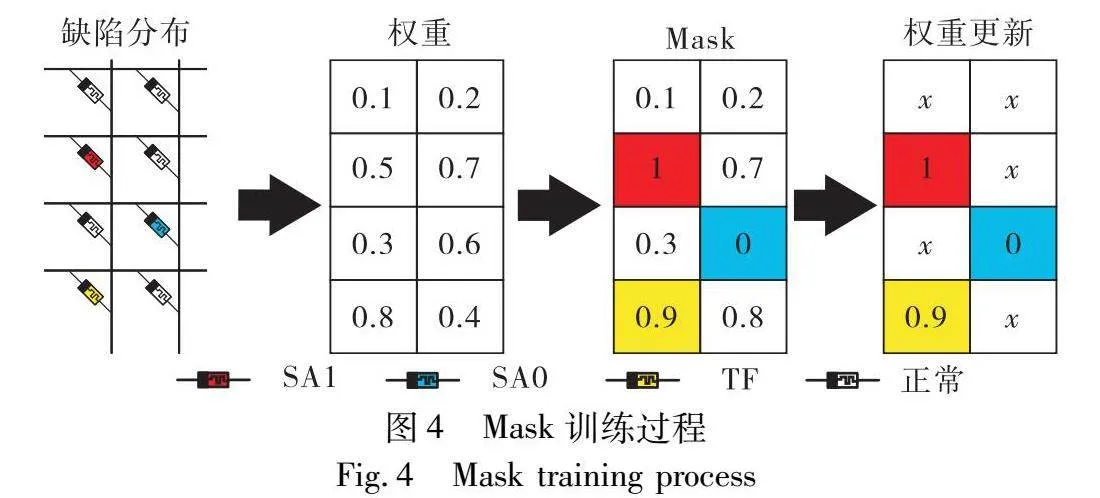
根据缺陷分布，Mask函数用于在训练阶段将有SAF缺陷的RRAM固定，将有TF缺陷的RRAM根据噪声波动改变到其对应值。假设RRAM上包含SAF和TF缺陷，为保证再训练阶段能够容忍权重变化，对有缺陷的RRAM单元进行掩码，权值更新情况如图4所示，根据缺陷分布获得缺陷类型及位置，将缺陷位置的权重值固定后，更新无缺陷位置的权重值来容忍缺陷。

2.3 算法优化

为了进一步优化离线再训练的恢复精度，对神经网络的结构进行调整，在卷积层后加入归一化层，并采取Huber损失函数作为再训练的蒸馏损失。

2.3.1 归一化层

批归一化应用于每个卷积层之后，将每层的输出x进行如式（8）的变换处理。由文献［28］可知，BN层可以减少内部变量的移位问题，并被广泛应用于提高训练性能。由式（8）可以看出，BN层有5个参数，其中ε参数仅在训练期间更新。（μ，σ）是前向传播阶段更新的每批输入统计数据，（β，γ）是在反向传播阶段通过梯度下降更新。为了进行推断，通常用常数值替换μ、σ。本文将BN层设置为服从均值μ为0，方差σ为1的标准正态分布，将卷积层的输出进行归一化处理，可使梯度变大，避免梯度消失问题。

y=γ（x-μσ2+ε）+β（8）

2.3.2 损失函数

机器学习中的所有算法都需要最大化或最小化目标函数。一般把最小化的一类函数称为损失函数。损失函数大致可以分为两类：分类问题的损失函数和回归问题的损失函数。本文中最小化教师模型与学生模型的块间输出，本质上是回归问题，常用的损失函数有平均绝对值误差（MAE）、均方误差（MSE）和Huber损失函数。三种损失函数的表达式如下：

MAE=∑ni=1|yi-f（x）|，

MSE=∑ni=1（yi-f（x））2（9）

Huber = 12（yi-f（x））2 yi-f（x）≤δ

δyi-f（x）-12δ2otherwise（10）

其中：yi表示真实值; f（x）是目标值;超参数δ表示临界选择条件。比较三种损失函数的表达式可以看出：MAE是真实值与目标值之差的绝对值之和，在处理异常数据时有更好的鲁棒性，但它的梯度为定值，容易错过最优解，求解效率低；MSE对误差取了平方，放大了误差，与MAE相比，MSE对异常值更敏感，得到的模型会更加精确，但鲁棒性不够好；Huber结合了MAE与MSE的优点，使模型对异常数据敏感的同时也能够具有较好的鲁棒性，MSE与MAE的临界值由δ控制。考虑到所处理对象缺陷比率较大，本文采用Huber函数作为块间损失函数，δ取值为1。损失函数表示为

L=1c·w·hHuber（11）

为了让每一块的权重更新都能根据对应区块的通道数和通道大小获得一个合适的损失函数，这里对区块的损失函数进行了数据处理，c、w、h分别表示通道数、区块输出宽和高。为了保证每个区块学生模型的稳定性，区块的训练是独立的，前一个区块的输出作为下一个区块的输入，区块内部使用反向传播进行训练。

2.4 算法实现

所提出的分区再训练算法的伪代码如算法1所示，输入为数据集和缺陷信息，输出为训练好的学生模型。首先根据式（5）的划分方法对模型进行划分，逐层确定卷积层所属区块，对应步骤a）；然后进行前向传播训练并根据式（8）对卷积层进行归一化处理，获得理想情况下的无缺陷模型即教师模型，并获得教师模型各区块的输出，对应步骤b）；根据式（3）的建模方法对教师模型添加缺陷信息获得学生模型，对应步骤c）；根据式（12）进行反向传播训练并更新权重，对应步骤d）；重复执行Z次步骤d），最后获得训练好的学生模型即容错模型，对应步骤e）。

算法1 基于分区的多缺陷容忍算法

输入：数据集，缺陷信息。

输出：训练好的学生模型。

a）根据式（5）逐层确定卷积层所属区块。

b）进行前向传播训练并根据式（8）进行归一化处理，获得教师模型。

c）根据式（3）对教师模型添加缺陷信息获得学生模型。

d）根据式（12）计算区块损失进行反向传播训练并更新权重。

e）重复执行Z次步骤d）获得训练好的学生模型。

3 实验结果

3.1 数据集和实验设置

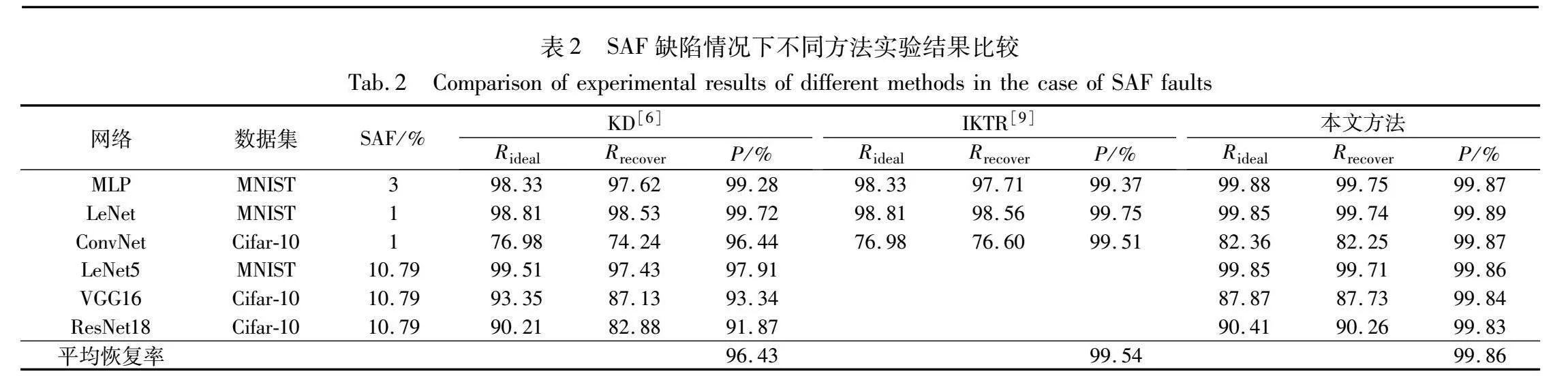
本文方法在Linux系统，配置为GeForce RTX 3090 GPU的VMware环境下，用PyTorch机器学习框架实现DNN模型，使用MNIST和Cifar-10数据集来验证有效性。借鉴文献［24］的数据，在SAF和TF同时存在的情况下，缺陷率设置为25.03%，其中TF为14.24%，SA1为9.04%，SA0为1.75%。TF的波动值σ设置为0.2。在仅有SAF的情况下，缺陷率设置与对比文献［6，9］一致。使用Adam优化器，训练轮次Z为20，学习率为0.001。在相同的缺陷环境下，将本文方法与同样采用知识蒸馏框架的文献［6，9］进行比较，通过比较不同算法下神经网络的恢复效果，证明本文的网络划分和算法优化的有效性。

3.2 结果分析

为了更好地对比不同方法的恢复效果，本文采用恢复百分比来比较各种方法的有效性，如式（13）所示，其中Rrecover表示训练后的测试准确率，Rideal表示理想情况下的测试准确率。由于训练是一个不断迭代的过程，其计算结果具有随机性，所以采用算法恢复率P来表示不同训练方法的有效性。

P=RrecoverRideal（12）

本文方法与基于传统知识蒸馏的KD［6］和面向小电路的IKTR［9］进行比较，在只有SAF环境下进行实验，实验结果如表2所示，采用算法恢复率的平均结果表示算法的恢复程度，在表2中用“平均恢复率”表示。MLP、LeNet和ConvNet的网络规模较小，其中MLP仅有三层全连接层，LeNet有两层卷积两层全连接层，ConvNet也只有三层卷积两层全连接层。LeNet5、VGG16和ResNet18的结构与文献［6］相同。SAF的缺陷率如表2所示。KD方法在小规模网络上的恢复效果较好，随着网络规模的增大和缺陷率的增加，其算法恢复率明显降低，6个网络的平均恢复率为96.43%。这是因为，KD方法采用传统的知识蒸馏，训练过程中学生模型仅学习到教师模型的最后输出结果，不能拟合教师模型的中间特征，缺陷的增加导致网络训练过程中数据产生的偏差过大，恶化了反向传播的数据更新，进一步造成算法恢复率的降低。IKTR方法仅针对3个小规模网络进行基于中间特征的知识蒸馏训练，其中SAF的缺陷率也较低，最大仅有3%，IKTR算法平均恢复率为99.54%。本文方法在6个小规模网络上的算法恢复率达到99.86%以上，这是因为本文区块划分较为合理，在缺陷率增加的情况下，神经网络训练过程中区块划分可以在保证中间特征的稳定提取下，限定了缺陷对数据偏差的影响，防止逐层累积影响到后面层级的训练，从而实现损失函数的稳定；卷积层的归一化操作保证反向传播中梯度大小适当，防止出现梯度消失问题影响数据更新。

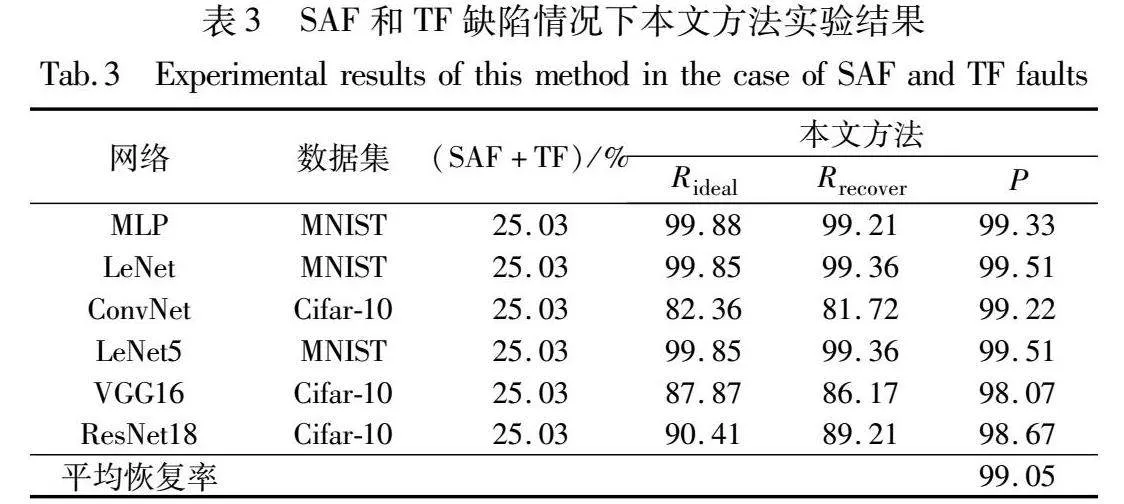
为了进一步验证本文方法在多缺陷模型上的有效性，本文综合考虑SAF和TF两种缺陷，在缺陷率为25.03%的情况下进行实验，结果如表3所示。本文方法在多缺陷且缺陷率高达25.03%的情况下，6个网络的平均恢复率仍能达到99%以上。这是因为本文方法在训练时通过区块划分有效限制缺陷对数据的累积影响，学生模型通过区块输出拟合教师模型的中间特征，归一化处理增加反向传播的梯度来加快网络收敛速度，损失函数使模型在对异常数据敏感的同时具有较好的鲁棒性，从而在缺陷率较大的情况下得到较好的恢复效果。

4 结束语

不同于传统方法只针对RRAM阵列的SAF缺陷进行容忍，本文针对RRAM单元的多缺陷进行容忍。为此，本文对TF和SAF缺陷进行统一建模，在传统知识蒸馏的基础上，采用分区知识蒸馏的方法进行掩码再训练。实验结果表明，本文方法在算法级将网络的测试准确率恢复到98%以上，证明了本文方法的有效性。但是，本文方法仅在仿真阶段对神经网络的计算进行容错，没有在实际RRAM单元中进行进一步的精度恢复，因此将在后期对硬件系统进行进一步设计。

参考文献：

［1］Chi Ping， Li Shuangchen， Xu Cong， et al. Prime： a novel processing-in-memory architecture for neural network computation in ReRAM-based main memory［J］. ACM SIGARCH Computer Architecture News， 2016， 44（3）： 27-39.

［2］Shafiee A， Nag A， Muralimanohar N， et al. ISAAC： a convolutional neural network accelerator with in-situ analog arithmetic in crossbars［J］. ACM SIGARCH Computer Architecture News， 2016，44（3）： 14-26.

［3］Wong H， Lee H， Yu Shimeng， et al. Metal-oxide RRAM［J］. Proceedings of the IEEE， 2012， 100（6）： 1951-1970.

［4］Tosson A， Yu Shimeng， Anis M， et al. Analysis of RRAM reliability soft-errors on the performance of RRAM-based neuromorphic systems［C］//Proc of the 16th IEEE Computer Society Annual Symposium on VLSI. Piscataway， NJ： IEEE Press， 2017： 62-67.

［5］Long Yun， She Xueyuan， Mukhopadhyay S. Design of reliable DNN accelerator with un-reliable ReRAM［C］//Proc of the 23rd Design， Automation & Test in Europe Conference & Exhibition. Piscataway， NJ： IEEE Press， 2019： 1769-1774.

［6］Charan G， Mohanty A， Du Xiaocong， et al. Accurate inference with inaccurate RRAM devices： a joint algorithm-design solution［J］. IEEE Journal on Exploratory Solid-State Computational Devices and Circuits， 2020， 6（1）： 27-35.

［7］Chen Lerong， Li Jiawen， Chen Yiran， et al. Accelerator-friendly neural-network training： learning variations and defects in RRAM crossbar［C］//Proc of the 21st Design， Automation & Test in Europe Conference & Exhibition. Piscataway， NJ： IEEE Press， 2017： 19-24.

［8］Liu Chen， Hu Miao， Strachan J， et al. Rescuing memristor-based neuromorphic design with high defects［C］//Proc of the 54th ACM/EDAC/IEEE Design Automation Conference. Piscataway， NJ： IEEE Press， 2017： 1-6.

［9］Li Wen， Wang Ying， Liu Cheng， et al. On-line fault protection for ReRAM-based neural networks［J］. IEEE Trans on Computers， 2023， 2（72） ： 423-437.

［10］He Zhezhi， Lin Jie， Ewetz R， et al. Noise injection adaption： end-to-end ReRAM crossbar non-ideal effect adaption for neural network mapping［C］//Proc of the 56th Annual Design Automation Confe-rence. New York： ACM Press， 2019： 1-6.

［11］Zhang Fan， Hu Miao. Defects mitigation in resistive crossbars for analog vector matrix multiplication［C］//Proc of the 25th Asia and South Pacific Design Automation Conference. Piscataway， NJ： IEEE Press， 2020： 187-192.

［12］Zhang Baogang， Uysal N， Fan Deliang， et al. Handling stuck-at-faults in memristor crossbar arrays using matrix transformations［C］//Proc of the 24th Asia and South Pacific Design Automation Confe-rence. New York： ACM Press， 2019： 438-443.

［13］Liu Mengyun， Xia Lixue， Wang Yu， et al. Fault tolerance in neuromorphic computing systems［C］//Proc of the 24th Asia and South Pacific Design Automation Conference. New York： ACM Press， 2019： 216-223.

［14］Chen C， Shih H， Wu Chengwen， et al. RRAM defect modeling and failure analysis based on march test and a novel squeeze-search scheme［J］. IEEE Trans on Computers， 2014， 64（1）： 180-190.

［15］Kivinen J， Smola A， Williamson R. Online learning with kernels［J］. IEEE Trans on Signal Processing， 2004， 52（8）： 2165-2176.

［16］Qiu Junfei， Wu Qihui， Ding Guoru， et al. A survey of machine learning for big data processing［J］. EURASIP Journal on Advances in Signal Processing， 2016， 2016： 1-16.

［17］Hoi S， Sahoo D， Lu Jing， et al. Online learning： a comprehensive survey［J］. Neurocomputing， 2021， 459： 249-289.

［18］Zhao Weisheng， Moreau M， Deng E， et al. Synchronous non-volatile logic gate design based on resistive switching memories［J］. IEEE Trans on Circuits and Systems I： Regular Papers， 2013， 61（2）： 443-454.

［19］Park S， Noh J， Choo M， et al. Nanoscale RRAM-based synaptic electronics： toward a neuromorphic computing device［J］. Nanotechnology， 2013， 24（38）： 384009.

［20］Li Boxun， Gu Peng， Shan Yi， et al. RRAM-based analog approximate computing［J］. IEEE Trans on Computer-Aided Design of Integrated Circuits and Systems， 2015， 34（12）： 1905-1917.

［21］Hinton G， Vinyals O， Dean J. Distilling the knowledge in a neural network［EB/OL］.（2015-03-09）. https：//arxiv.org/abs/1503.02531.

［22］Gou Jianping， Yu Baosheng， Maybank S， et al. Knowledge distillation： a survey［J］. International Journal of Computer Vision， 2021， 129： 1789-1819.

［23］邵仁荣， 刘宇昂， 张伟， 等. 深度学习中知识蒸馏研究综述［J］. 计算机学报， 2022， 45（8）： 1638-1673. （Shao Renrong， Liu Yu’ang， Zhang Wei， et al. A review of research on knowledge distillation in deep learning［J］. Chinese Journal of Computers， 2022， 45（8）： 1638-1673.）

［24］Yadav D， Thangkhiew P， Datta K， et al. FAMCroNA： fault analysis in memristive crossbars for neuromorphic applications［J］. Journal of Electronic Testing， 2022， 38（2）： 145-163.

［25］Krishnan G， Yang Li， Sun Jingbo， et al. Exploring model stability of deep neural networks for reliable RRAM-based in-memory acceleration［J］. IEEE Trans on Computers， 2022， 71（11）： 2740-2752.

［26］Howard A， Zhu Menglong， Chen Bo， et al. MobileNets： efficient convolutional neural networks for mobile vision applications［EB/OL］. （2017-04-17）. https：//arxiv. org/abs/1704. 04861.

［27］Torres-Huitzil C， Girau B. Fault and error tolerance in neural networks： a review［J］. IEEE Access， 2017， 5： 17322-17341.

［28］Ioffe S， Szegedy C. Batch normalization： accelerating deep network training by reducing internal covariate shift［C］//Proc of the 32nd International Conference on Machine Learning. Cambridge， MA： MIT Press， 2015： 448-456.